=== BENTUK KANONIK DAN BENTUK BAKU ===
Bentuk Kanonikyaitu “Fungsi Boolean yang diekspresikan dalam bentuk SOP atau POS
dengan minterm atau maxterm mempunyai literal yang lengkap”. Bentuk Baku yaitu “Fungsi Boolean yang diekspresikan dalam bentuk SOP atau POS
dengan minterm atau maxterm mempunyai literal yang tidak lengkap”.
SOP (Sum of Product) atau yang diistilahkan dengan jumlah dari hasil perkalian.
POS (Product of Sum) atau yang diistilahkan dengan perkalian dari hasil penjumlahan. Untuk mendapatkan ekspresi Boolean, yang diperhatikan hanyalah “keluaran yang bernilai
1”. Suku-suku bentuk SOP disebut minterm.
Untuk mendapatkan ekspresi Boolean, yang diperhatikan hanyalah “keluaran yang bernilai
0”. Suku-suku bentuk POS disebut maxterm.
Menggunakan Tabel Kebenaran
Tabel kebenaran adalah tabel yang memuat semua kemungkinan atau kombinasi masukan serta keluaran dari kombinasi tersebut.
Secara umum tabel kebenaran yang memiliki “n” buah masukan mempunyai “2n”
kombinasi masukan yang mungkin, jika kondisi keluaran yang diharapkan dari rangkaian logika diberikan untuk semua kemungkinan kondisi masukan, maka hasilnya dapat diperlihatkan dalam tabel kebenaran.
Contoh:
1. 1) Buatlah ekspresi Boolean dalam bentuk SOP dan POS dari tabel kebenaran ini.
A B C Y
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
0 1 0 1 0 1 0 1
Penyelesaian:
a) Dalam bentuk SOP, maka yang dilihat adalah Y = 1.
A B C Y
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
0 1 0 1 0 1 0 1
Y = ( A.B.C ) + ( A.B.C ) +( A.B.C ) + ( A.B.C )
C B A. .
C B A. .
C B A. .
Y = y1+ y3 + y5 + y7
Y = y (1,3,5,7)
b) Dalam bentuk POS, maka yang dilihat adalah Y = 0.
A B C Y
2. Buatlah suatu rangkaian gerbang logika sederhana sebagai alat pengamanan lemari untuk menyimpan dokumen penting pada suatu BANK yang mempunyai 3 buah kunci pembuka, lemari tersebut dapat dibuka bila minimal oleh 2 orang direktur yang memiliki kunci pembuka.
Pernyelesaian:
Dari soal menunjukkan bahwa lemari akan terbuka jika minimal 2 orang dari 3 orang yang ada (dapat menggunakan SOP).
a) Masukan (nilai “0” berarti tidak ada orang sedang nilai “1” berarti ada orang).
b) Keluaran (nilai “0” berarti pintu tertutup sedang nilai “1” berarti pintu terbuka). Tabel kebenarannya:
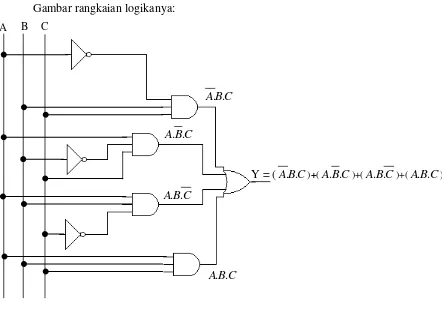
Gambar rangkaian logikanya:
Bentuk Kanonik
Beberapa bentuk kanonik fungsi Boolean 3 masukan variabel:
a). Y = ( A.B.C ) + ( A.B.C ) +( A.B.C ) + ( A.B.C ) SOP (outputnya “1”) b). Y = (ABC ) . (ABC ) . (ABC ) . (ABC ) POS (“0”) Contoh:
1). Nyatakan fungsi Boolean Y (x, y, z) = ( x + y ) . (y + z ) dalam bentuk kanonik SOP dan POS.
Penyelesaian:
a) Diambil suku ( x + y ) yang artinya jika nilai masukan 0 1 -, maka Y = 0 (POS) x y z Y
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
0 0
b) Diambil suku (y + z ) yang artinya jika nilai masukan - 1 0, maka Y = 0 (POS)
A B C
C B A. .
C B A. .
C B A. .
C B A. .
Semua suku telah dimasukan ke tabel kebenaran, nilai Y (keluaran) yang belum terisi akan berharga 1, sehingga tabel kebenarannya menjadi:
Berdasarkan tabel kebenaran, maka: Bentuk SOP-nya (minterm) adalah
Y (A, B, C) = y (0, 1, 4, 5, 7)
Bentuk POS-nya (maxterm) adalah
Semua suku telah dimasukan ke tabel kebenaran, nilai Y (keluaran) yang belum terisi akan berharga 1, sehingga tabel kebenarannya menjadi:
Berdasarkan tabel kebenaran, maka: Bentuk SOP-nya (minterm) adalah
Y (A, B, C) = y (0, 1, 2, 3, 4, 5, 6)
Bentuk POS-nya (maxterm) adalah
Y (A, B, C) = y ( 7 )
Konversi Antar Bentuk Kanonik
Apabila f ( x, y, z ) = ( 1, 2, 5, 7 ) dan f‟ adalah fungsi komplemen dari f, maka
f„ ( x, y, z ) = ( 0, 3, 4, 6 ) = y0 + y3 + y4 + y6.
Dengan menggunakan hukum De Morgan, maka diperoleh fungsi f dalam bentuk POS
sebagai berikut:
f ( x, y, z ) = (f„( x, y, z))‟ = (y0 + y3 + y4 + y6)‟ = y0‟ y3‟ y4‟ y6‟
= (x‟y‟z‟)‟ (x‟yz)‟ (xy‟z‟)‟ (x yz‟)‟
= ( x + y +z ) ( x + y‟ +z‟ ) ( x‟+ y +z‟ ) ( x‟+ y‟ +z ) = y0 y3 y4 y6
= y ( 0, 3, 4, 6 )
Jadi f ( x, y, z ) = y ( 1, 2, 5, 7 ) = y ( 0, 3, 4, 6 ) Contoh: Nyatakan fungsi dibawah ini.
a) f ( x, y, z ) = y ( 0, 2, 4, 5 ) dalam bentuk SOP.
b) g ( w, x, y, z ) = y ( 1, 2, 5, 6, 10, 15 ) dalam bentuk POS. Penyelesaian:
a) f ( x, y, z ) = y ( 1, 3, 6, 7 ).
b) g ( w, x, y, z ) = y ( 0, 3, 4, 7, 8, 9, 11, 12, 13, 14 ) Bentuk Baku
Beberapa bentuk baku fungsi Boolean 3 variabel:
a). Y = (A.B.C ) + ( A. ) + (B A. ) C (Bentuk baku dalam bentuk SOP) b). Y = (AB ) . (ABC ) . (BC ) (Bentuk baku dalam bentuk POS)
A B C Y
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
1 1 1 1 1 1 1 0
A B C Y
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
=== PETA KARNAUGH (K-MAP) ===
Peta Karnaugh adalah metode untuk menyederhanakan rangkaian logika.
Peta Karnaugh (K-map) mirip dengan tabel kebenaran yang menampilkan keluaran persamaan Boolean untuk tiap kemungkinan kombinasi variabel masukkan, menentukan jumlah sel identik dengan mencari jumlah kombinasi sebuah tabel kebenaran.
1. Variabel yang mempunyai 2n kotak (n adalah banyaknya masukkan), dimana dalam kotak-kotak atau sel-sel tersebut merupakan kombinasi masukkan yang terjadi.
Misal: a). 2 variabel masukkan membutuhkan 22 atau 4 sel (kombinasi yang terjadi). b). 3 variabel masukkan membutuhkan 23 atau 8 sel (kombinasi yang terjadi). c). dan seterusnya.
Contoh berbagai variabel pada Peta Karnaugh:
2. Peta Karnaugh dapat digunakan untuk:
a). Menyederhanakan rangkaian (miniaturisasi). b). Merancang rangkaian.
Langkah-Langkah Penyederhanaan Peta Karnaugh
1). Masukan keluaran sesuai dengan nomor minterm atau maxterm.
2). Untuk penyederhanaan, kelompokkan yang minterm bernilai 1 untuk SOP atau
maxterm yang bernilai 0 untuk POS.
3). Setiap kelompok harus berkelipatan 2n yaitu: 2, 4, 8, 16, dan seterusnya.
4). Usahakan mencari kelompok terbesar terlebih dahulu, lalu mencari kelompok yang lebih kecil.
a b c d
4-Input Function 3-Input
Function a
b c
y y
ab
00 01 11 10
0 1
c cd ab 00 01 11 10
00 01 11 10
Karnaugh Map ab
00 01 11 10 1 y
a
Peta Karnaugh Dengan 2 Variabel Masukan (22 = 4)
Aturannya yaitu:
a. Dalam masing-masing kotak kombinasi yang terjadi adalah AND GATE.
b. Antar kotak mempunyai hubungan OR GATE.
Contoh:
a). Dari gerbang OR.
Persamaan keluaran dapat ditulis sebagai berikut: X = A + B = 1
= A ( B + B ) + B ( A + A ) = AB + AB + AB + AB = AB + AB + AB
b). Dari gerbang EX-OR.
Untuk X = A B + AB Untuk X = A B + A B + AB
1). Aturan miniaturisasi untuk 2 variabel masukan.
Bila 4 kotak dari K-Map terisi bernilai “1” semua, maka persamaan tersebut adalah 1 (X = 1).
X = A B+ AB + AB + AB = A ( B + B ) + A (B + B ) = A + A = 1
0 1
0
00
AB
“0” 10
B A
“2”
0 1 00 01 11 10 0 1
0 0 2 AB AB AB AB 0 00 10
1 1 3 “0” “1” “3” “2” 1 01 11
1
01
B A
“1” 11
AB
“3”
A
B A
B
A B
A B
B A
X = A+B = AB
0 1 A
B 0 1
1 1 1 0
1 A
B 0 1
AB AB 1
AB
1
B A
1
B A X = A B + A B 0
1 A
B 0 1
1 1
0 1 A
B 0 1
1 1 1 0
1 A
B 0 1
2). Pernyataan persamaan Bokan dari 2 kotak yang berdekatan (bukan bersilangan), dapat disederhanakan dari 2 komponen menjadi satu kombinasi persamaan Bokan.
X = A B+ AB = A ( B + B ) = A
X = A B+ AB = B ( A + A ) = B
X = AB+ AB = B ( A + A ) = B
Contoh: Perhatikan peta disamping berikut ini, fungsi yang diplot ialah: Z = f (A,B) = A B +AB
Penyelesaian:
Dari lingkaran di atas, terlihat bahwa semua nilai 1 berada bagian A, Karenanya keluaran berupa A dan nilai B hilang. Dengan simplifikasi aljabar, dapat juga ditemukan penyederhanaan persamaan di atas sebagai berikut: Z = A B +AB = A( B +B) = A.
Contoh:
Perhatikan ekspresi Z = f (A,B) = A B +A B + A B yang diplot di Peta Karnaugh ini.
Penyelesaian:
Pasangan 1 dikelompokkan seperti gambar di atas, dan jawaban diperoleh dengan melihat nilai 1 yang masuk ke kelompok lingkaran yang menyebabkan nilai A dan B hilang.
Hasil dari penyederhanaan persamaan di atas ialah: Z = A + B .
0
1 A
B 0 1
AB 1
B A
1
B
B
A A
0
1 A
B 0 1
AB AB 1
AB
1 B
A 1
B
B
A
A
0 1
A
B 0 1
1
1
0 1
A
B 0 1
1
AB C
Peta Karnaugh Dengan 3 Variabel Masukan (23 = 8)
Aturannya yaitu:
a. Seluruh kotak (8 kotak) dapat disederhanakan dengan F = 1. b. 4 kotak dapat disederhanakan dari 3 variabel menjadi 1 variabel. c. 2 kotak dapat disederhanakan dari 3 variabel menjadi 2 variabel.
Dari 2 buah peta Karnaugh di atas dapat disederhanakan menjadi sebagai berikut:
Contoh:
Sederhanakan persamaan menggunakan Peta Karnaugh dari soal berikut: 1. Z = f (A,B,C) = A B C + A B + AB C + AC
2. Z = f (A,B,C) = A B + B C + BC + A B C Penyelesaian:
1. Z = f (A,B,C) = A B C + A B + AB C + AC
Menggunakan aturan simplifikasi, hasil persamaan yang disederhanakan ialah: B+A C . Peta Karnaugh Dengan 4 Variabel Masukan (24 = 16)
Aturannya yaitu:
a. Seluruh kotak (16 kotak) dapat disederhanakan dengan F = 1. b. 8 kotak dapat disederhanakan dari 4 variabel menjadi 1 variabel. c. 4 kotak dapat disederhanakan dari 4 variabel menjadi 2 variabel. d. 2 kotak dapat disederhanakan dari 4 variabel menjadi 3 variabel.
Pengelompokan Minterm
1). Pengelompokan dua-an (n = 1), yang perlu diperhatikan adalah variabel yang tidak berubah.
3). Pengelompokan delapan-an (n = 3), yang perlu diperhatikan adalah variabel yang tidak berubah.
4). Pengelompokan enam belas-an (n = 4), yang perlu diperhatikan adalah variabel yang tidak berubah.
Peristiwa Tumpang Tindih (Overleaping)
a). Tanpa tumpang tindih
b). Dengan tumpang tindih
Dari gambar-gambar di atas nampak bahwa dengan menggunakan peristiwa tumpang tindih persamaan menjadi lebih sederhana.
Peristiwa Penggulungan (Rolling)
a). Penggulungan dua-an (n = 1) b). Penggulungan delapan-an (n = 3)
c). Penggulungan empat-an (n = 2)
Peristiwa Kelebihan Pengelompokan (Redundant)
Peristiwa redundant adalah pengelompokan kembali semua suku baik minterm ataupun
maxterm yang sudah dikelompokkan. a). Tidak terjadi kelebihan pengelompokan
b). Terjadi kelebihan pengelompokan
Suku ini redundant : ACD Suku ini redundant : AB
Contoh:
1). Sederhanakan dengan K-Map tabel berikut ini:
A B C Y
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
Penyelesaian:
2). Y (A,B,C,D) = y (0,1,2,4,5,6,8,9,12,13,14) sederhanakan dengan K-Map: Penyelesaian:
C B A
D B A
1 1 1
AB AB AB AB D
C
D C
CD
D C
1
C A
1 1 1
AB AB AB AB D
C
D C
CD
D C
1 1
1
1
1 BC
AB
1 1
AB AB AB AB
C
C
C B
1 1
Y(A, B, C) = BC + AB
Y(A,B,C,D) = C + AD + B D
D A
C 1
1
1 1
AB AB AB AB D
C
D C
CD
D C
1 1
1 1
1 1 1
3). Y(A,B,C) = A B C + A B C + A B C + ABC sederhanakan dengan K-Map: Penyelesaian:
Kondisi Tidak Peduli (Don’t Care)
Suatu kondisi dimana keluaran suatu rangkaian logika sembarang (“1” atau “0”) yang tidak mempengaruhi kerja dari sistem rangkaian tersebut, kondisi ini dapat menyebabkan can’t happen (keadaan tak pernah terjadi) dan juga dapat menyebabkan keadaan redundant (kelebihan suku).
Langkah-langkah penyederhanaan:
a). Suku-suku pada K-map berisi kondisi don’t carediberi tanda “d”. b). “d” boleh bernilai “0” atau “1”.
c). “d” dipakai hanya bila menyumbang penyederhanaan. Contoh:
1). Cara kerja suatu rangkaian logika dapat dijelaskan pada tabel kebenaran berikut ini.
A B C Y
0 0 0 d
0 0 1 1
0 1 0 0
0 1 1 d
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 d
Penyelesaian:
a). Tanpa memanfaatkan kondisi don’t care: Y(A,B,C) = BC + ABC
b). Dengan memanfaatkan kondisi don’t care: Y(A,B,C) = C + AB
Y(A,B,C) = BC + AC AC
1
1 AB AB AB AB
C
C
C B
1 1
Tentukan fungsi Boolean yang telah
disederhanakan dengan:
a). Tanpa memanfaatkan kondisi don’t care. b). Dengan memanfaatkan kondisi don’t care.
1
AB AB AB AB
C
C 1 BC
1 ABC
C
B A
1
AB AB AB AB
C
2). F(A,B,C,D) = y ( 1, 3, 7, 11, 15 ) + d ( 0, 2, 5 ), tentukan persamaan Booleannya.
3). F(A,B,C,D) = y (0,3,4,7,13) .d(1,2,5,6,9), tentukan persamaan Booleannya. F(A,B,C,D) = AB + C D
1
1 1
AB AB AB AB D
C
D C
CD
D C
d
1 1 d
d
F(A,B,C,D) = AC + AD
1
1
AB AB AB AB D
C
D C
CD
D C
d
1
1 d d