Diferansiyel Denklemler ve Uygulamaları

Erciyes Üniversitesi

Mühendislik Fakültesi

Makina Mühendisliği Bölümü

DİFERANSİYEL DENKLEMLER

ve

UYGULAMALARI

(DERS NOTLARI)

Doç.Dr. Sebahattin ÜNALAN

BÖLÜM I

PROBLEM ve DİFERANSİYEL ÇÖZÜM 1.1 GİRİŞ.

Mühendislik bir problemin çözümüne yönelik araştırma yapan bir hesaplama bilimidir. Bir hesaplama işlemi ise, değişik metodlar neticesinde geliştirilmiş olan bağıntı-denklem-eşitlik ismi verilen, değişik fonksiyonların kullanılmasıyla mümkündür. Yani denklemsiz bir problem çözümünden bahsedilemez. “Doğru-Yanlış”, “Az-çok”, “Büyük-Küçük” gibi mantıksal yorumlar ancak bir denklemin vereceği sayısal sonuca göre veya eğrisel karekterestiğine göre yapılabilir. Bu bağıntılar veya denklemler, deneysel olarak bulunması halinde AMPİRİK, nümerik metodlarla bulunması halinde NÜMERİK ve teorik tekniklerle elde edilmesi halinde ise ANALİTİK bağıntılar ismini alırlar. Bir bağıntının çözüm aralığı ve hassasiyeti, sınırlı ve hatasız olabileceği gibi, (-∞, ∞) aralığı ve belirli bir hata olabilir. Bunun nedeni, bir denklemin üretimi sürecinde bazı ön şartların kabul edilmesi ve denklem üretimini imkansız kılan bazı parametreler ihmal edilmesidir. Dolayısıyla hem denklemleri kullanabilmek ve çözebilmek, hemde bu denklemlerden elde edilecek sonuçların doğruluğu hakkında yorum yapmak belirli bir bilgi birikimini gerektirecektir. Bu nedenle, hesaplama işleminde kullanılan denklemlerin nasıl ve hangi şartlarda bulunduğu çok önemli olacaktır. Başka bir ifadeyle, denklemlerin nasıl üretilildiğinin ve çözüm metodlarının ne olduğunun bilinmesi mühendisler için vazgeçilmez bir aşamadır.

Bu dersin amacı, bahsedilen denklemlerden TEORİK ve NÜMERİK çözümlerin uygulanabileceği temel yapının oluşturulabilmesi için gerekli olan matematiksel ve temel fiziki teknikleri vermektir. İlave olarak, çözüm modeli olarakta isimlendirilebilecek temel yapının ürünü olan denklemlerin nasıl çözüleceği sorusuda cevaplanacaktır. Çözüm teknikleri ve çözümün uygulanacağı temel yapı, tam olarak doğru olabileceğı gibi belirli bir hata payını baştan kabul ederek yaklaşık neticeler de verebililecektir. Önemli olan bu hatanın problem üzerinde etkisinin mühendislik açısından ihmal edilebilir seviyede olmasıdır. Bu nedenle bir mühendis kesin çözümlerin yanında yaklaşık çözümlerle de ilgilenen kişidir. Çözüme ulaşma yolunda, nelerden vazgeçileceğini ve bu vazgeçilen parametrelerin sonuç üzerindeki etkisi tahmin edebilen matematik ve fizik adamıdır.

Mühendis başka bir ifade ile “matemetiksel ve fiziksel olarak doğru olabilen bir çözümü mutlaka

bulmak için zorunlu olarak kabul edilen bir hatanın, çözüm sonrasında sonuç üzerine etkisini yansıtabilecek kadar, ilgili problemin gereği olan fiziksel ve matematiksel bilgiye sahip olan ” kişi

demektir. Diğer bir bakış açısıyla, mühendis problemi en kolay, mümkün olan en doğru şekilde çözüp, bulunan neticelerin geçerliliğinide tayin edebilen kişidir. Böyle bir kabiliyet ise ancak matematisel ve fiziksel bilgilerin olarak tam olarak bilinmesiyle ve bunların harmanlanmasıyla mümkün olabilir. Sonuçta, probleme ve problemin fiziğine olan hakimiyet, pratik mühendislikte oluşabilecek arızaların veya üretim hatalarının meydana geliş sebeplerinin kolay bir şekilde belirlenmesine ve en kısa zamanda arızanın giderilmesine de yardımcı olacaktır.

Örnek-1: İlk hızı 1 m/s olan maddesel nokta, 1

sin(0.25 )

a

t

= şeklinde zamana bağlı ivme ile hareketine devam etmektedir. Hareketin zamana bağlı hızını veren denklemi bulunuz. Denklemdeki t nin birimi saniyedir.

Çözüm : a dV dt

= , ise hız

ivmenin zaman üzerinden integrasyonundan bulunabilir. dV = adt

∫

∫

1 0 sin(0.25 ) V t dt dV t =

∫

∫

integrali

hareketin zamana bağlı hız denklemini verecektir. Bu integralin çözümü ile 0-∞ arasındaki herhangi bir t zamanı için geçerli V=V(t) şeklinde bir denklemi verecektir. Ancak verilen integral çözülemeyen bir integraldir. Dolayısıyla V=V(t) şeklinde bir bağıntı üretilemeyecektir. Buda hareketin hızının hesaplanamaması manasınadır. Bu aşamada tam bir çözüm yerine yaklaşık bir çözüm düşünülebilir. Bu yaklaşık çözümün birincisi analitik olarak çözülemeyen integralin sayısal (nümerik) olarak çözülmesidir. İkincisi ise, integralin çözümsüzlüğüne neden olan fonksiyonel yapının belirli bir hata ile giderilmeye çalışılmasıdır. İntegraldeki

sin(0.25t) yerine, küçük 0.25t değerleri için ≈

0.25t yazılabilir. Böylece integral çözülebilir hale dönüşür. Bu yaklaşımın doğruluğu, yandaki şekilden gözlenebilir. Zaman-t nin 0 ile 3 saniye değerleri arasında sin(0.25t) ve 0.25t arasında büyük bir uyum vardır. İntegral eğri altında kalan alanın hesabı manasınada geleceği için 0-3 saniye aralığında her iki eğri altındaki alanda hemen hemen aynı olacaktır. Ancak, 3 saniyeden büyük zaman değerlerinde aradaki fark büyümektedir. Böylece 0-3 arasında kullanılmak üzere hareketin hızını tanımlayan bir denklem üretilebilir.

1 0 sin(0.25 ) V t _dt dV t =

∫

∫

≈ 0 0.25 t _dt t

∫

ise

V(t) = 1+4 t

1/2 (t<3 s) 0 1 2 3 4 5 6 7 8 9 10 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 2 0 sin 0.25 t( ) 0.25 t 10 0 t

Çözülemeyen integral nümerik yöntemlerle çok hassas bir şekilde çözülebilir. Nümerik çözüm ve V(t)=1+4 t1/2 _{denklemiyle değişik}

zamanlar için hesaplanan hız değerleri mukayese edildiği zaman 3 s den sonraki hız değerlerinin çok farklı olduğu görülecektir. Yandaki tabloda MATHCAD ile yapılan

nümerik integrasyon ve V(t)=1+4t1/2

denklemi ile hesaplanan hız değerleri görülmektedir. İfade edildiği gibi 3 s den sonra hız değerleri arasında fark meydana gelmektedir. 10 saniye için V(t)=1+4t1/2 denkleminden hız hesaplanır- sa %12 lik [=(15.524-13.649)*100/15.524] bir hata yapılmış olur.

Değişik zamanlar için nümerik ve analitik hız değerleri [m/s] Zaman t [s] Nüm.Hes. V(t)=1+4t1/2 1 5.004 5.000 2 6.681 6.656 3 7.995 7.928 4 8.139 9.000 5 9.194 9.944 6 10.205 10.797 8 13.232 12.313 10 15.524 13.649 Örnek-2: Aynı kütleye sahip bir paraşütün ve bir çelik bilyanın H kadar yükseklikten serbest bırakılması halinde meydana gelen hareketlerin hız ve yol denklemlerini bulunuz.

Çözüm : Çelik bilyaya ve paraşüte etkiyen kuvvetler Ağırlık (W) ve Hava Direnç (FR)

kuvvetleridir. Hava direnci cismin yüzey alanıyla (A) yakından ilişkilidir. Büyük yüzeylere büyük direnç kuvvetleri, küçük yüzeylere küçük direnç kuvvetleri etkiyecektir. Genel olarak akışkan direnç kuvvetleri akışkan veya cisim hızıyla n.dereceden (Vn) orantılıdır. Bu durumda paraşüt ve çelik bilya için II.Newton Kanunu (∑F=ma) uygulanırsa ivme (a) şu şekilde bulunur.

∑F=ma ,

W-F

R

= ma , W=mg ve F

R

=AV

n

ise

n AV a g m = −

Son ifadeye göre ivme hızın fonksiyonudur. Hareket süresince hız değişeceği için ivme değişecektir. İvmeden hıza ve hızdan yola integrasyon ile geçilebilir.

_Vn m A g dt dV a = = − ise

∫

∫

− = n V m A g dV dt

Son integralin alınabilmesi n değerinin sayısal değerine bağlıdır. “n” sayısı cisim geometrisine, akışkan cinsine ve akış cinsine göre 0.5 ile 2 arasında değer alabilir. Bu durumda integral alma işlemi genel manada mümkün olamadığı için “çözümsüzlük var” denilebilir. Çözüm için çözümsüzlüğe sebep olan direnç kuvvet ihmal edilmesi düşünülebilir. Çok küçük yüzey alanına sahip çelik bilya için FR≈ 0 alınabilir. Bu durumda ivme yerçekimi

ivmesine eşit olup sabit olacaktır. Yeni durumda zamana bağlı hız ve yol denklemleri

g dt dV a = = ise V=gt ve 2 2 1 gt s=

olacaktır. Lise seviyesinde fizik bilgisi olarak verilen bu denklemler sadece direnç kuvvetinin yaklaşık sıfır olduğu veya hareket ivmesinin sabit olduğu durumlarda kullanılabilir. Bir paraşüt hareketinin analizinde kullanılamaz.

Yukarıdaki örneklerden görüldüğü gibi problem çözümünde amaç en doğru ve en kolay çözümü uygulamaktır. Tercih edilen bir denklem vasıtasıyla analitik çözüm aramaktır. Sonra nümerik ve gerekirse deneysel çözümler takip edilecektir. Genel olarak bir mühendislik probleminin çözümü için gerekli olan bir denklemin elde edilmesi için başlangıcından sonuna kadar gelişen genel olaylar Tablo-I‘ deki akış şeması ile açıklanabilir. Deneysel ve nümerik çözümlerin aşamaları Tablo-1 de açıktır. Bu çözüm metodları için gerekli alt yapı ve teknikler Ölçme Tekniği ve Nümerik Analiz dersleriyle verilir. Analitik veya teorik analizi içeren çözüm metodu ve aşamaları Diferansiyel

Denklemler Dersinin müfredatını kapsamaktadır. Bu dersin kapsamının daha iyi anlaşılması

bakımından, analitik çözüm için bu tabloda görünen aşamalar daha detaylı olarak alt bölümlerde incelemiştir:

1.2 Mühendislik Problemi:

Makina mühendisliğinin ilgi alanı olan Enerji, Termodinamik, İmalat-Konsrüksiyon, Makina

Dinamiği ve Mekanik anabilim dallarını ilgilendiren Dizayn, Üretim ve Kontrol hesaplamalarının

tamamıdır. Hata tayini, ayar işlemleri, üretim sonrası kontrol gibi tüm süreçler bir problemin kapsamı dahilindedir. Bir problem bu anabilim dallarından sadece biri ile alakalı olabileceği, birden fazla alanıda kapsayabilir. Bir problemin hem nümerik hem deneysel veya hem teorik hemde deneysel çözümü yapılabilir. Deney reel ortamı temsil edeceğinden, neticeleri daha sağlıklı olacaktır. Ancak deneysel çalışma pahalı ve hassas bir işlemdir. Bu nedenle literatürde teorinin doğruluğu deneysel çalışma ile doğrulandıktan sonra deneysel çalışma tercih edilmez. Daha ekonomik ve kolay olan analitik ve nümerik çözümler ile netice aranır.

Tablo - I : Bir Çözüm Denklemin Bulunması için Gerekli Aşamalar

Mühendislik Problemi

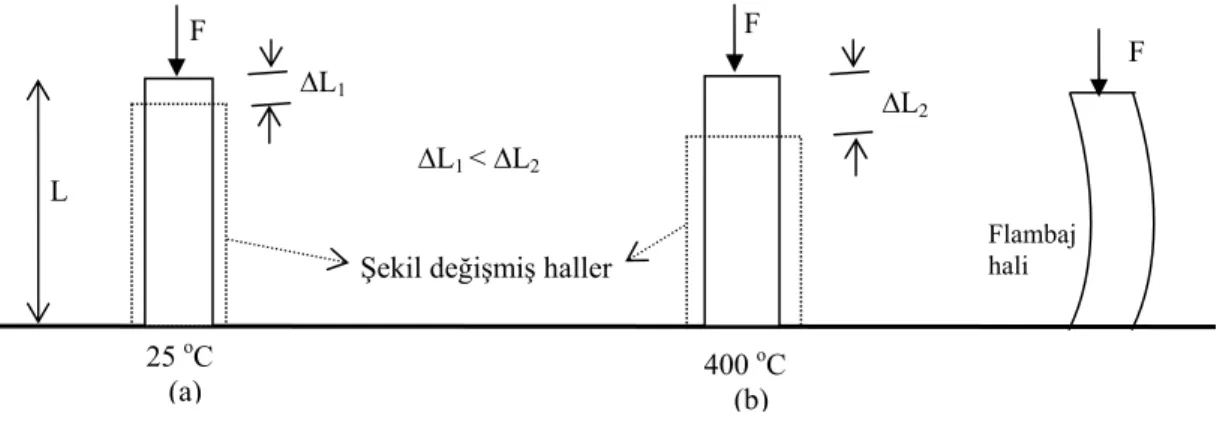
Örnek: F [N] luk bir basma kuvveti zorlanan A kesitli L uzunluğundaki makina elemanının 25 oC ve 400 oC sıcaklık ortamlarında çalışması halinde hesaplamalarda dikkate alınacak kriterler neler olabilir.

Değerlendirme : Bu makina elemanının F kuvvetini emniyetli bir şekilde taşıması için gerekli kesit ve uzunluk değeri Makine Elemanları, Malzeme, Isı transferi ve Mukavemet bilgileri dahilinde hesaplanmalıdır. Bu açıdan kullanılan malzemenin emniyetli gerilme değerleri F’ nin sebep olduğu basıncı ve L uzunluğunun maruz kaldığı burkulmayı (flambaj) karşılayacak seviyede olmalıdır. Basınç ve burkulma tesirinde malzeme bir şekil değişimine maruz kalacaktır. Bu şekil değişiminin

Uygun Koordinat Sisteminin Seçilmesi Teorik Çalışma Deneysel Çalışma ve Model Fiziksel Büyüklüklerin Tanımlanması Deney Setinin Hazırlanması Deneysel Ölçümler Sonuçların Yorumu ve Hata Analizi Deneysel Ölçümlerin AMPİRİK DENKLEME

Dönüştürülmesi Tüm Sonuçların Fiziki Olarak Yorumlanması. _{Teorik ve Deneysel Neticelerin Mukayesesi} ÖLÇME TEKNİĞİ İSTATİSTİK METODLAR Sınır ve Başlangıç Şartlarının Belirlenmesi Diferansiyel Denklemin Teşkil Edilmesi Diferansiyel Denklemin Çözümü Nümerik Çözüm Analitik Çözüm NÜMERİK ANALİZ F F L 25 o_C (a) 400 o_C (b) ∆L1 _∆L 2 ∆L1 < ∆L2

Şekil değişmiş haller

F

Flambaj hali

çalışılan ortam ve malzeme sıcaklığı ile yakın bir ilgisi vardır. a şıkkında malzeme oda sıcaklığındadır. Bu nedenle atomik yapıda bir değişim gözlenmez. Böyle bir halde sıcaklık sonucu mukavemette bir azalma veya plastik-elastik şekil değişiminin tehlikesinden bahsedilemez. Mukavemet hesaplamaları için L, A ve F ile malzemenin emniyet sınırını belirleyen gerilme değeri yeterlidir. Bu nedenle sadece mukavemet problemi olarak ele alınabilir. Oysaki b şıkkında malzeme yüksek sıcaklıktadır. Bu nedenle atomik (kristalik) yapı değişim gösterebilir. a şıkkına göre şekil değiştirme (elastik veya plastik deformasyon) kabiliyeti daha fazladır. Bu nedenle yüksek sıcaklık ortamında çalışmak istenmeyen neticeler doğuracaktır. Bu açıdan b şıkkında malzeme ek bir sistemle soğutulmalıdır. Dolayısıyla mukavemet hesaplarına ilave olarak ısı transferi hesaplamaları ve malzemenin mikroskobik analizide yapılmalıdır. Örnek olarak, mikroskopik yapı YMK yapıdan HMK yapıya kayabilir. Bu değişim malzemenin sertlik, elektrik iletkenliği, ısı iletme kabiliyeti, dayanımı gibi tüm özelliklerinin değişmesine neden olabilir. Hatta soğutmayı temin etmek için eleman yapısında meydana gelecek dizayn değişimleri, mukavemet analizinde tekrar dikkate alınmalıdır. Soğutma için eleman içerisinde soğtucu akışkan kanalları açılmalıdır. Bu kesitte ve diğer boyutlarda değişime neden olacaktır. Dolayısıyla konular birbirinden bağımsız olmayıp, birbirleriyle etkileşim halindedirler.

1.3 Fiziksel Büyüklükler:

İlgili probleme etkisi olan birimli (4 temel birim: m; metre, oC; santigrad derece, s; saniye ve kg; kilogram) veya birimsiz bütün büyüklüklerdir. Diğer bir ifade ile bulunacak çözüm denkleminde ve çözüm aşamasında karşımıza çıkacak Sabit ve Değişkenlerdir. Bu büyüklüklerin belirlenmesi ilgili problemin fiziğine hakim olmakla mümkündür. Bir probleme etkiyen fiziksel büyüklüklerin iyi belirlenmesi çözümün sıhhatini de direkt etkiliyecektir. Yanlış bir belirleme hasaplanan ve gerçekte meydana gelen değerler arasında bir farkın meydana gelmesine neden olacaktır. İyi bir fiziki bilgi aynı zamanda pratikte meydana gelebilecek problemlerin giderilmesinede yardımcı olacaktır. Fiziksel büyüklükler tespit edilirken probleme olan etkiside başlangıçta belirlenebilmelidir. Böylece, kolay çözüm açısından hangi fiziksel parametrelerin ihmal edilebileceği tayin edilebilir. Çünkü, fiziksel büyüklük sayısının artması, problemin daha komplex olmasına ve analitik çözümün daha zor olmasına neden olacaktır. Hiç çözüm bulamamak yerine, kabul edilebilir bir çözümün üretilmesi mühendislik formasyonunun bir sonucudur.

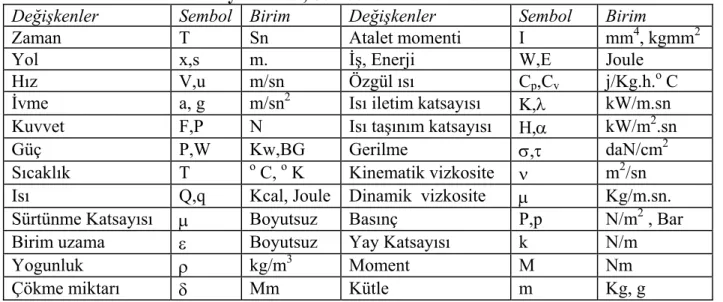
Tablo II : Temel Fiziksel Büyüklükler, Sembolleri ve Birimleri

Değişkenler Sembol Birim Değişkenler Sembol Birim

Zaman T Sn Atalet momenti I mm4, kgmm2

Yol x,s m. İş, Enerji W,E Joule

Hız V,u m/sn Özgül ısı Cp,Cv j/Kg.h.o C

İvme a, g m/sn2 Isı iletim katsayısı K,λ kW/m.sn

Kuvvet F,P N Isı taşınım katsayısı H,α kW/m2.sn

Güç P,W Kw,BG Gerilme σ,τ daN/cm2

Sıcaklık T o C, o K Kinematik vizkosite ν m2/sn

Isı Q,q Kcal, Joule Dinamik vizkosite µ Kg/m.sn.

Sürtünme Katsayısı µ Boyutsuz Basınç P,p N/m2 , Bar

Birim uzama ε Boyutsuz Yay Katsayısı k N/m

Yogunluk ρ kg/m3 Moment M Nm

Çökme miktarı δ Mm Kütle m Kg, g

Makina mühendisliği açısından önemli büyüklükler, bunların birimleri ve sembolleri Tablo II verilmiştir. Fiziksel büyüklüklerin problemin hiç bir safhasında değişiklik göstermeyen kısmına

sabit büyüklükler ismi verilir. Genelde, sabitlerin problem çözümünde bir zorlaştırıcı ve kolaylaştırıcı bir etkisi yoktur. Problem çözümünde asıl etkili olan değişken fiziksel büyüklükler’ dir. En basit problem için değişken sayısı en az iki tane olması gerekirken, üst sınırı yoktur. Fiziksel

büyüklüklerin değişebilir kısmı kendi arasında BAĞIMLI DEĞİŞKEN ve BAĞIMSIZ

DEĞİŞKEN şeklinde iki alt gruba ayrılır. Bu ayırma işlemi problemin çözümünde etkilidir. Kolay çözümü veren bir grublama tercih edilmelidir. Bağımsız değişken genelde keyfi değer alabilen değişkendir. Bağımlı değişken ise bağımsız değişkene karşı değer alabilen bir değişkendir. y=y(x)=f(x) fonksiyonel gösteriminde y bağımlı, x ise bağımsız değişkendir [Örnek: y(x)=4sinx]. Eğer x = x (y) şeklinde [Örnek: x(y)=4siny] bir düzenleme yapılırsa, x bağımlı y bağımsız değişkenler olacaktır. Önceki örnekte verilen hareket probleminde, V hız bağımlı değişken olarak, t zaman ise bağımsız değişken olarak isimlendirilir. Genelde, “hangi zaman da hız ne olur?” şeklindeki soru sorulması nedeniyle V=V(t) şeklinde gösterim gerekir. Eğer “V=10 iken t=?” sorusunun cevabı önemli ise t=t(V) şeklinde bağımlı ve bağımsız değişkenlerin yerdeğiştirmesi de mümkündür.

Örnek: Atmosferde hızla hareket eden roketin uç kısmındaki sıcaklık değerinin doğru olarak hesaplanması için gerekli fiziksel büyüklükler ne olmalıdır?

Hareket

yönü _{Roket içindeki cihazlar}

Et kalınlığı

Hava akım çizgileri

Açıklama: Roketin atmosfer içerisindeki hareti esnasında hava taneciklerinin akım çizgileri roketin uç kısmından dolayı şekilde gösterilen yapıya sahip olur. Hava tanecikleri roket ucunun çarparak hareket doğrultusuna dik doğrultuda dağılırlar. Bu nedenle uç tarafta sürtünme meydana gelir. Bu sürtünme de aşırı ısınmaya neden olur. Meydana gelen ısınma roket ucunun geometrisi, roket hızı gibi değerlere büyük oranda bağlı olacaktır. Aerodinamik yapıya sahip bir uç geometrisi ile düzlem yüzeye (küt geometri) sahip bir uç geometrisi aynı etkiye neden olmayacaktır. Hatta havanın sıcaklığı nemi, gece gündüz gibi bir çok faktörle meydana gelecek ısınma değerini etkileyecektir. Meydana gelecek ısı uç taraftaki sıcaklığın yükselmesi ile neticelenir. Sıcaklık yükselmesi malzemenin ergime sınırını aşarsa istenmeyen, roket hareketini bozan etkileşimler meydana gelir. Burada amaç roket ucundaki sıcaklık değerinin rokete ve roket içindeki cihazlara zarar vermeyecek bir seviyede olmasıdır. Çünkü, roketin hedefine varmadan bozucu tesirin altına girmesi roketin imal edilme düşüncesine aykırıdır. Sıcaklığın düşürülmesi için bir soğutma sistemi düşünülebilir. Gerek ergime ve gerekse soğutma problemleri için roket ucundaki sıcaklık dağılımı bilinmelidir. İstenmeyen bir olayın meydana gelmemesi için roket ucundaki malzeme cinsinin ve et kalınlığının istenen şartları sağlayacak derecede olması gerekir. Sıcaklık değerinin hesaplanabilmesi için deneysel veya teorik çalışma sonunda bir bağıntının bulunması gerekir. Elde edilecek bu bağıntı bulunması gerekli veya kurulacak deney setinde ölçülecek fiziksel büyüklüklere şunlar olmalıdır:

Fiziksel büyüklükler :

- Sıcaklık, T Değişken parametre

- Roketin hızı, V Değişken parametre

- malzeme ve malzemenin ısı iletim katsayısı, k Sabit parametre

- roket ucunun geometrik yapısı ,A Sabit parametre

- hava yoğunlugu, ρ Değişken parametre

- hareket doğrultusu, x Değişken parametre

- sürtünme sonucu meydana gelen ısı , Q Değişken parametre

- yerçekimi ivmesi ,g Sabit parametre

Bu büyüklüklerden uç geometrisi, malzeme ve yerçekimi roketin hareketi süresince sabit kalırken, diğerleri değişir. Çünkü, malzeme yapısının değişmesi başlangıçta yapılan hesaplamalarıda

etkileyecektir. Bu nedenle malzeme özellikleri hareket süresince sabit kalmalıdır. Değişken büyüklüklerden sıcaklık bağımlı, diğerleri bağımsız değişken olarak isimlendirilebilir. Çünkü, T=T(ρ,x,Q,V) şeklinde bir bağıntı araştırılıyor. Böylece keyfi ve bağımsız ρ, x, Q ve V değerlerine karşılık T nin bağlı olarak hangi değerleri alacağı hesaplanabilir.

1.4 Deneysel Çalışma

Oldukca karışık ve analitik çözümü mümkün olmayan bazı problemlerde pratik hesaplamalar için kullanılan bir takım bağıntılar-denklemler deneysel çalışmalar neticesinde bulunur. Bunlara deneysel olarak bulunmaları sebebiyle AMPİRİK BAĞINTI ismi verilir. Böyle bir bağıntının bulunması için deney yapan kişinin ölçüm cihazlarının kullanım kapasitesi ve hata yapma büyüklüğü hakkında uzman olması gerekir. Deney seti, sonucun mümkün olduğunca doğru olması için gerçek problemin küçük bir maketi olmalıdır. Aynı zamanda deneysel ölçümler sonucu bulunmuş datalar iyi bir istatiksel bilgi ile değerlendirilmelidir. Deneysel çalışmalarla bulunan bu bağıntıların kullanılabilme aralığı analitik denklemlere göre oldukça sınırlıdır. Ancak gerçek bir uygulamadan (deney bir nevi uygulama sahası olarak alınabilir) bulunması nedeniyle neticeleri analitik denklemlere göre daha sağlıklı olacaktır. Yinede her hal için çok sayıda yapılması gereken deneylerin getirdiği yüksek maliyet nedeniyle teorik analizin mümkün olmadığı veya büyük oranda hatalı olduğu hallerde deneysel yönteme başvurulur. Çünkü, herhangi bir problemin deneysel olarak analizi çok kapsamlı deney setini ve çok sayıda deney yapılmasını gerekli kılar. Bir çok mühendislik probleminin var olduğu düşünülürse sonsuza giden sayıda deney seti ile ancak tüm mühendislik problemleri çözüme kavuşturulabilir. Hiç süphesiz ki, sonsuza giden sayıdaki deney seti ise o kadar büyük sayıda personel ve maddi desteği gerekli kılacaktır. Yani, deneysel çalışma ancak, teorik analizin iyi neticeler vermediği, çözümsüzlüğün olduğu durumlarda kullanılmalıdır. Günümüzde, mühendislik problemlerinin çoğu teorik ve deneysel neticelerin birlikte değerlendirildiği özelliktedirler. Örneğin, yoğunluk, ısı iletim katsayısı (katıların ısı transfer etme kabiliyetini gösterir), ısı taşınım katsayısı (akışkanların ısı transfer etme yeteneğini gösterir), viskozite (akışkanların sıvılık kabiliyetini gösterir), yerçekimi ivmesi gibi fiziksel büyüklükler ancak deneysel olarak tesbit edilebilirler. Bununla birlikte, yoğunluğu ve ısı iletim kabiliyeti deneysel olarak belirlenmiş bir metal plaka içerisindeki sıcaklık dağılımı oldukca iyi bir hassasiyetle teorik olarak hesaplanabilir. Verilen bir denklemin ampirik olduğu, değişkenlerin önünde ve üst olarak bulunan sabitlerin çok küsüratlı olmasından anlaşılabilir. İlgili kitaplarada, denklemin ampirik olup olmadığı belirtilir. Aynı zamanda ampirik denklemin sağlıklı kullanılma aralığı da belirtilmiştir. Denklemlerde bulunan değişkenlerin birimlerinin ne olması gerektiği de açıklanmıştır.

Örnek: Aşağıda verilen denklemleri analitik ve ampirik olması durumuna göre değerlendiriniz.

a) V(t)=Vo-at , y(t)=Vot-0.5at2 : Vo ilk hızıyla başlamış bir hareketin zamana bağlı hız ve

yol denklemleridir. Bu denklemler ivmenin sabit olduğu ve hareketin yavaşlayan bir karaktere sahip olduğunu göstermektedir. Bu denklemler ile hesaplama bağımsız değişken olan zamanın 0 < t < ∞ aralığı içindeki tüm değerleri için geçerlidir. Verilen denklemler II.Newton Kanunu ve integrasyonla bulunduğu için ANALİTİK DENKLEM’lerdir. Dikkat edilirse, denklemlerde sabitler çok küsüratli değildir ve V(hız), y(yol), a(ivme) ve t(zaman) değişkenleri için bir birim mecburiyeti verilmemiştir. Sadece değişkenlerin birimleri birbirleriyle uyumlu olmalıdırlar. Yol ve zaman km (kilometre) ve h (saat) olarak verilmişse hız ve ivme km/h veya km/h2; cm ve s (saniye) verilmiş ise cm/s veya cm/s2 olacaktır. Bu denklemler, sabit olmasından dolayı, g yerçekimi etkisinde gelişen hareketler içinde kullanılabilir. Bu durumda a=g olacaktır. Böylece deneysel olarak belirlenebilen yerçekimi ivmesi teorik bir analizle birleştirilerek denklem üretiminde kullanılabildiğine dikkat edilmelidir.

b) P P H T o o = ⎡ − ⎣ ⎢ ⎤ ⎦ ⎥ 1 0 0065 5 26 . .

: Bu bağıntı atmosferin değişik yüksekliklerinde (H) ölçülen basınç (P) değerlerinin nümerik ve istatistik metodlarla denklem haline dönüştürülmesinden belirlenmiş olup, havanın atmosferik basıncınının denklemsel ifadesidir. Daha önce çeşitli ölçüm cihazlarıyla basınç değerleri ölçülmüştür. Daha sonra Nümerik Teknikler kullanılarak, ölçüm değerleri formülize edilmişlerdir. Po ve To deniz seviyesindeki basınç ve sıcaklıklardır. Denklemdeki sabitler

çok küsüratlıdır ve değişkenler H ve P , sırasıyla m ve Atm. birimlerinde olmak zorundadırlar. Başka birimlerde, (örnek olarak mm ve N/m2), H ve P’ nin bu denklemde kullanılması yanlış netice verecektir. Bu denklem ile sağlıklı bir hesaplama için maksimum H yüksekliği 11000 m olabilir. Daha yükseklerde yanlış netice verecektir. Yani denklemin kullanımına bir sınır getirilmiştir. Dolayısıyla bu bir AMPİRİK DENKLEM’dir. Bu denklemde 0 ile 11000 metre arasındaki herhangi yükseklik yazılarak, o irtifa seviyesindeki basınç hesaplanabilir.

1.5 Teorik Çalışma ve Diferansiyel Çözüm

Teorik çalışma deneysel çalışmaya göre ucuz olması nedeniyle tercih edilir. Genelde bir teorinin neticesi deneysel bir çalışmayla doğrulanmaya çalışılır. Bu doğrulama işlemi bir problemin birkaç sahası için içra edildikten sonra ileri sürülen teorinin doğru neticeler verdiği kanaatine ulaşılır. Teorik çalışmada problemin seyri üzerinde etkili olan fiziksel büyüklükler tesbit edildikten sonra, bu değişkenlerin problemin geçerliliği süresince oynadığı rol de tespit edilmelidir. Bu işlemde amaç fiziksel büyüklükleri sabit ve değişken şeklinde iki gruba ayırmaktır. Değişken fiziksel büyüklüklerin artan sayısı teorik analizin yapılabilirliğini azaltır. Genel olarak, belirlenmiş fiziksel büyüklükler arasında direkt olarak bir denklem türetmek pek mümkün değildir. Çünkü direkt bir denklem yazmak için mantiken ve fiziksel olarak gerekçe bulunamaz. Dolayısıyla, bu gerekçelerin üretilebileceği yeni ortamlar düşünülmelidir. Bu nedenle, çözülemeyen mühendislik problemlerinde genellikle süperpozisyon ilkesi uygulanır. Bu prensibe göre çözülemeyen bir problem çözülebilir daha küçük parçalara ayrılır. Ayrılan bu parçalar teker teker birbirlerinden ayrı olarak çözüme tabii tutulurlar. Daha sonra sonuçta elde edilen çözümler belirli fizik kaidelerine göre toplanır. Bu şekilde asıl problem için lazım olan genel çözüm elde edilmiş olur. Parçalama işlemi makas veya testere ile gerçekleştirilen bir olgu olmayıp, çözüm gayesi ile üretilmiş, hayali-sanal olarak düşünülen, ana probleme göre çok daha küçük olan problemciklerdir. Bahsedilen parçalama işleminin sayısı arttıkca, düşünülecek parametre sayısıda azaldığı için, elde edilen neticenin daha sağlıklı olmasıda sözkonusudur. Daha büyük problemleri ve yapıları daha küçük problemler veya yapılar şeklinde düşünmenin temel mantığı, çözülebilirlik şartına ulaşılabilmesidir. Sonuç olarak büyük sistemlerin belirli sayıda alt sistemlere bölünerek, 1 büyük problemin N sayıda küçük probleme ayrılması esastır. Şayet, çözülemeyen problemin sonsuza (N→∞ ) giden sayıda parçalama ile çözümü aranırsa, elde edilen her bir parçaya DİFERANSİYEL ELEMAN ismi verilir. Başka bir ifade ile en küçük fiziksel yapıya diferansiyel eleman demek de mümkündür. Ancak, en küçük olmakla birlikte hiçbir zaman sıfır değere sahip değildir. Sıfıra en yakın ve en küçük şeklindeki bir yorum daha doğrudur. Diferansiyel eleman, matematisel olarak, zaman (t) için (zamanın diferansiyel elemanı veya diferansiyeli );

dt N t t O N = = ∆ →

lim

şeklinde bir örnekle tariflenebilir. Parçalama işlemi diğer bir tanımla türetmedir. Bir fiziksel büyüklüğün en küçük parçası, onun matematisel olarak türevi (ingilizcede diferansiyel) dir. Bu diferansiyel eleman duruma göre Diferansiyel Aralık, Diferansiyel Yüzey veya Diferansiyel

Hacim isimlerinide alabilir. Özellikle, termodinamikte ve akışkanlar mekaniğinde Kontrol Hacmi olarakda isimlendirilir. Çözülemeyen problemde, parçalama işlemi bağımsız değişkenler olarak belirlenen fiziksel büyüklükler esas alınarak gerçekleştirilir. Genel olarak, çözülen problem bir geometrik problem ise, diferansiyel eleman esas problemin bir minik minyatürü şeklinde olur. Esas

problem bir prizma ise diferansiyel elemanda minik bir prizma, bir küre ise diferansiyel eleman küçük bir bir küre parçası, esas problem bir silindir ise diferansiyel eleman da küçük bir silindir parçası şeklindedir. Diferansiyel eleman ile ana problem üzerinde etkili olan fiziksel büyüklükler arasında belirli fiziki kaidelere göre geliştirilmiş bağıntılara ise DİFERANSİYEL DENKLEM ismi verilir. Genelliklede, denklem teşkil edilirken bağımsız değişkenin diferansiyel boyutunda, bağımlı değişkenin nasıl değiştiği araştırılır. Mantıksal olarak en küçük yapı içerisinde bağımlı değişkenin bağımsız değişkene göre değişimi ancak lineer olabilirler. Yani diferansiyel boyutta parobolik, sinuziodal ve logaritmik eğriler veya değişimler meydana gelmez. Bu tür eğriler veya değişimler asıl problem boyutunda meydana gelir. Bir problemde bağımlı değişkenin bağımsız değişkene göre değişimi herhengi bir eğridir. Bu eğrinin bilinen fonsiyonlar (sinüs, cosinüs, log, tan, exp veya porabolik) cinsinden açık ifadesinin yazılabilmesi problemin çözülmüş olduğunu gösterir. Mühendislik problemlerinde bağımlı değişkenin bağımsız değişkene göre değişimi başlangıçta bilinmez. Dolayısıyla bir çözümsüzlük mevcuttur. Ancak, çözülemeyen bu problemin en küçük parçası olan diferansiyel eleman içerisinde tüm değişimler lineerdir. Başka bir bakış açısıyla, lineer bir değişim yakalamak için, sistem sonsuza giden sayıda parçalara ayrılarak süperpoze edilir. Çünkü, en basit eğri-en basit denklem-en basit değişim lineer (y=ax+b) bir denklemdir. Lineer denklemden daha basit ifade ise sabitlerdir. Dolayısıyla çözülemeyen ana problemler süperpoze edilirken genel çözüm grubunu oluşturan herhangi bir eğri çok sayıda doğrulara bölünmektedir. Sonuç olarak, en küçük parçalara ayırarak meydana getirilen çözüm tekniğine ise DİFERANSİYEL ÇÖZÜM denir. Bir diferansiyel denklem, bildiğimiz klasik denklemlerden farklıdır. Direkt hesaplamalar için kullanılamazlar. Bu nedenle ya nümerik olarak yada analitik olarak tekrar çözülmelidirler. Daha önce verilmiş olan İntegraller en basit

diferansiyel denklemlerdir. “ integralinde x=1.5 için y ne olmalıdır?” sorusu

cevaplanamaz. Ancak, bu integralin çözümü olan y = 0.5x y=

∫

xdx

2_{+C den, y=0.5(1.5)}2_{+C şeklinde}

hesaplama yapılması mümkündür. Çünkü, “x=1.5 ise dx = ?” sorusu hiç bir zaman netice bulamaz. Bilinen dx en küçük ama, sıfır olmayan bir büyüklüktür. İntegrallerin çözümünde karşılaşılan değişken dönüşümleri, kısmi integrasyon, yarım açı formülleri vb çözüm şekilleri gibi, diferansiyel denklemlerin çözümlerinde de çeşitli teknikler vardır. Diferansiyel denklemlerinde, alınabilen veya alınamayan integrallerde olduğu gibi, analitik olarak çözülebilen ve çözülemeyen tipleri mevcuttur. Diferansiyel çözümün anlaşılabilmesi için aşağıdaki kinematik probleminin üzerinde durulmasında büyük fayda vardır.

Örnek : İki değişik harekette yolun zamana göre değişimleri aşağıdaki şekilde verilmiştir. Buna göre hareketleri tanımlamak için gerekli olan bağıntıları tanımlayınız.

Açıklama : Dikkat edilirse bir hesaplama için mutlaka gerekli olan bir denklem veya bağıntı isteniyor. Aslında soruda “Şeklin yazı ifadesi nedir” sorusuna cevap isteniyor. Bu nedenle “Bu bağıntı nasıl olmalıdır? Nasıl elde edilir?

Hangi aralıklarda çözüm sağlıklıdır. Bulunacak bu bağıntı benzer hangi problemlerde kullanılabilir.” gibi sorulara cevapların

mutlaka bilinmesi gereklidir.

Bu şekle göre I. Harekette yol zamana göre lineer olarak artmaktadır. Lineer bir değimin eğimi (θ) tüm t değerleri için aynıdır. Herhangi bir t anındaki θ değeri bulunursa bu tüm t ler için kullanılabilir. Şekilden

1 0 1 0 S S tg t t θ = − − yazılabilir. Bu denklemdeki

tgθ yol/zaman kavramına uygun olarak m/s birimine sahip olmalıdır. Dolayısıyla I. Hareket için s ve t böyle bir kavramla birbirine bağlanmakta ve bir denkleme dönüşmektedir. Sonuç olarak I. Hareketin tam olarak tanımlanabilmesi için s ve t ye

S(yol) 0 _t(zaman) Eğrisel Değişim (II.Hareket) Lineer Değişim (I.hareket) S1 S0 t0 t1 θ

ilave olarak m/s birimine sahip yeni bir fiziksel büyüklük gereklidir. Bu büyüklüğe literatürde HIZ ismi verilmiş ve V harfi ile simgeselleşmiştir. Neticede I. Hareketin denklemi, V bağımlı ve t bağımsız

değişkenler olmak üzere 1 0

1 0 ( ) S S S V t t t t − = = −

şeklindeki olup tüm zamanlar için hareketin hızını verir. Bu denklem eğimin sabit olduğu, yani, yolun zamana göre düzgün değiştiği tüm hareketler için geçerlidir. II. Harekette olduğu gibi yol zamana göre düzgün değişmiyorsa kullanılamaz. II. Harekette ise yolun zamana göre değişimi herhangi bir eğridir. Eğrinin eğimi zamanla değişmektedir. Dolayısıyla I. Hareketteki yaklaşımla hızı bulmak mümkün değildir. Çünkü, herhangi bir an için bulunmuş olan eğim diğer zaman dilimleri için yanlış olacaktır. Bu eğriyi bilinen fonksiyonların çarpımı, toplamı veya bölümü şeklinde direkt yazmak, mantıksal bir tabanı olmadığı için yanlış olacaktır. Örneğin, II. Hareket için V=2sint + lnt veya V = 5t2-et gibi bir tanımlamalar doğru olmayacaktır. Çünkü, “Niçin böyle bir fonksiyon?” sorusu her seferinde cevap bulamayacaktır. Böylece, II. Hareket için bu noktada bir çözümsüzlük mevcuttur. Çözmek içinde hareket daha kısa süreli hareketciklere bölünmelidir. V=V(t) veya S = S(t) şeklinde bir bağlantı arandığı için t bağımsız değişken olarak tercih edilmelidir. Çünkü, kinematik problemlerde herhangi bir andaki hız ve yol merak edilir. Çözüm için II. Hareket 4 ve 8 parçaya ayrılırsa, aşağıdaki S-t grafikleri elde edilir.

I.hareketin çözümünden s ve t arasında lineer bir değişim için çözümün olabileceği sonucu ortaya çıkmıştır. Bu nedenle, II.hareket çözüm gayesiyle daha küçük parçalara ayrılırken, zamana göre değişimlerin lineer olması prensibi gözetilmelidir. II.hareket ∆t1

lik zamana sahip 4 eşit hareketciğe bölündüğü zaman her hareketcik içerisinde s-t değişiminin biraz daha basit olduğu görülecektir. Bu nedenle her dilim içerindeki değişim lineer olarak kabul edilirse, gerçek eğri ve lineer eğri arasında bir ε1 kadar Hata

farkı meydana gelecektir. Bu hata kabul

edilirse her bir hareketcik için I.hareketten elde edilen hız bağıntısı uygulanabilir. Böylece 4 küçük hareket için 4 tane denklem ve hız değeri bulunacaktır. Fakat, bu çözüm küçükte olsa hatalı olacaktır. Bu hatayı azaltmak için çözüm düşünülen küçük hareket sayısının artırılmasıdır. Bu amaçla dilim sayısı bölüm sayısının 8 olursa, her bir hareketin zamanı ∆t2=∆t1/2 olacaktır.

Bununla birlikte lineer değişim ve gerçek değişim arasındaki farkta ε1 den yarı yarıya

azalarak ε2 ye düşecektir. I.hareket

uygulamasından elde edilecek hız ve denklem sayısıda 8 e çıkacaktır. Bu denklemler birbirine bağlı olup birinin neticesi bir sonraki hareketciğin input bilgisi olacaktır. Dolayısıyla 4 hareketcik için 4 bilinmeyenli, 8 parçacık için 8 bilinmeyenli denklem sistemi ortaya çıkacaktır. Netice olarak, bölüm veya dilim sayısının artması halinde meydana gelen hata azalacaktır. Yani gerçek ve lineer değişimler birbirine yaklaşacaktır. Bu yaklaşımdan hareketle

parçalama sayısı arttıkca, gerçek değişimler çözüm için olması arzu edilen lineer değişimler birbirlerine yaklaşacaktır

şeklinde genel sonuç elde edilir. Bununla

S(yol)

0 _t(zaman)

∆t2 ∆t2 ∆t2

I.hareketin 8 parçaya bölünmesi ε2

1 4

8

S(yol)

0 _t(zaman)

I.hareketin 4 parçaya bölünmesi ∆t1 ∆t1 ∆t1 ∆t1 Lineer değişim kabulu ε1 1 2 3 4

birlikte ele daha fazla bilinmeyenli denklem sistemi elde edilmektedir. Bu denklem sisteminin çözümü ayrı bir zorluk olarak düşünülmelidir. Yinede, hata sıfır değildir.

En az hata için dilim sayısı olabildiğince artırılmalıdır. Ancak meydana gelecek çok bilinmeyenli denklem sistemini çözümü bu artırıma engel olacaktır.

Eğer parçalanma sayısı sonsuza giden miktarda büyük alınırsa hata değeride sıfıra ve hareketciğin zamanı gidecektir. Hareketciğin meydana geldiği bu en kısa zaman aralığı

DİFERANSİYEL ELEMAN olacaktır. Sonsuzluk matematiksel ve fiziksel olarak yorumlanamayan bir büyüklüktür. ∞ sn, ∞ N, ∞ m/sn veya ∞ o_{C gibi ifadeler ölçüm aletlerinin}

ve insan hafsalasının ötesinde bir olgudur. Bu nedenle herhangi bir ifadeyi sonsuz kabul etmek mümkün değildir. Ancak, sonsuz veya tanımsız olmadan önceki, tanımlı olan son değere matematikten bildiğimiz LİMİT ile ulaşılabilir. Bu açıdan II.hareket için herhengi bir zaman diliminde hız ifadesi matematiksel yaklaşımla şu şekilde yazılabilir: n, parçalama sayısı

0 0

_lim

n t S n dt n t ε→∞→ dS V dt ∆ → ∞ ⇒ → → ⇒ = = ∆

Bu prosesle bulunan denklem DİFERANSİYEL DENKLEM olacaktır. Bu denkleme ulaşmak için uygulanan sonsuz küçük parçalara ayırma mantığı ve süreci DİFERANSİYEL ÇÖZÜM olarak bilinmektedir. İşlemlerdeki ∆t ve ∆S sonlu küçük zaman ve yol, dt ve dS ise sonsuz küçük zaman ve yol olarak isimlendirilir. Yolun (S) diferansiyeli dS, zamanın (t) diferansiyeli dt, hızın (V) diferansiyeli dV ve sıcaklığın (T) diferansiyeli dT olacaktır. Bu son ifadeden hızın, yolun zamana göre birinci türevi olduğu sonucu çıkarılabilir. Dolayısıyla, II.hareketin S = S(t) fonksiyonu belirlenip zamana göre türetilirse hız bulunmuş olur. Bulunan bu denklem tüm hareketler için geçerlidir. Yolun zamana göre değişimi ne olursa olsun bu denklemle cevap almak mümkündür. Ancak, “Çok bilinmeyenli denklem sistemi nasıl çözülecek?” ve “yukarıdaki ifadeden S nasıl çekilecel?” soruları cevaplanmalıdır. En az hata ile çözüm için sistem en küçük parçasına ayrılır; buna türev veya diferansiyel, elde edilen denklem sistemi bir toplama işlemi gerektirir ki bunada integrasyon ismi verilir. Başka bir ifadeyle birbirinin tersi olan, türev ve integrasyon, çözüm için bir sistemin sonsuz küçük parçalara ayrılması ve bunların tekrar toplanması olarak tariflenebilir.

Daha önce bahsedilen ve asıl problem üzerinde etkili olan fiziksel büyüklüklerin değişken olanları diferansiyel denklemlerin bağımlı ve bağımsız değişkenlerini meydana getirirler. Bu değişkenlerin sayılarına göre diferansiyel eleman üzerinden elde edilecek diferansiyel denklemin isimlendirilmesi yapılabilir. Bağımsız değişken sayısı ve bağımlı değişken sayısı birer tane ise diferansiyel denklem

ADİ DİFERANSİYEL DENKLEM ismini alır. Bağımsız değişken sayısı birden fazla ise KİSMİ

DİFERANSİYEL DENKLEM, bağımlı değişken sayısı birden fazla ise DİFERANSİYEL

DENKLEM SİSTEMİ ismini alır. Hem bağımlı hemde bağımsız değişken sayısı birden fazla ise

KİSMİ DİFERANSİYEL DENKLEM SİSTEMİ sözkonusu olacaktır. Diferansiyel denklem sistemlerinin çözümü için bağımlı değişken sayısınca diferansiyel denklem elde bulunmalıdır. Adi diferansiyel denklemler “ d “ , operatörü ile, kısmi diferansiyel denklemler “ “ operatörü ile gösterilirler. Diferansiyel denklemler aynı zamanda bağımlı ve bağımsız değişkenlerin diferansiyellik derecesine (türev mertebesine) göre Mertebe olarak, bağımlı değişkenin veya türevlerinin en büyük kuvvet derecesine görede Derece olarakta sınıflandırılabilir. Çözüm aşamasında bağımlı değişken ve türevleri eşitliğin sol tarafında, bağımsız değişken ve sabitler ise eşitliğin diğer tarafında toplanırlar. Bu işlem sonucu, eğer eşitliğin sağ tarafı sıfır ise Homejen, sıfır değilse Homojen Olmayan (non-homojen) diferansiyel denklem olarakta isimlendirilir. Bu kavramlar diferansiyel denklemin çözümünü de belirlemektedir. Bu tanımlamalara ilave olarak, çözüm tekniğini ve diferansiyel denklemi ilk bulan bilim adamlarının isimleriyle anılan diferansiyel denklemlerde mevcuttur.

Örnek : Aşağıdaki diferansiyel denklemleri isimlendiriniz.

1) dy

dx+4y=sin x : y bağımlı, x bağımsız değişken. 1.mertebe, 1.derece (lineer) non-homojen 2) d y

dx y

2

2 +4 = sin x : y bağımlı, x bağımsız değişken. 2.mertebe, 1.derece (lineer) non-homojen

3) dy

dx+4y =

3 _{sin x : y bağımlı, x bağımsız. 1. Mertebe, 3.derece (non-lineer) non-homojen}

4) dy dx y ⎡ ⎣⎢ ⎤ ⎦⎥ + = 2

4 sin x : y bağımlı, x bağımsız değişken. 1. Mertebe, 2.derece non-homojen

5) d y

dx y

4

4 +4 = 0: y bağımlı, x bağımsız değişken. 4. mertebe, 1.derece homojen

6) q kdT dr

= − : Fourier Dif. Denklemi ; Isı transferinde kullanılır. 1. mertebe 1.derece 7) ∂ ∂ ∂ ∂ 2 2 2 2 0 T x T y

+ = : T bağımlı değişken, x ve y bağımsız değişkenler. Kısmi dif.denklem

8) ds dt d r dt dr dt s t + = − = 2 3 3 ln

: s ve r bağımlı, t bağımsız değişkenler. Adi dif.denk.sistemi

9) ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ u x v y u x v y x y + = + = + 0 2 2 2 2

:u ve v bağımlı , x ve y bağımsız değişkenler. Kısmi dif.denk. sistemi

1.5.1 Bazı Diferansiyel Uygulamaları

Diferansiyel yaklaşım denklem üretiminin yanında varolan bazı denklemlerin çözümünde de kullanılır. Açık formu bilinmeyen birden fazla bağımsız değişkene bağlı bir bağıntının diferansiyeli alınabilir ve bu diferansiyel form minimum-maksimum hesabı veya başka çözüm amacıyla kullanılabilir. Bir z=z(x,y) fonsiyonunun 1. ve 2. türevleri şu şekildedir.

dy dy z dx x z dz +∂ ∂ ∂ = 2 2 2 2 2 2 2 2 _{2 dy} dy z dxdy y x z dx x z z d +∂ ∂ ∂ ∂ + ∂ ∂ =

Özellikle extramum (minimum veya maksimum) noktaların belirlenmesi noktasında çok faydalıdır. Bir extramum noktada bağımlı değişkenin diferansiyeli sıfırdır. Fakat bağımsız değişken bu

noktalarda kesinlikle sıfır değildir. Böylece yukaridaki örnek için dx≠0 ve dy≠0

yazılabilecektir. Bu noktada bazı örnekler şu şekilde verilebilir.

, 0 = ∂z

Problem-1: Bir akış ortamında akışkan taneciklerinin hızını veren hız profilini veya hız alanını belirleyiniz. Taneciklerin ivmesi için bir bağıntı türetiniz.

0 V

y

x z

Çözüm için gerekli koordinat sistemi kartezyen (x:y:z) olarak seçilirse akışkan taneciklerinin hızı x, y ve z ye göre değişecektir. Hız bir vektörel büyüklük olup her 3 eksen üzerinde de izdüşümü meydana gelebilir. Yukarıdaki şekilden görüleceği üzere seçilen orijin noktasından uzaklaştıkca farklı hız değerlerine ulaşılacaktır. Akış kanalının boyutları, dolayısyla akış kesiti değiştiği için kütlenin korunumuna göre hızda değişmelidir. Aynı zamanda her noktadaki hız değeri zamanlada değişebilir. Bu durumda hız x,y,z ve t nin fonksiyonu olacaktır. V hızının x, y ve z üzerindeki izdüşümleri U, V ve W olarak gösterilirse hız için şu işlemler yapılabilir.

k W j V i U VG= G+ G+ G, V=V(x,y,z,t) ise dt t V dz z V dy y V dx x V dV ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ = yazılabilir.

Bulunan diferansiyel ifade dt’ye bölünerek ivme bağıntısı bulunabilir.

t V dt dz z V dt dy y V dt dx x V a dt dV ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ = = ise t V W z V V y V U x V a ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ =

Son ifadedeki ilk üç terim konuma bağlı konvektif ivme, son terim ise zamana bağlı ivme olarak bilinir. Dolayısıyla hız sabit olsada akışkanlar için ivme sıfır olmayabilir.

Problem-2: 25 o_{C lık ortam sıcaklığında 300} o_{C lık sıcaklığa sahip 1000 m}3 _{lük bir sıcak sıvıyı}

saklamak üzere iki farklı geometriye sahip depo düşünülmektedir. 1. geometri R yarıçapında ve H yüksekliğindeki bir silindirik yapı, 2. geometri ise KxLxM boyutlarında prizmatik yapıdır. Sıcak sıvının soğumasının en az düzeyde olabilmesi için düşünülen geometrilerin boyutları ne olmalıdır. En az ısı kaybı için hangi geometri uygundur.

M

L K

H R

Açıklama: Isı yüksek sıcaklık ortamından düşük sıcaklık ortamına akar. Isı akış doğrultuları şekilde oklarla gösterilmiştir. Meydana gelen ısı transferi Q=C.A.(Tiç-Tdış)=C.A.(300-25) denklemiyle

basitce hesaplanabilir. Burada C depo malzemesinin ve ortamın bir sabit değeridir. A ise ısının transfer olduğu yüzeydir. Bu durumda ısının en az miktarda kaybı için sadece A yüzeyi ile

oynanabilir. Q ve A doğru orantılı olacağı için, en az ısı tranferi için A değeride en küçük olmalıdır. 1000 m3 lük hacmi veren en küçük A yüzeyi aranmalıdır.

Silindirik yapı için çözüm:

2 2 ₁₀₀₀ 1000 R H H R π π = ⇒ = HACİM= ve ₂ 2 _{2 2} 2 ₂ 1000₂ R R R RH R A π π π π π + = + =

A nın en küçük değerini bulmak için türevi sıfır olmalıdır. A nın R ye göre değişimi şekilde verilmiştir. Bu şekle göre R nin 5 m civarlarında A yüzey alanının minumum bir değeri vardır.

5 10 15 20 0 1000 2000 3000 2.613 10× 3 553.582 A r( ) 20 1 r m R R R dR dA R R A 419 . 5 4 2000 0 2000 4 2000 2 3 / 1 2 2 = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = = − = ⇒ + = π π π m R H 10.838 4 2000 1000 1000 3 / 2 2 = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = = π π π , 2 2 2 min 553.58 419 . 5 2000 ) 419 . 5 ( 2 2000 2 m R R A = π + = π + =

Prizmatik yapı için çözüm:

HACİM= ve 2( ) 2(1000 1000 LM) L M LM KM KL A= + + = + + LM K KLM =1000⇒ =1000

Öncekinden farklı olarak burada A hem L hemde M nin fonksiyonu olarak elde edilebildi. Silindir için sadece R’nin fonksiyonu olarak değişiyordu. A=A(M,L) ise diferansiyeli şu şekildedir.

dM M A dL L A dA ∂ ∂ + ∂ ∂ = ise dL≠0 ve dM≠0, 0 =0 ∂ ∂ = ∂ ∂ M A L A , olmalıdır.

A’nın en küçük değerini bulmak için türevi (dA) sıfır olmalıdır. Bunun içinde A’nın L ve M ye göre kısmi türevleri sıfır olmalıdır.

) 1000 1000 ( 2 LM L M A= + + ise 2( 1000₂ ) 0 1000₂ L M M L L A = ⇒ = + − = ∂ ∂ 2 2 1000 0 ) 1000 ( 2 M L L M M A _{= − + = ⇒ =} ∂ ∂ ,

[

1000/

]

1000 1000 3 2 2 ⇒ = = L L L ise L=10 m M=1000/102 =10 m ve K=1000/(10.10)=10 m dir . Amin=2(10.10+10.10+10.10)=600 m2

1000 m3 lük hacim silindir yapı ile daha düşük yüzey alanı ile sağlanmaktadır. Silindirin yüzey alanı (553.58 m2), prizmanın yüzey alanından (600 m2 ) daha küçüktür. Silindir yapının tercih edilmesiyle ısı kaçağından %7.7 (=[600-553.58]x100/600) daha tasarruf edilebilir.

Problem-3: 500 m uzunluğundaki bir tel ile bir saha çevrelenecektir. Dikdötgen şeklinde olması istenen sahanın, alanının maksimum

olması için kenar uzunlukları ne olmalıdır.? Çevre=2a+2b=500 m, a=250-b

Alan=A=a.b =b(250-b) = 250b-b2 dA/db=0 ise 250-2b=0 ise b=125 m ve a=125 m bulunur

a

b

1.5.2 Seriler

Analitik veya teorik çözümlerin üretilmesinde en çok kullanılan yötemlerden biride seri açılımlardır. Değişik seri ifadeler olmakla birlikte en temel seri “kuvvet serisi” olarak bilinir. Bu serinin bir xo noktası civarında gösterimi şu şekildedir:

n o n o o o o n n o n x x C C x x C x x C x x C x x C x x C y ( ) ( ) ( ) ( ) ( )4 .... ( ) 4 3 3 2 2 1 0 0 − + + − + − + − + − + = − =

∑

∞ =

Bu ifade n. Derece bir polinomu gösterir. Herhangi bir triginometrik veya logaritmik fonksiyonun kendisi çarpımı veya toplamı bu açılım ile gösterilebilir. Çözüm süreci içerisinde fonksiyonun kendisi işlemin devamını mümkün kılmaz ise seri açılımıyla devam edilir. Bu serideki xo çözüm

sahasının alt ve üst noktaları arasını veya çözüm civarını tarif eder. Örnek olması açısından bir integralin alt ve üst sınırının ortalaması, bir aranılan kök değerinin yaklaşık değeri veya bir türevin noktası olabilir. Bu serilerin xo=0 açılımı Maclaurin ve xo≠0 açılımı ise Taylor serisi olarak

bilinmektedir.

∑

∞ = = + + + + + + = 0 ) ( 5 ) ( 4 ) ( 3 2 ! ) 0 ( .... 2 . 3 . 4 . 5 2 . 3 . 4 2 . 3 ) 0 ( '' ' 2 ) 0 ( '' ) 0 ( ' ) 0 ( ) ( n n n V IV x n y x y x y x y x y x y y x y

∑

∞ = − = + − + − + − + = 0 ) ( 3 2 _{( )} ! ) ( .... ) ( 2 . 3 ) ( '' ' ) ( 2 ) ( '' ) )( ( ' ) ( ) ( n n o o n o o o o o o o x x n x y x x x y x x x y x x x y x y x y

Bu açılımlar yardımıyla çözümsüzlüğe sebep olan bir türevlenebilir bir fonksiyon polinom haline dönüştürülerek çözümsüzlük aşılmaya çalışılır.

Problem: Şekilde görülen taralı alanda Z vektörü düzlemsel değişim göstermektedir. Koordinat sistemini (x:y) seçerek diferansiyel elemanı oluşturunuz. Seriler yardımıyla dx.dy lik diferansiyel elamanın sınırları arasında bir bağıntı geliştiriniz.

dx dy Zx Zy

?

?

y x 0 dx dy Z Zx Zy Diferansiyel Eleman Diferansiyel yüzey x0 x0+dx y0 y0+dy

Çözüm için taralı alan diferansiyel yüzeylere bölünmüştür. Sonsuza giden sayıda olan diferansiyel yüzeylerden bir tanesi ele alınarak istenen bağıntı kurulabilir. Bu elemanın koordinatları (x0:y0) ve

(x0+dx:y0+dy) olacaktır. Buradaki x, x0, y ve y0 değişken oldukları için seçilen bir eleman tüm

diferansiyel elemanları temsil edecektir. Diferansiyel elemanın bir yüzeyindeki (x0:y0) veya

girişindeki değerler Zx ve Zy ise karşılık yüzeylerdeki (x0+dx:y0+dy) veya çıkıştaki değeri nedir? Bu

soru diferansiyel eleman üzerinden denklem üretiminde, özellikle sürekli ortamlar için (ısı akışı veya akışkan akışının oluşturduğu ortam katı cisimler gibi belirli bir sınıra sahip olmadığı için sürekli ortam olarak isimlendirilir) önemlidir. Nasıl bir eğri değişimi ile iki sınır birbirine bağlanmaktadır. Bir yüzeydeki Zx ve Zy değerleri hangi fonksiyonel değişimle diğer yüzeylere

ulaşmaktadır. Bu soru seri açılım ile cevaplanabilir. Sadece diferansiyel eleman için değil, tüm sistemler için bir değişimi seri ile ifade etmek mümkündür. Çünkü tüm fonksiyonlar seriye açılabilir. Diferansiyel eleman üzerinde x0≠0 ve y0≠0 olduğu için Taylor Serisi bu amaçla

kullanılabilir. Daha önce verilen seride y yerine Z yazarak x ve y yönündeki değişimler Taylor Serisi belirlenmiş olur. Ancak Z hem x hemde y ile değiştiğinden türevler kısmi türev olacaktır. Bu durumda Z nin x ve y’ ye göre x0 ve y0 daki Taylor açılımları şu şekilde olacaktır:

2 2 3 3 2 3 0 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) .... 2 3.2 n n o o o o o o o o n n ! o Z x Z x x x Z x x x Z x x x Z x Z x x x x x x x ∞ = ∂ ∂ − ∂ − ∂ = + − + + + = ∂ ∂ ∂

∑

∂ n − 2 2 3 3 2 3 0 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) .... 2 3.2 n n o o o o o o o o n n ! o Z y Z y y y Z y y y Z y y y Z y Z y y y y y y y ∞ = ∂ ∂ − ∂ − ∂ = + − + + + = ∂ ∂ ∂

∑

∂ n −

Daha önce diferansiyel elemanın sonsuz küçük olduğu ve içerisindeki tüm değişimlerin lineer olduğu söylenmişti. Dolayısıyla yukarıdaki ifadede, Z x ve y’ ye göre lineer olarak artacağı veya azalacağı için, Z=ax+b ve Z=cy+d ise 1.türev sabit olacaktır. Daha yüksek mertebeden türevler bu durumda sıfır olacaktır. Böylece yukarıdaki açılımlar şu şekle dönüşürler,

( ) ( ) ( ) o ( ) o o Z x Z x Z x x x x ∂ = + − ∂ , ( ) ( ) ( ) o ( ) o o Z y Z y Z y y y y ∂ = + − ∂

Bu ifadeler diferansiyel eleman içerisinde Z’ nin x ve y’ ye göre değişimini göstermektedir. (x0:y0)

daki Z değerleri biliniyor kabul edilirse, (x0+dx:y0+dy) daki Z değerleri bu denklemler yardımıyla

belirlenebilir. Bu amaçla, yukarıdaki denklemde x=x0+dx ve y=y0+dy yazılmalıdır:

( _o ) ( )_o Z x( )o ( _{o o}) ( o ) ( )o ( )o ( o o) Z y Z y dy Z y y dy y y ∂ + = + + − ∂ Z x dx Z x x dx x x ∂ + = + + − ∂ ,

Bulunan son ifadelerde gerekli yoketmeler yapılarak ve yeniden düzenlenirse

Z x( _o dx) Z x( )_o Z x( )o dx x ∂ + = + ∂ , ( ) ( ) ( ) o o o Z y Z y dy Z y dy y ∂ + = + ∂

bulunur Bulunan sonuçlar mühendislikte kullanılan değişik fiziksel büyüklükler için gemelleştirilebilir. Örnek olarak diferansiyel elemanın bir yüzeyindeki gerilme σ ise dx kadar ve dy kadar sonraki değerleri şöyledir.

( ) (x dx) ( )x x dx x

σ

σ

+ =

σ

+∂ ∂ ( ) (y dy) ( )y y dy y

σ

σ

+ =

σ

+∂ ∂

Bir hava akımında akış sıcaklığına ve basıncına bağlı olarak hava yogunluğu çok değişecektir. (x:y) düzleminde hava yoğunluğu hesabı yapılmak istenirse yukarıdakine benzer işlemler yapılır. Direkt bir denklem yazmak mümkün olduğu için, akış ortamı bir denklemin yazılabileceği

diferansiyel elemanlara bölünür. Elemanın bir yüzeyindeki belirli kabul edilerek diğer yüzeyindeki yogunluklar yazılabilir. Yoğunluk (ρ) için bu değerler;

( ) (x dx) ( )x x dx x

ρ

ρ

+ =

ρ

+∂ ∂ ( ) (y dy) ( )y y dy y

ρ

ρ

+ =

ρ

+∂ ∂

Diferansiyel eleman üzerinden çeşitli fiziksel kanunlar, kütlenin korunumu, enerjinin korunumu, II.Newton Yasası vb kullanılarak yukarıdaki eşitlikler ile bir diferansiyel denklem bulunur. Bu diferansiyel denklemin çözümünden hesaplamalarda kullanılabilecek analitik bağıntılar bulunur.

1.6 Başlangıç ve Sınır Şartları

İntegrallerin en basit diferansiyel denklem oldukları noktasından hareketle başlangıç ve sınır şartlarının tarifi ve gereği integrasyon işleminden verilebilir. Bilindiği gibi belirli integrasyon

(sınırlı integrasyon) ve belirsiz integrasyon (sınırsız integrasyon) şeklinde iki integral alma yöntemi

mevcuttur. Diferansiyel denklemlerin çözümü daha ziyade belirsiz integral çözüm mantığı ile

çözülürler. Dolayısıyla, diferansiyel denklemlerin çözümü esnasında da belirsiz integral çözümünde karşımıza çıkan integral sabitlerine benzeyen “C” diferansiyel denklem sabitleri karşımıza çıkar. Yani, integrasyon işlemi veya diferansiyel denklem çözümü sonrasında elde edilecek çözüm denklemi bu C sabitlerinide içerecektir. “C” bir sabit olup reel, tamsayı, negatif, pozitif veya complex sayısal karşılığı belirli olmayan büyüklüktür. Sonuç olarak nümerik karşılığı belli olmayan C’ li denklem ile direkt olarak sayısal bir hesaplama yapılamaz. Örnek olarak;

C x y dx x y=

∫

⇒ = + 3 3 2 _{x=3 ⇒ y=? y= +C} 3 33

(C den dolayı y tam belli değil) Belirsiz integral ile sadece bir C sabiti karşımıza çıkmaktadır. Diferansiyel denklem çözümlerinde bu sabitlerin sayısı daha fazla olabilir. Bu sabitlerin sayısı diferansiyel denklemin mertebesine göre değişir. 1. mertebe için 1 tane C sabiti, 2. mertebe için 2 tane C sabiti , 3. mertebe için 3 tane C sabiti bulunur. Eğer bağımsız değişken sayısı biden fazla ise bu sayılar bağımsız değişken adedi ile çarpılmalıdır. 2. Mertebe, bağımsız değişken sayısı 2 olan bir kısmi diferansiyel denklemin C sabiti sayısı 4 tür. İşte bu C sabitlerinin sayısal karşılıklarının bulunmasını sağlayan hallere

BAŞLANGIÇ ve SINIR ŞARTLARI ismi verilir. Görülebileceği gibi çözüm için belirli olması gereken şart sayısının C sabiti sayısına eşit olması gerekir. Bu şartlar aynı zamanda diferansiyel denklemin çözümü sonrasında bulunan analitik ifadenin sağlaması gereken değerlerdir. Bir noktada çözüm denkleminin fiziki olarak doğru olup olmadığı hakkında karar vermemizi sağlayan en temel büyüklüklerdir. Eğer bu şartlar yerine gelmezse rahatlıkla çözümün yanlışlığından bahsedebiliriz. Diğer taraftan, diferansiyel denklemim çözümü mutlaka bir koordinat sistemine (kartezyen koordinatlar, silindirik koordinatlar veya küresel koordinatlar ) göre yapılmak zorundadır. Her koordinat sistemi mutlaka bir orijin noktasına sahiptir. Başlangıç ve sınır sartları tariflenirken bu orijin noktası ve koordinat sisteminin tipi dikkate alınmalıdır. Eğer proplem geometrisi üzerindeki orijin noktası yer değiştirirse, başlangıç ve sınır şartlarının değeride değişecektir. Bu şartlar, özellikle kısmi diferansiyel denklemlerin çözümünde çok etkilidirler. Çözüm fonksiyonu bulunabilmesine rağmen, başlangıç ve sınır şartları şartlar sağlanamadığı için çözümsüzlük mümkün olabilmektedir. Sonuç olarak başlangıç ve sınır şartlarının bilinmesi veya problem üzerinden çıkarılabilmesi gerekir.

Diferansiyel denklemin bağımsız değişkeni zaman ise bulunması gereken şart BAŞLANGIÇ

ŞARTI, bağımsız değişken geometri veya boyut ise bulunması gereken şart SINIR ŞARTI olarak isimlendirilir. Literatürde, kullanılacak şartların durumlarına göre problemler SINIR DEĞER

PROPLEMİ veya BAŞLANGIÇ DEĞER PROBLEMİ olarak da isimlendirilebilir. Bir problem sadece sınır veya sadece başlangıç şartı gerektirebileceği gibi her ikisinide birden isteyebilir. Bu şartlar problemin yapısından elde edilir. İyi tesbit edilmeleri çözümün sağlığı üzerinde müspet yönde etkili olacaktır. Bu şartların anlaşılması için, makine mühendisliği eğitimi sürecinde mutlaka

görülecek en temel konuları ihtiva eden, aşağıdaki uygulama problemlerinin iyi analiz edilmesinde fayda vardır. Bu problemlerde ilk önce diferansiyel denklemin meydana getirilmesi araştırılacak daha sonra başlangıç ve sınır şartları bulunacaktır. En son olarakta, elde edilen diferansiyel denklemlerin çözümüyle bulunması gereken eğriler araştırılacaktır. Bulunan diferansiyel denklemlerin belirlenen sınır veya başlangıç şartları vasıtasıyla çözümleri ileriki bölümlerde verilecektir.

PROBLEM-1:

L kalınlığındaki levha veya duvarın iki yüzeyindeki sıcaklıklar T1 ve T2 dir. Bu sıcaklık değerleri

T1>T2 şeklinde birbirinden farklı olarak verilmiş ise levha-duvar içerisinden geçen ısı miktarını ve

levha-duvar içerisindeki sıcaklık dağılımını problem üzerinde etkili olan fiziksel büyüklüklere bağlı olarak bulunuz. Başlangıç ve sınır şartlarını belirleyiniz. Doğru olması mümkün olabilecek veya beklenen çözümler neler olabilir?

ileyen Sınır Şartları

in noktası sağda . Transfer olan ısı mıktarı ; q 1. x = 0 ıse T=T1 x = 0 ıse T=T2

∆T=T1-T2

ir duvar veya levha ile iki ayrı sıcaklığa sahip iki ayrı ortam oluşturulmuştur. Termodinamik

er mühendislik probleminin çözümünde mutlaka bir referans sistem olarak bir eksen takımı

Problemi etk

Fiziksel büyüklükler: orijin noktası solda orij 1

2. Sıcaklık ; T 2. x = L ise T=T2 x = L ise T=T1

3. Malzeme (yoğunluk, ısı iletim yeteneği ) 4. Kalınlık ; L

5. Zaman ; t 6. Yüzey alanı ; A B

kanunlara göre iki ortam arasında ısı transferinin olabilmesi için ortamlar arasındaki sıcaklık farkının sıfırdan farklı olması gerekir (∆T=T1-T2≠ 0). Isı yüksek sıcaklık ortamından düşük sıcaklık

ortamına akar. Böyle bir durumda iki ortam arasındaki levha veya duvar üzerinden bir miktar ısı geçecektir. Böylece duvarın bir yüzeyi T1, diğer yüzeyi T2 sıcaklığına sahip olacaktır. Duvarın veya

levhanın iç bölgesindeki sıcaklıklarda bu iki değerin arasında olacaktır. Isının yüksek sıcaklıktan düşük sıcaklığa akması gerektiği için, duvarın iç noktalarındaki sıcaklık değerleri T1 ve T2 den

büyük veya küçük olamaz. Böylece duvar içerisindeki sıcaklık değişimi T(x) eğrisi veya denklemi şekildeki a, b ve c eğrilerinden biri olacaktır. Doğru bir çözüm için, çözüm fonksiyonunun bu eğrilerden birini vermesi gerekir. Aksi halde, şekilde görülen kesik çizgilerle verilmiş eğrileri tanımlayan, minimum veya maksimum noktalara sahip çözümler fiziken yanlış olacaktır. Çünkü, duvar veya levha içindeki sıcaklık yükselirse bir ısı üreticisi, düşerse bir ısı absorberi olmalıdır. Böyle bir bilgi olmadığı için doru sıcaklık dağılımları a,b ve c eğrilerinden biri olacaktır

H

(Kartezyen koordinat sistemi, Silindirik veya küresel koordinatlardan birisi) seçilmeli ve problem geometrisinin bir yeride eksen takımının orijin noktası olarak tercih edilmelidir. Çünkü, bulunması

Isı akış Doğrultusu T _a T1 T1 b q Duvar veya Levha c T2 T₂ x x=L 0 L

Duvar içerinde sıcaklık değişimi Beklenen sıcaklık eğrileri

q=q(T,x,malzeme,A,t) (1)

eklinde bir denklem geliştirmektir. Direkt böyle bir bağıntının yazılması şu aşamada mümkün

- Levhanın veya duvarın kalınlığı arttıkca q miktarı azalmalıdır. Yani q ile L ters orantılıdır. Fakat - Termodinamiğin 2. yasasına göre ısı yüksek sıcaklık ortamından düşük sıcaklık ortamına akar.

- Levha veya duvar malzemesinin ısı iletme kabiliyeti iyi ise daha çok ısı, kötü ise daha az ısı

- A ısı akış doğrultusuna dik yüzey alanı olup transfer olan ısı ile doğru orantılıdır. ukarıdaki yorumların ilk ikisi birleştirilerek şu şekide bir denklem elde edilir.

gerekli başlangıç ve sınır şartları ancak orijini belirli olan bir sistem için belirlenebilir. Aynı zamanda bulunacak çözümün formuda eksen takımının tipinden ve orijin noktasının yerinden etkilenecektir. Seçilen eksen takımının her eksenine (her doğrultusuna) fiziksel büyüklüklerden bir tanesi atanmalıdır. Bu işlem yapılırken mutlaka fiziksel büyüklüklerin DEĞİŞKEN olan tipi ele alınmalıdır. Yukarıdaki fiziksel büyüklüklerin 2, 4 ve 5 nolu elemanları değişken olurken diğerleri sabittirler. Kalınlık sabit değer gibi görülebilir. Ancak duvar veya levha içerisinde her nokta için bir sıcaklık değeri sözkonusudur. Yani sıcaklık duvar içerisindeki noktadan noktaya değişmektedir. Duvar içerisi koordinat sisteminin x boyutu ile temsil edildiğinden T x’e göre değişecektir. Böylece çözüm düzlemi düşey doğrultu T ve yatay ısı akış doğrultusu x olacaktır. Böylece 2 boyutlu-değişkenli (T ve x) çözüm aranacaktır. Eğer x yönü q doğrultusuna göre 30o açılı seçilseydi T ve q hem x hemde x’ e dik doğrultuda (y doğrultusu) değişim göstereceğinden 3 boyutlu (T,x ve y) bir problem meydana gelecekti. Malzeme, yüzey alanı ve transfer olan ısı sabittir. Çünkü, cözüm süresince veya çözüm alanında değişmezler. Bununla beraber sıcaklık kalınlığın her noktasında farklı değerler aldığı için değişkendir. Başka bir ifade ile sıcaklık (T) kalınlığa (L,x) bağlı olarak değişmektedir. Eksen takımı olarak, problem geometrisi bir düzlem yapı arzettiği için, düzlemsel kartezyen koordinatlar seçilmiş ve eksen doğrultularıda T ve x olarak alınmıştır. Eksen takımının orijin noktası olarak levhanın sol tarafı tercih edilmiştir. Bu şartlar altında gerekli olan sınır şartları çıkarılmıştır. Eksen takımı ve orijin noktasının yeri değiştirilmiş olsa sınır şartlarınında değişeceği açıkca görülebilir. 5 nolu fiziksel büyüklük olan zaman da bir değişkendir. Ancak, mühendisliğin pratik uygulamalarında zamana göre bir değişme istenmez. Çünkü, zaman problemin çözümünü zorlaştırmasının yanında, problem parametrelerinin zamana göre değişimi istenmeyen ve beklenmeyen bazı olumsuzlukları beraberinde getirir. Bu tür zamana bağlı olarak değişmeyen problemler DAİMİ (steady) veya SÜREKLİ REJİM olarak isimlendirilir. Zaman bağlı olarak değişen problemlere DAİMİ OLMAYAN (unsteady) problem ismi verilir. Şayet T ve x zamana bağlı olarak değişmiş olsaydı eksenlerin biri zaman boyutunu temsil ederken, sınır şartlarına ilaveten birde başlangıç sartı gerekecekti. Bu problemin çözümünde amaç fiziksel büyüklükler arasında

ş

değildir. Ancak bir denklemin veya bağıntının geliştirilmesine yardımcı olabilecek, fiziksel büyüklükler arasında şu yorumlar çıkarılabilir:

bu orantının derecesi bilinemez. ( q ≈ 1/ Lm ; m: orantı derecesi)

Başka bir ifade ile iki ortam arasında ısı transferinin olması için aralarında bir sıcaklık farkının (∆T=T1-T2 ) olması gerekir. Bu sıcaklık farkı sıfır ise ısı transferi olmaz. Dolayısı ile sıcaklık farkı

büyüdükce transfer olan ısı miktarınında artması gerekir. Yani transfer olan ısı miktarı sıcaklık farkı ile doğru orantılıdır. ( q ∝ ∆Tn _{; n:orantının derecesi)}

iletilmelidir. Yani malzemenin ısı iletme kabiliyeti ısı yükü ile doğru orantılıdır. Malzemenin ısı iletme kabiliyeti malzemeye ait bir sabit olup, deneysel çalışmalarla düzenlenmiş tablolardan malzeme tipine göre seçilir. Bu değer literatürde ISI İLETİM KATSAYISI olarak bilinmektedir.

Y

q T L

n m

∝ ∆ (2)

Bu orantı bir katsayı ile ( k ) eşitliğe dönüştürülebilir. q k T L n m = ∆ (3)

Son ifadedeki k bir orantı sabiti olup yukarıdaki 3. yorumu temsil edebilir. Çünkü, hem malzeme ısı iletme yeteneği hemde orantı katsayısı sabittirler. Bulunan son denklem daha ileriye götürülemez. Dolayısı ile m ve n bilinmediği için sayısal hesaplamada yapılamaz. Çünkü, sıcaklığın levha içerisinde kalınlığa bağlı olarak ne şekilde değiştiği bilinmemektedir. Bu değişim m ve n nin değerlerine göre şekil alacaktır. Sıcaklığın levha içerisindeki değişimi a, b ve c eğrilerinden hangisidir. Sonuç olarak, bu aşamada bir tıkanma meydana gelmiştir. Eğer, duvar veya levha içerisindeki sıcaklık dağılımının bilindiği bir yapı bulunursa çözüm ileriye götürülebilir. Süperpozisyon prensibi gereği çözülemeyen bir bütün çözülebilir daha basit ve kontrol edilebilir küçük parçalara ayrılır. Bölünen her parça içerisinde değişimler biraz daha basitleşir. Bu parçalama sayısı artıkca her parça içerisindeki değişimler lineer hale yaklaşacaktır. Şayet bölüm işlemi sonsuza giden sayıda yapılacak olursa sistem en küçük parçasına ayrılmış olur. Bu en küçük yapıya DİFERANSİYEL ELEMAN ismi verilir. Bu diferansiyel eleman genelde problem geometrisinin çok küçültülmüş bir minyatürü olur ve genelde diferansiyel eleman ile ana problemin geometrisi birbirine benzerler. Çözüm için bundan sonra fiziksel büyüklükler ile diferansiyel eleman arasında yukarıdaki mantıkla bağıntı elde edilmeye çalışılır. Bu eleman çok küçük olduğu için içerisinde sıcaklığın kalınlığa göre değişimide LİNEER olacaktır. Sıcaklığın duvar veya levha içerisindeki değişimi a, b ve c eğrilerinden hangisi olursa olsun, bu eğrilerin diferansiyel eleman üzerindeki izdüşümleri mutlaka bir doğru olacaktır. Diğer bir ifade ile a,b ve c eğrileri diferansiyel elemanlar vasıtasıyla sonsuza giden sayıda lineer doğruya ayrılmıştır. Sonsuz giden sayıdaki doğrucuklar yanyana gelerek herhangi bir eğriyi oluşturmaktadırlar. Dolayısıyla diferansiyel eleman içinde m=n=1 olacaktır. Duvarın en ince dx kalınlığındaki dilimlere ayrıldığı düşünülürse, bunların bir tanesi aşağıdaki gibi olacaktır: Bu incecik duvarın yüzey sıcaklıkları olacaktır. Bu sıcaklıklar T ' 1 T ' 2 T

1 ve T2 nin arasında olacaktır. Sonuç olarak, dx sonsuz küçük levha kalınlığı olduğu için, bu

kalınlığın iki kenarı arasındaki sıcaklık farkıda sonsuz küçük (dT= - ) olacaktır. Matematik ifadeyle, i sonsuz küçük parçalama sayısı ise

' 1 T ' 2 T ⇒ dx i L i→∞ = lim T dT i→∞∆ = lim T _Lineer değişimler

Diferansiyel eleman ve üst taraftaki açıklamalar 3 nolu ifadeye taşınarak yeni haliyla denklem şu şekilde yazılabilir. dx dT k q= (4) 0 x x T1 T2 x+dx Lineer değişim dT Diferansiyel Eleman ve içerisindeki sıcaklık dağılımı dx x _x+dx