I PENDAHULUAN
1.1 Latar Belakang
Pada kondisi-kondisi tertentu keheterogenan unit percobaan tidak bisa dikendalikan hanya dengan pengelompokkan satu sisi keragaman unit-unit percobaan namun memerlukan penanganan yang lebih kompleks. Kondisi ini tentunya memerlukan bentuk rancangan yang lain. Salah satu rancangan yang mampu mengendalikan komponen keragaman unit-unit percobaan lebih dari satu sisi komponen adalah rancangan bujursangkar latin (latin square). Tulisan ini menawarkan prosedur sederhana yang dapat digunakan untuk membangun sekuen (rangkaian) dari petemuan berpasang-pasangan diantara pelaku yang berasal dari populasi yang finite (terbatas) dengan menggunakan rancangan bujursangkar latin tersebut. Proses pertemuan yang dipelajari memiliki dua sifat, pertama rangkaian dari pertemuan tersebut adalah eksogen yang berarti bahwa setiap pelaku bertemu dengan pelaku yang lain tepat satu kali. Kedua, dalam setiap periode proses ini memaksimumkan banyaknya dari pemasangan dalam populasi.
Dalam ilmu ekonomi proses pertemuan berpasang-pasangan dengan sifat ini
digunakan untuk meyatakan konsep dari persaingan dagang secara eksplisit.
Dalam mengembangkan prosedur untuk menciptakan rangkaian pemasangan yang diinginkan digunakan bentuk khusus dari permutasi yang disebut involusi. Dengan memanfaatkan beberapa hasil matematis dari bujursangkar latin, alasan untuk bekerja dengan objek matematika ini adalah proses pemasangan yang merupakan cara untuk membagi populasi X ke dalam himpunan agen-agen yang disjoint secara berulang-ulang. Karena diketahui bahwa pertemuan yang dipandang adalah bilateral, maka proses pemasangan dapat dilihat sebagai rangkaian involusi dari X ke X.
1.2 Tujuan
Adapun tujuan dari penulisan makalah ini adalah memasangkan agen satu dengan agen lainnya dalam populasi yang terbatas di mana setiap agen bertemu dengan agen lainnya tepat satu kali dengan memperagakan bagaimana membangun bujursangkar latin sedemikian rupa sehingga setiap baris, pada awalnya adalah involusi dari baris pertama yang akhirnya didapatkan suatu matriks pemadanan.
II. LANDASAN TEORI
2.1 Matriks
Matriks adalah kumpulan bilangan yang disusun dalam bentuk persegi panjang atau bujur sangkar yang tersusun dalam baris dan kolom. Ukuran atau ordo dari suatu matriks ditentukan oleh banyaknya baris dan kolom yang membentuknya.
Secara umum matriks dapat ditulis sebagai berikut
= elemen matrik A yang terletak pada baris ke-i, kolom ke-j ; i=1,2,…,m ; j=1,2,…..,n
= ukuran atau ordo matriks A, yaitu
11 12 1 21 22 2 1 2 n n m m mn
a
a
a
a
a
a
A
a
a
a
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
L
L
M
M
O
M
L
[Leon 2001] 2.2 Bujursangkar Latin Definisi 1 (Bujursangkar Latin)Diketahui ada n symbol berbeda, bujursangkar latin adalah matriks
dengan entri simbol-simbol yang diketahui yang disusun sedemikian rupa sehingga setiap simbol muncul tepat satu kali dalam setiap baris dan kolom.
[Aliprantis, et al 2006] Contoh 1 :
Diberikan himpunan simbol-simbol {1, 2, 3, 4} dan {@, #, $, &}, matriks
1 2 3 4 @ # $ & 2 3 4 1 $ & @ # dan 3 4 1 2 # $ & @ 4 1 2 3 & @ # $ ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦
adalah dua contoh dari bujursangkar latin. Tentu saja bila diketahui himpunan n simbol,
secara umum dapat diperoleh banyak bujursangkar latin yang berbeda, dan juga banyaknya bujursangkar latin yang terbentuk akan semakin bertambah bergantung pada n. Walaupun bujursangkar latin telah dipelajari secara rinci dalam matematika banyaknya bujursangkar latin yang ada telah dihitung hanya untuk 10.
[Aliprantis, et al 2006]
Diketahui himpunan populasi 1, … … … , dengan n agen. Ada tiga prosedur pembangunan bujursangkar latin yang masing-masing menghasilkan matriks
yang spesifik.
2.2.1 Konstruksi Bujursangkar Latin1 Bujursangkar latin ini dinotasikan dengan dan baris pertamanya adalah vektor (1, 2, . . . . , n). Baris lainnya dari dihasilkan secara rekursif dengan cara menggeser satu tempat ke kiri baris yang sebelumnya secara
siklik. Yang berarti baris kedua diperoleh dengan cara menggeser baris pertama satu tempat ke kiri, dalam contoh di atas baris kedua adalah (2, 3, . . . . , n, 1) dan baris ke tiga adalah vektor (3, 4, . . . ., n, 1, 2). Dengan demikian adalah matriks seperti berikut : 1 2 ... 2 1 2 3 1 1 3 4 1 2 1 4 3 2 1 3 2 1 n n n n n n n n n n n n n n n − − − − − − − − − −
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
L L M M O M M M L LJika menggunakan notasi standar untuk bujursangkar latin ini maka setiap entri diberikan formula sebagai berikut: jika 1 dan 1 1 ( 1) 1 jika 2 dan 1 ( ) 1 jika 2 dan 2 j i j n aij i j n Y i j i j i i j n i j n i i n i j n χ = ≤ ≤ = + − − + − = + − ≥ ≤ ≤ − + − − − ≥ − + ≤ ≤
⎧⎪
⎨
⎪⎩
di mana χY N: →{0,1} adalah fungsi karakteristik dari himpunan1, 2, … dengan
( ) 1 jika dan ( ) 0 jika . Y k k Y Y k k Y
χ = ∈ χ = ∉
Contoh 2
Saat 4 konstruksi ini akan menghasilkan bujursangkar latin
1 2 3 4 2 3 4 1 3 4 1 2 4 1 2 3 L− =
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
.2.2.2 Konstruksi Bujursangkar Latin2 Misalkan notasi untuk bujursangkar latin ini adalah . Matriks ini memiliki baris pertama (1, 2, . . ., n) dan konstruksinya dibuat secara rekursif tepat seperti cara pertama, tetapi satu-satunya perbedaan terletak pada
cara penggeserannya yang ke arah kanan bukan ke arah kiri. Hal ini berarti baris kedua dari diperoleh dengan cara menggeser baris pertama ke kanan secara siklik, dalam contoh, baris ke dua adalah vektor (n, 1,…, n-2, n-1), dan baris ketiga adalah vektor (n-1, n, 1, …, n-2), dan seterusnya. Bujursangkar latin yang terbentuk adalah 1 2 2 1 1 3 2 1 1 4 3 2 3 4 1 2 2 3 1 1 n n n n n n n n n n n n L n n n − − − − − − − − − + = − ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ L L L M M O M M M L L
Dengan notasi maka formula untuk entri dari adalah
jika 1dan1 1 ( 1 1) ( ) 1 jika 2 dan1 1 1 jika 2 dan j i j n aij n j i n Y n j n i j i j i j i i i j n χ = ≤ ≤ = + + − − + + − = − + + ≥ ≤ ≤ − − + ≥ ≤ ≤
⎧⎪
⎨
⎪⎩
Contoh 3
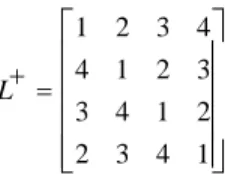
Di mana saat 4 kita mendapatkan
1 2 3 4 4 1 2 3 3 4 1 2 2 3 4 1 L+ =
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
.2.2.3 Konstruksi Bujursangkar Latin3 Bujursangkar latin dinotasikan dengan
di mana baris pertama adalah (n, n-1, …1) dan baris lainnya dibentuk dengan cara mengikuti prosedur rekursif dengan cara menggeser baris pertama satu tempat ke kiri, sehingga baris ke dua yang terbentuk adalah (n-1,n-2, …, 1, n). Dengan mengulang proses
ini sebanyak 1 maka diperoleh bujursangkar latin seperti berikut :
1 2 1 1 2 1 1 3 2 2 1 4 3 1 3 2 n n n n n L n i n i n i n i n − − − = − + − − + − + ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ L L M M O M M L M M O M M M M
Dengan maka formula untuk entri dari L adalah
1 jika 1dan1 1 ( 1) ( 1) 2 jika 2dan1 1 2 2 jika 2dan 2 n j i j n aij n i j n Y i j n i j i j n i n i j i n i j n χ + − = ≤ ≤ = + − + − + + − = + − − ≥ ≤ ≤ − + − + − ≥ − + ≤ ≤
⎧⎪
⎨
⎪⎩
Contoh 4Saat 4 bujursangkar latin L adalah seperti berikut : 4 3 2 1 3 2 1 4 2 1 4 3 1 4 3 2 L=
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Berdasarkan dari ketiga konstruksi bujursangkar latin di atas maka untuk sembarang populasi berukuran n terdapat beberapa bujursangkar latin yang dapat dibentuk. Banyaknya bujursangkar latin yang dapat dibentuk dari populasi berukuran n dapat dilihat dari Tabel 1 berikut:
Tabel 1 Banyak bujursangkar latin dari populasi berukuran n sebarang. Ukuran Contoh bujursangkar latin standar A B C B C A C A B A B C D B C D A C D A B D A B C A B C D E B A E C D C D A E B D E B A C E C D B A A B C D E F B C F A D E C F B E A D D E A B F C E A D F C B F D E C B A A B C D E F G B C D E F G A C D E F G A B D E F G A B C E F G A B C D F G A B C D E G A B C D E F ABC...N BCD...A CDE...B . . . PAB...(P-1) Banyaknya bujursangkar latin standar 1 4 56 9408 16.942.080 --- Banyaknya bujursangkar latin yang terbentuk 12 576 161.280 818.851.200 61.479.419.904.000 ! 1 ! Banyaknya bujursangkar latin standar [Montgomery 2001]
2.3 Fungsi Definisi 2 (Fungsi)
Fungsi (pemetaan) f dari himpunan A ke himpunan B, dinotasikan , adalah suatu relasi dari A ke B yang setiap anggota dari A muncul hanya sekali sebagai komponen pertama dari pasangan terurut keanggotaan relasi yang bersangkutan.
Kurtz 1992] Dari definisi dia atas, jika , , maka dapat ditulis b = f (a). Dalam hal ini b disebut imej dari a dibawa oleh f, sedangkan a disebut preimej dari b oleh f. Penulisan ringkas dengan menerapkan lambang logika dari definisi di atas dapat dinyatakan sebagai berikut.
jika dan hanya jika
! , atau
: jika dan hanya jika ( )
[ ( ) ( )] maka . f A B a A b f a c f a b c → ∀ ∈ = ∧ = = Contoh 5 Misalkan 1,2,3 dan , , , , perhatikan bahwa 1, , 2, , 3,
adalah fungsi dari A ke B, sedangkan
1, , 2, dan
1, , 2, , 2, , 3, bukan merupakan fungsi dari A ke B.
Definisi 3 (Fungsi Injektif)
Fungsi f disebut fungsi injektif (satu-satu) apabila f tidak pernah mencapai nilai yang sama dua kali; yakni,
jika maka
[Stewart 2001] Contoh 6
Misalkan 1,2,3 dan B = {a,b,c,d,e}.
fungsi 1, , 2, , 3, adalah
injektif, sedangkan fungsi 1, , 2, , 3, bukan merupakan
fungsi injektif.
Perhatikan Contoh 6 di atas komponen ke dua dari semua anggota f muncul hanya sekali, sehingga f adalah fungsi injektif. Sekarang perhatikan fungsi , unsur a muncul dua kali sebagai komponen ke dua di dalam kenggotaan , sehingga tidak injektif. Definisi 4 (Fungsi Surjektif)
Suatu fungsi : disebut fungsi surjektif, jika , artinya
. [Kurtz 1992] Contoh 7 Jika 1,2,3,4 dan , , , 1, , 2, , 3, , 4, dan 1, , 2, , 3, , 4, adalah dua fungsi surjektif dari A ke B, sedangkan fungsi
1, , 2, , 3, , 4, tidak surjektif.
Dalam Contoh 7 terlihat bahwa semua anggota B muncul sebagai komponen ke dua di dalam ke anggotaan f1 dan f2, sehingga f1 dan f2 adalah fungsi surjektif. Sekarang perhatikan fungsi , ada anggota B yaitu z yang tidak muncul sebagai komponen ke dua di dalam kenggotaan , sehingga tidak surjektif.
Definisi 5 (Fungsi Bijektif)
f fungsi bijektif jika dan hanya jika f fungsi injektif dan f fungsi surjektif
[Kurtz 1992] Contoh 8
Jika 1,2,3 dan , , ,
1, , 2, , 3, adalah fungsi bijektif karena merupakan fungsi injektif dan surjektif.
Contoh 9
Jika 1,2,3 dan , , , ,
1, , 2, , 3, bukan fungsi bijektif karena merupakan fungsi injektif tetapi tidak surjektif.
2.4 Permutasi Definisi 6 (Permutasi)
Permutasi dari himpunan terbatas X yang tidak kosong adalah fungsi bijektif dari X ke X.
[Biggs 1989] Dalam pemasangan dari anggota X ke X yang biasa dijumpai permutasi dapat dipandang sebagai suatu susunan yang dapat dibentuk dari sekumpulan objek yang dapat dipilih sebagian atau seluruhnya.
Jika ada n benda yang berbeda maka banyaknya susunan yang berbeda (permutasi) dari n benda tersebut adalah:
, ! 1 … 2 1.
Permutasi merupakan penyusunan kembali suatu kumpulan objek dalam urutan yang berbeda dari urutan yang semula. Sebagai contoh, kata-kata dalam kalimat sebelumnya “permutasi merupakan penyusunan kembali suatu kumpulan objek dalam urutan yang
berbeda dari urutan yang semula” dapat disusun kembali sebagai "merupakan Permutasi suatu urutan yang berbeda urutan yang kumpulan semula objek penyusunan kembali dalam dari". Proses mengembalikan objek-objek tersebut pada urutan yang baku (sesuai ketentuan) disebut sorting.
Jika terdapat suatu untai abjad abcd, maka untai itu dapat dituliskan kembali dengan urutan yang berbeda: acbd, dacb, dan seterusnya. Selengkapnya ada 24 cara menuliskan ke empat huruf tersebut dalam urutan yang berbeda satu sama lain. Setiap untai baru yang tertulis mengandung unsur-unsur yang sama dengan untai semula abcd, hanya saja ditulis dengan urutan yang berbeda. Maka setiap untai baru yang memiliki urutan berbeda dari untai semula ini disebut dengan permutasi dari abcd.
Contoh 10
Berikut ini adalah permutasi dari abcd abcd abdc acbd acdb adbc adcb bacd badc bcad bcda bdac bdca cabd cadb cbad cbda cdab cdba dabc dacb dbac dbca dcab dcba
[Wikipedia Indonesia 2008] 2.5 Involusi
Definisi 7 (Aturan pemadanan bilateral) Aturan pemadanan bilateral untuk populasi X adalah fungsi yang
memenuhi artinya
o untuk semua
, dengan yang merupakan pemetaan identitas pada X.
[Aliprantis, et al 2006] Berdasarkan definisi di atas, jika
merupakan aturan pemadanan bilateral, maka fungsi invertible dan adalah permutasi dari X karena adalah fungsi surjektif satu-satu. Bagaimanapun juga,
merupakan bentuk khusus dari permutasi yang inversnya adalah dirinya sendiri. Sebagai contoh ; fungsi ini dalam ilmu matematika kita kenal sebagai “involusi”. Secara sederhana dapat dikatakan bahwa cara apapun untuk memasangkan agen-agen dalam populasi haruslah sedemikian rupa sehingga
pasangan dari agen tersebut adalah agen itu sendiri.
Oleh karena itu, jika adalah aturan pemadanan dan agen x dipadankan dengan agen , maka kita sebut adalah pasangan dari x. Dengan cara serupa,
adalah pasangan dari jadi himpunan , dapat disebut aturan pemadanan bilateral.
Contoh 11
Berikut contoh sederhana dari aturan pemadanan bilateral (involusi)
Andaikan 0, ∞ dan didefinisikan
dengan .
[Aliprantis, et al 2006] Contoh 12
Misal diberikan bujursangkar latin dengan 4 1 2 3 4 2 1 4 3 3 4 1 2 4 3 2 1 L=
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Perhatikan matriks L di atas, misalkan saja matriks di atas menggambarkan pemadanan pada populasi 4 dan diasumsikan populasi agen 1,2,3,4 sehingga dari matriks tersebut dapat diperoleh pemadanan yang setiap barisnya diartikan sebagai periode pemadanannya. Dengan demikian baris pertama merupakan periode pemadanan pertama di mana belum ada agen yang dipadankan. Selanjutnya perhatikan pada baris ke dua atau periode ke dua, diperoleh pemadanan {(1,2),(2,1),(3,4),(4,3)}, kemudian dapat dilihat bahwa dari pemadanan ini agen 1 dipadankan dengan agen 2, pada baris yang sama agen 2 dipadankan dengan agen 1. Begitu juga untuk agen 3 yang dipadankan dengan agen 4, pada baris yang sama juga agen 4 dipadankan dengan agen 3. Dapat dilihat dengan jelas bahwa baris ke tiga dan ke empat pada matriks L di atas dikenakan hal yang sama seperti pada baris ke dua. Oleh karena itu, hal inilah yang menyebabkan matriks L tersebut memiliki sifat involusi di mana baris lainnya merupakan involusi dari baris pertama.