T1 662011010 Full text

(1)

PEMBENTUKAN HYPOCYCLOID 3 DIMENSIDAN KOMPUTASI LUAS

PERMUKAANNYA

THE FORMATION AND COMPUTATION OF THREE-DIMENSIONAL

HYPOCYCLOID AND SURFACES

Oleh

PURWOTO NIM : 662011010

TUGAS AKHIR

Diajukankepada Program Studi Matematika, Fakultas Sains dan Matematika guna memenuhi sebagian dari persyaratan untuk mencapai gelar Sarjana Sains

(Matematika)

Program Studi Matematika

Fakultas Sains dan Matematika Universitas Kristen Satya Wacana

(2)

(3)

(4)

(5)

PERNYATAAN KEASLIAN KARYA TULIS TUGAS AKHIR

Yang bertanda tangan dibawah ini,

Nama : Purwoto

NIM : 662011010

Program Studi : Matematika

Fakultas : Fakultas Sains dan Matematika, Universitas Kristen Satya Wacana

Menyatakan dengan sesungguhnya bahwa tugas akhir, Judul:

PEMBENTUKAN HYPOCYCLOID 3 DIMENSI DAN

KOMPUTASI LUAS PERMUKAANNYA

Yang dibimbing oleh:

1. Dr. Hanna Arini Parhusip, M.Sc.

2. Tundjung Mahatma, S.Pd, M.Kom

adalah benar-benar hasil karya saya.

Di dalam laporan tugas akhir ini tidak terdapat keseluruhan atau sebagian tulisan atau gagasan orang lain yang saya ambil dengan cara menyalin atau meniru dalam bentuk rangkaian kalimat atau gambar serta simbol yang saya aku seolah-olah sebagai karya saya sendiri tanpa memberikan pengakuan kepada penulis atau sumber aslinya.

Salatiga, Januari 2015 Yang memberikan

pernyataan

(6)

(7)

MOTTO

“Takut akan Tuhan adalah permulaan pengetahuan, tetapi orang bodoh menghina hikmat dan didikan.”

(Amsal 1:7)

“Dia memberi kekuatan kepada yang lelah dan menambah semangat kepada yang tiada berdaya “

(Yesaya 40:29)

“Jangan seorangpun mengganggap engkau rendah karena engkau muda. Jadilah teladan bagi orang-orang percaya, dalam perbuatanmu, dalam tingkah lakumu,

dalam kasihmu, dalam kesetiaanmu dan dalam kesucianmu” (1 Timotius 4:12)

“Doa dilanjutkan dalam karya, karya dibawa dalam doa” (Santo Vincentius A. Paulo)

“Keberhasilan adalah kemampuan untuk melewati dan mengatasi dari satu kegagalan ke kegagalan berikutnyatanpa kehilangan semangat.

(Winston Churchill)

Semua orang ingin mengubah dunia , tetapi tidak semua orang mau mengubah dirinya sendiri. Diri kita sendiri yang mau berubah dan bergerak adalah kunci. Hidup memang kadang menumbangkan kita, tapi kita bisa memilih untuk tetap bangkit. Jangan hanya diam dan menunggu kesempatan hadir menyapa kita, tapi

bagaimana jika kita yang menciptakan kesempatan itu bagi orang lain untuk sebuah proses keberhasilan.

(8)

KATA PENGANTAR

Puji syukur dan terima kasih kepada Tuhan Allah yang penuh kasih atas segala berkat dan penyertaan-Nya. Oleh karena bimbingan serta kasihnya penulis dapat menyelesaikan tugas akhir (Skripsi) sebagai prasyaratan Studi S1 pada Program Studi Matematika Fakultas Sains dan Matematika Universitas Kristen Satya Wacana. Di dalam Skripsi ini disajikan dua bentuk makalah . Makalah pertama berjudul “ PERLUASAN KURVA PARAMETRIK HYPOCYCLOID 2 DIMENSI MENJADI 3 DIMENSI DENGAN SISTEM KOORDINAT BOLA’’ dan telah dipublikasikan dalam Seminar Nasional Matematika VIII tahun 2014 dengan tema “ Peran Serta Cendekia Matematika dan Pendidikan Matematika dalam Akselerasi Perubahan Karakter Bangsa” yang diselenggarakan oleh jurusan Matematika FMIPA Universitas Negeri Semarang pada tanggal 8 November 2014. Kemudian dilanjutkan penelitian pada makalah yang kedua dengan judul

“KOMPUTASI LUAS PERMUKAAN PADA HYPOCYCLOID 3 DIMENSI”.

Makalah kedua ini dipresentasikan dalam ujian skripsi pada tanggal 28 Januari 2015.

Dari penulisan skripsi ini penulis berharap apa yang tersaji di dalam skripsi ini dapat bermanfaat bagi yang membacanya. Dapat memberikan wawasan lebih dan juga ilmu pengetahuan tentang matematika serta dimungkinkan sebagai salah satu referensi di dalam penulisan penelitian yang lain. Penulis menyadari bahwa masih banyak kekurangan dalam penyusunan skripsi ini.Oleh karena itu, penulis menerima kritik, saran dan pendapat yang bersifat membangun untuk penyempurnaan laporan tugas akhir (Skripsi).

Salatiga, Januari 2015

(9)

UCAPAN TERIMA KASIH

Penulis menyadari bahwa banyak pihak yang telah mendukung dan membantu di dalam penyusunan skripsi ini sehingga dapat berjalan dengan baik dan lancar. Oleh karena itu, pada kesempatan ini penulis mengucapkan terima kasih atas segala doa, nasihat, bimbingan dan dorongan baik materi maupun spiritual kepada :

1. Dr. Bambang Susanto, M.Sc selaku Ketua Program Studi Matematika. 2. Dr. Hanna Arini Parhusip, M.Sc selaku pembimbing utama yang dengan sabar dan tak kenal lelah membimbing dan mengarahkan penulis selama proses penulisan skripsi ini sehingga laporan skripsi ini dapat diselesaikan dengan baik.

3. Tundjung Mahatma, S.Pd, M.Kom selaku pembimbing pendamping yang juga membimbing serta mengarahkan penulis sehingga laporan skripsi ini dapat diselesaikan dengan baik.

4. Dra. Lilik Linawati, M.Kom selaku wali studi angkatan 2011 yang secara tidak langsung menjadi ibu pendamping bagi penulis dan juga teman-teman. Trima kasih untuk motivasi, nasihat dan juga semangat didalam proses perkuliahan kami.

5. Dosen pengajar, Dr. Bambang Susanto, Dra. Lilik Linawati, M.Kom, Dr. Adi Setiawan, M.Sc, Tundjung Mahatma,S.Pd, M.Kom, Didit Budi Nugroho, D.Sc, Dr. Hanna Arini Parhusip, M.Sc, Leopoldus Ricky Sasongko, S.Si yang telah memberikan ilmu pengetahuan kepada penulis selama studi di FSM UKSW.

6. Staf TU FSM, Pak Edy, Mbak Eny, Mas Basuki, Bu Ketut yang telah banyak memberikan bantuan kepada penulis.

7. Bapak dan ibu orang tuapenulisyang selalu mendoakan dan mendukung demi menyelesaikan studi ini baik dalam bentuk materi juga motivasi dan semangat.

(10)

maupun melalui motivasinya sehingga penulis dapat menyelesaikan skripsi dengan semangat .

9. Bu Titi dan sahabat-sahabat yang luar biasa Titis, Dewi, Priska, Daivi, Rafen, Dwi ,Yohanes Huwae, Lelono, Ferry, Happy, Yaya, Kukuh Azis, Yodi, dan semua yang tidak bisa disebutkan satu demi satu yang selalu memberikan semangat, motivasi, bantuan dan doa kepada penulis. Terimakasih untuk keceriaan yang penulis dapatkan dari kalian semua.

10. Semua pihak yang tidak dapat penulis sebutkan satu persatu yang juga mendukung penulis selama penulisan skripsi ini.

Penulis menyadari sepenuhnya bahwa dalam penulisan skripsi ini masih terdapat banyak kekurangan dan jauh dari kesempurnaan. Oleh karena itu, penulis sangat mengharapkan segala saran dan nasihat dari pembaca. Harapan penulis, semoga skripsi ini bermanfaat bagi semua pihak.

Salatiga, Januari 2015

(11)

DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

LEMBAR PENGESAHAN ... ii

LEMBAR PERNYATAAN KEASLIAN ... iii

LEMBAR PERNYATAAN BEBAS ROYALTY DAN PUBLIKASI ... iv

MOTTO DAN PERSEMBAHAN ... v

KATA PENGANTAR ... vi

UCAPAN TERIMA KASIH ... vii

DAFTAR ISI ... ix

DAFTAR LAMPIRAN ... x

ABSTRAK ... xi

BAB I : PENDAHULUAN ... 1

BAB II : ISI ... 3

MAKALAH I ... 4

JUDUL MAKALAH 1 MAKALAH II... 5

JUDUL MAKALAH 2 BAB III : PENUTUP ... 6

(12)

DAFTAR LAMPIRAN

LAMPIRAN 1 : Program MATLAB kurva Deltoid dan perluasannya LAMPIRAN 2 : Program MATLAB kurva Astroid dan perluasannya LAMPIRAN 3 : Program MATLAB kurva Star dan perluasannya LAMPIRAN 4 : Program MATLAB kurva Bentuk 4 dan perluasannya LAMPIRAN 5 : Program perluasan turunan kedua epicycloid

LAMPIRAN 6 : Program perluasan turunan kedua hypocycloid

LAMPIRAN 7 : Program menghitung luas permukaan dari perluasan 3D

(13)

ABSTRAK

Skripsi ini membahas tentang pengembangan kurva hypocycloid menjadi permukaan hypocycloid. Hypocycloid merupakan salah satu bentuk kurva dari persamaan parametrik. Bentuk-bentuk hypocycloid dipengaruhi oleh nilai-nilai parameternya. Berbagai macam bentuk kurva hypocycloid diperluas ke dalam 3 dimensi dengan menggunakan sistem koordinat bola, dimana setiap titik dari permukaan mempunyai jari-jari dan dua sudut. Turunan dari persamaan-persamaan permukaanterhadap parameter-parameternya memberikan persamaan-persamaan parametrik baru. Kombinasi persamaan-persamaan tersebut menghasilkan berbagai bentuk permukaan.

(14)

ABSTRACT

This research is about the development of hypocycloid curve into hypocycloid surface. Hypocycloid is one of the parametric equations. Hypocycloid curves are influenced by the values of the parameters. Various forms of hypocycloid curve are expanded into their three dimensional forms by using the spherical coordinate system, where each point of the surface has a radius and angle. The derivative of the surface’s equation generates new parametric equations. The combination of these equations generates various of surfaces. Some of the surfaces are then formulated in vector notation and calculated by using MATLAB.

(15)

BAB I PENDAHULUAN

.

Pada skripsi ini akan dicari persamaan permukaan dari kurva parametrik 2 dimensi yang diperluas dalam 3 dimensi. Pernyataan diperluas disini adalah menggunakan pasangan (x,y) dari kurva parametrik atau polar 2 dimensi yang sudah diketahui dari literatur sedangkan untuk membuat pasangan titik (x,y,z) dibuat dengan modifikasi bebas tergantung fungsi yang dipilih. Hal ini dilakukan dalam 2 tahap penelitian.

Pada penelitian pertama skripsi ini dibahas perluasan dari persamaan parametrik

hypocycloid 2 dimensi menjadi 3 dimensi dengan sistem koordinat

bola.Hypocycloidmerupakankurva dari satu bentuk persamaan parametrik.Hypocycloid

mempunyai berbagai macam bentuk yang terbuat dari kombinasi nilai-nilai parameternya. Kemudian dari situ kurva-kurva hypocycloid divisualisasikan ke dalam bentuk 3 dimensi. Visualisasi 3 dimensi dikerjakan dengan program MATLAB. Hasil penelitian telah dipresentasikan pada Seminar Nasional Matematika VIII tahun 2014 yang diselenggarakan oleh jurusan Matematika FMIPA Universitas Negeri Semarang pada tanggal 8 November 2014 (Purwoto, dkk, 2014).

Pada penelitian tahap kedua, setiap permukaan yang diperoleh akan dicari luas permukaannya dengan menggunakan rumus luas permukaan. Pembahasan dibatasi pada salah satu permukaan yang sudah diperoleh pada penelitian tahap pertama.

Rumusan Masalah

1. Bagaimana membentuk kurvahypocycloidkedalam 3 dimensi dengan program MATLAB?

(16)

Tujuan

1. Membentuk kurvahypocycloid ke dalam 3 dimensi dengan program MATLAB. 2. Menghitung luas permukaan 3 dimensihypocycloiddengan program MATLAB

Batasan Masalah

1. Pembahasan pada bentuk kurva hypocycloid yang sudah umum dikenal seperti deltoid,

astroid, dan stars.

2. Pembahasan luas permukaan untuk permukaan yang dianggap sederhana yaitu 3 dimensihypocycloiddari kurvadeltoid.

Manfaat Penelitian

(17)

BAB II ISI

Makalah I.

Judul :Perluasan Kurva Parametrik Hypocycloid 2 Dimensi menjadi 3 Dimensi dengan Sistem Koordinat Bola

Dipresentasikan :Seminar Nasional MatematikaVIII tahun 2014 yang diselenggarakan oleh Jururan Matematika FMIPA Universitas Negeri Semarang pada tanggal 8 November 2014.

Makalah II.

Judul : Komputasi Luas Permukaan pada Hypocycloid3 Dimensi

(18)

(19)

(20)

A. Tinjauan Pustaka

Visualisasi 2 dimensi dalam model dekoratif

Beberapa visualisasi kurva parametrik klasik, seperti hypocycloid telah dipelajari dan digunakan di dalam menyusun motif dekoratif. Persamaan parametrik yang berbentuk

) (t x

x dan y y(t) mempunyai pasangan titik (x,y) sehingga membentuk motif-motif dekoratif.

Persamaan hypocycloid merupakan salah satu dari persamaan parametrik. Persamaan

hypocycloid telah dipelajari sebagai domain dari beberapa pemetaan seperti pemetaan

kompleks dan pemetaan Voronoi (Parhusip,2014). Sebagai contoh pemetaan fungsi kompleks yang digunakan adalahfungsi kompleks � � =1

�dan � � = cos(�). Hasil visualisasi dibuat dengan menggunakan program MATLAB (Suryaningsih,dkk,2013). Hasil yang diperoleh ditunjukkan sebagai berikut

Gambar 1.Komposisi transformasi � � = cos(�) terhadap � � = 1_� yang kemudian di gabungkan (Suryaningsih,dkk,2013)

Selain itu terdapat juga pemetaan kurva parametrik hypocycloid oleh fungsi kompleks

 

z

 

z

f cos ,

 

z z

f 1, f

 

z sin

 

z dan dipetakan dengan pemetaan voronoi (Parhusip,2014). Hasil yang diperoleh ditunjukan sebagai berikut

Gambar 2.Hasilpemetaanpersamaan hypocycloid dalam f(z)cos(z)dan dipetakan dengan pemetaan voronoi (Parhusip,2014)

Visualisasi 3 dimensi

(21)

geometri. Geometri yang merupakan salah satu bidang dalam matematika dipandang sebagai sesuatu yang sangat menarik dan diekspresikan dalam sebuah gambar dengan program komputer untuk matematika. Program-program matematika yang digunakan dalam memvisualisasikan beberapa diantaranya adalah 3D_XplorMath , Cinderella, dan Surfer. 3D_XplorMath merupakan program yang paling luas di dalam memvisualisasikan objek matematika (Greuel,2008). Beberapa objek oleh tim IMAGINARY ditunjukkan

Gambar 3. Hasil visualisasi Algebraic sculpturesyang diornamenkan oleh tim IMAGINARY (Greuel,2008)

B. Metode Penelitian

Mengenal bentuk dan persamaan hypocycloid.

Hypocycloid terbentuk oleh sebuah titik P pada keliling sebuah lingkaran kecil dengan

radius b yang menggelinding di dalam lingkaran yang lebih besar dengan radius a (a>b)

(Hsu,et.al,2008). Bermacam ukuran dari lingkaran menghasilkan hypocycloid yang berbeda. Secara umum persamaan parametrik dapat dituliskan sebagai berikut





cos cos ;





sin sin _;

  

 

       

     

 

       



    

b b a b

b a y b

b a b

b a

x (1)

Persamaan (1) tersebut pada dasarnya merupakan persamaan umum dari epicycloid

dan juga hypocycloid. Parameter b menjadi parameter yang menentukan bentuk yang diperoleh. Ketika b bernilai positif akan menghasilkan epicycloid dan ketika b bernilai negatif akan menghasilkan hypocycloid. Hypocycloid mempunyai beberapa bentuk yang berbeda-beda tergantung dari parameter yang diberikan. Dengan ditetapkan a=1 sebagai radius lingkaran besar dan b sebagai radius lingkaran kecil dengan

q p

b bentuk hypocycloid

akan dijumpai ketika p <q . Sedangkan ketika p>q akan terbentuk kurva epicycloid sekalipun b bernilai negatif. Secara umum persamaan hypocycloid dapat dituliskan sebagai berikut





cos cos ;





sin sin _;

  

 

       

     

 

       



    

b b a b

b a y b

b a b

b a

x (2)

Sistem Koordinat bola

(22)

Gambar 4. Titik P di dalam sistem koordinat bola (Purcell,1987)

Sebuah titik P mempunyai koordinat bola



,,



jikaadalah jarak |OP| dari titik asal ke P, adalah kutub yang berhubungan dengan proyeksi P’ dari P ke bidang xy, dan  adalah sudut antara z positif dan ruas garis OP.

Hasil yang diperoleh dari perluasan kurva parametrik hypocycloidoleh sistem koordinat bola memberikan persamaan dengan dua parameter yaitu dan . Hasil persamaan yang diperoleh diturunkan terhadap parameter-parameter tersebut .

Turunan Persamaan Parametrik

Diasumsikan persamaan parametrikx f

 

u dan yg

 

u maka turunan pertama

persamaan parametrik adalah

dx dy

(Ayres,2009) . Turunan persamaan parametrik dirumuskan

            

du dx du

dy dx dy

(3)

Contoh 1:

Persamaan parametrik xacos4dan yasin4



; tentukan

dx dy

Penyeleseian

   4acos3 sin

d dy

 

   4asin3 cos

d dx



 

2 2

sin cos  

dx dy

C. Hasil dan Pembahasan

Persamaan (1) mempunyai bentuk yang bermacam-macam dipengaruhi oleh nilai parameter a dan b. Dengan parameter a=1 sebagai radius lingkaran besar maka bentuk-bentuk hypocycloid hanya tergantung parameter b. Dengan

q p

(23)

Tabel 1. Program Matlab untuk mengetahui pola bentuk persamaan parametrik clear

close all

n=100; %banyaknya titik p=1;

for q=1:9; %Pengulangan terhadap nilai q

a=1;b=-(p/q); % menegatifkan b untuk menyelidiki hypocycloid syms theta

x=(a+b).*cos(theta)+ b.*cos((a+b)./b.*theta); y=(a+b).*sin(theta)+ b.*sin((a+b)./b.*theta); subplot(3, 3, q) ; ezplot(x, y, [0 2*p*pi]); end

Gambar 5. Bentuk kurva persamaan parametrik untuk

p=1 dan q=1,2,3,4 (kolom 1-2) ,q=5,6,7,8 (kolom 3-4)

Gambar 9. Bentuk kurva persamaan parametrik dengan

Gambar 10. Bentuk kurva persamaan parametrik dengan

Persamaan (1) denganp6danq8didapatkan beberapa hal mengenai hypocycloid

dan juga epycicloid. Berikut diantaranya adalah (Rovenskii,2000)

a. Apabila parameter b bernilai positif maka bentuk kurva epycicloid

b. Apabila parameter b bernilai negatif maka bentuk kurva hypocycloid

c. Jika nilai 0

q p

maka kurva berbentuk epicycloid , sebaliknya jika 0

q p

kurva berbentuk hypocycloid

-2-1.8-1.6-1.4-1.2-1-0.8-0.6-0.4-0.20 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-1-0.8-0.6-0.4-0.200.20.40.60.81 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-1 -0.5 0 0.5 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-0.8-0.6-0.4-0.200.20.40.60.8 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8

-1-0.8-0.6-0.4-0.200.20.40.60.81 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-3-2.5-2-1.5-1-0.500.511.5 -3 -2 -1 0 1 2 3

-2-1.8-1.6-1.4-1.2-1-0.8-0.6-0.4-0.20 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-0.5 0 0.5 1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-1-0.8-0.6-0.4-0.200.20.40.60.81 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-1 -0.5 0 0.5 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-1-0.8-0.6-0.4-0.200.20.40.60.81 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-0.8-0.6-0.4-0.200.20.40.60.8 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8

-5-4-3-2-1012345 -5 -4 -3 -2 -1 0 1 2 3 4 5

-2-1.5-1-0.500.511.52 -1.5 -1 -0.5 0 0.5 1 1.5

-2-1.8-1.6-1.4-1.2-1-0.8-0.6-0.4-0.20 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-0.8-0.6-0.4-0.200.20.40.60.8 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8

-1-0.8-0.6-0.4-0.200.20.40.60.81 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-8 -6 -4 -2 0 2 4 6 8 -8 -6 -4 -2 0 2 4 6 8

-3-2.5-2-1.5-1-0.500.511.5 -3 -2 -1 0 1 2 3

-2 -1.5 -1 -0.5 0 0.5 1 1.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2

-2-1.8-1.6-1.4-1.2-1-0.8-0.6-0.4-0.20 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-1-0.8-0.6-0.4-0.200.20.40.60.81 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-0.5 0 0.5 1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-1-0.8-0.6-0.4-0.200.20.40.60.81 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-10-8-6-4-20246810 -10 -8 -6 -4 -2 0 2 4 6 8 10

-4 -3-2 -1 01 23 4 -4 -3 -2 -1 0 1 2 3 4

-2.5-2-1.5-1-0.500.511.522.5 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5

-1.5 -1 -0.5 0 0.5 1 1.5 -1.5 -1 -0.5 0 0.5 1 1.5

-2-1.8-1.6-1.4-1.2-1-0.8-0.6-0.4-0.20 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-1-0.8-0.6-0.4-0.200.20.40.60.81 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-15 -10 -5 0 5 10 15 -15 -10 -5 0 5 10 15

-5-4-3-2-1012345 -5 -4 -3 -2 -1 0 1 2 3 4 5

-3-2.5-2-1.5-1-0.500.511.5 -3 -2 -1 0 1 2 3

-2-1.5-1-0.500.511.5 2 -1.5 -1 -0.5 0 0.5 1 1.5

-1.5 -1 -0.5 0 0.5 1 1.5 -1.5 -1 -0.5 0 0.5 1 1.5

-2-1.8-1.6-1.4-1.2-1-0.8-0.6-0.4-0.20 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-1-0.8-0.6-0.4-0.200.20.40.60.81 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

(24)

d. Nilai penyebut q pada parameter b menjadi jumlah ujung pada kurva

hypocycloid. Namun jika nilai

q p

dapat disederhanakan ,maka nilai q yang

paling sederhana tersebut yang akan menjadi jumlah ujung kurva hypocycloid.

Beberapa bentuk hypocycloid sudah diberikan nama seperti deltoid dan juga astroid. Berikut adalah kurva yang akan diperluas ke dalam 3 dimensi dengan sistem koordinat bola

Gambar 11. Bentukhypocycloid yang akandiperluaske 3 dimensi dengan sistem koordinat bola

Persamaan (1) akan dibentuk ke dalam persamaan 3 dimensi dengan mengikuti sistem koordinat bola. Permukaan bola dianggap sebagai perluasan dari titik-titik yang setiap titiknya mempunyai jari-jaridan juga sudutdari pusat bola. Demikian pula setiap titik di permukaan hasil perluasan kurva hypocycloid juga mempunyai jari-jari dan juga sudut.Persamaan hypocycloid menjadi





cos cos ; sin





sin sin ;

sin _                                                  b b a b b a y b b a b b a

x (4)

dengan   sin ; 2

2 _y r

x

r   maka dikonstruksi

 cos 

z (5)

Terdapat dua parameter berbeda pada persamaan (4) dan (5) yaitu dan. Dari hasil turunan persamaan tersebut akan diperoleh persamaan baru yang kemudian dikombinasikan sebagai bentuk perluasan yang baru.

Persamaan (4) diturunkan terhadap 

                                                    b b a b b a d dy b b a b b a d dx sin sin ) ( cos cos cos ) ( cos

Persamaan (4) diturunkan terhadap 

; cos ) ( cos ) ( sin _                           b b a b a b a d dy ; sin ) ( sin ) ( sin _                            b b a b a b a d dx

Persamaan (5) diturunkan terhadap  

   sin

d dz

-1 -0.5 0 0.5 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-0.8-0.6-0.4-0.200.20.40.60.8 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8

-1-0.8-0.6-0.4-0.200.20.40.60.81 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

(25)

Bentuk 1 (Deltoid)

Bentuk deltoid diperoleh dari persamaan (1) dengan parameter a=1 dan b mempunyai bentuk sederhana bernilai −1

3dan − 2

3. Bentukumum deltoid ini kemudian diperluas dengan sistem koordinat bola . Hasil turunan dari masing-masing parameternya dikombinasikan sehingga menghasilkan persamaan baru dan divisualisasikan. Perlakuan ini juga diterapkan pada bentuk astroid, star, dan juga bentuk 4. Hasil perluasan ditunjukkan oleh gambar 12.

Gambar 12. Deltoid dan perluasan 3 dimensi dengan sistem koordinat bola dilanjutkan visualisasi dari

kombinasi turunannya _

                 z d dy d dx z d dy d dx d dz d dy d dx , , , , , , , ,        dan                                    d dz d dy d dx d dz d dy d dx d dz d dy d dx z d dy d dx , , , , , , , , , , ,

Bentuk 2 (Astroid)

Bentuk Astroid diperoleh dari persamaan (1) dengan parameter a=1 dan b mempunyai bentuk sederhana bernilai −1

4dan − 3

4. Hasil perluasan ditunjukan oleh gambar 13.

(26)

Gambar 13. Astroid dan perluasan 3 dimensi dengan sistem koordinat bola dilanjutkan visualisasi dari

Bentuk 3 (Star)

Bentuk star diperoleh dari persamaan (1) dengan parameter a=1 dan b mempunyai bentuk sederhana bernilai −2

5dan − 3

5. Hasil perluasan ditunjukkan oleh gambar 14.

Gambar 14. Star dan perluasan 3 dimensi dengan sistem koordinat bola dilanjutkan visualisasi dari kombinasi

turunannya _

                 z d dy d dx z d dy d dx d dz d dy d dx , , , , , , , ,        dan                                    d dz d dy d dx d dz d dy d dx d dz d dy d dx z d dy d dx , , , , , , , , , , , -0.8 -0 .6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 -0.8 -0 .6 -0 .4 -0.2 0 0.2 0.4 0.6 0.8

(27)

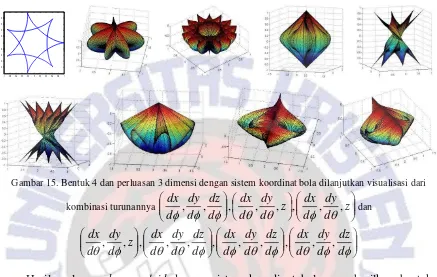
Bentuk 4

Bentuk 4 diperoleh dari persamaan (1) dengan parameter a=1 dan b mempunyai bentuk sederhana bernilai −2

7dan − 5

7. Hasil perluasan ditunjukan oleh gambar 15.

Gambar 15. Bentuk 4 dan perluasan 3 dimensi dengan sistem koordinat bola dilanjutkan visualisasi dari

Hasil perluasan hypocycloid dengan sistem koordinat bola menghasilkan bentuk 3 dimensi yang mempunyai kemiripan dengan bentuk bola. Bentuk yang dihasilkan mempunyai Hanya saja kontur dari hasil perluasan dipaksakan seperti bentuk dasar dari

hypocycloid yang diperluas dan bukan lagi lingkaran yang menjadi bentuk dasar bola. Hasil

turunan persamaan yang kemudian dikombinasikan juga menghasilkan berbagai bentuk 3 dimensi yang bermacam-macam.

D. Simpulan dan Saran

Hypocycloid merupakan persamaan parametrik yang mempunyai berbagai bentuk

tergantung nilai parameternya. Bentuk-bentuk dasar hypocycloid dapat diperluas kedalam bentuk 3 dimensi dengan menggunakan sistem koordinat bola. Persamaan perluasan

hypocycloid 3 dimensi yang diturunkan terhadap parameter-parameternya membentuk

persamaan baru yang dapat dikombinasikan dan membentuk perluasan baru. Setiap gambar yang diperoleh dengan masing-masing bentuk dasarnya didapatkan kemiripan dalam setiap kombinasi yang dibuat. Setiap kombinasi hypocycloid yang diperluas dengan sistem koordinat bola tersebut dipolakan ke dalam bentuk 3 dimensi dan menjadi satu bentuk keluarga.

Hypocycloid merupakan satu dari berbagai persamaan parametrik, sehingga sangat

dimungkinkan persamaan-persamaan yang lain untuk diperluas ke dalam 3 dimensi dengan sistem koordinat bola. Terdapat banyak program komputer yang dapat digunakan sebagai alat bantu visualisasi 3 dimensi seperti 3D-XplorMath, Surfer, dan lain-lain.

(28)

E. Daftar Pustaka

[1] Ayres.F., Mendelson.E. 2009. Schaum’s Outlines Calculus, FifthEdition. McGraw-Hill, Singapore.

[2] Hsu MH, Yan HS, Liu JY, Hsieh LC (2008). Epicycloid (Hypocycloid) Mechanisms Design Proceedings of the International Multi Conference of Engineers and Computer Scientists, IMECS, Hong Kong,(2).

[3] Greuel G.M, Matt A.D ,” IMAGINARY-Through the eyes of mathematics” Mathematisches Forschungsinstitut Oberwolfach (2008),ISBN 978-3-00-026939-4, Oberwolfach-German.

[4] Parhusip H.A, 2014. Arts revealed in calculus and its extension. International Journal of Statistics and Mathematics, 1(3): 002-009, Premier-Publisher,(online).

:https://www.academia.edu/8236790/Arts_revealed_in_calculus_and_its_extension or https://www.facebook.com/premierpublisher/posts/788548327863008 or

http://premierpublishers.org/ijsm/articles

[4] Purcell,Edwin J. Dale Varberg, Kalkulus dan Geometri Analitis jilid 2, edisi kelima,Terj. I Nyoman Susila, Jakarta: Erlangga.

[5] Rovenskii, Vladimir Y,2000. Geometry of Curves and Surfaces with Maple. New York: Birkhauser Bolton

[6] Suryaningsih, V, Parhusip,H.A, Mahatma, T, 2013. Kurva Parametrik dan Transformasinya untuk Pembentukan Motif Dekoratif, Prosiding, Seminar Nasional Matematika dan Pendidikan Matematika UNY,9 Nov, ISBN:978-979-16353-9-4,hal. MT – 249-258.

[7] O’Connor, J.J, Robertson,E.F, 2006. Famous curves index.

(29)

Hasil review 28 Januari 2015:

1. Perubahan pada pendahuluan paragraph pertama kalimat terakhir: Rujukan Web 1 menjadi (O’Connor,2006)

2. Perubahan pada tinjauan pustaka paragraf pertama kalimat kedua : xx(t)dan )

(t y

y menjadi xx()dan xx()

3. Perubahan pada metode penelitian: mengganti judul Mengenal bentuk dan persamaan hypocycloidmenjadiKeterkaitan kurva hypocycloid dan epicycloid di dalam satu persamaan parametrik.

4. Penambahan rujukan(Rovenskii,2000) pada metode penelitian paragraf pertama kalimat kedua.

5. Contoh 1 pada turunan persamaan parametrik :    

   

 

 

  

 b

b a b a b

a d

dx

xˆ ( )sin ( )sin

   

   

 



  

 b

b a b

a b

a d dy

yˆ ( )cos ( )cos

6. Penulisan daftar pustaka [7] menjadi

O’Connor, J.J, Robertson,E.F, 2006. Famous curves index. (http://www-history.mcs.st-andrews.ac.uk/Curves/Curves.html Di akses pada 29 September 2014) 7. Perubahan pada penjelasan gambar 5-10 : Bentuk Hypocycloid diubah menjadi

(30)

(31)

KOMPUTASI LUAS PERMUKAAN PADA HYPOCYCLOID 3 DIMENSI

Purwoto1), Hanna Arini Parhusip2), Tundjung Mahatma3) 1)3)

Program Studi Matematika,Fakultas Sains dan Matematika, Universitas Kristen SatyaWacana

Jl. Diponegoro 52-60 Salatiga 50711

1)

662011010@student.uksw.edu, 2)hannaariniparhusip@yahoo.co.id,

3)

t.mahatma@staff.uksw.edu

A. Pendahuluan

Persamaan parametrik hypocycloid dalam 2 dimensi telah dikembangkan sebagai permukaan 3 dimensi (Purwoto,dkk,2014) yaitu





cos cos ; sin





sin sin ;

sin _

  

 

   

 

       

 

   

 

   

 

       



      

b b a b

b a y

b b a b

b a

x (a)

 cos 

z (b)

dengan ; .

sin

2 2

y x r

r _ _





 Perluasan ini didasarkan oleh sistem koordinat bola.

Koordinat bola merupakan salah satu dari banyak cara pemerincian posisi titik di ruang dimensi-tiga (Purcell,1987). Permukaan bola dianggap sebagai perluasan dari titik-titik yang setiap titik-titiknya mempunyai jari-jari  dan sudut  dari pusat bola. Demikian pula setiap titik di permukaan hasil perluasan kurva hypocycloid juga mempunyai jari-jari dan sudut.

Hasil persamaan hypocycloid yang diperluas menjadi persamaan baru yang mempunyai kemiripan dengan persamaan bola dengan jari-jari yang lebih bervariasi. Selain itu, persamaan-persamaan yang diperoleh dapat diturunkan dan diperoleh persamaan baru. Persamaan-persamaan itu dikombinasikan sehingga didapatkan berbagai macam bentuk perluasan permukaan 3 dimensi. Ilustrasi untuk berbagai permukaan ditunjukkan pada penelitian pertama (Purwoto,dkk,2014).

(32)

Setiap permukaan yang diperoleh dicari luasnya yang dinyatakan dalam bentuk vektor. Pembahasan dibatasi untuk permukaan yang dianggap sederhana yaitu pada perluasan kurva hypocycloid dalam koordinat bola.

B. Metode Penelitian

Persamaan Hypocycloid dan Epicycloid

Secara umum terdapat sebuah persamaan parametrik yang dituliskan sebagai berikut





cos cos ;





sin sin _;

                                   b b a b b a y b b a b b a

x (1)

Persamaan (1) merupakan sebuah persamaan parametrik yang mendasari kurva

hypocycloid dan epicycloid. Perlakuan berbeda pada nilai-nilai parameter a dan b yang

membuat kedua bentuk kurva berbeda.

Hypocycloid terbentuk oleh sebuah titik P pada keliling sebuah lingkaran kecil

dengan radius b yang menggelinding di dalam lingkaran yang lebih besar dengan radius a

(a>b) (Hsu,et al.2008). Bermacam ukuran dari lingkaran menghasilkan hypocycloid yang

berbeda.

Secara umum persamaan hypocycloid sendiri dapat dituliskan sebagai berikut





cos cos ;





sin sin _;

                                   b b a b b a y b b a b b a

x (2)

Sedikit berbeda dengan hypocycloid, epicycloid terbentuk oleh sebuah titik P pada keliling lingkaran kecil dengan radius b yang menggelinding di luar lingkaran dengan radius a (Hsu,et al.2008). Secara umum persamaan epicycloid dapat dituliskan sebagai berikut





cos cos ;





sin sin _;

                                   b b a b b a y b b a b b a

x (3)

Turunan Persamaan parametrik

Persamaan (1) diturunkan terhadap  sehingga membentuk sebuah persamaan parametrik baru. Hasil dari turunannya adalah

                b b a b a b a d dx

(33)

               b b a b a b a d dy

yˆ ( )cos ( )cos (5)

Kurva pada persamaan (2) dan (3) dianggap sebagai persamaan x()dan y() yang baru. Dengan memperhatikan koordinat bola persamaan (2) dan (3) dikonstruksi menjadi

                     b b a b a b a

xˆ sin ( )sin ( )sin (6)

                    b b a b a b a

yˆ sin ( )cos ( )cos (7)

denganr x2  y2;dan

 

sin

r

 maka

 cos ˆ

z (8)

Persamaan (6), (7), dan (8) kembali diturunkan , sehingga terjadi dua kali penurunan pada persamaan hypocycloid. Hasil persamaan dikombinasikan untuk mendapat permukaan-permukaan yang baru pada satu persamaan parametrik sebagai berikut:

                      b b a b a b a d x d sin ) ( sin ) ( cos ˆ                      b b a b a b a d y d cos ) ( cos ) ( cos ˆ                       b b a b b a b a d x d cos ) ( cos ) ( sin ˆ 2                       b b a b b a b a d y d sin ) ( sin ) ( sin ˆ 2    sin ˆ __ d z d

Notasi Vektor permukaan

Sebuah permukaan parametrik dengan dua parameter (Hopkins, 2013) dinyatakan )

, ( 

x

x , y y(,), z z(,) (9)

(34)

Sekarang  T(,j)dan vT(i,) adalah kurva pada permukaan, oleh karena itu

k z j y i x T T

 

 _

  

      

 T T xi y j z k

 

 _

          

merupakantangent vectors dari permukaan.

Secara analitik luas dari permukaan parametrik adalah



  

 ( )~ _ _( , )  

)

(S Area S_ij T T _i _j

Area (10)

dengan

) ( _ij*

ij T R

S 

sebagai sebuah persegi kecil



        



 i i i i

ij

R* ( , ); , (11)

dan dalam limit dengan ,0didapatkan rumus sebagai berikut 

  



 T d d

T S

Area( )



 ( _i, _j)

(12)

C. Hasil dan Pembahasan Kasus 1.

Persamaan parametrik hypocycloid (2) diturunkan terhadap parameter  yang kemudian di desain menjadi persamaan baru . Persamaan baru yang menjadi persamaan dengan dua parameter (,) kembali diturunkan terhadap parameter-parameter tersebut dan dikombinasikan, sehingga mendapatkan bentuk-bentuk perluasan yang lain. Bentuk yang diperoleh adalah sebagai berikut

Bentuk turunan dari deltoid

Bentuk turunan deltoid diperoleh dengan parameter a=1 dan b mempunyai bentuk

sederhana bernilai 1 3dan

2

(35)

[image:35.612.107.535.74.377.2]

kombinasi turunannya _                  z d y d d x d z d y d d x d d z d d y d d x d _ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ        dan                                    d z d d y d d x d d z d d y d d x d d z d d y d d x d z d y d d x d ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ

.

Gambar 1. Hasil perluasan 3 dimensi dari turunan kurva hypocycloid (deltoid)

Hasil perluasan kurva deltoid ditunjukan oleh gambar 2 berturut turut adalah kurva deltoid dan perluasan 3 dimensi dengan sistem koordinat bola dilanjutkan visualisasi dari

                 z d dy d dx z d dy d dx d dz d dy d dx , , , , , , , ,        dan                                    d dz d dy d dx d dz d dy d dx d dz d dy d dx z d dy d dx , , , , , , , , , ,

, (Purwoto dkk, 2014).

Gambar 2. Hasil perluasan 3 dimensi dari kurva hypocycloid (deltoid).

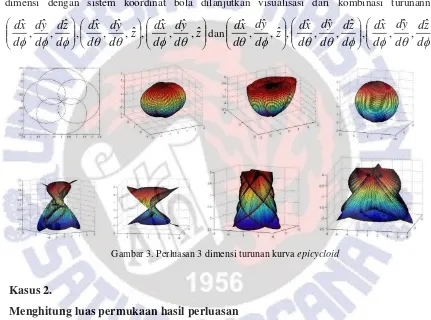
[image:35.612.73.543.212.664.2]

(36)

Kurva turunan Epicycloid

Hasil turunan kurva epicycloids persamaan (3) dibentuk menjadi persamaan baru dalam 3 dimensi dengan 2 parameter

 

, . Persamaan yang diperoleh diturunkan dengan parameter-parameternya. Hasil turunan tersebut menjadi turunan kedua dari kurva epicycloids yang kemudin dikombinasikan membentuk permukaan baru. Dengan nilai

a=1 dan b mempunyai bentuk sederhana bernilai 1

4 diperoleh bentuk-bentuk yang ditunjukan oleh gambar 3. Berturut-turut adalah bentuk turunan epicycloid dan perluasan 3 dimensi dengan sistem koordinat bola dilanjutkan visualisasi dari kombinasi turunannya

                  z d y d d x d z d y d d x d d z d d y d d x d _ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ      

 dan _

[image:36.612.99.530.230.550.2]

                        d z d d y d d x d d z d d y d d x d z d y d d x d ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ , ˆ

Gambar 3. Perluasan 3 dimensi turunan kurva epicycloid

Kasus 2.

Menghitung luas permukaan hasil perluasan

Luas yang akan dihitung adalah dari kurva persamaan parametrik hypocycloid

dengan berbagai parameternya. Untuk menyelesaikannya digunakan alat bantu program MATLAB.

Persamaan parametrik hypocycloid adalah





cos cos ;





sin sin _;

                                   b b a b b a y b b a b b a x

(37)

 sin

x

x _,y  ysin

 cos  z dengan   sin r

 dan r x2 y2

didalam notasi vektor sebagai

k z j y i x

T(,)  



T danT_merupakan tangent vector permukaan dengan

k z j y i x T T      _              xcos

x _

 

, 

 ycos

y _   ,   2 sin r

z _ 

  dan k z j y i x T T      _            dengan     sin

  

x x

, 

   sin

  

y y

,              r z sin cos

denganr  x2  y2









                                    2 2 2 1 2 2 2 1 2 2 . 2 . sin cos sin

cos x y x y x y

z





                   y y x x y x z 2 2 . 2 . sin

cos 2 2 12

(38)

                                   y z z y T

T . . i - _

                              x z z x .

. j + _

                        x y y x . . k

luas permukaan didapat dari jumlah norm cross product T_T_ atau



  

 ( )~  ( , )  

)

(S Area S_ij T T _i _j

Area

yang kemudian penyelesaian dilanjutkan dengan program MATLAB (Lampiran 2).

Bentuk yang dibahas adalah permukaan dari kurva deltoid yang diperluas.

Hasil yang didapatkan adalah hasil dari pendekatan , sehingga semakin besar n

[image:38.612.101.526.231.601.2]

(banyaknya titik yang digunakan) pada program akan semakin mendekati luas permukaan yang sebenarnya. Dengan program MATLAB diperoleh luas dari gambar (4) adalah 13.8245 untuk n=100 dan 14.0958 untukn=1000 pada gambar (5).

Gambar 4. Bentuk permukaandeltoid dari program MATLAB dengan nilai n=100

Gambar 5. Hasil permukaan deltoid dari program MATLAB dengan nilai n=1000

(39)

Untuk membuktikan hasil luas permukaan yang didapat, dibuat program yang sama untuk luas permukaan bola. Secara umum luas permukaan bola dapat dihitung dengan rumus luas permukaan sehingga menghasilkan rumus4r2(Lampiran 1).

D. Kesimpulan dan Saran

(40)

E. Daftar Pustaka

[1] Hsu MH, Yan HS, Liu JY, Hsieh LC,2008. Epicycloid (Hypocycloid) Mechanisms Design Proceedings of the International Multi Conference of Engineers and Computer Scientists, IMECS, Hong Kong,(2).

[2] Hopkins, Johns, 2013. Parameterized surface.

http://www.math.jhu.edu/~lindblad/211/l17.pdf (Di akses pada 16 Desember 2014)

[3] Purcell,Edwin J. Dale Varberg, Kalkulus dan Geometri Analitis jilid 2, edisi kelima,Terj. I Nyoman Susila, Jakarta: Erlangga.

[4] Purwoto, Parhusip,H.A, Mahatma, T, 2014. Perluasan Kurva Parametrik Hypocycloid 2

Dimensi Menjadi 3 Dimensi Dengan Sistem Koordinat Bola, telah diseminarkan pada

(41)

Lampiran 1 :Program perhitungan Luas Permukaan Hypocycloid (Deltoid)

Program Menghitung Luas Permukaan dari perluasan 3D kurva Hypocycloid clear

close all

n=100; %banyaknya titik phi=linspace(0,pi,n); a=1;b=1/3;

theta=linspace(0,2*pi,n); dtheta=2*pi/n;

dphi=pi/n;

%persamaan parametrik Hypocycloid xhipo=(a-b)*cos(theta)+ b*cos((a-b)/b*theta);

yhipo=(a-b)*sin(theta)- b*sin((a-b)/b*theta);

[Phi,Theta]=meshgrid(phi,theta);

X=sin(Phi).*((a-b).*cos(Theta)+b.*cos((a-b)/b.*Theta));

Y=sin(Phi).*((a-b).*sin(Theta)-b.*sin((a-b)/b.*Theta));

r=sqrt(X.^2 + Y.^2); Z=r.*cos(Phi)./sin(Phi);

[image:41.612.75.537.95.662.2]

%bentuk gambar yang akan dihitung luasannya

figure surf(X,Y,Z)

%==================================== =

%mencari Tphi = dXdphi i +dYdphi j +dZdphi k

dXdphi=cos(Phi).*((a-b).*cos(Theta)+b.*cos((a-b)/b.*Theta)); dYdphi=cos(Phi).*((a-b).*sin(Theta)-b.*sin((a-b)/b.*Theta));

dZdphi=-r./(sin(Phi)).^2; Tphi=[dXdphi dYdphi dZdphi]; %==============================

%mencari Ttheta=dXdtheta i +dYdtheta j +dZdtheta k

dXdtheta=sin(Phi).*(-(a-b).*sin(Theta)-(a-b).*sin((a-b)/b.*Theta));

dYdtheta=sin(Phi).*((a-b).*cos(Theta)-(a-b).*cos((a-b)/b.*Theta));

dZdtheta=cos(Phi).*(X.*dXdtheta +Y.*dYdtheta)./(r.*sin(Phi));

%================================== %norm |Tphi x Ttheta|

komponeni=(dYdphi.*dZdtheta)-(dZdphi.*dYdtheta);

komponenj=(dXdphi.*dZdtheta)-(dZdphi.*dXdtheta);

komponenk=(dXdphi.*dYdtheta)-(dYdphi.*dXdtheta);

Ttheta=[dXdtheta dYdtheta dZdtheta]

for i=1:n for j=2:n

vT=[komponeni(i,j) komponenj(i,j) komponenk(i,j)]

HasilnormTcros=norm(vT)

dR(j)=HasilnormTcros*dtheta*dphi; end

jumdR(i)=sum(dR); end

(42)

Lampiran 2

Contoh: mencari luas permukaan pada bola dengan jari-jari r

Persamaan parametrik bola adalah  cos sin r x  sin sin r y  cos r x Dibentuk k r j r i r

T sincos  sinsin  cos

k z j y i x T T      _             

 rcos cos

T  i +rcossinj - rsink

k z j y i x T T      _           





 rsin sin

T  i +rsincosj

0 cos sin sin sin sin sin cos cos cos            r r r r r k j i T T       

 T r2sin2 cos

T   i + r2sin2



sin



j + r2cos



sin



k













 T r2sin sin2 cos2 sin2 sin2 cos2 r2sin

T     

Area (S)=

 





 





   _         2 0 0 2 0 2 0 2 2 0 2 2 4 2 cos

sin d d r d r d r

r

Luas bola dengan r = 7 adalah .49 616 7

22 . 4

4r2  

(43)

Tabel 1. Program luas permukaan bola

clear close all n=100;

phi=linspace(0,pi,n); theta=linspace(0,2*pi,n); dtheta=2*pi/n;

dphi=pi/n; r=7;

x=r*cos(theta) y=r*sin(theta) plot(x,y)

[Phi,Theta]=meshgrid(phi,theta); X=r.*sin(Phi).*cos(Theta);

[image:43.612.68.580.89.672.2]

Y=r.*sin(Phi).*sin(Theta); Z=r.*cos(Phi);

figure surf(X,Y,Z)

%============================= %mencari Tphi=dXdphi i +dYdphi j +dZdphi k

dXdphi=r.*cos(Phi).*cos(Theta); dYdphi=r.*cos(Phi).*sin(Theta); dZdphi=-r.*(sin(Phi));

Tphi=[dXdphi dYdphi dZdphi]; %============================== %mencari Ttheta=dXdtheta i +dYdtheta j +dZdtheta k

dXdtheta=-r.*sin(Phi).*sin(Theta); dYdtheta=r.*sin(Phi).*cos(Theta); %dZdtheta=cos(Phi).*(X.*dxh +Y.*dyh)./r;

%dZdtheta=cos(Phi).*(X.*dXdtheta +Y.*dYdtheta)./r;

dZdtheta=zeros(n,n);

%============================== %norm |Tphi x Ttheta|

komponeni=(dYdphi.*dZdtheta)-(dZdphi.*dYdtheta);

komponenj=(dXdphi.*dZdtheta)-(dZdphi.*dXdtheta);

komponenk=(dXdphi.*dYdtheta)-(dYdphi.*dXdtheta);

Ttheta=[dXdtheta dYdtheta dZdtheta]

for i=1:n for j=2:n

vT=[komponeni(i,j) komponenj(i,j) komponenk(i,j)]

HasilnormTcros=norm(vT)

dR(j)=HasilnormTcros*dtheta*dphi; end

jumdR(i)=sum(dR); end

(44)

(45)

BAB III PENUTUP

Kesimpulan

Berdasarkan kedua makalah dapat disimpulkan :

1. Dari satu persamaan parametrikhypocycloiddapat diperoleh berbagai macam bentuk permukaan 3 dimensi yang divisualisasikan dengan program MATLAB. Hasil permukaan yang didapat merupakan bentuk permukaan baru yang mempunyai persamaan di dalamnya.

2. Hasil permukaan 3 dimensi hypocycloid dapat dihitung luas permukaannya yang dipaparkan di dalam program (lampiran 7) pada MATLAB. Program perhitungan luas dapat diterapkan untuk menghitung permukaan dengan bentuk-bentuk dasar hypocycloid

yang lain dengan mengganti nilai-nilai parameternya.

Saran

Berdasarkan kedua makalah yang telah dikaji, saran yang dapat diberikan adalah :

1. Persamaan-persamaan parametrik yang lain dimungkinkan untukdapat diperluas ke dalam bentuk 3 dimensi . Terdapat banyak pula program dan aplikasi yang membantu dalam memvisualisasikan bentuk-bentuk tersebut seperti 3D-XplorMath, Surfer, dan lain-lain.. 2. Hasil perhitungan luas permukaan masih terbatas pada bentuk yang sederhana. Masih

perlu dikembangkan ketika hasil perluasan mempunyai bentuk dengan tingkat kerumitan tertentu.

(46)

Lampiran 1

Program MATLAB kurva Deltoid

dan Perluasannya:

clear close all

n=100; %banyaknya titik

phi=linspace(0,pi,n); p=1;q=3;

a=1;b=-(p/q);

theta=linspace(0,2*pi,n);

%Fungsi parametric

[image:46.612.71.537.96.687.2]

x=(a+b).*cos(theta)+ b.*cos((a+b)./b.*theta); y=(a+b).*sin(theta)+ b.*sin((a+b)./b.*theta); figure

plot(x,y)

% Desain persamaan 3 dimensi

X=sin(Phi).*((a+b).*cos(Theta)+b.*cos( (a+b)/b.*Theta));

Y=sin(Phi).*((a+b).*sin(Theta)+b.*sin((a +b)/b.*Theta));

r=sqrt(X.^2 + Y.^2); rho=r./sin(Phi); Z=rho.*cos(Phi); figure

surf(X,Y,Z) %hasil perluasan

%Turunan pers 3dimensi dalam Phi

dXdPhi=cos(Phi).*((a+b).*cos(Theta)+b .*cos((a+b)/b.*Theta));

dYdPhi=cos(Phi).*((a+b).*sin(Theta)+b. *sin((a+b)/b.*Theta));

dZdPhi=-rho.*sin(Phi); figure

surf(dXdPhi,dYdPhi,dZdPhi)

% Turunan pers 3 dimensi dalam

Theta

dXdt=sin(Phi).*((a+b).*-(sin(Theta))-(a+b)*sin((a+b)/b.*Theta));

dYdt=sin(Phi).*((a+b).*cos(Theta)+(a+b )*cos((a+b)/b.*Theta));

r=sqrt(X.^2 + Y.^2); rho=r./sin(Phi); Z=rho.*cos(Phi);

%Hasil Figure kombinasi dari masing

masing turunan

figure

surf(dXdt,dYdt,Z) figure

surf(dXdPhi,dYdt,Z) figure

surf(dXdt,dYdPhi,Z) figure

surf(dXdt,dYdt,dZdPhi) figure

surf(dXdPhi,dYdt,dZdPhi) figure

(47)

Lampiran 2

Program MATLAB kurva

Astroid dan Perluasannya:

clear close all

a=1;b=-(p/q);

theta=linspace(0,2*pi,n);

[image:47.612.68.541.94.700.2]

plot(x,y)

Theta

masing turunan

figure

(48)

Lampiran 3

Program MATLAB kurva Star

dan Perluasannya:

clear close all

a=1;b=-(p/q);

theta=linspace(0,2*pi*p,n);

[image:48.612.68.541.96.700.2]

plot(x,y)

Theta

masing turunan

figure

(49)

Lampiran 4

Program MATLAB kurva Bentuk

4 dan Perluasannya:

clear close all

a=1;b=-(p/q);

plot(x,y)

Theta

masing turunan

figure

(50)

Lampiran 5

Program Perluasan turunan kedua epicycloid

clear close all

n=100; % banyaknya titik phi=linspace(0,pi,n); p=1;q=4; %

a=1;b=(p/q);

theta=linspace(0,2*pi*p,n); % Fungsi Parametrik Epicycloid x=(a+b).*cos(theta)-

b.*cos((a+b)./b.*theta); y=(a+b).*sin(theta)- b.*sin((a+b)./b.*theta);

%Xbaru dan Ybaru adalah turunan dari kurva mula2

Xbaru=-(a+b).*sin(theta)+ b*(a+b)/b*sin((a+b)/b*theta); Ybaru=(a+b).*cos(theta)- b*(a+b)/b*cos((a+b)/b*theta); %gambar turunan pertama kurva epicycloid figure

plot(Xbaru,Ybaru) %1

%memperluas bidang 3dimensi [Phi,Theta]=meshgrid(phi,theta); %pers parametrik epicycloid x=(a+b).*cos(Theta)-

b.*cos((a+b)./b.*Theta); y=(a+b).*sin(Theta)- b.*sin((a+b)./b.*Theta);

% Turunan mula2 kurva epicycloid XBARU=-(a+b).*sin(Theta)+

b*(a+b)/b*sin((a+b)/b*Theta); YBARU=(a+b).*cos(Theta)- b*(a+b)/b*cos((a+b)/b*Theta);

%Mendesain pers kurva ke dalam 3D dg system koor bola

X=sin(Phi).*(XBARU); Y=sin(Phi).*(YBARU); r=sqrt(X.^2 + Y.^2);

rho=r./sin(Phi); Z=rho.*cos(Phi);

%gambar perluasan 3D figure

surf(X,Y,Z) %2 figure

contour(X,Y,Z)%3

dXdPhi=cos(Phi).*(XBARU); dYdPhi=cos(Phi).*(YBARU); dZdPhi=-rho.*sin(Phi); figure

surf(dXdPhi,dYdPhi,dZdPhi) % 4

%TURUNAN DARI XBARU=TURUNAN KE-2 DARI X MULA-MULA

dxBARU=-(a+b).*cos(Theta)+ b*((a+b)/b)^2*cos((a+b)/b*Theta); dyBARU=-(a+b).*sin(Theta)+

b*((a+b)/b)^2*sin((a+b)/b*Theta); dXdt=sin(Phi).*(dxBARU);

dYdt=sin(Phi).*(dyBARU); r=sqrt(X.^2 + Y.^2); rho=r./sin(Phi); Z=rho.*cos(Phi); figure

surf(dXdt,dYdt,Z) % 5 figure

surf(dXdPhi,dYdt,Z) %6 figure

surf(dXdt,dYdPhi,Z)%7 figure

surf(dXdt,dYdt,dZdPhi) %8 figure

surf(dXdPhi,dYdt,dZdPhi)%9 figure

(51)

Lampiran 6

Program Perluasan turunan kedua hypocycloid

clear close all n=100;

a=1;b=(p/q);

% Fungsi Parametrik Hypocycloid x=(a-b).*cos(theta)+ b.*cos((a-b)./b.*theta);

y=(a-b).*sin(theta)- b.*sin((a-b)./b.*theta);

%Xbaru dan Ybaru adalah turunan dari kurva mula2

Xbaru=-(a-b).*sin(theta)- b*(a-b)/b*sin((a-b)/b*theta); Ybaru=(a-b).*cos(theta)- b*(a-b)/b*cos((a-b)/b*theta);

%gambar turunan pertama kurva epicycloid

figure

plot(Xbaru,Ybaru) %1

%memperluas bidang 3dimensi [Phi,Theta]=meshgrid(phi,theta); x=(a-b).*cos(Theta)+ b.*cos((a-b)./b.*Theta);

y=(a-b).*sin(Theta)- b.*sin((a-b)./b.*Theta);

% Turunan mula2 kurva hypocycloid XBARU=-(a-b).*sin(Theta)- b*(a-b)/b*sin((a-b)/b*Theta);

YBARU=(a-b).*cos(Theta)- b*(a-b)/b*cos((a-b)/b*Theta);

%Mendesain pers kurva ke dalam 3D dg system koor bola

X=sin(Phi).*(XBARU); Y=sin(Phi).*(YBARU); r=sqrt(X.^2 + Y.^2); rho=r./sin(Phi);

Z=rho.*cos(Phi);

%gambar perluasan 3D figure

surf(X,Y,Z) %2 figure

contour(X,Y,Z)

dXdPhi=cos(Phi).*(XBARU); dYdPhi=cos(Phi).*(YBARU); dZdPhi=-rho.*sin(Phi); figure

surf(dXdPhi,dYdPhi,dZdPhi) % figure 4

%TURUNAN DARI XBARU=TURUNAN KE-2 DARI X MULA-MULA

dxBARU=-(a-b).*cos(Theta)- b*((a-b)/b)^2*cos((a-b)/b*Theta); dyBARU=-(a-b).*sin(Theta)+ b*((a+b)/b)^2*sin((a-b)/b*Theta); dXdt=sin(Phi).*(dxBARU);

dYdt=sin(Phi).*(dyBARU); r=sqrt(X.^2 + Y.^2); rho=r./sin(Phi); Z=rho.*cos(Phi); figure

surf(dXdt,dYdt,Z) % 5 figure

surf(dXdPhi,dYdt,Z) %6 figure

surf(dXdt,dYdPhi,Z)%7 figure

surf(dXdt,dYdt,dZdPhi) %8 figure

surf(dXdPhi,dYdt,dZdPhi)%9 figure

(52)

Lampiran 7

Program Menghitung Luas Permukaan dari perluasan 3D kurva Hypocycloid clear

close all

n=100; %banyaknya titik phi=linspace(0,pi,n); a=1;b=1/3;

theta=linspace(0,2*pi,n); dtheta=2*pi/n;

dphi=pi/n;

%persamaan parametrik Hypocycloid xhipo=(a-b)*cos(theta)+ b*cos((a-b)/b*theta);

yhipo=(a-b)*sin(theta)- b*sin((a-b)/b*theta);

X=sin(Phi).*((a-b).*cos(Theta)+b.*cos((a-b)/b.*Theta));

Y=sin(Phi).*((a-b).*sin(Theta)-b.*sin((a-b)/b.*Theta));

r=sqrt(X.^2 + Y.^2); Z=r.*cos(Phi)./sin(Phi);

[image:52.612.73.532.67.695.2]

%bentuk gambar yang akan dihitung luasannya

figure surf(X,Y,Z)

%==================================== =

%mencari Tphi = dXdphi i +dYdphi j +dZdphi k

dXdphi=cos(Phi).*((a-b).*cos(Theta)+b.*cos((a-b)/b.*Theta)); dYdphi=cos(Phi).*((a-b).*sin(Theta)-b.*sin((a-b)/b.*Theta));

dZdphi=-r./(sin(Phi)).^2; Tphi=[dXdphi dYdphi dZdphi]; %==============================

%mencari Ttheta=dXdtheta i +dYdtheta j +dZdtheta k

dXdtheta=sin(Phi).*(-(a-b).*sin(Theta)-(a-b).*sin((a-b)/b.*Theta));

dYdtheta=sin(Phi).*((a-b).*cos(Theta)-(a-b).*cos((a-b)/b.*Theta));

dZdtheta=cos(Phi).*(X.*dXdtheta +Y.*dYdtheta)./(r.*sin(Phi));

%================================== %norm |Tphi x Ttheta|

komponeni=(dYdphi.*dZdtheta)-