PENDUGAAN SELANG KEPERCAYAAN RATA-RATA POPULASI DENGAN KONDISI ADANYA PENCILAN

i

PENDUGAAN SELANG KEPERCAYAAN RATA-RATA

POPULASI DENGAN KONDISI ADANYA PENCILAN

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh :

Petronela Yuni Iswari NIM: 133114001

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

ii

ON THE ESTIMATION OF POPULATION MEAN

CONFIDENCE INTERVAL IN THE PRESENCE OF

OUTLIERS

A Thesis

Presented as a Partial Fulfillment of the Requirements to Obtain the Degree of Sarjana Sains

Mathematics Study Program

Written by : Petronela Yuni Iswari Student Number: 133114001

MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

v

HALAMAN PERSEMBAHAN

Skripsi ini dipersembahkan untuk:

Tuhan Yesus Kristus dan Bunda Maria yang senantiasa menyertai, memberikan berkat-Nya, dan memberi perlindungan sepanjang perjalanan hidup saya.

Kedua orangtua, Bapak Hendricus Bagyo dan Ibu Margaretta Istikomah, S.Pd, serta kakak Heribertus Henta Nooristyanto, S.T yang selalu mendokan, memberi kasih sayang, serta menjadi penyemangat dalam hidup saya.

“Aku tahu, bahwa Engkau sanggup melakukan segala sesuatu, dan tidak ada rencana-Mu yang gagal.” (Ayub 42:2)

“Banyaklah rancangan di hati manusia, tetapi keputusan Tuhanlah yang terlaksana.” (Amsal 19:21)

vii

ABSTRAK

Pencilan adalah nilai ekstrim yang muncul di dalam suatu analisis data. Adanya pencilan dapat mengakibatkan bias kesimpulan atas hasil analisis. Untuk mendeteksi pencilan digunakan metode grafis, Boxplot, Uji Grubbs, dan Uji MAD. Penulisan skripsi ini bertujuan untuk menduga selang kepercayaan rata-rata populasi dengan kondisi adanya pencilan. Untuk menyimpulkan hasil analisis pada data yang memuat pencilan digunakan statistik robust (kekar) yang menghasilkan kesimpulan data tetap akurat meskipun dalam keadaan yang tidak ideal. Statistik robust yang digunakan adalah penduga median (Fraiman, et al) dan penduga 𝑀

(penduga Huber). Dalam skripsi ini digunakan empat metode selang kepercayaan, yaitu metode selang kepercayaan dengan penduga rata-rata, median (Kendall and Stuart), median (Fraiman, et al), dan penduga Huber. Selang kepercayaan robust dengan simulasi data acak diperoleh dari distribusi Normal, Cauchy, dan Chi-Square dengan ukuran 𝑛 = 10, 50, 100, dan 500 untuk setiap distribusi. Hasil simulasi menunjukkan bahwa selang kepercayaan robust bagi parameter lokasi dengan penduga median (Fraiman, et al) dan penduga Huber adalah selang kepercayaan robust yang insensitif terhadap adanya pencilan. Hal ini disebabkan karena hasil dari standard error (galat standar) dan lebar selang kepercayaan yang tetap, meskipun nilai pencilan semakin besar untuk setiap ukuran sampel yang diberikan.

Kata Kunci: Pencilan, Pendeteksian Pencilan, Statistik Robust, Penduga Robust, Selang Kepercayaan Robust.

viii

ABSTRACT

An outlier is an extreme value which is appeared in data analysis. The presence of outliers will affect to the bias conclusion of analytical results. Graphical method, Boxplot, Grubbs Test, and MAD Test can be applied to detect the presence of outliers. The purpose of this thesis is to estimate the population mean confidence interval in the presence of outliers. To summarize the results of the analysis on the data contains the outliers, robust statistics is used so that the result in the conclusion of the data remains accurate although it is not ideal. Robust statistics for location parameters which were used are median estimators (Fraiman, et al) and M estimators (Huber estimators). We apply four confidence interval methods that are confidence interval method for mean estimators, median estimators (Kendall and Stuart), median estimators (Fraiman, et al), and Huber estimators. Robust confidence interval with random data simulation was obtained from Normal, Cauchy, and Chi-Square distributions of sample sizes 𝑛 = 10, 50, 100, and 500 for each distributions. From the simulation, robust confidence interval for location parameters with the median estimators (Fraiman, et al) and Huber estimators were insensitive robust confidence interval to the presence of outliers while two others were sensitive. It is due to the value of the standard error and the width of the confidence interval which remains constant although the value of the outlier becomes bigger for each sample size.

Keywords: Outlier, Detection of Outlier, Robust Statistics, Robust Estimators, Robust Confidence Intervals.

x

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus yang selalu mencurahkan rahmat dan Roh KudusNya sehingga penulis mampu mengerjakan dan menyelesaikan skripsi ini dengan baik. Skripsi ini dibuat dengan tujuan memenuhi salah satu syarat dalam menyelesaikan studi Strata satu (S1) dan memperoleh gelar Sarjana Sains (S.Si.) pada Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma Yogyakarta.

Penulis menyadari bahwa proses penulisan skripsi ini melibatkan banyak pihak untuk membantu dalam menghadapi berbagai macam tantangan, kesulitan dan hambatan selama proses penulisan skripsi. Oleh karena itu, pada kesempatan ini penulis mengucapkan terima kasih kepada:

1. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., selaku dosen pembimbing skripsi yang telah meluangkan waktu, tenaga, dan pikiran, serta dengan penuh kesabaran telah memberikan masukan, nasihat dan arahan kepada penulis.

2. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., selaku Dekan Fakultas Sains dan Teknologi.

3. Bapak YG. Hartono, S.Si., M.Sc., Ph.D., selaku Kaprodi Matematika. 4. Ibu M. V. Any Herawati, S.Si., M.Si., selaku Wakaprodi Matematika

dan Dosen Pembimbing Akademik angkatan 2013.

5. Romo Prof. Dr. Frans Susilo, S.J., Bapak Dr. rer. nat. Herry P. Suryawan, S.Si., M.Si., Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., Bapak YG. Hartono, S.Si., M.Sc., Ph.D., Ibu M. V. Any Herawati, S.Si., M.Si., dan Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku dosen Prodi Matematika yang telah memberikan banyak pengetahuan dan pengalaman kepada penulis selama proses perkuliahan.

6. Perpustakaan Universitas Sanata Dharma dan Bapak/Ibu dosen/karyawan Fakultas Sains dan Teknologi yang telah banyak membantu selama penulis berkuliah.

xii

DAFTAR ISI

HALAMAN JUDUL ...i

HALAMAN JUDUL DALAM BAHASA INGGRIS ...ii

HALAMAN PERSETUJUAN PEMBIMBING ...iii

HALAMAN PENGESAHAN ...iv

HALAMAN PERSEMBAHAN ...v

PERNYATAAN KEASLIAN KARYA ...vi

ABSTRAK ...vii

ABSTRACK ...viii

LEMBAR PERNYATAAN PERSETUJUAN ...ix

KATA PENGANTAR ...x

DAFTAR ISI ...xii

DAFTAR TABEL ...xvi

DAFTAR GAMBAR ...xvii

BAB I PENDAHULUAN ...1 A. Latar Belakang ...1 B. Rumusan Masalah ...2 C. Pembatasan Masalah...3 D. Tujuan Penulisan ...3 E. Manfaat Penulisan ...4 F. Metode Penulisan ...4 G. Sistematika Penulisan ...4

BAB II PENDUGAAN PARAMETER ...6

A. Statistika ...6

B. Distribusi Probabilitas ...11

1. Variabel Acak ...11

2. Fungsi Probabilitas bagi Variabel Acak ...12

3. Fungsi Distribusi Kumulatif ...14

xiii

C. Distribusi Sampling ...30

1. Teorema Limit Pusat ...30

2. Distribusi 𝑡 ...32

D. Pendugaan Parameter ...33

1. Pendugaan (Estimasi) ...33

2. Macam-macam Pendugaan Parameter...34

E. Konsistensi Penduga ...45

F. Metode Kemungkinan Maksimum ...47

G. Pencilan ...51

1. Definisi Pencilan ...51

2. Pengaruh Pencilan ...55

3. Pendeteksian Pencilan ...56

BAB III SELANG KEPERCAYAAN ROBUST ...69

A. Statistik Robust ...69

B. Pengujian Robustness ...70

C. Penduga 𝑀 (Penduga Huber) ...75

D. MAD (Median Absolute Deviation) ...79

E. Selang Kepercayaan Robust bagi Parameter Lokasi ...82

BAB IV SELANG KEPERCAYAAN ROBUST DENGAN SIMULASI DATA ACAK ...85 BAB V PENUTUP ...89 A. Kesimpulan ...89 B. Saran ...90 DAFTAR PUSTAKA ...92 LAMPIRAN ...94

xiv

DAFTAR TABEL

Tabel 2.1 Fungsi probabilitas banyaknya laptop yang rusak ... 13

Tabel 2.2 Nilai harapan dan galat standar beberapa penduga titik ... 38

Tabel 2.3 Banyaknya barang yang terjual dan harga barang ... 52

Tabel 2.4 Produksi hasil hutan rimba (kayu pertukangan) menurut jenisnya di provinsi D. I. Yogyakarta ... 53

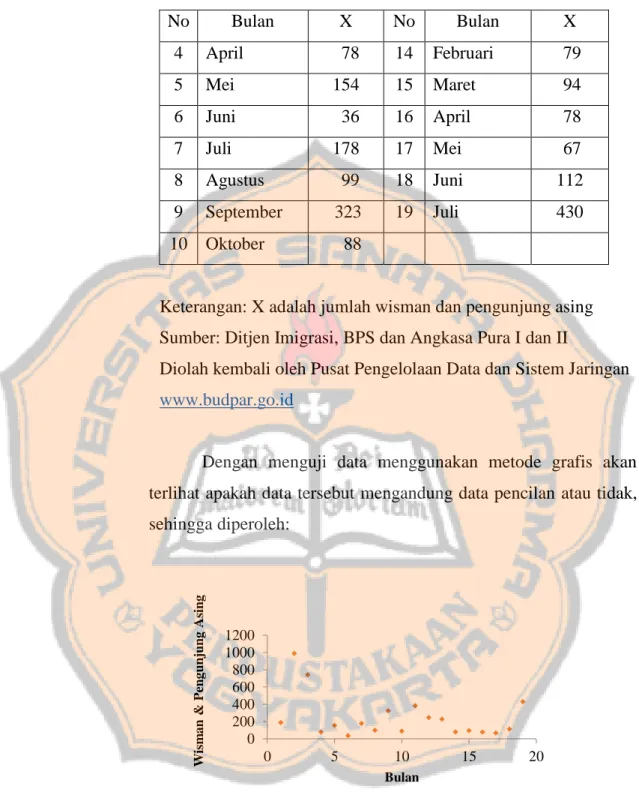
Tabel 2.5 Jumlah wisatawan yang masuk melalui pintu Makassar ... 56

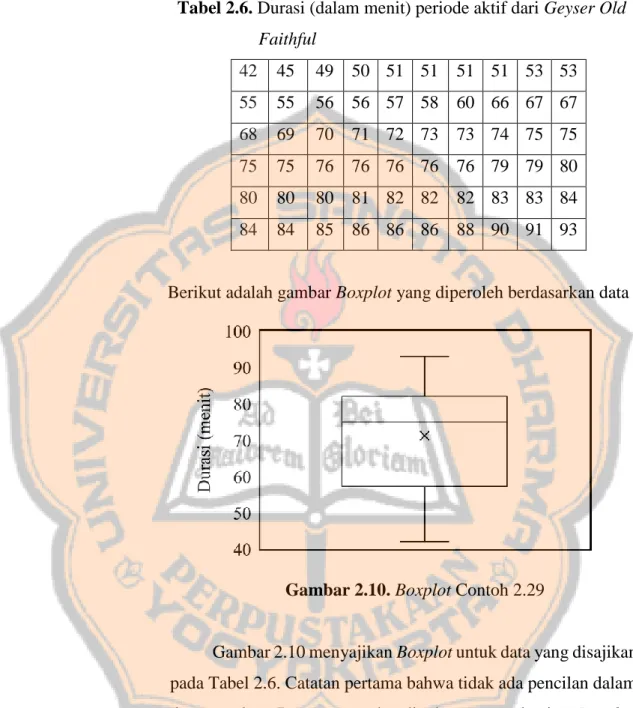
Tabel 2.6 Durasi (dalam menit) periode aktif dari Geyser Old Faithful ... 61

Tabel 2.7 Ketebalan lapisan oksida bagi silicon wafers ... 63

xv

DAFTAR GAMBAR

Gambar 2.1 Fungsi probabilitas Normal ... 24

Gambar 2.2 Distribusi nilai dugaan ... 35

Gambar 2.3 Distribusi sampling untuk penduga titik bias positif ... 35

Gambar 2.4 Fungsi probabilitas bagi 𝑈 ... 42

Gambar 2.5 Letak −𝑧_{𝛼 2}⁄ dan 𝑧𝛼 2⁄ ... 44

Gambar 2.6 Harga barang terhadap banyaknya barang yang terjual ... 53

Gambar 2.7 Produksihasil hutan rimba terhadap waktu ... 54

Gambar 2.8 Scatter-plot jumlah wisman dan pengunjung asing ... 57

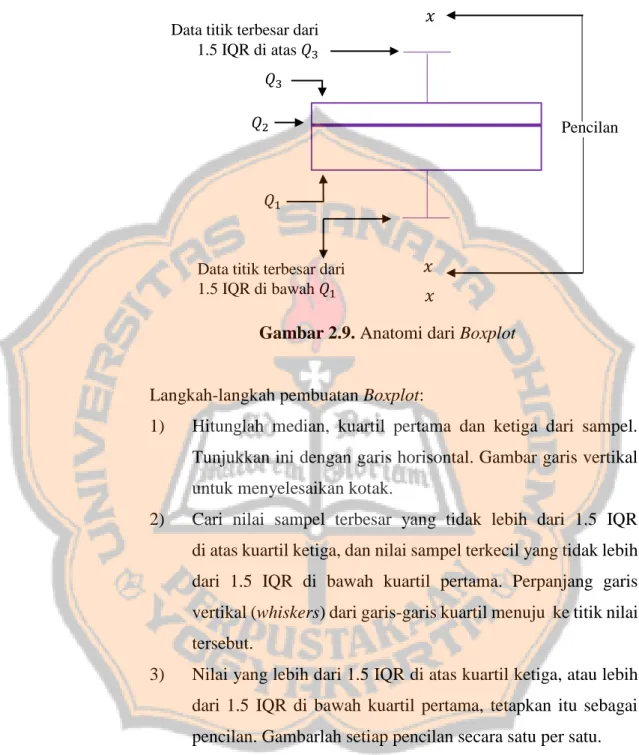
Gambar 2.9 Anatomi dari Boxplot ... 60

Gambar 2.10 Boxplot contoh 2.29 ... 61

Gambar 2.11 Perbandingan boxplot untuk data ketebalan lapisan oksida ... 64

Gambar 3.1 Kurva sensitivitas untuk rata-rata ... 72

Gambar 3.2 Kurva sensitivitas untuk median ... 73

Gambar 3.3 Kurva sensitivitas untuk median contoh 3.4 ... 74

Gambar 3.4 (a) Fungsi tujuan, 𝜌(𝑥; 𝑡) = (𝑥 − 𝑡)2 ... 76

(b) Fungsi 𝜓, 𝜓(𝑥; 𝑡) = 𝑥 − 𝑡... 77

Gambar 3.5 Pendugaan dengan fungsi tujuan mutlak residual. (a) Fungsi tujuan, 𝜌(𝑥; 𝑡) = |𝑥 − 𝑡|; (b) Fungsi 𝜓, 𝜓(𝑥; 𝑡) = sgn(𝑥 − 𝑡) ... 79

Gambar 3.6 Hasil pendeteksian uji MAD ... 80

Gambar 3.7 (a) Kurva sensitivitas untuk MAD ... 81

1

BAB I PENDAHULUAN

A. Latar Belakang Masalah

Pendugaan sering muncul di lingkungan sekitar dalam kehidupan sehari-hari yang tidak dapat dihindari. Permasalahan yang sering terjadi adalah bagaimana dugaan tersebut dapat mendekati kebenaran. Terdapat dua jenis pendugaan, yaitu pendugaan titik dan pendugaan selang. Pendugaan titik adalah penentuan suatu nilai tunggal berdasarkan atas sampel yang dengan baik menduga parameter sasaran, sedangkan pendugaan selang adalah penentuan batas-batas selang nilai, yang disebut batas atas (𝜃_𝑈) dan batas bawah (𝜃_𝐿). Batas-batas itu dihitung berdasarkan pengukuran sampel dan hasilnya mempunyai peluang tertentu yang memuat parameter sasaran (Wackerly, et al, 2008: 391). Peluang tersebut disebut tingkat kepercayaan. Tingkat kepercayaan itu sering dinyatakan dengan persen (%) dan memuat parameter tertentu (𝜃)

yang disebut koefisien kepercayaan. Selang yang dihasilkan dengan tingkat kepercayaan tertentu disebut selang kepercayaan. Bentuk selang kepercayaan yang sering digunakan adalah

𝑷(𝜃̂𝐿 < 𝜃 < 𝜃̂𝑈) = 1 − 𝛼, 0 < 𝛼 < 1,

dengan 1 − 𝛼 adalah koefisien kepercayaan dan 𝜃̂_𝐿 < 𝜃 < 𝜃̂_𝑈 adalah selang kepercayaan.

Pada umumnya bentuk selang kepercayaan (1 − 𝛼)100% bagi 𝜇 adalah

𝑥̅ − 𝑧_{𝛼 2}⁄ ∙ 𝜎

√𝑛< 𝜇 < 𝑥̅ + 𝑧𝛼 2⁄ ∙ 𝜎 √𝑛

dengan 𝜎 adalah standar deviasi populasi yang diketahui dan 𝑧_{𝛼 2}⁄ adalah kuartil ke (𝛼 2⁄ ) dari distribusi Normal standar 𝑍 dengan 𝑛 ≥ 30 menurut Teorema Limit Pusat.

Suatu pendugaan yang dilakukan tidak tertutup kemungkinan akan terjadi kesalahan (error). Kondisi tersebut kerap kali dipengaruhi oleh adanya pencilan (outlier) yang dapat mengganggu proses analisis data, sehingga pendeteksian pencilan sangat penting untuk dilakukan. Pencilan (outlier)

adalah data yang memiliki perbedaan cukup ekstrim bila dibandingkan dengan data lainnya (Barnett, 1978: v). Pengaruh pencilan pada proses analisis data, salah satunya adalah terhadap nilai rata-rata dan standar deviasi. Adanya pencilan dapat menunjukkan kesalahan pengukuran dalam distribusi data, serta dapat menyebabkan variansi data menjadi besar, selang data menjadi lebar, dan rata-rata tidak dapat menunjukkan nilai yang sebenarnya (bias). Oleh karena itu, akan lebih baik jika pencilan dihapuskan supaya tidak ada kejanggalan dalam analisis data, tetapi diupayakan terlebih dahulu untuk menyelidiki penyebab adanya pencilan. Di sisi lain, adakalanya pencilan tidak dapat dihapuskan begitu saja karena pencilan dapat memberikan suatu informasi yang tidak dapat diberikan oleh data lainnya.

Skripsi ini akan membahas tentang selang kepercayaan yang robust (kekar). Sifat robust (kekar) sendiri memiliki kinerja yang baik dalam menghasilkan pendugaan yang dapat mencapai kebenaran yang memuaskan dengan selang kepercayaan yang cenderung lebih sempit. Kata “robust” (kekar) seringkali muncul di dalam proses analisis data yang menginginkan pencilan tetap ada, namun tidak menyebabkan adanya kejanggalan. Dengan demikian, akan diperoleh selang kepercayaan baru yang menjadikan selang kepercayaan dapat tetap kekar untuk digunakan dalam pendugaan rata-rata populasi. Akan diperkenalkan selang kepercayaan robust bagi parameter lokasi dengan penduga median dan penduga Huber. Selang kepercayaan robust bagi parameter lokasi dengan penduga Median dibedakan menjadi dua berdasarkan galat standar yang diberikan oleh Fraiman, et al (2001) dengan Kendall dan Stuart (2001).

B. Rumusan Masalah

Perumusan masalah yang akan dibicarakan pada skripsi ini adalah: 1. Bagaimana cara mengetahui data yang mengandung pencilan?

2. Apa pengaruh pencilan dalam pendugaan selang kepercayaan rata-rata populasi?

3. Bagaimana penduga robust (kekar) dapat membuat selang kepercayaan menjadi lebih baik dengan adanya pencilan?

4. Bagaimana perbandingan selang kepercayaan yang robust dengan selang kepercayaan yang biasa?

C. Pembatasan Masalah

Penulis akan membatasi penulisan agar menjadi lebih terarah dan tidak menyimpang dari masalah yang akan dibahas, yaitu:

1. Data yang digunakan dalam penulisan hanyalah data yang mengandung pencilan univariat.

2. Metode yang digunakan dalam pengujian sifat robust yang dimiliki oleh suatu pendugahanya dengan menggunakan kurva sensitivitas.

3. Penulis hanya menggunakan dua penduga robust dengan menggunakan penduga median (Fraiman, et al) dan penduga M (Huber) bagi parameter lokasi.

4. Galat standardan lebar selang yang dihasilkan dari selang kepercayaan bagi suatu penduga akan dibandingkan dengan galat standar dan lebar selang yang dihasilkan dari selang kepercayaan bagi penduga lainnya.

D. Tujuan Penulisan

Tujuan yang ingin dicapai penulis, selain untuk memenuhi syarat skripsi dalam Program Studi Matematika Universitas Sanata Dharma, juga untuk: 1. Mengetahui penduga robust dalam menduga parameter lokasi untuk data

yang memuat pencilan.

2. Mengetahui seberapa robust (kekar) selang kepercayaan yang terbentuk dari suatu data yang memuat pencilan.

E. Manfaat Penulisan

Manfaat dari penulisan skripsi ini adalah sebagai berikut:

1. Penulis memperoleh pengetahuan baru selama mengerjakan tulisan ini. 2. Pembaca mendapat gambaran tentang pendugaan selang kepercayaan

bagi rata-rata populasi dengan kondisi adanya pencilan di dalam suatu data.

3. Skripsi ini dapat dijadikan referensi bagi penganalisis lain.

F. Metode Penulisan

Metode penulisan yang digunakan penulis dalam penulisan skripsi ini adalah metode studi pustaka, yaitu dengan membaca dan mempelajari buku-buku atau jurnal yang berkaitan dengan pendugaan selang kepercayaan rata-rata populasi, pencilan, serta sifat robust (kekar) dari selang kepercayaan.

G. Sistematika Penulisan

Skripsi ini ditulis menggunakan sistematika berikut: BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan BAB II PENDUGAAN PARAMETER

A. Statistika

B. Distribusi Probabilitas C. Distribusi Sampling D. Pendugaan Parameter E. Konsistensi Penduga

G. Pencilan

BAB III SELANG KEPERCAYAAN ROBUST A. Statistik Robust

B. Pengujian Robustness C. Penduga M

D. MAD (Median Absolute Deviation)

E. Selang Kepercayaan yang Robust bagi Parameter Lokasi

BAB IV SELANG KEPERCAYAAN ROBUST DENGAN SIMULASI DATA ACAK

BAB V PENUTUP A. Kesimpulan B. Saran DAFTAR PUSTAKA

6

BAB II

PENDUGAAN PARAMETER

A. Statistika

Teknik statistik hampir digunakan dalam setiap fase kehidupan banyak orang di berbagai bidang. Contohnya, para ahli ekonomi yang mengamati berbagai indeks kesehatan ekonomi selama periode waktu dan menggunakan informasi tersebut untuk meramalkan kondisi ekonomi di masa depan, serta pelaksanaan survey yang dirancang untuk mengumpulkan data pada hari pemilihan dan meramalkan hasil pemilu.

Definisi dari statistika sendiri muncul dari para statistikawan. Stuart dan Ord (1991) menyatakan: "Statistika adalah cabang dari metode ilmiah yang berkaitan dengan data yang diperoleh dengan menghitung atau mengukur sifat dari populasi. Rice (1995) dalam komentarnya mengenai eksperimen dan aplikasi dalam statistika, menyatakan bahwa statistika pada dasarnya berkaitan dengan prosedur untuk menganalisis data, terutama data yang memiliki karakter acak. Freund dan Walpole (1987) menyatakan statistika adalah ilmu yang mendasarkan kesimpulan pada data yang diamati dan seluruh masalah dalam membuat keputusan dalam menghadapi ketidakpastian. Mood, Graybill, dan Boes (1974) mendefinisikan statistika sebagai teknologi dari metode ilmiah dan menambahkan bahwa statistika berkaitan dengan desain eksperimen dan penyelidikan, serta statistika inferensi. Dari beberapa definisi tersebut dapat disimpulkan bahwa statistika adalah sekumpulan metode untuk merencanakan eksperimen, mengumpulkan data, menganalisis, menafsirkan dan mengambil kesimpulan berdasarkan data.

Pengambilan sampel dari populasi yang akan diteliti diperlukan untuk mengambil kesimpulan.

Definisi 2.1

Populasi adalah kumpulan yang lengkap dari semua elemen (nilai, orang, benda, hasil, dan lain-lain) yang menjadi pusat perhatian untuk dipelajari dan diteliti. Lengkap berarti mencakup semua obyek yang akan diambil kesimpulannya.

Banyaknya observasi dalam populasi didefinisikan sebagai ukuran populasi. Di bidang statistika inferensi, statistik tertarik pada kesimpulan mengenai populasi bila tidak memungkinkan untuk mengamati seluruh pengamatan yang membentuk populasi. Misalnya, dalam upaya untuk menentukan rata-rata hidup dari suatu lampu merk tertentu. Hal ini tidak mungkin untuk menguji semua lampu. Biaya yang terlalu tinggi juga bisa menjadi faktor penghalang dalam mengamati seluruh populasi. Oleh karena itu, pengamatan bergantung pada bagian dari populasi, yang disebut sampel, untuk membantu memperoleh kesimpulan tentang populasi yang diamati berdasarkan informasi yang terdapat di dalam sampel .

Definisi 2.2

Sampel adalah himpunan bagian dari populasi yang menjadi perhatian kita.

Jika menginginkan kesimpulan yang valid, maka harus didapatkan sampel yang mewakili populasi. Oleh karena itu, diperlukan pemilihan sampel secara acak, yaitu setiap individu dalam populasi mempunyai peluang tertentu untuk dipilih sebagai anggota sampel. Tujuan utama dalam memilih sampel secara acak adalah untuk memperoleh informasi tentang parameter populasi yang tidak diketahui.

Definisi 2.3

Parameter adalah karakteristik dari populasi yang biasa dinyatakan dalam suatu nilai/konstanta.

Secara umum, parameter dilambangkan dengan 𝜃. Parameter 𝜃 dapat berupa rata-rata µ, variansi 𝜎2 dan proporsi 𝑝. Parameter dibagi menjadi dua bagian, yaitu parameter lokasi dan parameter skala yang definisi eksaknya akan dibahas kemudian pada Definisi 2.15 dan Definisi 2.18. Parameter lokasi dirancang untuk memenuhi analisis dengan banyaknya nilai pada data yang berada di pusat. Contohnya adalah rata-rata µ dan median. Sedangkan parameter skala dirancang untuk mengetahui penyebaran data analisis. Contoh dari parameter skala adalah variansi 𝜎2 _{dan standar deviasi 𝜎.}

Definisi 2.4

Statistik adalah fungsi dari variabel-variabel acak yang diamati dalam sampel dan dinyatakan dalam suatu bilangan.

Ada beberapa contoh statistik, yaitu rata-rata sampel 𝑥̅, standar deviasi sampel

𝑠, dan proporsi sampel 𝑝̂. Parameter 𝜇, 𝜎2 dan 𝑝 adalah parameter yang nilainya sama sekali tidak terpengaruh atau dipengaruhi oleh pengamatan sampel acak. Statistik yang paling umum digunakan adalah mean (rata-rata), median (nilai tengah) dan modus.

Definisi 2.5

Misalkan pengamatan di dalam sampel berukuran 𝑛 adalah 𝑥₁, 𝑥₂, … , 𝑥_𝑛. Rata-rata sampel dilambangkan dengan 𝑥̅ yang didefinisikan sebagai

𝑥̅ =𝑥1 + 𝑥2 + ⋯ + 𝑥𝑛

𝑛 =

∑𝑛𝑖=1𝑥𝑖 𝑛 .

Definisi 2.6

Diberikan pengamatan sampel 𝑥₁, 𝑥₂, … , 𝑥_𝑛. Sampel disusun dari data yang nilainya terkecil hingga data yang nilainya terbesar, maka nilai tengah (median) sampel adalah:

𝑥̃ = {

𝑥_(𝑛+1)/2 , jika 𝑛 bilangan ganjil, 1

2(𝑥𝑛/2+ 𝑥𝑛2+1) , jika 𝑛 bilangan genap, dengan 𝑥_(𝑛+1)/2 adalah pengamatan ke- (𝑛 + 1)/2 dari variabel acak 𝑋.

Definisi 2.7

Modus sampel adalah nilai dari sampel yang paling sering muncul atau memiliki frekuensi yang paling besar.

Ukuran variasi yang lebih umum digunakan dalam statistika adalah variansi yang merupakan fungsi deviasi (atau jarak) ukuran sampel dari rata-ratanya.

Definisi 2.8

Variansi dari sampel berukuran 𝑛, diberikan sebagai berikut

𝑠2 =∑ (𝑥𝑖− 𝑥̅) 2 𝑛

𝑖=1

𝑛 − 1 .

Variansi populasi yang sesuai, dilambangkan dengan 𝜎2_.

Definisi 2.9

Standar deviasi dari sampel berukuran 𝑛 adalah akar kuadrat positif dari variansi yang diberikan sebagai berikut

𝑠 = √𝑠2_.

Standar deviasi populasi yang sesuai, dilambangkan dengan 𝜎 = √𝜎2_.

Contoh 2.1

Dari hasil penelitian mengenai nilai ujian matematika dari 50 mahasiswa diperoleh data sebagai berikut:

Carilah rata-rata, median, modus, variansi serta standar deviasi dari sampel penelitian tersebut. Solusi:  Rata-rataSampel 𝑥̅ =∑ 𝑥𝑖 50 𝑖=1 50 = 3292 50 = 65.8.  Median Sampel

Data penelitian yang sudah urut adalah sebagai berikut:

sehingga diperoleh, 𝑥̃ =1 2(𝑥25+ 𝑥26) = 1 2(67 + 68) = 67.5.  Modus Sampel

Nilai yang sering muncul dalam pengamatan sampel adalah 74, yaitu sebanyak empat kali. Oleh karena itu, modus sampel dari pengamatan adalah 74.

 Variansi Sampel 𝑠2 = ∑ (𝑥𝑖 − 65.8) 2 50 𝑖=1 49 = 19080.04 49 = 389.3886. 42 74 68 54 78 57 83 71 41 89 64 50 76 100 90 74 59 89 98 23 84 64 90 95 33 45 71 87 66 67 57 78 62 38 79 65 87 67 42 74 71 50 34 57 90 69 59 23 74 34 23 23 33 33 34 38 41 42 42 45 50 50 54 57 57 57 59 59 62 64 64 65 66 67 67 68 69 71 71 71 74 74 74 74 76 78 78 79 83 84 87 87 89 89 90 90 90 95 98 100

 Standar Deviasi Sampel

𝑠 = √389.3886 = 19.73.

B. Distribusi Probabilitas 1. Variabel Acak Definisi 2.10

Variabel acak adalah fungsi bernilai bilangan real yang domainnya adalah ruang sampel.

Variabel acak dinotasikan dengan huruf kapital dan nilainya dinotasikan dengan huruf kecil. Misalkan 𝑋 menyatakan variabel acak, maka nilai dari 𝑋 adalah 𝑥.

Definisi 2.11

Variabel acak 𝑋 dikatakan variabel acak diskrit jika himpunan dari kemungkinan hasilnya adalah terbilang. Jika hal ini tidak terpenuhi, maka variabel acak 𝑋 disebut variabel acak kontinu.

Contoh 2.2

Para statistikawan menggunakan perencanaan pengambilan sampel untuk menerima atau menolak sekumpulan barang. Misalnya, salah satu rencana pengambilan sampel yaitu sampel diambil secara acak sebanyak 10 dari

100 barang. Dari 100 barang tersebut terdapat 12 barang yang rusak. Misalkan 𝑋 adalah variabel acak yang didefinisikan sebagai banyaknya barang yang ditemukan rusak dalam sampel dari 10 barang. Dalam hal ini, variabel acak bernilai 0,1,2, . . . ,9,10.

Contoh 2.3

Pusat survey melakukan percobaan dengan mengirimkan surat pada para responden dan melihat proporsi responden dalam merespon surat tersebut. Misalkan 𝑋 adalah variabel acak yang didefinisikan sebagai proporsi

responden. 𝑋 akan memuat semua nilai 𝑥 dalam selang

0 ≤ 𝑥 ≤ 1.

2. Fungsi Probabilitas bagi Variabel Acak

Fungsi probabilitas dibagi menjadi dua macam, yaitu fungsi probabilitas diskrit dan kontinu.

a. Fungsi Probabilitas Diskrit Definisi 2.12

Himpunan pasangan terurut (𝑥, 𝑝(𝑥)) adalah suatu fungsi probabilitas, atau distribusi probabilitas dari suatu variabel acak diskrit 𝑋, jika

1. 0 ≤ 𝑝(𝑥) ≤ 1 untuk setiap 𝑥, 2. ∑ 𝑝(𝑥)𝑥 = 1,

3. 𝑃(𝑋 = 𝑥) = 𝑝(𝑥).

Contoh 2.4

Pengiriman 20 laptop ke toko pengecer berisi 3 yang rusak. Apabila ada sekolah yang membeli laptop secara acak sebanyak 2 laptop, temukanlah distribusi probabilitas untuk banyaknya laptop yang rusak.

Solusi:

Misalkan 𝑋 adalah variabel acak yang nilainya 𝑥, yaitu kemungkinan banyaknya laptop rusak yang dibeli oleh sekolah. Kemudian 𝑥 hanya dapat berisi nilai 0,1, dan 2, sehingga diperoleh

𝑝(0) = 𝑃(𝑋 = 0) =( 3 0)( 17 2) (20₂) = 136 190, 𝑝(1) = 𝑃(𝑋 = 1) =( 3 1)( 17 1) (20₂) = 51 190, 𝑝(2) = 𝑃(𝑋 = 2) =( 3 2)( 17 0) (20₂) = 3 190.

Tabel 2.1. Fungsi probabilitas banyaknya laptop yang rusak

b. Fungsi Probabilitas Kontinu Definisi 2.13

Fungsi 𝑓(𝑥) adalah fungsi probabilitas untuk variabel acak kontinu

𝑋, jika

1. 𝑓(𝑥) ≥ 0, untuk setiap 𝑥 ∈ 𝑅, 2. ∫_−∞∞ 𝑓(𝑥)𝑑𝑥 = 1,

3. 𝑃(𝑎 < 𝑋 < 𝑏) = ∫ 𝑓(𝑥)𝑑𝑥_𝑎𝑏 .

Contoh 2.5

Misalkan suhu dalam ℃ yang diuji dalam pengontrolan laboratorium adalah suatu variabel acak kontinu 𝑋 yang mempunyai fungsi probabilitas

𝑓(𝑥) = { 𝑥2

3 , 𝑑𝑎𝑛 − 1 < 𝑥 < 2, 0 , lainnya.

a) Periksalah bahwa 𝑓(𝑥) adalah fungsi probabilitas. b) Temukan 𝑃(0 < 𝑋 ≤ 1).

Solusi:

a) Dengan jelas, 𝑓(𝑥) ≥ 0.

Untuk memeriksa syarat kedua dalam Definisi 2.13, diperoleh

∫ 𝑓(𝑥)𝑑𝑥 = ∫₋₁2 𝑥₃2𝑑𝑥 =𝑥3 9| 2 −1= 1 ∞ −∞ . b) 𝑃(0 < 𝑋 ≤ 1) = ∫₀1𝑥₃2𝑑𝑥 =𝑥3 9| 1 0= 1 9. 𝑥 0 1 2 𝑝(𝑥) 136 190 51 190 3 190

3. Fungsi Distribusi Kumulatif Definisi 2.14

Fungsi distribusi kumulatif 𝐹(𝑥) dari variabel acak 𝑋 dengan fungsi probabilitas 𝑝(𝑥) adalah 𝐹(𝑥) = 𝑃(𝑋 ≤ 𝑥) = { ∑ 𝑝(𝑡) ∀𝑡≤𝑥 , 𝑑𝑎𝑛jika 𝑋 diskrit ∫ 𝑓(𝑡)𝑑𝑡 𝑥 −∞ , 𝑑𝑎𝑛jika 𝑋 kontinu

4. Karakteristik Distribusi Probabilitas

Distribusi probabilitas suatu variabel acak dicirikan dengan parameter lokasi dan parameter skala.

Definisi 2.15

Misalkan 𝑓(𝑥; 𝜃, 𝜆) adalah sembarang fungsi probabilitas suatu variabel acak 𝑋. Parameter 𝜃 adalah parameter lokasi jika fungsi probabilitas dapat ditulis sebagai fungsi dari 𝑥 − 𝜃; yaitu 𝑓(𝑥; 𝜃, 𝜆) = ℎ(𝑥 − 𝜃; 𝜆) untuk setiap fungsi ℎ(∗; 𝜆) yang tidak bergantung pada 𝜃.

Contoh 2.6

Diberikan fungsi probabilitas sebagai berikut

𝑓(𝑥; 𝜇, 𝜎) = 1 𝜎√2𝜋𝑒

−(1/2) [(𝑥−𝜇)/𝜎]2_.

Misalkan 𝑦 = 𝑥 − 𝜇, maka fungsi 𝑓(𝑥; 𝜇, 𝜎) dapat ditulis sebagai

ℎ(𝑦; 𝜎) = 1 𝜎√2𝜋𝑒

−(1/2) [𝑦/𝜎]2_.

Dengan demikian, 𝜇 adalah parameter lokasi.

Contoh 2.7

Jika 𝑋~𝑁(0, 𝜃), maka 𝑋 − 𝜃~𝑁(−𝜃, 𝜃) mempunyai distribusi yang tidak bebas dari 𝜃. Dengan demikian, 𝜃 adalah bukan parameter lokasi.

Definisi 2.16

Misalkan 𝑥1, 𝑥2, … , 𝑥𝑛 adalah variabel acak dari suatu distribusi dengan fungsi probabilitas 𝑓(𝑥; 𝜇); 𝜇 ∈ Ω, Ω adalah ruang parameter. Penduga

𝑡(𝑥₁, … , 𝑥_𝑛) didefinisikan sebagai ekuivarian lokasi jika dan hanya jika

𝑡(𝑥₁+ 𝑐, … , 𝑥_𝑛+ 𝑐) = 𝑡(𝑥₁, … , 𝑥_𝑛) + 𝑐,

untuk semua nilai 𝑥₁, … , 𝑥_𝑛 dan sebuah konstanta 𝑐.

Dengan kata lain, penambahan konstanta 𝑐 pada variabel acak akan menambah nilai dugaan sebesar 𝑐.

Definisi 2.17

Misalkan 𝑥₁, 𝑥₂, … , 𝑥_𝑛 adalah variabel acak dari suatu distribusi dengan fungsi probabilitas 𝑓(𝑥; 𝜇); 𝜇 ∈ Ω, Ω adalah ruang parameter. Penduga

𝑡(𝑥1, … , 𝑥𝑛) didefinisikan sebagai invarian lokasi jika dan hanya jika 𝑡(𝑥1+ 𝑐, … , 𝑥𝑛 + 𝑐) = 𝑡(𝑥1, … , 𝑥𝑛),

untuk semua nilai 𝑥₁, … , 𝑥_𝑛 dan sebuah konstanta 𝑐.

Dengan kata lain, penambahan konstanta 𝑐 pada variabel acak tidak akan mengubah nilai penduga.

Contoh 2.8

Apakah 𝑥̅ adalah penduga invarian atau ekuivarian lokasi? Solusi: Misalkan 𝑡(𝑥₁, … , 𝑥_𝑛) = 𝑥̅. Kemudian, 𝑡(𝑥₁+ 𝑐, … , 𝑥_𝑛 + 𝑐) =∑ (𝑥𝑖 + 𝑐) 𝑛 𝑖=1 𝑛 =∑ 𝑥𝑖 𝑛 𝑖=1 + 𝑛𝑐 𝑛 = 𝑥̅ + 𝑐 = 𝑡(𝑥₁, … , 𝑥_𝑛) + 𝑐.

Oleh karena penambahan konstanta 𝑐 pada variabel acak akan menambah nilai dugaan 𝑥̅ sebesar 𝑐, maka 𝑥̅ adalah penduga ekuivarian lokasi dan tidak invarian.

Contoh 2.9

Apakah 𝑠2 _{adalah penduga invarian atau ekuivarian lokasi?} Solusi: Misalkan 𝑡(𝑥₁, … , 𝑥_𝑛) = 𝑠2 ₌ ∑ (𝑥𝑖−( ∑𝑛_{𝑖=1𝑥𝑖} 𝑛 )) 2 𝑛 𝑖=1 𝑛−1 . Kemudian,

Oleh karena penambahan konstanta 𝑐 pada variabel acak tidak

mengalami perubahan nilai dugaan 𝑠2, maka 𝑠2 adalah penduga invarian lokasi dan tidak ekuivarian.

Definisi 2.18

Misalkan 𝑓(𝑥; 𝜃) adalah sembarang fungsi probabilitas suatu variabel acak 𝑋. Keluarga fungsi probabilitas 𝑓(𝑥/𝜃) 𝜃⁄ , untuk 𝜃 > 0, parameter

𝜃 adalah parameter skala bagi 𝑓(𝑥) jika dan hanya jika distribusi dari 𝑥 𝜃⁄

tidak bergantung pada 𝜃.

𝑡(𝑥₁+ 𝑐, … , 𝑥_𝑛+ 𝑐) ₌ ∑ (𝑥𝑖 + 𝑐 − ( ∑𝑛_𝑖=1𝑥_𝑖 + 𝑐 𝑛 )) 2 𝑛 𝑖=1 𝑛 − 1 = ∑ (𝑥𝑖+ 𝑐 − (𝑥̅ + 𝑐)) 2 𝑛 𝑖=1 𝑛 − 1 = ∑ (𝑥𝑖 − 𝑥̅) 2 𝑛 𝑖=1 𝑛 − 1 = ∑ (𝑥𝑖 − ( ∑𝑛_𝑖=1𝑥_𝑖 𝑛 )) 2 𝑛 𝑖=1 𝑛 − 1 = 𝑠2 = 𝑡(𝑥1, … , 𝑥𝑛).

Contoh 2.10

Diberikan fungsi probabilitas sebagai berikut

𝑓(𝑥) =1 𝜃𝑒

−(𝑥/𝜃)_.

Misalkan 𝑦 = 𝑥/𝜃, maka keluarga fungsi probabilitas 𝑓(𝑥/𝜃) 𝜃⁄ dapat ditulis sebagai 𝑓(𝑦) 𝜃 = 1 𝜃𝑒 −(𝑦) 𝑓(𝑦) = 𝑒−(𝑦)_{, untuk 𝑦 > 0}

Dengan demikian, 𝜃 adalah parameter skala.

Definisi 2.19

Misalkan 𝑥₁, 𝑥₂, … , 𝑥_𝑛 adalah variabel acak dari suatu distribusi dengan fungsi probabilitas 𝑓(𝑥; 𝜇); 𝜇 ∈ Ω, Ω adalah ruang parameter. Penduga

𝑡(𝑥₁, … , 𝑥_𝑛) didefinisikan sebagai ekuivarian skala jika dan hanya jika

𝑡(𝑐𝑥1, … , 𝑐𝑥𝑛) = 𝑐𝑡(𝑥1, … , 𝑥𝑛), untuk semua nilai 𝑥₁, … , 𝑥_𝑛 dan sebuah konstanta 𝑐 > 0.

Definisi 2.20

Misalkan 𝑥1, 𝑥2, … , 𝑥𝑛 adalah variabel acak dari suatu distribusi dengan fungsi probabilitas 𝑓(𝑥; 𝜇); 𝜇 ∈ Ω, Ω adalah ruang parameter. Penduga

𝑡(𝑥1, … , 𝑥𝑛) didefinisikan sebagai invarian skala jika dan hanya jika 𝑡(𝑐𝑥₁, … , 𝑐𝑥_𝑛) = 𝑡(𝑥₁, … , 𝑥_𝑛),

untuk semua nilai 𝑥₁, … , 𝑥_𝑛 dan sebuah konstanta 𝑐 > 0.

Dengan kata lain, penduga bersifat invarian terhadap skala jika nilainya tidak mengalami perubahan dengan adanya perkalian dengan 𝑐.

Contoh 2.11

Solusi: Misalkan 𝑡(𝑥1, … , 𝑥𝑛) = 𝑥̅. Kemudian, 𝑡(𝑐𝑥1, … , 𝑐𝑥𝑛) = ∑𝑛_𝑖=1𝑐𝑥_𝑖 𝑛 =𝑐 ∑ 𝑥𝑖 𝑛 𝑖=1 𝑛 = 𝑐𝑥̅ = 𝑐𝑡(𝑥1, … , 𝑥𝑛).

Oleh karena penambahan konstanta 𝑐 pada variabel acak akan mengubah nilai dugaan 𝑥̅, maka 𝑥̅ adalah penduga ekuivarian terhadap skala dan tidak invarian.

a. Nilai Harapan atau Rata-rata dari Variabel Acak Definisi 2.21

Misalkan 𝑋 adalah variabel acak dengan fungsi probabilitas 𝑝(𝑥). Nilai harapan atau rata-rata dari 𝑋 adalah

𝜇 = 𝐸(𝑋) = { ∑ 𝑥𝑝(𝑥) 𝑥 , 𝑑𝑎𝑛jika 𝑋 diskrit ∫ 𝑥𝑓(𝑥)𝑑𝑥 ∞ −∞ , 𝑑𝑎𝑛jika 𝑋 kontinu Teorema 2.1

Diberikan 𝑎, 𝑏 suatu konstanta, 𝐸(𝑎𝑋 + 𝑏) = 𝑎𝐸(𝑋) + 𝑏. Bukti:

Berdasarkan Definisi 2.21, diperoleh: untuk variabel acak diskrit,

𝐸(𝑎𝑋 + 𝑏) = ∑(𝑎𝑥 + 𝑏) 𝑝(𝑥) 𝑥

= ∑(𝑎𝑥 𝑝(𝑥) + 𝑏 𝑝(𝑥)) 𝑥

= 𝑎 ∑ 𝑥 𝑝(𝑥) + 𝑏 ∑ 𝑝(𝑥) 𝑥 𝑥

= 𝑎𝐸(𝑋) + 𝑏. Untuk variabel acak kontinu,

𝐸(𝑎𝑋 + 𝑏) = ∫ (𝑎𝑥 + 𝑏)𝑓(𝑥)𝑑𝑥 ∞ −∞ = 𝑎 ∫ 𝑥𝑓(𝑥)𝑑𝑥 ∞ −∞ + 𝑏 ∫ 𝑓(𝑥)𝑑𝑥 ∞ −∞ = 𝑎𝐸(𝑋) + 𝑏. ∎ Lemma 2.1 Diberikan 𝑎 = 0, maka 𝐸(𝑏) = 𝑏. Bukti:

Untuk variabel acak diskrit,

𝐸(𝑏) = ∑ 𝑏𝑝(𝑥) = 𝑏 ∑ 𝑝(𝑥) = 𝑏(1) = 𝑏_{𝑥 𝑥} . Untuk variabel acak kontinu,

𝑥𝐸(𝑏) = ∫ 𝑏𝑓(𝑥)𝑑𝑥 = 𝑏 ∫ 𝑓(𝑥)𝑑𝑥 = 𝑏. ∎

Lemma 2.2

Diberikan 𝑏 = 0, maka 𝐸(𝑎𝑋) = 𝑎𝐸(𝑋). Bukti:

Untuk variabel acak diskrit,

𝐸(𝑎𝑋) = ∑ 𝑎𝑥𝑝(𝑥) = 𝑎 ∑ 𝑥𝑝(𝑥) = 𝑎𝐸(𝑋)𝑥 𝑥 . Untuk variabel acak kontinu,

𝐸(𝑎𝑋) = ∫ 𝑎𝑥𝑓(𝑥)𝑑𝑥 = 𝑎 ∫ 𝑥𝑓(𝑥)𝑑𝑥 = 𝑎𝐸(𝑋). ∎

Teorema 2.2

Misalkan 𝑋 adalah variabel acak dengan fungsi probabilitas 𝑝(𝑥) dan

𝑔₁(𝑋), 𝑔₂(𝑋), … , 𝑔_𝑘(𝑋) adalah 𝑘 buah fungsi dari 𝑋; maka

𝐸[𝑔1(𝑋) + 𝑔2(𝑋) + ⋯ + 𝑔𝑘(𝑋)]

Bukti:

Akan dibuktikan dengan 𝑘 = 2, tetapi langkah tetap sama untuk setiap 𝑘. Menurut Definisi 2.21, diperoleh:

untuk 𝑋 diskrit, 𝐸[𝑔₁(𝑋) + 𝑔2(𝑋)] = ∑[𝑔1(𝑥) + 𝑔2(𝑥)]𝑝(𝑥) 𝑥 = ∑ 𝑔1(𝑥)𝑝(𝑥) + 𝑥 ∑ 𝑔2(𝑥)𝑝(𝑥) 𝑥 = 𝐸[𝑔1(𝑋)] + 𝐸[𝑔2(𝑋)]. Untuk 𝑋 kontinu, 𝐸[𝑔₁(𝑋) + 𝑔₂(𝑋)] = ∫ [𝑔₁(𝑥) + 𝑔₂(𝑥)]𝑝(𝑥)𝑑𝑥 ∞ −∞ = ∫ 𝑔₁(𝑥)𝑓(𝑥)𝑑𝑥 + ∞ −∞ ∫ 𝑔₂(𝑥)𝑓(𝑥)𝑑𝑥 ∞ −∞ = 𝐸[𝑔₁(𝑥)] + 𝐸[𝑔₂(𝑥)]. ∎

b. Variansi dari Variabel Acak Definisi 2.22

Jika 𝑋 adalah variabel acak dengan rata-rata 𝐸(𝑋) = 𝜇, maka variansi dari

𝑋 didefinisikan sebagai nilai harapan dari (𝑋 − 𝜇)2_{, yaitu} 𝜎2 _{= 𝑉(𝑋) = 𝐸[(𝑋 − 𝜇)}2_] = { ∑(𝑥 − 𝜇)2𝑝(𝑥) 𝑥 , 𝑑𝑎𝑛jika 𝑋 diskrit, ∫ (𝑥 − 𝜇)2_{𝑓(𝑥)𝑑𝑥} ∞ −∞ , jika 𝑋 kontinu.

Standar deviasi dari 𝑋 adalah akar dari 𝑉(𝑋).

Contoh 2.12

Diberikan 7 komponen sebagai sampel yang terdiri atas 4 komponen tidak rusak dan 3 komponen rusak. Penguji mengambil sampel secara acak

sebanyak 3 komponen. Temukan nilai harapan dan variansi dari banyaknya komponen rusak di dalam pengambilan sampel tersebut. Solusi:

Misalkan 𝑋 adalah variabel acak yang menunjukkan banyaknya komponen rusak di dalam sampel. Fungsi probabilitas dari 𝑋 adalah

𝑝(𝑥) =( 3 𝑥)( 4 3−𝑥) (7₃) , 𝑥 = 0,1,2,3. Diperoleh: 𝑝(0) =( 3 0)( 4 3) (7₃) = 4 35, 𝑝(1) =( 3 1)( 4 2) (7₃) = 18 35, 𝑝(2) =( 3 2)( 4 1) (7₃) = 12 35, 𝑝(3) =( 3 3)( 4 0) (7₃) = 1 35. Oleh karena itu,

𝜇 = 𝐸(𝑋) = (0) (4 35) + (1) ( 18 35) + (2) ( 12 35) + (3) ( 1 35) = 1.3. 𝜎2 = 𝑉(𝑋) = ∑(𝑥 − 1.3)2𝑝(𝑥) 3 𝑥=0 = (0 − 1.3)2(4 35) + ⋯ + (3 − 1.3) 2₍1 35) = 0.49. Contoh 2.13

Diberikan variabel acak 𝑋 yang mempunyai fungsi kontinu sebagai berikut:

𝑓(𝑥) = {(3 8)𝑥 2

⁄ , 0 ≤ 𝑑𝑎𝑛𝑥 ≤ 2 0 , 𝑑𝑎𝑛lainnya

Temukanlah nilai harapan dan variansi bagi 𝑋. Solusi:

𝜇 = 𝐸(𝑋) = ∫ 𝑥 (2 3₈) 𝑥2_𝑑𝑥 0 = ( 3 8) ( 1 4) 𝑥 4_] 0 2 = 1.5. 𝜎2 _{= 𝑉(𝑋) = ∫ (𝑥 − 1.5)}2₍3 8) 𝑥 2_𝑑𝑥 2 0 = (3 8) ∫ (𝑥 2_{− 3𝑥 + 2.25)𝑥}2_𝑑𝑥 2 0 = (3 8) ∫ (𝑥 4_{− 3𝑥}3_{+ 2.25𝑥}2_)𝑑𝑥 2 0 = (3 8) (( 1 5) 𝑥 5 _{− (}3 4) 𝑥 4_{+ (}2.25 3 ) 𝑥 3_)] 0 2 = (3 40𝑥 5₋ 9 32𝑥 4_{+ (}6.75 24 ) 𝑥 3_)] 0 2 = 0.15. Teorema 2.3

Misalkan 𝑋 adalah variabel acak diskrit dengan fungsi probabilitas 𝑝(𝑥)

dan rata-rata 𝐸(𝑋) = 𝜇; maka

𝑉(𝑋) = 𝜎2 _{= 𝐸[(𝑋 − 𝜇)}2_{] = 𝐸(𝑋}2_{) − [𝐸(𝑋)]}2_. Bukti: 𝑉(𝑋) = 𝜎2 = 𝐸[(𝑋 − 𝜇)2] = 𝐸(𝑋2− 2𝜇𝑋 + 𝜇2) = 𝐸(𝑋2_{) − 2𝜇𝐸(𝑋) + 𝐸(𝜇}2₎ = 𝐸(𝑋2_{) − 2𝜇}2_{+ 𝜇}2 = 𝐸(𝑋2) − 𝜇2 = 𝐸(𝑋2) − [𝐸(𝑋)]2_{. ∎}

Contoh 2.14. Distribusi Normal

Distribusi probabilitas kontinu yang paling banyak digunakan adalah distribusi Normal.

Definisi 2.23

Variabel acak 𝑋 dikatakan berdistribusi Normal jika dan hanya jika untuk

𝜎 > 0 dan −∞ < 𝜇 < ∞, fungsi probabilitas dari 𝑋 adalah

𝑓(𝑥) = 1 𝜎√2𝜋𝑒

−(𝑥−𝜇)2/(2𝜎2)_{, −∞ < 𝑥 < ∞.}

Teorema 2.4

Jika 𝑋 adalah variabel acak berdistribusi Normal dengan parameter 𝜇 dan

𝜎, maka

𝐸(𝑋) = 𝜇 dan 𝑉(𝑋) = 𝜎2. Bukti:

Rata-rata dari distribusi Normal diberikan dengan

𝐸(𝑋 − 𝜇) = ∫ 𝑥 − 𝜇 √2𝜋𝜎𝑒 −1₂(𝑥−𝜇_𝜎 )2 𝑑𝑥. ∞ −∞

Misalkan 𝑧 = (𝑥 − 𝜇) 𝜎⁄ dan 𝑑𝑥 = 𝜎 𝑑𝑧, maka

𝐸(𝑋 − 𝜇) = 𝜎 √2𝜋∫ 𝑧𝑒 −𝑧₂2 𝑑𝑧 = 0 ∞ −∞

karena fungsi dari 𝑧 adalah fungsi ganjil. Dengan menggunakan Teorema 2.1, diperoleh:

𝐸(𝑋 − 𝜇) = 0 𝐸(𝑋) − 𝜇 = 0

𝐸(𝑋) = 𝜇. Variansi dari distribusi Normal diberikan dengan

𝐸[(𝑋 − 𝜇)2_{] = ∫} (𝑥 − 𝜇) 2 𝜎√2𝜋 𝑒 −1₂(𝑥−𝜇_𝜎 )2 𝑑𝑥 ∞ −∞ .

Misalkan 𝑧 = (𝑥 − 𝜇) 𝜎⁄ dan 𝑑𝑥 = 𝜎 𝑑𝑧, maka

𝐸[(𝑋 − 𝜇)2_{] =} 𝜎 2 √2𝜋∫ 𝑧 2_𝑒−𝑧 2 2 _𝑑𝑧 ∞ −∞ .

Misalkan 𝑢 = 𝑧 dan 𝑑𝑣 = 𝑧𝑒−𝑧22 𝑑𝑧_{, maka} 𝑑𝑢 = 𝑑𝑧 _dan 𝑣 = −𝑒− 𝑧2

2_,

𝐸[(𝑋 − 𝜇)2] = 𝜎 2 √2𝜋(−𝑧𝑒 −𝑧₂2 | −∞ ∞ + ∫ 𝑒−𝑧 2 2 _𝑑𝑧 ∞ −∞ ) = 𝜎2(0 + 1) = 𝜎2_{. ∎}

Teorema 2.4 menunjukkan bahwa parameter 𝜇 berada pada pusat distribusi dan 𝜎 mengukur penyebarannya. Grafik fungsi probabilitas Normal ditunjukkan pada gambar berikut.

Gambar 2.1. Fungsi probabilitas Normal

Variabel acak Normal 𝑋 dapat diubah ke variabel acak Normal standar 𝑍

dengan menggunakan hubungan

𝑍 =𝑋 − 𝜇 𝜎 .

Kemudian melalui Tabel distribusi Normal Standar (Tabel 𝑍), dapat digunakan untuk menghitung probabilitas. Nilai rata-rata 𝑍 harus 0 dan standar deviasinya harus 1.

Contoh 2.15

Skor prestasi untuk ujian masuk perguruan tinggi memiliki rata-rata 75

dan standar deviasi 10. Hitunglah 𝑃(80 < 𝑋 < 90). Solusi:

Ingat bahwa

𝑍 =𝑋−𝜇 𝜎 .

Dengan demikian, 𝑃(80 < 𝑋 < 90) = 𝑃 (80 − 75 10 < 𝑋 − 𝜇 𝜎 < 90 − 75 10 ) = 𝑃(0.5 < 𝑍 < 1.5) = 𝑃(𝑍 > 0.5) − 𝑃(𝑍 > 1.5) = 0.3085 − 0.0668 = 0.2417

Hasil tersebut dapat diperoleh dengan menggunakan Tabel 𝑍 (terlampir).

Contoh 2.16

Misalkan 𝑍 adalah variabel acak Normal dengan rata-rata 0 dan standar deviasi 1.

a) Temukan 𝑃(𝑍 > 2).

b) Temukan 𝑃(−2 ≤ 𝑍 ≤ 2).

Solusi:

a) Karena 𝜇 = 0 dan 𝜎 = 1, maka dengan menggunakan Tabel distribusi Normal, diperoleh 𝑃(𝑍 > 2) = 0.0228.

b) Karena fungsi probabilitas Normal simetri pada rata-rata

𝜇 = 0, maka dengan menggunakan Tabel 𝑍 (terlampir), diperoleh

𝑃(−2 ≤ 𝑍 ≤ 2) = 1 − 2(𝑃(𝑍 > 2))

= 1 − 2(0.0228) = 0.9544.

Contoh 2.17. Distribusi Chi-Square

Variabel acak kontinu 𝑋 berdistribusi chi-square dengan derajat bebas 𝑣, jika fungsi probabilitasnya diberikan dengan

𝑓(𝑥; 𝑣) = { 1 2𝑣2_{Γ(𝑣 2)}⁄ 𝑥𝑣2−1_𝑒− 𝑥 2_{, 𝑑𝑎𝑛𝑥 > 0,} 0 , 𝑑𝑎𝑛lainnya,

dengan 𝑣 adalah bilangan bulat positif dan Γ(𝑣 2)⁄ adalah fungsi Gamma.

Teorema 2.5

Jika 𝑋 adalah variabel acak berdistribusi chi-square dengan derajat bebas

𝑣, maka nilai harapan (rata-rata) dan variansinya adalah

𝜇 = 𝐸(𝑋) = 𝑣 dan 𝜎2 _{= 𝑉(𝑋) = 2𝑣.} Bukti: Misalkan 𝑐 = 1 2 𝑣 2Γ(𝑣 2)⁄ . 𝐸(𝑋) = ∫ 𝑥𝑐𝑥𝑣2−1_𝑒− 𝑥 2_𝑑𝑥 ∞ 0 = 𝑐 ∫ 𝑥𝑣2_𝑒− 𝑥 2_𝑑𝑥 ∞ 0 = 𝑐 {[−2𝑥𝑣2_𝑒− 𝑥 2_] 0 ∞ + ∫ 2𝑣 2𝑥 𝑣 2−1_𝑒− 𝑥 2_𝑑𝑥 ∞ 0 } = 𝑐 {(0 − 0) + 𝑣 ∫ 𝑥𝑣2−1_𝑒− 𝑥 2_𝑑𝑥 ∞ 0 } = 𝑣 ∫ 𝑐𝑥𝑣2−1_𝑒− 𝑥 2_𝑑𝑥 ∞ 0 = 𝑣. (berdasarkan Definisi 2.13 (2)) Berdasarkan Teorema 2.3, 𝑉(𝑋) = 𝐸[(𝑋 − 𝜇)2_{] = 𝐸(𝑋}2_{) − [𝐸(𝑋)]}2_. 𝐸(𝑋2) = ∫ 𝑥2𝑓(𝑥)𝑑𝑥 ∞ −∞ = ∫ 𝑥2𝑐𝑥𝑣2−1_𝑒− 𝑥 2_𝑑𝑥 ∞ 0 = 𝑐 ∫ 𝑥𝑣2+1_𝑒− 𝑥 2_𝑑𝑥 ∞ 0

= 𝑐 {−2𝑥𝑣2+1_𝑒− 𝑥 2_] 0 ∞ + ∫ 2 (𝑣 2+ 1) 𝑥 𝑣 2_𝑒− 𝑥 2_𝑑𝑥 ∞ 0 } = 𝑐 {(0 − 0) + (𝑣 + 2) ∫ 𝑥𝑣2_𝑒− 𝑥 2_𝑑𝑥 ∞ 0 } = 𝑐(𝑣 + 2) {∫ 𝑥𝑣2_𝑒− 𝑥 2_𝑑𝑥 ∞ 0 } = 𝑐(𝑣 + 2) {[−2𝑥𝑣2_𝑒− 𝑥 2_] 0 ∞ + ∫ 2𝑣 2𝑥 𝑣 2−1_𝑒− 𝑥 2_𝑑𝑥 ∞ 0 } = 𝑐(𝑣 + 2) {(0 − 0) + 𝑣 ∫ 𝑥𝑣2−1_𝑒− 𝑥 2_𝑑𝑥 ∞ 0 } = 𝑣(𝑣 + 2) {∫ 𝑐𝑥𝑣2−1_𝑒− 𝑥 2_𝑑𝑥 ∞ 0 } = 𝑣(𝑣 + 2){∫ 𝑥𝑓(𝑥)𝑑𝑥₀∞ } = 𝑣(𝑣 + 2), (berdasarkan Definisi 2.13 (2)) [𝐸(𝑋)]2 _{= 𝑣}2 𝑉(𝑋) = 𝐸(𝑋2) − [𝐸(𝑋)]2 = 𝑣(𝑣 + 2) − 𝑣2 = 𝑣(𝑣 + 2 − 𝑣) = 2𝑣. ∎

c. Momen dan Fungsi Pembangkit Momen (FPM) Definisi 2.24

Momen ke-𝑘 dari variabel acak 𝑋 didefinisikan sebagai 𝐸(𝑋𝑘) dan dinotasikan dengan 𝜇′_𝑘 dengan 𝑘 = 1,2,3, … .

Definisi 2.25

Fungsi pembangkit momen dari variabel acak 𝑋 diberikan dengan 𝐸(𝑒𝑡𝑋)

dan dinotasikan dengan 𝑀_𝑋(𝑡), 𝑡 ∈ ℝ. Oleh karena itu,

𝑀𝑋(𝑡) = 𝐸(𝑒𝑡𝑋) = { ∑ 𝑒𝑡𝑥_𝑝(𝑥) 𝑥 , jika 𝑑𝑎𝑛𝑋 diskrit, ∫ 𝑒𝑡𝑥𝑓(𝑥) 𝑑𝑥 ∞ −∞ , jika 𝑑𝑎𝑛𝑋 kontinu. Contoh 2.18

Temukanlah FPM dari Contoh 2.12 dan Contoh 2.13. Solusi:

Untuk Contoh 2.12, diperoleh:

Untuk Contoh 2.13, diperoleh:

Dengan menggunakan integral parsial, diperoleh hasil sebagai berikut:

𝑀_𝑋(𝑡) = 𝐸(𝑒𝑡𝑋) = ∑ 𝑒𝑡𝑥𝑝(𝑥) 𝑥 = 𝑒0𝑡𝑝(0) + 𝑒𝑡𝑝(1) + 𝑒2𝑡𝑝(2) + 𝑒3𝑡𝑝(3) = 4 35+ 18 35𝑒 𝑡₊12 35𝑒 2𝑡₊ 1 35𝑒 3𝑡_. = 1 35(4 + 18𝑒 𝑡_{+ 12𝑒}2𝑡_{+ 𝑒}3𝑡_{); 𝑡 ∈ ℝ.} 𝑀_𝑋(𝑡) = 𝐸(𝑒𝑡𝑋) = ∫ 𝑒𝑡𝑥_{𝑓(𝑥) 𝑑𝑥} ∞ −∞ =3 8∫ 𝑥 2_𝑒𝑡𝑥_𝑑𝑥 2 0

Dengan menggunakan kembali integral parsial, diperoleh: 𝑀_𝑋(𝑡) =3 8{[ 𝑥2_𝑒𝑡𝑥 𝑡 ] 0 2 −2 𝑡∫ 𝑥𝑒 𝑡𝑥_𝑑𝑥 2 0 } =3 8[( 4𝑒2𝑡 𝑡 ) − 2 𝑡∫ 𝑥𝑒 𝑡𝑥_𝑑𝑥 2 0 ] 𝑀_𝑋(𝑡) =3 8[( 4𝑒2𝑡 𝑡 ) − 2 𝑡( 𝑥𝑒𝑡𝑥 𝑡 ] 0 2 −1 𝑡∫ 𝑒 𝑡𝑥_𝑑𝑥 2 0 )] =3 8[( 4𝑒2𝑡 𝑡 ) − 2 𝑡( 2𝑒2𝑡 𝑡 − 1 𝑡[ 𝑒𝑡𝑥 𝑡 ] 0 2 )] =3 8[( 4𝑒2𝑡 𝑡 ) − 2 𝑡( 2𝑒2𝑡 𝑡 − 1 𝑡( 𝑒2𝑡 𝑡 − 1 𝑡))] =3 8[( 4𝑒2𝑡 𝑡 ) − 2 𝑡( 2𝑒2𝑡 𝑡 − 𝑒2𝑡 𝑡2 + 1 𝑡2)] =3 8[ 4𝑒2𝑡 𝑡 − 4𝑒2𝑡 𝑡2 + 2𝑒2𝑡_{+ 2} 𝑡3 ] =3 8[ 2 𝑡(2𝑒 2𝑡₋2𝑒2𝑡 𝑡 + 𝑒2𝑡_{+ 1} 𝑡2 )] = 3 4𝑡(2𝑒 2𝑡₋2𝑒 2𝑡 𝑡 + 𝑒2𝑡 + 1 𝑡2 ).

C. Distribusi Sampling

Kesimpulan pada statistika pada dasarnya berkaitan dengan generalisasi dan dugaan yang diperoleh dari sampel. Oleh karena itu, sampel yang diamati harus memiliki distribusi probabilitas.

Definisi 2.26

Distribusi probabilitas dari statistik disebut sebagai distribusi sampling.

Distribusi sampling dari statistik bergantung pada distribusi populasi, ukuran sampel, dan metode pemilihan sampel. Distribusi probabilitas dari 𝑥̅ disebut distribusi sampling dari rata-rata.

Distribusi sampling dari 𝑥̅ dan 𝑠2 dapat digunakan untuk membuat kesimpulan pada parameter 𝜇 dan 𝜎2.

1. Teorema Limit Pusat

Jika dilakukan penarikan sampel dari populasi dengan distribusi yang tidak diketahui, maka distribusi sampling dari 𝑥̅ akan tetap mendekati Normal dengan rata-rata 𝜇 dan variansi 𝜎2⁄_𝑛, asalkan ukuran sampelnya besar. Hal ini adalah akibat langsung dari Teorema Limit Pusat (TLP).

Teorema 2.6 (TLP)

Misalkan 𝑥₁, 𝑥₂, … , 𝑥_𝑛 merupakan variabel acak saling bebas dan terdistribusi dengan 𝐸(𝑥_𝑖) = 𝜇 dan 𝑉(𝑥_𝑖) = 𝜎2 _{< ∞. Variabel acak 𝑈}

𝑛 didefinisikan sebagai 𝑈𝑛 = ( 𝑥̅−𝜇 𝜎/√𝑛) dengan 𝑥̅ = 1 𝑛∑ 𝑥𝑖. 𝑛 𝑖=1

Fungsi distribusi dari 𝑈𝑛 konvergen ke fungsi distribusi Normal standar untuk 𝑛 → ∞, yaitu lim 𝑛→∞𝑃(𝑈𝑛 ≤ 𝑢) = ∫ 1 √2𝜋𝑒 −𝑡2⁄2_{𝑑𝑡, ∀𝑢} 𝑢 −∞ .

Teorema 2.7

Misalkan 𝑋 dan 𝑋1, 𝑋2, … , 𝑋𝑛 adalah variabel acak dengan FPM 𝑚(𝑡) dan 𝑚₁(𝑡), 𝑚2(𝑡), 𝑚3(𝑡), …, dan seterusnya.

Jika

lim

𝑛→∞𝑚𝑛(𝑡) = 𝑚(𝑡), ∀𝑡 ∈ ℝ,

maka fungsi distribusi dari 𝑋𝑛 konvergen ke fungsi distribusi dari 𝑋 untuk 𝑛 → ∞.

Bukti:

Bukti terdapat pada buku Williams, David. (1991). Probability with Martingales. New York: Cambridge University Press. Halaman: 185.

Bukti Teorema Limit Pusat Diketahui: 𝑈_𝑛 = √𝑛 (𝑥̅ − 𝜇 𝜎 ) = √𝑛 ( ∑𝑛𝑖=1𝑥𝑖 𝑛 − 𝜇 𝜎 ) = √𝑛 (∑𝑛𝑖=1𝑋𝑖−𝑛𝜇 𝑛𝜎 ) = √𝑛 𝑛 ( ∑𝑛𝑖=1𝑋𝑖−𝑛𝜇 𝜎 ) = 1 √𝑛(∑ 𝑧𝑖 𝑛 𝑖=1 ), dengan 𝑧_𝑖 = 𝑋𝑖−𝜇 𝜎 .

Karena variabel acak 𝑥_𝑖 saling bebas dan berdistribusi secara identik, maka

𝑧𝑖 dengan 𝑖 = 1,2, . . . , 𝑛 juga saling bebas dan berdistribusi secara identik dengan 𝐸(𝑧_𝑖) = 0 dan 𝑉(𝑧_𝑖) = 1.

Karena fpm dari banyaknya variabel acak saling bebas masing-masing adalah hasil kali dari masing-masing fpm, maka

𝑚∑ 𝑍_𝑖(𝑡) = 𝑚𝑍1(𝑡) × 𝑚𝑍2(𝑡) … × 𝑚𝑍𝑛(𝑡) = [𝑚𝑍1(𝑡)] 𝑛 dan 𝑚_𝑈𝑛(𝑡) = 𝑚∑ 𝑍_𝑖(_√𝑛𝑡) = [𝑚𝑍1( 𝑡 √𝑛)] 𝑛 .

Dengan menggunakan Teorema Deret Taylor di sekitar 0 dan dengan suku sisa bentuk Lagrange,

𝑚_𝑍1(𝑡) = 𝑚𝑍1(0) + 𝑚′𝑍1(0)𝑡 + 𝑚′′𝑍1(𝜉)

𝑡2

sehingga 𝑚_𝑈𝑛(𝑡) = [1 +𝑚′′𝑍1(𝜉𝑛) 2 ( 𝑡 √𝑛) 2 ] 𝑛 = [1 +𝑚′′𝑍1(𝜉𝑛)𝑡 2 2𝑛 ] 𝑛 , dengan 0 < 𝜉_𝑛 < 𝑡 √𝑛. Perhatikan bahwa karena 𝑛 → ∞, 𝜉_𝑛 → 0 dan

𝑚′′_𝑍1(𝜉𝑛)(𝑡2⁄ ) → 𝑚′′2 𝑍1(0)(𝑡

2_{⁄ ) = 𝐸(𝑍2}

12)(𝑡2⁄ ) = (𝑡2 2⁄ )2 dengan 𝐸(𝑍₁2) = 𝑉(𝑍1) = 1.

Perlu diingat bahwa jika lim

𝑛→∞𝑏𝑛 = 𝑏, maka lim𝑛→∞(1 + 𝑏𝑛 𝑛) 𝑛 = 𝑒𝑏. Akhirnya diperoleh, lim 𝑛→∞𝑚𝑈𝑛(𝑡) = lim𝑛→∞[1 + 𝑚′′_𝑍1(𝜉𝑛)(𝑡2⁄ )2 𝑛 ] 𝑛 = 𝑒(𝑡2⁄ )2 ,

fpm untuk variabel acak Normal standar. Dengan menerapkan Teorema 2.7, dapat disimpulkan bahwa 𝑈_𝑛 memiliki fungsi distribusi yang konvergen ke fungsi distribusi dari variabel acak Normal standar. ∎

2. Distribusi 𝑡 Definisi 2.27 Misalkan 𝑍 = 𝑥̅−𝜇

𝜎/√𝑛 adalah variabel acak Normal standar dan 𝑊 =

(𝑛−1)𝑠2 𝜎2

berdistribusi 𝜒2 dengan derajat bebas 𝑣. Jika 𝑍 dan 𝑊 saling bebas, maka

𝑇 = 𝑍

√𝑊/𝑣

berdistribusi 𝑡 dengan derajat bebas 𝑣.

Lemma2.3

Misalkan 𝑥₁, 𝑥₂, … , 𝑥_𝑛 sebagai variabel acak saling bebas berdistribusi Normal dengan rata-rata 𝜇 dan standar deviasi 𝜎; maka variabel acak 𝑇 =

𝑥̅−𝜇

𝑠/√𝑛 berdistribusi 𝑡 dengan derajat bebas 𝑣 = 𝑛 − 1. Bukti:

𝑇 = 𝑍 √𝑊/𝑣 = (𝑥̅ − 𝜇) (𝜎/√𝑛)⁄ √[(𝑛 − 1)𝑠2_/𝜎2_{] (𝑛 − 1)⁄} =√𝑛(𝑥̅ − 𝜇) 𝜎⁄ √𝑠2_/𝜎2 =√𝑛(𝑥̅ − 𝜇) 𝜎⁄ 𝑠/𝜎 = √𝑛(𝑥̅ − 𝜇) 𝑠

berdistribusi 𝑡 dengan derajat bebas 𝑣 = (𝑛 − 1). ∎

Contoh 2.19

Temukan 𝑃(−𝑡0.025 < 𝑇 < 𝑡0.025). Solusi:

Dari tabel distribusi 𝑡 (terlampir) diperoleh,

𝑃(−𝑡_0.025 < 𝑇 < 𝑡_0.025) = 1 − 0.05 − 0.025 = 0.925.

D. Pendugaan Parameter

Pendugaan adalah pokok bahasan dalam statistika yang berhubungan dengan pendugaan nilai-nilai parameter berdasarkan data yang diukur/data empiris yang berasal dari sampel acak. Tujuan dari percobaan atau penelitian statistik adalah untuk menduga satu atau lebih parameter yang relvan. Pendugaan parameter adalah suatu proses untuk membuat kesimpulan tentang parameter populasi berdasarkan sampel acak.

1. Pendugaan (Estimasi)

Di dalam statistika, pendugaan-pendugaan dilakukan untuk menyimpulkan karakteristik dari populasi (parameter).

Definisi 2.28 (Wackerly, et al., 2008: 391)

Penduga adalah suatu aturan, yang dinyatakan dalam bentuk rumus, yang memberitahukan bagaimana cara menghitung nilai suatu dugaan berdasarkan pengukuran yang termuat di dalam sampel.

Penduga dari parameter 𝜃 adalah statistik 𝜃̂. Contoh dari parameter

𝜃 dapat berupa rata-rata µ, standar deviasi 𝜎, dan proporsi 𝑝 yang diduga dengan rata-rata 𝑥̅, standar deviasi 𝑠, dan proporsi 𝑝̂.

2. Macam-Macam Pendugaan Parameter

Nilai parameter dapat diduga dengan dua cara, yakni: penduga titik dan penduga selang.

2.1. Penduga Titik Definisi 2.29

Penduga titik adalah penentuan suatu nilai tunggal berdasarkan atas sampel yang dengan baik menduga parameter yang sebenarnya.

Bias dan Rata-rata Galat Kuadrat dari Penduga Titik

Dalam pemilihan sampel, hal yang sering dilakukan adalah memilih anggota yang paling cocok dari populasi. Cara tersebut dapat menyebabkan kesimpulan yang keliru mengenai populasi dan dapat dikatakan sebagai bias. Oleh karena itu, diperlukan pemilihan sampel secara acak.

Misalkan seorang pria menembak satu tembakan pada suatu sasaran dan mengenai sasaran tersebut. Apakah dapat disimpulkan bahwa pria tersebut adalah penembak jitu? Apakah ingin disimpulkan dugaan sementara pada tembakan kedua? Jelas, tidak bisa disimpulkan bahwa pria tersebut adalah seorang ahli menembak berdasarkan bukti yang sedikit. Di sisi lain, jika 100 tembakan berturut-turut dapat menembak tepat sasaran, mungkin dapat diperoleh keyakinan bahwa orang tersebut adalah seorang penembak jitu dan berkeyakinan besar untuk menembak tepat sasaran. Dapat dikatakan bahwa hal itu adalah distribusi dari pendugaan yang tepat mengenai parameter sasaran, seperti yang ditunjukkan pada Gambar 2.2. Dengan kata lain, rata-rata atau nilai yang diharapkan dari distribusi nilai dugaan akan sama dengan parameter nilai dugaan,

𝜃̂ 𝜃

yaitu 𝐸(𝜃̂) = 𝜃. Penduga titik yang memenuhi sifat ini dikatakan sebagai penduga tak bias. Distribusi sampling untuk suatu penduga titik bias positif adalah 𝐸(𝜃̂) > 𝜃, ditunjukkan pada Gambar 2.3.

Gambar 2.2. Distribusi Nilai Dugaan

Gambar 2.3. Distribusi Sampling untuk Penduga Titik Bias Positif

Definisi 2.30

Misalkan 𝜃̂ adalah penduga titik dari parameter 𝜃, maka 𝜃̂ adalah penduga tak bias bagi 𝜃 jika 𝐸(𝜃̂) = 𝜃. Jika 𝐸(𝜃̂) ≠ 𝜃, maka 𝜃̂

dikatakan penduga yang bias bagi 𝜃.

Definisi 2.31

Bias dari penduga titik 𝜃̂ didefinisikan sebagai 𝐵(𝜃̂) = 𝐸(𝜃̂) − 𝜃.

Contoh 2.20

Misalkan 𝑥1, 𝑥2, … , 𝑥𝑛 adalah sampel acak dengan 𝐸(𝑥𝑖) = 𝜇 dan 𝑉(𝑥𝑖) = 𝜎2. Tunjukkan bahwa 𝑠′2= 1 𝑛∑ (𝑥𝑖 − 𝑥̅) 2 𝑛 𝑖=1 adalah

penduga bias bagi 𝜎2 dan bahwa 𝑠2 = 1

𝑛−1∑ (𝑥𝑖− 𝑥̅) 2 𝑛

𝑖=1 adalah

Solusi: ∑(𝑥𝑖 − 𝑥̅)2 = 𝑛 𝑖=1 ∑(𝑥_𝑖2− 2𝑥̅𝑥𝑖 + 𝑥̅2) 𝑛 𝑖=1 = ∑ 𝑥_𝑖2− 2𝑥̅ ∑ 𝑥_𝑖 + ∑ 𝑥̅2 𝑛 𝑖=1 𝑛 𝑖=1 𝑛 𝑖=1 = ∑ 𝑥_𝑖2− 2𝑥̅𝑛 𝑛 𝑖=1 𝑥̅ + 𝑛𝑥̅2 = ∑ 𝑥_𝑖2− 2𝑛𝑥̅2 𝑛 𝑖=1 + 𝑛𝑥̅2 = ∑ 𝑥_𝑖2− 𝑛𝑥̅2 𝑛 𝑖=1 sehingga, 𝐸 [∑(𝑥_𝑖− 𝑥̅)2 𝑛 𝑖=1 ] = 𝐸 [∑ 𝑥_𝑖2− 𝑛𝑥̅2 𝑛 𝑖=1 ] = 𝐸 [∑ 𝑥_𝑖2 𝑛 𝑖=1 ] − n𝐸[𝑥̅2_] = ∑ 𝐸[𝑥_𝑖2] 𝑛 𝑖=1 − n𝐸[𝑥̅2]

Karena 𝐸[𝑋_𝑖2] sama untuk ∀𝑖 = 1,2, … , 𝑛 dan

𝑉(𝑋) = 𝐸[𝑋2_{] − (𝐸[𝑋])}2 _{= 𝐸[𝑋}2_{] − 𝜇}2_, maka 𝐸[𝑋2] = 𝑉(𝑋) + 𝜇2 dan 𝐸 [∑(𝑥_𝑖 − 𝑥̅)2 𝑛 𝑖=1 ] = ∑ 𝐸[𝑥_𝑖2] 𝑛 𝑖=1 − n𝐸[𝑥̅2] = ∑[𝑉(𝑥_𝑖) + 𝜇2_{] − 𝑛[𝑉(𝑥̅) + 𝜇}2_] 𝑛 𝑖=1 = ∑(𝜎2+ 𝜇2) − 𝑛 (𝜎 2 𝑛 + 𝜇 2₎ 𝑛 𝑖=1 = 𝑛(𝜎2_{+ 𝜇}2_{) − 𝑛 (}𝜎 2 𝑛 + 𝜇 2₎ = 𝑛𝜎2_{+ 𝑛𝜇}2 _{− 𝜎}2_{− 𝑛𝜇}2 = (𝑛 − 1)𝜎2

Oleh karena itu, 𝐸(𝑠′2_{) =} 1 𝑛𝐸[∑ (𝑥𝑖− 𝑥̅) 2 𝑛 𝑖=1 ] = 1 𝑛[(𝑛 − 1)𝜎 2_{] =}𝑛−1 𝑛 𝜎 2_{, maka} 𝑛 𝑛−1𝐸(𝑠 ′2_{) = 𝜎}2_.

Dengan demikian, 𝑠′2 _{adalah penduga bias bagi 𝜎}2 _karena 𝐸(𝑠′2) ≠ 𝜎2. Akan tetapi, 𝐸(𝑠2) = 1 𝑛 − 1𝐸 [∑(𝑥𝑖 − 𝑥̅) 2 𝑛 𝑖=1 ] = 1 𝑛 − 1[(𝑛 − 1)𝜎 2_] =𝑛 − 1 𝑛 − 1𝜎 2 _{= 𝜎}2_,

sehingga 𝑠2 adalah penduga tak bias bagi 𝜎2 karena 𝐸(𝑠2) = 𝜎2_.

Definisi 2.32

Rata-rata kuadrat galat (Mean Square Error) dari penduga titik 𝜃̂

adalah

𝑀𝑆𝐸(𝜃̂) = 𝐸 [(𝜃̂ − 𝜃)2].

𝑀𝑆𝐸(𝜃̂) adalah fungsi dari variansi dan biasnya.

Definisi 2.33

Teorema 2.8

Jika 𝐵(𝜃̂) menunjukkan bias dari penduga titik 𝜃̂, maka

𝑀𝑆𝐸(𝜃̂) = 𝑉(𝜃̂) + [𝐵(𝜃̂)]2. Bukti:

Petunjuk:

(𝜃̂ − 𝜃) = [𝜃̂ − 𝐸(𝜃̂)] + [𝐸(𝜃̂) − 𝜃] = [𝜃̂ − 𝐸(𝜃̂)] + 𝐵(𝜃̂). Dengan menggunakan petunjuk di atas, diperoleh:

𝑀𝑆𝐸(𝜃̂) = 𝐸 [(𝜃̂ − 𝜃)2] = 𝐸 [((𝜃̂ − 𝐸(𝜃̂)) + 𝐵(𝜃̂)) ∙ ((𝜃̂ − 𝐸(𝜃̂)) + 𝐵(𝜃̂))] = 𝐸 [(𝜃̂ − 𝐸(𝜃̂))2+ 2 (𝜃̂ − 𝐸(𝜃̂)) 𝐵(𝜃̂) + (𝐵(𝜃̂))2] = 𝐸 [(𝜃̂ − 𝐸(𝜃̂))2] + 2𝐵(𝜃̂)𝐸[𝜃̂ − 𝐸(𝜃̂)] + [𝐵(𝜃̂)]2 = 𝑉(𝜃̂) + 2𝐵(𝜃̂)(𝐸[𝜃̂] − 𝐸[𝐸(𝜃̂)]) + [𝐵(𝜃̂)]2 = 𝑉(𝜃̂) + 2𝐵(𝜃̂)[𝐸(𝜃̂) − 𝐸(𝜃̂)] + [𝐵(𝜃̂)]2 = 𝑉(𝜃̂) + [𝐵(𝜃̂)]2. ∎

Tabel 2.2. Nilai Harapan dan galat standar Beberapa Penduga Titik Parameter Sasaran 𝜃 Ukuran Sampel Penduga Titik 𝜃̂ Galat standar 𝐸(𝜃̂) 𝜎𝜃 𝜇 𝑛 𝑋̅ 𝜇 𝜎 √𝑛 𝑝 𝑛 𝑝̂ =𝑋 𝑛 𝑝 √ 𝑝𝑞 𝑛 𝜇1− 𝜇2 𝑛1dan 𝑛2 𝑋̅₁− 𝑋̅₂ 𝜇₁− 𝜇_{2 √}𝜎1 2 𝑛1 +𝜎2 2 𝑛2 𝑝1− 𝑝2 𝑛1dan 𝑛2 𝑝̂1− 𝑝̂2 𝑝̂1− 𝑝̂2 √ 𝑝1𝑞1 𝑛1 +𝑝2𝑞2 𝑛2

2.2. Penduga Selang Kepercayaan Definisi 2.33

Penduga selang adalah suatu penentuan selang nilai yang dihitung berdasarkan pengukuran sampel dan mempunyai peluang tertentu, akan memuat parameter yang sebenarnya.

Idealnya, selang yang dihasilkan akan memiliki dua sifat: Pertama, akan memuat parameter sasaran 𝜃; kedua, menghasilkan selang yang relatif sempit. Salah satu atau kedua batas dari selang menjadi fungsi dari pengukuran sampel, yang akan bervariasi secara acak dari sampel yang satu ke sampel lainnya.

Penduga selang biasa disebut “Selang Kepercayaan”. Pro-babilitas bahwa selang kepercayaan akan memuat parameter sasaran

𝜃 disebut “Koefisien Kepercayaan”. Jika diketahui bahwa koefisien kepercayaan memiliki nilai yang tinggi, maka dapat dipercaya bahwa setiap selang kepercayaan yang dibentuk dengan mengguna-kan hasil dari sampel amengguna-kan memuat parameter sasaran 𝜃.

Misalkan 𝜃̂_𝐿 dan 𝜃̂_𝑈 adalah batas bawah dan atas untuk parameter 𝜃. Jika

𝑃(𝜃̂𝐿 ≤ 𝜃 ≤ 𝜃̂𝑈) = 1 − 𝛼,

untuk 0 < 𝛼 < 1, maka probabilitas (1 − 𝛼) adalah koefisien kepercayaan. Selang 𝜃̂𝐿 ≤ 𝜃 ≤ 𝜃̂𝑈 dihitung dari sampel yang diseleksi, ini adalah selang kepercayaan 100(1 − 𝛼)%, dan titik akhir 𝜃̂_𝐿 dan 𝜃̂_𝑈 sebagai titik batas terbesar dan terkecil dari selang kepercayaan. Jadi, sebagai contohnya, ketika 𝛼 = 0.05, berarti diperoleh selang kepercayaan 95%, dan ketika 𝛼 = 0.01, diperoleh selang kepercayaan 99%. Semakin lebar selang kepercayaan, maka selang kepercayaan tersebut memuat parameter yang tidak diketahui. Akan tetapi, lebih baik jika menghasilkan selang yang relatif pendek dengan tingkat kepercayaan yang tinggi.

Selang acak yang dihasilkan didefinisikan dengan [𝜃̂𝐿, 𝜃̂𝑈] yang disebut sebagai “Selang Kepercayaan Dua Sisi”.

Definisi 2.34

Selang kepercayaan satu sisi yang dinyatakan dengan

𝑃(𝜃̂𝐿 ≤ 𝜃) = 1 − 𝛼

akan menghasilkan selang kepercayaan satu sisi bawah, yaitu

[𝜃̂_𝐿, ∞), dan

𝑃(𝜃 ≤ 𝜃̂𝑈) = 1 − 𝛼

akan menghasilkan selang kepercayaan satu sisi atas, yaitu

(−∞, 𝜃̂_𝑈].

Salah satu metode yang sangat berguna untuk mencari selang kepercayaan adalah Metode Pivot. Metode ini tergantung pada suatu nilai yang disebut besaran Pivot. Besaran ini memiliki dua karak-teristik, yaitu:

i. Merupakan fungsi dari pengukuran sampel dan parameter 𝜃 yang tidak diketahui.

ii. Distribusi probabilitas dari besaran ini tidak tergantung pada parameter 𝜃.

Jika distribusi probabilitas dari besaran Pivot diketahui, maka besaran tersebut dapat digunakan untuk membentuk nilai dugaan selang yang diinginkan.

Contoh 2.21

Diberikan pengamatan tunggal 𝑋 dari distribusi eksponensial dengan rata-rata 𝜃. Gunakan 𝑋 untuk membentuk selang kepercayaan bagi

𝜃 dengan koefisien kepercayaan 0.90. Solusi:

Fungsi densitas probabilitas bagi 𝑋 diberikan dengan 𝑓(𝑥) = {( 1 𝜃) 𝑒−𝑥 𝜃 ⁄ _{, 𝑑𝑎𝑛𝑥 ≥ 0} 0 , danlainnya

Dengan menggunakan Metode Pivot, akan diperiksa apakah 𝑈 = 𝑋 𝜃 memenuhi syarat sebagai besaran Pivot?

1) 𝑈 = 𝑋

𝜃 adalah fungsi dari 𝑋 (ukuran sampel) dan 𝜃 tidak diketahui. 2) 𝑈 = 𝑋 𝜃 𝑓_𝑢(𝑢) = ⋯ ? Untuk 𝑥 < 0, 𝐹(𝑥) = 0. Untuk 𝑥 ≥ 0, 𝐹(𝑥) = ∫ 0 𝑑𝑡 + 0 −∞ ∫ (1 𝜃) 𝑒−𝑡 𝜃 ⁄ _{𝑑𝑡 =} 𝑥 0 1 𝜃(−𝜃)𝑒−𝑡 𝜃 ⁄ _]𝑥 0 = −𝑒−𝑥 𝜃⁄ + 1. 𝐹(𝑥) = {0 , 𝑑𝑎𝑛𝑥 < 0 −𝑒−𝑥 𝜃⁄ + 1, 𝑑𝑎𝑛𝑥 ≥ 0 𝐹_𝑢(𝑢) = 𝑃(𝑈 ≤ 𝑢) = 𝑃 (𝑋 𝜃 ≤ 𝑢) = 𝑃(𝑋 ≤ 𝑢𝜃) = 𝐹(𝑢𝜃) = −𝑒−𝑢𝜃 𝜃⁄ + 1 = −𝑒−𝑢+ 1. 𝐹_𝑢(𝑢) = {0 , 𝑑𝑎𝑛𝑢 < 0 −𝑒−𝑢+ 1, 𝑑𝑎𝑛𝑢 ≥ 0 𝑓𝑢(𝑢) = {0 ,_𝑒−𝑢 _{, 𝑑𝑎𝑛𝑢 ≥ 0}𝑑𝑎𝑛𝑢 < 0

 Kedua syarat besaran Pivot terpenuhi

Gambar 2.4. Fungsi probabilitas bagi 𝑈

Selanjutnya akan dicari selang kepercayaan bagi 𝜃 ∗ 𝑃(𝑈 < 𝑎) = ∫ 𝑒𝑎 −𝑢 _{𝑑𝑢 =} 0 0.05 −𝑒−𝑢]𝑎 0 = 0.05 1−𝑒−𝑎 = 0.05 𝑒−𝑎 _{= 0.95} ln(𝑒−𝑎) = ln(0.95) −𝑎 = −0.051 𝑎 = 0.051 *𝑃(𝑈 > 𝑏) = ∫ 𝑒_𝑏∞ −𝑢 𝑑𝑢 =0.05 −𝑒−𝑢_]∞ 𝑏 = 0.05 𝑒−𝑏 = 0.05 ln(𝑒−𝑏) = ln(0.05) −𝑏 = −2.996 𝑏 = 2.996 sehingga, 0.9 = 𝑃(0.051 ≤ 𝑈 ≤ 2.996) = 𝑃 (0.051 ≤ 𝑋 𝜃 ≤ 2.996). Karena akan dicari penduga selang bagi 𝜃, maka diperoleh:

0.9 = 𝑃 (0.051 ≤𝑋 𝜃 ≤ 2.996) = 𝑃 ( 0.051 𝑋 ≤ 1 𝜃≤ 2.996 𝑋 ) 0.9 = 𝑃 ( 𝑋 0.051≥ 𝜃 ≥ 𝑋 2.996) = 𝑃 ( 𝑋 2.996 ≤ 𝜃 ≤ 𝑋 0.051) 0.90 a _b f(u) 0.05 0.05 u

Dengan demikian, diperoleh batas bawah dan batas atas untuk selang kepercayaan 𝜃 adalah 𝑋

2.996 dan 𝑋 0.051.

2.3. Selang Kepercayaan Sampel Besar

Untuk sampel besar, semua penduga titik akan mendekati distribusi sampling Normal dengan galat standar yang telah ditunjukkan pada Tabel 2.2.

Jika parameter sasaran 𝜃 adalah 𝜇, 𝑝, 𝜇₁− 𝜇₂, atau 𝑝1− 𝑝2, maka untuk sampel besar,

𝑍 =𝜃̂ − 𝜃 𝜎_𝜃̂

akan mendekati distribusi Normal standar. Akibatnya, 𝑍 adalah suatu besaran Pivot dan Metode Pivot dapat digunakan untuk menghasilkan selang kepercayaan untuk parameter sasaran 𝜃.

Contoh 2.22

Misalkan 𝜃̂ adalah statistik berdistribusi Normal dengan rata-rata 𝜃

dan galat standar 𝜎𝜃. Temukan selang kepercayaan bagi 𝜃 yang memiliki koefisien kepercayaan (1 − 𝛼).

Solusi: Nilai 𝑍 =𝜃̂−𝜃

𝜎_𝜃̂ berdistribusi Normal. Sekarang, pilih dua nilai di

dalam selang, yaitu 𝑧𝛼 2⁄ dan −𝑧𝛼 2⁄ , sehingga 𝑃(−𝑧𝛼 2⁄ ≤ 𝑍 ≤ 𝑧𝛼 2⁄ ) = 1 − 𝛼.