ANALISIS DAMPAK PROGRAM SKRINING DAN TERAPI
HIV DALAM MODEL PENYEBARAN HIV
Marsudi1
1Jurusan Matematika, Universitas Brawijaya, Malang, Indonesia e-mail: [email protected]
Abstrak. Sebuah model matematika nonlinear telah digunakan untuk mengkaji dampak program skrining dan terapi HIV dalam model penyebaran HIV/AIDS. Pembahasan difokuskan pada analisis sensitivitas dari angka reproduksi efektif dan simulasi numeriknya untuk mengetahui parameter-parameter dalam model yang mempuyai dampak signifikan dalam penyebaran HIV. Angka reproduksi efektif diperoleh menggunakan metode matriks generasi berikutnya. Dampak dari program skrining dan terapi HIV pada tingkat populasi diukur menggunakan indeks sensitifitas dari angka reproduksi efektif, yaitu mengukur perubahan relatif dalam angka reproduksi efektif jika suatu parameter model berubah. Berdasarkan simulasi numerik menggunakan nilai-nilai parameter dan populasi awal yang diberikan dapat disimpulkan bahwa program skrining pada unaware infectives dan program terapi pada screened infectives mempunyai pengaruh signifikan dalam mereduksi penyebaran HIV/AIDS.
Kata Kunci: analisis sensitivitas, skrining dan terapi, angka reproduksi efektif, HIV
1. Pendahuluan
Infeksi Human Immunodeficiency Virus (HIV)/Acquired Immune Deficiency Syndrome
(AIDS) merupakan salah satu masalah kesehatan yang menimbulkan dampak yang sangat luas dan sampai saat ini belum ditemukan vaksin. HIV adalah virus yang menyerang dan
menghancurkan sistem kekebalan dalam tubuh manusia. Sistem kekebalan merupakan
sistem pertahanan tubuh yang alami untuk melawan segala jenis infeksi dan penyakit. AIDS merupakan kondisi pada pengidap HIV yang mengalami sakit serius karena sistem kekebalan tubuhnya tidak dapat lagi berfungsi secara efektif melawan penyakit. Penderita AIDS kehilangan begitu banyak sel darah putih (sel CD4). Jika sel CD4 yang tersedia 200
sel/mm3 darah, maka tubuh tidak cukup terlindungi.
Sepanjang sejarah epidemi infeksi HIV/AIDS, program pencegahan ditujukan terutama untuk menurunkan resiko penularan pada individu yang negatif HIV atau individu yang tidak mengetahui status HIVnya. Menurut Anonim [2], salah satu prioritas kegiatan penanggulangan HIV/AIDS adalah perubahan perilaku resiko tinggi pada kelompok rentan (susceptible aktif-seksual), kelompok beresiko tertular (Infected HIV tanpa gejala AIDS) dan kelompok tertular (Infected HIV dengan gejala AIDS). Salah satu intervensi program
untuk meminimalisasi prevalensi HIV/AIDS adalah skrining VCT (voluntary counselling
and testing) dan terapi ARV (antiretroviral) bagi orang yang terdeteksi positif HIV.
Skrining adalah salah satu dari strategi atau intervensi yang paling umum untuk mengontrol penyebaran infeksi HIV. Program skrining memiliki pengaruh substantif pada penyebaran HIV. Banyak orang yang terinfeksi tetapi mereka tidak tahu bahwa ia terinfeksi dan orang yang tahu bahwa ia terinfeksi melalui skrining VCT tidak selalu mengambil tindakan pencegahan saat melakukan hubungan seksual. Oleh karena itu, diharapkan promosi
skrining sukarela atau skrining acak terus ditingkatkan dengan sasaran terutama pada kelompok berisiko tinggi. Pada individu yang terdeteksi infeksinya dapat termotivasi untuk mengubah perilakunya dan mengambil tindakan pencegahan seperti menggunakan kondom, menerima terapi HIV menggunakan obat ARV sehingga resiko penyebaran infeksi HIV berkurang dan sebaiknya individu-individu yang tidak terinfeksi.
Saat ini, perkembangan efektifitas program skrining dan terapi HIV belum memadai meskipun cakupan program meningkat. Banyak aspek penanggulangan yang belum diketahui, misalnya fenomena penyebaran epidemik HIV. Disinilah perlunya penelitian melalui pemodelan matematika untuk membantu menjelaskan fenomena penyebaran epidemik penyakit menular seperti HIV/AIDS. Beberapa penelitian yang menggunakan model matematika berkaitan dengan masalah-masalah epidemiologi (lihat [1], [4], [7], [9], [10] dan [11]). Berdasarkan uraian di atas, tujuan penulisan makalah ini adalah menentukan dampak setiap parameter pada dinamika model HIV dengan intervensi skrining dan terapi HIV melalui model matematika menggunakan analisis sensitivitas.
2. Model Matematika
Model HIV dengan skrining dan terapi HIV dideskripsikan menggunakan model kompartemen di mana secara demografi populasi dibagi menjadi lima subpopulasi:
susceptibles atau negatif HIV (S), unaware infectives (I1), screened infectives (I2), treated
population (T) dan AIDS population (A). Diasumsikan bahwa: Laju penyebaran adalah proporsional dengan populasi susceptible dan rasio antara anggota-anggota populasi
terinfeksi dengan total populasi, unaware infectives dapat bergerak menuju screened
infectives dengan laju , unaware infectives, screened infectives dan treated population
yang bergerak menjadi AIDS population dengan laju masing-masing 1, 2dan di mana
,
1
2 hanya individu-individu screened infectives yang menjadi treated population
dan menerima terapi HIV dengan laju dan unaware infectives, screened infectives dan
treated population dapat menginfeksi populasi unaware infectives dengan laju
masing-masing 1, 2 dan 3 di mana 3 2 1.Parameter adalah laju rekruitmen
susceptible, adalah laju kematian karena penyakit dan adalah laju kematian alami. Berdasarkan asumsi di atas, transisi antara kelima subpopulasi dapat disajikan ke dalam
model matematika berbentuk sistem persamaan diferensial nonlinear (Marsudi dkk. [7])
sebagai berikut: A T I I dt dA T I dt dT I I dt dI I S dt dI S S dt dS ) ( ) ( ) ( ) ( 2 2 1 1 2 2 2 1 2 1 1 1 (1)
di mana N T c I c I c1 1 1 2 2 2 3 3 , N S I I T A 2
1 dengan kondisi inisialS(0) S0,
. ) 0 ( , ) 0 ( , ) 0 ( , ) 0 ( 10 2 20 0 0 1 I I I T T A A
I Himpunan solusi fisibel dari sistem (1) adalah
N A T I I S A T I I S 5 1 2 2 1, , , ) , ( R
di mana merupakan himpunan invariant positif terhadap (1).
Sebuah ukuran penting dari penyebaran penyakit adalah konsep secara epidemiologi angka reproduksi dasar. Angka reproduksi efektif (Ref) mengukur rata-rata jumlah infeksi baru
yang disebabkan oleh satu individu terinfeksi selama dalam periode keinfeksian ([6]) di mana program skrining dan terapi HIV digunakan sebagai strategi kontrol. Ref eigen
terbesar untuk sistem (1) yang ternormalisasi dan diperoleh menggunakan metode matriks generasi selanjutnya (lihat [8])..
. ) )( )( ( ) ( ) )( ( 2 1 3 3 2 2 2 1 1 c c c Ref
Untuk menilai kontribusi dari I1, I2 and T dalam parameter-parameter 1, 2, 3 dari
persamaan (3), misalkan 1 1 1 1 c ReI ) )( ( 1 2 2 2 2 c ReI ) )( )( ( 1 2 3 3 c ReT maka . 2 1 eI eT eI ef R R R R
Dari persamaan-persamaan (4)-(5) di atas, tampak bahwa ReI ReI ReT
2
1 yang
mengimplikasikan bahwa unaware infectives (I1) mempunyai kontribusi signifikan pada
penyebaran infeksi HIV/AIDS diikuti oleh screened infectives (I2) dan menjaga
endemisitas penyakit dalam populasi masing-masing melalui c1 1d a nc2 2 sedangkan untuk therapy infectives (T) melalui c3 3. Dalam ketidakhadiran infeksi, ukuran populasi
mendekati keadaan mantab / .
Selanjutnya akan dianalisis empat keadaan model dengan skrining dan terapi HIV secara epidemiologi dalam populasi:
(i) Jika model dengan therapy infectives tidak menularkan infeksi ( 0dan 3 0),
maka Ref menjadi angka reproduksi induksi-terapi
. ) )( ( ) ( 2 1 2 2 2 1 1 c c RT (2) (3) (8) (4) (5) (6) (7)
(ii) Jika model dengan screened infectives dan therapy infectives tidak menularkan infeksi
( 0, 2 0, 0dan 3 0), maka Ref menjadi angka reproduksi induksi-skrining
dan terapi . 1 1 1 c RST
(iii) Jika model dengan skrining tanpa terapi ( 0 dan 0 ), maka Ref menjadi
angka reproduksi induksi-skrining
. ) )( ( ) ( 2 1 2 2 2 1 1 c c RS
(iv) Jika model tanpa skrining ( 0), maka Ref menjadi angka reproduksi dasar
. 1 1 1 0 c R
Dari analisis keempat keadaan epidemiologi di atas, disimpulkan bahwa endemisitas HIV
dapat direduksi menggunakan program skrining pada unaware infectives dan program
terapi pada screened infectives dalam populasi.
3. Analisis Sensitivitas
Analisis sensitivitas dilakukan untuk menemukan parameter-parameter model yang berpengaruh tinggi pada nilai ambang. Oleh karena itu, perlu dihitung indeks sensitifitas dari nilai ambang menggunakan pendekatan seperti yang dilakukan oleh [5]. Indeks sensitivitas menunjukkan ukuran perubahan relatif dari nilai ambang jika suatu parameter berubah. Indeks sensitivitas pada semua parameter yang mempunyai pengaruh tinggi pada
nilai ambang dapat dijadikan sasaran untuk diberikan intervensi dalam mengendalikan
penyebaran penyakit.
Definisi 1 Indeks sensitivitas normalisasi maju dari variabel u yang bergantung diferensial
pada parameter p, didefinisikan sebagai
. u p p u
I
u p3.1. Analisis Sensitivitas Ref, RT, RST, RS dan R0
Jika menggunakan nilai-nilai parameter, 1 0.86, 2 0.15, 3 0.1, 0.6, 0.1,
, 99 .
0 1 0.8, 2 0.01,c1 3,c2 2,c3 1 dan 700, diperoleh indeks sensitivitas dari Ref, RT, RST, RS dan R0 terhadap parameter-parameter model ditunjukkan dalam Tabel
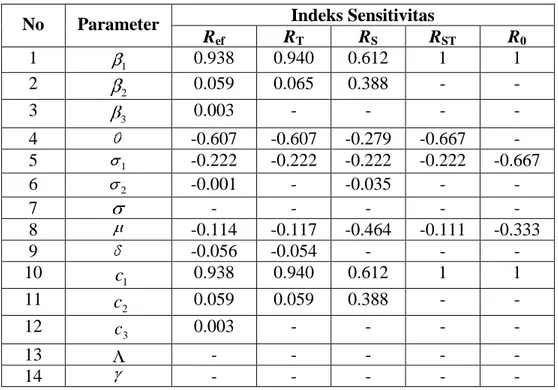
1. Tabel 1 menunjukkan bahwa indeks sensitivitas yang bernilai positif adalah parameter-parameter 1, 2, 3,c1,c2 danc3. Hal ini menunjukkan bahwa jika salah satu parameter dari 1, 2, 3,c1,c2 danc3dinaikkan sementara parameter yang lain dibuat konstan akan
menaikkan nilai Ref dan akibatnya menaikkan endemisitas penyakit HIV. Sedangkan
parameter-parameter , 1, 2, dan mempunyai nilai indeks sensitivitas negatif,
artinya jika salah satu parameter dari , 1, 2, dan dinaikkan sementara parameter
lain dibuat konstan akan menurunkan nilai Ref dan akibatnya menurunkan endemisitas
(9)
(10)
(11)
penyakit HIV. Hal yang sama juga berlaku untuk nilai indeks sensitivitas terhadap RT, RST,
RS dan R0.
Tabel 1. Indeks sensitivitas angka reproduksi
No Parameter Indeks Sensitivitas
Ref RT RS RST R0 1 1 0.938 0.940 0.612 1 1 2 2 0.059 0.065 0.388 - - 3 3 0.003 - - - - 4 -0.607 -0.607 -0.279 -0.667 - 5 1 -0.222 -0.222 -0.222 -0.222 -0.667 6 2 -0.001 - -0.035 - - 7 - - - - - 8 -0.114 -0.117 -0.464 -0.111 -0.333 9 -0.056 -0.054 - - - 10 1 c 0.938 0.940 0.612 1 1 11 2 c 0.059 0.059 0.388 - - 12 c3 0.003 - - - - 13 - - - - - 14 - - - - -
Parameter yang paling sensitif adalah laju kontak (frekwensi hubungan) dari unaware
infectives dengan suscepribles ( 1(c1))diikuti ah laju progresi dari unaware infectives ke screened infectives ( ). Parameter yang kurang sensitif adalah laju oleh laju progresi dari
screenedinfectiveske AIDS population ( 2). 3.2. Simulasi Numerik
Simulasi numerik dari sistem (1) diselesaikan menggunakan nilai-nilai parameter seperti di
atas dan kondisi inisial S0 20.000.000.000,I10 2.000.000,I20 250.000,
000 . 50 0
T dan A0 20.000. Waktu akhir tf 10 tahun dan komputasi menggunakan
Matlab dengan skema ode45. Fungsi ini mengimplementasikan metode Runge-Kutta. Gambar 1 menunjukkan solusi sistem (1) dengan nilai-nilai parameter yang diberikan dalam Tabel 1 untuk susceptibles, unaware infectives, screened infectives, therapy infectives dan AIDS patient.
Gambar 1 menunjukkan bahwa proporsi dari populasi susceptible turun dengan
meningkatnya waktu sementara proporsi populasi therapy infectives naik dan mencapai
titik kesetimbangannya. Pada awalnya proporsi dari unaware infectives naik tetapi karena
meningkatnya skrining dan terapi dengan laju masing-masing adalah dan menjadi
turun dan mencapai posisi titik kesetimbangannya. Hal ini mengakibatkan turunnya proporsi dari AIDS patients. Selanjutnya, juga diperoleh nilai-nilai angka reproduksi
3.057, 2.87, 0.182, 0.055, 2.87, 0.182, 0.055, 2 1 2 1 eI eT eI eI eT eI ef R R R R R R R RT 3.048,RS 4.685,RST 2.867 dan R0 8.60. 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 0 0.5 1 1.5 2x 10 8 P ro p o rs i P o p u la s i Waktu (tahun) Susceptibles Unware infectives Screened infectives Therapy infectives AIDS patient
Gambar 1. Proporsi populasi dalam kelas berbeda
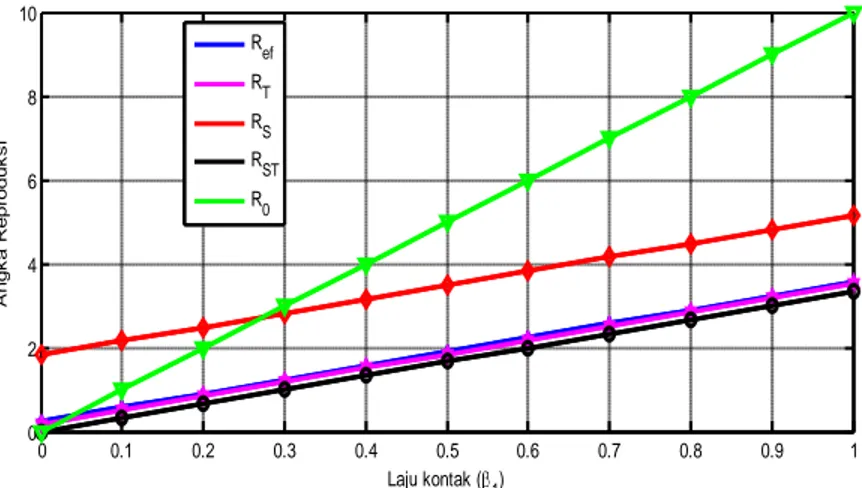
Gambar 2 menunjukkan perilaku angka reproduksi (Ref, RT, RS, RST dan R0) terhadap
perubahan laju penularan (kontak) 1. Dari Gambar 2 tampak bahwa jika 1 naik, maka
angka reproduksi juga naik. R0 naik lebih cepat kemudian diikuti oleh RS, Ref, RT dan RST.
Ini menunjukkan pentingnya skrining dan terapi HIV. Jadi, laju kontak dengan populasi terinfeksi mempunyai dampak langsung pada dinamika penyebaran penyakit HIV.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 2 4 6 8 10 Laju kontak (1) A n g k a R e p ro d u k s i Ref RT RS RST R0
Gambar 2. Perilaku dari angka reproduksi terhadap perubahan laju penularan 1
4. Kesimpulan
Sebuah model matematika nonlinear telah digunakan untuk menganalisis dampak program skrining dan terapi HIV dalam penyebaran infeksi HIV. Menggunakan metode matriks
generasi berikutnya diperoleh angka reproduksi efektif Ref. yang merepresentasikan dinamika penyebaran HIV dengan intervensi skrining dan terapi HIV.
Berdasarkan simulasi numerik menggunakan nilai-nilai parameter dan populasi awal (data simulasi), angka reproduksi efektif adalah 3.057, angka reproduksi induksi-terapi adalah 3.048, angka reproduksi induksi-skrining adalah 4.685, angka reproduksi induksi-skrining dan terapi adalah 2.867 dan angka reproduksi dasar adalah 8.60. Dampak dari program skrining dan terapi HIV pada tingkat populasi diukur menggunakan indeks sensitifitas dari angka reproduksi. Indeks sensitifitas digunakan untuk mengukur perubahan relatif dalam angka reproduksi jika suatu parameter berubah. Dengan menurunkan nilai parameter-parameter 1, 2, 3,c1,c2 danc3, angka reproduksi juga turun. Demikian juga halnya,
dengan menaikkan nilai-nilai , 1, 2, dan , angka reproduksi akan turun. Parameter
yang paling sensitif adalah laju kontak dari unaware infectives dengan suscepribles
)) (
( 1 c1 diikuti laju progresi dari unaware infectives ke screened infectives ( ). Jadi,
dapat disimpulkan bahwa skrining terhadap unaware infectives and terapi dari screened infectives mempunyai dampak mereduksi penyebaran HIV/AIDS.
5. Ucapan Terimakasih
Isi makalah adalah bagian dari penelitian yang didanai oleh Direktorat Jenderal Pendidikan Tinggi, Kementerian Pendidikan dan Kebudayaan, melalui DIPA Universitas Brawijaya Nomor : DIPA-023.04.2.414989/2014.
Referensi
1. Anderson, R.M.,: The Role of Mathematical Models in The Study of HIV Transmission
and The Epidemiology of AIDS, J. AIDS 1, 214-256 (2001)
2. Anonim: Strategi Nasional Penanggulangan HIV dan AIDS 2010-2014. Komisi
Penanggulangan AIDS Nasional (2010)
3. Brauer, F. and Castillo-Chavez, C.: Mathematical Models in Population Biology and Epidemiology, Text in Applied Mathematics, Springer Verlag (2001)
4. Chavez-Castillo and Song, B. (2004) Dynamical Models of Tuberculosis and their
Applications, Mathematical Bioscience and Engineering, 1, 361-404
5. Chitnis, N., Hyman, J.M., Cushing, J.M.: Determining Important Parameter in the
Spread of Malaria Through the Sensitivity Analysis of Mathematical Model, Department
of Public Health and Epidemiology, 70, 1272-1296 (2008)
6. Diekmann, O., Heesterbeek, J.A.P. , Metz, J.A.P., On the definition and computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous
7. Gumel, A.B., Moghadas,, S.M. and Mickens, R.E.: Effect of a preventive Vaccine on the
Dynamics of HIV Transmission. Nonlinear Science and Numerical Simulations, 9, 649-
659 (2004),
8. Marsudi, Marjono dan Andari, A.: Evaluasi Dampak Program Skrining dan Terapi HIV dalam Upaya Pencegahan Penyebaran HIV di Malang Melalui Analisis Sensitivitas
Model Matematika, Laporan Hibah Penelitian Unggulan Perguruan Tinggi, LPPM
Universitas Brawijaya (2013)
9. Mukandavire, Z., Garira, W. and Tchuenche, J.M.: Modelling Effects of Public Health
Educational Campaigns on HIV/AIDS Transmission Dynamics, Applied Mathematical
Modelling, 33, 4, 2084–2095 (2009)
10. Tripathi, A. Naresh R. and Sharma D.: Modeling the Efect of Screening and Unaware Infective on the Dynamics of HIV Transmission. England Journal of Medicine,
Applied Mathematics and computation, 184,1053-1068 (2007)
11. van den Driessche, P. and Watmough, J.: Reproduction Numbers and Subthreshold
Endemic Equilibria for Compartmental Models of DiseaseTransmission, Mathematical