Multisensor Fusion and Integration in the Wake of Big Data, Deep Learning and Cyber Physical System

Sukhan Lee · Hanseok Ko

Songhwai Oh   

Editors

Multisensor Fusion

and Integration in the

Wake of Big Data, Deep

Learning and Cyber

Physical System

Volume 501

Board of Series editors

Leopoldo Angrisani, Napoli, Italy Marco Arteaga, Coyoacá_{n, M}é_xico Bijaya Ketan Panigrahi, New Delhi, India Samarjit Chakraborty, Mü_{nchen, Germany} Jiming Chen, Hangzhou, P.R. China Shanben Chen, Shanghai, China Tan Kay Chen, Singapore, Singapore Rü_{diger Dillmann, Karlsruhe, Germany} Haibin Duan, Beijing, China

Gianluigi Ferrari, Parma, Italy Manuel Ferre, Madrid, Spain Sandra Hirche, Mü_{nchen, Germany} Faryar Jabbari, Irvine, USA Limin Jia, Beijing, China

Janusz Kacprzyk, Warsaw, Poland Alaa Khamis, New Cairo City, Egypt Torsten Kroeger, Stanford, USA Qilian Liang, Arlington, USA

Tan Cher Ming, Singapore, Singapore Wolfgang Minker, Ulm, Germany Pradeep Misra, Dayton, USA Sebastian Mö_{ller, Berlin, Germany}

Subhas Mukhopadyay, Palmerston North, New Zealand Cun-Zheng Ning, Tempe, USA

Toyoaki Nishida, Kyoto, Japan Federica Pascucci, Roma, Italy Yong Qin, Beijing, China

Gan Woon Seng, Singapore, Singapore Germano Veiga, Porto, Portugal Haitao Wu, Beijing, China

SCOPUS, MetaPress, Springerlink **

Lecture Notes in Electrical Engineering (LNEE)is a book series which reports the latest research and developments in Electrical Engineering, namely:

• Communication, Networks, and Information Theory • Computer Engineering

• Signal, Image, Speech and Information Processing • Circuits and Systems

• Bioengineering • Engineering

The audience for the books in LNEE consists of advanced level students, researchers, and industry professionals working at the forefront of theirfields. Much like Springer_’s other Lecture Notes series, LNEE will be distributed through Springer’s print and electronic publishing channels.

For general information about this series, comments or suggestions, please use the contact address under“service for this series”.

To submit a proposal or request further information, please contact the appropriate Springer Publishing Editors:

Asia:

China,Jessie Guo, Assistant Editor(jessie.guo@springer.com) (Engineering) India,Swati Meherishi, Senior Editor(swati.meherishi@springer.com) (Engineering) Japan,Takeyuki Yonezawa, Editorial Director(takeyuki.yonezawa@springer.com) (Physical Sciences & Engineering)

South Korea,Smith (Ahram) Chae, Associate Editor(smith.chae@springer.com) (Physical Sciences & Engineering)

Southeast Asia,Ramesh Premnath, Editor(ramesh.premnath@springer.com) (Electrical Engineering)

South Asia,Aninda Bose, Editor(aninda.bose@springer.com) (Electrical Engineering) Europe:

Leontina Di Cecco, Editor(Leontina.dicecco@springer.com)

(Applied Sciences and Engineering; Bio-Inspired Robotics, Medical Robotics, Bioengineering; Computational Methods & Models in Science, Medicine and Technology; Soft Computing; Philosophy of Modern Science and Technologies; Mechanical Engineering; Ocean and Naval Engineering; Water Management & Technology)

(christoph.baumann@springer.com)

(Heat and Mass Transfer, Signal Processing and Telecommunications, and Solid and Fluid Mechanics, and Engineering Materials)

North America:

Songhwai Oh

Editors

Multisensor Fusion

and Integration in the Wake

of Big Data, Deep Learning

and Cyber Physical System

An Edition of the Selected Papers

from the 2017 IEEE International Conference

on Multisensor Fusion and Integration

for Intelligent Systems (MFI 2017)

Sukhan Lee

Intelligent Systems Research Institute Sungkyunkwan University

Suwon

Korea (Republic of) Hanseok Ko

School of Electrical Engineering Korea University

Seoul

Korea (Republic of)

Songhwai Oh

Department of Electrical and Computer Engineering

Seoul National University Seoul

Korea (Republic of)

ISSN 1876-1100 ISSN 1876-1119 (electronic) Lecture Notes in Electrical Engineering

ISBN 978-3-319-90508-2 ISBN 978-3-319-90509-9 (eBook) https://doi.org/10.1007/978-3-319-90509-9

Library of Congress Control Number: 2018940915

©Springer International Publishing AG, part of Springer Nature 2018

This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.

The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.

The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Printed on acid-free paper

This Springer imprint is published by the registered company Springer International Publishing AG part of Springer Nature

Multisensor fusion and integration is playing a critical role in harnessing the smart technologies as we ride the big wave of the 4th Industrial Revolution. Deployment of the Internet of Things, Cyber-Physical Systems and Robotics in distributed environment is rapidly rising as our society seeks to transition from being ambient to being smart and, at the same time, to enable human to curate information and knowledge between ubiquitous and collective computing environments. What surround us are the networks of sensors and actuators that monitor our environment, health, security and safety, as well as the service robots, intelligent vehicles and autonomous systems of ever heightened autonomy and dependability with inte-grated heterogeneous sensors and actuators. Developing fundamental theories and advancing implementation tools to address the emerging key issues in multisensor fusion and integration in the wake of big data and deep learning would make the above transition smooth and rewarding.

This volume is an edition of the papers selected from the 13th IEEE International Conference on Multisensor Integration and Fusion, IEEE MFI 2017, held in Daegu, Korea, 16–22 November 2017. Only 17 papers out of the 112 papers accepted for IEEE MFI 2017 were chosen and requested for revision and extension to be included in this volume. The 17 contributions to this volume are organized into two chapters: Chapter 1 is dedicated to the theories in data and information fusion in distributed environment and Chapter 2 to the multisensor fusion in robotics. To help readers understand better, a chapter summary is included in each chapter as an introduction.

It is the wish of the editors that readers find this volume informative and enjoyable. We would also like to thank Springer-Verlag for undertaking the pub-lication of this volume.

Sukhan Lee Hanseok Ko Songhwai Oh

Multi-sensor Fusion: Theory and Practice

Covariance Projection as a General Framework of Data Fusion

and Outlier Removal . . . 5 Sukhan Lee and Muhammad Abu Bakr

State Estimation in Networked Control Systems with Delayed

and Lossy Acknowledgments . . . 22 Florian Rosenthal, Benjamin Noack, and Uwe D. Hanebeck

Performance of State Estimation and Fusion with Elliptical

Motion Constraints. . . 39 Qiang Liu and Nageswara S. V. Rao

Relevance and Redundancy as Selection Techniques

for Human-Autonomy Sensor Fusion. . . 52 Justin D. Brody, Anna M. R. Dixon, Daniel Donavanik,

Ryan M. Robinson, and William D. Nothwang

Classi_fication of Reactor Facility Operational State Using SPRT

Methods with Radiation Sensor Networks . . . 76 Camila Ramirez and Nageswara S. V. Rao

Improving Ego-Lane Detection by Incorporating Source Reliability . . . 98 Tran Tuan Nguyen, Jens Spehr, Jonas Sitzmann, Marcus Baum,

Sebastian Zug, and Rudolf Kruse

Applying Knowledge-Based Reasoning for Information Fusion

in Intelligence, Surveillance, and Reconnaissance. . . 119 Achim Kuwertz, Dirk Mü_{hlenberg, Jennifer Sander, and Wilmuth M}ü_ller

Multiple Classi_fier Fusion Based on Testing Sample Pairs. . . 140 Gaochao Feng, Deqiang Han, Yi Yang, and Jiankun Ding

Multi-sensor Fusion Applications in Robotics

Bayesian Estimator Based Target Localization in Ship Monitoring System Using Multiple Compact High Frequency

Surface Wave Radars. . . 157 Sangwook Park, Chul Jin Cho, Younglo Lee, Andrew Da Costa,

SangHo Lee, and Hanseok Ko

SLAM-Based Return to Take-Off Point for UAS. . . 168 Daniel Bender, Wolfgang Koch, and Daniel Cremers

Underwater Terrain Navigation During Realistic Scenarios. . . 186 Må_{rten Lager, Elin A. Topp, and Jacek Malec}

Supervised Calibration Method for Improving Contrast

and Intensity of LIDAR Laser Beams . . . 210 Mohammad Aldibaja, Noaki Suganuma, Keisuke Yoneda, Ryo Yanase,

and Akisue Kuramoto

Multi-object Tracking Based on a Multi-layer Particle Filter

for Unclustered Spatially Extended Measurements. . . 219 Johannes Buyer, Martin Vollert, Mihai Kocsis, Nico Suß_mann,

and Raoul Zö_llner

Ensemble Kalman Filter Variants for Multi-Object Tracking

with False and Missing Measurements. . . 239 Fabian Sigges and Marcus Baum

Fall Detection with Unobtrusive Infrared Array Sensors. . . 253 Xiuyi Fan, Huiguo Zhang, Cyril Leung, and Zhiqi Shen

Subtle Hand Action Recognition in Factory Based

on Inertial Sensors. . . 268 Yanyan Bao, Fuchun Sun, Xinfeng Hua, Bin Wang, and Jianqin Yin

Kinematics, Dynamics and Control of an Upper Limb

Rehabilitation Exoskeleton. . . 284 Qingcong Wu and Ziyan Shao

Sukhan Lee and Hanseok Ko

Multisensor fusion and integration in a distributed environment is becoming of utmost importance, especially, in the wake of the growing deployment of Internet of Things (IoT) as well as Cyber Physical Systems (CPS). Although the fundamental theory behind multisensor fusion and integration has been well-established through several decades of investigations, in practice, there still remain a number of technical chal-lenges to overcome, in particular, for dealing with multisensor fusion and integration in a distributed environment. Specifically speaking, multisensor fusion with the known cross-correlations among multiple data sources can be handled ideally, for instance, by Bar-Shalom Campo and Generalized Millman’s formula. However, in a distributed environment, a number of critical issues arise that are yet to be addressed and solved, including (1) the difficulty of estimating exact cross-correlations among multiple data sources due to the physical relationships possibly existing among their observations as well as the possible double counting by sharing prior information or data sources, (2) the presence of inconsistency or outliers among data sources, (3) the existence of transmission delays as well as data losses and (4) the incorporation of various con-straints that may be available among states and observations into fusion. The papers collected for this chapter are to address some of the critical issues as described above in a theoretical and/or a practical point of view, as follows:

Framework of Data Fusion

and Outlier Removal

Sukhan Lee(&)and Muhammad Abu Bakr

Intelligent Systems Research Institute, Sungkyunkwan University, Gyeonggi-do, Suwon 440-746, South Korea

{lsh1,abubakr}@skku.edu

Abstract. A fundamental issue in sensor fusion is to detect and remove outliers as sensors often produce inconsistent measurements that are difficult to predict and model. The detection and removal of spurious data is paramount to the quality of sensor fusion by avoiding their inclusion in the fusion pool. In this paper, a general framework of data fusion is presented for distributed sensor networks of arbitrary redundancies, where inconsistent data are identified simultaneously within the framework. By the general framework, we mean that it is able to fuse multiple correlated data sources and incorporate linear constraints directly, while detecting and removing outliers without any prior information. The proposed method, referred to here as Covariance Projection (CP) Method, aggregates all the state vectors into a single vector in an extended space. The method then projects the mean and covariance of the aggregated state vectors onto the constraint manifold representing the constraints among state vectors that must be satisfied, including the equality constraint. Based on the distance from the manifold, the proposed method identifies the relative disparity among data sources and assigns confidence measures. The method provides an unbiased and optimal solution in the sense of Minimum Mean Square Error (MMSE) for distributed fusion architectures and is able to deal with correlations and uncer-tainties among local estimates and/or sensor observations across time. Simulation results are provided to show the effectiveness of the proposed method in iden-tification and removal of inconsistency in distributed sensors system.

Keywords: Covariance projection method

Constraint manifold Data fusion

Distributed sensor network

Inconsistent data

1 Introduction

Multisensor data fusion is to obtain a more meaningful and precise estimate of a state by combining data from multiple sources. One of the inherent issues in multisensor data fusion is that of uncertainty in sensor measurements. The sensor uncertainties may come from impreciseness and noise in the measurements, as well as, from ambiguities and inconsistencies present in the environment. The fusion methodologies should be able to model such uncertainties and combine data to provide a consistent and accurate fused solution.

©Springer International Publishing AG, part of Springer Nature 2018 S. Lee et al. (Eds.): MFI 2017, LNEE 501, pp. 5_–21, 2018.

Recently, distributed data fusion [1, 2] is widely explored in diverse fields of engineering and control due to its superior performance over the centralized fusion in terms offlexibility, robustness to failure and cost-effectiveness in infrastructure and communication. However, the distributed architecture needs to address statistical dependency among the local estimates received from multiple nodes for fusion. This is due to the fact that local state estimates at individual nodes can be subject to same process noise [3] and to double counting, i.e., sharing same data sources among them [4]. Ignoring such statistical dependency or cross-correlation among multiple nodes leads to inconsistent results, causing divergence in data fusion [5].

The fusion methodologies assume that the sensor measurements are affected by Gaussian noise only and thus the covariance of the estimate provides a good approximation of all the disturbances affecting the sensor measurements. However, in real applications, the sensor measurements may not only be affected by noise but also from unexpected situations such as short duration spike faults, sensor glitch, permanent failure or slowly developing failure due to sensor elements [6]. Since these types of uncertainties are not attributable to the inherent noise, they are difficult to model. Due to these uncertainties, the estimates provided by sensor nodes in a distributed network may be spurious and inconsistent. Fusing these imprecise estimates with correct esti-mates can lead to severely inaccurate results [7]. Hence, a data validation scheme is required to identify and eliminate the outliers from the fusion pool.

Detection of inconsistency needs either a priori information often in the form of specific failure model(s) or data redundancy [1]. The model-based approaches [1,8] uses the generated residuals between the model outputs and actual measurements to detect and remove faults. For instance in [9], Nadaraya-Watson estimator and a priori observations are used to validate sensor measurements. Similarly, a priori system model information as a reference is used to detect failures infiltered estimates [10]. Researchers have also used fuzzy logic [11] and neural network [12] based approaches for sensor validation. However, model-based methods either require an explicit mathematical model or need tuning and training for data validation. This restricts the usage of these methods in the case where prior information is not available or unmodeled failure occurs. A method to detect spurious data based on Bayesian framework is proposed in [13]. The method adds a term to the Bayesian formulation which has the effect of increasing the posterior distribution when measurement from one of the sensor is inconsistent with respect to the other. However, the method assumes independence of the sensor estimates in its analysis and may lead to incorrect rejection of true estimates or incorrect retaining of false estimates.

This paper presents a general data fusion framework, referred to as Covariance Projection (CP) Method, tofind an optimal and consistent fusion solution for multiple correlated data sources. The proposed method provides a framework for identifying and removing outliers in a distributed sensor network where only the sensor estimates may be available at the fusion center.

1.1 Problem Statement

covariance. Assume that each local system predicts the underlying states using fol-lowing equation,

xk ¼ A xk 1 þ Buk 1 þ wk 1

whereA is the system matrix,Binput matrix, uk 1 input vector and^xk 1 is the state vector. The system process is affected by zero mean Gaussian noise wk 1 with covariance matrixQ. The sensor measurements are approximated as,

zki ¼ Hixk þ vki þ eki;i ¼ 1;. . .;n

wherevki is Gaussian noise with covariance matricesRi;i ¼ 1;2;. . .;n. The sensor measurements are also affected by unmodeled faultseki. The state prediction of each local system is updated by its own sensor measurement to compute local state estimates as (^xk;Pk). The local estimates are then communicated among sensor nodes or sent to a central node for obtaining a global estimate. However, the local estimates may be correlated due to common process noise [3] or double counting [4]. Furthermore, the estimates provided by local systems may be spurious and inconsistent due to the unmodeled sensor faults. As stated in the introduction, the majority of work needs a priori information in the form of particular failure model(s) to detect sensor faults [9, 10]. While in a distributed architecture, the fusion node may have access to the estimated mean and covariance of the data sources only. Moreover, the cross-correlation among data sources is overlooked in traditional data validation schemes and outliers removal is mostly based on heuristics [13].

This paper presents a general framework to validate and fuse correlated and uncertain data from multiple sources without any prior information. The proposed method assigns confidence measure to multiple data sources based on the distance from the constraint manifold. The method then statistically removes the inconsistent sensor estimates of arbitrary dimensions and correlations.

2 Proposed Approach

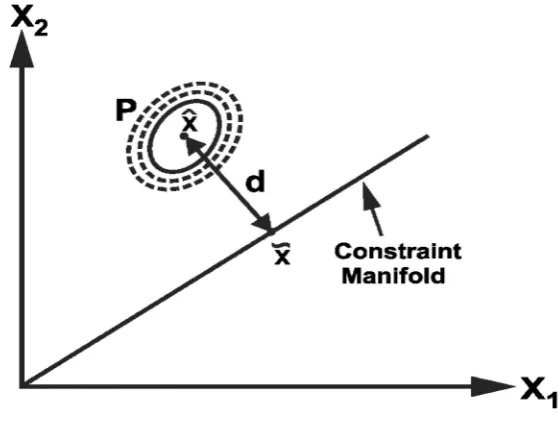
Consider unbiased estimates^x1and^x2, of the true statex, with covariancesP1,P2and cross-covariance matrixP12. The statistical distribution, that is, the mean and covari-ance from individual sensors in RN is aggregated such that it is transformed to an extended space ofR2Nalong with the equality constraint between the two data sources, that is,

^x ¼ ^x1 ^x2

; P ¼ P1 P12

PT₁₂ P2

; ^x1 ¼ ^x2 ð1Þ

transformation that can be defined as,W ¼ D 1=2ET_{, where D and E is the respective} eigenvalue and eigenvector matrix of P. Applying Whitening transform, we get,

^

xW ¼ W^x; PW ¼ WPWT ¼ I; MW ¼ WM

Figure1(b) shows the transformation of the ellipsoid into a unit circle after W. The mean and covariance are then projected on the constraint manifoldMW _{to get a fused} result in the transformed space as shown in Fig.1(b). Inverse Whitening Transform is applied to obtain the optimal fused mean and covariance in the original space as,

~x ¼ W 1PrW^x ð2Þ

~

P ¼ W 1PrPTrW

T _ð3Þ

wherePris the projection matrix computed asPr ¼ MW MW T

MW

MWT

. It should be

noted that the framework of CP method can incorporate any linear constraints among data sources without any additional processing. Using definition of various components in (2) and (3), we get the closed-form simplification of fused mean and covariance for CP method as,

~

x ¼ MTP 1M 1MTP 1^x ð4Þ

~

P ¼ MTP 1M 1

The details of the simplification are provided in Appendix1. Using the values of identity matrix and N the dimension of individual data source. The proposed CP method provides an unbiased and optimal fused solution in the sense of Minimum Mean Square Error (MMSE) for a multisensor system of arbitrary redundancies.

Theorem 1: The fused estimate~xgiven by the CP method in Eq. (2) is an unbiased estimator ofx, that is,Eð Þ ¼~x E xð Þ:

Proof: Using (2) we can write

x ~x ¼ W 1PrW xð ^xÞ Taking expectation on both sides, we get

E xð x~Þ ¼W 1PrWE xð ^xÞ

E xð _~xÞ ¼0

E xð Þ ¼Eð Þ~x

where the assumption of unbiasedness is used forE xð Þ ¼ Eð Þ. This conclude that the_^x

fused state estimate~xis an unbiased estimate of x.

Theorem 2: The fused covarianceP~ of the CP method is smaller than the individual covariances, that is,P~ Pi;i ¼ 1;2;. . .;n:

Proof: From Eq. (5), we can write

~

P ¼ MTP 1M 1

By Schwartz matrix inequality, we have

where M is the constraint among data sources andMi ¼ ½INi;0;. . .;0Š T

is the con-straint matrix forPi. The equality holds forPi ¼ Pij;that is,P~ ¼ Pi;whenPi ¼ Pij;

j ¼ 1;2;. . .;n.

Since the estimates of the state provided by sensors in a distributed architecture are correlated, computation of cross-covariancePij;is needed to compute the fused mean (4) and covariance (5). The cross-covariance between the sensor estimates can be computed as [15],

ij represent the cross covariance of the previous cycle between sensoriandj.

3 Con

_fi

dence Measure of Data Sources

The working of fusion algorithms is based on assumption that the input sensor esti-mates are consistent and consequently fails in the case of inconsistent estiesti-mates. Hence, a data validation scheme is required to identify and eliminate the outliers before fusion. The proposed approach identifies relative disparity and confidence measure of the multi-sensory data by utilizing the relationship among data sources. Assuming that the data sources can be represented jointly as a multivariate normal distribution, the confidence of data sources can be measured by calculating the distance from the constraint manifold as depicted in Fig.2. Suppose that we have n Gaussian data sources inRN with corresponding joint mean and covariance matrices as,

^x ¼

Then the distanced from the manifold representing confidence measure can be com-puted as,

d ¼ ð^x _~xÞTP 1ð_^x _~xÞ ð9Þ

where~xis the point on the manifold and can be obtained by using (4). For instance, given two data sources with mean as^x1,^x2 2 RNand respective covariance matrices

The point on the manifold is given as,

~

x ¼ P2ðP1 þ P2Þ 1^x1 þ P1ðP1 þ P2Þ 1^x2

Simplifying we get,

d ¼ ½^x1 ^x2ŠTðP1þP2Þ 1½^x1 ^x2Š ð10Þ

The details of simplifications are provided in Appendix 2. From (10), it can be observed that distance d is a weighted distance between the two data sources and it can provide a measure of nearness or farness of the two data sources to each other. A large value of d implies a large separation while a small d signifies closeness of the data sources. In other words, the distance from the manifold provides an indication of the relative disparity among the data sources.

Theorem 3: ForNdimension ofndata sources, the d distance (9) follow a chi-squared distribution withnN degrees of freedom (DOF), that is,dv2ðNnÞ.

Proof: From (9) we can write

d ¼ ð^x ~xÞTP 1ð^x ~xÞ ð11Þ Applying Whitening Transformation, we get,

^x ~x

ð ÞTP 1ð^x ~xÞ ¼ð^xW ~xWÞTð^xW ~xWÞ

)ðWð^x ~xÞÞTðWð^x x~ÞÞ ¼yTy ð12Þ

wherey¼Wð_^x _~xÞ Nð0;1Þis an independent standard normal distribution. For N dimensions of state vector, the right-hand side of (12) is PN

i¼1y2i, thus distance d follows a chi-square distribution withNDOF, that is, dv2ð Þ. ForN n data sources withNstates,

dv2ðnNÞ

Sinced is a chi-square distribution withnN DOF, then for any significance level a2ð0;1Þ,v2_aðNnÞis defined such that the probability,

P d v2_aðNnÞ¼a

Hence, to have a confidence of 100 1ð aÞpercent, d should be less than respective critical value. A value of a ¼ 0:05 is assumed in this paper unless specified. Chi-square table [16] can be used to obtain the critical value for the confidence distance with a particular significance level and DOF.

3.1 Inconsistency Detection and Exclusion

To obtain reliable and consistent fusion results, it is important that the inconsistent estimates in a multisensor distributed system be identified and excluded before fusion. For this reason, at each time step when the fusion center receives computed estimates from sensor nodes, distance d is calculated. A computed distancedless than the critical value mean that we are confident about the closeness of sensor estimates and that they can be fused together to provide better estimate of the underlying states. On the other hand, a distancedgreater than or equal to the critical value indicate spuriousness of the sensor estimates. At least one of the sensor estimate is significantly different than the other sensor estimates. To exclude the outliers, a distance from the manifold is com-puted for every estimate and compared with the respective critical values. Fornsensor estimates the hypothesis and decision rule are summarized as follow,

Hypotheses: H0: ^x1¼^x2 ¼ ¼^xn

H1: ^x16¼^x2 6¼ 6¼^xn

Decision Rule: AcceptH0ifd \_v2 aðNnÞ RejectH0 ifd v2_aðNnÞ

If the hypothesisH0 is accepted then the estimates are optimally fused using (4) and (5). On the other hand, rejection of null hypothesis means that at least one of the sensor estimate is significantly different than the other sensor estimates. The next step is to identify the inconsistent sensor estimates. A distance from the manifold is computed for each of the estimates as,

di ¼ ð^xi ~xÞ T

The outliers are identified and eliminated based on the respective critical value, that is, ifdiv2_að ÞN they are rejected. Where Nis the dimension of individual data source.

3.2 Effect of Correlation ond Distance

Since the estimates provided by sensor nodes in a distributed fusion architecture are correlated, it is important to consider the effect of cross-correlation in the calculation of confidence distance. The d distance for a pair of multivariate Gaussian estimates

^x1;r2₁

and ^x2;r2₂, with cross-correlationr2₁₂ can be written as,

d ¼ ½^x1 ^x2Š 2

r2₁þr2₂ r2₁₂ r2₂₁ ð13Þ It is apparent that the distance between the mean values is affected by the correlation between the data sources. Figure3illustrates the dependency of confidence distance d on the correlation coefficient. Figure3(a) shows the scenario in which a data source (with changing mean and constant variance) is moving away from another data source (with constant mean and constant variance). The distance d is plotted for various values of correlation coefficients. The y-axis shows the percentage of rejection of the null hypothesisH0. Figure3(b) shows the distance d with changing correlation coefficient from−1 to 1. It can be noted that ignoring the cross-correlation in distance d result in

underestimated or overestimated confidence and may lead to incorrect rejection of true null hypothesis (Type I error) or incorrect retaining of false null hypothesis (Type II error). The proposed framework inherently takes care of any cross-correlation among multiple data sources in the computation of distanced.

Example: Consider a numerical simulation with the constant state,

xk ¼ 10

Three sensors are used to estimate the state xk, where the measurements of the sensors are corrupted with respective variance of R1; R2 andR3. The values for the parameters assumed in the simulation are,

Q ¼ 2; R1 ¼ 0:5; R2 ¼ 1; R1 ¼ 0:9

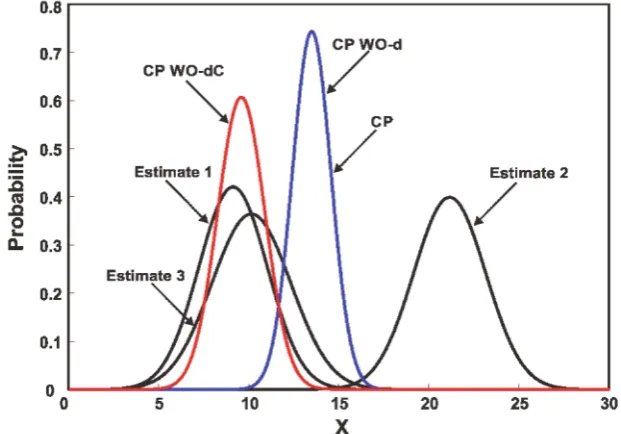
The sensors measurements are assumed to be cross-correlated. It is also assumed that the sensor 1, sensor 2 and sensor 3 measurements are independently affected by unmodeled random noise and produce inconsistent data for 33, 33 and 34% of the time respectively. The sensors compute local estimates of the state and send it to the fusion center. Three strategies for fusing the local sensor estimates are compared: (1) CP, which fuses the three sensor estimates using (4) and (5) without removing outliers, (2) CP WO-d means the outliers were identified and rejected based on (13) with r212¼0 before fusion, that is, correlation in computation ofd is ignored and, (3) CP WO-dC, reject the outliers based on (13) with taking into account the cross-correlation. Figure4 shows the fused solution of three sensors when the estimate provided by sensor 2 is in disagreement with sensor 1 and 3. It can be observed from Fig.4 that neglecting the cross-correlation in CP WO-d result in Type II error, that is, all the three estimates are fused despite the fact that estimate 2 is inconsistent. CP WO-dC correctly identifies and eliminates the spurious estimate before the fusion process. Figure 5

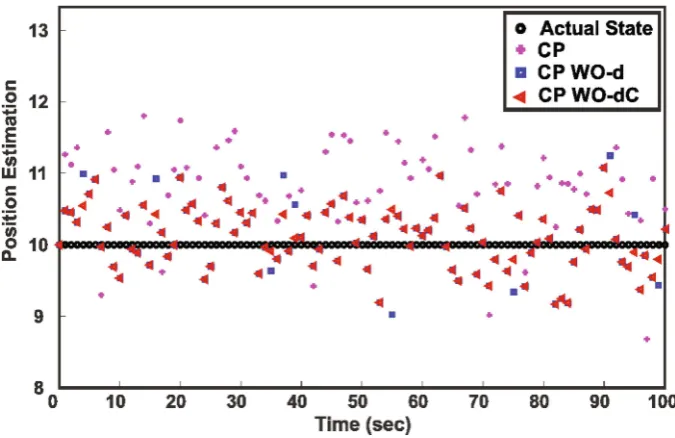
shows the estimated state after fusion of three sensors estimates for 100 samples. It can be seen that the presence of outliers greatly affects the outcome of multisensor data fusion. As depicted in Fig.5, eliminating outliers before fusion can improve the esti-mation performance. The fused samples of CP WO-d and CP WO-dC on average lies closer to the actual state. Figure5also shows the fusion performance when outliers are identified with and without cross-correlation. It can be noted that inconsideration of correlation affects the estimation quality because of Type I and Type II error.

4 Simulation Results

In this section, simulation results are provided to demonstrate the effectiveness of the proposed method for fusion of spurious data. The performance is assessed by root mean square error (RMSE) over the simulation time computed as,

SRMSE ¼ 1

V

X V

i¼1

ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi

xActualð Þi xEstimatedð Þi

ð Þ2

L

s

where L is the length of simulation and V is the Monte-Carlo runs.

Consider a target tracking scenario characterized by the following dynamic system model,

xk ¼ 1 target at time t respectively. T is the sampling period and assumed as 3 s. The system process is affected by zero mean Gaussian noisewk 1with covariance matrixQ. Three sensors are employed to track the movement of the target, where the sensor mea-surements are approximated by the following equation,

zki ¼ 1 0 0 1

xk þ vki þ eki; i ¼ 1;2;3 ð15Þ

The measurements of the sensors are corrupted by noisevkiwith respective covariance of Ri;i ¼ 1;. . .;3. The covariance of the process noise assumed is Q ¼ 10 and sensor measurement noises are,

R1 ¼ diagð50;30Þ; R2 ¼ diagð70;20Þ; R3 ¼ diagð10;60Þ

The control inputuk 1 ¼ 1 ifv\30 otherwise it is changed to₋1 untilv\5:It is assumed that the sensor 1, sensor 2 and sensor 3 measurements are independently affected by unmodeled random noiseeki for 33, 33 and 34% of the time respectively and thus the estimates provided by sensors are sometimes spurious.

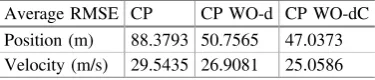
Starting from an initial value, in each time step the individual sensor uses local state prediction, that is, (14) to predict the state of the target and then update the state prediction by its own sensor measurements obtained through (15). The local estimates are assumed to be correlated and (8) is used to calculate the track-to-track cross-correlation. The estimated states and covariances by each sensor are sent to the fusion center, where they are fused by CP Method, which takes care of the cross-correlation among the estimates. The three fusion strategies of CP (fusion without outlier removal), CP WO-d (outlier removal without considering cross-correlation) and CP WO-dC (taking care of correlation in outlier removal) are compared based on RMSE between the actual state value and fused estimate of the state for 1000 Monte Carlo runs. In the simulation setup, the inconsistency is detected with significance level a= 0.05. Figure6(a) and (b) illustrate the RMSE of the target position and velocity respectively versus time. Table1summarizes the average RMSE for 1000 Monte Carlo runs.

5 Conclusion

Sensors often produce inconsistent and spurious data. Detection and removal of such inconsistencies before fusion is essential for accurate state estimation. In this paper, we propose a general approach to the fusion of correlated and uncertain data sources. The proposed method provides an unbiased and optimal fusion rule for arbitrary sensors in a distributed sensor architecture. The method automatically detects and remove inconsistent estimates from multiple data sources by assigning statistical confidence measure. Simulation results verified the effectiveness of the proposed method in the identification of spuriousness in distributed sensor data. It was shown that the proposed method improves the estimation quality by effectively identifying and removing the incorrect sensor data. It was also observed that consideration of cross-correlation by the proposed method in the detection of outliers result in lower RMSE due to avoidance of Type I and II errors.

Acknowledgments. The original idea of the proposed approach is due to Sukhan Lee. This research was supported, in part, by the“Space Initiative Program”of National Research Foun-dation (NRF) of Korea (NRF-2013M1A3A3A02042335), sponsored by the Korean Ministry of Science, ICT and Planning (MSIP), and in part, by the“3D Visual Recognition Project”of Korea Evaluation Institute of Industrial Technology (KEIT) (2015-10060160), and in part, by the

“Robot Industry Fusion Core Technology Development Project”of KEIT (R0004590).

Appendix 1

The fused mean and covariance of Covariance Projection (CP) Method are given as,

~x¼W 1PrW^x ðA1Þ

~

P¼W 1PrWPWTPTrW

T _ðA2Þ

Putting W ¼D 1=2ET_{; P}

r¼MW MW T

MW

1

MWT

and MW_{¼WM in (A2), we} get,

~

P¼W 1WM M TWTWM 1MTWTWM M TWTWM 1MTWT

T

W T

Leta¼MTWTWM, then,

~

P¼W 1WMa 1MTWTWMa TMTWTW T ~

P¼Ma TMT

ðA3Þ

Putting the value of ain (A3) and simplifying, we get,

~

TheP~ in (A5) is the projection of the ellipsoid on the equality constraint. Projecting it on the subspace of individual data source will result in fused covariance as,

~

P¼MTP 1M 1

ðA6Þ

Similarly, using definitions of various components in fused mean (A1), we have,

~

The fused mean on the subspace of individual data source can then be obtained as,

~x¼MTP 1M 1

MTP 1^x ðA9Þ

Appendix 2

Similarly

Putting (B2) and (B3) in (B1) and simplifying, we get,

d¼ ½^x1 ^x2Š

1. Bakr, M.A., Lee, S.: Distributed multisensor data fusion under unknown correlation and data inconsistency. Sensors17, 2472 (2017)

2. Liggins II, M., Hall, D., Llinas, J.: Handbook of Multisensor Data Fusion: Theory and Practice. CRC Press, Boca Raton (2017)

3. Bar-Shalom, Y.: On the track-to-track correlation problem. IEEE Trans. Automat. Contr.26, 571–572 (1981)

4. Smith, D., Singh, S.: Approaches to multisensor data fusion in target tracking: a survey. IEEE Trans. Knowl. Data Eng.18, 1696–1710 (2006)

5. Maybeck, P.: Stochastic Models, Estimation, and Control. Academic Press, New York (1982)

6. Khaleghi, B., Khamis, A., Karray, F., Razavi, S.: Multisensor data fusion: a review of the state-of-the-art. Inf. Fusion14, 28–44 (2013)

7. Abdulhafiz, W., Khamis, A.: Handling data uncertainty and inconsistency using multisensor data fusion. Adv. Artif. Intell.2013, 1–11 (2013)

8. Hwang, I., Kim, S., Kim, Y., Seah, C.E.: A survey of fault detection, isolation, and reconfiguration methods. IEEE Trans. Control Syst. Technol.18, 636–653 (2010) 9. Wellington, S., Atkinson, J.: Sensor validation and fusion using the Nadaraya-Watson

statistical estimator. In: Information Fusion 2002 (2002)

10. Doraiswami, R., Cheded, L.: A unified approach to detection and isolation of parametric faults using a Kalmanfilter residual-based approach. J. Franklin Inst.350, 938–965 (2013) 11. Jeyanthi, R., Anwamsha, K.: Fuzzy-based sensor validation for a nonlinear bench-mark boiler under MPC. In: 2016 10th International Conference on Intelligent Systems and Control (ISCO), pp. 1–6. IEEE (2016)

12. Abbaspour, A., Aboutalebi, P., Yen, K.K., Sargolzaei, A.: Neural adaptive observer-based sensor and actuator fault detection in nonlinear systems: application in UAV. ISA Trans.67, 317–329 (2017)

14. Lee, S., Bakr, M.A.: An optimal data fusion for distributed multisensor systems. In: Proceedings of the 11th International Conference on Ubiquitous Information Management and Communication - IMCOM 2017, pp. 1–6. ACM Press, New York (2017)

15. Shin, V., Lee, Y., Choi, T.: Generalized Millman’s formula and its application for estimation problems. Signal Process.86, 257–266 (2006)

Systems with Delayed and Lossy

Acknowledgments

Florian Rosenthal(B)_{, Benjamin Noack, and Uwe D. Hanebeck}

Intelligent Sensor-Actuator-Systems Laboratory (ISAS), Institute for Anthropomatics and Robotics,

Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany {florian.rosenthal,noack}@kit.edu, uwe.hanebeck@ieee.org

Abstract. In this article, we are concerned with state estimation in Net-worked Control Systems where both control inputs and measurements are transmitted over networks which are lossy and introduce random transmission delays. We focus on the case where acknowledgment pack-ets transmitted by the actuator upon reception of applicable control inputs are also subject to delays and losses, as opposed to the com-mon notion of TCP-like communication where successful transmissions are acknowledged instantaneously and without losses. As a consequence, the state estimator in the considered setup has only partial and belated knowledge concerning the actually applied control inputs which results in additional uncertainty. We derive an estimator by extending an existing approach for the special case of UDP-like communication which main-tains estimates of the applied control inputs that are incorporated into the estimation of the plant state. The presented estimator is compared to the original approach in terms of Monte Carlo simulations where its increased robustness towards imperfect knowledge of the underlying net-works is indicated.

Keywords: State estimation

·

Networked control systems

·

Delays Packet losses

·

Markov jump linear systems

·

IMM filter

1

Introduction

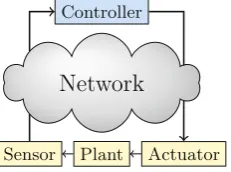
Networked Control Systems (NCSs), such as the one sketched in Fig.1, are a spe-cial class of control loops where the individual components, i.e., plant/actuator, sensor, and controller, communicate over packet-based and typically general-purpose networks such as WiFi or Ethernet. In comparison to traditional con-trol loops, where dedicated point-to-point connections are utilized, such sys-tems profit from reduced expenditure for installation and maintenance, and from enhanced flexibility and reliability [1]. On the downside, they have to cope with effects and constraints induced by the networks and constraints like random

c

Springer International Publishing AG, part of Springer Nature 2018 S. Lee et al. (Eds.): MFI 2017, LNEE 501, pp. 22–38, 2018.

packet losses, delays and limited bandwidth. Since these factors affect the over-all system performance and stability, communication and control should not be addressed independently from each other [2–4]. Consequently, several control methods have been proposed in recent years that explicitly consider the under-lying network. Among these, the approach ofsequence-based control has gained much attention [5–9]. Here the idea is to compute control inputs for the next, sayN, time steps in addition to the one for the current time instant. By trans-mitting this control sequence in a single data packet which is buffered at the actuator upon reception, the problem of delayed or missing control inputs can be alleviated. Such controllers, often called predictive controllers, are usually based on model predictive control approaches [6,7], or adapted from nominal controllers which disregard the network [10,11]. Also, controllers which directly minimize a quadratic cost function with respect to the control sequence have been proposed [8,9]. Since most of the derived control algorithms either explic-itly demand a state estimate or assume a perfectly known state or noise-free plants and measurements, state estimation is generally required in an NCS. This article is an extended version of our previous paper [12], where we devel-oped an estimator based on the minimum mean squared error (MMSE) criterion for a given predictive controller in an NCS scenario. Due to the presence of the networks, the estimator is confronted with the problem that measurements and control inputs can arrive delayed or get lost so that out-of-sequence and burst arrivals are probable. In particular, the resulting uncertainty about the actual applied control inputs poses a major challenge.

Network

Controller

Plant

Sensor Actuator

Fig. 1.Schematical overview of a Networked Control System.

the acknowledgment packets sent from the actuator to the controller also suffer from random delays and losses. Consequently, the setup in [19] can be seen as a special case of the scenario we consider in that acknowledgments are provided by the actuator but always get lost.

Outline. This article is structured as follows. First, in Sect.2we give a detailed description of the considered scenario. Then, in Sect.3 we derive an estimator based on a formal model of the considered problem. The performance of the presented estimator is then assessed in Sect.4. Finally, Sect.5 concludes this work.

Notation. Throughout the article, vectors will be indicated by underlined let-ters (x) while random vectors will be underlined and in bold (x). To denote matrices, we will employ boldface capital letters, e.g., A. We useIn to denote

then-dimensional identity matrix,0to denote zero matrices of arbitrary dimen-sion, and a subscript k, e.g., x_k, to indicate the time step. Transposition of a vector or a matrix is indicated by xT and AT. Finally, δi,j stands for the

Kronecker delta, i.e.,δi,j= 1 ifi=j and 0 otherwise.

2

Problem Formulation

Consider an NCS where both plant and sensor are linear and described by

x_k+1=A_kx_k+B_ku_k+w_k,

y_k=Ckxk+vk,

(1)

withxk ∈IRn, andy_k ∈IRmstate and measurement, respectively, anduk∈IRl

the control input provided by a given controller. The zero mean white noise sequencesw_kandv_kare Gaussian and independent of each other with covariance matricesW_k and V_k. The initial plant statex₀ is Gaussian with mean ˆx₀ and covariance matrixΣ0and is independent ofwiandvj. Furthermore, we assume

that all components are synchronized and that the networks assign time stamps to data packets upon transmission.

Uk=

to be applied at time k+i. The buffer located at the actuator side employs the so called past packets rejection logic[1]: From the set of all received control sequences, the one with the largest time index, that is, only the most recent sequence, is maintained while all others are discarded. The control inputs pro-vided by this sequence are then successively applied at the corresponding time steps until a newer sequence reaches the actuator. However, in case of subsequent packet losses or large delays it may occur that the next control sequence arrives too late so that the control inputs from the buffered sequence are not applicable anymore. In such a case, the default input udf_k = 0 is applied.

Remark 1. Applying the default control input udf_k = 0 is known as zero-input strategy in literature. Another common alternative is to apply the previous con-trol input, i.e.,udf_k =u_k−1, which is known as hold-input strategy. While the first one is mathematically more convenient, it has been shown in [20] that even for scalar systems and when only packet dropouts are considered neither strategy is superior.

Each time the stored control sequence is replaced by a more recent one, an acknowledgment (ACK) is sent back by the actuator to indicate a successful transmission of the corresponding sequence. It is important to emphasize that these ACKs are application layer acknowledgments, since not every received data packet is acknowledged by the actuator, but only that one containing the actually utilized control sequence. From the perspective of the underlying CA-network they are just regular payload to be delivered. Consequently, the ACKs are also subject to delays and losses (infinite delays) which are modeled by the i.i.d. random variables τAC_k with PMFfAC. Due to this acknowledgment procedure, the controller is able to infer applied control inputs upon the reception of ACKs from the actuator.

Remark 2. Note that, besides the actuator acknowledgment procedure, the transport layer protocol employed by the CA-network might send out dedicated acknowledgment packets upon successful reception of data packets. A common example is the TCP protocol, while UDP is an example for a transport layer pro-tocol that does not acknowledge received packets. TCP implementations enhance the reliability of the communication compared to UDP, since they issue packet retransmissions in case such an acknowledgment packet is delayed or missing. However, it is known that this behavior often poses a severe problem for rela-tively short transfers [21,22]. Also, data losses are traded for large delays, which is typically not desired in Networked Control Systems [3].

regard, the setup we consider could be summarized as UDP-like network with application layer acknowledgments.

Finally, at each time step, a sensor takes a noisy measurement of the state and sends it over another network (SC-network) to an estimator which is attached to the controller. Delays and losses in this network are described by the i.i.d. random variablesτSC_k with given PMFfSC_{, so that at each time instant multiple}

measurements (or none) can arrive at the estimator. Note that in contrast to the CA-network, (i) all delayed packets do provide valuable information about past states and hence should be processed by the estimator and (ii) this net-work appears deterministic for the estimator since the packet delays are known due to the assigned time stamps. However, as the estimator’s buffer is finite, only up to M ∈ IN measurements can be stored at the same time. As will be discussed in Sect.3, an appropriate approach to deal with burst and out-of-sequence arrivals of measurements is to maintain a fixed measurement history. The following assumption is thus justified.

Assumption 1. Measurements with a delay larger than M −1 time steps are discarded by the estimator upon reception.

Remark 4. Discarding measurements according to the above assumption always results in a suboptimal estimator. However, for the case that all measurement packets either arrive with a delay of at mostM−1 time steps or do not arrive at all, that is, for the case that no measurements have to be discarded, the optimal estimator was presented [14].

The complete setup is depicted in Fig.2. Our goal is to design an estimator which, at each time stepk, supplies the controller with an estimate ˆxe_k of the plant state based on the MMSE criterion for the given setup. We do so by extending the filter proposed by Fischer et al. [19] for a UDP-like CA-network.

Network

Network

Fig. 2.Considered NCS Setup. A control sequenceUk computed by the controller is

transmitted to the actuator which buffers the most recent sequence. From this sequence, the control inputuk corresponding to the current time step is selected and applied to

3

Derivation of the Proposed Estimator

The estimator from [19] relies on a stochastic model which jointly describes the CA-network and the actuator as dynamical system. With this model and a suitable state augmentation, the considered NCS is then expressed in terms of a Markov jump linear system (MJLS) [23]. As we build upon this estimator, we provide a condensed summary of the resulting model in Sect.3.1. A more detailed derivation can be found in [8,19]. We then present the proposed esti-mator in Sect.3.2.

3.1 Modeling the NCS as a Markov Jump Linear System

Main ingredients of the network-actuator model are a vector η

k which

encom-passes all control inputs from the sequencesU_k−N, . . . , Uk−1that are still appli-cable at time kor later, and an additional discrete, scalar random variable θk.

Formally,η

Fig. 3. Visualization of the elements ofη

k (

k−2 k−1 k k+ 1 k+ 2

Fig. 4.Illustration of the relationship betweenη

k+1(dashed),ηk (solid), andUk for

N= 2. Applicable control inputs for the same time step are shown one below another.

with

k−t if the currently buffered control sequence isU_t

N+ 1 else , (4)

where k−N ≤t ≤k, we have that θk ∈ {0, . . . , N + 1} and thatθk =N+ 1

corresponds to the case when the buffer ran empty and the default inputudf_k = 0 is applied. In [19] it was shown thatθkis a Markov chain with transition matrix

Tgiven by

wherepj=fCA(j) denotes the probability that a control sequence arrives with

a delay ofj time steps, and qj = 1−ji=0pi. By means of η_k and θk, we can

write the actual applied control input according to

with

which is a MJLS with parameter θk, usually referred to as the mode of the

system. Recall from (4) thatθk ∈ {0, . . . , N+ 1}, the augmented system hence

possessesN+ 2 modes.

3.2 Estimator Design

A major challenge for the design of an estimator for (7) is that in the given setup only a subset Ik of the mode historySk ={θ0, θ1, . . . , θk} is available to

the estimator. More precisely, Ik contains those modes that could be inferred

from ACKs that have been received by the controller up to time k. It is well-known that a time-varying Kalman filter is the optimal MMSE estimator for MJLS if Ik =Sk, i.e., if the complete mode history is available. However, it is

also well-known that for the other extreme case Ik =∅, that is, the case of a

completely unknown mode history, the optimal estimator is not only nonlinear but also intractable [24,25]. This is mainly due to the fact that an exponentially increasing number of hypotheses about the true mode trajectory must be tracked. The computational complexity thus grows exponentially in time. Consequently, a variety of approximations to the optimal solution have been proposed, ranging from LMMSE estimators [26–28] to approaches which at each time instant main-tain only a fixed number of hypotheses about the mode history by applying some hypothesis reduction strategy [29]. Among the latter, the Interacting Multiple Model (IMM) filter [24] has gained much attraction as it exhibits a good trade-off between estimation quality and complexity. A variant of the IMM filter for a UPD-like NCS scenario, which corresponds to this extreme case Ik =∅, has

been introduced in [19]. As already mentioned, we will build upon this estimator and generalize it to the caseIk ⊂ Sk.

measurements. For instance, the estimators proposed in [31,32] only consider packet losses, and the MMSE estimator from [33] assumes fixed measurement delays. On the downside, applying retrodiction in our setup necessitates that the system matrix Ak in (1) is invertible which is not always given. Fischer et al.

[19] thus proposed to adapt the approach from [34] and to instead maintain a history of past estimates which is updated upon the reception of a delayed measurement. Besides being simple, this approach has the advantage that it is inherently suited for dealing with burst arrivals of measurements which can be, for instance, processed one by one. Moreover, it can be easily extended to deal with delayed mode observations. We introduce this extension in the following.

In essence, the IMM filter is composed of a bank of Kalman filters, one for each mode, which are individually reinitialized at each time step by mixing all mode-conditioned estimates from the previous time step [29]. For the given system (7) with N + 2 different modes the IMM filter thus requires N + 2 individual filters, so that the state estimate is maintained as a Gaussian mixture distribution withN+ 2 components. Each component is weighted according to the estimated mode probability distributionπ_k. At the end of each measurement update, the mode distribution is updated according to the mode-conditioned measurement likelihoods. The point estimate ˆxe_kfor the controller is then simply the mean of the mixture. Suppose now, that at time k, the estimator can infer a mode realization θt=L,t≤k,L∈ {0, . . . , N}, due to a received ACK. The

proposed extension exploits that the distribution ofθtthen reduces to

π_t=e_L+1, (8)

where e_L+1 is the (N + 2)-dimensional unit vector with one at position L+ 1 and zero elsewhere.1_{Please note that the mode realizationθ}

t=N+ 1 will never

be available to the filter since this indicates that at timetthe default input was applied. In such a case, no applicable control sequence would have been received in time by the actuator, and hence no ACK would have been sent back. Note also that, since the measurement equation in (7) is independent of the mode,

θt only affects the prediction step at t+ 1. Combined with Assumption1 this

means that it is reasonable to discard all ACKs with a delay larger than M time steps. Integrating a delayed mode observation at time kfinally consists of updatingπ_taccording to (8) and then recomputing the estimates fromt+1 tok. This procedure is also well-suited to handle burst arrivals of ACKs, which means that multiple modes can be inferred at once. Starting with the oldest one, they are simply integrated into the recomputation of the state estimates one after another. One cycle of the proposed estimator is summarized in Algorithm1. For a detailed description of the IMM-specific steps in lines 5, 9, 13, 14 and 16 refer to, for instance, [24,29]. We can clearly get from the algorithm that both computational complexity and required memory increase with the buffer length. In particular, it necessary to store at least the mode observationsθk−M, . . . , θk−1, the control sequencesU_k−M, . . . , U_k−1, the measurementsy

k−M+1, . . . , yk, and

the Gaussian mixture denoting the estimate from timek−M. To represent the

1

latter,N+2 mode-conditioned means and covariance matrices and the estimated mode distributionπ_k−M must be stored.

A reference implementation of the algorithm is available on github as part of the CoCPN-Sim simulation framework [35].

Algorithm 1. One Cycle of the Proposed IMM-based Estimator

Input: Estimate from timek−M, i.e., Gaussian mixture

Output: Point estimate ˆxek

1: fori=M−1to0do

2: if modeθk₋i₋1 is availablethen

3: Updateπk

−i−1according to (8)

4: end if

5: Reinitialize the mode-conditioned Kalman filters 6: Createη

k

−i−1

according to (2) // Prediction Step

7: for allmode-conditioned filtersdo

8: Compute mode-conditioned input by usingη_k

−i−1

,Uk

−i−1 in (6)

9: Perform prediction using the mode-conditioned input 10: end for

// Measurement Update 11: if measurementy

k₋i is availablethen

12: for allmode-conditioned filtersdo

13: Perform measurement update usingy_k

−i

14: Evaluate measurement likelihood

15: end for

16: Updateπk

−iusing to the individual measurement likelihoods

17: end if

18: end for

19: Compute mixture mean ˆxe k

20: return xˆek

Remark 5. We conclude this section with the remark that θk describes an

ergodic Markov chain and hence possesses a stationary distribution [9]. As an alternative to the proposed algorithm, the Kalman filter approach from [18], equipped with the stationary distribution, could also be used in the given setup. However, using this stationary distribution is clearly an approximation and in [19] it was shown that this approach is inferior to an IMM-based filter.

4

Evaluation

Table 1.Parameters of the inverted pendulum used in the evaluation.

Mass of the cart 0.5 kg Mass of the pendulum 0.5 kg Coefficient of friction for the cart 0.1 N s/m Length to pendulum center of mass 0.3 m Moment of inertia of the pendulum 0.006 kg m2

Gravitational acceleration 9.81 m/s2

history Ik. Our aim is to evaluate to what extent the information advantage of

the proposed filter results in improved estimates.

To that end, consider the state of the pendulum given by x_k =

sk s˙k φk φ˙k

T

. Here, sk denotes the position of the cart (in m) and φk is

the deviation (in rad) of the pendulum from the upward equilibrium. Lineariz-ing the nonlinear pendulum dynamics (cf., for instance, [36]) with parameters given in Table1 around the upward equilibrium and performing a subsequent discretization with sampling timetA=0.01 s results in the linear model (1) with

A_k =

The state variablesskandφkare thus directly accessible, i.e., the are measured,

while ˙skand ˙φkare non-accessible state variables. The covariances ofwkandvk

are chosen to beWk = 0.01I4andVk = 0.2I2. As in [19], we employ a nominal predictive state feedback linear quadratic regulator [36] and compute the control sequences U_k based on the true state of the plant. State and input weighting matrix for the calculation of the regulator gainLare given by

Q=

Overall, we carried out two Monte Carlo simulations with 2000 runs each where each run comprised 250 time steps. In each run, the initial plant state was randomly drawn from a Gaussian distribution with mean and covariance matrix

ˆ x0=

0 0.2 0.2 0T

0 1 2 3 4 5 ≥6

Fig. 5. PMFs of the packet delays. Delays larger than five time steps in the SC-link are treated as packet losses (infinite delay) by the estimators.

The probability mass functionsfCA,fAC andfSC used to model the networks employed in the simulations are depicted in Fig.5. In each simulation run the actual delay of each packet was independently drawn according to the corre-sponding PMF.

We chose to set the length of the measurement history toM = 6. Accordingly, measurements with a delay larger than five time steps and ACKs with a delay larger than six time steps were discarded. For the SC-network described by the PMFshown in Fig.5a the measurement loss rate was thus 4. For the ACKs sent from the actuator to the controller, we decided to utilize a distribution (cf. Fig.5b) according to which delays larger than three time steps were very unlikely. As mentioned above, the plant operates in a transient state, i.e., set point changes occur. Thus, in each simulation run, the initial set point of the pendulum was [2 0 0 0]T _{which changed to [−2 0 0 0]}T _{after 100 time steps and then changed} back after another 100 time steps. The length of the control sequences computed by the controller was N + 1 = 7, resulting in an MJLS with 8 modes. In each run, the mode-conditioned Kalman filters of both estimators were initialized with a Gaussian with mean ˆx₀ and covariance matrix Σ0 and the initial mode distribution wasπ₀ =e₈∈IR8. Note that neither estimator had impact on the computation of the control sequences because the control inputs were computed based on the true state.

In the first simulation, the true PMFfCA _{from Fig.5a was used in (5) to}

compute the transition matrix T of the Markov chain θk, while in the second

simulation we assumed that the filters were completely unaware of the behavior of the CA-link. Hence, we employed a uniform PMFinstead in (5) to obtainT. This decision was motivated by the time-varying nature of real networks, due to which model mismatches are likely in practical applications.

The simulation results in terms of the root mean squared error (RMSE) are shown in Fig.6 for the directly accessible statessk andφk and in Fig.7for the

non-accessible states ˙skand ˙φk. We can immediately see from the results that the

0 50 100 150 200 250

(b)Uniform PMF assumed forτCA_k Estimator from [19] Proposed Estimator

Fig. 6.Results of the proposed estimator and the original approach from [19]: Com-parison of the RMSE for the directly accessible statesskandφk.

pays off at a single time step (k = 190) in both simulation scenarios. At that time step, the estimation error of the filter from [19] increases drastically while it remains at the same level for the proposed filter. An additional interesting observation is that the estimation quality of both filters is not affected by the model mismatch introduced in the second simulation.

As opposed to this, the RMSE curves of the non-accessible states ˙sk and

˙

φ_k exhibit that the overall estimation quality of both filters is corrupted by the wrong PMFassumed forτCA

k . However, although both filters achieve almost

equal performance most of the time, the proposed approach can yield signifi-cantly lower estimation errors compared to the approach from [19] even in case of a model mismatch. In particular for the angular velocity component of the state ˙φ_k, the original approach is not able to improve its estimates at times where the proposed approach achieves considerable improvements.

Overall, we can conclude that the additional available information in terms of the partial mode historyIk can result in an enhanced estimation quality and

0 50 100 150 200 250

(b)Uniform PMF assumed forτCA_k

Estimator from [19] Proposed Estimator

Fig. 7.Results of the proposed estimator and the original approach from [19]: Com-parison of the RMSE for the non-accessible states ˙skand ˙φk.

nature of the networks. Finally, it is worth to remark that the set point changes do not result in an increased estimation error, in contrast to what was reported in [19].

5

Conclusions

networks, we derived a state estimator which is able to incorporate the informa-tion on applied past control inputs retroactively into the estimate of the current state.

The evaluation results indicated that the integration of this belated infor-mation can be an appropriate means to make the filter more robust towards imperfect knowledge of the network characteristics, in particular for components of the state that are not directly accessible.

Prospective research in this context will address scenarios with time-varying packet delays and losses. This is especially of interest with regards to the increas-ing number of cyber-physical systems where usually multiple control loops share a network. We will focus on the derivation of an estimator which does not require a priori knowledge of the underlying network delay distributions or relies on assumptions. Here, the joint estimation of the plant state and the properties of θk seems promising. Likewise, approaches from robust estimation, such as

H∞ estimation, which exploit the structure of the transition matrix, could be

employed. Future work should also be concerned with the incorporation of the hold-input strategy into the presented estimator. Finally, it is worth to exam-ine whether an additional, similar state augmentation which explicitly takes the network between sensor and estimator into account, can serve as a starting point for the derivation of an estimator for the given setup.

Acknowledgments. This work is supported by the German Science Foundation (DFG) within the Priority Programme 1914 “Cyber-Physical Networking”.

References

1. Zhang, L., Gao, H., Kaynak, O.: Network-induced constraints in networked control systems a survey. IEEE Trans. Ind. Inform.9(1), 403–416 (2013).https://doi.org/ 10.1109/TII.2012.2219540

2. Hespanha, J.P., Naghshtabrizi, P., Xu, Y.: A survey of recent results in net-worked control systems. Proc. IEEE 95(1), 138–162 (2007). https://doi.org/10. 1109/JPROC.2006.887288

3. Baillieul, J., Antsaklis, P.J.: Control and communication challenges in net-worked real-time systems. Proc. IEEE 95(1), 9–28 (2007). https://doi.org/10. 1109/JPROC.2006.887290

4. Heemels, W.M.H., Teel, A.R., Van de Wouw, N., Nesic, D.: Networked control systems with communication constraints: tradeoffs between transmission intervals, delays and performance. IEEE Trans. Autom. Control 55(8), 1781–1796 (2010). https://doi.org/10.1109/TAC.2010.2042352

5. Bemporad, A.: Predictive control of teleoperated constrained systems with unbounded communication delays. In: Proceedings of the 37th IEEE Conference on Decision and Control, vol. 2, pp. 2133–2138. IEEE (1998).https://doi.org/10. 1109/CDC.1998.758651

7. Quevedo, D.E., Nesic, D.: Input-to-state stability of packetized predictive control over unreliable networks affected by packet-dropouts. IEEE Trans. Autom. Control

56(2), 370–375 (2011).https://doi.org/10.1109/TAC.2010.2095950

8. Fischer, J., Hekler, A., Dolgov, M., Hanebeck, U.D.: Optimal sequence-based LQG control over TCP-like networks subject to random transmission delays and packet losses. In: 2013 American Control Conference, Washington, D.C., USA, pp. 1543– 1549 (2013).https://doi.org/10.1109/ACC.2013.6580055

9. Dolgov, M., Fischer, J., Hanebeck, U.D.: Infinite-horizon sequence-based networked control without acknowledgments. In: 2015 American Control Conference (ACC), Chicago, Illinois, USA, pp. 402–408 (2015). https://doi.org/10.1109/ACC.2015. 7170769

10. Liu, G.P., Xia, Y., Chen, J., Rees, D., Hu, W.: Networked predictive control of systems with random network delays in both forward and feedback channels. IEEE Trans. Ind. Electron.54(3), 1282–1297 (2007).https://doi.org/10.1109/TIE.2007. 893073

11. Liu, G.: Predictive controller design of networked systems with communication delays and data loss. IEEE Trans. Circuits Syst. II Express Briefs57(6), 481–485 (2010).https://doi.org/10.1109/TCSII.2010.2048377

12. Rosenthal, F., Noack, B., Hanebeck, U.D.: State estimation in networked control systems with delayed and lossy acknowledgments. In: 2017 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Daegu, Korea, pp. 435–441 (2017).https://doi.org/10.1109/MFI.2017.8170359 13. Sinopoli, B., Schenato, L., Franceschetti, M., Poolla, K., Jordan, M.I., Sastry,

S.S.: Kalman filtering with intermittent observations. IEEE Trans. Autom. Control

49(9), 1453–1464 (2004).https://doi.org/10.1109/TAC.2004.834121

14. Schenato, L.: Optimal estimation in networked control systems subject to random delay and packet drop. IEEE Trans. Autom. Control 53(5), 1311–1317 (2008). https://doi.org/10.1109/TAC.2008.921012

15. Thapliyal, O., Nandiganahalli, J.S., Hwang, I.: Optimal state estimation for LTI systems with imperfect observations. In: 2017 IEEE 56th Annual Conference on Decision and Control (CDC), pp. 2795–2800. IEEE (2017). https://doi.org/10. 1109/CDC.2017.8264065

16. Epstein, M., Shi, L., Murray, R.M.: An estimation algorithm for a class of net-worked control systems using UDP-like communication schemes. In: Proceedings of the 45th IEEE Conference on Decision and Control, pp. 5597–5603. IEEE (2006). https://doi.org/10.1109/CDC.2006.377481

17. Schenato, L., Sinopoli, B., Franceschetti, M., Poolla, K., Sastry, S.S.: Foundations of control and estimation over lossy networks. Proc. IEEE95(1), 163–187 (2007). https://doi.org/10.1109/JPROC.2006.887306

18. Moayedi, M., Foo, Y.K., Soh, Y.C.: Filtering for networked control systems with single/multiple measurement packets subject to multiple-step measurement delays and multiple packet dropouts. Int. J. Syst. Sci.42(3), 335–348 (2011).https://doi. org/10.1080/00207720903513335

19. Fischer, J., Hekler, A., Hanebeck, U.D.: State estimation in networked control systems. In: 2012 15th International Conference on Information Fusion, Singapore, pp. 1947–1954 (2012)