www.elsevier.com/locate/orms
Simplicial with truncated Dantzig–Wolfe decomposition
for nonlinear multicommodity network ow problems
with side constraints
(
Siriphong Lawphongpanich
∗Department of Operations Research, Naval Postgraduate School, 1411 Cunningham Road, Monterey, CA 93943, USA
Received 1 June 1998; received in revised form 1 July 1999
Abstract
The simplicial decomposition (SD) subproblem for a nonlinear multicommodity network ow problem is simply its linear approximation. Instead of solving the subproblem optimally, this paper demonstrates that performing one iteration of Dantzig– Wolfe decomposition is generally sucient for SD to eciently converge to an optimal solution. c2000 Elsevier Science B.V. All rights reserved.
Keywords:Multicommodity network; Trac assignment problem; Decomposition technique
1. Introduction
The nonlinear multicommodity network ow prob-lem with side constraints can be stated as follows:
NMNFP-SC : min x f
K X
k=1
x(k) !
s:t: Bx(k) =b(k); ∀k= 1; : : : ; K;
K X
k=1
Sx(k)6u;
x(k)¿0; ∀k= 1; : : : ; K;
(This research was partially supported by the U.S. Army’s Oce of the Deputy Chief of Sta for Personnel and the Naval Postgraduate School Institutionally Funded Research Program.
∗Fax: +1-831-656-2595.
E-mail address:[email protected] (S. Lawphongpanich)
where B is the node-arc incidence matrix for the underlying network,b(k) is the supply–demand vec-tor for commodity k; S and u are a matrix and a vector, respectively, forming the side constraints, x(k) is the ow vector for commodity k, and f(x) is a pseudo-convex cost function. For the remain-der, X represents the aggregate ow vector, i.e., X =PKk=1x(k).
One important instance of NMNFP-SC and the main motivation of this work is the capacitated trac as-signment problem (see, e.g., [13,18]) whereS is the identity matrix and u is a vector of arc capacities. However, there are other applications such as those in, e.g., [2,22,23].
Simplicial decomposition (SD) as applied to NMNFP-SC can be stated as follows:
Simplicial Decomposition
Step0: LetX1be a feasible aggregate ow vector
and set= 1.
wherey(k) and Y are dened in a manner similar to x(k) andX, respectively.
Step2: If 3f(X)t(Y−X)¿0, stop and X is
In Step 1, problem SD-SP() is a linear multicom-modity network ow problem with side constraints. (See, e.g., [2].) Because of its size, solving SD-SP() optimally, or nearly so, is time consuming. To avoid doing so, many (see, e.g., [13,23,18]) have dualized or penalized the side constraints in NMNFP-SC. The resulting dual or penalty problem is a nonlinear mul-ticommodity network ow problem without the side constraints for which there are several ecient algo-rithms (see, e.g., [7]). On the other hand, Gon et al. [10] and Hearn and Lawphongpanich [11] used varia-tions of the cutting plane technique (see, e.g., [3]) to solve a Lagrangian dual of NMNFP-SC instead.
Using a dierent strategy for decomposing NMNFP-SC, Rutenberg [24] (see also [16]), Marin [22], and Wu and Ventura [28] delete the side con-straints from SD-SP() and add them to the master problem. Doing so reduces the resulting subproblem
to a set of shortest path problems. On the other hand, the resulting master problem, i.e.,
+1= arg min
is larger and more complex. Below, it is demonstrated that the master problem can be kept as simple as the one in Step 3 while maintaining the shortest path struc-ture of the subproblem.
To solve SD-SP(), it is natural to consider de-composition techniques (see, e.g., [17]), especially for large networks. One such technique is the Dantzig– Wolfe (DW) decomposition (see [5]) which decom-poses SD-SP() into the following two problems, a master (DW-MP) and a subproblem (DW-SP). The master problem can be stated as follows:
DW-MP : min
initially. The remaining extreme points are generated as needed by solving the following subproblem:
DW-SP : min
whereis the dual vector corresponding to the side constraints (or the rst set of constraints) in DW-MP. Observe that DW-SP can be decomposed into K separate shortest path problems.
To establish a benchmark for his own algorithms, Stefek [25] implemented a restricted version of SD (see, e.g., [12]) and solved SD-SP() by DW decom-position to near optimality. This typically requires a large number of DW iterations, i.e., solving a large number of DW-MP and DW-SP problems.
Instead of obtaining a near optimal solution to SD-SP(), the next section demonstrates that DW decomposition, when ‘nested’ in simplicial decompo-sition, can be truncated after one iteration. The idea of ‘nesting’, or recursively applying DW decompo-sition, is described earlier in [14,9] for staircase or multi-stage linear programs. (For additional enhance-ments, see [27] and references cited therein.) The term ‘nesting’ is used here because SD is essentially DW decomposition generalized to nonlinear problems.
Finally, Section 3 summarizes the numerical results from an implementation of the algorithm in an alge-braic modeling system, GAMS [4].
2. Simplicial with truncated Dantzig–Wolfe decomposition
Below is a version of SD nested with truncated DW decomposition. In this version, superscripts dis-tinguish dierent vectors and subscripts denote dier-ent compondier-ents of a vector. Among the superscripts, andnindex extreme points in the SD and DW master problems, respectively.
Simplicial with truncated Dantzig–Wolfe (STDW) decomposition
Step 0: Let X1 be a feasible aggregate ow
vec-tor such thatPKk=1Sx1(k)6(1−)u for some small
whereq is the weight for theqth extreme point and = (1; 2; : : : ; n)t.
Letnandnbe optimal dual variables correspond-ing to the capacity and convexity constraints, respec-tively. SetZn=Pn
q=1qnPq.
Step2: If3f(X)t(Zn−X)¡0, then setY=Zn and go to Step 5. Otherwise, go to step 3.
Step3: For eachk= 1; : : : ; K, solve
Step 0 requires a solution,X1, that is both feasible
none is available, apply DW decomposition to the fol-lowing problem until the articial vectorw becomes zero:
min y
K X
k=1
3f( ˆX)ty(k) +Metw
s:t: By(k) =b(k); ∀k= 1; : : : ; K;
K X
k=1
Sy(k)−w6u;
y(k)¿0; ∀k= 1; : : : ; K;
w¿0;
where M is a suitably large constant, e is a (col-umn) vector of ones, and the aggregate ow vector
ˆ
X is arbitrary. Alternately, 3f( ˆX) can be replaced by a zero vector and the above problem becomes the Phase-I problem of the 2-Phase method for lin-ear programs. However, our numerical study suggests that using 3f( ˆX) can lead to a faster convergence. In any case, when DW decomposition terminates, it must yield a set of extreme points, i.e., {P1; : : : ; Pn}
where nis a positive integer, and a vectorsuch that X1 =Pn
q=1qPq is feasible to NMNFP-SC. At this
point, setY0=X1; = 1 andn= nand go to Step 1.
In Step 1, problem DW-MP(; n) as stated in-cludes all of the previously generated extreme points of F. (This requirement may be relaxed and it is a subject for a subsequent article.) Then, Step 2 checks whether a new feasible solution, Zn, leads to an improvement or generates a descent direction. If so, solving the SD-MP() in Step 5 would yield a new aggregate ow vector, X+1, with a smaller
objective function. When Zn does not satisfy the condition in Step 2, Step 3 generates a new extreme point, Pn+1, and adds it to the next master problem, DW-MP(; n+ 1), solved in Step 4. The theorem below shows that the next feasible point, Y, de-rived from the solution of DW-MP(; n+ 1) must yield a descent direction under a mild condition.
Theorem 2.1. Assume that X is not optimal
and DW-MP(; n) has a unique optimal solution. If 3f(X)t(Zn − X)¿0; then 3f(X)t(Y − X)¡0; where Y is derived from a solution to DW-MP(; n+ 1).
Proof. Since each Yr; r = 0; : : : ;( − 1), is in the convex hull of {P1; : : : ; Pn} and X is a con-vex combination of Y0; : : : ; Y(−1); X must be in the convex hull as well. From the condition that
3f(X)t(Zn−X)¿0, the unique solution, n, to DW-MP(; n) must be such thatX=Pn
q=1nqPq. To verify,3f(X)t(Zn−X)¿0 implies that
3f(X)tX63f(X)tZn= n X
q=1
(3f(X)tPn)n q:
Sincensolves DW-MP(; n) uniquely, the inequality in the above expression must hold at equality andX= Pn
q=1nqPq.
To obtain a contradiction, assume that3f(X)t(Y
−X)¿0. This implies that a solutionn+1such that
nq+1= (n
q if q= 1; : : : ; n;
0 if q=n+ 1
is optimal to DW-MP(; n+1). Moreover, (n; n), the optimal dual variables for DW-MP(; n), must be op-timal to the dual of DW-MP(; n+1) also. Given these dual values, the reduced cost for q is (3f(X)− Stn)tPq −n, which must be nonnegative for all q= 1; : : : ; n+ 1. In particular,
(3f(X)−Stn)tPq−n= 0; ∀q:n+1
q ¿0;
n X
q=1
[(3f(X)−Stn)tPq−n]qn+1= 0;
(3f(X)−Stn)tX−n= 0;
where the last equality follows from the construction of n+1 and the fact that n
q sums to one. Since the reduced cost for n+1 is nonnegative, the following
must hold:
(3f(X)−Stn)tPn+1−n
¿(3f(X)−Sn)tX−n= 0;
(3f(X)−Stn)t(Pn+1−X)¿0;
where the last inequality follows from the fact that pn+1(k) solves the kth shortest path problem in
DW-SP(n). However, this shows thatXsatises the optimality condition for NMNFP-SC (see, e.g., [22]) which is a contradiction.
Because solving DW-SP(n) in Step 3 and DW-MP(; n+ 1) in Step 4 constitutes one iteration of DW decomposition, the above theorem demon-strates that a descent direction for SD-MP() can be obtained by truncating the decomposition after one iteration.
When3f(X)t(Zn−X)¿0, an alternate optimal solution to DW-MP(; n) may exist. In such a case,Zn may not equalXand the wrong set of dual variables (i.e., those associated withZninstead ofX) may be transferred to DW-SP(n). Thus, 3f(X)t(Y−X) may not be negative as in Theorem 2.1. To ensure the same result when3f(X)t(Zn−X)¿0 andZn 6= X, one method is to let (n; n) be a solution to the following problem:
max
(;) u
t+
s:t: [SPq]t+63f(X)tPq; ∀q= 1; : : : ; n;
60;
t= 0 ∀i: [SX]i¡ ui:
Without the last constraint, the above problem is the dual of DW-MP(; n) in Step 1. On the other hand, the last constraint is derived from the complementary slackness condition associated with the rst constraint in DW-MP(; n) and the optimal primal solutionX. This ensures that the dual solution (n; n) and X form an optimal primal–dual pair.
When the algorithm terminates in Step 3, two con-ditions are satised. The rst condition is in Step 2 and veries thatZn does not produce a descent direc-tion. The second is in Step 3 and it ensures that no descent direction is possible. The justication of these two criteria is given in the following theorem.
Theorem 2.2.If3f(X)t(Zn−X)¿0and(3f(X)
−Stn)tPn+1−n¿0;thenXis optimal.
Proof. In a manner similar to the proof of Theorem 2.1, it can be demonstrated that these two conditions
lead to the following optimality condition:
(3f(X)−Stn)t(P−X)¿0; ∀P∈S:
Steps 1– 4 produce a descent direction for the master problem in Step 5 or they verify that the current solution is optimal. This observation forms a basis for the convergence of STDW, which can be established in the same manner as that of simplicial decomposition. (See, e.g., [15,26].)
3. Implementation
The STDW algorithm in Section 2 was implemented in GAMS, see [4]. In our implementation, the aggre-gate ow vectorPq is disaggregated into K vectors, one for each demandk(see, [19]), and DW-MP(; n) is replaced with the following.
DDW-MP(; n):
n= arg min
n X
q=1
K X
k=1
(3f(X)tpq(k))q(k)
s:t: n X
q=1
K X
k=1
q(k)Spq(k)6u;
n X
q=1
q(k) = 1; ∀k= 1; : : : ; K;
q¿0; ∀q= 1; : : : ; n:
Although not implemented here, Yr can also be disaggregated or represented as (yr(1); : : : ; yr(K)) in SD-MP(). Doing so, some components of the vec-torPKk=1Pr=1r(k)yr(k) may violate the side con-straints even though no component of Yr does. So, the side constraints must be added to the SD-MP() to ensure that they are not violated. This results in a larger and more complex master problem.
Also, the condition in Step 2 is replaced by the following:
3f(X)tZn63f(X)tX for some 0¡ ¡1:
Table 1
Information on ve nonlinear multicommodity network ow problems
Problem # Nodes # Arcs # OD pairs References
Nine-node 9 18 4 Hearn and Ribera [13]
Sioux falls 24 76 528 LeBlanc et al. [21] and Abdulaal and LeBlanc [1]
Hull 501 798 142 Florian et al. [6]
NDO22 14 22 23 Gon et al. [10]
NDO148 61 148 122 Gon et al. [10]
Table 2
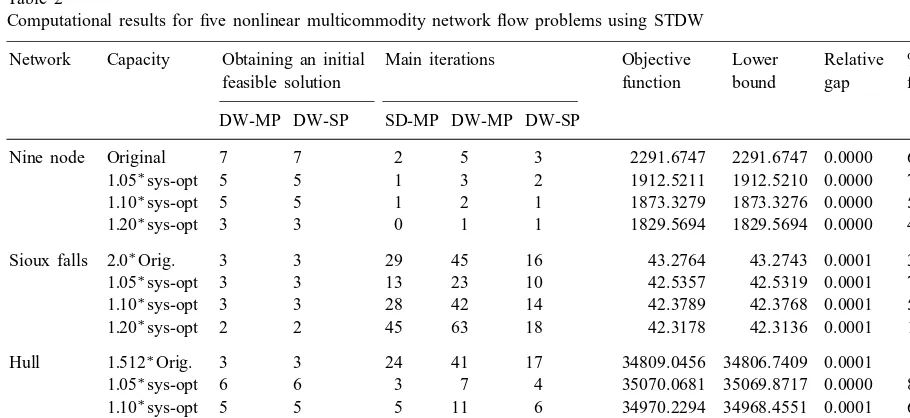
Computational results for ve nonlinear multicommodity network ow problems using STDW
Network Capacity Obtaining an initial Main iterations Objective Lower Relative % Arcs with
feasible solution function bound gap ow¿0:9∗cap
DW-MP DW-SP SD-MP DW-MP DW-SP
Nine node Original 7 7 2 5 3 2291.6747 2291.6747 0.0000 66.67
1:05∗sys-opt 5 5 1 3 2 1912.5211 1912.5210 0.0000 71.43 1:10∗sys-opt 5 5 1 2 1 1873.3279 1873.3276 0.0000 57.14 1:20∗sys-opt 3 3 0 1 1 1829.5694 1829.5694 0.0000 42.86 Sioux falls 2:0∗Orig. 3 3 29 45 16 43.2764 43.2743 0.0001 36.84 1:05∗sys-opt 3 3 13 23 10 42.5357 42.5319 0.0001 76.32 1:10∗sys-opt 3 3 28 42 14 42.3789 42.3768 0.0001 55.26 1:20∗sys-opt 2 2 45 63 18 42.3178 42.3136 0.0001 17.11 Hull 1:512∗Orig. 3 3 24 41 17 34809.0456 34806.7409 0.0001 1.80 1:05∗sys-opt 6 6 3 7 4 35070.0681 35069.8717 0.0000 81.52 1:10∗sys-opt 5 5 5 11 6 34970.2294 34968.4551 0.0001 63.24 1:20∗sys-opt 4 4 10 18 8 34930.6648 34927.2595 0.0001 18.48
NDO22a Original 2 2 7 14 7 103.4121 103.4120 0.0001 9.09
NDO148a Original 2 2 58 75 16 151.9368 151.9269 0.0001 0.00
aLower bounds for communication networks are from [10] and they are rounded to four digits.
Finally, our implementation of STDW begins by using DW decomposition to nd an initial feasi-ble solution and terminates when the relative gap, (f(X)− lower bound)=lower bound, is less than 0.0001. Whenever Step 3 is executed, the lower bound of the optimal objective function value can be obtained via the following result.
Theorem 3.1. Let X∗
denote an optimal solution to NMNFP-SC. Then;
f(X∗
)¿f(X) +3f(X)t(Pn+1−X)
+ (u−SPn+1)tn:
Proof. The result follows from the inequalities below.
f(X∗
)¿f(X) + min y
(
3f(X)t
×
K X
k=1
y(k)−X !
: K X
k=1
Sy(k)6u;
By(k) =b(k); y(k)¿0; ∀k )
¿f(X) +L(∗
)
¿f(X) +L(n)
=f(X) +3f(X)t(Pn+1−X)
S.
Lawphongpanich
/Operations
Research
Letters
26
(2000)
33–41
39
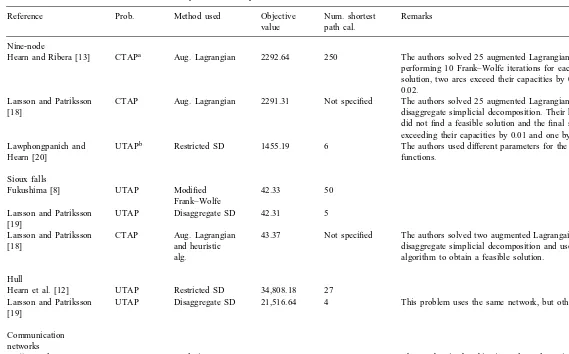
Previous results for ve nonlinear multicommodity network ow problems
Reference Prob. Method used Objective Num. shortest Remarks value path cal.
Nine-node
Hearn and Ribera [13] CTAPa Aug. Lagrangian 2292.64 250 The authors solved 25 augmented Lagrangian problems by
performing 10 Frank–Wolfe iterations for each one. In the nal solution, two arcs exceed their capacities by 0:01 and one by 0:02.
Larsson and Patriksson CTAP Aug. Lagrangian 2291.31 Not specied The authors solved 25 augmented Lagrangian problems via [18] disaggregate simplicial decomposition. Their heuristic algorithm
did not nd a feasible solution and the nal solution has two arcs exceeding their capacities by 0:01 and one by 0:02.
Lawphongpanich and UTAPb Restricted SD 1455.19 6 The authors used dierent parameters for the travel cost
Hearn [20] functions.
Sioux falls
Fukushima [8] UTAP Modied 42.33 50 Frank–Wolfe
Larsson and Patriksson UTAP Disaggregate SD 42.31 5 [19]
Larsson and Patriksson CTAP Aug. Lagrangian 43.37 Not specied The authors solved two augmented Lagrangain problems via [18] and heuristic disaggregate simplicial decomposition and used a heuristic
alg. algorithm to obtain a feasible solution.
Hull
Hearn et al. [12] UTAP Restricted SD 34,808.18 27
Larsson and Patriksson UTAP Disaggregate SD 21,516.64 4 This problem uses the same network, but other data are dierent. [19]
Communication networks
Gon et al. [10] NDO22 Analytic center 103.41202 14 The number in the objective value column is the best known cutting plane Lagrangain dual value, i.e., lower bound.
Gon et al. [10] NDO148 Analytic center 151.92687 16 The number in the objective value column is the best known cutting plane Lagrangain dual value, i.e., lower bound.
whereL() is the following Lagrangian dual function:
The rst three inequalities above hold, respectively, because f(X) is pseudo-convex, the Weak Duality Theorem applies, andndoes not solve the dual prob-lem. The last equality follows from the fact thatPn+1=
PK
k=1 pn+1(k) solves the DW-SP(n).
Five problems from the literature were selected for testing. Three are trac assignment problems and the remaining two are problems in network communica-tion. Their statistics are given in Table 1.
For all problems, the travel cost function is separa-ble, i.e.,f(x) =P
(i; j)∈fij(xij), where is the set of arcs in the network, and each arc cost,fij(xij), is generally a convex function of its capacity. For Sioux Falls and Hull, these capacities are too small, for they make the resulting capacitated trac assignment prob-lem (CTAP) infeasible. To construct feasible CTAP, the original capacities are multiplied by a factor ¿1, when necessary. Alternately, the system optimal so-lution (see [7]) can serve as arc capacities. However, using system optimal ows as arc capacities tends to reduce the feasible region of CTAP to a single point and STDW would terminate as soon as it nds an ini-tial feasible solution. To generate more meaningful problems, the capacities are set to×(system optimal solution) where ¿1.
Table 2 summarizes the results for the ve test problems using STDW. The table primarily lists the number of times each problem (SD-MP, DW-MP, and DW-SP) must be solved to achieve 0.0001 relative gap or better. For large networks, a good indicator of an algorithm’s eciency is the number of shortest path calculations or the num-ber of DW-SPs solved. (See, e.g., [12].)
Com-paring these numbers in Table 2 (particularly those in the main iterations, i.e., the iterations af-ter an initial feasible solution has been obtained) with those reported in the literature (see Table 3) demonstrates that STDW is competitive with the existing algorithms solving the same or sim-ilar problems. When compared with penalty or dual-based algorithms, STDW oers an added ad-vantage, in that it always produces a feasible solu-tion when terminated prior to reaching an optimal solution.
Acknowledgements
This research was completed while the author was spending his sabbatical leave at the Center for Ap-plied Optimization and Department of Industrial and Systems Engineering at the University of Florida. He is grateful for the support provided by these two orga-nizations. He would like to also thank Prof. Hearn for providing the data for this research, Prof. Ramana for suggesting the use of system optimal solutions, and Prof. Morton for Ref. [27].
References
[1] M. Abdulaal, L.J. LeBlanc, Methods for combining modal split and equilibrium assignment models, Transportation Sci. 13 (1979) 292–314.
[2] R.K. Ahuja, T.L. Magnanti, J.B. Orlin, Network Flows: Theory, Algorithms, and Applications, Prentice-Hall, Englewood Clis, NJ, 1993.
[3] M.S. Bazaraa, H.D. Sherali, C.M. Shetty, Nonlinear Pro-gramming: Theory and Algorithms, Wiley, New York, 1993. [4] A. Brooke, D. Kendrick, A. Meeraus, GAMS: A User’s
Guide, Release 2.25, The Scientic Press, 1992.
[5] G.B. Dantzig, P. Wolfe, Decomposition principle for linear programs, Oper. Res. 8 (1960) 101–111.
[6] M. Florian, J. Guelat, H. Spiess, An ecient implementation of the PARTAN variant of the linear approximation method for the network equilibrium problem, Networks 17 (1987) 319–339.
[7] M. Florian, D.W. Hearn, Network equilibrium models and algorithms, in: M.O. Ball et al. (Eds.), Network Routing, Handbooks in OR and MS, Vol. 8, Elsevier Science, 1995, pp. 485 –550 (Chapter 6).
[8] M. Fukushima, A modied Frank–Wolfe algorithm for solving the trac assignment problem, Transportation Res. B 18B (1984) 169–177.
[10] J.L. Gon, J. Gondzio, R. Sarkissian, J.-P. Vial, Solving nonlinear multicommodity ow problem by the analytic center cutting plane method, Math. Programming 76 (1996) 131– 154.
[11] D.W. Hearn, S. Lawphongpanich, A dual ascent algorithm for trac assignment problems, Transportation Res. B 24B (1990) 423–430.
[12] D.W. Hearn, S. Lawphongpanich, J.A. Ventura, Restricted simplicial decomposition: computation and extensions, Math. Programming Study 31 (1987) 99–118.
[13] D.W. Hearn, J. Ribera, Bounded ow equilibrium problems by penalty methods, Proceedings of the IEEE International Conference on Circuits and Computers, 1980, pp. 162–166. [14] J.K. Ho, J.S. Mann, Nested decomposition for dynamic
models, Math. Programming 6 (1974) 121–140.
[15] C. Holloway, An extension of the Frank–Wolfe method of feasible directions, Math. Programming 6 (1974) 14–27. [16] W.S. Hsia, On Rutenberg’s decomposition method,
Management Sci. 21 (1974) 10–12.
[17] J.L. Kennington, R.V. Helgason, Algorithms for Network Programming, Wiley, New York, 1980.
[18] T. Larsson, M. Patriksson, An augmented Lagrangian dual algorithm for link capacity side constrained trac assignment problems, Transportation Res. B 29 (1995) 433–455. [19] T. Larsson, M. Patriksson, Simplicial decomposition with
disaggregated representation for the trac assignment problem, Transportation Sci. 26 (1992) 4–17.
[20] S. Lawphongpanich, D.W. Hearn, Restricted simplicial decomposition with application to the trac assignment problem, Ricerca Operativa 38 (1986) 97–120.
[21] L.J. LeBlanc, E.K. Morlok, W.P. Pierskalla, An ecient approach to solving the road network equilibrium trac assignment problem, Transportation Res. 9 (1975) 309–318. [22] A. Marin, Restricted simplicial decomposition with side
constraints, Networks 26 (1995) 199–215.
[23] M.C. Pinar, S.A. Zenios, Solving nonlinear programs with embedded network structures, in: D.-Z. Du, P.M. Pardalos (Eds.), Network Optimization Problems, World Scientic Publishing, Co., Singapore, 1993, pp. 177–202.
[24] D.P. Rutenberg, Generalized networks, generalized upper bounding and decomposition of the convex simplex method, Management Sci. 16 (1970) 388–401.
[25] D. Stefek, Extensions of simplicial decomposition for solving the multicommodity ow problem with bounded arc ows and convex costs, Ph.D. Dissertation, Decision Sciences Department, University of Pennsylvania, 1988.
[26] B. Von Hohenbalken, Simplicial decomposition in nonlinear programming algorithms, Math. Programming 13 (1977) 49– 68.
[27] R.J. Wittrock, Advances in a nested decomposition algorithm for solving staircase linear programs, Technical Report SOL 83-2, Department of Operations Research, Stanford University, 1983.