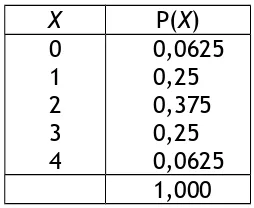
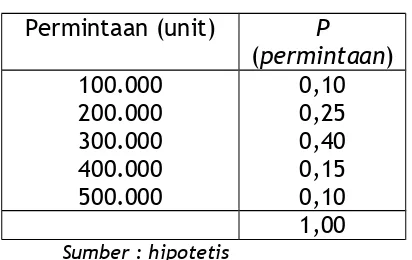
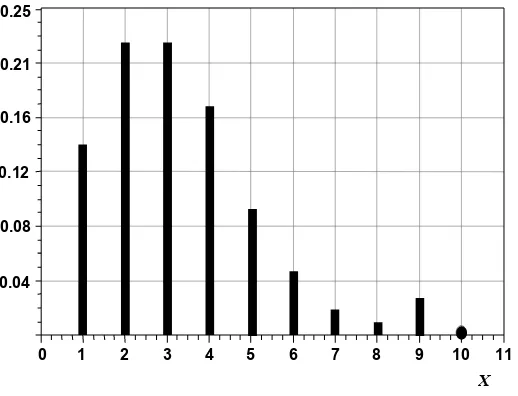
Modul 8 Dist Peluang Diskrit
Teks penuh
Gambar

Garis besar
Dokumen terkait
Adapun bentuk terapi Ruqyah pada gangguan kejiwaan yang disebabkan karena gangguan jin ditetapkan pada orang yang di Ruqyah di Pondok Ruqyah Center Kalinyamat
Ketiga pesan Paulus bagi jemaat Efesus dapat kita jadikan senjata untuk memelihara kebersamaan dalam komunitas/kelompok kita : keluarga, pekerjaan, gereja,
Penelitian ini memiliki dua tujuan, (1) mengidentifikasi bentuk-bentuk pemakaian interferensi dalam bahasa Indonesia, dan (2) mendeskripsikan faktor-faktor yang
Sebagaimana telah dirumuskan sebelumnya bahwa dalam penelitian ini sesuai dengan hipotesis : terdapat hubungan yang nyata jaringan komunikasi (tingkat keterkaitan,
Penerapan media audio visual mempunyai peran yang sangat penting yaitu dapat memberikan banyak manfaat asalkan guru berperan aktif dalam proses pembelajaran,
Tanah vertisol dan mineral zeolit yang memiliki kelengasan sesuai dengan ekologi nematoda entomopatogen Steinernema carpocapsae sehingga dapat hidup pada jangka
Uji ini dimaksudkan untuk mengetahui apakah variabel independen yang ada secara bersama-sama mempengaruhi variabel dependennya. Pada penelitian ini digunakan untuk menguji
Perusahaan yang melaksanakan program keselamatan dan kesehatan kerja secara serius, akan dapat menekan angka resiko kecelakaan dan penyakit kerja dalam tempat kerja, sehingga