PEMILIHAN BANDWIDTH PADA ESTIMATOR NADARAYA-WATSON DENGAN TIPE KERNEL GAUSSIAN PADA DATA TIME SERIES (Studi Kasus: Penutupan Indeks Harga Saham Harian Jakarta Islamic Index (JII)
Periode 1 Januari 2016 −30April 2016) SKRIPSI
Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta
untuk Memenuhi Sebagian Persyaratan guna Memperoleh Gelar Sarjana Sains HALAMAN JUDU L
Oleh : Joko Andy Saputra NIM : 12305141003
PROGRAM STUDI MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA
ii HALAMAN P ERSETUJUAN
iii HALAMAN P ENG ESA HAN
iv
HALAMAN PERNYATAAN
Yang bertanda tangan dibawah ini, saya: Nama : Joko Andy Saputra NIM : 12305141003 Program Studi : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam
Judul Skripsi :PEMILIHAN BANDWIDTH PADA ESTIMATOR NADARAYA-WATSON DENGAN TIPE KERNEL GAUSSIAN PADA DATA TIME SERIES
Menyatakan bahwa skripsi ini benar-benar karya saya sendiri dan sepanjang pengetahuan saya, tidak terdapat karya atau pendapat yang ditulis atau diterbitkan orang lain, kecuali pada bagian-bagian tertentu yang diambil sebagai acuan atau kutipan dengan mengikuti tata penulisan karya ilmiah yang telah lazim.
Apabila terbukti pernyataan saya ini tidak benar maka sepenuhnya menjadi tanggung jawab saya dan saya bersedia menerima sanksi sesuai ketentuan yang berlaku.
Yogyakarta, ... agustus 2016 Yang menyatakan,
Joko Andy Saputra NIM 12305141003
v
MOTTO
Boleh jadi kamu membenci sesuatu, padahal ia amat baik bagimu, dan boleh jadi (pula) kamu menyukai sesuatu, padahal ia amat buruk bagimu, Allah mengetahui, sedang kamu tidak mengetahui.
(Q.S Al-Baqarah 216)
Sesungguhnya sesudah kesulitan itu ada kemudahan. Maka apabila kamu telah selesai (dari suatu urusan), kerjakanlah dengan
sungguh-sungguh (urusan) yang lain. (Q.S Al-Insyirah 6-7)
Berusahalah jangan sampai terlengah walau sedetik saja, karena atas kelengahan kita tak akan bisa dikembalikan seperti semula
vi
HALAMAN PERSEMBAHAN
Alhamdulillahirabbil’alamin, dengan mengucap rasa syukur kepada Allah SWT skripsi ini telah selesai disusun . Skripsi ini
dipersembahkan untuk:
Ibu dan Ayah, orangtua yang telah memberikan kasih sayang, nasihat, teguran, motivasi, doa yang tiada hentinya, dan selalu
memberikan kekuatan untuk mencapai kesuksesanku
Lala , siti, Fatma, nuri, tyas, humam, muhsin, yoga, dan fajar sahabat yang terus memberikan candaan, hiburan, semangat dan
sudah menjadi saudaraku sendiri
Bu Endang, dosen pembimbing yang telah membimbingku selama ini dengan kesabaran dan dukungan beliau lah yang telah
memberikan manfaat besar bagiku
Teman-Teman Matsub 2012, yang telah memberikanku kesadaran betapa pentingnya kerjasama itu
vii
PEMILIHAN BANDWIDTH PADA ESTIMATOR
NADARAYA-WATSON DENGAN TIPE KERNEL GAUSSIAN PADA DATA
TIME SERIES
(Studi Kasus: Penutupan Indeks Harga Saham Harian Jakarta Islamic Index (JII) Periode 1 Januari 2016 −30April 2016)
Oleh:
JOKO ANDY SAPUTRA 12305141003
ABSTRAK
Regresi nonparametrik merupakan analisis regresi dengan pendugaan model dilakukan berdasarkan pendekatan yang tidak terikat asumsi bentuk kurva regresi tertentu, namun dibentuk sesuai dengan informasi yang ada dalam data. Salah satu jenis fungsi yang dapat digunakan untuk menduga bentuk regresi nonparametrik adalah fungsi kernel Gaussian.
Pada regresi kernel, terdapat beberapa estimator yang dapat digunakan untuk memodelkan harga saham Jakarta Islamic Index (JII) dalam rentang waktu 1 januari 2016 sampai dengan 30 april 2016, salah satunya adalah estimator Nadaraya-Watson. Dalam melakukan analisis regresi kernel, diperlukan suatu konstanta penghalus yang disebut dengan bandwidth. Beberapa metode yang dapat digunakan untuk mendapatkan nilai bandwidth yang sesuai dengan data adalah metode bandwidth “Rule of Thumb”, metode Unbiased Cross Validation (UCV), metode Biased Cross Validation (BCV), dan metode Complete Cross Validation (CCV).
Perhitungannya menggunakan bantuan software R 3.2.3 dan SPSS versi 20. Untuk mengetahui metode yang lebih baik dalam mengestimasi kasus harga saham Jakarta Islamic Index (JII) tersebut digunakan perbandingan nilai Mean Square Error (MSE). Nilai MSE yang paling kecil diperoleh menggunakan metode bandwidth “Complete Cross Validation”. Hasil estimasi menunjukkan bahwa pada nilai parameter bandwidth “Complete Cross Validation” menghasilkan kurva yang tidak cukup mulus tetapi nilai hasil estimasinya dekat dengan titik data aktual. Kata kunci: Regresi Nonparametrik, Regresi Kernel, Fungsi Gaussian, Estimator Nadaraya-Watson, Cross Validation, Bandwidth.
viii
KATA PENGANTAR
Puji syukur kehadirat Allah SWT sehingga penulis dapat menyelesaikan skripsi berjudul “PEMILIHAN BANDWIDTH PADA ESTIMATOR NADARAYA-WATSON DENGAN TIPE KERNEL GAUSSIAN PADA DATA TIME SERIES”. Penulisan skripsi ini dibuat untuk memenuhi sebagian persyaratan guna memperoleh gelar Sarjana Sains Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta.
Skripsi ini tidak dapat diselesaikan tanpa bantuan, dukungan serta bimbingan beberapa pihak. Penulis mengucapkan terimakasih kepada:
1. Bapak Dr. Hartono selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta yang telah memberikan kelancaran pelayanan dalam urusan akademik.
2. Bapak Dr. Ali Mahmudi selaku Ketua Jurusan Pendidikan Matematika Universitas Negeri Yogyakarta yang telah memberikan kelancaran pelayanan dalam urusan akademik.
3. Bapak Dr. Agus Maman Abadi, M.Si selaku Ketua Program Studi Matematika Universitas Negeri Yogyakarta serta Penasehat Akademik yang telah memberikan serta motivasi selama studi.
4. Ibu Endang Listyani, M.S dosen pembimbing yang telah berkenan memberikan waktu luang, arahan, bimbingan serta dengan penuh kesabaran meneliti setiap kata demi kata dalam skripsi ini.
5. Seluruh dosen Jurusan Pendidikan Matematika Universitas Negeri Yogyakarta yang telah memberikan ilmu kepada penulis.
ix
6. Orangtua dan keluarga yang telah memberikan doa, dukungan, serta semangat kepada penulis.
7. Seluruh teman-teman matematika angkatan 2012 yang telah menghibur serta menyemangati penulis.
8. Semua pihak yang telah membantu penulisan skripsi ini hingga selesai. Penulis menyadari adanya ketidaktelitian, kekurangan dan kesalahan dalam penulisan tugas akhir skripsi ini. Oleh karena itu, penulis menerima kritik dan saran yang bersifat membangun. Semoga penulisan tugas akhir ini dapat bermanfaat bagi pembaca dan pihak yang terkait.
Yogyakarta, ... Agustus 2016 Penulis
x
DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN ... ii
HALAMAN PENGESAHAN ... iii
HALAMAN PERNYATAAN ... iv
MOTTO ... v
HALAMAN PERSEMBAHAN ... vi
ABSTRAK ... vii
KATA PENGANTAR ... viii
DAFTAR ISI ... x
DAFTAR GAMBAR ... xii
DAFTAR TABEL ... xiii
BAB I PENDAHULUAN ... 1
A. Latar Belakang Masalah ... 1
B. Rumusan Masalah ... 6
C. Tujuan Penelitian ... 6
D. Manfaat penelitian ... 6
BAB II LANDASAN TEORI ... 7
A. Integral Tak Tentu... 7
B. Variabel Random ... 9
C. Ekspektasi dan Variansi Variabel Random ... 12
D. Distribusi Peluang Bersama ... 14
E. Distribusi Bersyarat ... 15
F. Mean Square Error (MSE) ... 16
G. Uji Normalitas ... 18
H. Uji Kolmogorov Smirnov ... 19
I. P-value ... 20
J. Analisis Regresi Linear Sederhana ... 21
K. Metode Kuadrat Terkecil ... 21
L. Saham ... 24
M. Indeks Harga Saham ... 25
BAB III PEMBAHASAN ... 28
A. Estimasi Nonparametrik... 28
xi
C. Estimasi Bias ... 33
D. Mean Square Error dan Mean Integrated Square Error ... 36
E. Regresi Kernel ... 39
F. Estimator Nadaraya-Watson ... 39
G. Estimator Nadaraya-Watson dengan Tipe Kernel Gaussian ... 43
H. Pemilihan Bandwidth ... 43
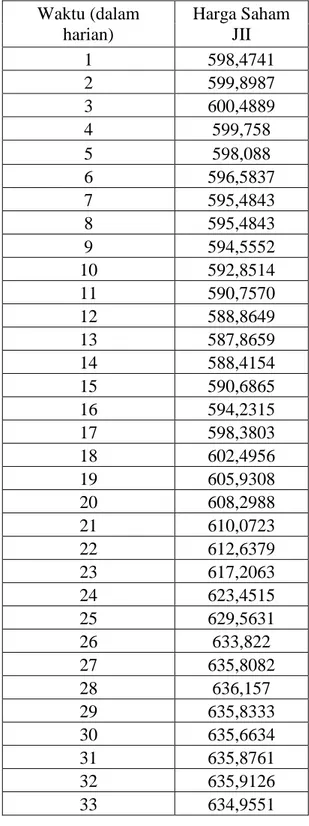
I. Deskripsi Data ... 48
J. Uji Linearitas dan Uji Normalitas ... 49
K. Deskripsi Regresi Kernel ... 51
L. Pemilihan Bandwidth Pada Data Harga Saham Jakarta Islamic Indeks. 51 M. Estimator Nadaraya-Watson ... 52
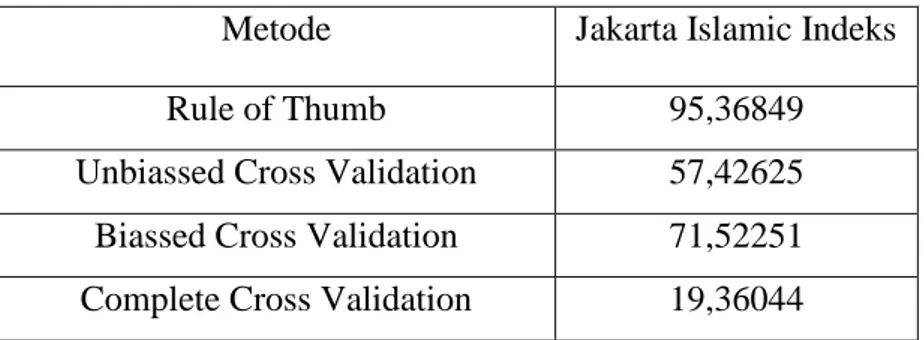
N. Perbandingan MSE ... 53
O. Hasil Estimasi Harga Saham Jakarta Islamic Indeks ... 55
BAB IV PENUTUP ... 58
A. Kesimpulan ... 58
B. Saran ... 59
DAFTAR PUSTAKA ... 61
xii
DAFTAR GAMBAR
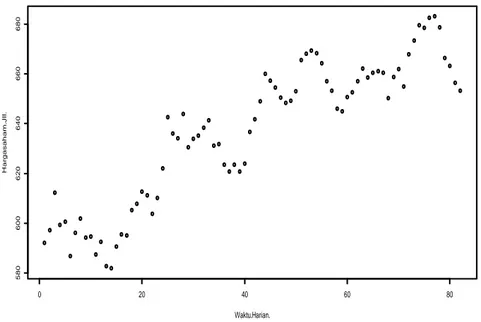
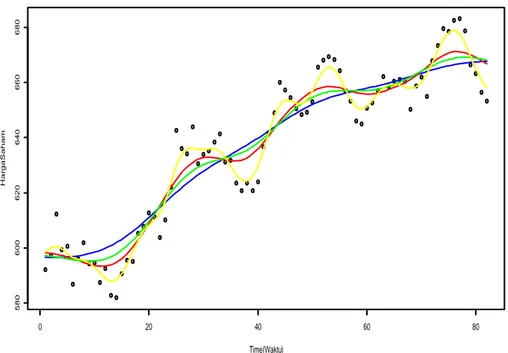
Gambar 2.1 Grafik Residual ... 18 Gambar 3.1 Plot Harga Saham Jakarta Islamic Index ... 50 Gambar 3.2 Kurva Hasil Estimasi Harga Saham Jakarta Islamic Index ... 53
xiii
DAFTAR TABEL
Tabel 3.1 Macam-macam Fungsi Kernel ... 33
Tabel 3.2 Nilai ∫(𝐾(𝑢))2𝑑𝑢 dan ∫ 𝑢2𝐾(𝑢)𝑑𝑢 fungsi kernel ... 46
Tabel 3.3 Nilai Parameter Bandwidth untuk data Jakarta Islamic Index ... 52
Tabel 3.4 Nilai MSE ... 54
1
BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Analisis regresi merupakan metode analisis data yang menggambarkan hubungan antara variabel respon dengan satu atau beberapa variabel prediktor. Misalkan X adalah variabel prediktor dan Y adalah variabel respon untuk n pengamatan berpasangan {𝑥, 𝑦}, maka hubungan linear antara variabel prediktor dan variabel respon tersebut dapat dinyatakan sebagai berikut:
𝑌𝑖= 𝑚(𝑋𝑖)+ 𝜀𝑖 , i=1, 2, 3 ,…,n ,
dengan 𝜀𝑖 adalah sisaan yang diasumsikan independen dengan mean nol dan variansi 𝜎𝑖, serta m(𝑋𝑖) adalah fungsi regresi atau kurva regresi. Menurut Hardle (1990:4) mengungkapkan bahwa untuk mengestimasi m(𝑋𝑖) ada dua pendekatan yang dapat digunakan dalam menentukan kurva regresi yaitu pendekatan regresi parametrik dan pendekatan regresi nonparametrik.
Pendekatan regresi parametrik mengasumsikan bentuk hubungan antara variabel respon dan variabel prediktor diketahui atau diperkirakan dari kurva regresi. Menurut Hardle (1990:6) mengungkapkan bahwa pendekatan regresi nonparametrik digunakan untuk mengestimasi kurva regresi memiliki beberapa tujuan utama, yaitu memberikan metode untuk menghubungan antara dua variabel secara umum, menghasilkan prediksi dari observasi walaupun dibuat tanpa referensi, serta merupakan metode yang fleksibel untuk mensubstitusi nilai-nilai yang hilang antara variabel prediktor yang berdekatan. Pendekatan regresi
2
nonparametrik merupakan pendekatan regresi yang sesuai untuk pola data yang tidak diketahui bentuknya, atau tidak terdapat informasi masa lalu tentang pola data, I Nyoman Budiantara (2010:1).
Dalam jurnal Siana Halim dan Indriati Bisono (2006:74) yang berjudul Fungsi-Fungsi Kernel pada Metode Regresi Nonparametrik dan Aplikasinya pada Priest River Experimental Forest’s Data memberikan kesimpulan jika asumsi terhadap sebuah model parametrik dibenarkan, maka fungsi regresi dapat diestimasi dengan cara yang lebih efisien jika dibandingkan dengan menggunakan sebuah metode nonparametrik. Tetapi jika asumsi terhadap model parametrik salah, maka hasilnya akan memberikan kesimpulan yang salah terhadap fungsi regresi. Menurut I Komang Gede Sukarsa (2012:21) dalam jurnalnya yang berjudul regresi kernel dalam model regresi nonparametrik mengungkapkan bahwa regresi kernel adalah teknik statistik nonparametrik untuk mengestimasi nilai 𝐸(𝑌|𝑋) = 𝑚(𝑋) atau 𝑦 = 𝑚(𝑋) dalam suatu variabel. Tujuan regresi kernel yaitu untuk memperoleh hubungan nonlinear antara X dengan Y.
Pada regresi nonparametrik data akan mencari bentuk estimasinya sendiri tanpa di pengaruhi oleh subjektifitas dari peneliti, sehingga pendekatan regresi nonparametrik memiliki fleksibilitas yang tinggi, Eubank (1988:3). I Nyoman Budiantara (2010:1) mengungkapkan bahwa terdapat beberapa teknik untuk mengestimasi kurva regresi dalam regresi nonparametrik, yaitu kernel, histogram, spline, Deret Fourier, Wavelets, orthogonal. Salah satu pendekatan regresi nonparametrik yang digunakan dalam penelitian ini adalah regresi kernel.
Regresi kernel merupakan salah satu analisis nonparametrik dengan metode smoothing. Smoothing telah menjadi sinonim dengan metode–metode
3
nonparametrik yang digunakan untuk mengestimasi fungsi-fungsi. Tujuan dari smoothing adalah untuk membuang variabilitas dari data yang tidak memiliki efek sehingga ciri-ciri dari data akan tampak jelas. Regresi kernel memiliki bentuk yang fleksibel dan perhitungan matematisnya mudah disesuaikan. Pada regresi kernel dikenal suatu estimator yang biasanya digunakan untuk mengestimasi fungsi regresi yaitu estimator Nadaraya-Watson.
Estimasi dengan pendekatan kernel tergantung pada dua parameter yaitu bandwidth dan fungsi kernel. Ada tujuh fungsi kernel antara lain Uniform, Triangle, Epanechnicov, Quartic, Triweight, Gaussian, dan Cosinics. Diantara ke-tujuh fungsi kernel tersebut pada penelitian ini dipilih fungsi kernel Gaussian. Sedangkan bandwidth adalah parameter pemulus (smoothing) yang berfungsi untuk mengontrol kemulusan kurva yang diestimasi. Bandwidth yang terlalu kecil akan menyebabkan fungsi yang diestimasi tersebut menjadi sangat kasar sehingga hubungan variansinya tinggi dan memiliki potensi bias yang rendah. Sebaliknya jika bandwidth yang terlalu besar menyebabkan fungsi yang diestimasi tersebut menjadi sangat mulus sehingga hubungan variansinya rendah dan memiliki potensi bias yang besar. Oleh karena itu, diperlukan pemilihan bandwidth optimal.
Pemilihan bandwidth yang optimal dilakukan dengan cara memperkecil tingkat kesalahan. Semakin kecil tingkat kesalahan semakin baik estimasinya. Untuk mengetahui ukuran tingkat kesalahan suatu estimator dapat dilihat dari Mean Squared Error (MSE). Bandwidth yang digunakan pada jurnal Guidom (2015: 1-22) yaitu Bandwidth Rule of Thumb, Unbiased Cross Validation, Biased Cross Validation, Complete Cross Validation. Dari ke-empat bandwidth tersebut akan dipilih bandwidth yang memiliki nilai MSE yang paling kecil.
4
Pada regresi nonparametrik kernel Gaussian dengan estimator Nadaraya-Watson dalam data time series dapat mengggunakan data harga saham Jakarta Islamic Index (JII). Saham adalah tanda bukti penyertaan atau kepemilikan seseorang atau sesuatu institusi dalam suatu badan usaha atau perusahaan dengan menerbitkan saham, memungkinkan perusahaan-perusahaan yang membutuhkan pendanaan jangka panjang untuk menjual kepentingan dalam bisnis saham dengan imbalan uang tunai. Indikator atau cerminan harga saham disebut indeks harga saham.
Indeks harga saham merupakan salah satu pedoman bagi investor untuk melakukan investasi di pasar modal, khususnya saham. Saham merupakan salah satu komoditas yang diperdagangkan dipasar modal yang paling popular. Investasi saham oleh investor diharapkan memberikan keuntungan yang sudah barang pasti dalam saham juga mengandung risiko. Pengertian saham adalah surat berharga yang dapat dibeli atau dijual oleh perorangan atau lembaga di pasar tempat surat tersebut diperjual-belikan. Saham merupakan instrumen ekuitas, yaitu tanda penyertaan atau kepemilikan seseorang atau badan usaha dalam suatu perusahaan atau perseroan terbatas. Jadi, saham merupakan surat berharga sebagai bukti penyertaan atau kepemilikan individu maupun institusi dalam suatu perusahaan.
Dengan menyertakan modal tersebut, maka pihak tersebut memiliki klaim atas pendapatan perusahaan, klaim atas asset perusahaan dan berhak hadir dalam Rapat Umum Pemegang Saham (RUPS). Berkembangnya pasar modal yang telah mengembangkan pengertian mengenai pasar modal berbasis syariah. Pasar modal syari’ah merupakan pasar modal berbasis syariah. Pasar modal syari’ah merupakan pasar modal yang menerapkan prinsip-prinsip syari’ah dalam transaksi ekonomi.
5
Pasar modal syari’ah menggunakan prinsip, prosedur, asumsi dan aplikasi bersumber dari epistemologi islam. Di dunia interasional indeks saham syari’ah telah berkembang di Negara bagian Timur Tengah maupun Barat. Seiring dengan perkembangan ekonomi Islam secara global, indeks syariah merupakan alternatif investasi yang aman khususnya bagi kaum muslim yang ingin berinvestasi secara syari’ah. Indonesia yang sebagian besar penduduknya muslim, memunculkan instrumen pasar modal yang menggunakan prinsip syari’ah, salah satunya dengan adanya Jakarta Isamic Index (JII) yang dikhususkan untuk perusahaan-perusahaan dengan prinsip syari’ah.
Salah satu indeks saham yang menunjukkan pergerakan harga saham yaitu Jakarta Islamic Index (JII). Jakarta Islamic Index (JII) merupakan suatu rangkaian informasi historis mengenai pergerakan harga saham JII yang mencerminkan suatu nilai yang berfungsi sebagai pengukur kinerja suatu saham. Saham JII sebagai acuan investasi yang berbasis syari’ah guna melihat pergerakan harga saham syari’ah, sehingga untuk mengetahui kemungkinan kenaikan atau penurunan harga saham diperlukan suatu metode analisis.
Dengan melihat kondisi-kondisi di atas, maka penulis akan membahas cara mengestimasi harga saham Jakarta Islamic Indeks menggunakan regresi nonparametrik kernel Gaussian dengan estimator Nadaraya-Watson serta metode pemilihan bandwidth adalah bandwidth “Rule of Thumb”, Unbiased Cross Validation, Biased Cross Validation dan Complete Cross Validation.
6 B. Rumusan Masalah
Berdasarkan latar belakang di atas, maka dapat dirumuskan masalah sebagai berikut:
1. Bagaimana analisis estimator Nadaraya-Watson dengan tipe kernel Gaussian? 2. Bagaimana pemilihan bandwidth pada Rule of Thumb, Unbiased Cross
Validation, Biased Cross Validation dan Complete Cross Validation? 3. Bagaimana hasil estimasi setelah dilakukan pemilihan bandwidth? C. Tujuan Penelitian
Sesuai dengan rumusan masalah, maka tujuan penulisan skripsi ini adalah:
1. Menjelaskan analisis estimator Nadaraya-Watsom dengan tipe kernel Gaussian 2. Menjelaskan pemilihan bandwidth pada Rule of Thumb, Unbiased Cross
Validation, Biased Cross Validation dan Complete Cross Validation 3. Menentukan hasil estimasi setelah dilakukan pemilihan bandwidth. D. Manfaat penelitian
Penulisan skripsi ini diharapkan dapat memberikan manfaat diantaranya:
1. Bagi mahasiswa dapat memberikan gambaran dan ilmu tentang penggunaan Estimator Nadaraya-Watson dengan tipe kernel Gaussian.
2. Bagi perpustakaan Jurusan Pendidikan Matematika UNY, dapat dijadikan sebagai referensi maupun menambah wawasan.
7
BAB II
LANDASAN TEORI
A. Integral Tak TentuDefinisi 2.1 Integral Tak Wajar Tipe 1 (Purcell dan Varberg, 2010: 37) Jika 𝑓 kontinu pada selang [−∞, ∞], dan hanya jika lim
𝑥→𝑐|𝑓(𝑥)| = ∞, maka
∫−∞∞ 𝑓(𝑥) 𝑑𝑥 dapat dikatakan konvergen dan bernilai
∫−∞∞ 𝑓(𝑥) 𝑑𝑥 = ∫−∞0 𝑓(𝑥) 𝑑𝑥+ ∫ 𝑓(𝑥) 𝑑𝑥0∞ ∫ 𝑓(𝑥) 𝑑𝑥 = lim 𝑐→−∞∫ 𝑓(𝑥) 𝑑𝑥 0 −𝑐 + lim𝑐→+∞∫ 𝑓(𝑥) 𝑑𝑥 𝑐 0 ∞ −∞ (2.1) Contoh 2.1
Tentukan apakah integral berikut konvergen atau divergen,jika konvergen tetntukan nilainya ∫−∞∞ 𝑥𝑒−𝑥2𝑑𝑥 ! Penyelesaian : ∫ 𝑥𝑒−𝑥2𝑑𝑥 =1 2∫ 𝑒 −𝑥2(−2𝑥 𝑑𝑥) −1 𝑎 −1 𝑎 ∫ 𝑥𝑒−𝑥2𝑑𝑥 = [−1 2𝑒 −𝑥2 ] 𝑎 1 −1 𝑎 ∫ 𝑥𝑒−𝑥2𝑑𝑥 = −1 2𝑒 −1+1 2𝑒 −𝑎2 −1 𝑎 maka, ∫ 𝑥𝑒−𝑥2𝑑𝑥 = lim 𝑎→−∞− 1 2𝑒 −1+1 2𝑒 −𝑎2 = 1 2𝑒 −1 𝑎
Dapat disimpulkan bahwa integral konvergen dan bernilai −1 2𝑒⁄ .
Definisi 2.2 Integral Tak Wajar Tipe 2 (Purcell dan Varberg, 2010: 47)
Jika 𝑓 kontinu pada selang [𝑎, 𝑏], kecuali di suatu bilangan 𝑐 dengan 𝑎 < 𝑐 < 𝑏, dan hanya jika lim
8 ∫ 𝑓(𝑥) 𝑑𝑥 = ∫ 𝑓(𝑥) 𝑑𝑥𝑎𝑏 𝑎𝑐 + ∫ 𝑓(𝑥) 𝑑𝑥𝑐𝑏 ∫ 𝑓(𝑥) 𝑑𝑥 = lim 𝑢→𝑐−∫ 𝑓(𝑥) 𝑑𝑥 𝑢 𝑎 + lim𝑢→𝑐+∫ 𝑓(𝑥) 𝑑𝑥 𝑏 𝑢 𝑏 𝑎 (2.2)
asalkan kedua integral di ruas kanan konvergen. Jika tidak demikian, maka dapat dikatakan ∫ 𝑓(𝑥) 𝑑𝑥𝑎𝑏 divergen.
Contoh 2.2
Tentukan apakah integral berikut konvergen atau divergen, jika konvergen tentukan nilainya ! ∫ 𝑥𝑒−𝑥2 𝑑𝑥 ∞ −∞ Penyelesaian : ∫ 𝑥𝑒−𝑥2 𝑑𝑥 ∞ −∞ = ∫ 𝑥𝑒−𝑥2 𝑑𝑥 + ∫ 𝑥𝑒−𝑥2 𝑑𝑥 ∞ 0 0 −∞ ∫ 𝑥𝑒−𝑥2 𝑑𝑥 ∞ −∞ = lim 𝑥→∞ ∫ 𝑥𝑒 −𝑥2 𝑑𝑥 0 −∞ + lim 𝑥→∞∫ 𝑥𝑒 −𝑥2 𝑑𝑥 ∞ 0 ∫ 𝑥𝑒−𝑥2 𝑑𝑥 ∞ −∞ = lim 𝑥→∞− 1 2 𝑒 −𝑥2] 𝑡 0 + lim 𝑥→∞− 1 2 𝑒 −𝑥2] 0 𝑡 ∫ 𝑥𝑒−𝑥2 𝑑𝑥 ∞ −∞ = lim 𝑥→∞(− 1 2+ 1 2 𝑒 −𝑡2 ) + lim 𝑥→∞(− 1 2 𝑒 −𝑡2 + 1 2)]0 𝑡 ∫ 𝑥𝑒−𝑥2 𝑑𝑥 ∞ −∞ = −1 2+ 0 + 0 + 1 2 ∫ 𝑥𝑒−𝑥2 𝑑𝑥 ∞ −∞ = 0
9 B. Variabel Random
Definisi 2.3 (Bain dan Engelhardt, 1992:53)
Variabel random 𝑋 adalah suatu fungsi yang didefinisikan pada ruang sampel 𝑆
yang menghubungkan setiap hasil yang mungkin 𝑒 di 𝑆 dengan suatu bilangan riil, yaitu 𝑋(𝑒) = 𝑥.
Definisi 2.4 (Bain dan Engelhardt, 1992:56)
Jika himpunan hasil yang mungkin dari variabel random 𝑋 merupakan himpunan terhitung, {𝑥1, 𝑥2, … , 𝑥𝑛} atau {𝑥1, 𝑥2, …} maka 𝑋 disebut variabel random diskrit. Fungsi 𝑓(𝑥) = 𝑃[𝑋 = 𝑥]; 𝑥 = 𝑥1, 𝑥2, … , 𝑥𝑛 yang menentukan peluang untuk masing–masing nilai 𝑥 yang mungkin disebut dengan fungsi densitas peluang diskrit.
Contoh 2.3
Misalkan 𝑥1 < 𝑥2 < 𝑥3 < ... barisan bilangan real dan 𝑝𝑛, 𝑛 = 1,2,3, … barisan bilangan real nonnegatif sedemikian hingga ∑∞ 𝑝𝑛 = 1
𝑛=1 . Dapat dinyatakan 𝐹(𝑥) = {∑ 𝑝𝑖 𝑛 𝑖=1 𝑥𝑛 ≤ 𝑥 < 𝑥𝑛+1, 𝑛 = 1,2,3, … 0 − ∞ < 𝑥 < 𝑥1
Dengan demikian, 𝐹(𝑥) merupakan fungsi distribusi kumulatif tangga. Fungsi tersebut mempunyai lompatan dengan ukuran 𝑝𝑛 pada setiap 𝑥𝑛 dan mendatar diantara 𝑥𝑛 dan 𝑥𝑛+1, 𝑛 = 1,2,3, … .Fungsi distribusi kumulatif sedemikian disebut fungsi distribusi kumulatif diskrit dan variabel random yang bersesuaian merupakan variabel random diskret.
10
Sebaliknya, misalkan ada fungsi distribusi kumulatif 𝐹(𝑥) dalam fungsi F(x). Misalkan 𝑆 = {𝑥1, 𝑥2, 𝑥3, … }, 𝐴 = 2𝑆, dan dapa dinyatakan
𝑃(𝐴) = ∑ 𝑝𝑖, 𝐴 ∈ 𝐴
𝑖:𝑥𝑖𝜖𝐴
dan 𝑋(𝜔) = 𝜔, maka P adalah ukuran probabilitas dan fungsi distribusi kumulatif
𝑥 adalah F(x).
Definisi 2.5 (Bain dan Engelhardt, 1992:57)
Suatu fungsi dapat dikatakan sebagai distribusi peluang dari variabel random diskrit jika dan hanya jika memenuhi kedua persamaan berikut untuk semua nilai x:
𝑓(𝑥𝑖) ≥ 0 untuk semua 𝑥𝑖 (2.3)
∑𝑛 𝑓(𝑥𝑖) = 1
𝑖=1 (2.4)
Bukti:
Dengan mengikuti persamaan (2.7), diketahui bahwa nilai pdf diskrit merupakan suatu peluang yang positif. Karena [𝑋 = 𝑥𝑖],... , [𝑋 = 𝑥𝑛] merupakan suatu partisi lengkap dari ruang sampel.
Sehingga,
∑𝑛𝑖=1𝑓(𝑥𝑖)=∑𝑛𝑖=1𝑃[𝑋 = 𝑥𝑖]= 1 (2.5) Akibatnya, setiap fungsi densitas harus memenuhi sifat (2.3) dan (2.4) dan setiap fungsi yang memenuhi sifat (2.3) dan (2.4) akan menetapkan definisi peluang.
11 Contoh 2.4
Misalkan 𝑝(𝑥) = 𝑐 (2
3 ) 2
, 𝑥 = 1,2,3, … akan menentukan 𝑐 agar 𝑝(𝑥) merupakan fungsi massa probabilitas. Dengan sendirinya 𝑐 (2
3 ) 𝑥
> 0 untuk c positif. Supaya
𝑝(𝑥) merupakan fungsi massa probabilitas, ∑ 𝑝(𝑥) = 𝑐 ∑ (2
3 ) 𝑥 = 1 ∞ 𝑥=1 ∞ 𝑥=1 . Karena ∑ (2 3 ) 𝑥 = 1 1−23 ∞ 𝑥=1 = 3, yang berati ∑ ( 2 3 ) 𝑥 = 3 − 1 = 2 ∞ 𝑥=1 , maka 𝑐 ∑ (2 3 ) 𝑥 = 𝑐. 2 = 1 ∞ 𝑥=1 atau 𝑐 = 1 2.
Definisi 2.6 (Bain dan Engelhardt, 1992:58)
Fungsi distribusi kumulatif dari variabel random 𝑋 yang didefinisikan untuk bilangan riil 𝑥 adalah sebagai berikut :
𝐹(𝑥) = 𝑃(𝑋 ≤ 𝑥) (2.6) Contoh 2.5 𝐹(2,4) = 𝑃(𝑋 ≤ 2,4) = 𝑓(0) + 𝑓(1) = (1 3) + ( 1 2) = 5 6
Definisi 2.7 (Bain dan Engelhardt, 1992:61)
Jika 𝑋 variabel random diskrit dengan fungsi densitas peluang dari (𝑋), maka nilai ekspektasi dari 𝑋 didefinisikan sebagai berikut :
𝐸(𝑥) = ∑ 𝑥𝑓(𝑥)𝑥 (2.7)
Definisi 2.8 (Bain dan Engelhardt, 1992:67)
Jika 𝑋 variabel random kontinu dengan fungsi densitas peluang dari (𝑋), maka nilai ekspektasi dari 𝑋 didefinisikan sebagai berikut :
𝐸(𝑥) = ∫−∞∞ 𝑥𝑓(𝑥) 𝑑𝑥 (2.8)
12 Contoh 2.6
Misalkan X mempunyai fungsi kepadatan probabilitas
𝑓(𝑥) = {2(1 − 𝑥) 0 < 𝑥 < 1 0 yang lain dengan demikian, 𝐸(𝑋) = ∫ 𝑥𝑓(𝑥) 𝑑𝑥 = ∫(𝑥) 2(1 − 𝑥) 𝑑𝑥 = 1 3 1 0 ∞ −∞
Definisi 2.9 (Wand dan Jones, 1995:14)
Jika X suatu variabel random kontinu dengan pdf 𝑓(𝑥), maka
𝑣𝑎𝑟[𝑓̂(𝑥)] = 𝐸 [𝑓̂(𝑥) − 𝐸[𝑓̂(𝑥)]]2 (2.9) Definisi 2.10 (Wand dan Jones, 1995:15)
Jika X suatu variabel random maka bias dari estimator fungsi kepadatan dari 𝑓(𝑥)
adalah
[𝐵𝑖𝑎𝑠[𝑓̂(𝑥)]]2 = [𝐸[𝑓̂(𝑥)] − 𝑓̂(𝑥)]2 (2.10) C. Ekspektasi dan Variansi Variabel Random
Definisi 2.11 (Bain dan Engelhardt, 1992:72)
Jika X adalah variabel random dengan fungsi densitas peluang 𝑓(𝑥), maka nilai ekspektasi dari X didefinisikan sebagai berikut:
𝐸(𝑋) = { ∑ 𝑥𝑓(𝑥), jika 𝑥 diskrit 𝑥 ∫ 𝑥𝑓(𝑥)𝑑𝑥, jika 𝑥 kontinu ∞ −∞
Jika X variabel random dengan fungsi densitas 𝑓(𝑥) dan 𝑢(𝑥) adalah fungsi riil dengan domain elemen dari X, maka:
13 𝐸[𝑢(𝑋)] = { ∑ 𝑢(𝑋)𝑓(𝑥), jika 𝑥 diskrit 𝑥 ∫ 𝑢(𝑋)𝑓(𝑥)𝑑𝑥, jika 𝑥 kontinu ∞ −∞
Jika X variabel random dengan fungsi densitas 𝑓(𝑥), 𝑎 dan 𝑏 suatu konstanta, dan
𝑔(𝑥) dan ℎ(𝑥) fungsi real dengan domain elemen dari X, maka
𝐸[𝑎𝑔(𝑥) + 𝑏ℎ(𝑥)] = 𝑎𝐸[𝑔(𝑥)] + 𝑏𝐸[ℎ(𝑥)] (2.11)
𝐸(𝑎𝑋 + 𝑏) = 𝑎𝐸(𝑥) + 𝑏 (2.12)
Sifat-sifat ekspektasi adalah sebagai berikut: 1. 𝐸(𝑋 + 𝑌) = 𝐸(𝑋) + 𝐸(𝑌)
2. 𝐸(𝑋 − 𝑌) = 𝐸(𝑋) − 𝐸(𝑌)
3. 𝐸(𝑎𝑋 + 𝑏) = 𝑎𝐸(𝑋) + 𝑏, dengan a dan b adalah konstanta 4. 𝐸(𝑋𝑌) = 𝐸(𝑋)𝐸(𝑌), jika X dan Y independen.
Contoh 2.7
Misalkan X mempunyai fungsi kepadatan probabilitas
𝑓(𝑥) = {2(1 − 𝑥) 0 < 𝑥 < 1 0 yang lain dengan demikian, 𝐸(𝑋) = ∫ 𝑥𝑓(𝑥) 𝑑𝑥 = ∫(𝑥) 2(1 − 𝑥) 𝑑𝑥 = 1 3 1 0 ∞ −∞ 𝐸(𝑋2) = ∫ 𝑥2𝑓(𝑥) 𝑑𝑥 = ∫(𝑥2) 2(1 − 𝑥) 𝑑𝑥 = 1 6 1 0 ∞ −∞
Dengan menggunakan definisi 2.11 maka,
𝐸(6𝑥 + 3𝑥2) = 6 (1 3) + 3 ( 1 6) = 5 2
14 Teorema 2.1 (Bain dan Engelhardt, 1992:74) Jika 𝑋 adalah variabel random, maka :
𝑉𝑎𝑟(𝑋) = 𝐸[(𝑥 − 𝜇)2] (2.13) Bukti 𝑉𝑎𝑟(𝑋) = 𝐸(𝑋2− 2𝜇𝑋 + 𝜇2) 𝑉𝑎𝑟(𝑋) = 𝐸(𝑋2) − 2𝜇𝐸(𝑋) + 𝜇2 𝑉𝑎𝑟(𝑋) = 𝐸(𝑋2) − 2𝜇2+ 𝜇2 𝑉𝑎𝑟(𝑋) = 𝐸(𝑋2) − 𝜇2
Teorema 2.2 (Bain dan Engelhardt, 1992:74)
Jika 𝑋 adalah variabel random 𝑎 dan 𝑏 adalah konstanta, maka :
𝑉𝑎𝑟(𝑎𝑋 + 𝑏) = 𝑎2𝑉𝑎𝑟(𝑋) (2.14) Bukti 𝑉𝑎𝑟(𝑎𝑋 + 𝑏) = 𝐸[((𝑎𝑋 + 𝑏) − (𝑎𝜇 + 𝑏))2] 𝑉𝑎𝑟(𝑎𝑋 + 𝑏) = 𝐸[(𝑎𝑋 + 𝑏 − 𝑎𝜇 − 𝑏)2] 𝑉𝑎𝑟(𝑎𝑋 + 𝑏) = 𝐸[𝑎2(𝑋 − 𝜇)2] 𝑉𝑎𝑟(𝑎𝑋 + 𝑏) = 𝑎2𝐸[(𝑋 − 𝜇)2] 𝑉𝑎𝑟(𝑎𝑋 + 𝑏) = 𝑎2𝑉𝑎𝑟(𝑋)
D. Distribusi Peluang Bersama
15
Distribusi peluang bersama merupakan suatu tabel atau rumus yang mendaftarkan semua kemungkinan nilai x dan y bagi variabel random diskrit X dan Y berikut peluang padanannya 𝑓(𝑥, 𝑦).
Bila X dan Y adalah dua variabel random diskrit, distribusi peluang bersamanya dapat dinyatakan sebagai sebuah fungsi 𝑓(𝑥, 𝑦) untuk sembarang pasangan nilai
(𝑥, 𝑦) yang dapat diambil oleh variabel random X dan Y. Jadi, dalam kasus variabel random diskrit,
𝑓(𝑥, 𝑦) = 𝑃(𝑋 = 𝑥, 𝑌 = 𝑦) (2.15)
nilai 𝑓(𝑥, 𝑦) menyatakan peluang bahwa x dan y terjadi secara bersamaan. Contoh 2.8
Empat mata uang seimbang dilemparkan secara independen. Probabilitas mendapatkan dua muka dan dua belakang adalah
𝑃(𝑥 = 2) = (4 2) ( 1 2) 2 (1 2) 2 = 3 8 E. Distribusi Bersyarat
Definisi 2.13 (Walpole dan Raymond, 1995:113 )
Distribusi bersyarat untuk variabel random diskrit Y, untuk 𝑋 = 𝑥, diberikan rumus sebagai berikut:
𝑓(𝑦|𝑥) =𝑓(𝑥,𝑦)
𝑓(𝑥) , 𝑓(𝑥) > 0 (2.16)
Begitu pula distribusi bersyarat untuk variabel random diskrit X, untuk Y=y, diberikan rumus sebagai berikut:
𝑓(𝑥|𝑦) =𝑓(𝑥,𝑦)
16 Contoh 2.9
Misalkan bahwa X bagian dari pelari pria dan Y bagian dari pelari wanita yang menyelesaikan lomba-lomba maraton dapat dinyatakan sebagai fungsi padat gabungan
𝑓(𝑥, 𝑦) = { 8 𝑥𝑦, 0 ≤ 𝑥 ≤ 1 0 ≤ 𝑦 ≤ 𝑥 0 untuk nilai 𝑥, 𝑦 lainnya
Hitunglah 𝑓(𝑥), 𝑓(𝑦|𝑥)! Penyelesaian : 𝑓(𝑥) = ∫ 𝑓(𝑥, 𝑦) 𝑑𝑦 = ∫ 8 𝑥𝑦 𝑑𝑦 𝑥 0 ∞ −∞ 𝑓(𝑥) = 4𝑥𝑦2] 𝑦=0 𝑦=𝑥 = 4𝑥3, 0 < 𝑥 < 1 lalu, 𝑓(𝑦|𝑥) = 𝑓(𝑥, 𝑦) 𝑓(𝑥) = 8 𝑥𝑦 4 𝑥3 = 2𝑦 𝑥2, 0 < 𝑦 < 𝑥 F. Mean Square Error (MSE)
Kesalahan kuadrat rerata atau mean square error (MSE) adalah nilai harapan dari kuadrat perbedaan antara estimator dengan parameter populasi. Teorema 2.3 (Haeruddin, 1997:14)
Diketahui 𝜃 merupakan suatu parameter dan 𝜃̂ merupakan taksiran dari parameter
𝜃, maka MSE dari suatu taksian parameter 𝜃 didefinisikan sebagai berikut:
𝑀𝑆𝐸[𝜃̂] = 𝐸 [(𝜃̂ − 𝜃)2]
17 Bukti
terdapat 𝑉𝑎𝑟[𝜃̂] = 𝐸 [𝜃̂ − 𝐸[𝜃̂]]2
[𝑏𝑖𝑎𝑠[𝜃̂]]2=[𝐸[𝜃̂]− 𝜃]2
dengan memisalkan 𝐸[𝜃̂] = 𝑚 sehingga
𝑀𝑆𝐸[𝜃̂] = 𝐸 [(𝜃̂ − 𝜃)2] 𝑀𝑆𝐸[𝜃̂] = 𝐸 [(𝜃̂ − 𝐸[𝜃̂] + 𝐸[𝜃̂] − 𝜃)2] 𝑀𝑆𝐸[𝜃̂] = 𝐸 [(𝜃̂ − 𝑚 + 𝑚 − 𝜃)2] 𝑀𝑆𝐸[𝜃̂] = 𝐸 [(𝜃̂ − 𝑚)2+ 2(𝜃̂ − 𝑚)(𝑚 − 𝜃) + (𝑚 − 𝜃)2] 𝑀𝑆𝐸[𝜃̂] = 𝐸 [(𝜃̂ − 𝑚)2] + 2𝐸[(𝜃̂ − 𝑚)(𝑚 − 𝜃)]+(𝑚 − 𝜃)2 𝑀𝑆𝐸[𝜃̂] = 𝐸 [(𝜃̂ − 𝑚)2] +(𝑚 − 𝜃)2+ 2𝐸[(𝜃̂ − 𝑚)(𝑚 − 𝜃)] 𝑀𝑆𝐸[𝜃̂] = 𝐸 [(𝜃̂ − 𝑚)2] + (𝑚 − 𝜃)2+ 0 𝑀𝑆𝐸[𝜃̂] = 𝑉𝑎𝑟[𝜃̂] + [𝑏𝑖𝑎𝑠[𝜃̂]]2
Jadi 𝑀𝑆𝐸[𝜃̂] sama dengan varians ditambah bias kuadrat. Jika 𝜃̂ adalah penduga yang tak bias maka 𝑀𝑆𝐸[𝜃̂] merupakan variannya. Dengan kata lain, MSE adalah jumlah dari dua kuantitas, yaitu varians dan bias kuadrat.
18 G. Uji Normalitas
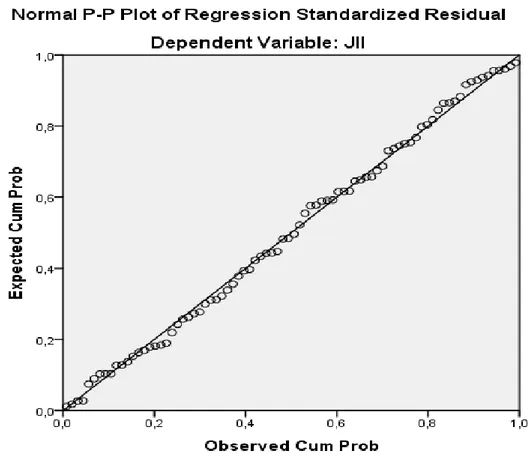
Menurut Imam Ghozali (2013:160) menyatakan bahwa uji normalitas digunakan untuk menguji apakah dalam model regresi, variabel dependennya memiliki distribusi normal atau tidak. Model regresi yang baik adalah memiliki distribusi data normal atau mendekati normal. Pada prinsipnya normalitas data dapat diketahui dengan melihat penyebaran data (titik) pada sumbu diagonal dari grafik dependennya seperti gambar 2.1
Gambar 2. 1 Grafik Residual Normal Data normal dan tidak normal dapat diuraikan sebagai berikut:
1. Jika data menyebar di sekitar garis diagonal dan mengikuti arah garis diagonal atau grafik histogramnya, menunjukan pola berdistribusi normal, maka model regresi memenuhi asumsi normalitas.
19
2. Jika data menyebar jauh dari garis diagonal dan tidak mengikuti arah garis diagonal atau grafik histogramnya, tidak menunjukkan pola terdistribusi normal, maka model regresi tidak memenuhi asumsi normalitas.
Uji normalitas dengan grafik dapat menyesatkan apabila tidak hati-hati, secara visual kelihatan normal, namun secara statistik bisa sebaliknya. Oleh sebab itu dianjurkan selain menggunakan uji grafik dilengkapi dengan uji statistik. Uji statistik sederhana yang sering digunakan untuk menguji asumsi normalitas adalah dengan menggunakan uji normalitas dari Kolmogorov-Smirnov. Metode pengujian normal tidaknya distribusi data dilakukan dengan melihat nilai signifikan variabel (p-value). Jika residualnya tidak normal, maka dapat dilakukan beberapa langkah yaitu:
1. Data tidak berdistribusi normal 2. Melakukan transformasi data
3. Menggunakan alat analisis nonparametrik. H. Uji Kolmogorov Smirnov
Prosedur ini diperkenalkan pada tahun 1933 oleh ahli matematik Rusia A.N. Kolmogorov. Menurut Imam Ghozali (2013:165) mengungkapkan bahwa metode Kolmogorov-Smirnov menggunakan data dasar yang belum diolah dalam tabel distribusi frekuensi. Data ditransformasikan dalam nilai Z untuk dapat dihitung luasan kurva normal sebagai probabilitas kumulatif normal. Probabilitas tersebut dicari bedanya dengan probabilitas kumulatif empiris. Uji Kolmogorov-Smirnov dilakukan dengan membuat hipotesis dengan membuat hipotesis:
20
𝐻1 ∶ Data tidak berdistribusi normal Statistik uji:
𝐷 = 𝑚𝑎𝑥((𝐹𝑌) − (𝐹𝑌𝑖)) (2.19)
dengan F adalah distribusi kumulatif teoritis dari distribusi yang sedang diuji. Dari statistik uji tersebut didapatkan nilai kritisnya yaitu jika nilai D lebih besar dari nilai kritis yang diperoleh dari tabel. Seiring berkembangnya teknologi, kini pengujian normalitas bisa dilakukan dengan memanfaatkan software yang mengandung analisis pengujian normalitas. Penerapan pada uji Kolmogorov-Smirnov adalah jika signifikansi dibawah 0,05 maka uji tersebut menolak hipotesis nol yang menyatakan data tidak berdistribusi normal.
I. P-value
P-value adalah peluang terkecil sehingga nilai suatu uji statistik yang sedang diamati masih mempunyai arti. P-value lebih banyak digunakan daripada kriteria uji lain seperti tabel distribusi dan selang kepercayaan. Hal ini disebabkan karena p-value memberikan dua informasi sekaligus, disamping petunjuk apakah 𝐻0 pantas ditolak, p-value juga memberikan informasi mengenai peluang terjadinya kejadian yang disebutkan di dalam 𝐻0 (dengan asumsi 𝐻0 dianggap benar).
P-value dapat juga diartikan sebagai besarnya peluang melakukan kesalahan pada saat memutuskan untuk menolak 𝐻0. Pada umumnya p-value dibandingkan dengan taraf nyata 𝑎 tertentu, biasanya 0,05 atau 5%. Taraf nyata 𝑎
diartikan sebagai peluang melakukan kesalahan untuk menyimpulkan bahwa 𝐻0 salah, padahal 𝐻0 benar. Kesalahan semacam ini dikenal sebagai galat atau kesalahan jenis I.
21 J. Analisis Regresi Linear Sederhana
Analisis regresi adalah analisis statistik yang mempelajari bagaimana memodelkan sebuah model fungsional dari data menjelaskan ataupun meramalkan suatu fenomena alami atas dasar fenomena lain. Analisis regresi juga merupakan salah satu teknik statistika yang digunakan secara luas dalam ilmu pengetahuan terapan dalam bidang ekonomi maupun eksakta.
Analisis regresi merupakan alat statistika yang bermanfaat untuk mengetahui hubungan antara dua variabel atau lebih, sehingga salah satu variabel dapat diduga dua variabel lainnya. Model regresi dasar yang melibatkan satu variabel independen dan fungsi regresinya linear dapat ditulis sebagai berikut :
𝑌𝑖= 𝛽0+ 𝛽1𝑋𝑖+ 𝜀𝑖, 𝑖 = 1, … , 𝑛 (2.20) dengan,
𝑌𝑖 adalah nilai variabel respon pada pengamatan ke-i
𝑋𝑖 adalah variabel prediktor pada pengamatan ke-i
𝛽0 dan 𝛽1 adalah parameter-parameter yang tidak diketahui
𝜀𝑖 adalah error atau galat K. Metode Kuadrat Terkecil
Untuk mendapatkan estimasi yang baik bagi parameter koefisien regresi 𝛽0
dan 𝛽1, digunakan metode kuadrat terkecil (LSE). Metode kuadrat terkecil adalah metode yang digunakan untuk menduga parameter dengan cara meminimumkan nilai ∑𝑛𝑖=1𝜀𝑖2 dengan 𝜀 adalah galat atau error, Supramono (1993:210). Metode
22
kuadrat terkecil dapat menduga parameter dari model regresi linear. Misalkan terdapat model regresi linear sederhana yaitu
𝑌𝑖 = 𝛽0+ 𝛽1𝑋𝑖+ 𝜀𝑖
Persamaan diatas kemudian dibentuk menjadi persamaan sebagai berikut:
𝜀𝑖=𝑌𝑖−𝛽0− 𝛽1𝑋𝑖
jika 𝜀𝑖 adalah galat yang terkecil, maka kuadrat dan jumlah kuadratnya adalah yang paling kecil. Pada persamaan tersebut mempunyai parameter 𝛽0 dan 𝛽1 yang belum diketahui. Maka dengan metode kuadrat terkecil akan ditentukan penduga untuk parameter 𝛽0
dan 𝛽1 adalah 𝑏0 dan 𝑏1, menentukan persamaan 𝜀𝑖 kemudian dikuadratkan, sehingga diperoleh:
∑𝑛 𝜀𝑖2
𝑖=1 = ∑𝑛𝑖=1(𝑌𝑖−𝑏0− 𝑏1𝑋𝑖)2 = 𝑄
Untuk menentukan penduga parameter 𝑏0 dan 𝑏1 yang menghasilkan nilai Q yang minimum maka diselesaikan sistem persamaan berikut:
∂Q ∂𝑏0= 2∑(𝑌𝑖−𝑏0− 𝑏1𝑋𝑖)(−1) = 0 𝑛 𝑖=1 ∂Q ∂𝑏1= −2∑(𝑌𝑖−𝑏0− 𝑏1𝑋𝑖)(𝑋𝑖) = 0 𝑛 𝑖=1
Dari kedua persamaan diatas diperoleh penduga parameter 𝑏0 dan 𝑏1, sebagai berikut: 1. Pendugaan Parameter 𝑏0 ∂Q ∂𝑏0 = 2∑(𝑌𝑖−𝑏0− 𝑏1𝑋𝑖)(−1) = 0 𝑛 𝑖=1
23 ∂Q ∂𝑏0= ∑ (𝑌𝑖−𝑏0− 𝑏1𝑋𝑖) = 0 𝑛 𝑖=1 ∂Q ∂𝑏0= ∑𝑌𝑖 𝑛 𝑖=1 − ∑𝑏0 𝑛 𝑖=1 −∑𝑏1𝑋𝑖 𝑛 𝑖=1 = 0 ∂Q ∂𝑏0= ∑𝑌𝑖 𝑛 𝑖=1 − 𝑛𝑏0− 𝑏1∑𝑋𝑖 𝑛 𝑖=1 = 0 𝑛𝑏0+ 𝑏1∑𝑋𝑖 𝑛 𝑖=1 = ∑𝑌𝑖 𝑛 𝑖=1 𝑛𝑏0 = ∑ 𝑌𝑖 𝑛 𝑖=1 − 𝑏1∑ 𝑋𝑖 𝑛 𝑖=1 𝑏0 = 𝑌̅ − 𝑏1𝑋̅ 2. Pendugaan parameter 𝑏1 ∂Q ∂𝑏1= 2∑(𝑌𝑖−𝑏0− 𝑏1𝑋𝑖)(−𝑋𝑖) = 0 𝑛 𝑖=1 ∂Q ∂𝑏0= ∑(𝑌𝑖−𝑏0− 𝑏1𝑋𝑖)(𝑋𝑖) = 0 𝑛 𝑖=1 ∂Q ∂𝑏0= ∑𝑌𝑖𝑋𝑖 𝑛 𝑖=1 − ∑𝑏0𝑋𝑖 𝑛 𝑖=1 −∑𝑏1𝑋𝑖2 𝑛 𝑖=1 = 0 ∂Q ∂𝑏0= ∑ 𝑌𝑖 𝑛 𝑖=1 𝑋𝑖−𝑏0∑𝑋𝑖 𝑛 𝑖=1 − 𝑏1∑𝑋𝑖2 𝑛 𝑖=1 = 0 𝑏0∑𝑋𝑖 𝑛 𝑖=1 − 𝑏1∑𝑋𝑖2 𝑛 𝑖=1 = ∑𝑌𝑖 𝑛 𝑖=1 𝑋𝑖
24 𝑌̅ − 𝑏1𝑋̅ ∑ 𝑋𝑖 𝑛 𝑖=1 − 𝑏1∑ 𝑋𝑖2 𝑛 𝑖=1 =∑ 𝑌𝑖 𝑛 𝑖=1 𝑋𝑖 𝑌̅ ∑ 𝑋𝑖 𝑛 𝑖=1 − 𝑏1𝑋̅ ∑ 𝑋𝑖 𝑛 𝑖=1 − 𝑏1∑ 𝑋𝑖2 𝑛 𝑖=1 = ∑ 𝑌𝑖 𝑛 𝑖=1 𝑋𝑖 𝑏1(∑ 𝑋𝑖2 𝑛 𝑖=1 −𝑋̅ ∑ 𝑋𝑖 𝑛 𝑖=1 )=∑ 𝑌𝑖 𝑛 𝑖=1 𝑋𝑖− 𝑌̅ ∑ 𝑋𝑖 𝑛 𝑖=1 𝑏1 =∑ 𝑌𝑖 𝑛 𝑖=1 𝑋𝑖 − 𝑌̅ ∑𝑛𝑖=1𝑋𝑖 ∑𝑛 𝑋𝑖2 𝑖=1 −𝑋̅ ∑𝑛𝑖=1𝑋𝑖 =∑ 𝑌𝑖 𝑛 𝑖=1 𝑋𝑖− 𝑌̅ ∑𝑛𝑖=1𝑋𝑖 ∑𝑛 𝑋𝑖2 𝑖=1 − 𝑛𝑋̅2 L. Saham
Saham adalah surat berharga yang menunjukkan kepemilikan terhadap sebuah perusahaan. Masing-masing lembar saham biasa mewakili suatu suara tentang segala hal dalam pengurusan perusahaan dan menggunakan suara tersebut dalam rapat tahunan perusahaan dan pembagian keuntungan (Nor Hadi, 2013:85). Saham berwujud selembar kertas yang menerangkan bahwa pemilik kertas tersebut adalah pemilik perusahaan yang menerbitkan surat berharga tersebut. Porsi kepemilikan ditentutan oleh seberapa besar penyertaan yang ditanamkan di perusahaan tersebut. Walaupun demikian tidak semua saham memiliki hak tersebut. Tergantung dari jenis saham yang dimiliki oleh seorang investor. Ada beberapa sudut pandang untuk membedakan saham (Warsini, 2009:32):
1. Berdasarkan cara pengalihan/pemindahan tangan dibedakan:
a. Saham atas nama (registered stocks) yaitu dimana identitas pemiliknya tertera pada lembaran saham.
25
b. Saham atas unjuk (bearer stock), tanpa identitas pemilik, sehingga pemegang saham itulah pemilik saham.
2. Berdasarkan hak tagihan ada dua jenis saham: a. Saham Biasa (common stocks)
Saham biasa merupakan jenis efek yang paling sering dipergunakan oleh emiten untuk memperoleh dana dari masyarakat dan merupakan jenis yang paling populer di pasar modal.
b. Saham Preferen (preferred stocks)
Pemegang saham preferen tidak mempunyai hak suara didalam RUPS tetapi mempunyai hak untuk didahulukan dalam hal pembagian deviden maupun klaim terhadap aktiva perusahaan.
M. Indeks Harga Saham
Definisi 2.14 Pengertian Indeks Harga Saham
Indeks saham adalah harga saham yang dinyatakan dalam angka indeks. Indeks saham digunakan untuk tujuan analisis dan menghindari dampak negatif dari penggunaan harga saham (Hadi, 2013:96). Corporate action merupakan salah satu tindakan yang dilakukan oleh perusahaan yang dapat merusak analisis apabila menggunakan harga saham dalam rupiah tanpa korekai terlebih dahulu. Dengan menggunakan indeks saham dalam dapat dihindari kesalahan analisis walaupun tanpa koreksi.
Setiap bursa efek akan menetapkan angka basis indeks yang berbeda, yaitu ada yang dimulai dengan basis 100, 500, atau 1000. Pada tanggal 10 agustus 1982
26
ditetapkan sebagai hari dasar (nilai indeks = 100). Sebelum transaksi pertama terjadi di bursa efek, saham tersebut diberi indeks harga sebagai angka dasar. Kemudian ketika jam perdagangan mulai berlangsung dari pagi pukul 10.00 dan berakhir pada sore pukul 16.00, sudah pastipuluhan kali harga terbentuk dalam transaksi pada hari tersebut. Dari sekian banyak harga yang terbentuk lalu dibagi menjadi tiga, yaitu harga terendah (low), harga tertinggi (high) dan harga penutup (close). Ketiga jenis harga tersebut tertera dalan Daftar Informasi Perdanganan Efek Harian (DIPEH) yang ditertibkan oleh bursa efek. Indeks harga saham dihitung berdasarkan harga pasar penutupan (closing price).
Definisi 2.15 Jakarta Islamic Index (JII)
Jakarta Islamic Index (JII) merupakan salah satu indeks saham yang ada di Indonesia yang menghitung indeks dengan rata-rata saham untuk jenis saham-saham yang memenuhi kriteria syari’ah (Hadi, 2013:136). Pembentukan JII tidak lepas dari kerja sama antara Pasar Modal Indonesia (dalam hal ini Bursa Efek Jakarta) dengan PT Danareksa Invesment Management (PT DIM). JII telah dikembangkan sejak tanggal 3 juli 2000. Setiap periodenya, saham yang masuk JII berjumlah 30 (tiga puluh saham) yang memenuhi kriteria syari’ah dan akan diperbarui setiap tiga bulan sekali.
Penentuan kriteria dalam pemilihan saham dalam JII melibatkan Dewan Pengawas PT DIM, ada 4 syarat yang harus dipenuhi agar saham-saham tersebut dapat masuk JII:
1. Emiten tidak menjalankan usaha perjudian dan permainan yang tergolong judi atau perdagangan yang dilarang.
27
2. Bukan lembaga keuangan konvensional yang menerapkan sistem riba, termasuk perbankan dan asuransi konvensional.
3. Usaha yang dilakukan bukan memproduksi, mendistribusi, dan memperdagangkan makanan/minuman yang haram.
4. Tidak menjalankan usaha memproduksi, mendistribusi, dan menyediakan baran/jasa yang merusak moral dan besifat mudharat.
28
BAB III
PEMBAHASAN
A. Estimasi Nonparametrik
Tujuan dasar dalam sebuah analisa regresi adalah untuk mempelajari bagaimana respon sebuah peubah Y terhadap perubahan yang terjadi pada peubah lain yaitu X. Hubungan antara X dan Y dapat ditulis sebagai berikut:
𝑌𝑖= 𝑚(𝑋𝑖)+ 𝜀𝑖; 𝑖 = 1,2,3, … , 𝑛 (3.1) Dimana 𝑚(𝑋𝑖) adalah fungsi matematik yang disebut sebagai fungsi regresi dan 𝜀𝑖
adalah sisaan yang diasumsikan independen dengan mean nol. Pada aplikasi, terdapat sekumpulan data {(𝑋1,𝑌1), . . ,(𝑋𝑖, 𝑌𝑖)} yang berisi informasi tentang fungsi
𝑚(𝑋𝑖). Dari data-data ini diduga ataupun diestimasi fungsi 𝑚(𝑋𝑖) tersebut. Dalam beberapa penelitian, sering dijumpai permasalahan pada hubungan fungsional antara 2 variabel 𝑌 dan 𝑋 di mana bentuk –bentuk hubungan secara parametrik tidak dapat digunakan yang diakibatkan dari sedikitnya pengetahuan yang diperoleh tentang fungsi 𝑚(𝑋𝑖) ini, maka estimasi terhadap fungsi 𝑚(𝑋𝑖) ini dapat didekati secara nonparametrik. Agar pendekatan nonparametrik ini menghasilkan estimasi terhadap fungsi 𝑚(𝑋𝑖) yang masuk akal, maka hal yang harus diperhatikan adalah asumsi bahwa 𝑚(𝑋𝑖)memiliki derajat kemulusan. Biasanya kontinuitas dari 𝑚(𝑋𝑖)
merupakan syarat yang cukup untuk menjamin sebuah estimator akan konvergen pada 𝑚(𝑋𝑖) yang sesungguhnya bila jumlah data bertambah tanpa batas. Estimasi nonparametrik secara umum tidaklah efektif digunakan untuk ukuran sampel yang kecil (Suyono, 1997:3). Dalam aplikasi-aplikasi yang lain, dapat digunakan kemajuan fasilitas-fasilitas perhitungan dan metode-metode perhitungan untuk
29
mengembangkan hubungan fungsional antara Y dan X. Hal inilah yang mungkin menjadi pertimbangan untuk menggunakan metode dan teknik nonparametrik.
Kelebihan statistika nonparametrik dibanding dengan statistika parametrik adalah :
1. Asumsi yang digunakan minimum sehingga mengurangi kesalahan penggunaan 2. Perhitungan dapat dilakukan dengan cepat dan mudah
3. Konsep dan metode nonparametrik mudah dipahami
4. Dapat diterapkan pada skala kualitatif (nominal dan ordinal).
Estimator-estimator nonparametrik yang banyak digunakan adalah estimator-estimator smoothing, dimana error dari observasi direduksi dari rata-rata data dengan bermacam cara.
B. Estimator Densitas Kernel
Estimator densitas kernel merupakan pengembangan dari estimator histogram. Estimator densitas kernel adalah suatu metode pendekatan terhadap fungsi densitas yang belum diketahui dengan menggunakan fungsi kernel. Estimator diperkenalkan oleh Rosenblatt (1956), Parzen (1962) sehingga disebut estimator densitas kernel Rosenblatt-Parzen (Hardle, 1994). Penghalusan dengan pendekatan kernel selanjutnya dikenal sebagai penghalusan kernel (kernel
smoother) sangat tergantung pada fungsi kernel dan bandwidth.
Definisi (Hardle, 1994:32)
Didefinisikan X adalah variabel random dengan distribusi kontinu F(x) dan densitas 𝑓̂(𝑥)=𝑑𝑥𝑑 𝐹(𝑥). Estimator densitas kernel untuk fungsi𝑓̂(𝑥)adalah
𝑓 ̂(𝑥)=1𝑛∑𝑛𝑖=1𝐾ℎ(𝑋𝑖− 𝑥) 𝑓 ̂(𝑥)=𝑛ℎ1 ∑ 𝐾(𝑋𝑖−𝑥 ℎ ) 𝑛 𝑖=1 (3.2)
30
dengan x adalah sebuah angka spesifik yang nilainya tetap. Persamaan (3.2) dapat disederhanakan dengan 𝐾ℎ(𝑢) =
1 ℎ(
𝑢
ℎ), dengan memisalkan 𝑢 = 𝑋𝑖 − 𝑥 sehingga dapat ditulis
𝑓̂(𝑥) = 1
𝑛∑ 𝐾ℎ(𝑋𝑖− 𝑥) 𝑛
𝑖=1 (3.3)
dengan K adalah sebuah fungsi yang merupakan fungsi kontinu, berharga real, terbatas dan memenuhi ∫𝐾(𝑥)𝑑𝑥 = 1, fungsi ini dinamakan fungsi kernel, dan h
adalah bilangan positif yang disebut dengan bandwidth. Jika K(u) adalah fungsi densitas kernel, maka 𝐾ℎ(𝑢) juga.
Estimator kernel memenuhi asumsi-asumsi sebagai berikut: (Silverman, 1986) (i) 𝐾ℎ(𝑥)≥ 0, untuk semua x
(ii) 𝐾(𝑥) bersifat simetris
𝐾(−𝑥) = 𝐾(𝑥), untuk semua x
(iii) ∫𝐾(𝑥)𝑑𝑥 = 1
(iv) ∫𝑥𝐾(𝑥)𝑑𝑥 = 0
(v) ∫𝑥2𝐾(𝑥)𝑑𝑥 = 𝜇
2(𝐾) ≠ 0, dengan 𝜇2(𝐾) momen kedua tertentu
(vi) ∫[𝐾(𝑥)]2𝑑𝑥 =∫𝐾2(𝑥) 𝑑𝑥 =‖𝐾‖ 2
2= 𝑅(𝐾)
Jika fungsi kernel merupakan fungsi densitas, maka estimator fungsi dengan menggunakan fungsi kernel juga merupakan suatu fungsi densitas probabilitas. Akan dibuktikan fungsi densitas kernel memang memenuhi ∫𝑓̂(𝑥)𝑑𝑥 = 1.
Bukti
∫𝑓̂(𝑥)𝑑𝑥 =∫1
𝑛∑𝐾ℎ(𝑋𝑖− 𝑥)𝑑𝑥 𝑛
31 ∫𝑓̂(𝑥)𝑑𝑥 = ∫ 1 𝑛 ∞ −∞ ∑1 ℎ𝐾( 𝑋𝑖− 𝑥 ℎ )𝑑𝑥 𝑛 𝑖=1 dengan subtitusi : −𝑢 =𝑋𝑖−𝑥
ℎ dan 𝑑𝑥 = ℎ 𝑑𝑢 maka diperoleh
∫𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ ∫𝐾(−𝑢)𝑑𝑢 𝑛 𝑖=1 ∫𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ ∫𝐾(𝑢)𝑑𝑢 𝑛 𝑖=1 ∫𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑1 𝑛 𝑖=1 ∫𝑓̂(𝑥)𝑑𝑥 =1 𝑛𝑛 ∫𝑓̂(𝑥)𝑑𝑥 = 1
Jadi, 𝑓̂(𝑥) merupakan suatu fungsi densitas.
Akan digunakan kembali subtitusi −𝑢 =𝑋𝑖−𝑥
ℎ , maka mean densitas yang di
estimasi adalah ∫𝑥𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ ∫𝑥 1 ℎ𝐾( 𝑋𝑖− 𝑥 ℎ )𝑑𝑥 ∞ −∞ 𝑛 𝑖=1 ∞ −∞ ∫𝑥𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ ∫ (𝑋𝑖+ 𝑢ℎ)𝐾(𝑢)𝑑𝑢 ∞ −∞ 𝑛 𝑖=1 ∞ −∞ ∫𝑥𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑𝑋𝑖 ∫𝐾(𝑢)𝑑𝑢 ∞ −∞ 𝑛 𝑖=1 ∞ −∞ +1 𝑛∑ℎ ∫𝑢𝐾(𝑢)𝑑𝑢 ∞ −∞ 𝑛 𝑖=1
32 ∫𝑥𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑𝑋𝑖 𝑛 𝑖=1 ∞ −∞
merupakan mean sampel dari 𝑋𝑖.
Momen kedua dari 𝑥 dengan pdf merupakan densitas yang diestimasi, yaitu
∫𝑥2𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ ∫𝑥2 1 ℎ𝐾( 𝑋𝑖− 𝑥 ℎ )𝑑𝑥 ∞ −∞ 𝑛 𝑖=1 ∞ −∞ ∫𝑥2𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ ∫ (𝑋𝑖+ 𝑢ℎ)2𝐾(𝑢)𝑑𝑢 ∞ −∞ 𝑛 𝑖=1 ∞ −∞ ∫𝑥2𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑𝑋𝑖 2 ∫𝐾(𝑢)𝑑𝑢 ∞ −∞ 𝑛 𝑖=1 ∞ −∞ +2 𝑛∑𝑋𝑖ℎ ∫𝑢𝐾(𝑢)𝑑𝑢 ∞ −∞ +1 𝑛∑ℎ 2 ∫𝑢2𝐾(𝑢)𝑑𝑢 ∞ −∞ 𝑛 𝑖=1 𝑛 𝑖=1 ∫𝑥2𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑𝑋𝑖 2 + ℎ2𝜇2(𝐾) 𝑛 𝑖=1 ∞ −∞
dengan 𝜇2(𝐾)=∫𝑢2𝐾(𝑢)𝑑𝑢 adalah momen kedua dari u.
Selanjutnya, dapat dicari variansi dari densitas 𝑓̂(𝑥) sebagai berikut
∫𝑥2𝑓̂(𝑥)𝑑𝑥 −( ∫𝑥2𝑓̂(𝑥)𝑑𝑥 ∞ −∞ ) 2 =1 𝑛∑𝑋𝑖 2+ ℎ2 𝜇2(𝐾) 𝑛 𝑖=1 −(1 𝑛∑𝑋𝑖 𝑛 𝑖=1 ) 2 ∞ −∞ ∫𝑥2𝑓̂(𝑥)𝑑𝑥 −( ∫𝑥2𝑓̂(𝑥)𝑑𝑥 ∞ −∞ ) 2 = 𝜎̂2+ ℎ2𝜇2(𝐾) ∞ −∞
33
dengan 𝜎̂ adalah variansi sampel. Dengan demikian, estimasi densitas menaikkan variansi sampel sebesar ℎ2𝜇2(𝐾).
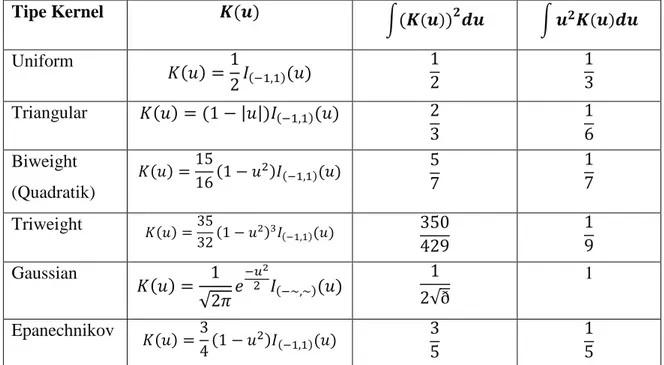
Menurut Sukarsa dan Srinadi (2012:20) menyatakan bahwa fungsi kernel ada bermacam-macam, contohnya kernel Gaussian, kernel Uniform, kernel Biweight. Tabel 3.1 menyajikan bermacam-macam fungsi kernel dan bentuknya, sebagai berikut:
Tabel 3.1 Macam-macam Fungsi Kernel
Tipe Kernel 𝐅𝐮𝐧𝐠𝐬𝐢 𝐊𝐞𝐫𝐧𝐞𝐥 Uniform 𝐾(𝑢) = 1 2𝐼(−1,1)(𝑢) Triangular 𝐾(𝑢) = (1 − |𝑢|)𝐼(−1,1)(𝑢) Biweight (Quadratik) 𝐾(𝑢) =15 16(1 − 𝑢 2)𝐼 (−1,1)(𝑢) Triweight 𝐾(𝑢) =35 32(1 − 𝑢 2)3𝐼 (−1,1)(𝑢) Gaussian 𝐾(𝑢) = 1 √2𝜋𝑒 −𝑢2 2 𝐼(−∞,∞)(𝑢) Epanechnikov 𝐾(𝑢) =3 4(1 − 𝑢 2)𝐼 (−1,1)(𝑢)
dengan I adalah Indikator.
C. Estimasi Bias
Estimator densitas kernel 𝑓̂(𝑥) merupakan estimator tak bias asimtotik dari suatu fungsi kepadatan 𝑓(𝑥). Menurut Haeruddin (1997:27) andaikan 𝑓̂(𝑥) adalah estimator densitas kernel dari suatu fungsi kepadatan 𝑓(𝑥) pada titik 𝑥 ∈ 𝑅 dan andaikan 𝑋𝑖 berdistribusi identik dengan fungsi kepadatan 𝑓(𝑥), maka
𝐸[𝑓̂(𝑥)] = 𝐸 [1 𝑛ℎ∑ 𝐾 ( 𝑋𝑖 − 𝑥 ℎ ) 𝑛 𝑖=1 ]
34 𝐸[𝑓̂(𝑥)] = 1 𝑛ℎ∑ 𝐸 [𝐾 ( 𝑋𝑖 − 𝑥 ℎ )] 𝑛 𝑖=1 𝐸[𝑓̂(𝑥)] =1 ℎ𝐸 [𝐾 ( 𝑋𝑖− 𝑥 ℎ )] 𝐸[𝑓̂(𝑥)] =1 ℎ∫ 𝐾 ( 𝑦 − 𝑥 ℎ ) 𝑓(𝑦)𝑑𝑦 misalkan 𝑠 =𝑦−𝑥 ℎ , maka 𝑑𝑦 = ℎ𝑑𝑠. Sehingga, 𝐸[𝑓̂(𝑥)] =1 ℎ∫ 𝐾(𝑠)𝑓(𝑥 + 𝑠ℎ)ℎ𝑑𝑠 𝐸[𝑓̂(𝑥)] = ∫ 𝐾(𝑠)𝑓(𝑥 + 𝑠ℎ) 𝑑𝑠
integral tersebut tidak dapat diselesaikan kecuali menggunakan pendekatan ekspansi taylor dari 𝑓(𝑥 + 𝑠ℎ) dengan 𝑠ℎ = 0, ketika ℎ → 0. Untuk setiap kernel order ke v, maka dapat menggunakan aturan sebagai berikut
𝑓(𝑥 + 𝑠ℎ) = 𝑓(𝑥) + 𝑓′(𝑥)𝑠ℎ +1 2𝑓 ′′(𝑥)ℎ2𝑠2+ 1 3!𝑓 ′′′(𝑥)ℎ3𝑠3+ ⋯ + 1 𝑣!𝑓 𝑣(𝑥)ℎ𝑣𝑠𝑣+ 𝑜(ℎ𝑣)
𝑜(ℎ𝑣) adalah sisa dari order yang lebih rendah dari ℎ𝑣 saat ℎ → 0. Maka, ekspansi taylor order dua untuk 𝑓(𝑥 + 𝑠ℎ) sebagai berikut:
𝑓(𝑥 + 𝑠ℎ) = 𝑓(𝑥) + 𝑓′(𝑥)𝑠ℎ +1 2𝑓
′′(𝑥)ℎ2𝑠2+ 𝑜(ℎ2)
Selanjutnya, dengan aturan ∫−∞∞ 𝐾(𝑠)𝑑𝑠 = 1 dan ∫ 𝑠𝑗𝐾(𝑠)𝑑𝑠 = 𝜇 𝑗(𝐾) ∞
35 𝐸[𝑓̂(𝑥)] = ∫ 𝐾(𝑠) [𝑓(𝑥) + 𝑓′(𝑥)𝑠ℎ +1 2𝑓 ′′(𝑥)ℎ2𝑠2+ 𝑜(ℎ2)] 𝑑𝑠 𝐸[𝑓̂(𝑥)] = 𝑓(𝑥) ∫ 𝐾(𝑠)𝑑𝑠 + 𝑓′(𝑥)ℎ ∫ 𝑠 𝐾(𝑠)𝑑𝑠 +1 2𝑓 ′′(𝑥)ℎ2∫ 𝑠2 𝐾(𝑠)𝑑𝑠 + 𝑜(ℎ2) ∫ 𝐾(𝑠)𝑑𝑠 𝐸[𝑓̂(𝑥)] = 𝑓(𝑥)(1) + 𝑓′(𝑥)ℎ(0) +1 2𝑓′′(𝑥)ℎ 2 ∫ 𝑠2 𝐾(𝑠)𝑑𝑠 + 𝑜(ℎ2) (1) 𝐸[𝑓̂(𝑥)] = 𝑓(𝑥) +1 2𝑓 ′′(𝑥)ℎ2𝜇 2(𝐾) + 𝑜(ℎ2) (3.4)
Akan dihitung bias, integrated squared bias, dan variansi dari 𝑓̂(𝑥) sebagai berikut (i) Bias dari 𝑓̂(𝑥)
𝐵𝑖𝑎𝑠 𝑓̂(𝑥) = 𝐸(𝑓̂(𝑥)) − 𝑓(𝑥) 𝐵𝑖𝑎𝑠 𝑓̂(𝑥) = 𝑓(𝑥) +1 2𝑓 ′′(𝑥)ℎ2𝜇 2(𝐾) + 𝑜(ℎ2) − 𝑓(𝑥) 𝐵𝑖𝑎𝑠 𝑓̂(𝑥) =1 2𝑓 ′′(𝑥)ℎ2𝜇 2(𝐾) + 𝑜(ℎ2) (3.5)
(ii) Integrated Squared Bias dari 𝑓̂(𝑥) ∫Bias (𝑓̂(𝑥))2𝑑𝑥 =ℎ 4 4 𝜇2(𝐾) 2 ∫(𝑓′′(𝑥))2𝑑𝑥 + (𝑜(ℎ2))2 ∫Bias (𝑓̂(𝑥))2𝑑𝑥 =ℎ4 4 𝜇2(𝐾) 2𝑅(𝑓′′)+ 𝑜(ℎ4) (3.6)
(iii) Variansi dari 𝑓̂(𝑥)
Selanjutnya akan dihitung variansi dari 𝑓̂(𝑥). Akan digunakan pendekatan Taylor order satu. Faktanya 𝑛−1 lebih kecil dari (𝑛ℎ)−1 jika ℎ → 0 dan 𝑛 →
36 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛2𝑉𝑎𝑟 (∑ 𝐾ℎ(𝑋𝑖− 𝑥) 𝑛 𝑖=1 ) 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛2∑ 𝑉𝑎𝑟(𝐾ℎ(𝑋𝑖− 𝑥)) 𝑛 𝑖=1 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛𝑉𝑎𝑟(𝐾ℎ(𝑋𝑖− 𝑥)) 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛{𝐸[𝐾ℎ 2(𝑋 𝑖 − 𝑥)] − (𝐸[𝐾ℎ(𝑋𝑖 − 𝑥)])2} 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛{ 1 ℎ2∫ 𝐾2( 𝑦 − 𝑥 ℎ ) 𝑓(𝑦)𝑑𝑦 − (𝑓(𝑥) + 𝑜(ℎ)) 2} Substitusi 𝑠 =𝑦−𝑥 ℎ dan 𝑑𝑦 = ℎ𝑑𝑠, maka 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛ℎ2∫ 𝐾2(𝑠)𝑓(𝑥 + 𝑠ℎ)ℎ𝑑𝑠 − 1 𝑛(𝑓(𝑥) + 𝑜(ℎ)) 2 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛ℎ∫ 𝐾 2(𝑠)𝑑𝑠 𝑓(𝑥 + 𝑠ℎ) −1 𝑛(𝑓(𝑥) + 𝑜(ℎ)) 2 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛ℎ𝑅(𝐾)𝑓(𝑥) + 𝑜(ℎ) − 1 𝑛(𝑓(𝑥) + 𝑜(ℎ)) 2 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛ℎ𝑓(𝑥)𝑅(𝐾) + 𝑜 ( 1 𝑛ℎ) 𝑉𝑎𝑟(𝑓̂(𝑥)) = ((𝑛ℎ)−1)𝑓(𝑥)𝑅(𝐾) + 𝑜((𝑛ℎ)−1), 𝑛ℎ → ∞ (3.7) dengan 𝑅(𝐾) = ∫ 𝐾2(𝑠)𝑑𝑠
D. Mean Square Error dan Mean Integrated Square Error
Menurut Suyono (1997:41) mengungkapkan bahwa suatu estimasi densitas kernel yang dibuat tergantung dari beda antara densitas yang sebenarnya 𝑓 dengan hasil estimasi 𝑓̂. Cara pengukuran beda antara densitas sebenarnya 𝑓 dengan hasil estimasi 𝑓̂ adalah dengan square error (SE) di suatu titik
37
𝑆𝐸𝑥(𝑓̂)={𝑓̂(𝑥)− 𝑓(𝑥)}2 (3.8)
Sehingga mean square error (MSE) dapat dirumuskan
𝑀𝑆𝐸𝑥(𝑓̂)= 𝐸[{𝑓̂(𝑥)− 𝑓(𝑥)} 2 ] 𝑀𝑆𝐸𝑥(𝑓̂)= 𝐸{𝑓̂(𝑥)− 𝐸[𝑓̂(𝑥)]+ 𝐸[𝑓̂(𝑥)]− 𝑓(𝑥)} 2 𝑀𝑆𝐸𝑥(𝑓̂)= 𝐸[(𝑓̂(𝑥)− 𝐸[𝑓̂(𝑥)])2]+ 𝐸[{𝐸[𝑓̂(𝑥)]− 𝑓(𝑥)}2] + 2𝐸{(𝑓̂(𝑥)− 𝐸[𝑓̂(𝑥)])(𝑓̂(𝑥)− 𝑓(𝑥))} 𝑀𝑆𝐸𝑥(𝑓̂)= 𝐸[(𝑓̂(𝑥)− 𝐸[𝑓̂(𝑥)])2]+[{𝐸[𝑓̂(𝑥)]− 𝑓̂(𝑥)}2] 𝑀𝑆𝐸𝑥(𝑓̂)= 𝑣𝑎𝑟 𝑓̂(𝑥)+(𝑏𝑖𝑎𝑠 𝑓̂(𝑥))2 (3.9) Maka, berdasarkan persamaan (3.9) dapat dicari nilai MSE dari 𝑓̂(𝑥) sebagai berikut: 𝑀𝑆𝐸 (𝑓̂(𝑥)) = 𝑣𝑎𝑟𝑓̂(𝑥) + [𝑏𝑖𝑎𝑠2𝑓̂(𝑥)]2 𝑀𝑆𝐸 (𝑓̂(𝑥)) = 1 𝑛ℎ𝑓(𝑥)𝑅(𝐾) + 𝑜((𝑛ℎ) −1) + [1 2𝑓 ′′(𝑥)ℎ2ì 2(𝐾) + 𝑜(ℎ2)] 2 𝑀𝑆𝐸 (𝑓̂(𝑥)) = 1 𝑛ℎ𝑓(𝑥)𝑅(𝐾) + ℎ4 4 (𝑓 ′′(𝑥)ì 2(𝐾)) 2 + 𝑜((𝑛ℎ)−1) + 𝑜(ℎ4) (3.10) untuk ℎ → 0, 𝑛ℎ → ∞
sedangkan pengukuran keseluruhan beda antara densitas yang sebenarnya 𝑓 dengan hasil estimasi 𝑓̂ disebut MISE yaitu mean integrated square error (Haeruddin,1997:17).
38 𝑀𝐼𝑆𝐸(𝑓̂) = ∫ 𝑀𝑆𝐸𝑥(𝑓̂)𝑑𝑥 𝑀𝐼𝑆𝐸(𝑓̂) = ∫ 𝐸{𝑓̂(𝑥) − 𝑓(𝑥)}2𝑑𝑥 𝑀𝐼𝑆𝐸(𝑓̂) = ∫ 𝐸 [(𝑓̂(𝑥) − 𝐸[𝑓̂(𝑥)])2] 𝑑𝑥 + ∫ 𝐸 [{𝐸[𝑓̂(𝑥)] − 𝑓(𝑥)}2] 𝑑𝑥 𝑀𝐼𝑆𝐸(𝑓̂) = ∫ 𝑣𝑎𝑟𝑓̂(𝑥) 𝑑𝑥 + ∫ (𝑏𝑖𝑎𝑠 𝑓̂(𝑥))2𝑑𝑥 (3.11) Maka, 𝑀𝐼𝑆𝐸[𝑓̂(𝑥)] = ∫ 𝑀𝑆𝐸[𝑓̂(𝑥)]𝑑𝑥 ∞ −∞ 𝑀𝐼𝑆𝐸[𝑓̂(𝑥)] = ∫ { 1 𝑛ℎ𝑓(𝑥)𝑅(𝐾) + ℎ4 4 (𝑓 ′′(𝑥)𝜇 2(𝐾)) 2 + 𝑜((𝑛ℎ)−1) ∞ −∞ + 𝑜(ℎ4)} 𝑑𝑥 𝑀𝐼𝑆𝐸[𝑓̂(𝑥)] = ∫ 1 𝑛ℎ𝑓(𝑥)𝑅(𝐾)𝑑𝑥 + ∫ ℎ4 4 (𝑓 ′′(𝑥)𝜇 2(𝐾)) 2 𝑑𝑥 ∞ −∞ + 𝑜((𝑛ℎ)−1) ∞ −∞ + 𝑜(ℎ4) 𝑀𝐼𝑆𝐸[𝑓̂(𝑥)] = 1 𝑛ℎ𝑅(𝐾) ∫ 𝑓(𝑥)𝑑𝑥 ∞ −∞ +ℎ 4 4 𝜇2(𝐾) 2 ∫ (𝑓′′(𝑥))2𝑑𝑥 ∞ −∞ + 𝑜((𝑛ℎ)−1) + 𝑜(ℎ4) 𝑀𝐼𝑆𝐸[𝑓̂(𝑥)] = 1 𝑛ℎ𝑅(𝐾) + ℎ4 4 𝜇2(𝐾) 2 ∫ (𝑓′′(𝑥))2𝑑𝑥 ∞ −∞ + 𝑜((𝑛ℎ)−1) + 𝑜(ℎ4)
39 𝑀𝐼𝑆𝐸[𝑓̂(𝑥)] = 1 𝑛ℎ𝑅(𝐾) + ℎ4 4 𝜇2(𝐾) 2𝑅(𝑓′′) + 𝑜((𝑛ℎ)−1) + 𝑜(ℎ4) (3.12) untuk ℎ → 0, 𝑛ℎ → ∞ E. Regresi Kernel
Salah satu teknik smoothing untuk mengestimasi fungsi penghalus m pada persamaan (3.1) adalah regresi kernel. Dalam jurnal Sukarsa dan Srinadi (2012:21), Regresi kernel merupakan metode untuk memperkirakan ekspektasi bersyarat dari variabel acak dengan menggunakan fungsi kernel. Metode alternatif dalam pendekatan regresi nonparametrik ini menggunakan pemulus kernel, yang menggunakan rata-rata terbobot dari data. Tujuan analisis regresi adalah menemukan hubungan antara sepasang variabel acak X dan Y, untuk mendapatkan dan menggunakan bobot yang sesuai. Menurut Hardle (1994:26), dalam setiap regresi nonparametrik, harapan bersyarat dari variabel Y relatif terhadap variabel 𝑋
dapat ditulis 𝐸(𝑌|𝑋) = 𝑚̂ (𝑥) atau 𝐸(𝑌|𝑋 = 𝑥) = ∫ 𝑦 𝑓(𝑥,𝑦)𝑑𝑦
𝑓(𝑥) . Dimana 𝑚 adalah
fungsi yang tidak diketahui untuk mendapatkan dan menggunakan bobot kernel yang sesuai.
Dalam regresi kernel terdapat berbagai estimator yang dapat digunakan untuk menduga bentuk 𝑚̂, diantaranya adalah estimator Nadaraya-Watson, estimator Polinomial Lokal, estimator Pristly-Chao dan estimator Gasser-Muller. Dalam bab ini akan dibahas mengenai estimator Nadaraya-Watson.
F. Estimator Nadaraya-Watson
Nadaraya dan Watson pada tahun 1964 mendefinisikan estimator regresi kernel sehingga disebut estimator Nadaraya-Watson (Wand dan Jones, 1995:130). Nilai dari fungsi 𝑚(𝑥) sesuai dengan nilai prediktor yang ekuivalen dengan
40
ekspektasi dari variabel target dibawah kondisi nilai dari prediktor tetap yaitu 𝑥, maka 𝑚̂ (𝑥)= 𝐸(𝑌|𝑋 = 𝑥) 𝑚̂ (𝑥)= ∫𝑦𝑓(𝑦|𝑥)𝑑𝑦 ∞ −∞ 𝑚̂ (𝑥) =∫ 𝑦𝑓(𝑥, 𝑦)𝑑𝑦 ∞ −∞ 𝑓(𝑥) (3.13)
Selanjutnya, Oryza (2013:22) menyatakan bahwa akan digunakan estimator densitas kernel sebagai metode yang sederhana untuk mengestimasi 𝑓(𝑥, 𝑦) dan
𝑓(𝑥). Estimasi dari 𝑓(𝑥, 𝑦) dan 𝑓(𝑥) dinotasikan sebagai 𝑓̂(𝑥, 𝑦) dan 𝑓̂(𝑥).
𝑓̂(𝑥, 𝑦)= 1 𝑛ℎ𝑥ℎ𝑦∑𝐾𝑥( 𝑋𝑖− 𝑥 ℎ𝑥 ) 𝑛 𝑖=1 𝐾𝑦(𝑌𝑖− 𝑦 ℎ𝑦 ) (3.14) 𝑓̂𝑥(𝑥)= 1 𝑛ℎ𝑥∑𝐾𝑥( 𝑋𝑖− 𝑥 ℎ𝑥 ) 𝑛 𝑖=1 (3.15) dimana 𝐾𝑥(𝑋𝑖−𝑥 ℎ𝑥 ) dan 𝐾𝑦( 𝑌𝑖−𝑦
ℎ𝑦 ) merupakan fungsi kernel, ℎ𝑥 dan ℎ𝑦 merupakan
konstan yang bernilai positif disebut dengan bandwidth. Telah disebutkan bahwa fungsi kernel memenuhi
∫ 𝐾𝑥(𝑢)𝑑𝑢 = ∫ 𝐾𝑦(𝑢)𝑑𝑢 = 1 ∞ −∞ ∞ −∞ (3.16) ∫−∞∞ 𝑢𝐾𝑥(𝑢)𝑑𝑢 = ∫−∞∞ 𝑢𝐾𝑦(𝑢)𝑑𝑢 = 0 (3.17) ∫ 𝑢2𝐾 𝑥(𝑢)𝑑𝑢 ∞ −∞ < ∞ (3.18)
41
∫ 𝑢2𝐾
𝑦(𝑢)𝑑𝑢 ∞
−∞ < ∞ (3.19)
dari persamaan (3.16) dan persamaan (3.17) diperoleh menjadi persamaan di bawah ini: 1 ℎ𝑥 ∫𝐾𝑥( 𝑋𝑖− 𝑥 ℎ𝑥 ) ∞ −∞ 𝑑𝑥 = 1 ℎ𝑦 ∫𝐾𝑦( 𝑌𝑖− 𝑦 ℎ𝑦 ) ∞ −∞ 𝑑𝑦 = 1 (3.20) 1 (ℎ𝑥)2 ∫𝑥𝐾𝑥( 𝑥 ℎ𝑥) ∞ −∞ 𝑑𝑥 = 1 (ℎ𝑦)2 ∫𝑦𝐾𝑦( 𝑦 ℎ𝑦) ∞ −∞ 𝑑𝑦 = 0 (3.21)
untuk mencari perhitungan yang sederhana yaitu 𝑚̂(𝑋) dapat menggunakan subtitusi dari persamaan (3.14) dan persamaan (3.15) ke dalam persamaan (3.13) sebagai berikut: 𝑚̂ (𝑥) =∫ 𝑦𝑓̂(𝑥, 𝑦)𝑑𝑦 ∞ −∞ 𝑓̂(𝑥) 𝑚̂ (𝑥)= ∫ 𝑦 1 𝑛ℎ𝑥ℎ𝑦∑ 𝐾𝑥( 𝑋𝑖− 𝑥 ℎ𝑥 ) 𝑛 𝑖=1 𝐾𝑦(𝑌𝑖ℎ− 𝑦 𝑦 ) 𝑑𝑦 ∞ −∞ 1 𝑛ℎ𝑥∑ 𝐾𝑥(𝑋𝑖ℎ− 𝑥 𝑥 ) 𝑛 𝑖=1 𝑚̂ (𝑥)= ∑ 𝐾𝑥(𝑋𝑖ℎ− 𝑥 𝑥 ) ∫ 𝑦𝐾𝑦( 𝑌𝑖− 𝑦 ℎ𝑦 )𝑑𝑦 ∞ −∞ 𝑛 𝑖=1 ℎ𝑦∑ 𝐾𝑥(𝑋𝑖ℎ− 𝑥 𝑥 ) 𝑛 𝑖=1 (3.22)
Selanjutnya, jika dimisalkan −𝑍 =𝑌𝑖−𝑦
ℎ𝑦 , maka 𝑑𝑦 = ℎ𝑦𝑑𝑍 1 ℎ𝑦 ∫𝑦𝐾𝑦( 𝑌𝑖− 𝑦 ℎ𝑦 )𝑑𝑦 = ℎ𝑦 ℎ𝑦 ∫ (𝑌𝑖+ ℎ𝑦𝑍)𝐾𝑦(𝑍)𝑑𝑍 ∞ −∞ ∞ −∞
42 1 ℎ𝑦 ∫𝑦𝐾𝑦( 𝑌𝑖− 𝑦 ℎ𝑦 )𝑑𝑦 = ∫𝑌𝑖𝐾𝑦(𝑍)𝑑𝑍 ∞ −∞ + ∫𝑍𝐾𝑦(𝑍)ℎ𝑦𝑑𝑍 ∞ −∞ ∞ −∞ 1 ℎ𝑦 ∫𝑦𝐾𝑦( 𝑌𝑖− 𝑦 ℎ𝑦 )𝑑𝑦 = 𝑌𝑖(1)+ ℎ𝑦(0) ∞ −∞ 1 ℎ𝑦∫ 𝑦𝐾𝑦( 𝑌𝑖−𝑦 ℎ𝑦 )𝑑𝑦 = 𝑌𝑖 ∞ −∞ (3.23)
Substitusi dari persamaan (3.23) ke dalam persamaan (3.22), dan penyederhanaan dari 𝐾𝑥(. ) menjadi 𝐾(. ) dan dari ℎ𝑥 menjadi ℎ menghasilkan:
𝑚̂ (𝑥)= 1 𝑛∑𝑛𝑖=1𝐾𝑥(𝑋𝑖ℎ− 𝑥)𝑌𝑖 1 𝑛∑𝑛𝑖=1𝐾𝑥(𝑋𝑖ℎ− 𝑥) 𝑚̂ (𝑥) = ∑𝑛𝑖=1𝐾 (𝑋𝑖ℎ− 𝑥) 𝑌𝑖 ∑ 𝐾 (𝑋𝑖 − 𝑥 ℎ ) 𝑛 𝑖=1 (3.24)
dengan mensubtitusikan persamaan (3.24) terhadap model regresi pada persamaan (3.1), maka estimator Nadaraya-Watson dari model regresi (3.1) adalah
𝑚̂ (𝑥)= ∑𝑛𝑖=1𝐾 (𝑋𝑖ℎ− 𝑥)𝑌𝑖 ∑𝑛𝑖=1𝐾 (𝑋𝑖ℎ− 𝑥) +𝜀𝑖, 𝑖 = 1,2,3, . . . , 𝑛 (3.25) dengan, K : fungsi kernel
h : nilai bandwidth tertentu