GRAPH, STARBARBELL GRAPH, AND Cm⊙kPn GRAPH
Ratih Yunia Mayasari, Tri Atmojo Kusmayadi, Santoso Budi Wiyono Department of Mathematics
Faculty of Mathematics and Natural Sciences Universitas Sebelas Maret
Abstract. LetG be a connected graph with vertex setV(G) and edge set E(G). For every pair of verticesu, v∈V(G), the intervalI[u, v] betweenuandvto be the collection of all vertices that belong to some shortestu−vpath. A vertexs∈V(G) strongly resolves two verticesuandv ifubelongs to a shortestv−spath orv belongs to a shortestu−s
path. A vertex setS ofGis a strong resolving set of Gif every two distinct vertices of
Gare strongly resolved by some vertex of S. The strong metric basis of G is a strong resolving set with minimal cardinality. The strong metric dimensionsdim(G) of a graph
Gis defined as the cardinality of strong metric basis. In this paper we determine the strong metric dimension of a broken fan graph, starbarbell graph, andCm⊙
k
Pn graph.
Keywords : strong metric dimension, strongly resolved set, broken fan graph, starbarbell graph,Cm⊙kPn graph
1. Introduction
The concept of strong metric dimension was presented by Seb¨o and Tannier [9]
in 2004. Oellermann and Peters-Fransen [8] defined for two vertices u and v in a
connected graphG, the intervalI[u, v] betweenuandvto be collection of all vertices
that belong to some shortest path. A vertex s strongly resolves two vertices u and
v if v ∈I[u, s] or u∈I[v, s]. A set S of vertices in a connected graph G is a strong
resolving set for Gif every two vertices ofGare strongly resolved by some vertex of
S. The smallest cardinality of a strong resolving set of Gis called its strong metric
dimension and is denoted by sdim(G).
Some researchers have investigated the strong metric dimension to some graph
classes. In 2004 Seb¨o and Tannier [9] observed the strong metric dimension of
complete graph Kn, cycle graph Cn, and tree. In 2012, Kuziak et al. [6] observed
the strong metric dimension of corona product graph. In the same year, Kratica et
al. [3] determined the metric dimension of hamming graph Hn,k. Kratica et al. [4]
determined the metric dimension of convex polytopeDn andTnin 2012 too. In 2013
Yi [10] determined the metric dimension of Pn. Kusmayadi et al. [5] determined
the strong metric dimension of some related wheel graph such as sunflower graph,
the strong metric dimension of a broken fan graph, starbarbell graph, andCm⊙kPn
graph.
2. Strong Metric Dimension
Let G be a connected graph with vertex set V(G), edge set E(G), and S =
{s1, s2, . . . , sk} ∈ V(G). Oellermann and Peters-Fransen [8] defined the interval
I[u, v] between u and v to be the collection of all vertices that belong to some
shortest u − v path. A vertex s ∈ S strongly resolves two vertices u and v if u ∈
I[v, s] or v ∈ I[u, s]. A vertex set S of G is a strong resolving set ofG if every two
distinct vertices of Gare strongly resolved by some vertex of S. The strong metric
basis of G is a strong resolving set with minimal cardinality. The strong metric
dimension of a graph G is defined as the cardinality of strong metric basis denoted
bysdim(G). We often make use of the following lemma and properties about strong
metric dimension given by Kratica et al. [4].
Lemma 2.1. Let u, v ∈ V(G), u ̸= v,
(1) d(w,v) ≤ d(u,v) for each w such that uw ∈ E(G), and
(2) d(u,w) ≤ d(u,v) for each w such that vw ∈ E(G).
Then there does not exist vertex a ∈ V(G), a ̸= u,v that strongly resolves vertices u and v.
Property 2.1. If S ⊂ V(G) is strong resolving set of graph G, then for every two vertices u,v ∈ V(G) satisfying conditions 1 and 2 of Lemma 2.1, obtained u ∈ S or v ∈ S.
Property 2.2. If S ⊂ V(G) is strong resolving set of graph G, then for every two vertices u, v ∈ V(G) satisfying d(u,v) = diam(G), obtained u ∈ S or v ∈ S.
3. The Strong Metric Dimension of a Broken Fan Graph
Gallian [2] defined the broken fan graph BF(a, b) is a graph withV(BF(a, b)) =
{c} ∪ {v1, v2, . . . , va} ∪ {u1, u2, . . . , ub} and E(BF(a, b)) ={(c, vi)|i= 1,2, . . . , a} ∪
{(c, ui)|i= 1,2, . . . , b} ∪E(Pa)∪E(Pb) (a ≥2 andb ≥2).
Lemma 3.1. For every integer a ≥ 2 and b ≥ 3, if S is a strong resolving set of broken fan graph BF(a, b) then |S |≥a+b−2.
Proof. We prove for every two distinct vertices (vi, ub) and (uj, ub). For every i =
orub ∈S and for everyj ∈ {1,2, . . . , b−2}sod(uj, ub) = 2 =diam(BF(a, b)) then
using Property 2.2, uj ∈ S or ub ∈ S. Therefore, S contains at least one vertex
from distinct set Xib = {vi, ub} for i ∈ {1,2, . . . , a} and one vertex from distinct
set Yjb ={uj, ub} for j ∈ {1,2, . . . , b−2}. The minimum number of vertices from
distinct set Xib is a and the minimum number of vertices from distinct set Yjb is
b−2. Therefore,|S |≥a+b−2.
Lemma 3.2. For every integera≥2andb≥3, a set S ={v1, v2, . . . , va, u1, u2, . . . ,
ub−2} is a strong resolving set of broken fan graph BF(a, b).
Proof. We prove that every two distinct vertices u, v ∈ (BF(a, b))\S, u̸= v there
exists a vertexs ∈Swhich strongly resolvesuandv. There are two pairs of vertices
from V(BF(a, b))\S.
(1) A pair of vertices (c, uj).
For every integer i = {1,2, . . . , a} and j ∈ {b − 1, b}, d(vi, uj) = 2 =
diam(BF(a, b)), we obtain the shortest vi −uj path : vi, c, uj. Thus, c ∈
I[vi, uj].
(2) A pair of vertices (ub−1, ub)
For j = b − 2, d(uj, ub) = 2 = diam(BF(a, b)), we obtain the shortest
ub−2−ub path: ub−2, ub−1, ub. Thus, ub−1 ∈I[uj, ub].
For every possible pairs of vertices, there exists a vertex s ∈ S which strongly
resolves every two distinct vertices BF(a, b)\S. Thus, S is a strong resolving set
of BF(a, b).
Theorem 3.1. Let BF(a, b) be the broken fan graph, then
sdim(BF(a, b)) =
{
3, a= 2 and n= 2;
a+b−2, a≥2 and b ≥3.
Proof. There are two cases to determine the strong metric dimension of broken fan graph.
(1) Case 1 (For a= 2 andb = 2).
By using Theorem from Kusmayadi et al. [5] thatsdim(fn) = 2n−1, so that
sdim(BF(2,2)) = 3 because of BF(2,2)∼=f2. Hence, sdim(BF(2,2)) = 3.
(2) Case 2 (For a≥2 and b≥3).
By using Lemma 3.2 a set S = {v1, v2, . . . , va, u1, u2, . . . , ub−2} is strong
re-solving set of broken fan graph BF(a, b) with a ≥ 2 and b ≥ 3. According
to Lemma 3.1, |S| ≥a+b−2, S is strong metric basis of broken fan graph
BF(a, b). Hence, sdim(BF(a, b)) =a+b−2.
4. The Strong Metric Dimension of Starbarbell Graph
Starbarbell graph SBm1,m2,...,mn is a graph obtained from a star graph Sn and n
complete graph Kmi by merging one vertex from each Kmi and the i
th-leaf of S
v, there exists a vertexs∈Swhich strongly resolvesuandv. There are four possible
(4) A pair of vertices (vi,1, vk,1).
From every possible pairs of vertices, there exists a vertex s ∈ S which strongly
resolves every two distinct vertices SBm1,m2,...,mn \S. Thus S is a strong resolving
set of starbarbell graph SBm1,m2,...,mn.
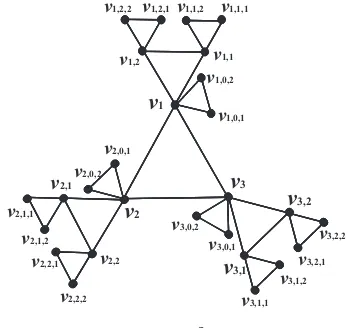
By using the definiton from Frucht and Harary [1], the corona product Cm⊙Pn
graph is graph obtained from Cm and Pn by taking one copy of Cm and n copies of
Pnand joining by an edge each vertex from ith-copy of Pn with theith-vertex of Cm.
Then, by using the definiton from Marbun and Salman [7], the k-multilevel corona
Lemma 5.1. For every integer m≥ 3, n = 2, and k ≥1, if S is a strong resolving set of Cm⊙kPn graph then |S |≥(mn(n+ 1)k−1)−1.
Proof. Let us consider a pair of vertices (va1,a2,...,ay, vb1,b2,...,bz) with y, z = k + 1,
1≤a1, b1 ≤m, 0≤ai, bi ≤2, and 2≤i≤k+ 1 satisfying both of the conditions of
Lemma 2.1. According to Property 2.1, we obtain va1,a2,...,ay ∈ S or vb1,b2,...,bz ∈ S.
It means that S contains one vertex from distinct sets Xyz= {va1,a2,...,ay, vb1,b2,...,bz}.
The minimum number of vertices from distinct sets Xyz is (mn(n + 1)k+1) −1.
Therefore, |S|≥(mn(n+ 1)k+1)−1.
Lemma 5.2. For every integer m≥3,n = 2, andk ≥1, a setS ={v1,0,...,1, v1,0,...,2,
. . . , v2,0,...,1, v2,0,...,2, . . . , vm,2,...,1} is a strong resolving set of Cm⊙kPn graph.
Proof. We prove that every two distinct verticesu, v ∈(Cm⊙kPn)\S, there exists
a vertex s∈S which strongly resolvesu andv. There are two pairs of vertices from
V(Cm⊙kPn)\S.
(1) A pair of vertices (va1,a2,...,ay, vb1,b2,...,bz).
For every integer 1 ≤ y, z ≤ k, 1 ≤ a1, b1 ≤ m, 0 ≤ ai, bi ≤ 2, and
2 ≤ i ≤ k, we obtain the shortest va1,a2,...,ay − vb1,b2,...,bz,bz+1,...,bk+1 path:
va1,a2,...,ay, va1,a2,...,ay−1, . . . , va1, . . . , vb1, . . . , vb1,b2,...,bz, vb1,b2,...,bz,bz+1,
. . . , vb1,b2,...,bz,,bz+1,...,bk+1. So that,vb1,b2,...,bz ∈I[va1,a2,...,ay, vb1,b2,...,bz,bz+1,...,bk+1].
(2) A pair of vertices (va1,a2,...,ay, vb1,b2,...,bz).
For every integer 1 ≤ y ≤ k, 1 ≤ a1 ≤ m−1, 0 ≤ ai ≤ 2, and 2 ≤ i ≤ k,
z = k + 1, b1 = m, bj = 2, and 2 ≤ j ≤ k + 1, we obtain the shortest
va1,a2,...,ay,ay+1,...,ak+1 −vb1,b2,...,bz path: va1,a2,...,ay,ay+1,...,ak+1, . . . , va1,a2,...,ay, . . . , va1, . . . , vb1, . . . , vb1,b2,...,bz. So that,va1,a2,...,ay ∈I[va1,a2,...,ay,ay+1,...,ak+1, vb1,b2,...,bz].
For every possible pairs of vertices, there exists a vertex s ∈ S which strongly
resolves every two distinct vertices (Cm⊙kPn)\S. Thus S is a strong resolving set
of Cm⊙kPn.
Lemma 5.3. For every integer m≥3, n≥3, and k ≥1, if S is a strong resolving set of Cm⊙kPn graph then |S |≥(mn(n+ 1)k−1)−2.
Proof. We know that S is strong resolving set of Cm ⊙kPn graph. Suppose that S
contains at most (mn(n+ 1)k−1)−3 vertices, then|S|<(mn(n+ 1)k−1)−2. LetV
1
is set of vertices va1,a2,...,ay with y =k+ 1, 1≤ a1 ≤m, 0≤ ai ≤ 2, and 2 ≤i ≤k
and V2 is set of vertices vb1,b2,...,bz with 1 ≤ z ≤ k, 1 ≤ b1 ≤ m, 0 ≤ bi ≤ 2, and
2≤i≤k. Now, we defineS1 =V1∩S andS2 =V2∩S. Without loss of generality,
we may take S1 =p, p >0 and S2 =q, q ≥0. Clearlyp+q≤(mn(n+ 1)k−1)−3,
for every s ∈ S we obtain va ∈/ I[vb, s] and vb ∈/ I[va, s]. This contradicts with the
supposition that S is a strong resolving set. Thus |S| ≥(mn(n+ 1)k−1)−2.
Lemma 5.4. For every integerm ≥3, n ≥3, andk ≥1, a setS ={v1,0,...,1, v1,0,...,2,
. . . , v1,0,...,n, . . . , v2,0,...,1, v2,0,...,2, . . . , v2,0,...,n, . . . , vm,n,...,1, vm,n,...,2, . . . , vm,n,...,n−2} is a
strong resolving set of Cm⊙kPn graph.
Proof. We prove that every two distinct verticesu, v ∈(Cm⊙kPn)\S, there exists
a vertex s ∈ S which strongly resolves u and v. There are three pairs of vertices
from V(Cm⊙kPn)\S.
(1) A pair of vertices (va1,a2,...,ay, vb1,b2,...,bz).
For every integer 1 ≤ y, z ≤ k, 1 ≤ a1, b1 ≤ m, 0 ≤ ai, bi ≤ n, and
2 ≤ i ≤ k, we obtain the shortest va1,a2,...,ay − vb1,b2,...,bz,bz+1,...,bk+1 path:
va1,a2,...,ay, va1,a2,...,ay−1, . . . , va1, . . . , vb1, . . . , vb1,b2,...,bz, vb1,b2,...,bz,bz+1, . . . , vb1,b2,...,bz,bz+1,...,bk+1. So that, vb1,b2,...,bz ∈I[va1,a2,...,ay, vb1,b2,...,bz,bz+1,...,bk+1].
(2) A pair of vertices (va1,a2,...,ay, vb1,b2,...,bz)
For every integer 1 ≤ y ≤ k, 1 ≤ a1 ≤ m − 1, 0 ≤ ai ≤ n, 2 ≤ i ≤
k, z = k + 1, b1 = m, bj = n, 2 ≤ j ≤ k, bz = {n − 1, n} we obtain
the shortest va1,a2,...,ay,ay+1,...,ak+1 −vb1,b2,...,bz path: va1,a2,...,ay,ay+1,...,ak+1, . . . ,
va1,a2,...,ay, . . . , va1, . . . , vb1, . . . , vb1,b2,...,bz. So that, va1,a2,...,ay ∈ I[va1,a2,...,ay,ay+1,...,ak+1, vb1,b2,...,bz].
(3) A pair of vertices (va1,a2,...,ay, va1,a2,...,az)
For every integer x, y, z = k + 1, a1 = m, ai = n, 2 ≤ i ≤ k, ay = n−
1, az = n ax = n −2 we obtain the shortest va1,a2,...,ax −va1,a2,...,az path:
va1,a2,...,ax, va1,a2,...,ay, va1,a2,...,az. So that, va1,a2,...,ay ∈I[va1,a2,...,ax, va1,a2,...,az].
For every possible pairs of vertices, there exists a vertex s ∈ S which strongly
resolves every two distinct vertices (Cm⊙kPn)\S. Thus S is a strong resolving set
of Cm⊙kPn.
Theorem 5.1. Let Cm⊙kPn be the corona product of cycle graph and path graph,
then
sdim(Cm⊙kPn) = {
(mn(n+ 1)k−1)−1, m≥3, k ≥1, dan n = 2;
(mn(n+ 1)k−1)−2, m≥3, k ≥1, dan n ≥3.
Proof. By Lemma 5.1 and Lemma 5.2, we havesdim(Cm⊙kPn) = (mn(n+1)k−1)−1
for m≥3, n= 2, and k ≥1. By Lemma 5.3 and Lemma 5.4, we have sdim(Cm⊙k
6. Conclusion
According to the discussion above it can be concluded that the strong metric
dimension of a broken fan graph BF(a, b), a starbarbell graph SBm1,m2,...,mn, and
a Cm ⊙kPn graph are as stated in Theorem 3.1, Theorem 4.1, and Theorem 5.1,
respectively.
References
[1] Frucht, and F. Harary, On The Corona of Two Graphs, Aequationes Math. Vol 4 (1970), 322-325.
[2] Gallian, J. A.,A Dynamic Survey of Graph Labeling, The Electronic Journal of Combinatorics #DS6, 2016.
[3] Kratica, J., V. Kovaˇcevi´c-Vujˇci´c, and M. ˇCangalovi´c,Minimal Doubly Resolving Sets and The Strong Metric Dimension of Hamming Graph, Applicable Analysis and Discrete Mathematics
6(2012), 63-71.
[4] Kratica, J., V. Kovaˇcevi´c-Vujˇci´c, and M. ˇCangalovi´c,Minimal Doubly Resolving Sets and The Strong Metric Dimension of Some Convex Polytope, Applied Mathematics and Computation
218(2012), 9790-9801.
[5] Kusmayadi, T. A., S. Kuntari, D. Rahmadi, and F. A. Lathifah, On the Strong Metric Dimension of Some Related Wheel Graphs, Far East Journal of Mathematical Sciences (FJMS)
99(2016), no. 9, 1322-1334.
[6] Kuziak, D., I. G. Yero, J. A. Rodr´ıguez-Vel´azquez,On The Strong Metric Dimension of Corona Product Graphs and Join Graph, Discrete Applied Mathematics161(2013), 1022-1027. [7] Marbun, H.T, and M. Salman,Wheel Supermagic Labelings for a Wheel k Multilevel Corona
with a Cycle, AKCE International Journal Graphs Combinatorics2(2013), 183-191.
[8] Oellermann, O. and J. Peters-Fransen,The Strong Metric Dimension of Graph and Digraph, Discrete Applied Mathematics155(2007), 356-364.
[9] Seb¨o, A. and E. Tannier, On Metric Generators of Graph, Mathematics and Operations Research29(2)(2004), 383-393.
[10] Yi, E.,On Strong Metric Dimension Graph and Their Complements, Acta Mathematica Sinica