Informasi Dokumen
- Penulis:
- Drs. Setiawan, M.Pd
- Sekolah: DIREKTORAT PENINGKATAN MUTU PENDIDIK DAN TENAGA KEPENDIDIKAN
- Mata Pelajaran: Matematika
- Topik: BAHAN AJAR DIKLAT PENGEMBANG MATEMATIKA SMA JENJANG DASAR
- Tipe: Bahan Ajar
Ringkasan Dokumen
I. Pendahuluan
Bab I menggariskan latar belakang modul Diklat Pengembangan Matematika SMA Jenjang Dasar ini, yang menekankan keperluan peningkatan mutu pengajaran Matematika di SMA berlandaskan Standar Nasional Pendidikan (SNP) 2005. Modul ini bertujuan untuk meningkatkan kompetensi guru dalam mengajar relasi, fungsi, persamaan dan pertidaksamaan, khususnya dalam fungsi aljabar, eksponen dan logaritma—topik yang sering menimbulkan kesulitan di kalangan pelajar. Sasarannya adalah peserta Diklat MGMP Matematika SMA dan guru Matematika SMA secara umum. Ruang lingkup modul merangkumi kaidah aljabar asas, persamaan dan pertidaksamaan aljabar serta fungsi eksponen dan logaritma, dan relasi dan fungsi aljabar, eksponen dan logaritma. Modul ini dirancang untuk pembelajaran kendiri dan diskusi kelompok, dengan soal latihan dan kunci jawapan untuk penilaian diri.
1.1 Latar Belakang
Bahagian ini membincangkan jurang antara harapan SNP 2005 untuk peningkatan pengajaran Matematika dan realiti di lapangan. Ia menyerlahkan cabaran dalam mengatasi persepsi negatif terhadap Matematika sebagai subjek yang sukar dan tidak menarik. Modul ini dibentangkan sebagai sebahagian daripada usaha menangani cabaran ini melalui peningkatan kemahiran guru.
1.2 Tujuan Penulisan Modul
Tujuan utama modul ini adalah untuk meningkatkan kompetensi dan pengetahuan guru dalam melaksanakan tugas pengajaran Matematika. Ia juga bertujuan untuk menyediakan bahan diskusi dalam forum MGMP Matematika SMA, khususnya berkaitan dengan topik relasi, fungsi, persamaan dan pertidaksamaan yang sering menjadi penghalang pembelajaran.
1.3 Sasaran
Sasaran utama modul ini ialah peserta Diklat Pemberdayaan MGMP Matematika SMA dan guru-guru Matematika SMA secara amnya. Ini menunjukkan fokus modul terhadap peningkatan profesionalisme guru dalam bidang Matematika.
1.4 Ruang Lingkup
Ruang lingkup modul meliputi kaedah asas aljabar yang menjadi asas kepada aljabar lanjutan, persamaan dan ketaksamaan aljabar dan fungsi eksponen, serta relasi dan fungsi aljabar termasuk fungsi eksponen dan logaritma. Ini menunjukkan pendekatan holistik modul terhadap topik-topik yang berkaitan.
1.5 Penggunaan Modul
Modul ini digalakkan digunakan melalui pembelajaran kendiri diikuti dengan refleksi diri melalui latihan-latihan yang disediakan. Guru digalakkan berdiskusi dalam forum MGMP sekiranya terdapat sebarang keraguan atau untuk berkongsi pengalaman. Ini mencerminkan pendekatan kolaboratif dalam peningkatan profesionalisme guru.
II. Persamaan dan Pertidaksamaan
Bab II menyelami topik persamaan dan pertidaksamaan, bermula dengan persamaan kuadratik, persamaan irasional, persamaan nilai mutlak, persamaan eksponen dan persamaan logaritma. Setiap subtopik dihuraikan dengan contoh-contoh penyelesaian dan latihan untuk mengukuhkan pemahaman. Bab ini kemudiannya meneroka pertidaksamaan linear satu pembolehubah, pertidaksamaan pecahan, pertidaksamaan irasional, pertidaksamaan nilai mutlak, pertidaksamaan eksponen dan pertidaksamaan logaritma. Setiap jenis pertidaksamaan dijelaskan dengan kaedah penyelesaian dan contoh-contoh.
2.1 Persamaan
Bahagian ini bermula dengan contoh-contoh masalah kontekstual yang membawa kepada model matematik persamaan kuadratik. Ia menerangkan penyelesaian persamaan kuadratik melalui pemfaktoran, melengkapkan kuasa dua sempurna, dan menggunakan formula abc. Contoh-contoh penyelesaian disertakan untuk setiap kaedah. Ia kemudiannya meneruskan kepada persamaan irasional, persamaan nilai mutlak, persamaan eksponen dan persamaan logaritma, setiap satunya diiringi dengan penjelasan dan contoh penyelesaian.
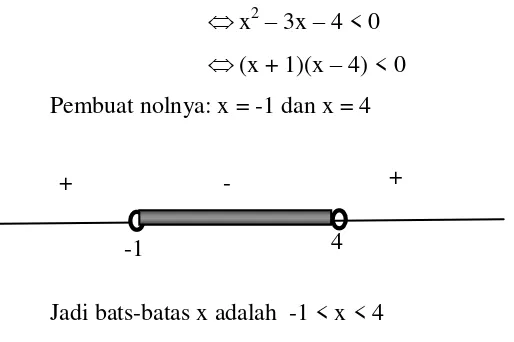
2.2 Pertidaksamaan
Bahagian ini bermula dengan asas pertidaksamaan, aksioma-aksioma dan teorema-teorema yang berkaitan. Ia meneroka pertidaksamaan linear satu pembolehubah, pertidaksamaan pecahan, pertidaksamaan irasional, pertidaksamaan nilai mutlak, pertidaksamaan eksponen, dan pertidaksamaan logaritma secara terperinci, disertakan dengan penjelasan konsep dan kaedah penyelesaian, serta contoh-contoh penyelesaian untuk setiap jenis pertidaksamaan.
III. Relasi dan Fungsi
Bab III memfokuskan kepada konsep relasi dan fungsi. Ia bermula dengan definisi relasi, diikuti dengan penerangan mengenai relasi determinatif, cara-cara penyajian relasi (diagram panah, himpunan pasangan tertib, dan diagram Cartesius), relasi songsang dan komposisi relasi. Bahagian fungsi pula menerangkan pengertian fungsi, fungsi surjektif, injektif dan bijektif, fungsi-fungsi khas, fungsi komposit, fungsi songsang, penentuan domain dan kodomain bagi fungsi songsang dan fungsi songsang bagi fungsi komposit.
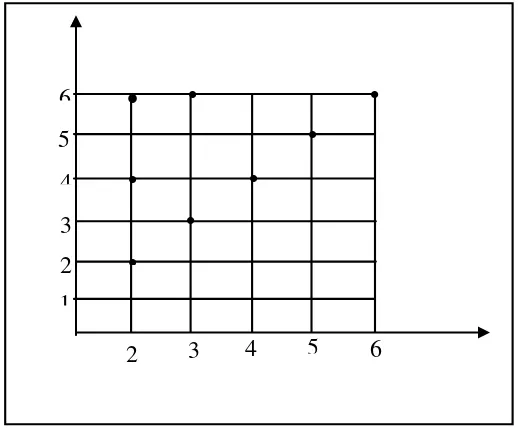
3.1 Relasi
Bahagian ini memperkenalkan konsep relasi melalui contoh-contoh kontekstual. Ia menjelaskan pelbagai jenis relasi, termasuk relasi binari, terner, kuarterner dan poliadik. Ia kemudiannya menerangkan relasi determinatif dan pelbagai kaedah untuk mewakili relasi, iaitu diagram panah, himpunan pasangan tertib dan diagram Cartesius. Konsep relasi songsang dan komposisi relasi turut dibincangkan.
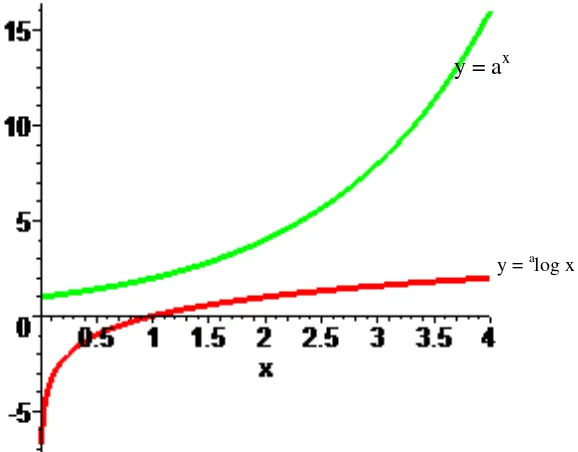
3.2 Fungsi
Bahagian ini mentakrifkan fungsi dan menerangkan jenis-jenis fungsi seperti fungsi surjektif, injektif dan bijektif. Ia juga membincangkan fungsi-fungsi khas, fungsi komposit, fungsi songsang, cara menentukan domain dan kodomain bagi fungsi songsang dan fungsi songsang bagi fungsi komposit. Contoh-contoh dan ilustrasi diberikan untuk menjelaskan setiap konsep.
IV. Kesimpulan
Bab IV merumuskan isi kandungan modul, menekankan pentingnya penguasaan konsep-konsep asas dalam aljabar, persamaan dan pertidaksamaan, relasi dan fungsi untuk kejayaan dalam pengajaran Matematika di peringkat SMA. Ia juga mencadangkan strategi pengajaran yang sesuai untuk memastikan pemahaman pelajar yang mantap.