I. Pengujian Hipotesis Satu Rata-rata a)
Bagian ini membahas pengujian hipotesis satu rata-rata pada sampel besar (n > 30) menggunakan distribusi Z. Materi ini relevan dengan tujuan pembelajaran statistik inferensial, khususnya dalam pengambilan keputusan berdasarkan data sampel. Mahasiswa diharapkan mampu memahami konsep pengujian hipotesis, merumuskan hipotesis nol dan alternatif, menentukan taraf signifikansi, memilih uji statistik yang tepat, dan menginterpretasikan hasil uji. Pengetahuan ini penting untuk menganalisis data kuantitatif dalam berbagai bidang studi, termasuk pendidikan, psikologi, dan ekonomi. Contoh soal yang diberikan memperlihatkan aplikasi praktis dalam konteks industri (pabrik susu) dan pengambilan sampel acak dari tabel angka acak, memperkaya pemahaman mahasiswa dengan penerapan di dunia nyata.
1.1 Formulasi Hipotesis
Sub-bab ini menjelaskan tiga jenis formulasi hipotesis yang mungkin: uji satu sisi kanan (H1: μ > μ0), uji satu sisi kiri (H1: μ < μ0), dan uji dua sisi (H1: μ ≠ μ0). Mahasiswa diajarkan untuk memilih formulasi yang sesuai dengan pertanyaan penelitian. Pemahaman tentang hipotesis nol (H0) dan alternatif (H1) merupakan dasar dalam pengujian hipotesis. Kemampuan untuk merumuskan hipotesis yang tepat sangat penting dalam penelitian karena menentukan arah pengujian dan interpretasi hasilnya. Hal ini melatih keterampilan berpikir kritis dan kemampuan memecahkan masalah secara sistematis.
1.2 Penentuan Nilai α dan Z tabel
Bagian ini menjelaskan bagaimana menentukan taraf signifikansi (α) dan nilai kritis Z dari tabel distribusi Z berdasarkan α yang telah ditentukan. Pemilihan α bergantung pada tingkat kepercayaan yang diinginkan dalam penelitian. Mahasiswa belajar untuk menghubungkan α dengan tingkat kesalahan Tipe I (menolak H0 saat H0 benar). Memahami tabel distribusi Z dan cara penggunaannya merupakan keterampilan penting dalam statistik inferensial. Ini mengasah kemampuan numerik dan pemahaman tentang probabilitas dalam konteks pengujian hipotesis.
1.3 Kriteria Pengujian
Sub-bab ini menjelaskan kriteria penerimaan dan penolakan H0 berdasarkan nilai statistik uji (Z hitung) dan nilai kritis Z. Mahasiswa mempelajari bagaimana membandingkan Z hitung dengan Z tabel untuk membuat keputusan. Ini memperkuat pemahaman tentang daerah kritis dan hubungannya dengan probabilitas membuat kesalahan dalam pengambilan keputusan statistik. Keterampilan interpretasi hasil uji statistik menjadi fokus utama di sini, mengasah kemampuan mahasiswa untuk mengambil kesimpulan yang valid berdasarkan bukti empiris.
1.4 Uji Statistik
Sub-bab ini memaparkan rumus uji statistik Z untuk dua kondisi: ketika simpangan baku populasi diketahui dan ketika simpangan baku populasi tidak diketahui (menggunakan simpangan baku sampel sebagai penduga). Mahasiswa perlu memahami perbedaan perhitungan dan implikasinya. Ini memperkuat pemahaman konseptual tentang estimasi parameter dan penggunaan statistik sampel untuk menguji hipotesis tentang parameter populasi. Kemampuan menghitung dan menganalisis data secara akurat menjadi penting dalam tahap ini.
1.5 Kesimpulan
Bagian ini menekankan pentingnya membuat kesimpulan yang tepat berdasarkan hasil uji statistik. Mahasiswa belajar untuk menghubungkan keputusan statistik (menerima atau menolak H0) dengan jawaban atas pertanyaan penelitian. Ini menekankan pentingnya interpretasi hasil yang benar dan menghindari generalisasi yang berlebihan. Keterampilan komunikasi ilmiah menjadi penting di sini, karena mahasiswa perlu menyajikan kesimpulan dengan jelas dan ringkas.
II. Pengujian Hipotesis Satu Rata-rata b)
Bagian ini melanjutkan pembahasan pengujian hipotesis satu rata-rata, namun kali ini untuk sampel kecil (n ≤ 30), menggunakan distribusi t. Perbedaan utama dengan bagian sebelumnya terletak pada penggunaan distribusi t Student, yang lebih tepat digunakan ketika ukuran sampel kecil dan/atau simpangan baku populasi tidak diketahui. Materi ini membangun pemahaman mahasiswa tentang pilihan uji statistik yang tepat berdasarkan karakteristik data. Contoh soal yang beragam, termasuk analisis data motivasi kerja dan berat kotor keranjang ampel, menunjukkan fleksibilitas aplikasi pengujian hipotesis ini dalam berbagai konteks.
1.1 Formulasi Hipotesis
Mirip dengan pengujian sampel besar, sub-bab ini membahas formulasi hipotesis nol dan alternatif, namun dalam konteks sampel kecil. Mahasiswa perlu memahami bahwa prinsip dasar formulasi hipotesis tetap sama, terlepas dari ukuran sampel. Kemampuan untuk secara tepat mendefinisikan hipotesis nol dan alternatif sesuai dengan pertanyaan penelitian tetap merupakan keterampilan yang sangat penting. Ini memperkuat dasar pemahaman konseptual tentang pengujian hipotesis.
1.2 Penentuan Nilai α dan t tabel
Sub-bab ini menjelaskan cara menentukan taraf signifikansi (α) dan nilai kritis t dari tabel distribusi t. Perbedaan utama dengan bagian sebelumnya adalah penggunaan derajat bebas (df = n-1) dalam mencari nilai kritis t. Mahasiswa belajar untuk menghubungkan derajat bebas dengan ukuran sampel dan memahami perbedaan distribusi t untuk ukuran sampel yang berbeda. Ini menguji pemahaman mahasiswa tentang distribusi probabilitas dan pengaplikasiannya dalam konteks statistik inferensial.
1.3 Kriteria Pengujian
Sub-bab ini menjabarkan kriteria penerimaan dan penolakan H0 menggunakan nilai t hitung dan t tabel. Mahasiswa belajar untuk membandingkan nilai t hitung dengan t tabel untuk membuat keputusan. Ini menguji pemahaman mahasiswa tentang daerah kritis dan pengambilan keputusan dalam konteks pengujian hipotesis dengan distribusi t. Keterampilan interpretasi hasil uji statistik menjadi fokus utama, memastikan mahasiswa dapat menarik kesimpulan yang tepat berdasarkan bukti statistik.
1.4 Uji Statistik
Bagian ini memberikan rumus uji statistik t untuk dua skenario: ketika simpangan baku populasi diketahui dan ketika tidak diketahui. Mahasiswa memahami perbedaan dalam perhitungan dan implikasinya. Ini menguji kemampuan mahasiswa untuk memilih rumus yang sesuai dan melakukan perhitungan yang benar. Keterampilan dalam melakukan perhitungan statistik dan menginterpretasikan hasilnya sangatlah penting.
1.5 Kesimpulan
Sub-bab ini menitikberatkan pada pentingnya kesimpulan yang tepat dan akurat berdasarkan hasil uji t. Mahasiswa menghubungkan keputusan statistik (menerima atau menolak H0) dengan jawaban pertanyaan penelitian. Ini melatih mahasiswa dalam keterampilan komunikasi ilmiah yang baik dan kemampuan menyajikan kesimpulan secara ringkas dan jelas.
III. Pengujian Hipotesis Beda Dua Rata-rata a)
Bagian ini membahas pengujian hipotesis untuk membandingkan dua rata-rata populasi pada sampel besar (n>30) menggunakan uji Z. Materi ini membangun pemahaman mahasiswa tentang pengujian hipotesis untuk data komparatif. Mahasiswa perlu memahami perbedaan antara pengujian satu rata-rata dan dua rata-rata. Contoh soal yang diberikan menggunakan data jam kerja buruh di dua daerah yang berbeda, membantu mahasiswa memahami aplikasi praktis dalam konteks sosial ekonomi.
2.1 - 2.5
Sub-bab 2.1 sampai 2.5 (Formulasi Hipotesis, Penentuan Nilai α dan Z tabel, Kriteria Pengujian, Uji Statistik, dan Kesimpulan) mengikuti struktur yang sama dengan bagian 1, namun diadaptasi untuk membandingkan dua rata-rata. Mahasiswa diajarkan untuk menghitung statistik uji Z untuk membandingkan dua rata-rata populasi, baik ketika varians populasi diketahui maupun tidak diketahui. Mereka juga belajar menginterpretasikan hasil uji untuk menentukan apakah terdapat perbedaan yang signifikan antara dua rata-rata tersebut. Contoh soal yang diberikan membantu mahasiswa dalam memahami langkah-langkah perhitungan dan interpretasi hasil.
IV. Pengujian Hipotesis Beda Dua Rata-rata b)
Bagian ini membahas pengujian hipotesis beda dua rata-rata untuk sampel kecil (n ≤ 30) menggunakan uji t. Ini melanjutkan materi pengujian komparatif dengan mempertimbangkan situasi ketika ukuran sampel kecil. Contoh soal yang diberikan, seperti membandingkan metode pembelajaran dan prestasi akademik mahasiswa, menunjukkan aplikasi dalam konteks pendidikan.
2.1 - 2.5
Struktur sub-bab 2.1 sampai 2.5 (Formulasi Hipotesis, Penentuan Nilai α dan t tabel, Kriteria Pengujian, Uji Statistik, dan Kesimpulan) serupa dengan bagian sebelumnya, tetapi menggunakan distribusi t dan derajat bebas yang sesuai. Mahasiswa belajar untuk membedakan antara uji t untuk data berpasangan dan tidak berpasangan. Contoh soal yang beragam memberikan kesempatan bagi mahasiswa untuk mempraktikkan keterampilan mereka dalam memilih uji statistik yang tepat dan menginterpretasikan hasilnya dalam berbagai konteks penelitian.
V. Pengujian Hipotesis Satu Proporsi
Bagian ini menjelaskan pengujian hipotesis untuk satu proporsi populasi. Materi ini memperkenalkan mahasiswa pada pengujian hipotesis untuk data kategorikal. Contoh soal yang diberikan fokus pada proporsi rumah dengan telepon di suatu kota, memberikan konteks yang relevan bagi mahasiswa.
3.1 - 3.4
Sub-bab 3.1 sampai 3.4 (Formulasi Hipotesis, Penentuan Nilai α dan Z tabel, Kriteria Pengujian, Uji Statistik, dan Kesimpulan) mengikuti struktur yang sudah dijelaskan sebelumnya, namun diadaptasi untuk pengujian proporsi. Mahasiswa belajar menghitung statistik uji Z untuk proporsi dan menginterpretasikan hasilnya untuk menentukan apakah proporsi sampel berbeda secara signifikan dari proporsi populasi yang telah ditetapkan. Mereka juga belajar bagaimana mengaplikasikan berbagai jenis hipotesis alternatif (satu sisi dan dua sisi).
VI. Pengujian Hipotesis Beda Dua Proporsi
Bagian ini membahas pengujian hipotesis untuk membandingkan dua proporsi populasi. Materi ini merupakan perluasan dari pengujian satu proporsi, mengajarkan mahasiswa untuk membandingkan dua proporsi dari kelompok yang berbeda. Contoh soal mengenai persetujuan terhadap pembangunan gedung serbaguna di dua wilayah berbeda, memberikan konteks penerapan yang bermakna.
4.1 - 4.4
Sub-bab 4.1 sampai 4.4 (Formulasi Hipotesis, Penentuan Nilai α dan Z tabel, Kriteria Pengujian, Uji Statistik, dan Kesimpulan) menjelaskan langkah-langkah pengujian hipotesis untuk membandingkan dua proporsi. Mahasiswa diajarkan menghitung statistik uji Z dan menginterpretasikan hasilnya untuk menentukan apakah terdapat perbedaan yang signifikan antara dua proporsi tersebut. Contoh soal yang diberikan membantu mahasiswa mempraktikkan keterampilan perhitungan dan interpretasi hasil.
VII. Pengujian Hipotesis dengan F (Rasio Variansi)
Bagian ini memperkenalkan pengujian hipotesis menggunakan distribusi F, khususnya untuk membandingkan varians dan rata-rata dari beberapa kelompok. Ini memperkenalkan teknik ANOVA (Analysis of Variance) yang penting dalam statistika. Materi ini relevan dengan tujuan pembelajaran statistika multivariat dan analisis data komparatif yang lebih kompleks.
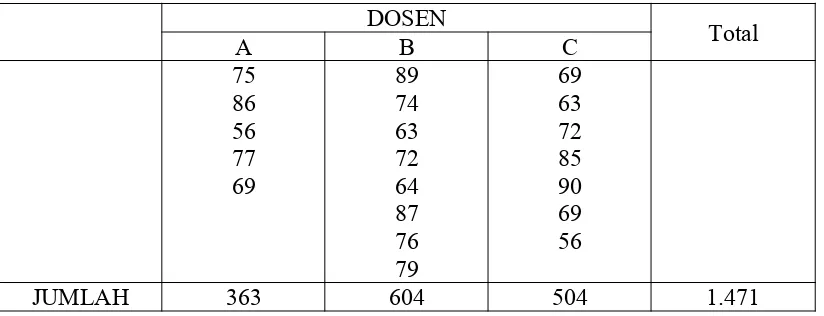
5.1 Pengujian Hipotesis Beda Tiga Rata-rata atau Lebih (ANOVA)
Sub-bab ini menjelaskan pengujian ANOVA satu arah, dua arah tanpa interaksi, dan dua arah dengan interaksi. Mahasiswa belajar tentang berbagai model ANOVA dan bagaimana memilih model yang tepat berdasarkan desain penelitian. Contoh soal yang diberikan, seperti membandingkan efektivitas beberapa jenis obat dan hasil panen berbagai varietas tanaman, menunjukkan aplikasi ANOVA dalam berbagai konteks penelitian. Sub-bab ini membutuhkan pemahaman mendalam tentang konsep varians, derajat bebas, dan tabel ANOVA.
5.2 Pengujian Hipotesis Beda Dua Varians
Sub-bab ini menjelaskan cara menguji kesamaan dua varians populasi menggunakan uji F. Mahasiswa belajar menghitung statistik uji F dan menentukan apakah terdapat perbedaan yang signifikan antara dua varians. Contoh soal yang diberikan memperlihatkan aplikasi uji F dalam membandingkan varians dua metode pembelajaran. Sub-bab ini menekankan pentingnya memahami asumsi uji F, seperti normalitas data dan kemerdekaan sampel.
VIII. Pengujian Hipotesis dengan χ²
Bagian ini membahas pengujian hipotesis menggunakan distribusi chi-square (χ²), yang terutama digunakan untuk data kategorikal. Materi ini memperluas pemahaman mahasiswa tentang pengujian hipotesis untuk berbagai jenis data. Contoh soal yang diberikan membahas pengujian proporsi produk rusak dan sikap karyawan terhadap kondisi kerja, memberikan ilustrasi aplikasi dalam konteks bisnis dan sumber daya manusia.
6.1 Pengujian Hipotesis Beda Tiga Proporsi atau Lebih
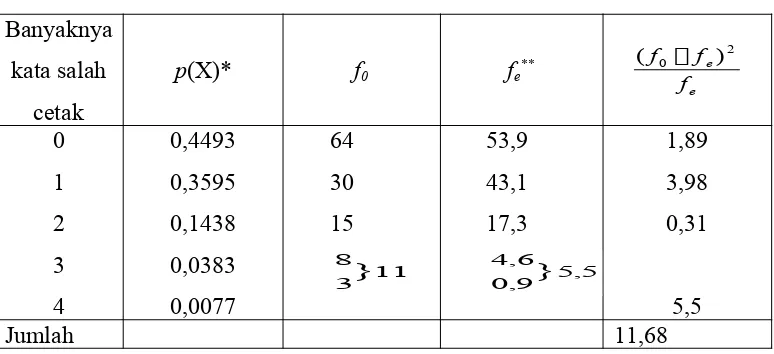
Sub-bab ini menjelaskan pengujian χ² untuk membandingkan tiga atau lebih proporsi populasi. Mahasiswa belajar menghitung statistik uji χ² dan menggunakan tabel χ² untuk menentukan signifikansi perbedaan proporsi. Contoh soal membahas pengujian kesamaan proporsi barang rusak selama beberapa hari, menunjukkan aplikasi dalam konteks pengendalian kualitas. Sub-bab ini menekankan pentingnya memahami frekuensi observasi dan harapan dalam pengujian χ².
6.2 Pengujian Hipotesis Independensi
Sub-bab ini menjelaskan bagaimana menggunakan uji χ² untuk menguji independensi antara dua variabel kategorikal. Mahasiswa belajar untuk membuat tabel kontingensi dan menghitung statistik uji χ² untuk menguji hipotesis independensi. Contoh soal yang diberikan memberikan ilustrasi penggunaan uji χ² dalam menguji hubungan antara variabel-variabel kategorikal. Sub-bab ini menekankan pentingnya memahami konsep independensi dan bagaimana uji χ² dapat digunakan untuk mengujinya.