Wahyuni Eka Sari1), Oyas Wahyunggoro2) 1) Teknologi Informasi,Politeknik Negeri Samarinda-Samarinda 2) Teknik Elektro dan Teknologi Informasi,Universitas Gadjah Mada-Yogyakarta
[email protected] 1), [email protected]2)
Abstrak
Salah satu bagian penanganan BMS adalah mengestimasi kapasitas baterai (State of Charge). Kapasitas baterai merupakan variabel yang tidak dapat diukur secara langsung melalui pengambilan data. Metode yang tepat diperlukan untuk melakukan estimasi kapasitas baterai. Salah satu metode yang digunakan untuk estimasi kapasitas baterai adalah sistem inferensi fuzzy. Pada penelitian ini dilakukan metode estimasi menggunakan Interval Type 2 Fuzzy Logic System dengan ANFIS (Adaptive Neuro Fuzzy Inference System) sebagai dasar untuk membangun fungsi keanggotaan dan basis aturan. Perbedaan daerah ketidakpastian digunakan untuk mengetahui model sistem fuzzy tipe 2 yang paling tepat berdasarkan nilai RMSE terkecil. Dua metode type reducer yaitu Enhanced Iterative Algorithm with Stop Condition (EIASC) dan Enhanced Opposite Direction Search (EODS) digunakan pada penelitian ini yang bertujuan untuk mengetahui hasil estimasi kapasitas baterai yang paling tepat. Dua jenis dataset digunakan untuk mengetahui kinerja metode yang diusulkan berdasarkan MSE, RMSE dan MAPE. Nilai RMSE terkecil diperoleh pada metode IT2FLS dengan nilai daerah ketidakpastian C 0,04 pada dataset beban konstan dan IT2FLS dengan nilai C 0,1 pada dataset beban bervariasi. Berdasarkan pengujian yang dilakukan terhadap tiga metode yaitu T1FLS, IT2FLS EIASC dan IT2FLS EODS, metode yang menghasilkan nilai RMSE terkecil adalah metode IT2FLS EIASC dengan nilai RMSE 0,033.
Kata Kunci – IT2FLS; baterai; BMS; SOC
1. PENDAHULUAN
Efisiensi energi dan permasalahan lingkungan merupakan isu yang hangat diperbincangkan di seluruh dunia. Demi mendukung gerakan efisiensi energi, Electric Vehicles (EV) atau kendaraan listrik merupakan salah satu solusi yang luar biasa dan menjanjikan. Salah satu jenis baterai yang banyak digunakan pada sistem EV adalah baterai Lithium Polymer (LiPo). Baterai LiPo telah banyak diadopsi dalam sistem EV karena memiliki kerapatan daya, low self-discharge, efisiensi energi yang tinggi dan tahan lama [1]. Namun proses charging yang lama (Over Charge) dan kurangnya proses charging (Over Discharge) dapat mengurangi kinerja baterai dalam menyimpan energi. Kondisi Charge dan Over-Discharge yang dapat mengakibatkan kerusakan irreversible (berubah-ubah) pada baterai LiPo dapat diidentifikasi dengan variabel State of Charge (SOC). Variabel SOC merupakan salah satu variabel yang tidak dapat dilakukan pengukuran secara langsung seperti pada variabel tegangan atau arus. Sehingga diperlukan metode yang tepat untuk mendapatkan nilai SOC yang optimal.
Terdapat berbagai macam metode untuk mengestimasi SOC. Metode Coulomb Counting (Ampere-Hour Integral) adalah teknik yang paling
banyak digunakan karena sederhana dan mudah diimplementasikan [2], [3]. Namun akurasi Coulomb Counting sangat tergantung pada keakuratan pengukuran arus dan algoritme inisialisasi. Tanpa mekanisme koreksi, kesalahan perhitungan metode ini akan diakumulasikan.
Pendekatan metode cerdas yang diterapkan untuk merancang model Black Box untuk estimasi SOC seperti jaringan saraf tiruan model [4][5][6], Fuzzy Logic Model [7][8][9] dan Support Vector Machine (SVM) [10][11][12]. Jaringan saraf tiruan dan SVM dapat memberikan perkiraan SOC yang cukup baik, jika dataset yang digunakan untuk pelatihan merupakan data yang tepat, karena fungsi yang kuat untuk pendekatan pada fungsi nonlinear. Namun, proses pelatihan membutuhkan komputasi yang berat dan beresiko overfitting. Model kinerja sangat bergantung pada jumlah dan kualitas data pelatihan yang dipilih. Berbeda dengan metode jaringan saraf tiruan dan SVM, metode estimasi fuzzy tidak menggunakan data latih sehingga komputasi menjadi lebih ringan.
54 beberapa tahun terakhir, fuzzy type 2 telah menarik
minat penelitian karena kemampuannya untuk memodelkan ketidakpastian dari himpunan fuzzy. Dibandingkan dengan himpunan fuzzy tipe-1 (T1FS), himpunan fuzzy tipe-2 (T2FS) lebih baik dalam merepresentasikan elemen himpunan fuzzy diwakili oleh sejumlah nilai fuzzy bukan nilai crisp. Perbedaan utama antara T1FLSs dan T2FLSs adalah T1FS memiliki dua fungsi dimensi dan T2FS memiliki derajat kebebasan (degree of freedom).
Penelitian ini membahas estimasi SOC pada baterai LiPo menggunakan IT2FLS dan menerapkan dua jenis type-reducer yang berbeda yaitu Enhanced Iterative Algorithm with Stop Condition (EIASC) dan Enhanced Opposite Direction Search (EODS). Dasar aturan fuzzy yang tepat dieksekusi menggunakan metode Adaptive Neuro Fuzzy Inference Systems (ANFIS). Hasil dari penelitian akan dibandingkan antara T1FLS, IT2FLS yang menggunakan EIASC dengan IT2FLS yang menggunakan EODS sebagai algoritme type-reducer sehingga dapat diketahui salah satu metode yang menghasilkan estimasi paling akurat.
Pada penelitian ini dibahas mengenai penelitian terkait estimasi state of charge pada bagian II. Pada bagian III dijelaskan perancangan estimasi dan bagian IV dijelaskan hasil serta pembahasan
.
2. METODE
2.1 Metode Matematis untuk Estimasi SOC
Metode estimasi SOC yang paling mudah adalah metode Coulomb Counting. Estimasi SOC secara online menggunakan Microcontroller dengan metode Coulomb Counting [2] menghasilkan akurasi antara 3 - 4%. Pengujian dilakukan terhadap kondisi konstan dan kondisi dinamis serta cycle charge-discharge yang berbeda terhadap baterai Lead Acid. Penelitian lain tentang peningkatan metode Coulomb Counting pada proses charging dan discharging terhadap baterai Lithium Ion [3]. Error estimasi dapat direduksi hingga 1,08% pada operasi cycle berikutnya. Terdapat 5 cycle yang berbeda untuk mengetahui karakteristik SOC.
Estimasi SOC juga dapat dilakukan dengan metode lain seperti Kalman Filter (KF). Penelitian menggunakan metode Improved Extended Kalman Filter (IEKF) untuk estimasi SOC [13] pada baterai Li-ion mampu mengurangi nilai error sampai 1,5%. Proses komputasi menjadi lebih cepat dengan akurasi
yang sangat baik. Algoritme KF telah mengalami banyak perkembangan. Salah satunya adalah Fading Kalman Filter (FDF) [14] pada baterai LiFePO4 (Lithium Iron Phosphate). Nilai OCV digunakan untuk mengestimasi hubungan linier dua stage filtering. Estimasi parameter baterai digunakan algoritme Recursive Least Square. Optimisasi fading factor menggunakan algoritme genetika dan Fading Kalman Filter (FKF). Error yang dihasilkan antara 3% sampai dengan 9%.
Perkembangan metode estimasi yang termasuk hard computing selain Coulomb Counting adalah OCV. Terdapat dua belas model OCV [15] yang dibandingkan untuk mengetahui hubungan OCV dengan SOC serta membahas time complexity dari kedua belas model OCV. Error maksimal yang dihasilkan menggunakan metode OCV adalah 10% dan error minimal adalah 2%.
Penelitan lain tentang metode OCV-SOC [16] digunakan untuk mengetahui pengaruh temperature terhadap kapasitas baterai. Sehingga penelitian ini membahas tentang estimasi SOC berbasis model suhu. Algoritme KF digunakan untuk proses tuning parameter pada setiap sampling. Kapasitas baterai aktif antara 25% - 85%. Percobaan didasarkan pada temperature 0oC, 10oC dan 40oC. Berdasarkan ketiga eksperimen, nilai RMSE paling besar 13% dan paling kecil 2%.
Selanjutnya penelitian yang membahas gabungan metode OCV dengan algoritme KF [17]. Hubungan antara OCV-SOC pada setiap baterai berbeda-beda sehingga hubungan antara SOC-OCV perlu dilakukan pengukuran untuk ketepatan nilai SOC. Peningkatan performa dari algoritme digunakan Extended Kalman Filter (EKF) untuk mengurangi noise. Hasil estimasi menggunakan EKF dibandingkan dengan metode ampere-hour counting. Nilai Error dari estimasi EKF sekitar 5%. Berbagai macam metode estimasi yang digunakan untuk mengindentifikasi kapasitas baterai tidak menutup kemungkinan adanya metode lain untuk memudahkan proses estimasi. Baterai yang memiliki karakteristik non-linier tidak selamanya dapat dilakukan proses estimasi dengan metode matematis.
2.2 Metode Kecerdasan Buatan untuk Estimasi SOC
55
kapasitas baterai lithium ion polymer (LiP). Pada penelitian ini metode Coulomb Counting digunakan sebagai pembanding dari metode SVM. Proses komputasi SVM dilakukan pada dua hardware yang berbeda. Hardware pertama mampu melakukan eksekusi selama 54 ms. Hardware kedua membutuhkan waktu 26 ms. SVM mampu mengeksekusi 4000 iterasi. Root mean square Error yang dihasilkan 2,5% dan maksimum error +13%.
Proses estimasi selanjutnya pada baterai LiFePO4 [11] menggunakan teknik SVM dengan input voltage, current dan temperature. Model prediksi SVM menggunakan optimisasi support vector regression menghasilkan koefisien R2 0,97. Error yang dihasilkan 3%. Pada Estimasi SOC berbasis SVM[10] untuk proses regresi dengan optimisasi pencarian berganda. Metode SVM dibandingkan dengan metode Artificial Neural Network. ANN yang digunakan adalah RBFNN. Error maksimal dari metode SVM adalah 4%. Penelitian lain yang menggunakan metode kecerdasan buatan adalah estimasi SOC menggunakan Neural Network [5]. Perbandingan metode estimasi state of available capacity dilakukan dengan metode backpropagation dan eksperimen data. Tiga dataset diuji coba pada penelitian ini. Error tertinggi yang dihasilkan menggunakan parameter Average Relative Percentage Error (ARPE) sekitar 2%. Penggunaan NN untuk estimasi menghasilkan akurasi yang lebih baik dari estimasi secara manual.
Terdapat penelitian lain yang juga menggunakan neural network [6] dan neuro controller. Algoritme yang digunakan untuk penyesuaian struktur neural adalah Recursive Least Square. Sedangkan neuro controller menggunakan algoritme backpropagation. Error yang dihasilkan maksimal adalah 1%. Estimasi SOC menggunakan baterai LiFePO4 berbasis aturan fuzzy [18]. Proses filter menggunakan model fuzzy menghasilkan akurasi SOC 95% dengan fuzzy model Sugeno. Kondisi baterai full 75% dengan proses charging selama 30 menit dan maksimum error 5.
2.3 Metode Interval Type-2 Fuzzy untuk Estimasi SOC
Type-reducer merupakan bagian penting dari IT2FLS. Pada bagian ini, himpunan fuzzy tipe 2 diubah menjadi himpunan tipe 1 sehingga mudah dalam proses defuzzifikasi. Terdapat berbagai macam algoritme untuk type-reducer. Salah satu algoritme yang
digunakan adalah Karnik Mendel [19]. Terdapat banyak pengembangan algoritme yang lahir dari algoritme Karnik Mendel (KM).
Iterative Algoritme with Stop Condition (IASC) merupakan algoritme pengembangan dari algoritme KM. IASC dibangun sebagai solusi alternatif untuk menghitung generalized centroid dari himpunan fuzzy interval type 2. Pada penelitian ini, IASC dibandingkan dengan Enhanced Karnik Mendel (EKM) [20] untuk mengetahui kecepatan komputasi dan tingkat presisi. Hasil eksperimen membuktikan bahwa IASC menghasilkan waktu komputasi yang lebih kecil sekitar 39% dibandingkan EKM. Namun untuk mendapatkan hasil yang lebih objektif, diperlukan analisis terhadap hardware yang digunakan untuk menjalankan algoritme.
Penelitian lain membandingkan algoritme pengembangan dari karnik mendel yaitu EIASC dengan EKM, EKMANI, dan IASC. Berdasarkan eksperimen yang telah dibuat, algoritme EIASC [21] memiliki waktu komputasi yang lebih cepat 50% dengan N ≤ 100. Kemudian pada penelitian lain, dilakukan perbandingan kinerja ketiga algoritme type-reducer yaitu karnik mendel, EKM dan EIASC. Waktu operasi algoritme EKM [22] lebih kecil 30% dibandingkan KM. EIASC lebih kecil dari EKM. Fungsi triangular dan Gaussian digunakan pada eksperimen. Fungsi triangular menghasilkan komputasi yang lebih cepat dibandingkan fungsi Gaussian.
Perkembangan penelitian type-reducer memunculkan metode baru yaitu Enhanced Opposite Direction Search (EODS) [23]. Metode ini merupakan pengembangan dari algoritme KM. EODS ini mampu menghasilkan komputasi yang lebih cepat dibandingkan EIASC. Berdasarkan keempat penelitian sebelumnya, pada penelitian ini digunakan dua algoritme terbaru yaitu EIASC dan EODS.
2.4 Alur Perancangan Sistem
56
Studi Lite rature Identifikasi m asalah
Perancangan
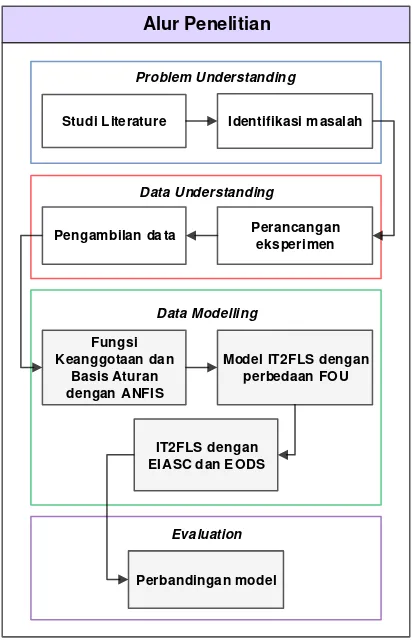
Gambar 1. Alur Penelitian Estimasi SOC
Pada penelitian ini dilakukan proses pemodelan baterai menggunakan rangkaian ekuivalen kemudian dilakukan identifikasi parameter dari rangkaian ekuivalen tersebut menggunakan algoritme adaptif. Setelah parameter diketahui, dilakukan proses estimasi SOC berdasarkan pemodelan tersebut menggunakan metode Interval Type 2 Fuzzy Logic System. Pada bagian ini dijelaskan tentang gambaran umum penelitian yang dilakukan berdasarkan Gambar diagram blok 2
Gambar 2. Diagram Blok Penelitian
Berdasarkan Gambar 2, algoritme adaptif yang digunakan pada penelitian ini yaitu: sistem fuzzy tipe 1 (T1FLS) dan Interval Type 2 Fuzzy Logic System (IT2FLS) sedangkan metode yang dijadikan acuan nilai SOC adalah Coulomb Counting
2.5 Pemodelan Interval Type-2 Fuzzy Logic System
Estimasi SOC menggunakan IT2FLS dibentuk berdasarkan beberapa kriteria. Pertama pada proses fuzzifikasi digunakan teknik singletone. Pada proses rule-based, digunakan fungsi triangular dengan tiga fungsi keanggotaan untuk setiap variabel input serta digunakan Takagi-Sugeno-Kang untuk konsekuen aturan. Pada proses inference-engine dipilih metode t-norm sehingga aturan yang terbentuk menggunakan operator AND. Pada blok type-reducer digunakan metode EIASC untuk mengeksekusi himpunan fuzzy tipe 2 menjadi himpunan tipe 1. Proses terakhir adalah defuzzifikasi. Pada proses defuzzifikasi dipilih teknik center of average untuk menghasilkan nilai output dalam bentuk crisp. Proses estimasi SOC menggunakan IT2FLS dijelaskan pada Gambar 3.
Fuzzifikasi
Gambar 3. Sistem Inferensi Fuzzy Interval Type 2 (IT2FLS)
Berdasarkan Gambar 3, pada penelitian ini akan dibangun sistem fuzzy menggunakan algoritme T1FLS (Type 1 Fuzzy Logic System), EIASC (Enhanced Iterative Algorithm with Stop Condition) dan EODS (Enhanced Opposite Directed Search). Tujuan dari penggunaan kedua algoritme ini untuk mengetahui nilai estimasi yang paling tepat berdasarkan ketiga algoritme ini
3. HASIL DAN PEMBAHASAN
Pada bagian pembahasan dipaparkan hasil eksperimen dan simulasi penerapan metode IT2FLS. Terdapat dua eksperimen untuk menguji kemampuan IT2FLS dalam mengestimasi kapasitas baterai.
3.1. Eksperimen 1
57
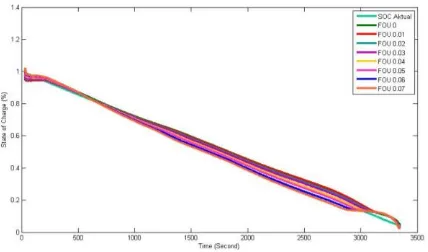
Gambar 4. Grafik Perbedaan FOU pada IT2FLS EIASC Data Beban Konstan
Berdasarkan Gambar 4 perbedaan nilai C untuk metode IT2FLS EIASC menunjukkan bahwa hasil estimasi yang paling mendekati adalah FOU 0,01, namun dengan daerah ketidakpastian 0,01 nilai RMSE dan MAE yang dihasilkan belum maksimal. Eksperimen ini menggunakan data beban konstan untuk proses estimasi kapasitas baterai.
Gambar 5. Grafik Perbedaan FOU Pada IT2FLS EIASC Data Beban Bervariasi
Pada Gambar 5, hasil estimasi SOC yang paling mendekati nilai SOC aktual adalah nilai C=0,1 dan C=0,025.
3.2. Eksperimen 2
Pada eksperimen ini, dua dataset beban konstan yang diambil pada waktu yang berbeda digunakan untuk proses pelatihan dan pengujian metode. Pada data beban konstan rentang nilai SOC terendah adalah 0,000345566 dan tertinggi 0,99138406 untuk SOC aktual. Pada Gambar 6 dijelaskan hasil estimasi SOC untuk dataset beban konstan dalam keadaan 100% hingga 50%.
Gambar 6. Grafik SOC Data Beban Konstan terhadap Waktu (a)
Pada Gambar 6 ditunjukkan grafik SOC Coulomb Counting, T1FLS, IT2FLS EIASC dan IT2FLS EODS terhadap waktu. Berdasarkan Gambar 6 kapasitas maksimal yang dihasilkan dari tiga metode adalah 0,96 atau 96%. Berbeda dengan SOC aktual yang memiliki kapasitas maksimal 99%.
Proses pengujian data beban bervariasi menggunakan data beban bervariasi pada waktu yang berbeda untuk data pelatihan dan data pengujian. Nilai kapasitas maksimal dari metode yang diusulkan adalah 98% sedangkan kapasitas minimal mencapai 14%. Berikut ini pada Gambar 7 dipaparkan grafik percobaan ketiga metode fuzzy.
Gambar 7. Grafik SOC Data Beban Bervariasi terhadap Waktu
Berdasarkan Gambar 7 hasil estimasi kapasitas baterai menggunakan metode IT2FLS EIASC dan IT2FLS EODS mendekati kapasitas baterai SOC aktual. Perbedaan yang cukup jauh terdapat pada metode T1FLS
3.3. Nilai Error
58 overcharge dan overdischarge baterai paling tinggi.
Kondisi overdischarge adalah kondisi dimana kapasitas baterai tersisa 20% sedangkan kondisi overcharge adalah kondisi dimana kapasitas baterai 80%. Berikut ini pada Gambar 8 diilustrasi nilai RMSE dalam bentuk grafik.
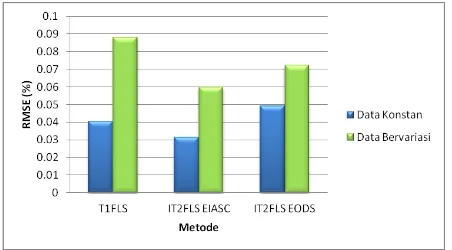
Gambar 8. Grafik RMSE Dua Dataset
Berdasarkan Gambar 8, nilai RMSE terkecil pada dataset beban konstan dihasilkan oleh metode IT2FLS EIASC. Hal yang sama terjadi pada dataset beban bervariasi, nilai RMSE dihasilkan dari metode IT2FLS EIASC. Berikut ini pada Gambar 9 dijelaskan Grafik MAE dari ketiga metode.
Gambar 9. Grafik MAE Dua Dataset
Pada Gambar 9 nilai MAE terkecil untuk kedua dataset dihasilkan oleh metode EIASC. Perbedaan nilai MAE pada kedua dataset tidak terlalu besar antara IT2LFS EIASC dengan IT2FLS EODS Hasil dan pembahasan dapat didukung dengan gambar, grafik, atau tabel yang dirujuk untuk memberikan penekanan dan visualisasi yang lebih mudah dipahami.
4.
K
ESIMPULANIT2FLS mampu merepresentasikan semua informasi tentang kinerja baterai untuk memperoleh estimasi yang lebih akurat dari kondisi penyimpanan daya. IT2FLS juga dapat mereduksi jumlah basis
aturan dibandingkan sistem fuzzy tipe 1 sehingga proses komputasi pencarian aturan berjalan lebih cepat. Metode IT2FLS dominan memberikan hasil estimasi yang lebih akurat dari dibandingkan Fuzzy Tipe 1 dengan nilai RMSE dan MAE yang lebih kecil dibandingkan Sistem Fuzzy tipe 1 untuk kedua dataset. Parameter input dan output dapat dipetakan menggunakan rentang nilai yang tepat sehingga karakteristik sistem dapat diketahui. Perbedaan nilai daerah ketidakpastian (Footprint of Uncertainty) mempengaruhi ketepatan hasil estimasi SOC.
IT2FLS menggunakan EIASC memberikan hasil estimasi yang lebih kecil dibandingkan IT2FLS menggunakan EODS dengan nilai RMSE 0,035 dan MAE 0,025 untuk dataset beban konstan sedangkan untuk dataset beban bervariasi RMSE 0,059 dan MAE 0,044. Metode ANFIS digunakan untuk membantu IT2FLS dalam hal mengindentifikasi hubungan tegangan, arus dan SOC dari baterai sehingga karakteristik baterai diketahui.
Pengembangan selanjutnya dapat menggunakan metode type-reducer lain selain dari pengembangan dari Karnik-Mendel untuk mengetahui kinerja dari Interval Type 2 Fuzzy Logic System dan menggunakan pemodelan baterai lain untuk mendapatkan parameter yang lebih bervariasi.
REFERENSI
[1] J. Kang, F. Yan, P. Zhang, and C. Du, “Comparison of
comprehensive properties of Ni-MH (nickel-metal hydride) and Li-ion (lithium-ion) batteries in terms of energy efficiency,”
Energy, vol. 70, no. 2014, pp. 618–625, 2014.
[2] Y. Çadirci and Y. Özkazanç, “Microcontroller-based on-line state-of-charge estimator for sealed lead-acid batteries,” J. Power Sources, vol. 129, no. 2, pp. 330–342, 2004.
[3] K. S. Ng, C.-S. Moo, Y.-P. Chen, and Y.-C. Hsieh, “Enhanced
coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries,” Appl. Energy, vol. 86, no. 9, pp. 1506–1511, 2009.
[4] K. T. Chau, K. C. Wu, and C. C. Chan, “A new battery capacity
indicator for lithium-ion battery powered electric vehicles using adaptive neuro-fuzzy inference system,” Energy Convers. Manag., vol. 45, no. 11–12, pp. 1681–1692, 2004.
[5] W. X. Shen, “State of available capacity estimation for
lead-acid batteries in electric vehicles using neural network,” Energy Convers. Manag., vol. 48, no. 2007, pp. 433–442, 2007. [6] Y. Shen, “Adaptive online state-of-charge determination based
on neuro-controller and neural network,” Energy Convers. Manag., vol. 51, no. 5, pp. 1093–1098, 2010.
[7] P. Singh, C. Fennie, and D. Reisner, “Fuzzy logic modelling of
state-of-charge and available capacity of nickel/metal hydride
batteries,” J. Power Sources, vol. 136, no. 2, pp. 322–333, 2004.
[8] P. Singh, R. Vinjamuri, X. Wang, and D. Reisner, “Design and
implementation of a fuzzy logic-based state-of-charge meter for Li-ion batteries used in portable defibrillators,” J. Power Sources, vol. 162, no. 2 SPEC. ISS., pp. 829–836, 2006. [9] C. Burgos, D. Sáez, M. E. Orchard, and R. Cárdenas, “Fuzzy
modelling for the state-of-charge estimation of lead-acid
batteries,” J. Power Sources, vol. 274, no. 2015, pp. 355–366,
59
[10] J. N. Hu, J. J. Hu, H. B. Lin, X. P. Li, C. L. Jiang, X. H. Qiu,
and W. S. Li, “State-of-charge estimation for battery management system using optimized support vector machine
for regression,” J. Power Sources, vol. 269, pp. 682–693, 2014.
[11] J. C. Álvarez Antón, P. J. García Nieto, F. J. de Cos Juez, F. Sánchez Lasheras, M. González Vega, and M. N. Roqueñí
Gutiérrez, “Battery state-of-charge estimator using the SVM
technique,” Appl. Math. Model., vol. 37, no. 8, pp. 6244–6253, 2013.
[12] T. Hansen and C.-J. Wang, “Support vector based battery state of charge estimator,” J. Power Sources, vol. 141, no. 2, pp.
351–358, 2005.
[13] S. Sepasi, R. Ghorbani, and B. Y. Liaw, “Improved extended Kalman filter for state of charge estimation of battery pack,” J. Power Sources, vol. 255, no. 2014, pp. 368–376, 2014. [14] K. Lim, H. Ayad, V. Duong, K. Wai, P. Zhang, and S. Xue,
“Fading Kalman filter-based real-time state of charge estimation in LiFePO 4 battery-powered electric vehicles,”
Appl. Energy, vol. 169, no. 2016, pp. 40–48, 2016.
[15] B. Pattipati, B. Balasingam, G. V. Avvari, K. R. Pattipati, and Y. Bar-Shalom, “Open circuit voltage characterization of
lithium-ion batteries,” J. Power Sources, vol. 269, no. 2014, pp. 317–333, 2014.
[16] Y. Xing, W. He, M. Pecht, and K. L. Tsui, “State of charge estimation of lithium-ion batteries using the open-circuit
voltage at various ambient temperatures,” Appl. Energy, vol. 113, no. 2014, pp. 106–115, 2014.
[17] S. Lee, J. Kim, J. Lee, and B. H. Cho, “State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge,” J. Power Sources, vol. 185, no. 2, pp. 1367–1373, 2008.
[18] L. Sánchez, I. Couso, and J. C. Viera, “Online SOC estimation
of Li-FePO4 batteries through a new fuzzy rule-based recursive
filter with feedback of the heat flow rate,” 2014 IEEE Veh. Power Propuls. Conf. VPPC 2014, pp. 1–6, 2015.
[19] J. M. Mendel, R. I. John, and F. Liu, “Interval Type-2 Fuzzy
Logic Systems Made Simple,” Fuzzy Syst. IEEE Trans., vol.
14, no. 6, pp. 808–821, 2006.
[20] K. Duran, H. Bernal, and M. Melgarejo, “Improved iterative
algorithm for computing the generalized centroid of an interval type-2 fuzzy set,” NAFIPS 2008 - 2008 Annu. Meet. North Am. Fuzzy Inf. Process. Soc., pp. 1–5, 2008.
[21] D. Wu and M. Nie, “Comparison and practical implementation
of type-reduction algorithms for type-2 fuzzy sets and
systems,” 2011 IEEE Int. Conf. Fuzzy Syst. (FUZZ-IEEE 2011), no. 6, pp. 2131–2138, 2011.
[22] Y. Chen and D. Wang, “Studies on Centroid Type-Reduction Algorithms for Interval Type-2 Fuzzy Logic Systems,” 2015 IEEE Fifth Int. Conf. Big Data Cloud Comput., pp. 344–349, 2015.
[23] D. Wu, “Approaches for reducing the computational cost of interval type-2 fuzzy logic systems: Overview and
comparisons,” IEEE Trans. Fuzzy Syst., vol. 21, no. 1, pp. 80–