PERFORMANSI METODE TRAPESIUM DAN METODE GAUSS-LEGENDRE DALAM PENYELESAIAN INTEGRAL DENGAN METODE NUMERIK MENGGUNAKAN BAHASA
PEMROGRAMAN MATLAB
Oleh :
MEILANY NONSI TENTUA
Dosen Program Studi Teknik Informatika, Universitas PGRI Yogyakarta [email protected]
INTISARI
Penggunaan integral ganda dua yang demikian telah digambarkan secara luas, sekarang terdapat penerapan lain yaitu massa, pusat massa, momen Inersia dari radius kitaran. Menurut definisi kamus, mengintegrasi berarti “memadukan bersama, sebagian kedalam suatu keseluruhan, menyatukan, menunjukkan jumlah total“, secara matematis integrasi dapat dinyatakan oleh:
b adx
x
f
I
(
)
Pada saat ini ada dua metode yang digunakan untuk menyelesaikan integral dan metode tersebut merupakan metode yang terbaik diantara metode yang lain. Metode tersebut adalah metode Trapesium dan metode kuadratur Gauss Legendre.
Kedua metode tersebut digunakan pada penyelesaian masalah integral yang sama sebagai contoh kasus. Algoritma kedua metode diselesaikan dengan bahasa pemrograman MATLAB
PENDAHULUAN
Dalam era globalisasi saat ini, ilmu pengetahuan dan teknologi berkembang sangat pesat, begitu juga dengan perkembangan matematika. Matematika pada dasarnya merupakan alat, sarana atau pelayanan ilmu lain. Hal ini tidak dapat dipungkiri dengan munculnya berbagai aplikasi matematika, baik dalam kehidupan sehari-hari maupun dalam berbagai disiplin ilmu lain yang membutuhkan banyak perhitungan. Banyak masalah ilmu pengetahuan (sciences) maupun teknologi yang perlu diselesaikan dengan menggunakan metode integral tunggal maupun integral lipat. Penerapan integral lipat dua yang paling jelas adalah dalam penghitungan volume benda pejal. Penggunaan integral ganda dua yang demikian telah digambarkan secara luas, sekarang terdapat penerapan lain yaitu massa, pusat massa, momen Inersia dari radius kitaran. Menurut definisi kamus, mengintegrasi berarti “memadukan bersama, sebagian kedalam suatu keseluruhan, menyatukan, menunjukkan jumlah total“, secara matematis integrasi dapat dinyatakan oleh:
b adx
x
f
I
(
)
Yang diartikan sebagai integrasi fungsi f(x) terhadap variabel x, yang dievaluasikan antara batas x = a hingga x = b. Sebagaimana makna persamaan diatas adalah jumlah total atau asumsi f(x) dx yang meliputi bentangan dari x = a hingga x = b. Kenyataannya, simbol sebenarnya merupakan huruf besar S yang
divariasikan untuk menandai hubungan yang dekat antara integrasi dan sumasi (Thomas dan Finney,1979). Fungsi yang akan diintegrasikan menurut jenisnya adalah:
(1) Fungsi kontinu sederhana, seperti sebuah polinomial, eksponensial atau sebuah fungsi trigonometri.
(2) Suatu fungsi kontinu yang rumit, yakni sukar atau tidak mungkin untuk mengintegrasi secara langsung.
(3) Suatu fungsi yang ditabulasikan di mana harga x dan f(x) diberikan pada sejumlah titik diskrit, seperti sering dijumpai pada data eksperimen.
Dalam kasus pertama, integral sebuah fungsi sederhana bisa dievaluasikan secara eksak dengan dievaluasikan secara eksak dengan menggunakan teknik analitis yang telah dipelajari dalam kalkulus. Tetapi untuk kedua kasus terakhir harus dilakukan metode aproksimasi. Suatu pendekatan sederhana dan intuitif ialah dengan memplot fungsi tersebut pada kedua kisi, dan menghitung banyaknya kotak untuk mengaproksimasikan luas. Jumlah ini dilakukan oleh luas setiap kotak, dan akan memberikan sebuah taksiran kasar dari luas total di bawah kurva. Taksiran ini dapat diperbaiki dengan melakukan upaya tambahan, yakni menggunakan kisi yang lebih halus. Pendekatan lain yang masuk akal ialah membagi luas tersebut ke dalam segmen - segmen vertikal, atau bilah - bilah (strips) yang tingginya sepada dengan harga fungsi pada titik tengah pada setiap bilah. Luas beberapa empat persegi panjang kemudian dapat dihitung, lalu dijumlahkan untuk menaksir luas total. Pada pendekatan ini dianggap bahwa harga yang terletak ditengah memberikan suatu aproksimasi yang berlaku untuk tinggi fungsi rata - rata untuk setiap bilah, seperti metode kisi, taksiran yang diperhalus memungkinkan dengan menggunakan bilah yang lebih banyak (dan lebih halus) untuk mengaproksimasikan integral tersebut. Walaupun pendekatan sederhana demikian mempunyai manfaat untuk menaksir secara cepat, teknik – teknik alternatif, yakni integrasi numerik atau metode kuadratur, tersedia untuk keperluan yang serupa. Metode - metode ini sebenarnya lebih mudah untuk dilaksanakan dibandingkan dengan pendekatan kisi, bertujuan sama seperti metode bilah (strip method). Artinya, tinggi fungsi dikali dengan lebar bilah lalu dijumlahkan untuk menaksir integralnya. Tetapi, melalui pemilihan faktor - faktor bobot yang baik, hasil taksiran dapat dibuat lebih akurat dibandingkan dengan “metode bilah” sederhana. Dengan berkembangnya teknologi komputer yang dewasa ini telah digunakan dihampir semua bidang kegiatan, tentu harus diikuti dengan teknik penyelesaian dan metode yang lebih baik. Artinya perlu dicari metode penyelesaian suatu masalah dengan ketelitian tinggi dan waktu proses yang lebih cepat.
Pada saat ini ada dua metode yang digunakan untuk menyelesaikan integral dan metode tersebut merupakan metode yang terbaik diantara metode yang lain. Metode tersebut adalah metode Trapesium dan metode kuadratur Gauss Legendre.
Kedua metode tersebut digunakan pada penyelesaian masalah integral yang sama sebagai contoh kasus. Algoritma kedua metode diselesaikan dengan bahasa pemrograman MATLAB
PEMBAHASAN
Dalam menyelesaikan suatu masalah yang menggunakan bantuan komputer, pemakai (user) diharapkan mampu membuat suatu proses atau prosedur yang merupakan urutan dari langkah-langkah atau instruksi-instruksi dalam menyelesaikan suatu permasalahan.
Menurut Yulikispartono (2004:12), sebuah algoritma pada hakikatnya merupakan suatu prosedur yang tepat untuk dapat memecahkan masalah dengan menggunakan bantuan komputer serta suatu bahasa pemrograman.
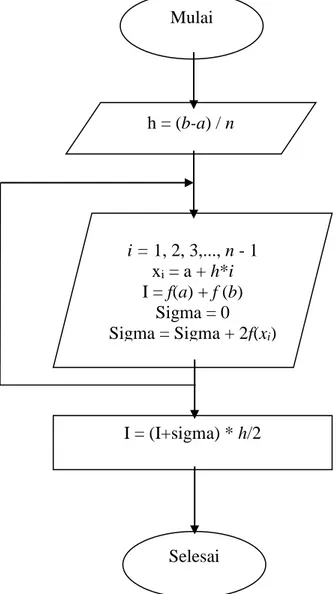
A. Kaidah Trapesium
Gambar 1. Flowchart Kaidah Trapesium
Mulai
h = (b-a) / n
I = (I+sigma) * h/2
Selesai
i = 1, 2, 3,..., n - 1
x
i= a + h*i
I = f(a) + f (b)
Sigma = 0
Sigma = Sigma + 2f(x
i)
Pada flowchart kaidah Trapesium (Gambar 3.1) dapat dijelaskan:
1) Langkah awal pada f(x) adalah membagi x menjadi n pias,
h = (b-a) / n
2) Dilakukan perhitungan dengan diketahui i = 1, 2, 3,..., n – 1,
xi = a + h*i, I = f(a) + f (b)
3) Jumlah awal Integrasi ditentukan dengan Sigma = 0,
4) Jumlah nilai integrasi berikutnya ditentukan dengan Sigma = Sigma + 2f(xi)
5) Sehingga nilai integrasi dengan I = (I+sigma) * h/2 B. Kaidah Gauss-Legendre Dua Titik
Mulai
Batas Bawah = (a)
Batas Atas = (b)
Fungsi awal = f(x)
dt
a
b
dx
t
a
b
b
a
x
2
2
)
(
)
(
Selesai
fT
1= f(
1
/
3
)
fT
2= f(
1
/
3
)
I = (b-a)/2 * (fT
1+ fT
2)
Gambar 2 Flowchart Kaidah Gauss-Legendre 2-titik
Pada flowchart kaidah Gauss-Legendre dua titik (Gambar 3.1) dapat dijelaskan 1. Menentukan Batas Bawah = (a), Batas Atas = (b), Fungsi awal = f(x)
2. Mentransformasikan
b adx
x
f
(
)
menjadi
1 1)
( dt
t
f
denganx
a
b
b
a
t
dx
b
a
dt
2
,
2
)
(
)
(
sehingga batas yang pada awalnya [a,b] menjadi [-1,1]
3. Memasuki proses pada perhitungan integrasi Gauss-Legendre dua titik dengan fT1 = f(
1
/
3
) dan fT2 = f(
1
/
3
). Sehingga nilai integrasididapatkan dari perhitungan dengan kaidah I = (b-a)/2 * (fT1 + fT2)
Dari hasil kedua metode tersebut akan dicari galat atau error relatif dengan menghitung nilai integral sejati dari permasalahan integral yang digunakan dalam penelitian ini. Selain itu ditampilkan juga kecepatan program dari perhitungan integral ini yang divisualisasikan dalam program MATLAB. Dari dua hal ini maka akan didapatkan performansi terbaik dari kedua metode tersebut.
Dalam penelitian ini program yang dibuat adalah program dinamis berdasarkan permasalahan integral yang berbeda. Permasalahan integral dan batas-batas integrannya dimasukkan ke dalam Command Windowyang memanggil program yang telah disimpan dalam M-File Work.
Program yang menggunakan metode trapesium dalam penelitian ini partisi yang dibuat adalah empat partisi, namun jika ingin memakai partisi dengan jumlah yang berbeda dapat dilakukan. Sedangkan dalam program yang menggunakan metode Gauss-Legendre bukan partisi yang menjadi tolak ukur, namun batas-batas yang dibawa dalam bentuk aturan transformasi Gauss.
Dalam setiap program telah dimasukkan fungsi integral yang akan dijalankan sehingga tinggan memasukkan batas-batas integrannya saja. Khusus untuk metode trapesium menggunakan partisi empat buah.
A. Program Metode Trapesium dalam M-File MATLAB
function trapezoid;
disp('FUNGSI TRAPEZOID');
a=input('Masukkan batas interval kiri:'); b=input('Masukkan batas interval kanan:'); n=input('Jumlah pembagian:');
fprintf('Nilai integral= %10.7e',Trapezoid (a,b,n)); function T = Trapezoid (a,b,n);
h=(b-a)/n; jumlah=0;
for i=1:1:n-1; x=a+h*i; jumlah=jumlah + F(x); end; T=(h/2)*(F(a)+F(b)+2*jumlah); function Fx = F(x); Fx=x^2+x-2 B. Program Metode Gauss-
Function Gauss;
disp('FUNGSI GAUSS LEGENDRE'); a=input('Masukkan batas interval kiri:'); b=input('Masukkan batas interval kanan:'); n=input('Jumlah pembagian:');
fprintf('Nilai integral= %10.7e',Gauss (a,b,t)); function G = Gauss (a,b,t);
x=(a+b)/2+(b-a)*t/2; I=int (t,-1,1); end; G=(b-a)*I/2; function Fx = F(x); Fx=x^2+x-2
Contoh Penyelesaian Integral secara Manual
dx
x
1
)
(
2 1 2
a. Secara Analitis
dx
x
1
)
(
2 1 2
=
2 1 2 1 21dx
dx
x
= 2 1 2 1 33
1
x
x
=
2
1
3
1
3
8
= 3,33333333333b. Secara Numerik menggunakan Metode Trapesium: 1) Integran yang diselesaikan adalah
(
x
1
)
dx
2 1
2
2) Batas bawah daerah integrasi (a) = 1 3) Batas atas daerah integrasi (b) = 2
4) Jumlah Pias n = 4, sehingga
0
,
25
4
b
a
h
dan
x
0
1
;x
1
1
,
25
;x
2
1
,
50
;x
3
1
,
75
;x
4
2
maka, penyelesaian secara numerik dengan metode trapesium adalah
(
1
)
(
2
)
2
(
1
,
25
)
(
1
,
50
)
(
1
,
75
)
2
4
/
)
1
2
(
)
1
(
2 1 2f
f
f
f
f
dx
x
=
2
5
2
(
2
,
625
3
,
25
4
,
0625
)
8
1
= 3,7813c. Secara Numerik menggunakan Metode Kuadratur Gauss-Legendre dua titik 1) Integran yang diselesaikan adalah
(
x
1
)
dx
2 1
2
2) Batas bawah daerah integrasi (a) = 1 3) Batas atas daerah integrasi (b) = 2
dt
dx
t
t
x
5
,
0
5
,
0
5
,
1
2
)
1
2
(
)
2
1
(
Transformasikanf
(
x
)
dx
2 1
menjadif
(
t
)
dt
2 1
:
1 1 1 1 2 2 2 1 21
)
5
,
0
5
,
1
(
5
,
0
5
,
0
1
)
5
,
0
5
,
1
(
)
1
(
x
dx
t
dt
t
dt
Jadi,dalam hal ini
1
)
5
,
0
5
,
1
(
)
(
t
t
2
f
Maka4673079295
,
2
1
)
3
1
5
,
0
5
,
1
(
)
3
/
1
(
1993587371
,
4
1
)
3
1
5
,
0
5
,
1
(
)
3
/
1
(
2 2
f
f
Dengan demikian
1
/
3
1
/
3
5
,
0
)
1
(
2 1 2
x
dx
f
f
3
,
33333333
Selesaikan persoalan integral berikut:
dx
x
1 04 , 01
a. Secara Analitisdx
x
1 04 , 01
=
x
dx
1 04 , 0 2 1 = 1 04 , 0 2 12x
=
2 1 2 104
,
0
2
1
2
= 2 - 0,4 = 1,6b. Secara Numerik menggunakan Metode Trapesium: 5) Integran yang diselesaikan adalah
dx
x
1 04 , 01
6) Batas bawah daerah integrasi (a) = 0,04 7) Batas atas daerah integrasi (b) = 18) Jumlah Pias n = 4, sehingga
0
,
24
4
b
a
dan
x
0
0
,
04
;x
1
0
,
28
;x
2
0
,
52
;x
3
0
,
76
;x
4
1
maka, penyelesaian secara numerik dengan metode trapesium adalah
(
1
)
(
2
)
2
(
1
,
25
)
(
1
,
50
)
(
1
,
75
)
2
4
/
)
1
2
(
)
1
(
2 1 2f
f
f
f
f
dx
x
=
2
5
2
(
2
,
625
3
,
25
4
,
0625
)
8
1
= 3,7813
(
0
,
04
)
(
1
)
2
(
(
0
,
28
)
(
0
,
52
)
(
0
,
76
))
2
4
/
)
04
,
0
1
(
1
1 04 , 0f
f
f
f
f
dx
x
7818
,
1
)
1471
,
1
3868
,
1
8898
,
1
(
2
1
5
2
24
,
0
c. Secara Numerik menggunakan Metode Kuadratur Gauss-Legendre dua titik 4) Integran yang diselesaikan adalah
dx
x
1 04 , 01
5) Batas bawah daerah integrasi (a) = 0,04 6) Batas atas daerah integrasi (b) = 1
dt
dx
t
t
x
48
,
0
48
,
0
52
,
0
2
)
04
,
0
1
(
)
04
,
0
1
(
Transformasikanf
(
x
)
dx
2 1
menjadif
(
t
)
dt
2 1
:dt
t
dx
x
0
,
52
0
,
48
0
,
48
1
1
1 1 1 04 , 0
Jadi,dalam hal ini
t
t
f
48
,
0
52
,
0
1
)
(
Maka0291
,
2
)
3
/
1
(
48
,
0
52
,
0
1
)
3
/
1
(
1200
,
1
)
3
/
1
(
48
,
0
52
,
0
1
)
3
/
1
(
f
f
Dengan demikian
1
/
3
1
/
3
48
,
0
1
1 04 , 0
dx
f
f
x
1
,
5116
Contoh 4.1.3 Contoh 4.5.2.Selesaikan persoalan integral berikut:
1
0 3 21
2x
x
a. Secara AnalitisPermasalahan ini akan diselesaikan dengan metode subtitusi.
1
0 3 21
2x
x
Misal:1
2
2
x
u
xdx
du
4
xdx
du
4
Sehingga menjadi:
* * * 3 * * * 3 24
1
1
2
4
1
u
du
x
du
1111
,
0
8
1
72
1
)
1
2
(
1
8
1
8
1
2
1
4
1
1 0 2 2 * * * 2 * * * 2
x
u
u
b. Secara Numerik menggunakan Metode Trapesium: 1) Integran yang diselesaikan adalah
1
0 3 21
2x
x
2) Batas bawah daerah integrasi (a) = 0 3) Batas atas daerah integrasi (b) = 1
4) Jumlah Pias n = 4, sehingga
0
,
25
4
b
a
h
dan
x
0
0
;x
1
0
,
25
;x
2
0
,
50
;x
3
0
,
75
;x
4
1
maka, penyelesaian secara numerik dengan metode trapesium adalah
(
0
)
(
1
)
2
(
0
,
25
)
(
0
,
50
)
(
0
,
75
)
2
4
/
)
0
1
(
)
1
2
(
1 0 3 2dx
f
f
f
f
f
x
x
=
0
0
,
0370
2
(
0
,
0741
0
,
0625
0
,
0480
)
8
1
= 0,0924c. Secara Numerik menggunakan Metode Kuadratur Gauss-Legendre dua titik
1) Integran yang diselesaikan adalah
1
0 3 21
2x
x
2) Batas bawah daerah integrasi (a) = 0 3) Batas atas daerah integrasi (b) = 1
dt
dx
t
t
x
5
,
0
5
5
,
0
2
)
0
1
(
)
0
1
(
Transformasikanf
(
x
)
dx
2 1
menjadif
(
t
)
dt
2 1
:
dt
t
t
x
x
1 0 1 1 3 2 3 21
)
5
,
0
5
,
0
(
2
5
,
0
5
,
0
5
,
0
1
2
Jadi,dalam hal ini
2
31
)
5
,
0
5
,
0
(
2
5
,
0
5
,
0
)
(
t
t
t
f
Maka
0
,
1635
1
))
3
/
1
(
5
,
0
5
,
0
(
2
5
,
0
5
,
0
)
3
/
1
(
0698
,
0
1
))
3
/
1
(
5
,
0
5
,
0
(
2
5
,
0
5
,
0
)
3
/
1
(
3 2 3 2
t
f
t
f
Dengan demikian
0
,
5
1
/
3
1
/
3
1
2
1 0 3 2
dx
f
f
x
x
0
,
1167
KESIMPULANPerformansi metode Trapesium dengan Kuadratur Gauss Legendre pada masalah integral dengan bahasa pemrograman MATLAB. Dapat dikatakan bahwa metode trapesium bersesuaian dengan kuadratur Gauss Legendre. Dapat dilihat bahwa nilai integrasi numerik dengan kaidah trapesium akan tepat (galat=0) untuk fungsi tetap dan fungsi lanjar. Misal f(x) = 1 dan f(x). dari dua buah fungsi tersebut, diperoleh dua persamaan:
1
)
(
x
f
maka, 1 2 1 1 1 12
)
1
(
1
1
dx
x
c
c
x x
Danx
x
f
(
)
maka, 2 2 1 1 2 2 1 1 1 1 20
)
1
(
2
1
)
1
(
2
1
2
1
x
c
x
c
x
xdx
x x
SARANSaran untuk penelitian ini adalah penyempurnaan pada sisi pemrograman MATLAB dapat di buat secara visual sehingga lebih interaktif.
DAFTAR PUSTAKA
Dash, Rajani B, and Debasish Das, A Mixed Quadrature Rule by Blending clenshaw-Curtis and GaussLegendre Quadrature Rules for Approximation of Real Definite Integrals in Adaptive Environment. 2011. Proceedings of the International MultiConference of Engineers and Computer Scientists.
Firmansyah.2007.
Dasar-dasar pemrograman MATLAB.Bandung:Universitas padjajaran Press. Munir, Rinaldi, Metode Numerik untuk Teknik Informatika. 1997. Jurusan Teknik