KAJIAN METODE BOOTSTRAP DALAM MEMBANGUN SELANG KEPERCAYAAN DENGAN MODEL ARMA (p,q)

1

KAJIAN METODE BOOTSTRAP DALAM MEMBANGUN SELANG KEPERCAYAAN

DENGAN MODEL ARMA (p,q)

Oleh :

Ratna Evyka E.S.A

1206 100 043

Dosen Pembimbing : Dra. Nuri Wahyuningsih, M.Kes

Dra. Laksmi Prita W, M.Si Jurusan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Sepuluh Nopember

Surabaya 2011 Abstrak

Data yang berukuran kecil tidak dapat di ramalkan secara langsung tetapi hal ini dapat disiasati dengan menggunakan teknik resampling, salah satu metode yang bisa digunakan dalam teknik resampling adalah metode resampling Bootstrap. Metode bootstrap ini merupakan suatu metode resampling untuk mengestimasi probabilitas suatu statistik dengan mendapatkan sampel baru

𝑥

∗

= (𝑥

₁∗

, 𝑥

₂∗

, … , 𝑥

₃∗

)

. Metode ini bagus sekali untuk ukuran data sampel yang relatif kecil. Dari hasil resampling tersebut dapat dianalisa selang kepercayaan dan model time series yang sesuai untuk digunakan dalam metode Bootstrap, serta digunakan untuk mendapatkan peramalan data untuk beberapa periode ke depan. Studi kasus dalam tugas akhir ini adalah meramalkan jumlah penjualan baju koko Dannis Collection pada periode yang akan datang. Hasil analisis menunjukkan bahwa selang kepercayaan untuk 𝑥 _𝑖,𝑗∗ adalah

𝑥 𝑖,𝑗∗ ± 𝑧𝛼 ₂

𝑥 _𝑖∗−𝑥 _𝑖,𝑗∗ 2

𝑁 𝑗=1

𝑁−1 𝑛𝑁 dengan model terbaik untuk peramalan penjualan Dannis Collection adalah

ARMA (10,10).

Kata kunci: Selang Kepercayaan, Estimasi, Resampling Bootstrap, ARMA(p,q)

1. Pendahuluan

Angka penjualan suatu produk memegang peranan penting dalam suatu proses produksi. Angka penjualan dan produksi suatu produk memiliki keterkaitan satu sama lain. Angka penjualan suatu produk dapat memberikan gambaran bagi produsen untuk mengetahui dan memperkirakan seberapa besar produk tersebut diproduksi untuk beberapa periode yang akan datang. Akan tetapi keterbatasan data (n<30) merupakan masalah yang sering dihadapi sehingga akan mempersulit peramalan untuk periode yang akan datang. Maka perlu dilakukan langkah-langkah untuk mengantisipasi masalah tersebut. Salah satunya adalah dengan cara resampling data yg sedikit tersebut agar mudah untuk untuk diramalkan. Salah satu metode

umum dalam resampling data adalah dengan menggunakan metode Bootstrap. Metode Bootstrap diciptakan oleh Bradley Efron pada tahun 1979. Metode Bootstrap ini merupakan suatu metode resampling untuk mengestimasi probabilitas suatu statistik dengan mendapatkan sampel baru

𝑥

∗

= (𝑥

₁∗

, 𝑥

₂∗

, … , 𝑥

₃∗

)

. Metode ini bagus untuk ukuran data sampel yang relatif kecil (n<30).

Untuk memperkirakan suatu nilai pada periode yang akan datang diperlukan suatu ilmu yang bernama forecasting (peramalan). Forecasting merupakan suatu proses analisis untuk meramalkan apa yang akan terjadi pada masa mendatang berdasarkan situasi dan kondisi yang terjadi sekarang dan masa lalu. Perspektif pada peramalan sama beragamnya dengan pandangan setiap kelompok metode ilmiah yang

2

dianut oleh pengambil keputusan. Untuk data yang belum stasioner perlu dilakukan transformasi terlebih dahulu, trasformasi yang biasa dipakai adalah transformasi Box-Cox. Dengan data yang telah stasioner bisa didapatkan estimasi parameter dan selang kepercayaan untuk parameter ARMA(p,q). Dalam tugas akhir ini digunakan metode resampling Bootstrap untuk memperoleh selang kepercayaan untuk parameter model ARMA(p,q) dengan studi kasus memprediksi jumlah penjualan baju koko dari Dannis Collection untuk periode yang akan datang.

2.

Metode Resampling Bootstrap

Metode bootstrap adalah prosedur pengambilan sampel baru secara berulang sebanyak N sampel baru dari data asal berukuran

𝑛, dimana untuk sebuah sampel baru dilakukan pengambilan titik sampel dari data asal dengan cara satu persatu sampai n kali dengan pengembalian. Misalkan terdapat data asal berukuran 𝑛, yaitu 𝑋 = (𝑥1, 𝑥2, … , 𝑥𝑛) maka

dengan metode bootstrap akan diperoleh sampel-sampel baru berukuran n sebagai berikut (Efron, 1993): Sampel ke-1, 𝑋∗1_{= (𝑥} 11∗ , 𝑥21∗ , 𝑥31∗ , … , 𝑥𝑛1∗ ) Sampel ke-2, 𝑋∗2_{= (𝑥} 12∗ , 𝑥22∗ , 𝑥32∗ , … , 𝑥𝑛2∗ ) ... ... Sampel ke-N, 𝑋∗𝑁_{= (𝑥} 1𝑁∗ , 𝑥2𝑁∗ , 𝑥3𝑁∗ , … , 𝑥𝑛𝑁∗ )

Jika di berikan ∅𝑁 𝑋 = ∅𝑁(𝑥1, 𝑥2, … , 𝑥𝑛) yang

ditetapkan sebagai estimator dari sampel

𝑋_{(𝑛 )}(𝑁)= (𝑥1𝑁∗ , 𝑥2𝑁∗ , 𝑥3𝑁∗ , … , 𝑥𝑛𝑁∗ ), dengan

parameternya adalah 𝜃 maka didapat estimasi mean untuk bootstrap adalah:

𝜃 = 1

𝑁 𝜃 𝑖

𝑁

𝑖=1

Jika diasumsikan estimator 𝜃 adalah distribusi normal dengan mean 𝜃 dan varian 𝜍2 maka sampel varian untuk bootstrap adalah:

𝑆2₌ 1

𝑁 − 1 (𝜃 𝑖− 𝜃 )

2 𝑁

𝑖=1

Sedangkan taksiran standar error bootstrap adalah: 𝑆𝑒 = 1 (𝑁−1) (𝜃 𝑖− 𝜃 ) 2 𝑁 𝑖=1 1 2 Selang

kepercayaan mean bootstrap 100 1 − 𝛼 % dengan 𝛼 = 0,05 untuk mean adalah:

𝜃 ± 𝑧𝛼 2𝑆𝑒 = 𝜃 ± 𝑧(𝛼 2) 1 𝑁 − 1 (𝜃 𝑖− 𝜃 ) 2 𝑁 𝑖=1

Untuk estimasi parameter dengan menggunakan MLE meliputi dua tahap, yaitu mengkontruksi fungsi Likelihood dan memperoleh fungsi Likelihood tersebut.

Misalkan 𝑥 adalah variabel random dengan fungsi probabilitas 𝑓(𝑥, 𝜃) merupakan himpunan parameter yang tidak diketahui dan untuk setiap

𝑥𝑖 saling independen maka pengkontruksian

fungsi Likelihood dapat dinyatakan dengan:

𝐿 𝜃, 𝑋 = 𝑓 𝑥1, 𝜃 𝑓 𝑥2, 𝜃 𝑓 𝑥3, 𝜃 … 𝑓 𝑥𝑛, 𝜃

𝐿 𝜃, 𝑋 = 𝑓(

𝑛

𝑖=1

𝑥𝑖, 𝜃) (2.1)

Probablitas bahwa nilai variabel acak 𝑥

berada dalam batas 𝑥1 dan 𝑥2 adalah:

𝑃 𝑥1< 𝑥 < 𝑥2 = 𝐹 𝑥2 − 𝐹𝑥1) = 𝑓 𝑥 𝑑𝑥 𝑥₂

𝑥₁

Probabilitas selang kepercayaan dengan selang kepercayaan sebesar 1 − 𝛼 100% untuk

𝑝 adalah:

𝑃(𝑝1< 𝑝 < 𝑝2 = 1 − 𝛼 (2.2)

Korelasi antara pengamatan pada waktu ke-t

(𝑍𝑡) dengan pengamatan pada waktu ke-t+k

(𝑍𝑡+𝑘) yang dipisahkan oleh lag k, sehingga

persamaan ACF dapat dirumuskan sebagai berikut:

𝜌𝑘 =

𝐶𝑜𝑣(𝑍𝑡, 𝑍𝑡+𝑘)

𝑉𝑎𝑟 𝑍𝑡 𝑉𝑎𝑟(𝑍𝑡+𝑘)

, 𝑘 = 1,2, …

Untuk mengukur keeratan hubungan 𝑍𝑡 dan

𝑍𝑡+𝑘 setelah dependensi linear dalam varian

𝑍𝑡+𝑘, … . , 𝑍𝑡+𝑘−1 dihilangkan [Wei, 1990]

disebut Partial Autocorrelation Function (PACF) dapat dihitung dengan menggunakan persamaan sebagai berikut:

∅k+1,k+1= ρ k+1− kj=1∅kj − ρ k−1+j 1 − kj=1∅kj ρ j ∅k+1,j = ∅kj − ∅k+1,k+1∅k,k+1−j k = 1,2, … ; j = 1,2, … , k − 1 dengan :

∅ : fungsi autokorelasi parsial 3. Model Time Series

Bentuk-bentuk umum model time series adalah sebagai berikut:

3

1. Autoregressive (AR)

Model untuk Autoregressive (AR) adalah:

Zt = ∅1Zt−1+ ∅2Zt−2+ ⋯ + ∅pZt−p+ ɑ𝑡 (3.1)

dengan :

Z_t :besarnya pengamatan (kejadian) pada waktu ke-t

ɑ𝑡 : nilai kesalahan (error) pada waktu ke-t

∅1, ∅2… , ∅p : parameter auturegresive

2. Moving Average (MA)

Model untuk Moving Average (MA) adalah:

𝑍𝑡= 𝜇 + ɑ𝑡− 𝜃1ɑ𝑡−1− 𝜃2ɑ𝑡−2− ⋯ − 𝜃𝑞 (3.2)

dengan:

𝜇 : nilai konstan

𝜃1, … , 𝜃𝑞: parameter-parameter Moving Average

ɑ𝑡 : nilai kesalahan pada saat 𝑡 − 𝑞

3. Autoregressive Moving Average (ARMA) Model Autoregressive Moving Average merupakan model campuran dari model autoregressive dan moving average. Bentuk umum model ARMA (p,q) menurut Wei (1994) adalah:

𝑍𝑡 = 𝜇 + 𝜙1Zt−1+ ⋯ + 𝜙𝑝Zt−p+ ɑ𝑡−

𝜃1ɑ𝑡−1− ⋯ − 𝜃𝑞ɑ𝑡−𝑞

(3.3)

3.1 Estimasi dan Uji Signifikansi Parameter Model ARMA yang baik adalah model yang menunjukkan bahwa penaksiran parameternya signifikan. Secara umum, misalkan 𝜃 adalah suatu parameter pada model ARMA dan 𝜃

adalah nilai taksiran dari parameter tersebut, serta 𝑆𝐸(𝜃 ) adalah standart error dari 𝜃 , maka uji kesignifikanan parameternya dapat dilakukan dengan hipotesa sebagau berikut :

Hipotesa :

𝐻𝑜 ∶ 𝜃 = 0 (paremeter tidak signifikan)

𝐻1 ∶ 𝜃 ≠ 0 (parameter signifikan) Statistik uji : 𝑡 = 𝜃 𝑆𝐸 (𝜃 ) Daerah kritis : 𝐻0 ditolak jika 𝑡 > 𝑡𝛼 2 ,𝑛−𝑝−𝑞

Atau 𝐻0 ditolak jika P-value < 𝛼 3.2 Pemeriksaan Diagnostik Model

Pemeriksaan diagnostik pada residual meliputi uji asumsi white noise (independen dan identik) dan berdistribusi normal.

1. Uji White noise

Pengujian yang digunakan untuk mengetahui apakah residual bersifat white noise digunakan statistik uji Ljung-Box.

Hipotesa

𝐻0: 𝜌1= 𝜌2= … = 𝜌𝑘= 0 (residual bersifat

white-noise)

𝐻1: minimal ada 𝜌𝑘 ≠ 0 (residual tidak bersifat

white-noise) Statistik uji: 𝑄 = 𝑛 𝑛 + 2 𝜌𝑘 2 𝑛 − 𝑘 𝐾 𝑘 =1 dengan:

𝐾 : lag maksimum yang diuji

𝑛 : banyak pengamatan

𝜌 𝑘 : ACF residual pada lag ke-𝑘

Daerah kritis

𝐻0 ditolak jika 𝑄 > 𝜒𝛼,𝐾−𝑝 −𝑞2 atau 𝑃 𝜒2 >

𝜒_{𝑕𝑖𝑡𝑢𝑛𝑔}2 < 𝛼 0,05

di mana 𝐾 adalah lag maksimum yang diuji, 𝑝

adalah jumlah parameter AR, dan 𝑞 adalah jumlah parameter MA.

2. Uji Normalitas

Untuk mengetahui residual berdistribsi normal dilakukan pengujian dengan menggunakan statistik uji Kolmogorov–Smirnov yaitu:

Hipotesa

𝐻0: 𝐹 𝑥 = 𝐹0 𝑥 (Residual berdistribusi

normal)

𝐻1: 𝐹 𝑥 ≠ 𝐹0 𝑥 (Residual tidak berdistribusi

normal) Statistik uji

𝐷 =𝑠𝑢𝑝

𝑥 𝑆 𝑥 − 𝐹0 𝑥

dengan:

𝑆 𝑥 : fungsi peluang komulatif yang dihitung dari data sampel

𝐹0 𝑥 : fungsi peluang komulatif distribusi yang

dihipotesakan

𝐹 𝑥 : fungsi distribusi yang belum diketahui

𝑠𝑢𝑝 : nilai supremum untuk semua 𝑥

Daerah kritis

H0 ditolak jika 𝐷 ≥ 𝐷𝛼,𝑛 atau 𝑃 𝐷 > 𝐷𝑕𝑖𝑡𝑢𝑛𝑔 <

𝛼 0,05

4

3.3 Kriteria Pemilihan Model Terbaik

Untuk menentukan model terbaik dari beberapa model yang memenuhi syarat tersebut dapat digunakan beberapa kriteria antara lain kriteria In-sampel (AIC dan SBC) dan Out-sampel (MSE dan MAPE ).

1. AIC (Akaike’s Information Criterion)

AIC (Akaike’s Information Criterion) adalah kriteria pemilihan model dengan mempertimbangkan jumlah parameter dalam model. Kriteria AIC dirumuskan sebagai berikut (Wei, 1990):

𝐴𝐼𝐶 = 𝑛 ln 𝜍 + 2𝑀𝑎2

dengan:

𝑛 : banyaknya residual

𝜍𝑎2 : estimasi dari varian residual (𝜍𝑎2)

𝑀 : jumlah parameter dalam model 2. SBC (Schwartz,s Bayesian Criterion)

SBC (Schwartz’s Bayesian Criterion) adalah kriteria pemilihan model dengan mempertimbangkan jumlah parameter dalam model yang digunakan untuk sampel yang kecil. Nilai-nilai SBC ditentukan dengan cara:

𝑆𝐵𝐶 𝑀 = 𝑛 ln 𝜍 + 𝑀 ln 𝑛𝑎2

3. MSE (Mean Square Error)

Kriteria MSE dirumuskan sebagai berikut:

𝑀𝑆𝐸 = 𝑍𝑡− 𝑍 𝑡

2 𝑛

𝑡=1

𝑛

dengan 𝑛 adalah banyaknya residual.

4. MAPE (Mean Absolute Percentage Error) Kriteria MAPE dirumuskan sebagai berikut:

𝑀𝐴𝑃𝐸 = 𝑍𝑡− 𝑍 𝑡 𝑍𝑡 𝑛 𝑡=1 𝑛 × 100%

dengan 𝑛 menyatakan banyaknya residual. 4. Metodelogi Penelitian

Metode yang digunakan pada tugas akhir dalam menyelesaikan permasalahan adalah: 1. Studi Literatur

2. Pengumpulan Data

3. Estimasi Parameter dari metode Bootstrap. 4. Membangun Selang Kepercayaan

5. Peramalan

6. Penarikan Kesimpulan dan Penulisan Laporan Tugas Akhir.

5. Hasil

Estimasi yang dilakukan menggunakan dua metode yaitu Maximum Likelihood Estimation dan Unbiassed Estimator.

1. Maximum Likelihood Estimation

Estimasi parameter menggunakan Maximum Likelihood Estimation (MLE) meliputi dua tahap yaitu mengkontruksi fungsi likelihood

𝐿 𝜑, 𝑍 , dan memperoleh nilai estimator 𝜑 yang memaksimumkan fungsi likelihood tersebut. Mean dari sampel asli adalah:

𝑥 = 1 𝑛 𝑥𝑖

𝑛

𝑖=1

(5.1)

Berdasarkan (2.1) pengkontruksian fungsi likelihood dapat dinyatakan dengan:

𝐿 𝜃, 𝑋 = 𝑓 𝑥1, 𝜃 𝑓 𝑥2, 𝜃 𝑓 𝑥3, 𝜃 … 𝑓 𝑥𝑛, 𝜃

𝐿 𝜃, 𝑋 = 𝑓(

𝑛

𝑖=1

𝑥𝑖, 𝜃) (5.2)

dengan 𝑥𝑖saling independen dan 𝑓 𝜃, 𝑥 adalah

fungsi probabilitas.

Karena data pengamatan pada resampling Bootstrap saling independent untuk setiap hasil resampling, maka pengkontruksian fungsi likelihood dinyatakan dengan:

𝐿 𝜇, 𝜍2 = 1

2𝜋 𝜍2 _𝑛𝑒

− 𝑥 _𝑖∗−𝜇 2 (2𝜍2 _𝑛)

𝑁

𝑗 =1

Diasumsikan resampling berdistribusi normal 𝑥_𝑖∗~𝑁 𝜇, 𝜍2 _{maka rata-rata tiap}

resampling 𝑥 𝑖∗ juga berdistribusi normal

𝑥 _𝑖∗~𝑁(𝜇, 𝜍2 _{)𝑛 Sehingga pdf dari 𝑥}

𝑖∗ adalah

𝑓 𝑥 _𝑖∗; 𝜇, 𝜍2 ₌ 1

2𝜋 𝜍2 _𝑛𝑒

− 𝑥 _𝑖∗−𝜇 2 (2𝜍2 𝑛)

dan pdf dari Likelihood adalah:

𝐿 𝜇, 𝜍2 = 1 2𝜋 𝜍2 _𝑛𝑒 − 𝑥 _𝑖∗−𝜇 2 (2𝜍2 _𝑛) 𝑁 𝑗 =1 ln 𝐿 𝜇, 𝑣 = −𝑁₂ ln 2𝜋 + ln𝜍_𝑛2 −_2𝜍𝑛2 𝑁𝑗 =1 𝑥 𝑖∗− 𝜇 2 (5.3) Kemudian, persamaan (5.3) diturunkan terhadap

𝜇 sehingga diperoleh persamaan berikut:

𝜕 ln 𝐿 𝜇, 𝜍2 𝜕𝜇 = − 𝑛 2𝜍2 2 𝑥 𝑖 ∗_{− 𝜇} 2 𝑁 𝑗=1 = 0 −𝑛 𝑥 𝑖∗ 𝑁 𝑗 =1 + 𝑛 𝜇 𝑁 𝑗 =1 = 0 𝜇 = 𝑥 𝑖 ∗ 𝑁 𝑗 =1 𝑁

5

𝜇 = 𝑥 𝑖𝑗∗ = 1 𝑛 1 𝑁 𝑥𝑖𝑗 ∗ 𝑁 𝑗 =1 𝑛 𝑖=1

Pengujian kedua adalah untuk varian:

ln 𝐿 𝜇, 𝑣 = −𝑁₂ ln 2𝜋 + ln𝜍_𝑛2 −_2𝜍𝑛2 𝑗 =1𝑁 𝑥 𝑖∗− 𝜇 2 (5.4) persamaan (5.4) diturunkan terhadap 𝜍2

sehingga diperoleh persamaan berikut:

𝜕 ln(𝜇,𝜍2₎ 𝜕𝑣 = − 𝑁 2 𝑛 𝜍2+ 𝑛 2(𝜍2₎2 𝑥 𝑖 ∗_{− 𝜇} 2 𝑁 𝑗=1 = 0 𝑛𝑁 2𝜍2= 𝑛 2(𝜍2₎2 𝑥 𝑖∗− 𝜇 2 𝑁 𝑗=1 𝜍2_{𝑁 = 𝑥} 𝑖 ∗_{− 𝜇} 2 𝑁 𝑗 =1 𝜍 2₌ 𝑥 𝑖 ∗_{− 𝜇} 2 𝑁 𝑗=1 𝑁 𝜍 2 𝑛 = 𝑥 _𝑖∗_{− 𝜇} 2 𝑁 𝑗=1 𝑁𝑛 (5.5) 2. Unbiassed Estimator

Pengujian dengan dengan menggunakan unbiassed estimator akan didapatkan bukti seberapa besar kesalahan atau error dari estimator tersebut. Pertama akan dilakukan untuk menguji apakah terdapat error pada saat

𝐸 𝑥𝑖,𝑗∗ = 𝜇.. Dengan rumus dasar ekspektasi

sebagai berikut:

Pengujian Unbiassed Estimatornya adalah:

𝜇 = 𝑥 𝑖𝑗∗ = 1 𝑛 1 𝑁 𝑥𝑖𝑗 ∗ 𝑁 𝑗 =1 𝑛 𝑖=1 𝐸 𝑥 _𝑖,𝑗∗ = 𝐸 1 𝑁 1 𝑛 𝑥𝑖𝑗 ∗ 𝑁 𝑗 =1 𝑛 𝑖=1 𝐸 𝑥 𝑖,𝑗∗ = 1 𝑁 1 𝑛𝐸 𝑥𝑖𝑗 ∗ 𝑁 𝑗 =1 𝑛 𝑖=1 𝐸 𝑥 _𝑖,𝑗∗ ₌1 𝑛 1 𝑁𝐸 𝑥11∗ + 𝑥21∗ + ⋯ + 𝑥𝑛1∗ + 𝑥12∗ + ⋯ + 𝑥𝑛𝑁∗ Karena setiap data dalam resampling Bootstrap bersifat independen maka:

𝐸 𝑥 _𝑖,𝑗∗ =1 𝑛 1 𝑁𝐸 𝑛𝑥𝑖1 ∗ _{+ 𝑛𝑥} 𝑖22 + ⋯ + 𝑛𝑥𝑖𝑁∗ 𝐸 𝑥 𝑖,𝑗∗ = 1 𝑛 1 𝑁𝐸 𝑛 𝑥𝑖1 ∗ _{+ 𝑥} 𝑖22 + ⋯ + 𝑥𝑖𝑁∗ 𝐸 𝑥 𝑖,𝑗∗ = 1 𝑛 1 𝑁𝐸(𝑛𝑁𝑥𝑖𝑗 ∗₎ 𝐸 𝑥 𝑖,𝑗∗ = 1 𝑛 1 𝑁𝑛𝑁𝜇 𝐸 𝑥 𝑖,𝑗∗ = 𝜇

Pengujian kedua dilakukan untuk menguji apakah terdapat error pada saat 𝐸 𝜍 2 ₌

𝜍2,maka dengan menggunakan persamaan (5.5) maka pengujian Unbiassed Estimatornya adalah:

𝜍 2₌1 𝑛 1 𝑁 𝑥 𝑖 ∗_{− 𝑥} 𝑖,𝑗∗ 2 𝑁 𝑗 =1 𝐸 𝜍 2 _{= 𝐸} 1 𝑛 1 𝑁 𝑥 𝑖 ∗_{− 𝑥} 𝑖,𝑗 ∗ 2 𝑁 𝑗 =1 𝐸 𝜍 2 ₌1 𝑛 1 𝑁𝐸 𝑥 𝑖 ∗_{− 𝑥} 𝑖,𝑗 ∗ 2 𝑁 𝑗 =1 𝐸 𝜍 2 =1 𝑛 1 𝑁𝐸 𝑥 𝑖 ∗2_{− 2𝑥} 𝑖∗𝑥 𝑖,𝑗∗ + (𝑥 𝑖,𝑗∗ )2 𝑁 𝑗 =1 𝐸 𝜍 2 ₌1 𝑛 1 𝑁𝐸 𝑥 𝑖∗2 𝑁 𝑗 =1 + 2𝑥 _𝑖∗_𝑥 𝑖,𝑗∗ 𝑁 𝑗 =1 + (𝑥 _𝑖,𝑗∗ ₎2 𝑁 𝑗 =1 𝐸 𝜍 2 ₌1 𝑛 1 𝑁 𝐸 𝑥 𝑖 ∗2_{− 2𝑁𝑥} 𝑖,𝑗∗ 2+ 𝑁𝑥 𝑖,𝑗∗ 2 𝑁 𝑗 =1 𝐸 𝜍 2 ₌1 𝑛 1 𝑁 𝐸 𝑁𝑥 𝑖 ∗2_{− 𝑁𝑥} 𝑖,𝑗 ∗ 2 𝐸 𝜍 2 ₌ 𝑁 𝑛𝑁 𝐸(𝑥 𝑖 ∗₎2_{− 𝐸(𝑥} 𝑖,𝑗∗ )2 Karena 𝜍2= 𝐸(𝑥 𝑖∗)2− 𝐸(𝑥 𝑖∗) 2 maka: 𝐸 𝜍 2 ₌1 𝑛 𝜍 2_{+ 𝐸(𝑥} 𝑖 ∗₎ 2 ₋𝜍 2 𝑁 − 𝐸(𝑥 𝑖,𝑗∗ ) 2 𝐸 𝜍 2 =1 𝑛 𝜍 2_{+ 𝜇}2₋𝜍 2 𝑁 − 𝜇 2 𝐸 𝜍 2 ₌1 𝑛 𝜍 2₋𝜍2 𝑁 = 1 𝑛 𝑁𝜍2_{− 𝜍}2 𝑁 = 𝑁 − 1 𝑛𝑁 𝜍 2 _(4.6)

Sehingga 𝜍 2 _{adalah estimator bias dari 𝜍}2_,

untuk menjadikan tak biasa maka menggunakan persamaan (5.6) akan dilakukan langkah-langkah sebagai berikut: 𝐸 𝜍 2 ₌𝑁 − 1 𝑛𝑁 𝜍 2 𝜍2= 𝑁 𝑛𝑁 − 1𝐸 𝜍 2 𝜍2₌ 𝑛𝑁 𝑁 − 1𝐸 𝜍 2 𝜍2= 𝐸 𝑛𝑁 𝑁 − 1 𝑥 _𝑖∗_{− 𝜇} 2 𝑁 𝑗=1 𝑁𝑛 𝜍2= 𝐸 1 𝑁 − 1 𝑥 𝑖 ∗_{− 𝜇} 2 𝑁 𝑗=1

6

Jadi dapat disimpulkan bahwa 1

𝑁−1 𝑥 𝑖 ∗₋ 𝑁

𝑗 =1

𝜇 2 _{adalah estimator unbiassed untuk 𝜍}2 _dan 1

𝑁−1 𝑥 𝑖 ∗_{− 𝜇} 2 𝑁

𝑗 =1 biasanya dinotasikan dengan

𝑆2_.

5.1 Selang Kepercayaan

Dalam metode Bootstrap, 𝑥 _𝑖,𝑗∗ dan 𝑠

merupakan rata-rata dan simpangan dari populasi dengan 𝜍2 _{yang tidak diketahui, maka selang}

kepercayaan 1 − 𝛼 100% untuk 𝜇 adalah sebagai berikut: 𝑥 _𝑖,𝑗∗ = 1 𝑁 1 𝑛 𝑥𝑖𝑗 ∗ 𝑛 𝑖=1 𝑁 𝑗 =1 𝜍 = 𝑆 = 1 𝑁 − 1 𝑥 𝑖 ∗_{− 𝑥} 𝑖,𝑗∗ 2 𝑁 𝑗=1 𝑍 =𝑥 𝑖,𝑗 ∗ _{− 𝜇} 𝜍 𝑛𝑁

Sehingga selang kepercayaannya adalah:

𝑃 −𝑧𝛼 2< 𝑍 < 𝑧𝛼2 = 1 − 𝛼 𝑃 −𝑧𝛼 2 < 𝑥 𝑖,𝑗∗ − 𝜇 𝜍 𝑛𝑁 < 𝑧𝛼 2 = 1 − 𝛼 𝑃 −𝑧𝛼 2< 𝑥 𝑖,𝑗∗ − 𝜇 𝑥 _𝑖∗− 𝑥 _𝑖,𝑗∗ 2 𝑁 𝑗=1 𝑁 − 1 𝑛𝑁 < 𝑧𝛼 2 = 1 − 𝛼 𝑃 −𝑧𝛼 2 𝑥 𝑖∗− 𝑥 𝑖,𝑗∗ 2 𝑁 𝑗 =1 𝑁 − 1 𝑛𝑁 < 𝑥 𝑖,𝑗∗ − 𝜇 < 𝑧𝛼₂ 𝑥 𝑖∗− 𝑥 𝑖,𝑗∗ 2 𝑁 𝑗 =1 𝑁 − 1 𝑛𝑁 = 1 − 𝛼 P 𝑥𝑖,𝑗∗ − zα 2 𝑥𝑖∗− 𝑥𝑖,𝑗∗ 2 𝑁 𝑗=1 𝑁 − 1 𝑛𝑁 < 𝜇 <𝑥𝑖,𝑗∗ + zα 2 𝑥𝑖∗− 𝑥𝑖,𝑗∗ 2 𝑁 𝑗=1 𝑁 − 1 𝑛𝑁 = 1 − α

Sehingga selang kepercayaan untuk 𝜇 adalah:

𝑥 _𝑖,𝑗∗ ± 𝑧𝛼 2 𝑥 _𝑖∗_{− 𝑥} 𝑖,𝑗 ∗ 2 𝑁 𝑗=1 𝑁 − 1 𝑛𝑁 5.2 Peramalan data

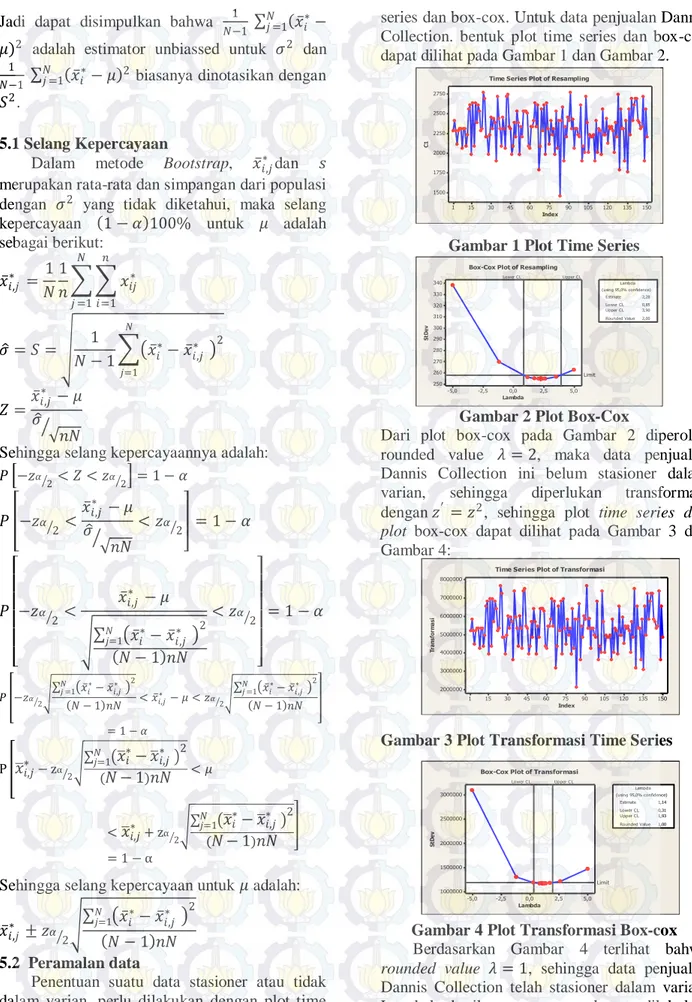
Penentuan suatu data stasioner atau tidak dalam varian, perlu dilakukan dengan plot time

series dan box-cox. Untuk data penjualan Dannis Collection. bentuk plot time series dan box-cox dapat dilihat pada Gambar 1 dan Gambar 2.

Gambar 1 Plot Time Series

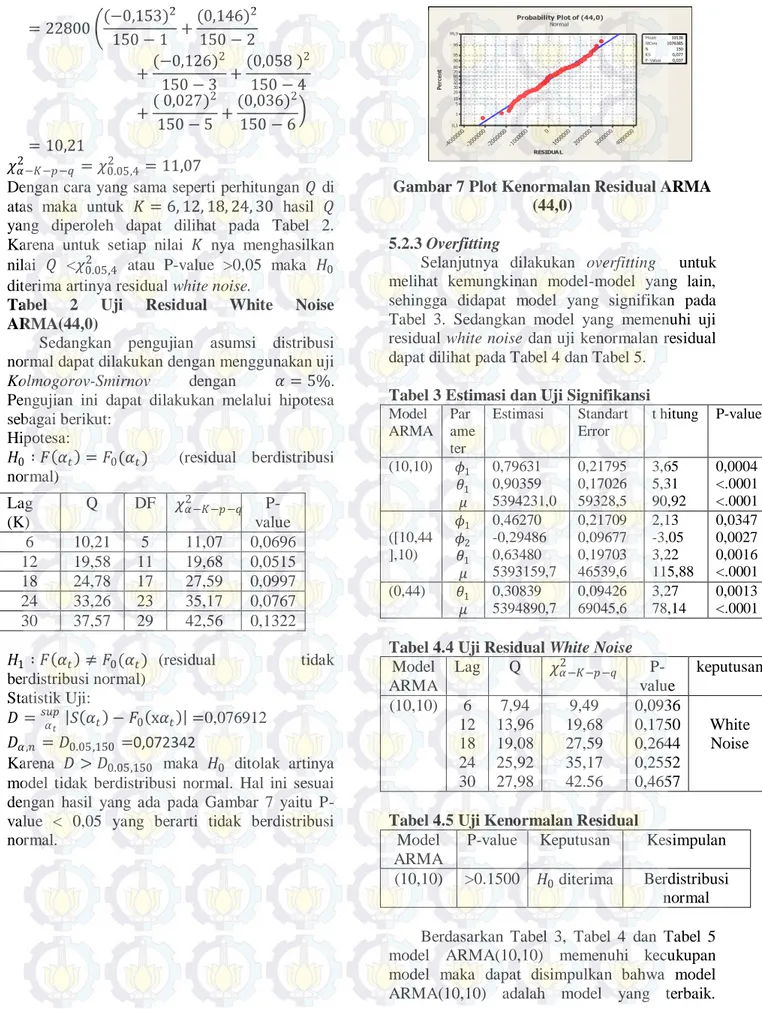
Gambar 2 Plot Box-Cox

Dari plot box-cox pada Gambar 2 diperoleh rounded value 𝜆 = 2, maka data penjualan Dannis Collection ini belum stasioner dalam varian, sehingga diperlukan transformasi dengan 𝑧′ _{= 𝑧}2_{, sehingga plot time series dan}

plot box-cox dapat dilihat pada Gambar 3 dan Gambar 4:

Gambar 3 Plot Transformasi Time Series

Gambar 4 Plot Transformasi Box-cox Berdasarkan Gambar 4 terlihat bahwa rounded value 𝜆 = 1, sehingga data penjualan Dannis Collection telah stasioner dalam varian. Langkah berikutnya yang harus dilakukan

Index C1 150 135 120 105 90 75 60 45 30 15 1 2750 2500 2250 2000 1750 1500

Time Series Plot of Resampling

Lambda St D ev 5,0 2,5 0,0 -2,5 -5,0 340 330 320 310 300 290 280 270 260 250 Lower CL Upper CL Limit Lambda 2,00 (using 95,0% confidence) Estimate 2,28 Lower CL 0,85 Upper CL 3,90 Rounded Value

Box-Cox Plot of Resampling

Index Tr an sf or m as i 150 135 120 105 90 75 60 45 30 15 1 8000000 7000000 6000000 5000000 4000000 3000000 2000000

Time Series Plot of Transformasi

Lambda St D ev 5,0 2,5 0,0 -2,5 -5,0 3000000 2500000 2000000 1500000 1000000 Lower CL Upper CL Limit Lambda 1,00 (using 95,0% confidence) Estimate 1,14 Lower CL 0,31 Upper CL 1,93 Rounded Value

7

adalah pengidentifikasi plot ACF dan PACF untuk menduga atau mengestimasi model awal peramalan data penjualan Dannis Collection. Plot ACF dan plot PACF ditunjukkan pada Gambar 5 dan Gambar 6.

Gambar 5 Plot ACF

Gambar 6 Plot PACF

Dari hasil output minitab yang ditunjukkan pada Gambar 4.5 dan Gambar 4.6, maka plot ACF (Gambar 4.5) dapat diketahui bahwa tidak ada lag yang keluar dari batas sedangkan plot PACF (Gambar 4.6) dapat diketahui ada dua lag yang keluar dari batas yaitu lag 10 dan 44 berarti ada dua parameter yang signifikan.

5.2.1 Estimasi dan Uji Signifikansi

Setelah melakukan pemeriksaan terhadap plot ACF dan PACF langkah selanjutnya adalah mengidentifikasikan kesignifikanan model dengan menggunakan software SAS. Maka untuk sementara model yang diduga adalah ARMA(44,0).

Tabel 1 Estimasi Parameter Data Penjualan Dannis Collection Model ARMA(44,0)

Param eter Estimasi Standart Error T hitun g P-value 𝜙1 -0.25343 0.09651 -2.63 0.0096 𝜇 5393182.8 74444.1 72.45 <.0001

Pengujian signifikan parameter dari model dalam Tabel 4.1 dengan menggunakan uji t-student dengan 𝛼 = 5%

Uji Signifikansi Parameter 𝝓1

Hipotesa:

𝐻0 ∶ 𝜙1= 0 (parameter tidak signifikan)

𝐻0 ∶ 𝜙1≠ 0 (parameter signifikan) Statistik Uji: 𝑡𝑕𝑖𝑡𝑢𝑛𝑔 = 𝜙1 𝑠𝑑(𝜙 )1 =−0.25343 0.09651 = −2.63 𝑡𝑡𝑎𝑏𝑒𝑙 = 𝑡𝛼 2 ,𝑛−𝑝−𝑞−1= 𝑡0.025,109 = 1,98 Karena 𝑡𝑕𝑖𝑡𝑢𝑛𝑔 > 𝑡𝑡𝑎𝑏𝑒𝑙 atau 𝑃 − 𝑣𝑎𝑙𝑢𝑒 =<

.0001 < 0,05 maka 𝐻0 ditolak artinya parameter

𝜙1 signifikan.

Uji Signifikansi Parameter 𝜇

Hipotesa:

𝐻0 ∶ 𝜇 = 0 (parameter tidak signifikan)

𝐻0 ∶ 𝜇 ≠ 0 (parameter signifikan) Statistik Uji: 𝑡𝑕𝑖𝑡𝑢𝑛𝑔 = 𝜇 𝑠𝑑(𝜇 )= 5393182.8 74444.1 = 72.45 𝑡𝑡𝑎𝑏𝑒𝑙 = 𝑡𝛼 2 ,𝑛−𝑝−𝑞−1= 𝑡0.025,109 = 1,98 Karena 𝑡_{𝑕𝑖𝑡𝑢𝑛𝑔} > 𝑡_{𝑡𝑎𝑏𝑒𝑙} atau 𝑃 − 𝑣𝑎𝑙𝑢𝑒 =< .0001 < 0,05 maka 𝐻0 ditolak artinya parameter

𝜇 signifikan.

5.2.2 Diagnoctic Checking

Ada dua asumsi yang harus dipenuhi dalam menentukan kecukupan model, yaitu residual bersifat white noise dan berdistribusi normal. Pengujian asumsi residual white noise dapat dilakukan dengan menggunakan uji Ljung-Box dengan 𝛼 = 5% sebagai berikut:

Hipotesa:

𝐻0 ∶ 𝜌1 = ⋯ = 𝜌𝑘 = 0

𝐻1 : minimal ada satu 𝜌𝑗 ≠ 0, dengan 𝑗 =

1, 2, … 𝐾

Statistik Uji Ljung-Box:

𝑄 = 𝑛(𝑛 + 2) 𝜌𝑘 2 𝑛 − 𝑘, 𝑛 > 𝑘 𝐾 𝑘=1 Untuk 𝐾 = 6 maka: 𝑄 = 150 150 + 2 𝜌𝑘 2 150 − 𝑘, 𝑛 > 𝑘 6 𝑘=1 Lag A ut oc or re la ti on 140 130 120 110 100 90 80 70 60 50 40 30 20 10 1 1,0 0,8 0,6 0,4 0,2 0,0 -0,2 -0,4 -0,6 -0,8 -1,0

Autocorrelation Function for Transformasi

(with 5% significance limits for the autocorrelations)

Lag Pa rt ia l A ut oc or re la ti on 140 130 120 110 100 90 80 70 60 50 40 30 20 10 1 0,2 0,0 -0,2

Partial Autocorrelation Function for Transformasi (with 5% significance limits for the partial autocorrelations)

8

= 22800 (−0,153) 2 150 − 1 + (0,146)2 150 − 2 +(−0,126) 2 150 − 3 + (0,058 )2 150 − 4 +( 0,027) 2 150 − 5 + (0,036)2 150 − 6 = 10,21 𝜒𝛼−𝐾−𝑝 −𝑞2 = 𝜒0.05,42 = 11,07

Dengan cara yang sama seperti perhitungan 𝑄 di atas maka untuk 𝐾 = 6, 12, 18, 24, 30 hasil 𝑄

yang diperoleh dapat dilihat pada Tabel 2. Karena untuk setiap nilai 𝐾 nya menghasilkan nilai 𝑄 <𝜒0.05,42 atau P-value >0,05 maka 𝐻0

diterima artinya residual white noise.

Tabel 2 Uji Residual White Noise ARMA(44,0)

Sedangkan pengujian asumsi distribusi normal dapat dilakukan dengan menggunakan uji Kolmogorov-Smirnov dengan 𝛼 = 5%. Pengujian ini dapat dilakukan melalui hipotesa sebagai berikut: Hipotesa: 𝐻0∶ 𝐹 𝛼𝑡 = 𝐹0(𝛼𝑡) (residual berdistribusi normal) 𝐻1 ∶ 𝐹 𝛼𝑡 ≠ 𝐹0(𝛼𝑡) (residual tidak berdistribusi normal) Statistik Uji: 𝐷 =𝑠𝑢𝑝_𝛼 𝑡 𝑆 𝛼𝑡 − 𝐹0 x𝛼𝑡 =0,076912 𝐷𝛼,𝑛 = 𝐷0.05,150 =0,072342

Karena 𝐷 > 𝐷0.05,150 maka 𝐻0 ditolak artinya

model tidak berdistribusi normal. Hal ini sesuai dengan hasil yang ada pada Gambar 7 yaitu P-value < 0,05 yang berarti tidak berdistribusi normal.

Gambar 7 Plot Kenormalan Residual ARMA (44,0)

5.2.3 Overfitting

Selanjutnya dilakukan overfitting untuk melihat kemungkinan model-model yang lain, sehingga didapat model yang signifikan pada Tabel 3. Sedangkan model yang memenuhi uji residual white noise dan uji kenormalan residual dapat dilihat pada Tabel 4 dan Tabel 5.

Tabel 3 Estimasi dan Uji Signifikansi

Model ARMA Par ame ter Estimasi Standart Error t hitung P-value (10,10) 𝜙1 𝜃1 𝜇 0,79631 0,90359 5394231,0 0,21795 0,17026 59328,5 3,65 5,31 90,92 0,0004 <.0001 <.0001 ([10,44 ],10) 𝜙1 𝜙2 𝜃1 𝜇 0,46270 -0,29486 0,63480 5393159,7 0,21709 0,09677 0,19703 46539,6 2,13 -3,05 3,22 115,88 0,0347 0,0027 0,0016 <.0001 (0,44) 𝜃1 𝜇 0,30839 5394890,7 0,09426 69045,6 3,27 78,14 0,0013 <.0001

Tabel 4.4 Uji Residual White Noise

Model ARMA Lag Q 𝜒_{𝛼−𝐾−𝑝 −𝑞}2 P-value keputusan (10,10) 6 12 18 24 30 7,94 13,96 19,08 25,92 27,98 9,49 19,68 27,59 35,17 42.56 0,0936 0,1750 0,2644 0,2552 0,4657 White Noise

Tabel 4.5 Uji Kenormalan Residual Model

ARMA

P-value Keputusan Kesimpulan (10,10) >0.1500 𝐻0diterima Berdistribusi

normal Berdasarkan Tabel 3, Tabel 4 dan Tabel 5 model ARMA(10,10) memenuhi kecukupan model maka dapat disimpulkan bahwa model ARMA(10,10) adalah model yang terbaik. Lag (K) Q DF 𝜒𝛼−𝐾−𝑝 −𝑞2 P-value 6 10,21 5 11,07 0,0696 12 19,58 11 19,68 0,0515 18 24,78 17 27,59 0,0997 24 33,26 23 35,17 0,0767 30 37,57 29 42,56 0,1322 RESIDUAL Pe rc en t 4000 000 3000 000 2000 000 1000 000 0 -10000 00 -20000 00 -30000 00 -40000 00 99,9 99 95 90 80 70 60 50 40 30 20 10 5 1 0,1 Mean 0,037 10138 StDev 1076385 N 150 KS 0,077 P-Value Probability Plot of (44,0) Normal

9

Model yang diperoleh selanjutnya akan digunakan meramalan data untuk 12 bulan yang akan datang mulai bulan Nopember 2010-Oktober 2011, hasil peramalannya disajikan dalam Tabel 6.

Tabel 6 Hasil Peramalan

Dari Tabel 6 dapat diketahui bahwa nilai-nilai dari data hasil ramalan tepat berada diantara nilai batas bawah untuk 𝛼 = 0,05 (L95) dan batas atas untuk 𝛼 = 0,05 (U95).

6. Penutup

Hasil yang diperoleh dari pembahasan di atas adalah:

1. Metode resampling Bootstrap dilakukan dengan pengestimasian dengan dua metode yaitu Maximum Likelihood Estimation (MLE) dan Unbiassed Estimation menghasilkan :

a. Maximum Likelihood Estimation

Untuk mean:

𝜇 = 𝑥

_𝑖𝑗∗

Untuk varian:

𝜍 2₌ 𝑥 𝑖 ∗_{− 𝜇} 2 𝑁 𝑗=1 𝑁 b. Unbiassed Estimatior

Untuk mean tidak terdapat error

pada saat

𝐸 𝑥

_𝑖,𝑗∗

= 𝜇

Untuk varian terdapat eror pada saat

𝐸 𝜍 2 _{= 𝜍}2

_sebesar

1

𝑁−1 𝑥 𝑖 ∗_{− 𝜇} 2 𝑁

𝑗 =1

dari hasil pengstimasian secara MLE dan Unbiassed estimation didapatkan selang kepercayaan 1 − 𝛼 100% dengan

𝑥

_𝑖,𝑗∗ dan

𝑠 yang merupakan rataan dan simpangan dari suatu populasi dengan 𝜍2 yang tidak diketahui adalah: 𝑥 𝑖,𝑗∗ ± 𝑧𝛼 ₂ 𝑥 _𝑖∗_{− 𝑥} 𝑖,𝑗∗ 2 𝑁 𝑗=1 𝑁 − 1 𝑛𝑁

2. Rata-rata penjualan baju koko Dannis Collection untuk 12 bulan ke depan adalah 2319 .

Saran yang dapat diberikan pada penelitian selanjutnya adalah menggunakan parameter lain seperti ARIMA atau Regresi, sehingga hasilnya bisa dibandingkan untuk mengetahui keakuratan hasilnya.

Daftar Pustaka

[1] Efron Bradley, 1994. The Jackknife, The Bootstrap and The Other Resampling Plans, Department of Statistics Stanford University.

[2] Makridakis, W. M. G. 1999. Metode dan Aplikasi Peramalan. Edisi kedua. Bina Rupa Aksara. Jakarta.

[3] Salamah, M., Suhartono., dan Wulandari S. 2003. Analisis Time Series. Surabaya: Jurusan Statistik ITS.

[4] Wei, W.W.S. 1990. “Time Series Analysis : Univariate and Multivariate Methods”. United State of America : Addison-Wesley Publishing Company. 52. Perio de Data Peramalan L95 U95 151 2262,434 1724,385 2695,128 152 2332,92 1815,877 2754,564 153 2305,145 1780,053 2731,08 154 2302,623 1776,786 2728,952 155 2410,9 1915,028 2820,912 156 2274,96 1740,786 2705,651 157 2354,209 1843,148 2772,617 158 2330,563 1812,849 2752,568 159 2314,039 1791,556 2738,591 160 2325,943 1806,905 2748,657 161 2274,808 1737,048 2707,797 162 2330,811 1809,769 2755,013