APLIKASI PROGRAM SOLVER DALAM PENYELESAIAN MASALAH OPTIMASI BERDASARKAN PERAMALAN DENGAN METODE TREND MUSIMAN PADA PERUSAHAAN KRUPUK UDANG SINAR JAYA BREBES.

(1)

APLIKASI PROGRAM SOLVER DALAM

PENYELESAIAN MASALAH OPTIMASI

BERDASARKAN PERAMALAN DENGAN METODE

TREND MUSIMAN

PADA PERUSAHAAN KRUPUK

UDANG SINAR JAYA BREBES

Skripsi

Disajikan sebagai salah satu syarat untuk memperoleh Gelar sarjana sains prodi matematika

oleh Siti Nurchotimah

4150405047

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS NEGERI SEMARANG

(2)

ii

Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Semarang pada:

Hari : Tanggal :

Panitia Ujian:

Ketua Sekretaris

Dr. Kasmadi Imam S, M.S. Drs. Edy Soedjoko, M.Pd NIP. 195111151979031001 NIP 19560419 198703 1 001

Penguji Utama,

Endang Sugiharti, S.Si., M.Kom. NIP. 132231407

Penguji / Pembimbing I, Penguji / Pembimbing II,

Dr. Dwijanto, M.S Drs. Mashuri, M.Si

(3)

iii

hasil karya saya sendiri, bukan jiplakan dari karya tulis orang lain baik sebagian atau seluruhnya. Pendapat atau temuan orang lain yang terdapat dalam skripsi ini dikutip dan dirujuk berdasarkan kode etik ilmiah.

Semarang, September 2009 Penulis,

(4)

iv

☺Sesungguhnya setelah ada kesulitan itu ada kemudahan (Q.S. An Nashr : 6). ☺Jenius adalah 1 % inspirasi dan 99 % keringat. Tidak ada yang dapat

menggantikan kerja keras. Keberuntungan adalah sesuatu yang terjadi ketika kesempatan bertemu dengan kesiapan (Thomas A. Edison).

☺The man who says he never has time is the laziest man (Lichtenberg).

Persembahan

☺ Bapak, ibu, adik-adikku dan budhe tercinta ☺ Sahabat-sahabat kost Griya Monesy

(5)

v

Optimasi Berdasarkan Peramalan dengan Metode Trend Musiman Pada Perusahaan Krupuk Udang Sinar Jaya Brebes. Skripsi, Jurusan Matematika. Fakultas Matematika dan Ilmu Pengetahuan Alam. Universitas Negeri Semarang. Dosen Pembimbing I: Dr. Dwijanto, M.S.; Dosen Pembimbing II: Drs. Mashuri, M.Si.

Kata Kunci : Program Solver, Peramalan, Metode Trend Musiman.

Perusahaan Krupuk Udang Sinar Jaya Brebes adalah perusahaan yang menjalankan proses produksinya berdasarkan pesanan atau permintaan. Jadi jumlah pemenuhan permintaan pasar atau konsumen di sini merupakan penjualan. Untuk memperkirakan banyaknya permintaan pasar di masa mendatang diperlukan peramalan sebagai bahan pertimbangan dalam mengambil keputusan banyaknya barang yang akan diproduksi. Salah satu metode peramalan adalah metode trend musiman. Metode ini cocok untuk data yang membentuk pola musiman. Hasil ramalan tersebut dijadikan sebagai fungsi kendala dalam model penyelesaian masalah optimasi pendapatan. Dalam hal ini penulis menggunakan program solver untuk menyelesaikan masalah optimasi tersebut.

Permasalahan dalam skripsi ini adalah bagaimana model ramalan masing-masing jenis krupuk pada Perusahaan Krupuk Udang Sinar Jaya agar bisa memprediksi jumlah krupuk yang dipesan pada masa yang akan datang, dan bagaimana penyelesaian model matematika dari suatu masalah optimasi pada perusahaan krupuk udang Sinar Jaya menggunakan program solver. Adapun tujuan dari penulisan skripsi ini adalah untuk mengetahui model ramalan masing-masing jenis krupuk pada Perusahaan Krupuk Udang Sinar Jaya agar bisa memprediksi jumlah krupuk yang dipesan pada masa yang akan datang, dan untuk menyelesaiakan model matematika dari suatu masalah optimasi pada perusahaan krupuk udang Sinar Jaya menggunakan program solver.

Metode penelitian dari skripsi ini adalah dengan menemukan masalah, merumuskan masalah, melakukan pengambilan data sekunder dari Perusahaan Krupuk Udang Sinar Jaya dan studi pustaka, menganalisis dan memecahkan masalah serta penarikan kesimpulan.

(6)

vi

banyaknya jenis krupuk PITA yang diproduksi=225, SPKK=1676, GNP=15494,

GND=31767, MB=5721, GNB=329, dan pendapatan yang diperoleh= Rp 507.773.100,-.

(7)

vii

Nya sehingga penulis dapat menyelesaikan skripsi dengan judul “ Aplikasi Program Solver dalam Penyelesaian Masalah Optimasi Berdasarkan Peramalan dengan Metode Trend Musiman Pada Perusahaan Krupuk Udang Sinar Jaya Brebes”. Skripsi ini disajikan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Prodi Matematika. Penulis menyadari sepenuhnya bahwa skripsi ini dapat terselesaikan karena bantuan dari banyak pihak, oleh karena itu penulis menyampaikan rasa terima kasih yang sebesar-besarnya pada:

1. Prof. Dr. Sudijono Sastroatmodjo, M.Si, Rektor Universitas Negeri Semarang. 2. Dr. Kasmadi Imam S, M.S, Dekan FMIPA Universitas Negeri Semarang. 3. Drs. Edy Soedjoko, M.Pd, Ketua Jurusan Matematika FMIPA Universitas

Negeri Semarang.

4. Dr. Dwijanto, M.S, Dosen pembimbing I yang telah memberikan bimbingan dan arahan kepada penulis dalam menyusun skripsi ini.

5. Drs. Mashuri, M.Si, Dosen pembimbing II yang telah memberikan bimbingan dan arahan kepada penulis dalam menyusun skripsi ini.

6. Bapak/Ibu Dosen khususnya jurusan Matematika FMIPA yang telah memberi bekal kepada penulis selama kuliah.

7. Bapak Dul Ali, Bendahara Perusahaan Krupuk Udang Sinar Jaya yang telah memberi kesempatan dalam pelaksanaan penelitian dan pengambilan data. 8. Kedua orang tua dan keluarga besar yang telah ikut berkorban dan

memberikan perhatian dalam meyelesaikan skripsi ini.

9. Sahabat-sahabatku di ”Alas Pete” yang sudah membagi pengalaman hidupnya. 10.Teman-teman Matematika angkatan 2005. Terima kasih atas semua kenangan

dan kita akan tetap berjuang.

(8)

viii

Semarang,

(9)

ix

HALAMAN JUDUL ... i

HALAMAN PENGESAHAN ... ii

PERNYATAAN ... iii

MOTTO DAN PERSEMBAHAN ... iv

ABSTRAK ... v

KATA PENGANTAR ... vii

DAFTAR ISI ... ix

DAFTAR TABEL ... xii

DAFTAR GAMBAR ... xiii

DAFTAR LAMPIRAN ... xiv

BABI. PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Rumusan Masalah... ... 6

1.3 Tujuan Penelitian ... 6

1.4 Manfaat Penelitian ... 6

1.5 Sistematika Skripsi ... 7

BABII. LANDASAN TEORI 2.1 Riset Operasi ... 9

2.2 Program Linear ... 11

2.2.1 Solusi PL dengan Metode Grafik ... 13

2.2.2 Solusi PL dengan Metode Simpleks ... 17

2.3 Metode Trend Musiman ... 23

2.3.1 Gerakan Musiman dan Indeks Musiman ... 23

2.3.1.1 Metode Rata-rata Sederhana ... 23

2.3.1.2 Metode Persentase terhadap Trend ... 24

2.3.1.3 Metode Rata-rata Bergerak ... 25

2.3.2 Membuat Tabel Deseasonalizing ... 26

(10)

x

2.5.1 Sejarah Berdirinya Perusahaan ... 38

2.5.2 Struktur Organisasi ... 38

2.5.3 Bahan Baku dan Proses Produksi ... 41

2.5.3.1 Bahan Baku ... 41

2.5.3.2 Proses Produksi ... 42

2.5.3 Pemasaran Produk ... 43

BABIII. METODE PENELITIAN 3.1 Menemukan Masalah ... 46

3.2 Merumuskan Masalah ... 47

3.3 Pengambilan Data ... 48

3.4 Analisis dan Pemecahan Masalah... ... 48

3.5 Penarikan Simpulan ... 51

BABIV. HASIL PENELITIAN DAN PEMBAHASAN 4.1. Hasil Penelitian ... 52

4.2 Pembahasan ... 72

BABV. PENUTUP 5.1 Simpulan ... 75

5.2 Saran ... 76

(11)

xi

1. Tabel Kebutuhan dan Waktu yang Tersedia ... 14

2. Tabel Nilai fungsi tujuan pada solusi fisibel titik ekstrim ... 17

3. Tabel Iterasi 0 awal ... 18

4. Tabel Iterasi 0 ... 19

5. Tabel Nilai Zj dan Zj-Cj ... 19

6. Tabel Iterasi 0 akhir ... 20

7. Tabel Baris dan Kolom Kunci Iterasi 0... 20

10. Tabel Baris dan Kolom Kunci Iterasi 1 ... 22

13. Tabel Kebutuhan Paket ... 29

14. Tabel Formula pada Sel ... 31

15. Tabel Data Penjualan Januari tahun 2006 sampai dengan Desember 2008 dalam Perkuartalan ... 52

16. Tabel Rata-rata Bergerak 4 Kuartal (PITA) ... 53

17. Tabel Indeks Musim Krupuk PITA... 54

18. Tabel Deseasonalizing Krupuk PITA ... 54

19. Tabel Rata-rata Bergerak 4 Kuartal (SPKK) ... 55

20. Tabel Indeks Musim Krupuk SPKK ... 56

21. Tabel Deseasonalizing Krupuk SPKK ... 56

22. Tabel Rata-rata Bergerak 4 Kuartal (GNP) ... 57

23. Tabel Indeks Musim Krupuk GNP ... 58

24. Tabel Deseasonalizing Krupuk GNP ... 58

25. Tabel Rata-rata Bergerak 4 Kuartal (GND) ... 59

26. Tabel Indeks Musim Krupuk GND ... 60

(12)

xii

31. Tabel Rata-rata Bergerak 4 Kuartal (GNB) ... 63

32. Tabel Indeks Musim Krupuk GNB ... 64

33. Tabel Deseasonalizing Krupuk GNB ... 64

34. Tabel Ramalan Tahun 2009 ... 65

(13)

xiii

1. Gambar 1 ….. ... 15

2. Gambar 2 ... 16

3. Gambar 3 ... 16

4. Tampilan Tabel Awal Kebutuhan Paket ... 30

5. Tampilan Solver Parameter ... 32

6. Tampilan Subject to the constraints ... 33

7. Tampilan Solver Options... 34

8. Tampilan Solver Results ... 34

9. Tampilan Lembar Answer ... 35

10. Tampilan Lembar Sensitivity... 36

11. Tampilan Lembar Limits ... 37

12. Struktur Organisasii Perusahaan Krupuk Udang Sinar Jaya ... 39

13. Grafik Penjualan per kuartal dan rata-rata bergerak terpusat (PITA) ... 53

14. Grafik Penjualan per kuartal dan rata-rata bergerak terpusat (SPKK) ... 55

15. Grafik Penjualan per kuartal dan rata-rata bergerak terpusat (GNP) ... 57

16. Grafik Penjualan per kuartal dan rata-rata bergerak terpusat (GND) ... 59

17. Grafik Penjualan per kuartal dan rata-rata bergerak terpusat (MB) ... 61

18. Grafik Penjualan per kuartal dan rata-rata bergerak terpusat (GNB) ... 63

19. Tampilan Hasil Optimasi Kuartal 1 ... 68

(14)

xiv

1. Data Penjualan bulan Januari tahun 2006 sampai dengan Juni tahun

2009 ... 78

2. Diagram Scatter Plot Data Penjualan Krupuk ... 79

3. Perhitungan Ramalan Penjualan Tahun 2009 ... 81

4. Perhitungan Harga Selisih Data Asli dan Data Ramalan ... 82

5. Model matematika yang terbentuk dari masalah optimasi pada Perusahaan Krupuk Udang Sinar Jaya Brebes ... 83

6. Formula pada Sel ... 84

7. Skema Proses Produksi Krupuk Udang Perusahaan Krupuk Udang Sinar Jaya Brebes ... 85

8. Usulan Pembimbing ... 86

(15)

1

BAB I

PENDAHULUAN

1.1

Latar Belakang

Kemajuan ilmu pengetahuan dan teknologi semakin dirasakan kegunaannya oleh manusia. Hal ini terjadi karena hasil kemajuan teknologi merupakan bagian yang tidak dapat dipisahkan dengan kebutuhan manusia itu sendiri. Pesatnya perkembangan ilmu pengetahuan dan teknologi tersebut tidak lepas dari peranan matematika. Tidak dapat dipungkiri bahwa matematika telah menjadi elemen dasar bagi perkembangan ilmu pengetahuan dan teknologi. Hampir dapat dipastikan bahwa setiap bagian dari ilmu pengetahuan baik dalam unsur kajian umum, ilmu murni maupun terapannya memerlukan peranan matematika sebagai alat bantunya.

(16)

Riset Operasi/Operation Research (OR) adalah bagian dari aplikasi matematika untuk memecahkan masalah optimasi. Masalah optimasi adalah masalah memaksimumkan dan meminimumkan sebuah besaran tertentu yang disebut tujuan objektif yang bergantung pada sejumlah berhingga variabel masukan (input variabel). Variabel ini dapat tidak saling bergantungan atau saling bergantungan melalui satu atau lebih kendala (constraints). Contoh untuk permasalahan yang dimaksimumkan adalah masalah keuntungan dan pendapatan sedangkan untuk masalah meminimumkan adalah masalah biaya, persediaan dan lain-lain. Banyak model OR yang sudah dikembangkan yang berhubungan dengan matematika untuk memecahkan masalah optimasi, salah satunya yaitu Program Linear.

Program linear adalah suatu alat yang digunakan untuk menyelesaikan masalah optimasi suatu model linear dengan keterbatasan-keterbatasan sumber daya yang tersedia. Masalah program linear berkembang pesat setelah ditemukan suatu metode penyelesaian program linear dengan metode simpleks yang dikemukakan oleh George Dantzig pada tahun 1947. Selanjutnya berbagai alat dan metode dikembangkan sampai pada masalah riset operasi hingga tahun 1950-an seperti pemrogram1950-an dinamik, teori 1950-antri1950-an, d1950-an teori persedia1950-an.

(17)

perusahaan tersebut menjalankan proses produksi berdasarkan pesanan atau permintaan. Jadi dalam hal ini pemenuhan permintaan konsumen tersebut merupakan penjualan. Jumlah permintaan itu sendiri tiap tahunnya mengalami naik turun karena dipengaruhi faktor-faktor seperti pendapatan masyarakat yang tidak tetap, persaingan pasar, selera konsumen, kualitas, pemasaran, dan lain-lain. Meskipun daerah pemasaran perusahaan tersebut semakin meluas hingga ke luar kota seperti Jakarta, Bandung, Solo, Yogyakarta, Magelang, Semarang, dan Riau, tetapi adanya faktor-faktor tadi menyebabkan permintaan konsumen dapat mengalami peningkatan pada periode tertentu dan penurunan pada periode lain.

Melihat kondisi tersebut maka pada suatu proses produksi tidak hanya bertujuan mengoptimalkan persediaan agar diperoleh sisa persediaan yang seminimal mungkin, tetapi juga harus memperhatikan kualitas penjualan suatu barang agar diperoleh pendapatan optimal. Sebagai contoh, dengan hanya mempertimbangkan optimalisasi persediaan, perhitungan program linear memberikan kebijakan memproduksi barang tipe A sebanyak 100 dan B sebanyak 200, padahal pasar tidak memungkinkan penjualan A dan B sebanyak itu pada periode tertentu. Jika keputusan yang diambil tetap memproduksi sebanyak itu maka sisa barang yang tidak terjual dapat menyebabkan kerugian. Oleh karena itulah diperlukan adanya peramalan penjualan pasar di masa yang akan datang sebagai bahan pertimbangan dalam mengambil kebijakan produksi.

(18)

secara pasti di masa mendatang karena perubahan tersebut dipengaruhi faktor-faktor yang sangat kompleks, misalnya kebudayaan masyarakat sekitar, penghasilan keluarga, keadaan pribadi dan sebagainya. Oleh karena itu diperlukan adanya ramalan untuk meminimumkan pengaruh ketidakpastian tersebut (Subagyo, 1986:1 ).

Ramalan yang akan dilakukan umumnya akan berdasarkan data masa lampau yang dianalisis dengan menggunakan cara-cara tertentu. Data masa lampau dikumpulkan, dipelajari, dan dianalisis kemudian dihubungkan dengan perjalanan waktu. Karena adanya faktor itu, maka dari hasil analisis itu dapat diprediksi kemungkinan yang akan terjadi pada masa yang akan datang. Jelas, dalam hal ini akan dihadapkan pada suatu ketidakpastian sehingga akan ada faktor akurasi yang harus diperhatikan.

(19)

produksi suatu barang akan lebih bagus. Masalah optimasi dapat diselesaikan dengan cara manual, tetapi membutuhkan waktu yang lama karena terdapat banyak variabel sehingga diperlukan bantuan komputer untuk menyelesaikannya.

Perkembangan yang terjadi pada teknologi komputer yang cukup pesat, telah merambah ke berbagai sektor kehidupan manusia. Saat ini telah tersedia berbagai macam software yang dapat digunakan sebagai alat bantu untuk menyelesaikan persoalan-persoalan di berbagai bidang, termasuk persoalan optimasi. Dengan bantuan software, permasalahan yang sebelumnya sulit karena melibatkan variabel yang cukup banyak sehingga tidak memungkinkan penyelesaian secara manual akan dapat dipecahkan dengan mudah. Dalam penyusunan skripsi ini, penulis memecahkan masalah optimasi tersebut menggunakan program Solver.

Solver adalah program add in yang berada di bawah program Excel. Program solver ini berisi perintah-perintah yang berfungsi untuk melakukan analisis terhadap masalah optimasi. Jika kita instal Microsoft Excel tidak secara otomatis Solver ini terinstal, jadi harus diinstal secara khusus setelah program Excel terinstal pada komputer. Program solver ini cukup baik untuk menyelesaikan masalah optimasi. Menjalankan programnya juga sederhana apalagi kalau sudah dapat menggunakan program Excel (Dwijanto, 2008:49).

(20)

1.2

Permasalahan

Dari uraian di atas penulis dapat merumuskan masalah sebagai berikut. (1) Bagaimana model ramalan masing-masing jenis krupuk pada Perusahaan

Krupuk Udang Sinar Jaya agar bisa memprediksi jumlah krupuk yang dipesan pada masa yang akan datang?

(2) Bagaimana penyelesaian model matematika dari suatu masalah optimasi pada perusahaan Krupuk Udang Sinar Jaya menggunakan program solver?

1.3

Tujuan

Tujuan dari skripsi ini adalah:

(1) Untuk mengetahui model ramalan masing-masing jenis krupuk pada Perusahaan Krupuk Udang Sinar Jaya agar bisa memprediksi jumlah krupuk yang dipesan pada masa yang akan datang.

(2) Untuk menyelesaikan model matematika dari suatu masalah optimasi pada perusahaan Krupuk Udang Sinar Jaya menggunakan program solver.

1.4

Manfaat

(1) Dengan mengetahui prediksi yang akan datang akan diperoleh kebijakan yang lebih bagus.

(2) Memberikan informasi untuk mendapatkan model matematikanya.

(21)

1.5

Sistematika Skripsi

Secara garis besar skripsi ini dibagi menjadi tiga bagian yaitu bagian awal skripsi, bagian pokok skripsi, dan bagian akhir skripsi.

Bagian awal skripsi meliputi Halaman Sampul, Halaman Judul, Abstrak, Halaman Pengesahan, Motto dan Persembahan, Kata Pengantar, Daftar Isi, Daftar Gambar, Daftar Tabel, Daftar Lampiran.

Bagian pokok skripsi secara garis besar terdiri dari lima bab, yaitu: BAB I PENDAHULUAN

Di dalam bab ini dikemukakan latar belakang masalah,

perumusan masalah, manfaat penelitian, dan sistematika

skripsi.

BAB II LANDASAN TEORI

Di dalam bab ini dikemukakan konsep-konsep yang dijadikan landasan teori sebagai berikut. Riset Operasi, Program Linear, Metode Trend Musiman, Program Solver untuk menyelesaikan masalah program linear. BAB III METODE PENELITIAN

Di dalam bab ini dikemukakan metode penelitian yang berisi langkah-langkah yang harus ditempuh untuk membahas permasalahan, yaitu identifikasi masalah, perumusan masalah, observasi, analisis data, dan penarikan simpulan.

BAB IV HASIL PENELITIAN DAN PEMBAHASAN

(22)

masalah optimasi berdasarkan peramalan dengan metode Trend Musiman pada perusahaan krupuk udang Sinar Jaya Brebes.

BAB V PENUTUP

Di dalam bab ini dikemukakan simpulan dari pembahasan dan saran yang berkaitan dengan simpulan.

(23)

9

BAB II

LANDASAN TEORI

2.1

Riset Operasi

Riset operasi yang berasal dari Inggris merupakan suatu hasil studi operasi-operasi militer selama Perang Dunia II. Setelah perang selesai, potensi komersialnya segera disadari dan pengembangannya telah menyebar dengan cepat di Amerika Serikat, dimana ia lebih dikenal dengan nama Riset Operasi atau Operatins Research (disingkat OR). Kini OR banyak diterapkan dalam menyelesaikan masalah-masalah manajemen untuk meningkatkan produktivitas atau efisiensi.

(24)

Pola dasar penerapan OR terhadap suatu masalah dapat dipisahkan menjadi beberapa tahap.

(1) Merumuskan masalah

Komponen penting dalam perumusuan masalah adalah sebagai berikut. a. Variabel keputusan yaitu unsur-unsur dalam penyelesaian yang dapat

dikendalikan oleh pengambil keputusan.

b. Tujuan (objective) yaitu hasil akhir yang hendak dicapai dengan cara memilih suatu tindakan yang paling tepat untuk sistem yang dipelajari. c. Kendala (constraints) yaitu pembatas-pembatas tehadap alternatif yang

tersedia.

(2) Pembentukan model

Sesuai dengan definisi persoalannya, maka pengambil keputusan menentukan model yang paling cocok untuk mewakili sistem.

(3) Mencari penyelesaian masalah

Proses penyelesaian dengan bermacam-macam teknik dan metode solusi kuantitatif untuk suatu model.

(4) Validasi model

Tahap untuk menguji validitas model, yaitu membandingkan performancenya dengan data masa lalu yang tersedia. Model dikatakan valid jika dengan kondisi input yang serupa, ia dapat menghasilkan kembali

performance seperti masa lampau. (5) Penerapan hasil akhir

(25)

2.2

Program Linear

Program linear (PL) merupakan suatu alat yang digunakan untuk menyelesaikan masalah optimasi suatu model linear dengan keterbatasan-keterbatasan sumber daya yang tersedia. PL banyak digunakan untuk menyelesaikan masalah optimasi di dalam industri, perbankkan, pendidikan dan masalah-masalah lain yang dapat dinyatakan dalam bentuk linear. Bentuk linear di sini berarti bahwa seluruh fungsi dalam model ini merupakan fungsi linear.

Secara umum, fungsi pada model ini ada dua macam yaitu fungsi tujuan dan fungsi pembatas. Fungsi tujuan dimaksudkan untuk menentukan nilai optimum dari fungsi tersebut yaitu nilai maksimal untuk masalah keuntungan dan nilai minimal untuk masalah biaya. Fungsi pembatas diperlukan berkenaan dengan adanya keterbatsan sumber daya yang tersedia, misalnya jumlah bahan baku yang terbatas, waktu kerja, jumlah tenaga kerja, luas gudang persediaan. Tujuan utama dari pogram linear ini adalah menentukan nilai optimum (maksimal/minimal) dari fungsi tujuan yamg telah ditetapkan (Dwijanto, 2008:13).

Pada dasarnya tidak semua masalah bisa diselesaikan dengan PL. Ada beberapa prinsip yang mendasari penggunaan PL, yaitu:

(1) Adanya sasaran. Sasaran dalam model matematika masalah PL berupa fungsi tujuan (fungsi objektif) yang akan dicari nilai optimalnya (maksimum/minimum).

(26)

(3) Adanya keterbatasan sumber daya. Sumber daya atau input dapat berupa waktu, biaya bahan dan sebagainya. Pembatas sumber daya disebut kendala (constraints) pembatas.

(4) Masalah harus dapat dituangkan dalam bahasa matematika yang disebut model matematika. Model matematika dalam PL memuat fungsi tujuan dan kendala. Fungsi tujuan harus berupa fungsi linear dan kendala berupa pertidaksamaan atau persamaan linear.

(5) Antar variabel yang membentuk fungsi tujuan dan kendala ada keterkaitan, artinya perubahan pada satu peubah akan mempengaruhi nilai peubah yang lain (Suyitno, 1997:8).

(27)

Banyak cara untuk menyelesaikan masalah dalam PL yaitu cara manual yaitu menggunakan perhitungan biasa sampai menggunakan bantuan komputer untuk penyelesaian masalah yang cukup rumit. Apabila banyaknya variabel (peubah) hanya dua buah, maka kita dapat menyelesaikan masalah PL dengan metode grafik, tetapi dengan keterbatasan metode ini, maka untuk masalah dengan banyaknya variabel yang lebih dari dua, metode ini kurang cocok (Dwijanto, 2008:13).

2.2.1 Solusi PL dengan Metode Grafik

Menyelesaikan masalah PL dengan metode grafik berarti menggambar pembatas sebagai grafik dalam ruang berdimensi dua, jika model matematikanya memuat dua variabel dan dalam ruang tiga jika model matematikanya memuat tiga variabel. Contoh masalah yang dapat diselesaikan dengan program linear menggunakan metode grafik adalah sebagai berikut.

Sebuah perusahaan mebel memproduksi dua jenis alat rumah tangga yaitu rak buku dan meja. Setiap hasil produksi harus melalui dua tahap yaitu pemotongan dan perampungan. Untuk pemotongan tiap rak buku memerlukan waktu 4 jam dan untuk meja juga sama. Untuk proses perampungan memerlukan 3 jam untuk rak buku dan 2 jam untuk meja. Rak buku jika dijual memberi laba Rp 8000,0/buah dan meja Rp 6000,-/buah. Waktu yang tersedia untuk pemotongan pada setiap periode waktu 100 jam dan untuk perampungan tersedia 60 jam. Perusahaan ingin menentukan jumlah produksi untuk masing-masing jenis barang agar diperoleh laba maksimal.

(28)

Untuk menyederhanakan masalah ini, kita buat tabel berkenaan dengan masalah pada contoh ini.

Tabel 1. Kebutuhan dan waktu yang tersedia

Barang

Lama Proses

Banyaknya Pemotongan (jam) Perampungan (jam)

Rak buku 4 3 X1

Meja 4 2 X2

Waktu yg

tersedia 100 60

Dari Tabel 1 di atas, kemudian dibuat model matemátikanya sebagai berikut.

Fungsi tujuan :

Maksimumkan Z = 8000x1 + 6000x2 Fungsi Pembatas:

4 x1 + 4 x2 ≤ 100 3 x1 + 2 x2 ≤ 60

x1 ≥ 0, x2 ≥0

Untuk membuat grafik, pertama-pertama buatlah sistem sumbu koordinat dengan sumbu x1 mendatar dan sumbu x2 tegak, kemudian buatlah garis dengan persamaan 4 x1 + 4 x2 = 100.

(29)

4 x1 + 4 * 0 = 100 4 x1 = 100

x1 = 25

diperoleh titik (25,0)

Titik potong dengan sumbu X2 yaitu dengan memberikan 0 pada nilai X1, sehingga diperoleh: 4 x1 + 4 x2 = 100

4 * 0 + 4 x2 = 100 4 x2 = 100

X2 = 25

diperoleh titik (0,25). Hubungkan kedua titik itu.

(25,0)

(0,25)

Gambar 1

(30)

(0,25)

Gambar 2. (25,0)

Selanjutnya dengan cara yang sama, digambar dari fungsi pembatas 3x1 + 2x2 ≤ 60, sehingga diperoleh grafik seperti pada Gambar 3 berikut.

(0,30)

(0,25)

(10,15)

(20,0) (25,0)

Gambar 3

(31)

Tabel 2. Nilai fungsi tujuan pada solusi fisibel titik ekstrim

Titik Nilai Z

(0,0) 0

(20,0) 160000

(10,15) 170000

(0,25) 150000

Dari Tabel 2. Terlihat bahwa nilai Z maksimum terjadi pada titik (10,15) dengan nilai Z = 170000.

Ini berarti supaya diperoleh laba maksimum, maka harus dibuat 10 buah rak buku dan 15 buah meja.

2.2.2 Solusi PL dengan Metode Simpleks

Metode simpleks merupakan teknik yang dikembangkan untuk memecahkan masalah PL yang mempunyai jumlah variabel keputusan dan pembatas yang besar. Contoh penyelesaian masalah dengan Metode Simpleks adalah sebagai berikut.

Maksimumkan Z = 20 X1 + 30 X2 + 40 X3 Harus memenuhi:

4 X1 + 5 X2 + 6 X3 ≤ 24000 2 X1 + 3 X2 + 4 X3 ≤ 15000 2 X1 + 5 X2 + 5 X3 ≤ 18000 X1, X2, X3 ≥ 0

(32)

Untuk menyelesaikan masalah di atas dengan metode simpleks kita ubah persamaan di atas menjadi sistem persamaan dengan menambahkan variabel tiruan, sebut saja variabel s1, s2 dan s3, sehingga terbentuk sistem persamaan berikut.

Maksimumkan Z = 20 X1 + 30 X2 + 40 X3 + 0 s1 + 0 s2 + 0 s3 Harus memenuhi:

4 X1 + 5 X2 + 6 X3 + s1 ≤ 24000 2 X1 + 3 X2 + 4 X3 + s2 ≤ 15000 2 X1 + 5 X2 + 5 X3 + s3 ≤ 18000 X1, X2, X3, s1, s2, s3 ≥ 0

Langkah awal kita tidak membuat apa-apa, sehingga variabel yang masuk terlebih dahulu adalah s1, s2, dan s3. Dari sistem persamaan ini kita buat tabel berikut Tabel 3. Iterasi 0 awal

Iterasi 0 20 30 40 0 0 0 Rasio

CB VDB Q X1 X2 X3 S1 S2 S3

S1

S2

S3

Zj

Zj-Cj

(33)

CB : koefisien variabel basis yang masuk pada fungsi tujuan VDB : variabel basis yang masuk

Q : banyaknya barang

Zj : nilai fungsi tujuan yaitu jumlah dari hasil kali variabel ke j dan CB

Cj : koefisien variabel pada fungsi tujuan (bilangan yang terletak di atas variabel)

Selanjutnya kita isi tabel sesuai dengan sistem persamaan di atas sehingga kita peroleh tabel berikut.

Tabel 4. Iterasi 0

CB VDB Q X1 X2 X3 S1 S2 S3

0 S1 24000 4 5 6 1 0 0

0 S2 15000 2 3 4 0 1 0 0 S3 18000 2 5 5 0 0 1

Zj

Zj-Cj

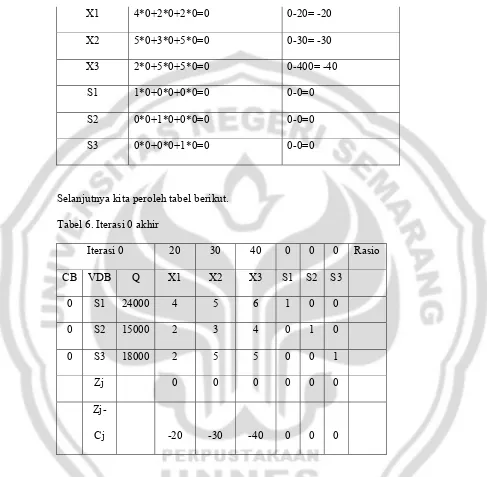
Kita hitung nilai Zj dan Zj-Cj sebagai berikut. Tabel 5. Nilai Zj dan Zj-Cj

Variabel Zj Zj-Cj

(34)

X1 4*0+2*0+2*0=0 0-20= -20

X2 5*0+3*0+5*0=0 0-30= -30

X3 2*0+5*0+5*0=0 0-400= -40

S1 1*0+0*0+0*0=0 0-0=0

S2 0*0+1*0+0*0=0 0-0=0

S3 0*0+0*0+1*0=0 0-0=0

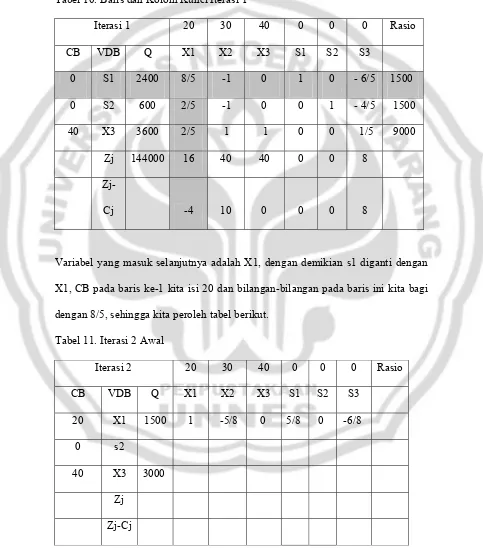
Selanjutnya kita peroleh tabel berikut. Tabel 6. Iterasi 0 akhir

CB VDB Q X1 X2 X3 S1 S2 S3

0 S1 24000 4 5 6 1 0 0

0 S2 15000 2 3 4 0 1 0

0 S3 18000 2 5 5 0 0 1

Zj 0 0 0 0 0 0

Zj-Cj -20 -30 -40 0 0 0

Kita tentukan kolom kunci (nilai yang nilai Zj-Cj paling kecil) yaitu kolom pada variabel X3. Lalu kita hitung rasionya. Rasio untuk baris pada variabel:

(35)

Jadi baris kuncinya adalah baris yang memuat variabel s3 (rasio paling kecil yaitu 3600), sehingga tabel menjadi.

Tabel 7. Baris dan Kolom Kunci Iterasi 0

CB VDB Q X1 X2 X3 S1 S2 S3

0 S1 24000 4 5 6 1 0 0 4000

0 S2 15000 2 3 4 0 1 0 3750

0 S3 18000 2 5 5 0 0 1 3600

Zj 0 0 0 0 0 0

Zj-Cj -20 -30 -40 0 0 0

Dari perhitungan di atas selanjutnya X3 menggantikan s3, CB kita isi koefisien X3 yaitu sebesar 40 dan pada baris ini bilangan kunci kita ubah menjadi 1 yaitu dengan membagi 3. Dengan demikian maka baris ini kita bagi dengan 3 sehingga diperoleh tabel berikut.

Tabel 8. Iterasi 1 Awal

CB VDB Q X1 X2 X3 S1 S2 S3

0 S1

0 S2

40 X3 10 1 2/3 2/3 0 0 1/3

B

(36)

Zj

Zj-Cj

Lakukan operasi baris elementer, sehingga bilangan pada kolom kunci menjadi 0. Untuk lebih mudahnya kita gunakan B1 (baris 1 adalah baris pertama yang berada pada matriks utama), B2 (baris 2 adalah baris ke-2 pada matriks utama) dan seterusnya, sehingga Bn adalah baris ke-n pada matriks utama. Selanjutnya Bn* adalah baris ke-n baru dalam suatu iterasi.

Pada baris ke-1, dengan rumusan B1-B3* dan pada baris ke-2 dengan rumusan B2-2*B3*, kemudian kita hitung nilai Zj dan Zj-Cj, sehingga kita peroleh tabel berikut.

Tabel 9. Iterasi 1

CB VDB Q X1 X2 X3 S1 S2 S3

0 S1 2400 8/5 -1 0 1 0 - 6/5

0 S2 600 2/5 -1 0 0 1 - 4/5

40 X3 3600 2/5 1 1 0 0 1/5

Zj 144000 16 40 40 0 0 8

(37)

Kolom kunci adalah kolom yang memuat X1, kemudian kita hitung rasio dan menentukan bilangan kunci. Sehingga kita peroleh tabel.

Tabel 10. Baris dan Kolom Kunci Iterasi 1

0 S1 2400 8/5 -1 0 1 0 - 6/5 1500

0 S2 600 2/5 -1 0 0 1 - 4/5 1500

40 X3 3600 2/5 1 1 0 0 1/5 9000

Zj 144000 16 40 40 0 0 8

Zj-Cj -4 10 0 0 0 8

Variabel yang masuk selanjutnya adalah X1, dengan demikian s1 diganti dengan X1, CB pada baris ke-1 kita isi 20 dan bilangan-bilangan pada baris ini kita bagi dengan 8/5, sehingga kita peroleh tabel berikut.

Tabel 11. Iterasi 2 Awal

CB VDB Q X1 X2 X3 S1 S2 S3

20 X1 1500 1 -5/8 0 5/8 0 -6/8

0 s2

40 X3 3000

Zj

(38)

Dengan melakukan OBE pada baris pertama dan ke-3, menghitung Zj dan Zj-Cj seperti perhitungan di atas, maka kita peroleh.

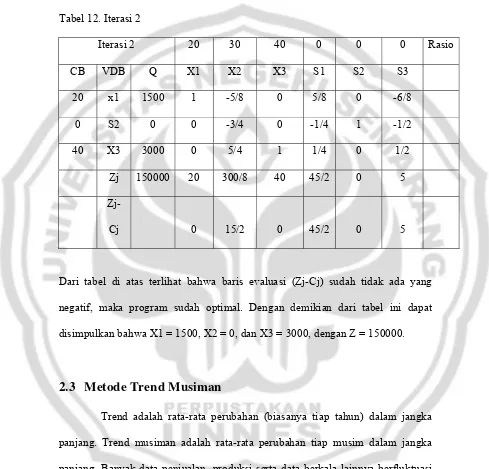
Tabel 12. Iterasi 2

20 x1 1500 1 -5/8 0 5/8 0 -6/8

0 S2 0 0 -3/4 0 -1/4 1 -1/2

40 X3 3000 0 5/4 1 1/4 0 1/2

Zj 150000 20 300/8 40 45/2 0 5

Zj-Cj 0 15/2 0 45/2 0 5

Dari tabel di atas terlihat bahwa baris evaluasi (Zj-Cj) sudah tidak ada yang negatif, maka program sudah optimal. Dengan demikian dari tabel ini dapat disimpulkan bahwa X1 = 1500, X2 = 0, dan X3 = 3000, dengan Z = 150000.

2.3

Metode Trend Musiman

(39)

2.3.1 Gerakan Musiman dan Indeks Musiman

Gerakan musiman (seasonal movement) merupakan gerakan yang teratur dan hampir terjadi pada waktu-waktu tertentu. Disebut gerakan musiman karena terjadinya bertepatan dengan pergantian musiman dalam suatu tahun. Untuk menunjukan ada tidaknya gerakan musiman, maka perlu dibuat indeks musiman (seasonal index). Indeks musiman dapat dihitung dengan beberapa metode yaitu metode rata sederhana, metode persentase terhadap trend, dan metode rata-rata begerak.

2.3.1.1Metode Rata-rata Sederhana (Simple Average Method)

Dalam metode ini, indeks musiman dihitung berdasarkan rata-rata tiap periode musim setelah bebas dari pengaruh trend. Adapun langkah-langkah yang harus dilakukan sebagai berikut.

(1) Menyusun data tiap kuartal atau bulan sesuai kebutuhan, untuk masing-masing tahun.

(2) Mencari rata-rata tiap kuartal pada tahun-tahun tersebut.

(3) Karena rata-rata tersebut masih mengandung unsur kenaikan (trend) maka dihilangkan terlebih dahulu pengaruh trend ini dengan mengurangkan dengan b secara kumulatif (disebut kolom sisa).

(4) Mencari rata-rata dari kolom sisa yaitu dengan membagi jumlah pada kolom sisa dengan empat.

(40)

2.3.1.2Metode Persentase Terhadap Trend (Ratio to Trend Method)

Untuk mencari indeks musim dengan metode ini, yang pertama dicari adalah nilai real dan nilai trendnya, kemudian berdasarkan persentase itu dicari indeks musim

(1) Mencari nilai trend pada setiap periode.

(2) Mencari persentase nulai real terhadap nilai trend dengan cara membagi nilai real dengan nilai trend kemudian dikalikan dengan 100.

(3) Dari langkah 2 di atas dicari median tiap kuartal dengan tidak memandang kapan terjadinya.

(4) Menghitung rata-rata dari median tersebut.

(5) Menghitung indeks musiman dengan cara median dibagi rata-rata median dikalikan 100.

2.3.1.3Membuat Tabel Rata-rata Bergerak

Dalam metode rata-rata bergerak ini, mula-mula dicari rata-rata bergerak dari data historis dan setelah ini kita tentukan indeks musimnya. Prosedur perhitungan sebagai berikut.

(1) Susunlah data historis yang ada ke dalam tabel pada kolom 1, menyatakan tahun, kolom 2 menyatakan periode musiman (kuartalan), kolom 3 menyatakan data yang sudah ada.

(41)

(3) Hitunglah rata-rata bergerak dengan membagi pada kolom 4 dengan 4 dan meletakan hasilnya pada kolom 5.

(4) Hitunglah rata-rata bergerak pusat dengan menjumlahkan dua periode pada kolom 5 kemudian dibagi 2, letakan hasilnya pada kolom 6 pada pertengahan dua periode.

(5) Hitung indeks musiman dengan membagi data asli dengan rata-rata bergerak pusatnya letakkan hasilnya pada kolom 7.

(6) Indeks musiman tersebut kita susun pada tabel indeks dibagi menurut tahun dan periode musiman yang dikehendaki.

(7) Lihat satu per satu menurut musim pada tahun tersebut lalu jumlahkan menurut musimnya.

(8) Cari rata-rata tiap musimnya, setelah itu jumlahkan rata-rata tiap musimnya tersebut.

(9) Menghitung Faktor Koreksi

rata rata keempat Jumlah koreksi faktor −

= 4,00

(10) Indeks tipe tri wulan (kuartalan) dapat dihitung dengan rumus:

pertahun musim jumlah musiman rata rata total x musim tiap rata rata

indeks= − −

(42)

2.3.2 Membuat Tabel Deseasonalizing

Prosedur pembuatan tabel Deseasonalizing adalah sebagai berikut. (1) Susunlah data historis yang ada ke dalam tabel pada kolom 1 menyatakan

tahun, kolom 2 menyatakan periode musiman, kolom 3 menyatakan data yang ada, kolom 4 menyatakan indeks setiap musim.

(2) Hitung Deseasonalizing (y) dengan cara membagi data yang ada dengan indeks musimnya, letakan hasilnya pada kolom 5.

(3) Nyatakan kolom 6 urutan musim tiap tahun (t). (4) Kalikan t dan y, letakan hasilnya pada kolom 7. (5) Kuadratkan t, letakan hasilnya kolom 8.

(Subagyo, 1986:65)

2.3.3 Membuat model Trend

Model trend dapat dirumuskan sebagai berikut. Y’ = a + b t

dimana,

Y’ adalah estimasi trend untuk periode t

a adalah titik perpotongan garis trend dengan 0 b adalah kemiringn (slope) dari garis trend t adalah nilai waktu yang dipilih

(43)

) ( ) ( ) )( ( 2 2 n t b n Y a n t t n t Y tY b

∑

− = − − =

(Mason, 1996: 348)

2.3.4 Peramalan Data

Peramalan data dalam hal ini dapat dirumuskan dengan: F = T x M

dengan F = Peramalan data.

T = Nilai trend musiman yang diramal. M = Indeks dari T.

2.4

Program Solver untuk Menyelesaikan Program Linear

(44)

Microsoft Excel Solver mengkombinasikan fungsi dari suatu Graphical User Interface (GUI), suatu algebraic modeling language seperti GAMS (Brooke, Kendrick, dan Meeraus 1992) atau AMPL (Fourer, Gay, and Kernighan 1993), dan optimizers untuk linear, nonlinear, dan integer program. Masing-masing fungsi ini terintegrasi ke dalam spreadsheet program. Fitur ini diinstal secara tersendiri karena merupakan fasilitas tambahan/optional.

Solver merupakan bagian dari serangkaian perintah/command yang seringkali disebut what-if analysis tool. Fasilitas ini bekerja dengan sel-sel suatu grup yang saling terhubung, baik secara langsung ataupun tidak langsung (directly-inderectly), untuk formula pada sel target. Solver terdiri dari tiga bagian: (1) Adjustable cells/sel pengatur

Solver mengatur perubahan nilai pada sel yang spesifik, untuk memproduksi hasil perlu spesifikasi dari formula pada sel target.

(2) Constrained cells/sel pembatas

Constraint digunakan untuk membatasi nilai solver yang dapat digunakan pada suatu model tertentu dan constraint mengacu pada sel lain yang memperngaruhi formula pada sel target.

(3) Target cells/sel target

Merupakan bagian solver sebagai tempat dimana hasil akhir pemrosesan/eksekusi suatu formula ditempatkan.

(45)

Paket A berisi 1 botol sirup, 3 bungkus biskuit dan 2 bungkus permen dan dijual Rp 65.000,00 per paket. Paket B berisi 1 botol sirup, 2 bungkus biskuit dan 1 bungkus permen dijual Rp 45.000,00. Paket C berisi 1 botol sirup, 1 bungkus biskuit dan 3 bungkus permen dijual Rp 50.000,00. Banyaknya sirup, biskuit dan ppermen yang tersedia berturut-turut adalah 400 botol sirup, 900 bungkus biskuit dan 800 bungkus permen. Toko Maju ingin memperoleh hasil penjualan yang sebesar-besarnya. Tentukan banyaknya masing-masing paket dengan asumsi semua paket terjual habis.

Penyelesaian:

Tabel yang dapat dibuat dari masalah ini adalah sebagai berikut. Tabel 13. Kebutuhan Paket

Paket A Paket B Paker C Jumlah

Barang

Sirup 1 1 1 400

Biskuit 3 2 1 900

Permen 2 1 3 800

Harga (dalam ribuan) 65 45 50

(46)

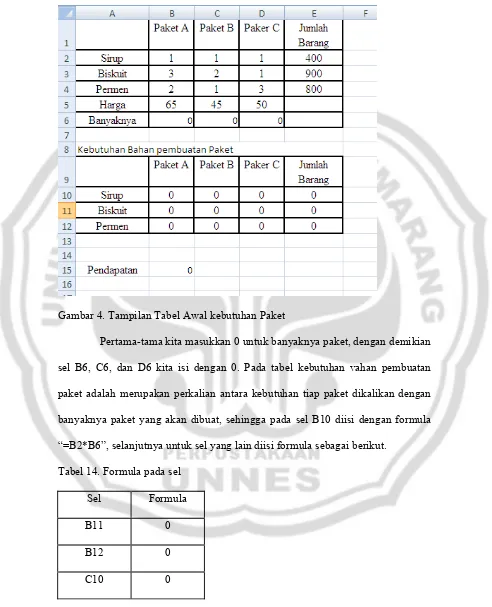
Gambar 4. Tampilan Tabel Awal kebutuhan Paket

Pertama-tama kita masukkan 0 untuk banyaknya paket, dengan demikian sel B6, C6, dan D6 kita isi dengan 0. Pada tabel kebutuhan vahan pembuatan paket adalah merupakan perkalian antara kebutuhan tiap paket dikalikan dengan banyaknya paket yang akan dibuat, sehingga pada sel B10 diisi dengan formula “=B2*B6”, selanjutnya untuk sel yang lain diisi formula sebagai berikut.

Tabel 14. Formula pada sel

Sel Formula

B11 0

B12 0

(47)

C11 0

C12 0

D10 0

D11 0

D12 0

Untuk praktisnya penulisan rumus di atas digunakan perintah copy-paste saja. Untuk itu pada sel B10 kita isi formula “=B2*$B$6 kemudian sel ini kita

copy, kemudian kita blok (sorot) pada sel B10 sampai D12 lalu kita paste, maka sel B10 dampai D12 akan terisi nilai 0.

Jumlah barang merupakan jumlah antara kebutuhan paket A, paket B, dan paket C, sehingga pada sel E10 kita isi dengan formula “=B10+C10+D10 atau dengan formula “=sum(B10:D10)” selanjutnya formula pada sel ini kita copykan ke dalam sel E11 dan E12.

Pendapatan merupakan hasil kali antara banyaknya barang (paket) dan harga satuan barang. Jadi sel B15 kita isikan formula “=B5*B6+C5*C6+D5*D6” atau dengan formula “=sumproduct(B5:D5;B6:D6). Dengan demikian persiapan untuk menjalankan program solver selesai.

(48)

Gambar 5. Tampilan Solver Parameter

Pada Set Target Cell kia isi Pendapatan, yaitu cukup mengklik sel B15, maka pada Set Target Cell akan terisi $B$15.

Equal To kita isi fungsi tujuan yaitu memaksimumkan, jadi kita pilih Max. By Changing Cells kita isi variabel yang kita cari, yaitu banyaknya barang (paket), jadi kita isi sel B6 sampai dengan D6 yaitu dengan melakukan drag pada sel-sel B6 sampai dengan D6.

(49)

E11 <= E3, dan E12 <= E4 yaitu dengan cara mengklik Add dan muncul menú berikut.

Gambar 6. Tampilan Subject to the constrains

(50)

Gambar 7. Tampilan Solver Options

Pilihlah Assume Linear Model dan Assume Non-Negative, kemudian pilih OK, maka akan kembali ke menu solver. Selanjutnya pilih Solve, maka diperoleh hasil.

(51)

Kita lihat hasil perhitungan, bahwa banyaknya paket A sebanyak 200 buah, paket B sebanyak 100 buah, dan paket C sebanyak 100 buah, dengan pendapatan 22500. Selanjutnya apabila kita pilih OK maka pekerjaan selesai, tetapi jika kita mengklik Answer, Sensitivity, dan Limits kemudian OK, maka akan kita peroleh kesimpulan atau uraian tentang jawaban (Answer), analisis Sensitivity, dan hasil Limitnya yang dituliskan pada lembar kerja sisipan (di depan sheet yang kita pakai). Lembar-lembar kerja ini kita buka maka akan terlihat sebagai berikut.

Gambar 9. Tampilan Lembar Answer

(52)

paket C adalah 100 buah. Sirup sebanyak 400 botol dipakai habis, demikian pula biscuit 900 bungkus dan permen 800 bungkus dipakai habis, yaitu terlihat pada Slack terisi 0.

Gambar 10. Tampilan Lembar Sensitivity

(53)

perubahan harga paket C bergerak diantara Rp 25.000 dan Rp 85.000. Sedangkan Tabel Constraints menunjukan bahwa jika persediaan biscuit dan permen tetap, maka sirup dapat berubah menjadi antara 357 dan 520. Dengan cara yang sama, jika persediaan sirup dan permen tetap, maka biscuit dapat berubah menjadi antara 600 dan 1200. Demikian pula jika persediaan sirup dan biscuit tetap, maka permen dapat berubah menjadi antara 500 dan 950.

Gambar 11. Tampilan Lembar Limits

(54)

2.5

Gambaran Umum Perusahaan Krupuk Udang Sinar Jaya

2.5.1 Sejarah Berdirinya Perusahaan

Perusahaan Krupuk Udang Sinar Jaya didirikan oleh Bapak H. Madnuri pada tahun 1971 di daerah Brebes. Pada awal berdirinya, perusahaan ini hanya memiliki karyawan sebanyak 15 orang dengan kapasitas produksi 300 Kg/ hari dan peralatan proses produksi yang masih sederhana. Perusahaan Krupuk Udang Sinar Jaya yang terletak di jalan Sunan Bonang Kaligangsa Kulon Brebes ini merupakan perusahaan perorangan yang dikelola secara kekeluargaan.

Perusahaan Krupuk Udang Sinar Jaya telah diakui keberadaannya dengan mendapat ijin usaha dari Depertemen Perindustrian pada Tahun 1971 kemudian diperbaharui dengan Surat Keputusan (SK) terbaru yaitu SK Menteri Perindustrian nomor 267/11/4/11/1990 tentang pemberian ijin usaha tetap.

Setelah beberapa tahun, dengan keuletan dalam berusaha perusahaan ini dapat berkembang. Baik dalam jumlah karyawan maupun kapasitas produksi mengalami peningkatan, proses produksi pun menggunakan mesin yang lebih modern.

2.5.2 Struktur Organisasi

(55)

oleh seorang kepala bagian yang bertanggung jawab kepada pemimpin perusahaan.

Struktur organisasi Perusahaan Krupuk Udang Sinar Jaya dapat dilihat pada gambar berikut.

Gambar 12. Struktur Organisasi Perusahaan Krupuk Udang Sinar Jaya Brebes Adapun uraian tugas dan tanggung jawab atas fungsi-fungsi yang ada dalam perusahaan adalah sebagai berikut.

(1) Pimpinan Perusahaan

Tugas dan tanggung jawabnya adalah:

• Memimpin dan mengawasi pelaksanaan tugas seluruh bawahannya dan

menetapkan kebijaksanaan perusahaan. Pimpinan Perusahaan

Wakil Pimpinan Perusahaan

Kabag. Dapur/Produksi

Bendahara

Kabag. Teknisi Kabag.

Penjemuran

Kabag. Pemasaran

(56)

• Bertanggung jawab atas maju mundurnya perusahaan dan mengendalikan

harta perusahaan.

(2) Wakil Pimipinan Perusahaan

• Membantu pemimpin perusahaan dalam mengelola perusahaan.

• Membantu beberapa koordinator bagian, meliputi bagian teknisi, dapur,

penjemuran, dan pemasaran. (3) Bendahara

• Bertanggung jawab atas keluar masuknya uang, langsung mengawasi

pembukuan, kasir, dan pengupahan.

• Mengatur dan mengawasi pembukuan serta surat-menyurat perusahaan.

(4) Kabag. Teknisi

• Mengkoordinir pekerja pada bagian teknisi.

(5) Kabag. Dapur/Produksi

• Mengkoordinir pekerja pada bagian dapur/produksi krupuk.

(6) Kabag. Penjemuran

• Mengkoordinir pekerja pada bagian penjemuran krupuk.

(7) Kabag. Pemasaran

(57)

• Mengkoordinir pekerja pada bagian pemasaran.

• Menjalin hubungan dengan para agen dan pihak perantara lain.

• Mencari informasi pasar dan konsumen.

2.5.3 Bahan Baku dan Proses Produksi

2.5.3.1 Bahan Baku

Bahan baku utama yang diperlukan oleh perusahaan krupuk udang ini, diantaranya:

(1) Tepung Tapioka

Tepung tapioka merupakan bahan baku utama yang diperlukan dalam pembuatan krupuk udang yang diperoleh dari daerah Bogor dan Bandung. Pembeliannya dengan cara memesan terlebih dahulu. Tepung tapioka yang digunakan ini khusus digunakan untuk pembuatan krupuk udang.

(2) Ikan

Ikan adalah salah satu bahan makanan dengan kandungan protein yang sangat tinggi. Daging ikan ini digunakan sebagai tambahan udang dalam pembuatan krupuk udang.

(3) Udang

Udang merupakan bahan dasar dalam pembuatan krupuk udang yang diperoleh perusahaan dari daerah sekitar Brebes.

(58)

2.5.2.2 Proses Produksi

Proses produksi krupuk udang Perusahaan Krupuk Udang Sinar Jaya meliputi beberapa tahap pengelolaan sebagai berikut.

(1) Pembersihan udang (kulit dan kepala udang dibuang) (2) Penggilingan dan pencampuran

Udang yang sudah bersih tadi digiling, lalu dicampur dengan bahan-bahan lain sesuai ukuran jenis krupuk. Selanjutnya, uleni hingga membentuk adonan.

(3) Pencetakan

Adonan yang sudah jadi dimasukkan dalam cetakan sesuai jenis krupuk. Kemudian atur cetakan-cetakan dalam ancak dan siap direbus.

(4) Perebusan/pengukusan

Cetakan-cetakan yang sudah diatur dalam ancak tadi direbus selama satu jam. Setelah matang, disiram dengan air dingin lalu diproses (dipres selama lima menit).

(5) Penirisan

Krupuk yang sudah dipres, lalu di atur di atas kreta, kemudian ditiriskan selama dua malam.

(6) Pemotongan

Setelah selesai ditiriskan, krupuk dimasukkan dalam mesin pemotong untuk diiris.

(7) Penjemuran

(59)

(8) Penyortiran krupuk

Setelah dijemur krupuk disortir ke bagian pengemasan/pengepakan.

(9) Pengemasan/pengepakan

Krupuk-krupuk yang sudah kering dan dengan hasil yang baik, dibungkus dalam plastik sesuai jenis krupuk kemudian dikemas dalam kardus.

(10) Penyimpanan di gudang

Krupuk yang sudah dikemas dalam kardus sementara disimpan dalam gudang, kemudian didistribusikan ke pemesan.

Produk yang dihasilkan oleh Perusahaan Krupuk Udang Sinar Jaya ada 14 jenis yang dibagi menjadi 3 macam yaitu:

(1) Krupuk udang kualitas super, meliputi: PITA, SJ-71, SPKK.

(2) Krupuk udang kualitas sedang, melliputi: SPK, GNP, GNO, UNYIL, PTR, GND.

(3) Krupuk udang kualitas umum, meliputi: GNB, GNM, JPT, SKP, MB.

2.5.3 PemasaranProduk

(60)

harga, pelayanan, dan kualitas produk. Dengan demikian adanya kebijaksanaan tersebut diharapkan hasil penjualan yang diperoleh Perusahaan Krupuk Udang Sinar Jaya di Kabupaten Brebes dapat meningkat sesuai dengan tujuan dan rencana yang telah ditetapkan.

Perusahaan Krupuk Udang Sinar Jaya dalam membuat produknya sangat memperhatikan kebutuhan dan keinginan konsumen agar produk yang ditawarkan dapat diterima di pasar konsumen karena sesuai dengan selera konsumen, sehingga produk memberikan kepuasan kepada kedua belah pihak. Masalah pemasaran ini sangat berpengaruh terhadap kelangsungan hidup perusahaan, untuk mengetahui hal tersebut pihak perusahaan menugaskan kepada bagian pemasaran untuk mencari informasi pasar dan konsumen, di sini mereka dibantu agen yang telah diajak untuk bekerja sama dalam penjualan produk.

Dalam perekonomian seperti sekarang ini sebagian produsen menjual barang melalui agen, tidak langsung ke konsumen akhir. Demikian pula dengan Perusahaan Krupuk Udang Sinar Jaya dalam menjual barangnya. Untuk mendistribusikan hasil produksinya perusahaan menggunakan saluran distribusi tidak langsung. Hasil produksinya dijual melalui agen yang ditunjuk kemudian ke pengecer.

Saluran distribusi produk yang dihasilkan perusahaan dapat dilakukan dalam beberapa jalur, yaitu:

(1) Perusahaan – Agen – Pedagang Besar - Pedagang kecil – Konsumen

(61)

Jakarta, Tasik Malaya, dan Riau. Dalam hal ini agen merupakan pedagang perantara yang berhubungan langsung dengan perusahaan, sedangkan pedagang besar, pedagang kecil dan konsumen akhir di daerah tersebut dilayani oleh agen.

(2) Perusahaan – Pedagang Besar – Pedagang kecil – Konsumen

Saluran pemasaran ini untuk wilayah yang agak jauh dari perusahaan misalnya : Semarang, Cirebon, Indramayu. Untuk pedagang kecil dan konsumen dilayani oleh pedagang besar.

(3) Perusahaan – Pedagang Kecil – Konsumen

(62)

48

BAB III

METODE PENELITIAN

Metode penelitian merupakan suatu cara yang digunakan dalam penelitian sehingga dapat dipertanggung jawabkan secara ilmiah. Dengan metode penelitian data yang diperoleh semakin lengkap untuk memecahkan masalah yang dihadapi. Pada penelitian ini prosedur/langkah-langkah yang digunakan adalah sebagai berikut.

3.1

Menemukan Masalah

Dalam tahap ini peneliti mengamati kenyataan-kenyataan yang ada di lapangan dan menemukan beberapa hal yang ingin dikaji. Pada bidang industri, salah satu masalah optimasi yang muncul adalah menentukan banyaknya produksi agar perusahaan memperoleh pendapatan maksimal. Permasalahan optimasi ini dapat diselesaikan dengan menggunakan program linear. Untuk menyelesaikan masalah program linear itu sendiri dapat digunakan metode grafik maupun metode simpleks pada masalah yang sederhana, sedangkan untuk masalah yang rumit dan memerlukan ketelitian yang tinggi sehingga cara manual sudah tidak efektif lagi dapat menggunakan software yang dapat menyelesaikan masalah optimasi.

(63)

proses produksi berdasarkan pesanan. Oleh karena itu diperlukan adanya peramalan penjualan pada masa yang akan datang untuk membantu dalam hal perencanaan, pengawasan dan pengambilan keputusan dalam memproduksi barang sehingga perusahaan dapat memaksimalkan pendapatan.

Dari kondisi tersebut peneliti mempunyai inisiatif untuk meramalkan penjualan perusahaan krupuk udang Sinar Jaya berdasarkan data penjualan tahun 2006 sampai dengan tahun 2008 dan dengan memasukan hasil peramalan penjualan tersebut dalam fungsi kendala diharapkan dapat memperoleh penyelesaian masalah optimasi yang berkaitan dengan jumlah produksi suatu barang akan lebih bagus.

3.2

Merumuskan Masalah

Masalah yang ditemukan kemudian dirumuskan ke dalam pertanyaan yang harus diselesaikan yaitu:

(1) Bagaimana model ramalan masing-masing jenis krupuk pada Perusahaan Krupuk Udang Sinar Jaya agar bisa memprediksi jumlah krupuk yang dipesan pada masa yang akan datang?

(64)

3.3

Pengambilan Data

Dalam penelitian ini, penulis memperoleh data dengan metode dokumentasi yaitu metode pengumpulan data dengan cara:

(1) Mengambil data sekunder yang diperoleh dari Perusahaan Krupuk Udang Sinar Jaya Brebes.

(2) Studi pustaka yaitu mengkaji sumber-sumber pustaka dengan cara mengumpulkan data atau informasi yang berkaitan dengan masalah, mengumpulkan konsep pendukung yang diperlukan dalam menyelesaikan masalah, sehingga didapatkan suatu ide mengenai bahan dasar pengembangan upaya pemecahan masalah.

3.4

Analisis dan Pemecahan Masalah

Sebelum analisis dan pemecahan masalah, penulis memiliki beberapa asumsi dalam penelitian ini sebagai berikut.

(1) Penelitian hanya dilakukan pada produksi krupuk udang jenis PITA, SPKK, GNP, GND, MB, dan GNB.

(2) Data yang diambil di Perusahaan Krupuk Udang Sinar Jaya Brebes adalah data dari bulan Januari tahun 2006 sampai dengan bulan Juni tahun 2009.

(65)

(1) Membuat plot data penjualan.

(2) Menyusun data tiap kuartal untuk masing-masing tahun.

(3) Menghitung indeks musiman dengan metode rata-rata bergerak.

a. Susunlah data historis yang ada ke dalam tabel pada kolom 1, menyatakan tahun, kolom 2 menyatakan periode musiman (kuartalan), kolom 3 menyatakan data yang sudah ada.

b. Hitung jumlah bergerak selama satu tahun dan letakkan hasilnya pada kolom 4 pada pertengahan data.

c. Hitunglah rata-rata bergerak dengan membagi pada kolom 4 dengan 4 dan meletakan hasilnya pada kolom 5.

d. Hitunglah rata-rata bergerak pusat dengan menjumlahkan dua periode pada kolom 5 kemudian dibagi 2, letakan hasilnya pada kolom 6 pada pertengahan dua periode.

e. Hitung indeks musiman dengan membagi data asli dengan rata-rata bergerak pusatnya letakkan hasilnya pada kolom 7.

f. Indeks musiman tersebut kita susun pada tabel indeks dibagi menurut tahun dan periode musiman yang dikehendaki.

g. Lihat satu per satu menurut musim pada tahun tersebut lalu jumlahkan menurut musimnya.

(66)

i. Menghitung Faktor Koreksi rata rata keempat Jumlah koreksi faktor −

= 4,00

(4) Menghitung indeks kuartalan.

Indeks tipe tri wulan (kuartalan) dapat dihitung dengan rumus:

pertahun musim jumlah musiman rata rata total x musim tiap rata rata

indeks= − −

(5) Menghitung tabel deseasonalizing dari data penjualan krupuk. Prosedur pembuatan tabel deseasonalizing adalah sebagai berikut.

a. Susunlah data historis yang ada ke dalam tabel pada kolom 1 menyatakan tahun, kolom 2 menyatakan periode musiman, kolom 3 menyatakan data yang ada, kolom 4 menyatakan indeks setiap musim. b. Hitung Deseasonalizing (y) dengan cara membagi data yang ada

dengan indeks musimnya, letakan hasilnya pada kolom 5. c. Nyatakan kolom 6 urutan musim tiap tahun (t).

d. Kalikan t dan y, letakan hasilnya pada kolom 7. e. Kuadratkan t, letakan hasilnya kolom 8.

(6) Membuat scatter plot data asli dengan data deseasonalized dengan bantuan Microsoft Excel.

(7) Mencari persamaan trend.

(8) Menghitung peramalan data penjualan krupuk dengan data deseasonalized. (9) Menentukan model matematika dari masalah optimasi pada Perusahaan

(67)

(10) Menambahkan hasil ramalan penjualan sebagai fungsi kendala.

(11) Menentukan penyelesaian model matematika masalah optimasi pada Perusahaan Krupuk Udang Sinar Jaya dengan menggunakan program Solver kemudian mengintrepetasikannya.

3.5

Penarikan Simpulan

(68)

54

BAB IV

HASIL PENELITIAN DAN PEMBAHASAN

4.1

Hasil Penelitian

Dari data penjualan yang tertera pada Lampiran 1 dan dengan bantuan Excel, penulis memperoleh ploting data yang membentuk pola musiman (Lampiran 2) pada setiap jenis krupuk sehingga penulis menggunakan analisis Trend Musiman untuk meramalkan penjualan krupuk pada masa yang akan datang. Data penjualan tersebut kemudian dibuat perkuartalnya untuk dianalisis dengan metode Trend Musiman. Penjualan yang dimaksud di sini adalah pemenuhan permintaan pasar atau konsumen.

Tabel 3. Data Penjualan Januari Tahun 2006 sampai dengan Desember 2008 dalam Perkuartalan

TAHUN KUARTAL

PENJUALAN

PITA SPKK GNP GND MB GNB

2006

1 986 1,225 16,535 2,655 14,148 1,650

2 457 2,225 22,713 16,140 5,159 1,660

3 1,137 2,855 27,935 10,135 17,999 3,045

4 194 1,330 14,232 24,260 4,950 240

2007

1 1,135 1,310 15,758 1,950 15,933 2,035

2 561 2,785 23,623 15,020 6,755 1,935

3 1,297 3,530 31,965 11,750 19,370 3,705

4 250 1,535 14,468 32,215 6,214 370

(69)

2 504 2,710 24,440 16,425 5,680 1,715

3 1,224 3,195 30,120 8,410 19,025 3,605

4 189 1,460 15,535 30,240 4,905 250

(1) Model Prediksi Penjualan dengan Trend Musiman a. Jenis Krupuk PITA (A)

Tabel 4. Rata-rata Bergerak 4 Kuartal

Tahun Kuartal penjualan

total rata2 bergerak

4 kuartal

rata2 bergerak

4 kuartal

rata2 bergerak

terpusat 4 kuartal indeks

2006

1 986

2 457

2,774 693.50

3 1,137 712.13 1.60

2,923 730.75

4 194 743.75 0.26

3,027 756.75

2007

1 1,135 776.75 1.46

3,187 796.75

2 561 803.75 0.70

3,243 810.75

3 1,297 796.38 1.63

3,128 782.00

4 250 774.88 0.32

3,071 767.75

2008

1 1,020 758.63 1.34

(70)

2 504 741.88 0.68

2,937 734.25

3 1,224

4 189

0 200 400 600 800 1,000 1,200 1,400

0 1 2 3 4 5 6 7 8 9 10 11 12 13

PENJUALAN

RATA2 BGRK TRPST

Gambar 10. Grafik penjualan per kuartal dan rata-rata bergerak terpusat Tabel 5. Indeks Musim Krupuk PITA

Tahun kuartal 1 kuartal 2 kuartal 3 kuartal 4 faktor koreksi

1.60 0.26 0.50

1.46 0.70 1.63 0.32

1.34 0.68

Jml 2.81 1.38 3.23 0.58 7.99

rata2 1.40 0.69 1.61 0.29 4.0

Indeks 2.80 1.38 3.22 0.58

Tabel 6. Deseasonalizing Krupuk PITA

penjualan indeks

penjualan

deseasonalized (y) t ty t^2

(71)

457 1.38 332.14 2 664.28 4

1,137 3.22 352.89 3 1,058.67 9

194 0.58 332.83 4 1,331.33 16

1,135 2.80 404.94 5 2,024.70 25

561 1.38 407.72 6 2,446.34 36

1,297 3.22 402.55 7 2,817.85 49

250 0.58 428.91 8 3,431.26 64

1,020 2.80 363.91 9 3,275.19 81

504 1.38 366.30 10 3,662.98 100

1,224 3.22 379.89 11 4,178.82 121

189 0.58 324.25 12 3,891.05 144

Jumlah 4448.12 78 29,134.24 650

Dari tabel deseasonalizing diperoleh Σy = 4448,12, Σty = 29134,24, Σt = 78,

Σt2 = 650, dengan rumus

∑

− − = n t t n t Y tY b ₂

2 ( )

) )( (

=1,55 dan

61 , 360 ) ( = − =

∑

n t b n Y

a sehingga diperoleh Model Trend Musiman

Y’ = (360,61 + 1,55 t) x Mt

b. Jenis Krupuk SPKK Tabel 7. Rata-rata Bergerak 4 Kuartal

Tahun Kuartal penjualan

total rata2

bergerak 4 kuartal

rata2

bergerak 4

kuartal

rata2 bergerak

(72)

2006

1 1,225

2 2,225

7,635 1,908.75

3 2,855 1,919.38 1.49

7,720 1,930.00

4 1,330 2,000.00 0.67

8,280 2,070.00

2007

1 1,310 2,154.38 0.61

8,955 2,238.75

2 2,785 2,264.38 1.23

9,160 2,290.00

3 3,530 2,331.25 1.51

9,490 2,372.50

4 1,535 2,363.13 0.65

9,415 2,353.75

2008

1 1,640 2,311.88 0.71

9,080 2,270.00

2 2,710 2,260.63 1.20

9,005 2,251.25

3 3,195

(73)

0 1,000 2,000 3,000 4,000

0 1 2 3 4 5 6 7 8 9 10 11 12 13

PENJUALAN

RATA2 BGRK TRPST

Gambar 11. Grafik penjualan per kuartal dan rata-rata bergerak terpusat Tabel 8. Indeks Musim Krupuk SPKK

1.49 0.67 0.50

0.61 1.23 1.51 0.65

0.71 1.20

Jml 1.32 2.43 3.00 1.31 8.06

rata2 0.66 1.21 1.50 0.66 4.0

Indeks 1.33 2.45 3.03 1.32

Tabel 9. Deseasonalizing Krupuk SPKK

penjualan indeks

penjualan

1,225 1.33 922.63 1 922.63 1

2,225 2.45 909.04 2 1,818.08 4

2,855 3.03 943.78 3 2,831.33 9

1,330 1.32 1,003.91 4 4,015.66 16

1,310 1.33 986.65 5 4,933.27 25

(74)

3,530 3.03 1,166.91 7 8,168.38 49

1,535 1.32 1,158.65 8 9,269.22 64

1,640 1.33 1,235.20 9 11,116.81 81

2,710 2.45 1,107.19 10 11,071.88 100

3,195 3.03 1,056.17 11 11,617.87 121

1,460 1.32 1,102.04 12 13,224.49 144

Jumlah 12,730.01 78 85,816.59 650

∑

− − = n t t n t Y tY b ₂

2 ( )

) )( ( =21,48 dan 22 , 921 ) ( = − =

∑

n t b n Y

Y’ = (921,22 + 21,48 t) x Mt c. Jenis Krupuk GNP

Tahun Kuartal Penjualan

Total bergerak

4 kuartal

Rata2 bergerak

4 kuartal

Rata2 bergerak

2006

1 16,535

2 22,713

81,415 20,353.75

3 27,935 20,256.63 1.38

80,638 20,159.50

4 14,232 20,273.25 0.70

(75)

2007

1 15,758 20,890.75 0.75

85,578 21,394.50

2 23,623 21,424.00 1.10

85,814 21,453.50

3 31,965 21,569.38 1.48

86,741 21,685.25

4 14,468 21,787.38 0.66

87,558 21,889.50

2008

1 16,685 21,658.88 0.77

85,713 21,428.25

2 24,440 21,561.63 1.13

86,780 21,695.00

3 30,120

4 15,535

0 10,000 20,000 30,000 40,000

0 1 2 3 4 5 6 7 8 9 10 11 12 13

bulan

pe

njua

la

n

penjualan

rata2 brgrk trpst

Gambar 12. Grafik penjualan per kuartal dan rata-rata bergerak terpusat Tabel 11. Indeks Musim Krupuk GNP

(76)

0.75 1.10 1.48 0.66

0.77 1.13

Jml 1.52 2.24 2.86 1.37 7.99

rata2 0.76 1.12 1.43 0.68 4.0

Indeks 1.52 2.23 2.86 1.36

Tabel 12. Deseasonalizing Krupuk GNP

penjualan indeks

penjualan

16,535 1.52 10,861.51 1 10,861.51 1

22,713 2.23 10,172.66 2 20,345.33 4

27,935 2.86 9,778.83 3 29,336.49 9

14,232 1.36 10,434.07 4 41,736.29 16

15,758 1.52 10,351.11 5 51,755.56 25

23,623 2.23 10,580.23 6 63,481.40 36

31,965 2.86 11,189.56 7 78,326.89 49

14,468 1.36 10,607.09 8 84,856.74 64

16,685 1.52 10,960.04 9 98,640.35 81

24,440 2.23 10,946.15 10 109,461.50 100

30,120 2.86 10,543.70 11 115,980.72 121

15,535 1.36 11,389.36 12 136,672.26 144

(77)

∑

− − = n t t n t Y tY b ₂

2 ( )

) )( (

=74,56 dan

56 , 10166 ) ( = − =

∑

n t b n Y

Y’ = (10166,56 + 74,56 t) x Mt

d. Jenis Krupuk GND

Total rata2

bergerak 4 kuartal

Rata2

bergerak 4

kuartal

Rata2 bergerak

2006

1 2,655

2 16,140

53,190 13,297.50

3 10,135 13,209.38 0.77

52,485 13,121.25

4 24,260 12,981.25 1.87

51,365 12,841.25

2007

1 1,950 13,043.13 0.15

52,980 13,245.00

2 15,020 14,239.38 1.05

60,935 15,233.75

3 11,750 15,485.63 0.76

(78)

4 32,215 15,913.13 2.02

64,355 16,088.75

2008

1 3,965 15,671.25 0.25

61,015 15,253.75

2 16,425 15,006.88 1.09

59,040 14,760.00

3 8,410

4 30,240

0 10,000 20,000 30,000 40,000

0 1 2 3 4 5 6 7 8 9 10 11 12 13

kuartal

pe

nj

ua

la

n PENJUALAN

RATA2 BRGRK TRPST

Gambar 13. Grafik penjualan per kuartal dan rata-rata bergerak terpusat Tabel 14. Indeks Musim Krupuk GND

0.77 1.87 0.50

0.15 1.05 0.76 2.02

0.25 1.09

Jml 0.40 2.15 1.53 3.89 7.97

rata2 0.20 1.07 0.76 1.95 4.0

Indeks 0.40 2.14 1.52 3.88

(79)

penjualan indeks

penjualan

2,655 0.40 6,619.91 1 6,619.91 1

16,140 2.14 7,536.54 2 15,073.08 4

10,135 1.52 6,665.48 3 19,996.43 9

24,260 3.88 6,253.81 4 25,015.25 16

1,950 0.40 4,862.08 5 24,310.39 25

15,020 2.14 7,013.56 6 42,081.35 36

11,750 1.52 7,727.61 7 54,093.29 49

32,215 3.88 8,304.47 8 66,435.80 64

3,965 0.40 9,886.23 9 88,976.03 81

16,425 2.14 7,669.62 10 76,696.20 100

8,410 1.52 5,531.00 11 60,840.98 121

30,240 3.88 7,795.35 12 93,544.24 144

Jumlah 85,865.66 78 573,682.95 650

∑

− − = n t t n t Y tY b ₂

2 ( )

) )( (

=108,78 dan

37 , 6448 ) ( = − =

∑

n t b n Y

Y’ = (6448,37 + 108,78 t) x Mt

e. Jenis Krupuk MB

(80)

Total rata2

bergerak 4 kuartal

Rata2

bergerak 4

kuartal

Rata2 bergerak

2006

1 14,148

2 5,159

42,256 10,564.00

3 17,999 10,787.13 1.67

44,041 11,010.25

4 4,950 11,209.75 0.44

45,637 11,409.25

2007

1 15,933 11,580.63 1.38

47,008 11,752.00

2 6,755 11,910.00 0.57

48,272 12,068.00

3 19,370 11,990.13 1.62

47,649 11,912.25

4 6,214 11,777.88 0.53

46,574 11,643.50

2008

1 15,310 11,600.38 1.32

46,229 11,557.25

2 5,680 11,393.63 0.50

44,920 11,230.00

3 19,025

(81)

0 5,000 10,000 15,000 20,000 25,000

0 1 2 3 4 5 6 7 8 9 10 11 12 13

kuartal

pe

nj

u

a

la

n

PENJUALAN

RATA2 BGRK TRPST

Gambar 14. Grafik pen