S¸.˙I. Birbil, K. B ¨ulb ¨ul, J.B.G. Frenk
Faculty of Engineering and Natural Sciences, Sabancı University, 34956 Istanbul, Turkey.
[email protected], [email protected], [email protected]
H.M. Mulder
Erasmus University Rotterdam,
Postbus 1738, 3000 DR Rotterdam, The Netherlands.
Abstract: We consider an economic order quantity type model with unit out-of-pocket holding costs, unit
opportunity costs of holding, fixed ordering costs and general transportation costs. For these models, we analyze the associated optimization problem and derive an easy procedure for determining a bounded interval containing the optimal cycle length. Also for a special class of transportation functions, like the carload discount schedule, we specialize these results and give fast and easy algorithms to calculate the optimal lot size and the corresponding optimal order-up-to-level.
Keywords: EOQ-type model; transportation cost function; upper bounds; exact solution.
1. Introduction. In inventory control the economic order quantity model (EOQ) is the most
funda-mental model, which dates back to the pioneering work of Harris [8]. The environment of the model is
somewhat restricted. The demand is known and constant, shortages are not permitted, there is a fixed
setup cost and the unit purchasing and holding costs are independent of the size of the replenishment order. In this simplest form, the model describes the trade-offbetween the fixed setup and the holding
costs. In the single item inventory control literature a lot of effort was put into weakening these
assump-tions [7,14]. However, as noticed by Carter [5] most of these models did not take into consideration the impact of the transportation costs as a separate cost component on the lot sizing decision. Carter
observes that typically in the lot sizing literature it is assumed that the transportation costs are managed
by the supplier (and hence part of the unit costs) or the transportation costs are fixed (and therefore part of the setup costs). Carter presents some examples, in which it is clear that the transportation costs
should be taken into consideration differently. Actually, only one paper by Lee [11] is known to the
authors that incorporates a special transportation cost function (a freight discount rate charge) into the classical EOQ model, where no shortages are allowed. The aim of the present paper is to include, in
a systematic way, the transportation costs as a separate cost component into an EOQ-type model and
investigate for which transportation cost functions it is still relatively simple to solve the corresponding optimization problem. One of the most well-known transportation cost functions is the carload discount
schedule [12]. We present a detailed analysis for this particular schedule and related transportation
functions.
The problem setting is as follows: We consider an EOQ-type model with complete backordering,
whereλ >0 is the arrival rate anda>0 is the fixed ordering cost. The inventory holding costs consist
of a unit out-of-pocket holding cost ofh > 0 per item per unit of time and a unit opportunity cost of holding with inventory carrying charger≥ 0. Moreover, the penalty cost of backlogging isb >0 per
item per unit of time. To avoid pathological cases we assume thatb > h. Clearly, whenb =∞ there
are no shortages in the problem. The functionp : [0,∞) → Rwithp(0)= 0 represents the purchase price function, and it is assumed thatp(·) is left continuous on (0,∞). This means that the well-known
all-units-discount scheme [14] is also included in, especially the first part of, our analysis. At the same
time, the functiont: [0,∞)→Rwitht(0)=0, denotes the transportation cost function and this function is also assumed to be left continuous on (0,∞). The structure of the functiont(·) allows us to model truck
costs. Consequently, the total transportation-purchase cost of an order of sizeQis given by
c(Q) :=t(Q)+p(Q), (1)
where c(·) denotes the transportation-purchase function. Since the addition of two left continuous
functions is again left continuous, the functionc(·) is, in general, a left continuous function. This means
for everyQ>0 that
c(Q)=c(Q−) :=limx↑Qc(x) and
c(Q+) :=limx↓Qc(x).
Using this left continuous transportation-purchase functionc(·) implies that the cost rate function of an
EOQ-type model is given by
For a detailed discussion of this cost rate function within a production environment, the reader is referred
to [2]. Since it is easy to see that for a given cycle lengthT>0, any order-up-to-levelS> λTis dominated in cost byS=λT, we only derive the average cost expression for (S,T) control rules within the interval
0≤S≤λT. For such control rules, the average costg(S,T) has the form
g(S,T)= a
+c(λT)+RT
0 f(T,S−λt)dt
T . (4)
Hence, to determine the optimal (S,T) rule, we need to solve the optimization problem
min{g(S,T) :T>0,0≤S≤λT}.
By relation (4), this problem reduces to
min of the optimization problem listed in relation (5) is given by
Hence, we obtain by relation (6) that
This shows by relation (3) forb < ∞ (shortages are allowed) that we need to solve the optimization problem Similarly forb=∞(no shortages allowed), we obtain the optimization problem
min{Φ∞(T) :T>0},
By the additivity of the costs, it is obvious that including the left continuous transportation-purchase
function c(·) as a separate cost component into the EOQ-type models does not change the structural form of the objective function. However, sincec(·) is left continuous, we can only conclude that the
objective functions in relations (7) and (8) are also left continuous, and hence, they may contain points
of discontinuity. In general, these functions (as a function of the length of the replenishment cycleT) are not unimodal anymore as in the classical EOQ models. Hence, they may contain several local minima
and so, it might be difficult to guarantee that a given solution is indeed optimal.
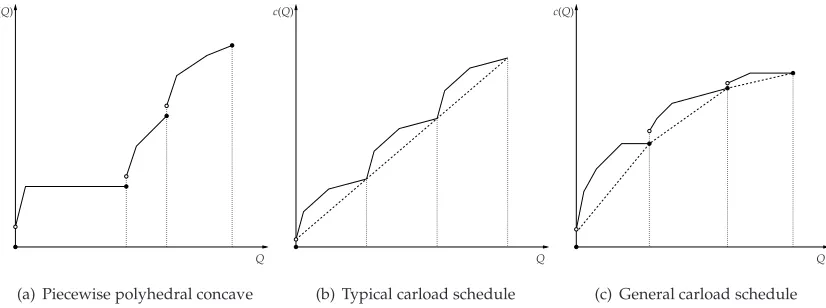
Our approach to these general models is to derive, in Section2, a bounded interval containing the
optimal cycle length T. We will first construct an upper bound on the optimal solution for a left
continuous and increasing transportation-purchase function as shown in Figure1(a). This upper bound is represented by an easy analytical formula for the special case of an increasing polyhedral concave
transportation-purchase function. Such a function is shown in Figure 1(c) and represents a typical
economies of scale situation. For the other more general transportation-purchase functions, it is possible to evaluate this upper bound by an algorithm. However, since this might take some computational
time, we also derive under some reasonable bounding condition on a transportation-purchase function,
a weaker analytical upper bound. To improve the trivial zero bound on an optimal solution, we only derive for an increasing concave transportation-purchase function as illustrated in Figure1(b), an
analytical positive lower bound.
We shall then show in Section3that there exists an important class of functions, for which the optimal solution can be identified by a fast algorithm. Figure2 shows some important instances that belong
to this class. Clearly, the well-known carload discount schedule in combination with linear purchase
costs [12] is a representative among these instances. To design these algorithms, we shall first show for an increasing linear transportation-purchase function that the resulting problem is a simple convex
optimization problem that can be solved very efficiently. In particular, we shall also derive analytic
solutions for two special cases: (i) when there are no shortages, or (ii) when there are shortages but the inventory carrying charge is zero. Having analyzed an increasing linear transportation-purchase
c(Q)
Q
(a) General
c(Q)
Q
(b) Concave
c(Q)
Q
(c) Polyhedral concave
Figure 1: Some transportation-purchase functions for which the bounds on optimalTare studied.
function is increasing piecewise polyhedral concave as shown in Figure2(a). This algorithm is based
on solving a series of simple problems that correspond to the increasing linear pieces on the piecewise
polyhedral concave function. To further improve the performance of the proposed algorithm, we shall then concentrate on two particular instances as shown in figures2(b)and2(c). The former is a
typical carload schedule with identical setups, and the latter represents a general carload schedule with
nonincreasing truck setup costs. Both cases admit a lower bounding function, which is linear in the former case and polyhedral concave in the latter case. These lower bounding functions, shown with
dashed lines in Figure2, allow us to concentrate on solving only a very few simple problems. Finally, in
Section4we will give some numerical examples to illustrate our results.
c(Q)
Q
(a) Piecewise polyhedral concave
Q c(Q)
(b) Typical carload schedule
c(Q)
Q
(c) General carload schedule
Figure 2: Some transportation-purchase functions for which fast algorithms are developed.
2. Bounding The Optimal Cycle Length. In this section we show that one can identify an upper
bound on the optimal cycle length of the previous EOQ-type models for left continuous increasing transportation-purchase functionsc(·) as shown in Figure1(a). For very general functionsc(·), it might
be difficult to compute this upper bound by means of an easy algorithm. Therefore, we show that under
an affine bounding condition on the functionc(·), this upper bound can be replaced by a weaker upper bound having an elementary formula. To derive these results, we first identify the general structure of
LetF: [0,∞)×(0,∞)→Rbe given by
F(x,T) := a+x
T + bλT
2 −
(λbT)2
2λ(h+b)T+2rx, (9)
then it follows from relation (7) that the EOQ-type optimization problem with shortages is given by
min{F(c(λT),T) :T>0}. (Pb) Similarly, we also introduce the functionG: [0,∞)×(0,∞)→Rgiven by
G(x,T) := a+x
T +
hλT+rx
2 . (10)
Then, it is clear from relation (8) that the EOQ-type model with no shortages allowed (b=∞) transforms
to
min{G(c(λT),T) :T>0}. (P∞)
By relations (9) and (10), it is obvious that the functionsF(·,·) andG(·,·) belong to the following class of functions.
Definition2.1 A function H : [0,∞)×(0,∞)→ Rbelongs to the setHif the function H(·,·)is continuous,
x7→H(x,T)is increasing on[0,∞)for every T>0, andlimT↓0H(x,T)=limT↑∞H(x,T)=∞for every x≥0.
Hence, both EOQ-type optimization models are particular instances of the optimization problem
min{H(c(λT),T) :T>0}, (P)
whereH(·,·) belongs to the setH andc(·) is an increasing left continuous function on [0,∞). We show in LemmaA.1of AppendixAthat the functionT7→H(c(λT),T) is lower semi-continuous for anyH(·,·)
belonging toH. Consequently, an optimal solution for problem (P) indeed exists, and hence, our search
for a bounded interval containing an optimal solution is justified.
2.1 Dominance Results. In this section, we shall give two simple dominance results that will be
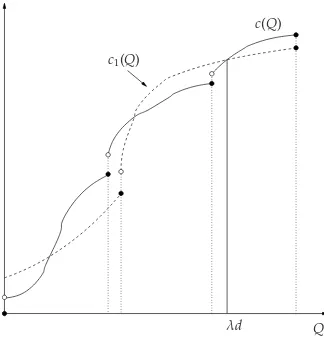
instrumental for finding a bounded interval for different EOQ-type models. We start with the following lemma, which has a straightforward proof. The functionsc(·) andc1(·) satisfying the conditions of the
lemma are exemplified in Figure3.
Lemma2.1 Let the functions c1(·), c(·)be left continuous on[0,∞)with c1(·)increasing and H(·,·)belong toH.
(i) If c(Q)≥c1(Q)for every Q> λd and c(λd)=c1(λd)and T7→H(c1(λT),T)is increasing on(d,∞),then H(c(λT),T)≥H(c(λd),d)for every T>d.
(ii) If c(Q)≥c1(Q)for every Q≤λd and c(λd)=c1(λd)and T7→H(c1(λT),T)is decreasing on(0,d),then
H(c(λT),T)≥H(c(λd),d)for every T<d.
Proof. Since the functionH(·,·) belongs toHand the functionc1(·) is left continuous and increasing,
it follows that
limT↓dH(c1(λT),T)=H(c1((λd)+),d)≥H(c1(λd),d)=H(c(λd),d).
Using againH(·,·)∈ H,c(λT)≥c1(λT) for everyT>d, andT7→H(c1(λT),T) is increasing on (d,∞), we have for everyT>dthat
Q c(Q)
λd c1(Q)
Figure 3: The increasing left-continuous functions used in Lemma2.1
By a similar proof the second part can also be shown.
An easy implication of Lemma2.1is given by the following result.
Lemma2.2 Let the functions c1(·), c(·)be left continuous on[0,∞)with c1(·)increasing and H(·,·)belong toH.
If
(i) c(Q)≥ c1(Q)for every Q≥0and c(λdn)=c1(λdn)for some strictly increasing sequence dn↑ ∞with d0:=0, and
(ii) there exists some y1 ≥ y0 > 0 such that the function T 7→ H(c1(λT),T)is decreasing on (0,y0)and
increasing on[y1,∞),
then for n∗ := max{n ∈ Z+ : dn < y0} and n∗ := min{n ∈ Z+ : dn ≥ y1}, the interval[dn∗,dn∗]contains an
optimal solution of the optimization problem(P).
Proof. Since the functionT 7→H(c1(λT),T) is decreasing on (0,dn
∗) and increasing on (dn∗,∞), and
c(λdn∗)=c1(λdn∗) andc(λdn∗)=c1(λdn∗), we can apply Lemma2.1to show the desired result.
Clearly, ifT7→H(c1(λT),T) is unimodal, then we obtain thaty1=y0and hencen∗=n∗+1. In the next
subsection we will apply the above localization results to the EOQ-type models.
2.2 Applications of The Dominance Results to The EOQ-Type Models. In this section we will
show some applications of Lemma2.1and Lemma2.2on different EOQ-type models. We first examine
the simple EOQ-type model with no shortages. To obtain an easily computable upper bound on an optimal solution, we impose on the functionc(·) the following bounding condition.
Assumption2.1 The transportation-purchase function c(·)satisfies
c(Q)≤αQ+β (11)
for someα, β >0.
By definition of a transportation-purchase function, Assumption2.1seems to be a reasonable condition.
function c(·) is increasing. Notice that the analysis up to this point applies toany type of EOQ-type model, but with this monotonicity assumption onc(·) we exclude the all-units discount model.
c(λT)
−a
D
d c1(λT)
c(λd)=c1(λd)
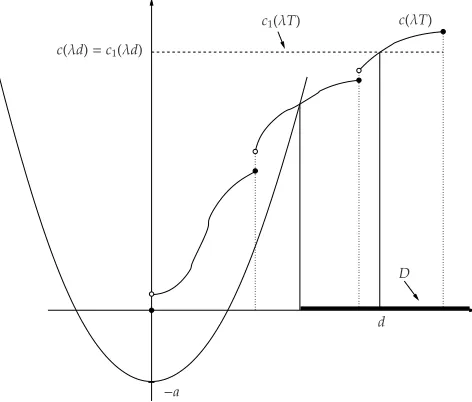
Figure 4: The construction used in Example2.1and Example2.2
Example2.1 (UpperBound forIncreasingc(·) WithNoShortages) If the transportation-purchase
func-tion c(·)is increasing and left continuous, consider the set
D:=
(
d≥0 :c(λd)≤ hλd2
2 −a )
, (12)
and assume D is nonempty (see Figure4). We will next show for any d ∈ D that an optimal solution of this problem can be found within the interval[0,d]. To verify this claim, consider some d ∈ D and introduce the
constant function c1: (0,∞)→Rgiven by
c1(Q) :=c(λd). (13)
Since c(·) is increasing, clearly c(Q) ≥ c1(Q) for every Q > λd and c(λd) = c1(λd). Moreover, if c1(·) is the considered transportation-purchase function and no shortages are allowed, then the objective functionΨd : (0,∞)→Rhas the form
Ψd(T)=G(c1(λT),T)=G(c(λd),T),
where G(·,·)is given in relation(10). By elementary calculus, it is easy to verify that the optimal solution Topt(d) of the optimization problemmin{Ψd(T) :T>0}is given by
Topt(d)= 2
r
2(a+c(λd))
hλ . (14)
Moreover, sinceΨd(·)is a strictly convex function, it is strictly decreasing on(0,Topt(d))and strictly increasing on (Topt(d),∞).Since d belongs to D, this implies by relation(14)that Topt(d)≤d. Consequently, we may conclude that the functionΨd(·)is increasing on(d,∞). By applying now the first part of Lemma2.1, it follows that an optimal solution of an EOQ-type model with no shortages is contained in[0,d]. To find the best possible upper
bound, we introduce
dmin:=inf{d≥0 :d∈D}. (15)
Since c(·)is increasing and left continuous, it follows that dmin also belongs to D, and so, an optimal solution is
difficult to give a fast procedure to compute the value of dmin. To replace dminby an easy computable bound, we now use Assumption2.1as c(λd)≤αλd+β. Observe this bounding condition guarantees that the set D is nonempty
and
we obtain by relation(16)that
vα,β≥dmin. (18)
Therefore, an optimal solution is contained in(0,vα,β].
Due to the specific form of the functionc1(·), it follows by relation (10) that for the EOQ-type model with
no shortages and transportation-purchase function c1(·), the inventory carrying charge is a fixed cost
independent of the decision variableT. Hence, the optimalTopt(d) given by relation (14) does not contain the value ofr. This means for our procedure discussed in Example2.1that the constructed upper bound
on an optimal solution does not contain this parameterrand holds uniformly for everyr≥0. Hence, it
seems likely that this upper bound might be far away from an optimal solution of an EOQ-type model with functionc(·) and a given inventory carrying charge. We explore this issue by our computational
study in Section4. In case we do not have any structure onc(·) –the structured case will be considered
in the next section– we might now use some discretization method over (0,wα,β] to approximate the optimal solution for the no shortages case.
We shall consider next the general EOQ-type model with shortages. Before discussing the construction of an upper bound for this model, we first need the following result.
Lemma2.3 If T(r)
opt(d)denotes the optimal solution of the EOQ model with shortages allowed, inventory carrying charge r≥0and the constant transportation-purchase function c1(·)listed in relation(13), then for all r≥0, we have
we obtain by relation (19) that
F(c1(λT),T)=F0(c1(λT),T)+K(T). (20)
By looking at relation (20), we observe that the function
T7→F0(c1(λT),T)
is the objective function of an EOQ-model with shortages allowed,r=0, and the transportation-purchase
functionc1(·). Also, it is easy to check in relation (20) that the remainder functionKis increasing with a
positive derivative. This shows that the derivative of the function
T7→F(c1(λT),T)
evaluated at the optimal solution T(0)opt(d) of an EOQ-type model with shortages allowed andr = 0 is positive. Using now relation (9) withr=0, it is easy to check that
Topt(0)(d)=
r
2(a+c(λd)) hλ
h+b b .
Since by the definition ofT(r)opt(d) the derivative of the functionT →F(c1(λT),T) evaluated at this point equals 0, the inequality
T(r)opt(d)≤T(0)opt(d)
holds once we have verified that the functionT 7→F(c1(λT),T) is unimodal. To show this property, we
first observe that the functionK1: (0,∞)→Rgiven by
K1(T) :=TK(T)
being the ratio of a squared convex function and an affine function is convex [4]. This implies that the function T 7→ TK1(T−1) = K(T−1) is convex [9]. Moreover, it is easy to verify by its definition
that the function T 7→ F0(c1(λT−1),T−1) is convex, and this shows by relation (20) that the function T7→F(c1(λT−1),T−1) is convex implyingT7→F(c1(λT),T) is unimodal.
Lemma2.3shows that the optimal solution of an EOQ-type model with the constant
transportation-purchase functionc1(·) and nonzero inventory carrying charge is bounded from above by the optimal solution of an EOQ-type model with the transportation-purchase function c1(·) and zero inventory
carrying charge. Using this result we will construct in the next example an upper bound on the
optimal solution of an EOQ-type model with shortages allowed, inventory carrying charger≥ 0 and left-continuous increasing transportation-purchase functionc(·).
Example2.2 (UpperBound forIncreasingc(·) WithShortages) If the transportation-purchase function c(·) is increasing and left continuous, consider the set
D:=
(
d≥0 :c(λd)≤ hλd
2
2 b h+b−a
)
, (21)
and assume that D is nonempty (see also Figure4). Let d∈D and consider the constant function c1: (0,∞)→R
given by
c1(Q) :=c(λd).
Since c is increasing clearly c(Q) ≥ c1(Q)for every Q > λd and c(λd) = c1(λd). Moreover, if shortages are
allowed, then the objective functionΨd: (0,∞)→Rhas the form
where F(·,·)is given in relation (9). In the proof of Lemma 2.3, it is shown that the objective function Ψd is unimodal, and for any r≥0we have
T(r)opt(d)≤T(0)opt(d)= 2
r
2(a+c(λd)) λh
h+b
b . (22)
Applying now the unimodality of the functionΨd(·)this yields thatΨd(·)is increasing on the interval(T(r)opt(d),∞), and since d belongs to D, we also obtain by relation (22) that
T(r)opt(d)≤T(0)opt(d)≤d.
This shows that the functionΨd(·)is increasing on(d,∞), and by applying part(i)of Lemma2.1, we conclude that an optimal solution of the EOQ-type model with the general transportation-purchase function c(·)is contained in the interval[0,d]. As in Example2.1the best possible upper bound is now given by
dmin:=inf{d≥0 :d∈D}. (23)
Again due to the particular instance of c(·)it might be difficult to compute dmin. To replace dminby an easily
computable upper bound, we again use the bounding condition given in Assumption2.1and obtain c(λd)≤αλd+β. This implies that D is nonempty and it follows as in Example2.1that dmin≤wα,βwith
wα,β:=αh−1(h+b)b−1+ 2 q
α2h−2((h+b)b−1)2+2h−1λ−1(a+β)(h+b)b−1. (24)
Therefore, under the bounding condition, wα,β serves as an upper bound on an optimal solution of the original problem.
Remark2.1 By relations(12) and (21), it is easy to see that an upper bound on an optimal solution for an EOQ-type model with no shortages (Example2.1) is always smaller than an upper bound on an optimal solution
of an EOQ-type model with shortages (Example2.2). Similarly, we obtain by relations(17)and(24)that this also
holds for the easily computable upper bounds under the bounding condition.
In case we additionally know that the functionc(·) is concave, which corresponds to some incremental
discount scheme [14] for either the purchase function or the transportation cost function, it is also possible to compute a (nontrivial) lower bound on the optimal solutions of the EOQ-type models considered in
the previous two examples. The next example discusses this lower bound explicitly for the no shortages
case.
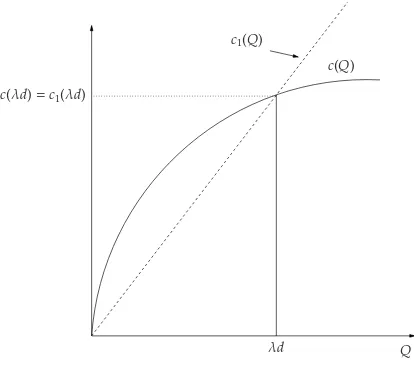
Example2.3 (LowerBound forIncreasingConcavec(·) WithNoShortages) If we know additionally
that the transportation-purchase function c(·) is concave, and hence continuous, it is also possible to give a lower bound on the optimal solution. Observe in this case that Assumption2.1is trivially satisfied (see Figure5).
Take for simplicity, Q 7→ c(λλdd)Q+c(λd), which clearly satisfies Assumption2.1withα= c(λd)
λd andβ= c(λd). Consider now for d>0, the function c1: (0,∞)→Rgiven by
c1(Q)= c(λd)
λd Q.
By the concavity of c(·)and c(0)=0, we obtain for every Q< λd that
Q c(Q)
λd c1(Q)
c(λd)=c1(λd)
Figure 5: The construction used in Example2.3
and this shows c(Q)≥c1(Q)for every Q< λd and c(λd)=c1(λd). As in Example2.1the objective function has
the form
Ψd(T)=G(c1(λT),T)
where G(·,·)is given in relation(10). By elementary calculus, it is easy to verify that the optimal solution Topt(d) of the optimization problemmin{Ψd(T) :T>0}is given by
Topt(d)= 2 r
2a
hλ+rc(λd)d−1. (25)
Since the function x7→c(λx)x−1is decreasing and continuous withlim
x↓0c(λx)x−1 ≤ ∞, it follows by relation (25)that the function Topt: (0,∞)→Ris increasing and continuous. Also, by the strict convexity of the function Ψdthis function is strictly decreasing on(0,Topt(d))and strictly increasing on(Topt(d),∞). This implies
Ψddecreasing on(0,d)⇔Topt(d)≥d.
Since the set{d≥0 :Topt(d)≥d}contains0it follows by the second part of Lemma2.1that an optimal solution of the EOQ-type model with no shortages allowed and a concave transportation-purchase function c(·)is contained
in[dmax,∞), where
dmax:=sup{d≥0 :Topt(d)≥d}=sup{d≥0 :hλd2+rdc(λd)≤2a}. (26)
Since the function d7→hλd2+rdc(λd)is strictly increasing and continuous on[0,∞), we obtain that dmaxis the
unique solution of the system
hλx2+rxc(λx)=2a.
Also, by the nonnegativity of c we obtain that
dmax∈[0,√22aλ−1h−1].
Thus, one can apply a computationally fast derivative free one-dimensional search algorithm [3] over the interval
of uncertainty[0,√22aλ−1h−1]to compute the lower bound dmax.
As shown in the above examples, under the affine bounding condition stated in Assumption2.1, it is possible to identify by means of an elementary formula a bounded intervalIcontaining an optimal
solution of the EOQ-type model with increasing transportation-purchase functionc(·). Hence, we obtain
for the two different cases represented by the optimization problems (Pb) and (P∞) that
minT>0H(c(λT),T)=minT∈IH(c(λT),T). (27)
However, for the general increasing left continuous transportation-purchase functions, the function T7→ H(c(λT),T) does not have the desirable unimodal structure. Since we are interested in finding an
optimal solution, the only thing we could do is to discretize the intervalIand select among the evaluated
function values on this grid the one with a minimal value. In case the objective function has a finite number of discontinuities and it is Lipschitz continuous between any two consecutive discontinuities
with known (maybe different) Lipschitz constants, it is possible by using an appropriate chosen grid to
give an error on the deviation of the objective value of this chosen solution from the optimal objective value. We leave the details of this construction to the reader and refer to the literature on one-dimensional
Lipschitz optimization algorithms [10].
However, for some left continuous increasing transportation-purchase functions c(·), it is possible to compute explicitly the value ofdminlisted in relations (15) and (23) by means of an easy algorithm. This means that for these functions we do not need the easily computable upper bound and so in
this case the upper bound on an optimal solution can be improved. An example of such a class of transportation-purchase functions is given in the next definition.
Definition2.2 ([13]) A function c: (0,∞)→Ris called a polyhedral concave function on(0,∞), if c(·)can be represented as the minimum of a finite number of affine functions on(0,∞). It is called polyhedral concave on an
interval I, if c(·)is the minimum of a finite number of affine functions on I.
We will now give an easy algorithm to identify the valuedminin casec(·) is an increasing polyhedral
concave function. Observe it is easy to verify that polyhedral concave functions defined on the same interval are closed under addition. Within the inventory theory, polyhedral concavity on [0,∞) of
the transportation-purchase functionc(·) describes incremental discounting either with respect to the
purchase costs or the transportation costs or both.
Clearly, a polyhedral concave function on (0,∞) can be represented for everyQ>0 as
c(Q)=min1≤n≤N{αnQ+βn}, (28)
whereNdenotes the total number of affine functions,α1> .... > αN ≥0, and 0≤β1< β2< ... < βN. An
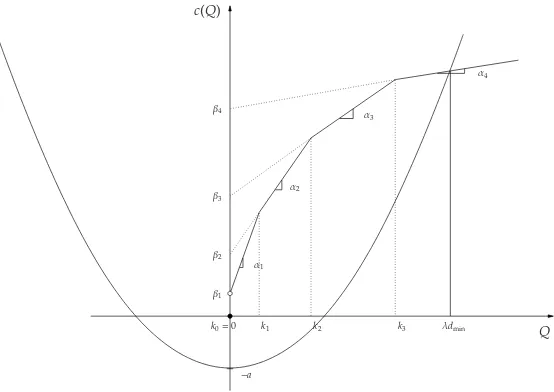
example of a polyhedral concave functionc(·) is given in Figure6. Betweenkn−1andknthe minimum in relation (28) is attained by the affine functionQ7→αnQ+βn. To compute the valuesαnandβnin terms
of our original data given by the finite set of breaking points 0 =k0 < k1 < ... < kN−1 <kN = ∞, and
function valuesc(kn),n=1, ...N−1 we observe that
αn=
c(kn)−c(kn−1) kn−kn−1
(29)
forn=1, ...,N−1 and
λdmin
α1
−a
c(Q)
Q
k0=0 k1 k2 k3
β2
β3
β4
β1
α4
α3
α2
Figure 6: A polyhedral concave transportation-purchase function.
Also, by the same figure we obtain forkn−1<Q≤kn,n=1, ..,Nthat c(Q)=c(kn−1)+αn(Q−kn−1)=αnQ+βn
and this implies
βn=c(kn−1)−αnkn−1 (31)
forn=1, ..,N.
We will now give an easy algorithm to identify the valuedmin, ifc(·) is a polyhedral concave function with the representation given in relation (28). Using now relations (15) and (23), we have
dmin=min{d>0 :c(λd)≤ hλd2ζ
2 −a}, (32)
where ζ = 1 for the no shortages case and ζ = b
h+b for the shortages case. Since c(·) is concave and increasing, and the functiond7→ hλ2d2ζ−ais strictly convex and increasing on [0,∞) (see Figure6), each regionD, given by relation (12) or relation (21), is an interval [dmin,∞). The next algorithm clearly yields dminas an output .
Algorithm 1: Findingdminfor polyhedralc(·)
n∗:=max{0≤n≤N−1 :c(kn)> hk
2
nζ 2λ −a} 1:
Determine in [kn∗,kn∗+1] or in [kn∗,∞) the unique analytical solutiond∗of the equation 2:
αn∗+1λd+βn∗+1= hλd2ζ
2 −a
given by
d∗=
αn∗+1λ+ p
(αn∗+1λ)2+2hλζ(a+βn∗+1) hλζ
dmin←d∗ 3:
In the next section we shall identify a subclass of the increasing left continuous
interval containing an optimal solution.
3. Fast Algorithms for Solving Some Important Cases. Unless we impose some additional structure
onc(·), it could be difficult to find a fast algorithm to solve optimization problem (P) due to the existence
of many local minima. Clearly, ifc(·) is an affine function given by
c(Q)=αQ+β
withα >0,β≥0, it is already shown in [2] that the objective functions of both EOQ-type models given
by (Pb) and (P∞) are unimodal functions. Also for the no shortages model (P∞), it is easy to check by relation (10) that the optimal solutionToptis given by
Topt = 2
s
2(a+β)
λ(h+rα), (33)
while for the shortages model (Pb) with zero inventory carrying charge (r=0), it follows by relation (9)
that the optimal solutionTopthas the form
Topt = 2
r 2(a+β)
λh
h+b
b . (34)
Finally, for the most general model with shortages allowed and nonzero inventory carrying charge, it
follows that the function
T7→F(c(λT−1,T−1)
is a convex function on [0,∞) (see [2, Lemma 3.2]). Hence, solving problem (Pb) using the decision variableT−1is an easy one-dimensional convex optimization problem, and so, we can findT
optrather quickly. Consequently, this observation helps us to come up with fast algorithms whenc(·) consists of
linear pieces. Among such functions, the most frequently used ones are the polyhedral concave functions given in (28). Using this representation andH(·,·)∈ H, the overall objective function for both EOQ-type
models becomes
H(c(λT),T)=min1≤n≤NH(αnλT+βn,T). (35) This shows by our previous observations that the functionT7→H(c(λT−1),T−1) is simply the minimum
ofNdifferent convex functions. In general this function is not convex anymore and even not unimodal. However, due to relation (35) it follows that
min T>0 H(c(λT
−1),T−1)= min
1≤n≤NminT>0 H(αnλT
−1+βn,T−1), (36)
and by relation (36), we need to solveNone-dimensional unconstrained convex optimization problems
to determine an optimal solution. Notice by relation (35) that each of theseNproblems involve an affine
function. This implies that if we consider the no shortages model (Pb) or the shortages model (P∞) with r=0, then we have the analytic solutions (33) and (34), respectively. Therefore, solving (36) boils down
to selecting the minimum amongNdifferent values in these cases.
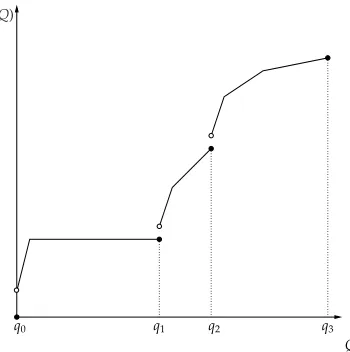
We next introduce a more general class containing as a subclass the polyhedral concave functions on [0,∞). An illustration of a function in this class is given in Figure7.
q0 q1 q2 q3 c(Q)
Q
Figure 7: A piecewise polyhedral concave transportation-purchase function.
A piecewise concave polyhedral function might be discontinuous at the pointsqn,n∈Z+. If the function
c(·) is a piecewise polyhedral concave function, then it follows by relation (28) that
c(Q)= min 1≤n≤Nk
{αnkQ+βnk} (37)
forqk−1 <Q≤qkand finiteNk. If, additionally, the functionc(·) satisfies Assumption2.1, then we have shown in Subsection2.2that an easily computable upper bound exists on the optimal solution. We
denote this upper bound byU. For problem (P∞),Uis given by relation (17), while for problem (Pb) it is given by relation (24). Sinceqn↑ ∞andUis a finite upper bound on an optimal solution it follows that
m∗:=min{n∈N:qn> λU}<∞ (38)
and an optimal solution is contained in the bounded interval [0, λ−1qm∗). Since c(·) is increasing this
implies that
minT>0H(c(λT),T) = min0<T≤λ−1qm∗H(c(λT),T)
= min1≤k≤m∗minλ−1q
k−1≤T≤λ−1qkH(c(λT),T).
By relation (37), it follows now that
min
λ−1qk−1≤T≤λ−1qkH(c(λT),T)
= min
1≤n≤Nk
min
λ−1qk−1≤T≤λ−1qkH(αnkλT
+βnk,T),
and so, we have to solve for 1≤k≤m∗andn≤Nk, the constrained convex one-dimensional optimization
problems
min λ−1q
k−1≤T≤λ−1qk
H(αnkλT−1+βnk,T−1).
Solving these subproblems can be done relatively fast, but since we have to solve Pm∗
k=1Nk of those subproblems this might take a long computation time for the most general case. Observe once again, if
we only consider the no shortages model or the shortages model with zero inventory carrying charge, the subproblems minT>0H(αnkλT+βnk,T) have analytical solutions given by relations (33) and (34), respectively. Hence, using the unimodality of the considered objective functions, the optimal solution
can be determined simply by checking whether the optimal solution of the unconstrained problem lies within [λ−1q
Algorithm 2: FindingToptfor piecewise polyhedralc(·)
DetermineUand determinem∗by relation (38) 1:
Solve fork=1, ...,m∗the optimization problems 2:
ϕk:= min
λ−1q
k−1≤T≤λ−1qk
H(c(λT),T)
nopt:=arg min{ϕk: 1≤k≤m∗}
3:
Topt←arg minλ−1q
nopt−1≤T≤λ−1qnoptH(c(λT),T) 4:
In Algorithm2we need to solve in Step2many relatively simple optimization problems. However, for m∗large this still might take some computation time. In the next example, we consider a subclass of the
set of piecewise polyhedral concave functions with some additional structure for which it is possible to
give a faster algorithm. For this class, we have to solve only one subproblem in Step2. The well-known carload discount schedule transportation function with identical trucks belongs to this class [12].
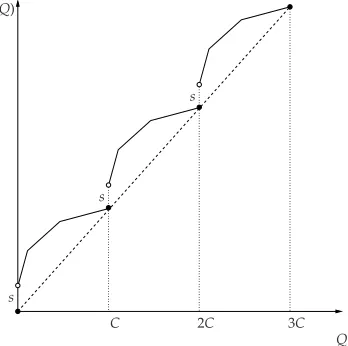
Example3.1 (CarloadDiscountScheduleWithIdenticalTrucks) Let C > 0 be the truck capacity, g :
(0,C] → Rbe an increasing polyhedral concave function satisfying g(0) = 0 and s ≥ 0 be the setup cost of using one truck. Here, g(Q) corresponds to the transportation cost for transporting an order of size Q with
0 <Q≤ C. If no discount is given on the number of used (identical) trucks, then the total transportation cost function t: [0,∞)→Rhas the form
t(Q)=
0, if Q=0;
g(Q)+s, if0<Q≤C,
and
t(Q)=ng(C)+g(Q−nC)+(n+1)s
for nC<Q≤(n+1)C with integer n≥1. Clearly, the above transportation function t(·)belongs to the class of
piecewise polyhedral concave functions with qn=nC. When we use the above transportation function t(·)with a
linear purchase function p(·), then we obtain a transportation-function c(·)similar to the one shown in Figure8.
c(Q)
C 2C 3C
Q s
s
s
For this class of functions it follows t(Q)≥t1(Q)for every Q≥0with
t1(Q) :=
g(C)+s C Q
and for dn:=λ−1nC the equality
t(λdn)=t1(λdn)
holds for every n ∈ Z+. If the price of each ordered item equals π > 0 (no quantity discount), and hence the
purchase function p: [0,∞)→Ris given by p(Q)=πQ, it follows that the lower bounding function c1(·)of the transportation-purchase function c(Q)=t(Q)+p(Q)is given by
c1(Q)=t1(Q)+p(Q)= g(C)+s
C +π !
Q
and
c(λdn)=c1(λdn)
for every n ∈ Z+. Adding a linear function p(·) to the piecewise polyhedral concave function t(·)yields that
c(·)is a piecewise polyhedral concave function (see also Figure 8). Since for the EOQ-type model with linear
function c1(·)both the no shortages objective function T 7→ G(c1(λT),T)and the shortages objective function
T 7→F(c1(λT),T)are unimodal, it follows by Lemma2.2that an optimal solution of the EOQ-type model with transportation-purchase function c(·)is contained within the interval[dn∗,dn∗+1]with
n∗:=max{n∈Z+:dn≤Topt}, (39)
where Toptis the optimal solution of the EOQ-type model with linear transportation-purchase function c1(·). Since dn=λ−1nC, this implies
n∗=⌊λToptC−1⌋, (40) where⌊·⌋denotes the floor function. In particular, if we consider the no shortages case (b=∞), then we obtain
using relation(33)that the optimal solution Toptof the EOQ-type model with function c1(·)has an easy analytical
form given by
Topt= 2 s
2a
λ(h+rp+r(g(C)+s)C−1). (41)
Likewise, for the EOQ-model with shortages (b<∞) and no inventory carrying charge(r=0), we obtain using
relation(34)that
Topt = 2 r
2a(h+b)
λhb . (42)
Finally, for the most general EOQ-type model with shortages allowed and positive inventory carrying charge r,
there exists a fast algorithm to compute its optimal solution Topt. If Toptequals dn∗or equivalently Toptis an integer multiple ofλ−1C the optimal solution of the EOQ model with function c(·)also equals Topt. Otherwise, as already observed, the optimal solution of this EOQ model with function c(·)can be found in the interval(dn∗,dn∗+1], and
so, we have to solve in the second step the optimization problem
mindn∗<T≤dn∗+1H(c(λT),T).
Algorithm3gives the details of solving the carload discount schedule with identical trucks.
When we generalize Example3.1to nonidentical trucks, we can use our results given for arbitrary
Algorithm 3: FindingToptfor carload discount schedule with identical trucks
T∗=arg min
T>0H(c1(λT),T) 1:
ifT∗is not an integer multiple ofλ−1Cthen 2:
n∗=⌊λToptC−1⌋
3:
T∗=arg min
dn∗<T≤dn∗+1H(c(λT),T) 4:
Topt←T∗
5:
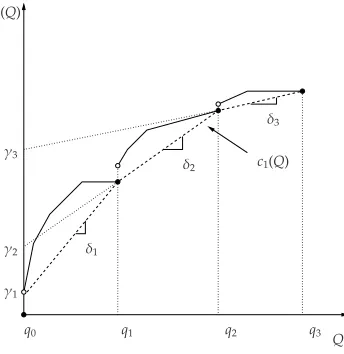
with nonincreasing truck setup costs as shown in Figure9, then the lower lower bounding functionc1(·)
becomes polyhedral concave. In this case, we can develop a faster algorithm. To obtain a polyhedral
concavec1(·), we assume forn≥1 that the sequence
δn:= c(qn)−c(qn−1)
qn−qn−1
is decreasing. Then, the functionc1: [0,∞)→Rbecomes
c1(Q)=c(qn−1)+δn(Q−qn−1)=δnQ+γn (43)
forqn−1 ≤ Q ≤ qn,n ≥ 1 withγn = c(qn−1)−δnqn−1. As shown in Figure9,c(qn) = c1(qn),n ∈ N, and c(Q)≥c1(Q) for everyQ≥0.
γ1 γ2 γ3
δ2
δ3
δ1 c(Q)
Q
q0 q1 q2 q3
c1(Q)
Figure 9: A transportation-purchase function for carload discount schedule with nonincreasing truck setup costs.
Since by constructionc(Q)≥c1(Q) it follows that
H(c(λT),T)≥H(c1(λT),T).
We will now show by means of the concavity of the lower bounding functionc1(·) that one can determine
a better upper bound than (38). We know for anydbelonging to the set
Dζ={d>0 :c1(λd)≤ hλd2ζ
2 −a} that
for anyT≥d. By the concavity ofc1(·), this implies for
n∗:=max{n∈N:c1(qn)> hqn2ζ
2λ −a} that
H(c1(λT),T)≥H(c1(qn∗+1), λ−1qn∗+1) (45)
for everyT≥λ−1q
n∗+1. This implies by relation (44) andc(qn∗+1)=c1(qn∗+1) that
H(c(λT),T)≥H(c(qn∗+1), λ−1qn∗+1)
for every T ≥ λ−1qn
∗+1. Hence we have shown that any optimal solution of the original EOQ model
with transportation-purchase function c(·) is contained in [0,λ−1qn∗+1]. By the discussion at the end
of Subsection2.2and relation (38), it follows thatn∗ ≤ m∗ and this shows that the newly constructed
upper bound is at least as good as the constructed bound for an arbitrary piecewise polyhedral concave function. Therefore, the number of subproblems to be solved could be far less thanm∗. We investigate
this issue in the next section.
4. Computational Study. We designed our numerical experiments with two basic goals in mind.
First, we would like to demonstrate that the EOQ model is amenable to fast solution methods in the presence of a general class of transportation functions introduced in this paper. Second, we aim to
shed some light into the dynamics of the EOQ model under the carload discount schedule which seems
to be the most well-known transportation function in the literature. Recall that in our analysis we assumed that there exists an affine upper bound on the transportation-purchase function (Assumption
2.1). Though straightforward, for completeness we explicitly give in AppendixBthe steps to compute
these affine bounds for the functions that are used in our computational experiments.
The algorithms we developed were implemented in Matlab R2008a, and the numerical experiments
were performed on a Lenovo T400 portable computer with an Intel Centrino 2 T9400 processor and 4GB of memory.
4.1 Tightness of The Upper Bounds on Topt for Polyhedral Concave and Piecewise Polyhedral
Concavec(·). In the final paragraph of Example2.1, we reckoned that the constructed upper bound
vα,β on dmin given in (17) for the no shortages case may be weak for problems with strictly positive
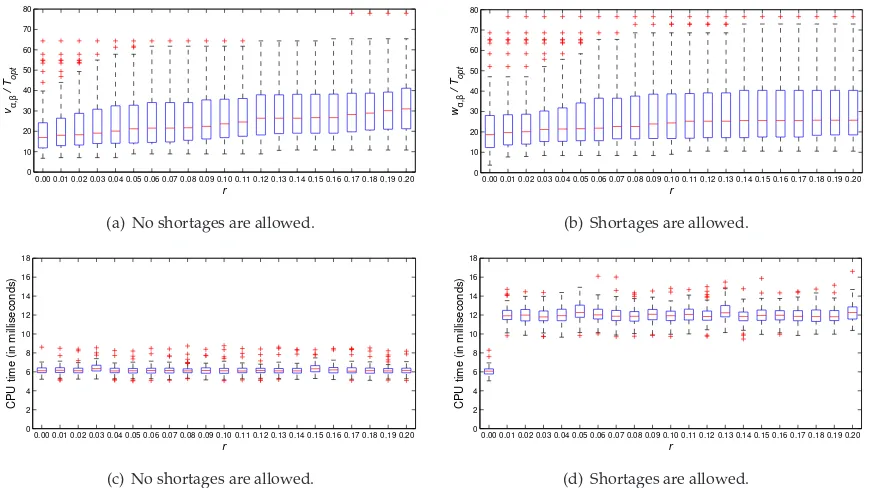
inventory carrying chargerbecausevα,βdoes not contain the value ofr. The same is true for the upper boundwα,βondmindefined in (24) if shortages are allowed. Thus, in the first part of our computational study we explore the strength of the upper bounds on Topt asr changes. To this end, 100 instances
are created and solved for varying values ofrfor both polyhedral concave and piecewise polyhedral concave transportation-purchase functions. For all of these instances, we setλ=1500,a=200,h=0.05.
Piecewise polyhedral concave functions consist of 20 intervals over which the transportation-purchase
functionc(·) is polyhedral concave. In this case, each polyhedral concave function is constructed by the minimum of a number of affine functions where this number is chosen randomly from the range [2,5].
Ifc(·) is polyhedral concave on [0,∞), then the number of linear pieces onc(·) is selected randomly from the range [2,20]. For both piecewise polyhedral concave and polyhedral concavec(·), the slope of the
first affine function on each polyhedral concave function is distributed asU[0.50,1.00]. The following
[0.80,1.00]. All (truck) setup costs are identical to 50, and the distance between two breakpoints onc(·) is generated randomly from the range [0.05λ,0.20λ]. If shortages are allowed,btakes a value of 0.25,
otherwiseb=∞. The inventory carrying chargeris varied in the interval [0,0.20] at increments of 0.01.
The results of these experiments are summarized in figures10-11.
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20 0
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20 0
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20 0
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20 0
Figure 10: Quality of the upper bound onToptfor polyhedral concave functions with respect to rand associated solution times.
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20 0
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20 0
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20 0
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20 0
Figure 11: Quality of the upper bound onTopt for piecewise polyhedral concave functions with respect
torand associated solution times.
problems with and without shortages. See figures10(a)-10(b). Unfortunately, we cannot computedmin exactly for piecewise polyhedral concave functions, and we can only determine the upper boundsvα,β
andwα,βondminfor problems with no shortages and with shortages, respectively. (See Examples2.1-2.2.)
Bothvα,β andwα,βrely on the existence of an affine upper bound onc(·) and are not particularly tight as depicted in figures11(a)-11(b). Thus, in the future we may formulate the problem of determining
the best affine upper bound as an optimization problem which would replace the approach described in
SectionB.2.
The values of the upper boundsdmin,vα,β, andwα,βonToptare invariant to the inventory carrying charge r; however, we observe that the ratiosdmin/Topt,vα,β/Topt, andwα,β/Toptare not significantly affected by
increasing values ofrin figures10(a)-10(b)and11(a)-11(b). These graphs exhibit only slightly increasing trends asrincreases from zero to 0.20.
Overall, figures10(c)-10(d)and 11(c)-11(d)demonstrate clearly that we can solve for the economic
order quantity very quickly even when a general class of transportation costs as described in this paper are incorporated into the model. This is important in its own right and also suggests that decomposition
approaches may be a promising direction for future research for more complex lot sizing problems with
transportation costs. The algorithms proposed in this paper or their extensions may prove useful to solve the subproblems in such methods very effectively.
Two major factors determine the CPU times. First, our algorithms are built on solving many EOQ problems with linear transportation-purchase functions. These subproblems possess analytical solutions
if no shortages are allowed or r = 0 when shortages are allowed. Otherwise, a line search must
be employed to solve these subproblems which is computationally more costly. This fact is clearly displayed in figures10(c)-10(d)and 11(c)-11(d). Second, the solution times depend on the number of
subproblems to be solved which explains the longer solution times for piecewise polyhedral concavec(·)
compared to those for polyhedral concavec(·). We will take up on this issue later again in this section.
4.2 Carload Discount Schedule. In the remainder of our computational study we focus our attention
on the carload discount schedule which is widely used in the literature [12]. We first start by providing
a negative answer to Nahmias’ claim that solving the EOQ model under the carload discount schedule
with two linear pieces may be very hard, and then propose some managerial insights into the nature of the optimal order policy under this transportation cost structure. Finally, we conclude by analyzing the
impact of the number of linear pieces onc(·) and the improved upper bound onToptgiven in relation (45)
on the solution times for the carload discount schedule with nonincreasing setup costs. (See Example 3.1.)
One hundred instances with transportation-purchase functions based on the carload discount
sched-ule with two linear pieces are generated very similarly to those with piecewise polyhedralc(·) described previously. We only point out the differences in the data generation scheme. The transportation-purchase
functionc(·) is polyhedral concave over each interval ((k−1)C,kC], k= 1,2, . . ., whereC = 250 is the
truck capacity. All truck setup costs are set to zero. The slope of the first piece of the carload discount schedule is distributed asU[0.50,1.00], and the cost of a truck increases linearly until the full truck load
contribute to the cost of a truck. These 100 instances are solved for varying values ofrboth with and without shortages. The CPU times for solving these instances are plotted in Figure12. The median CPU
time is below 1.5 milliseconds in all cases, and the maximum CPU time is about 4 milliseconds. Clearly,
the economic order quantity may be identified very effectively under the classical carload discount schedule [12].
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20 0
1 2 3 4
CPU time (in milliseconds)
r
(a) No shortages are allowed.
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20 0
1 2 3 4
CPU time (in milliseconds)
r
(b) Shortages are allowed.
Figure 12: Solution times for the classical carload discount schedule.
In the next set of experiments, our main goal is to illustrate the dynamics of the model if the
transporta-tion costs are dictated by the classical carload discount schedule. In particular, we focus on the interplay between the inventory holding costs and the structure of the classical carload discount schedule. We
create ten instances for each combination ofh∈ {0.50,1.00,1.50,2.00,2.50}andb∈ {∞,5h}. For all of these
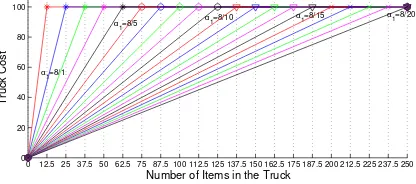
instances, we setλ =1500,a=100,r=0, andC= 250. Then, for each instance we keep the cost of a full truck load fixed at 100 but consider different slopes for the carload discount schedule as depicted
in Figure13. The main insight conveyed by the results in Figure14is that the optimal schedule strives
to use a truck at full capacity unless holding inventory is expensive. For instance, in Figure14(a)the optimal order quantity is always 3 full truck loads forh =0.50 until the carload schedule turns into an
(ordinary) linear transportation cost function. On the other hand, forh=2.50 the optimal order quantity
diverts from a full truck load if the full cost of a truck is incurred at 0.70Cor higher.
0 12.5 25 37.5 50 62.5 75 87.5 100 112.5 125 137.5 150 162.5 175 187.5 200 212.5 225 237.5 250 0
20 40 60 80 100
α1=8/1
α1=8/5 α1=8/10 α1=8/15 α1=8/20
Number of Items in the Truck
Truck Cost
Figure 13: Alternate carload discount schedules for the same capacity and full truck load cost.
Finally, we explore how the solution times scale as a function of the number of subproblems to be
solved. Recall that earlier in this section we argued that the solution times depend heavily on the number of linear pieces on the transportation-purchase functionc(·). We illustrate that this relationship
is basically linear - as expected - by solving the EOQ model under a general carload discount schedule.
That is, the truck setup costs are decreasing although the trucks are identical, and there may be multiple breakpoints on the transportation-purchase function. (See Figure9). We generate 100 instances where
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1
Full Truck Cost Incurred at (Expressed As a Fraction of Truck Capacity C)
Topt
Full Truck Cost Incurred at (Expressed As a Fraction of Truck Capacity C)
Topt
Full Truck Cost Incurred at (Expressed As a Fraction of Truck Capacity C)
Total Cost
Full Truck Cost Incurred at (Expressed As a Fraction of Truck Capacity C)
Total Cost
Figure 14: Optimal cycle length and cost for alternate carload discount schedules and differenthvalues.
As before, the truck capacity is C = 250, and the transportation-purchase functionc(·) is polyhedral concave over each interval ((k−1)C,kC],k= 1,2, . . .. The setup cost of the first truck is distributed as
U[50,100], and for each following truck the setup cost is computed by multiplying that of the previous truck with a random number in the range [0.50,1.00]. For each truck, the number of breakpoints on
the discount schedule is created randomly in the range [2,20], and the distance between two successive
breakpoints is calculated by multiplying the remaining capacity of the truck by a random number in [0.05,0.20]. The slope of the first linear piece is distributed asU[0.50,1.00] and subsequent slopes are
obtained by multiplying the slopes of the immediately preceding pieces by a random number in the
range [0.80,1.00]. The final slope is always zero. In Figure15, we plot the solution times against the number of subproblems solved and conclude that the relationship between these two quantities is linear.
The dotted lines in the figure are fitted by simple linear regression through the origin. We also observe
that the relatively tighter upper bound onToptgiven in relation (45) for carload discount schedules with nonincreasing setup costs provides computational savings of 22% and 28% on average for instances with
0 500 1000 1500 2000 2500 3000 3500 4000 4500 0
100 200 300 400 500 600
Number of Linear Pieces on the Transportation−Purchase Function
CPU Time (in milliseconds) Based on m*
Based on n*
(a) No shortages are allowed.
0 500 1000 1500 2000 2500 3000 3500 4000 4500 0
100 200 300 400 500 600
Number of Linear Pieces on the Transportation−Purchase Function
CPU Time (in milliseconds) Based on m*
Based on n*
(b) Shortages are allowed.
5. Conclusion and Future Research. In this work, we have analyzed the impact of the transportation cost in EOQ-type models. We investigated the structures of the resulting problems and derived bounds
on their optimal cycle lengths. Observing that the carload discount schedule is frequently used in
the real practice, we have identified a subclass of problems that also includes the well-known carload discount schedule. Due to their special structure, we have shown that the problems within this class are
relatively easy to solve. Using our analysis, we have also laid down the steps of several fast algorithms.
To support our analysis and results, we have setup a thorough computational study and discussed our observations from different angles. Overall, we have concluded that a large group of EOQ-type problems
with transportation costs can be considered as simple problems and they can be solved very efficiently
in almost no time. In the future, we intend to study the extension of the EOQ-type problems to stochastic single item inventory models with arbitrary transportation costs.
Acknowledgments. We would like to acknowledge The Scientific and Technological Research
Appendix A. Existence Result. In this appendix we show that the optimization problem (P) with H(·,·) belonging toHandc(·) an increasing left continuous function has an optimal solution.
DefinitionA.1 A function f : [0,∞)→Ris called lower semi-continuous at x≥0if
lim infk↑∞f(xk)≥ f(x)
for every sequence xksatisfyinglimk↑∞xk =x.The function is called lower continuous if it is lower semi-continuous at every x≥0.
It is well known (see for example [13] or [6]) that the function f : [0,∞)→Ris lower semi-continuous
if and only if for everyα∈Rthe lower level set
L(α)={x∈[0,∞) : f(x)≤α}
is closed. It is now possible to show the next result. Observe we extend the EOQ-type function
T7→H(c(T),T) defined on (0,∞) to [0,∞) by definingH(c(0),0)=∞.
LemmaA.1 If c(·)is an increasing left continuous function and H belongs toH(·,·), then the function T 7→ H(c(T),T)is lower semi-continuous on[0,∞).
Proof. By the previous remark we have to show that the lower level set L(α) := {T ∈ [0,∞) : H(c(T),T)≤α}is closed for everyα∈R.Letα∈Rbe given and consider some sequence (Tn)n∈N⊆L(α)
satisfying limk↑∞Tk = T.Consider now the following two mutually exclusive cases. If there exists an infinite setN0⊆NsatisfyingT≤Tnfor everyn∈ N0,then by the monotonicity ofcit followsc(T)≤c(Tn)
for everyn∈ N0.This implies by the monotonicity of the functionx7→H(x,T) for everyT>0 that
H(c(T),Tn)≤H(c(Tn),Tn)≤α
for every n ∈ N0. Since N0 is an infinite set and limn∈N0↑∞Tn = T we obtain by the continuity of x7→H(c(T),x) that
H(c(T),T)=limn∈N0↑∞H(c(T),Tn)≤α.
If there does not exist an infinite setN0⊆NsatisfyingT≤Tnfor everyn∈ N0, then clearly one can find a strictly increasing sequence (Tn)n∈N1 satisfying limn∈N1Tn↑ T.This implies by the left continuity ofc that limn∈N1c(Tn)=c(T) and applying now the continuity ofHit follows
α≥limn∈N1H(c(Tn),Tn)=H(c(T),T)
Hence for both cases we have shown thatH(c(T),T)≤αand soL(α) is closed.
By LemmaA.1andH(·,·) belonging toHimplying
limT↓0H(x,T)=limT↑∞H(x,T)=∞
for everyx≥0 we obtain by the Weierstrass-Lebesgue lemma [1] that the optimization problem (P) has
Appendix B. Computing The Affine Upper Bounds. In this appendix, we demonstrate how an
affine function may be computed that satisfies (11) for both the carload discount schedule and the
piecewise polyhedral concave transportation-purchase functions.
B.1 The Carload Schedule. Without loss of generality, we only consider carload discount schedules
with nonincreasing truck setup costs which also includes trucks with identical setup costs as a special
case. Similar to the construction in Example 3.1, we let g : (0,C] → R be an increasing polyhedral
concave function satisfyingg(0)=0 andsiwithsi≥si−1 ≥0,i≥1 be the setup cost of theith truck. We
LemmaB.1 For a discount carload schedule with nonincreasing setup costs si≥0, i≥1it follows that
c(Q)≤αQ+β,
B.2 Piecewise Polyhedral Concave Functions. We next compute an affine bound for a piecewise
Q
Figure 16: Construction of an upper bound for the carload discount schedule.
where 2≤k≤Kand
The result then follows by using relation (47).
q0 q1 q2 q3 Q c(Q)
u(Q)
αQ+β u(q3)
s2
u(0)
s3
s1