www.elsevier.nl / locate / econbase
‘Hydraulic’ rationing
a,b ,*
Marek M. Kaminski
a
Department of Politics, New York University, 715 Broadway, New York, NY 10003, USA
b
Central Eastern European Economic Research Centre(CEEERC), Warsaw University, Warsaw, Poland Received May 1998; received in revised form May 1999; accepted September 1999
Abstract
The problem of distributing a single homogeneous divisible good among a variable set of agents, or the ‘rationing problem,’ is analyzed. Examples of rationing include bankruptcy, taxation, claims settlement, cost allocation, surplus sharing, and social choice problems. Agents are described by their personal characteristics, or types. A type may be an agent’s utility function,
]]
preference ordering, claim to an estate, financial record, etc. A rule of division that can be represented as a system of connected vessels is called hydraulic. For separable spaces of types and
]]]
continuous rules, this property is equivalent to obeying the fundamental axioms of symmetry and ]]] consistency. A universal criterion is presented for deciding when a bilateral rule has a consistent ]]]
extension. 2000 Elsevier Science B.V. All rights reserved.
1. Introduction
Assignment of taxes, division of an estate among creditors, or mass privatization of state-owned enterprises are examples of the rationing of a single homogeneous divisible
]]]
good among a variable set of agents. Rationing problems in the context of bankruptcy were first considered by O’Neill (1982), and their mathematical analysis was developed by Aumann and Maschler (1985). Young (1994) introduced a general framework with the central concept of ‘type,’ or all relevant attributes of a claimant. For apportionment and bankruptcy for transplant for example, types were assumed to be the populations of the states and the agents’ claims, respectively. Young obtained a number of axiomatic characterizations of allocation rules for such specific contexts and results that were valid for any indivisible goods.
The current paper introduces Young’s framework in a unified way. The rationing
*Tel.: 11-212-998-8504; fax:11-212-995-4184.
E-mail address: [email protected] (M.M. Kaminski)
problem is described by three variables, types of agents, the amount of the good, and the restriction on the amount a type can get. A generic type may be interpreted as any piece of information about an individual. The type of a person may include welfarist information, i.e. preferences or the utility function, and / or non-welfarist characteristics, e.g. the size of a claim, a person’s health record, tax form entries, or sex, race and age. In the main results of this paper, a type is assumed to be an element of any relational structure (a set with relations) or any separable topological space. This general setting allows for various non-isomorphic interpretations. A result obtained in such a setting remains valid for every specific context. Various interpretation of types produce the results, or their generalizations, of Aumann and Maschler (1985), Dagan and Volij (1997), and Young (1987, 1994), or lead to new results for multi-claim bankruptcy or social choice.
Types and the maximal portion a type can get define a specific model of rationing, or the set of all rationing problems of a given kind. Solutions to rationing problems are provided by rules. For every problem, a rule specifies how a good is allocated among]] agents. Many rules are generated by standards, a concept invented by Young (1994). A]]] standard R is a weak ordering over all pairs consisting of a typeti and an amount of a ]]]
good g . We read ‘(ti i, g )R(ti j, g )’ as: typej ti has at least as high priority to g as typei tj has to g . A standard is numerical if there is a real-valued function r such thatj ]]] (ti, g )R(ti j, g ) iff r(tj i, g )i $r(tj, g ) (Young, 1994).j
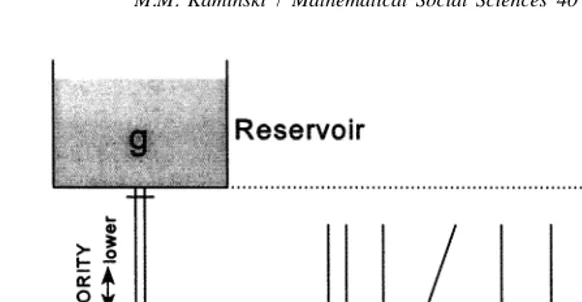
Consider the following solution to a rationing problem. Every agent gets one vessel from a system of connected vessels that are linked to a central reservoir through a system of pipes. The amount of water in a central reservoir is equal to the amount of good to be rationed. The allocation is obtained by opening the main sluice-gate and letting the water flow down and fill the vessels. When the water stops flowing, agents close their taps and enjoy the portions they received. Since the vessels are connected, the water levels in all vessels will be equal to one another. Solutions to all rationing problems are generated in a ‘hydraulic’ way, by the assignment of vessels to agents (Fig. 1).
The hydraulic metaphor conveniently enables one to visualize a numerical standard. Every such a standard R can be imagined as a specific system of connected vessels. In Fig. 1, different agents are assigned vessels that reflect their type. The representation of
R assigns to a typeti and his possible portion g , a number representingi ti’s priority to
g , r(i ti, g ). This numerical representation has a simple graphical representation. Let usi mount all vessels below some reference level, say, the bottom of main reservoir. Consider the vesselt4filled with g of water. The numerical priority of4 t4to get g can4
be represented by the distance from the surface of water in the vesselt4to the reference level. The farther from the surface to the reference level, the higher the priority assigned to (t4, g ). (Obviously, many different numerical representations of the same standard4
exist.)
Fig. 1. Hydraulic metaphor. Note: a problem (t1,t2,t3,t4; g) is solved by assigning to typest1,t2,t3,t4
appropriate vessels and pouring g water into the main reservoir.
properties a rule should satisfy. Among the most fundamental properties of rationing rules, which in fact are satisfied by almost all real-world rules, are continuity, symmetry and consistency. It turns out that for the class of continuous rules (in a separable topology), a rule is symmetric and consistent if and only if it is hydraulic. If continuity is substituted by monotonicity, then, for any space of types a rule is symmetric, monotone, and consistent if and only if it is ‘semi-hydraulic,’ i.e. if it is generated by a standard which is not necessarily hydraulic. This result leads to a corollary that provides simple necessary and sufficient conditions in order for any bilateral rationing rule to have a unique extension to a consistent rule.
The plan of the paper is as follows. Sections 2 and 3 introduce the formal framework and present the main results. Section 4 describes examples of hydraulic rules in claims settlement and bankruptcy, and develops applications to social choice. Section 5 discusses the relationship between the present results and the work of Dagan and Volij (1997), and Young (1987). The last section concludes with some general comments. Proofs omitted in the text are given in Appendix A.
2. Model
n
I begin with notational conventions. For any two points x, y[R , x$y means x $y i i for i51, . . . ,n and x.y means x$y and x ±y for some i. The non-negative orthant
i i
n n
in R is denoted as R15hx:x$0j. The framework introduced below is based on Young’s (1994) definitions.
Let T, a non-empty set of types, be any mathematical structure, i.e. a set with n ]]
relations. T may beRorR , a family of real-valued functions, a topological space, etc. A single type is denoted as ti and a finite vector of types is denoted as t orh. The cardinality of a vectort is denoted byutu, and the set of all vectors of such cardinality as
utu n
T .S 5< T is a set of all finite vectors. The number max(t) denotes the maximal
amount type t can get and the function max: (t)[(0, 1 `] is called the restriction.
i i ]]]
When max(ti)5 1 `, no effective restriction is imposed on the amount typetican get. Dom(ti) denotes all portions ti can get and is equal to the interval [0,max(ti)] when max(tutu i), 1 ` and to the interval [0,1`) when max(ti)5 1 `. Max(t) denotes
oi51max(ti), or the maximal total amount that can be divided among types in t. A rationing problem, or simply a problem, is defined as a pair (t; g) wheret[S and g is
]]]
the amount of a good to be divided; g#max(t) when max(t), 1 ` and g,max(t) when max(t)5 1 `. The class of all problems defined by a specific set T and a specific restriction max(T ) is denoted by P. Examples of P include claims and bankruptcy (O’Neill, 1982; Aumann and Maschler, 1985), surplus sharing (Moulin, 1985), taxation (Young, 1987), or social choice problems (Section 4.3). Rationing problems considered in this paper resemble compensation problems studied in Fleurbaey (1994, 1995).
For any P, I adopt the following definitions:
n
SYMMETRY (SYM): A rule F is symmetric if for all problems (t; g)[P, and for all
pairs of typest,t [t, ift 5 t then F(t; g) 5F(t; g) . i j i j i j
A rule is symmetric if identical types get equal portions regardless of their position as ]]]
a coordinate in a vector. We say that a vector of typeshis a restriction of]]] t ifh results from deleting some coordinates int.
CONSISTENCY (CONS): A rule F is consistent if for all problems (t; g)[Pand for
allvectors of typesh[osuch thathis a restriction oft, ift [t appears inhash
j m
then F(t; g)j5F(h;(oi :ti[hF(t; g) ) .i m
Consistency (Harsanyi, 1959; Balinski and Young, 1978; Aumann and Maschler, 1985) specifies properties of the rule when the vector of types is shrunk. Assume that some uhu types from t get a certain amount of a good oi :ti[h F(t; g) . Consistencyi requires that the agents from this subset divide this amount in the same way the good was divided in the larger set. (A review of literature on consistency is provided by Thomson, 1996.)
MONOTONICITY (MON): A rule F is monotonic if for all pairs of problems
** ** **
(t; g*),(t; g )[P, if g*.g then F(t; g*).F(t; g ).
Monotonicity (Balinski and Young, 1982; see also Kalai and Smorodinsky, 1975; Kalai, 1977) says that when the total amount increases, nobody loses. Note: the second ‘.’ denotes a vector inequality.
The axioms introduced so far are defined for all type spaces. Below, T is a topological space.
CONTINUITY (CONT): A rule F is continuous if, for every sequence of problems
k k k k k
Whenever continuity appears, it is assumed that T is a separable topological space, i.e. ]]]
that T contains a countable subset whose topological closure is T. Examples of separable n
constitute separable spaces. This makes separability a sound informational condition for all rationing problems.
The results of this paper will use a weaker, bilateral form of the four axioms. These weaker axioms, bilateral symmetry (B.SYM), bilateral consistency (B.CONS),
]]]]] ]]]]]]
bilateral continuity (B.CONT), and bilateral monotonicity (B.MON), require that the
]]]]] ]]]]]]
respective conditions hold for all pairs of agents. While each of the bilateral axioms alone is essentially weaker than its multi-agent version, the sets of bilateral axioms assumed in the results together are equivalent to their strong versions.
B.SYM, B.CONS and B.MON imply anonymity (Lemma 1(f) in Appendix A): ANONYMITY (AN): A rule F is anonymous if for all problems (t; g)[P, and for all
permutations of coordinates int, s, F(t+s; g)5F(t; g)+s.
Anonymity is stronger than symmetry and says that renaming types does not change their portions. Bilateral anonymity (B.AN) requires that the condition holds for all vectorst such thatutu52. Anonymity will be assumed in some subsequent definitions. The axioms introduced so far concerned rules. A second notion will lead to the next set of axioms. Let Y5h(t, g ): t[T, g [dom(t)j denote all types and the portions
i i i i i
they could get. Let R be a weak ordering over Y, i.e. a complete and transitive binary relation. Let I be the indifference part and P the strict part of R, i.e. (ti, g )I(ti j, g )j ↔h(ti, g )R(ti j, g ) and (tj j, g )R(tj i, g )i j; (ti, g )P(ti j, g )j ↔ h(ti, g )R(ti j, g ) andj
|(t, g )R(t, g )j. R is a standard if it is strictly monotone in the amount of good (Young,
j j i i ]]] 1994):
STANDARD STRICT MONOTONICITY (SSM): For all types t [T, and all i
allowable amounts of good g , g [dom(t), if g ,g then (t, g )P(t, g ).
1 2 i 1 2 i 1 i 2
A standard is interpreted as a comparison of priorities of different types to all portions of a good they can get. We read (ti, g )P(ti j, g ) as:j ti has a higher priority to g thani tjto
g . SSM means that a type has a higher priority to get less than to get more. R isj numerical if there exists a real-valued representation r:Y→Rsuch that (ti, g )R(ti j, g ) iffj ]]]
r(ti, g )i $r(tj, g ).j
SSM sets priorities for a given type and various amounts of the good. To define a specific standard, priorities between different types and different amounts of the good must be specified. In many cases, the definition of a standard can be completed in a very simple fashion. For instance, the egalitarian standard can be defined for all types with no restriction by asserting that ‘Everybody has an equal priority to the same amount of the
E
good.’ Formally, it is sufficient to say: R is a binary relation on Y that satisfies SSM E
and such that (t, g )I (t, g ) for allt,t [T and all g $0. A numerical representation of i i j i i j i
E E
R is simple as well, and we can define r (ti, g )i 5 2g for alli ti and g . Informali definitions of other familiar standards can implicitly require that a type carries some specific information, e.g. ‘Claimants have priorities proportional to their claims’ or ‘An agent who derives less utility from his portion of the good has a higher priority than the agent who derives more utility from his portion.’
The final axiom for standards specifies some technical topological requirement. Let us define B(t, g ,t)5hx[dom(t): (t, g )R(t,x)j. B(t, g ,t) is the set of all amounts x such
i i j j i i j i i j that tj has not higher priority to x asti to g .i
CLOSURE BELOW (CB): For all types with an allowable portion (t, g )[Y, and for i i
(a) if max(t)5 1 ` then B(t, g ,t)5 [ or inf B(t, g ,t)[B(t, g ,t); j i i j i i j i i j (b) if max(tj), 1 ` then B(ti, g ,ti j) is closed and non-empty.
Condition CB specifies topological requirements on R with no reference to any structure on T. This condition is closely related to one of Debreu’s (1954) classical conditions applied to the space T3Rand Young’s (1994, p. 191) axiom (see Section 3 for a more detailed discussion of the relationship).
Standards and rules can be linked via a concept of equity (Young, 1994). Let ( g , . . . , g ) be an allocation for (t; g) and 01 n ,´ #g . A transfer ofj ´ fromtj toti is
R-justified if (ti, g )P(ti j, gj2´).
]]]EQUITY: A rule F is R-equitable if for all (t; g)[P, no transfer is R-justified for ]]]
F(t; g).
Equity means that all allocations generated by a rule conform closely to the standard. (In the hydraulic language, a transfer fromtj toti is R-justified if the water level in the vesseltjis higher than inti. The reader is requested to go back to Fig. 1, fill the vessels with virtual water, and check how the metaphor works.) Consider a simple example of
E
the unconstrained equal division rule E and the egalitarian standard R . Since E(t; g)i5 E
(1 /utu)g for all i, for 0,´ #(1 /utu)g we can check that (ti, gi2´)P (tj, g ) for alli
E E
t,t [T and no transfer is R -justified. The rule E is R -equitable. i j
Now, the ‘hydraulic’ and ‘semi-hydraulic’ properties will be defined formally for any rule F. Both names denote concisely two classes of rules constructed on the basis of the concept of equity.
SEMI-HYDRAULIC PROPERTY: F is semi-hydraulic if it is R-equitable for some ]]]]
standard R.
HYDRAULIC PROPERTY: F is hydraulic if it is R-equitable for some numerical ]]]
standard R.
There exist semi-hydraulic rules that are not hydraulic. An example is the lex-icographic priority rule X, defined for T5Rand no restriction, which divides the whole
X X
good equally among agents with the lowest type. X is R -equitable for the standard R X
defined as ;t,t [T, ;g[dom(t), ;g [dom(t), [t , t →(t, g )P (t, g ); t 5 i j i i j j i j i i j j i
X X
tj→(ti, g )P (i tj, g ) iff gj i,g ]. Rj is not numerical and it is clear that X cannot be
R-equitable for any numerical standard R.
3. Results
In this section, T is any set of types and max(T ) any restriction. Theorems 1 and 2 generalize Young’s (1994) results which connect standards with rules. Theorem 1 will
1
be used as an intermediary step leading to Theorem 2 and Corollary 1.
Theorem 1. A rule satisfies B.SYM, B.CONS and B.MON if and only if it is
semi-hydraulic, i.e. if there exists a standard R such that F is R-equitable. For any standard R
1
that satisfies CB there exists a unique rule that satisfies B.SYM, B.CONS and B.MON and is R-equitable, and vice versa.
Theorem 11 of Young (1994, p. 192) connects rules with standards for claims, i.e. with T5R12h0j and max(ti)5ti. It says that if a standard R is representable and closed below then for every problem (t; g) there exists a unique allocation F(t; g) that is
R-equitable. The present result asserts that the relation of equity is two-sided, i.e. equity
is a one-to-one relation between all standards that satisfy CB and all rules that satisfy B.SYM, B.CONS and B.MON, and that it holds universally for all types.
The present axiom of closure below differs somewhat from Young’s formulation. Young’s axiom imposes a stronger topological condition than the present axiom but it does not require that, when max(ti), 1 `, the set B(ti, g ,ti j) be non-empty. However, without such a requirement, Young’s Theorem 11 is false since the relationship does not hold for some standards that satisfy his axioms. A counterexample to Young’s Theorem
CEA
*
11 is provided by a constrained equal award standard R with a following numerical
CEA
*
representation: r (t; g )5 2g for all g [dom(t). For t 51, t 52, g53, and i i i i i 1 2
t 5(t1,t2) a transfer of ´ is justified fromt2 tot1 for all 0,´ ,1 and no equitable
CEA
*
allocation exists since (1,2) is the only allocation for (t; g). The R standard satisfies Young’s condition of closure below but not the present condition. The difficulty
CEA
disappears when we add a provision that r (ti; g )i 5 2g only for all 0i #gi,max(ti)
CEA
while for g 5max(t), (t; g )R (t; g ) for all g [dom(t). i i j j i i j j
In Theorem 1, no structure on the set of types was postulated while in Theorem 2, some topological conditions are assumed.
Theorem 2. Let T be a separable topological space and let F be a continuous rule. F
satisfies B.SYM and B.CONS if and only if it is hydraulic, i.e. if it is R-equitable for some numerical standard R. In addition, F satisfies B.MON.
Theorem 2 says that, for continuous rules defined in a separable topology, the hydraulic property is equivalent to obeying bilateral symmetry and bilateral consistency. The assumption of continuity of F with respect to a separable topology on T cannot be dropped. Consider the lexicographic rule X introduced in Section 2. X is not hydraulic but it satisfies B.SYM and B.CONS. However, X is not continuous in the usual topology onR. If we change the topology, e.g. if we take the discrete topology onR, where any subset of reals is an open set, X becomes trivially continuous. However, such a topological space is not separable.
utility functions, when the rationing problem becomes a variant of the social choice problem. These cases are discussed in more detail in the next section.
The third general result concerns consistent extensions of bilateral rules. In the context of bankruptcy, Aumann and Maschler (1985) proved that the Contested Garment rule from the Talmud has a unique consistent extension. Dagan and Volij (1997) formulated necessary and sufficient conditions for deciding when any bilateral bankruptcy rule can be consistently extended. The following criterion is closely related to Dagan–Volij’s result (see discussion in Section 5.1).
2 2
Let us define P as the set of all two-type problems: P 5h(t; g)[P: utu52j. A
2 2 2
bilateral rule H:P →R1assigns to every bilateral problem (t,t; g)[P an allocation. i j
Anonymity of H guarantees that the relation R is well-defined. Bilateral symmetry and bilateral monotonicity alone do not imply anonymity of a bilateral rule. An example of a non-anonymous bilateral rule H* that satisfies B.SYM and B.MON is as follows:
T5R1, and for t , t1 2, H* is proportional; for t $ t1 2, H* is equal division.
Corollary 1. A bilateral rule H that satisfies B.AN and B.MON has a consistent
H
extension if and only if the relation R is transitive. This extension is unique.
The proof uses some concepts and results from Appendix A.
Proof. Only if : See Lemma 1(e,f).
H
If : R is a standard and satisfies CB [see the proof of Theorem 5(a)]. By Theorem 1, H
there exists a rule F that is R -equitable. We will show that F is a consistent extension of H. Let us assume, to the contrary, that for some (t; g)[P, F(t; g) 5g and
a transfer of´ from tj toti is justified and F cannot be R -equitable.
2 2
4. Examples
4.1. Single-claim bankruptcy
In this case T5R12h0jand max(ti)5ti. A type is interpreted as an agent’s ‘claim’ on a property and a problem is interpreted as a ‘bankruptcy’ or ‘bequest’ problem. Below, such problems will be called, in short, ‘claims.’
The formal analysis of claims was pioneered by O’Neill (1982) who introduced the claims problem with a story from the Babylonian Talmud, discussed several rules, and compared their properties. The mathematical analysis of claims was subsequently developed by Aumann and Maschler (1985), and Young (1987).
Aumann and Maschler’s analysis is focused on the Talmudic bequest problem. Marriage contracts for three wives of a deceased husband specify their claims as equal to 100, 200 and 300. How should the estate be divided if it is valued below the total of 600? In three discussed problems, the estate is worth 100, 200 and 300. The Talmudic solutions are clearly different from proportional division (Table 1). Aumann and Maschler noted that the Contested Garment (CG) solution from the other Mishna in the]]]]]] Talmud makes recommendations for any pair of claimants and the amounts they received, that are bilaterally consistent with the three-person problem.
Aumann and Maschler reconstructed a hypothetic general rule that generated the Talmudic numbers as a function of the estate. For two claimants, when the value of an estate rises continuously, CG divides the property equally up to the size of a smaller claim, next gives everything to the larger claimant up to the size of a larger claim, and finally divides the remaining part equally. Formally, for two claimstiandtj,t , ti j, the
1 1
] ]
CG rule is defined by the following formula: F(ti,tj; g)5( g, g) for 02 2 #g#ti;
1 1 1 1
] ] ] ]
F(ti,tj; g)5(2ti, g22ti) for t ,i g#tj; F(ti,tj; g)5( [ g2 2t 1 tj i], [ g2 2t 1 ti j]) for t ,j g#t 1 tj i. The CG rule can be compactly depicted as an appropriate ‘system of connected vessels’ (Fig. 2).
Some of Aumann–Maschler’s central results follow directly from Corollary 1. The CG rule clearly satisfies B.AN and B.MON. The reader can easily check that, in
CG
addition, the underlying binary relation R is transitive. Thus, Corollary 1 implies the existence of a unique extension of CG (Aumann and Maschler’s Theorem A) which is consistent (Aumann and Maschler’s Corollary 3.1).
The CG rule successfully challenges the apparently universal charm of proportional division. The two rules appeal to different value systems but, as many other claims rules, share the property of being hydraulic. Other examples of popular claims rules include
Table 1
Solutions to three claims problems recommended by the Talmud (Aumann and Maschler, 1985) Estate Claim
100 200 300
1 1 1
] ] ]
100 333 333 333
200 50 75 75
Fig. 2. A hydraulic CG solution to the three claims problems from the Talmud. Note: the size of a claim is equal to the area of the corresponding vessel.
Talmudic constrained equal award and its vertical mirror image, constrained equal loss,
]]]]]]] ]]]]]]
both by Maimonides (Aumann and Maschler, 1985, pp. 202–203; Thomson, 1995 provides a review of claims rules). Fig. 3 shows hydraulic systems for a few popular rules.
4.2. Multi-claim bankruptcy
B k k
Let us define the case of multi-claim bankruptcy as T 5R12h0jand max(ti)5oj51
x , where x is a jth coordinate ofj j ti. A type is interpreted as a vector of claims of various priorities and a creditor cannot get more than the sum of his claims. Claims are a special case of multi-claim bankruptcy with k51.
American bankruptcy law illustrates that multi-claim bankruptcy involves more complex information than a single claim. Every legal case in the United States constitutes a bankruptcy problem: ‘‘Once a bankruptcy petition is filed . . . the
2
bankruptcy priority system becomes applicable. There is no discretion in the court . . . ’’ Types are defined implicitly in the bankruptcy code by enlisting various ‘priority classes,’ since ‘‘[t]he general policy of the law is that there are no sub-classifications in priority classes.’’ The four major priority classes include the Federal Government,]]]]]] trustees and two kinds of creditors. Thus, a type can be represented formally as a vector
]] ]]]
of non-negative reals with different coordinates corresponding to claims from different priority classes.
Once the size of the estate and the types of creditors are reconstructed, the division of the estate is guided by the following ‘priority system.’ Among the four major classes of claims, the priority system is lexicographic. The highest priority is accorded to governmental taxes.]] These are followed, in order, by secured]] claims, administrative expenses of the trustee, and unsecured claims. Within the second and]]] ]]]]]]]
fourth classes of claims, the assets are being divided proportionally because the principle of ‘equal treatment of creditors’ is interpreted to be ‘a pro rata distribution.’ Thus, the actual American bankruptcy rule is mixed lexicographic–proportional.
In addition to four main classes of claims, a number of code sections describe a new category of claims. These ‘exceptions’ represent the introduction to the standard of some rarely met categories like lessors of property, whose priority is located between
]]]]]
administrative expenses and unsecured claims. As another exception, the ‘super-priority is confined to lien-holders,’ but ‘super super-priority’ to administrative expenses, ‘if a trustee is unable to obtain unsecured credit otherwise.’ Clearly, the code is intended to handle, in a somewhat awkward manner, priorities of all imaginable types of creditors and to set a corresponding lexicographic–proportional standard. The main idea of this complex system can be depicted in a remarkably simple way (Fig. 4).
The properties of bankruptcy laws around the world remain a question for empirical study. If a given bankruptcy code defines a rule that is symmetric, continuous, and consistent with respect to some set of types, Theorem 2 receives a remarkable empirical
Fig. 4. A hydraulic solution to a bankruptcy problem according to American bankruptcy law. Note: different levels represent four basic classes of claims. At levels 1 and 3, there is a single creditor. At levels 2 and 4, the rule is proportional division.
2
interpretation. It says that the code can be rewritten, and possibly simplified, so that it would provide an explicit list of types and their numerical priorities.
4.3. Social choice rationing
I
In this case T 5hu: R1→R s.t. u is continuous and strictly increasingj and no restriction is assumed. The following bilateral correspondences along with their multi-person versions are frequently considered in social choice theory:
2
UTILITARIAN LEXIMIN: L (u ,u ; g)i j 5Argmax minhu (x),u ( gi j 2x)j, for 0#x#g.
2
NASH PRODUCT: N (u ,u ; g)i j 5Argmax [u (x)i 2u (0)][u ( gi j 2x)2u (0)],j for 0#x#g.
2
UTILITARIAN SUMMATION: U (u ,u ; g)i j 5Argmaxhu (x)i 1u ( gj 2x)j, for 0#x#g.
One can ask under which conditions the bilateral correspondences are single-valued and can be consistently extended to multi-person rules. This question can be answered with Corollary 1.
2 2 2
L is single-valued and satisfies L (u ,u ; g)i j i1L (u ,u ; g)i j j5g for the original type
I 2 I
space T , which means that L is a bilateral rule on T . The other two rules are single-valued on narrower domains:
WC I
WEAK CONCAVITY: T 5hu[T :;x, y[R1;p[(0,1)
u( px1(12p)y)$pu(x)1(12p)u( y)j;
SC I
STRICT CONCAVITY: T 5hu[T :;x, y[R1;p[(0,1)
x±y→u( px1(12p)y).pu(x)1(12p)u( y)j.
2 2 WC SC 2
N and U are bilateral rules on T and T , respectively. It is also clear that L ,
2 2
N , and U are anonymous, non-decreasing in g, and that the corresponding binary relations R are transitive. Thus, Corollary 1 can be applied to obtain the next result.
Theorem 3. The following bilateral rules have unique consistent extensions for
respective spaces of types:
2 I
(a) L for T ;
2 WC
(b) N for T ;
2 SC
(c) U for T .
relation-ship between social choice problems and bargaining seems to be close indeed. The precise extent to which the results from one framework can be applied to the other framework depends on the assumed space of types.
With every social choice problem (u; g), where u5(u , . . . ,u ) and g1 n .0, the following bargaining problem can be associated: B(u; g)]]]]]] 5h(u ( g ), . . . ,u ( g )): all1 1 n n
n
gi$0 and oi51 gi#gj. Young (1994, pp. 210–212) noted that Lensberg’s (1987) results obtained for bargaining can be applied in the social choice setting, and he offered a preliminary discussion of the properties of anonymous, continuous and bilaterally
WC
consistent rules for T with respect to maximization of separately additive objective functions. However, the results for bargaining cannot be mechanically restated for the social choice setting, and vice versa, since the function B is not 1–1 and onto (Billera and Bixby, 1973). Moreover, almost all results in bargaining theory are obtained under the assumption of weak convexity of the bargaining set. This assumption rules out from consideration the utilitarian summation (since for a non-strictly convex bargaining set, U may be multi-valued) and makes the domain of L unnecessarily narrow (since some
I
bargaining problems corresponding to T are non-convex). More work remains to be done on the formal relationship between the two frameworks.
5. Related results
Below, I discuss informally the relationship between the present results and Dagan and Volij’s (1997) criterion for a consistent extension of a bilateral claims rule, and Young’s concept of parametric representation. The discussion exemplifies further applications of Theorem 2 and Corollary 1.
5.1. Consistent extension of a bilateral claims rule
For every vector of types t 5(t1,t2, . . . ,tn), a bilateral rule H, and any allocation H
g 5( g , g , . . . , g ), the following binary relation is defined: A :5h(i, j )[I3I:
1 2 n g
H
H (t,t; g 1g )$gj. iA j is interpreted as ‘g treats i no better than j according to H.’
i i j i j i g
H is consistent withg andt if for allt,t [t, H (t,t; g 1g )5g . Dagan and Volij’s i j i i j i j i
main Theorem, slightly reformulated, connects the possibility of a consistent extension H
of a bilateral claims rule and the transitivity of the strict part of Ag:
Theorem [Dagan and Volij, 1997]. Let T5R12h0j and max(ti)5ti. For any
anonymous bilateral rule H that satisfies B.MON and any problem (t; g)[P, there
exists a unique allocationg consistent with H andt if and only if for every allocation
H H H
x 5(x ,x , . . . ,x ),1 2 utu Ax is quasi-transitive, i.e. when ax, the strict part of Ax, is
transitive.
For claims, the Dagan–Volij’s theorem provides a criterion alternative to that of Corollary 1. We will show that both criteria are equivalent for all types.
H H extend it in a natural way to a global relation. Let us defineA as the sum of all Ag,
H H H
i.e. A :5<g[Rn, n[NAg. Since A depends only on typesti andtj, and all possible H
portions allotted to these types, we can interpretA as a binary relation on Y5h(t, g ):
i i
strictly monotone, A ;R as well. Thus, for strictly monotone bilateral rules, both
criteria are identical (this fact is reflected in the formulation of Dagan and Volij’s
H H
Theorem 4.9). In general, A substitutes some strict parts of R by indifferences. An
example is provided by the CG rule andt 5i 100,t 5j 200. All pairs ,(ti, g );(ti j, g )i .
The Dagan and Volij’s criterion, as well as the relation A , do not assume any
type-specific information. This fact suggests that a generalization is possible. In fact, the H criterion is valid for any space of types. Proposition 1 states the relationship betweenA
H
and R formally. The formulation of the criterion remains unchanged but the restrictions imposed on T and max can be dropped.
H
Proposition 1. For anyPand any anonymous bilateral rule H that satisfies B.MON, R
H
is transitive if and only if a is transitive for allg.
g
H
Proof (outline). The proof is based on the properties of binary relations a (Lemma A)
g
H H H
and R (Lemmas C and D), and the relationship between R and ag (Lemmas B and
E).
Comment. In the proof of Lemma A, ´ must be sufficiently small to preserve
H H
inequalities that are implied by iaxj and jaxk; the proof of Lemma B follows from
H
the definition of R . The details and the proofs of Lemmas C–E are left to the reader. H
Only if : Let us assume now that a is not transitive for someg, i.e. for somet,t,
H H H
quence for someg. By Lemmas C and D, we construct a following string (indices reflect the order of applying Lemma C): interval of the extended reals, with values inR<h1 `j. Following Young’s (1987, pp. 400–401) definition, f is called a parametric representation if for eachti: (a) f(ti,l) is
]]]]]]] claims rule F, F satisfies SYM and B.CONS iff it is representable by a continuous parametric function. Among parametric rules discussed by Young, who used the taxation setup, there are flat, head, leveling, and equal sacrifice taxes, as well as many other families of tax schedules. All these rules are hydraulic.
The concepts of a parametric representation and a numerical standard are in fact closely related. In terms of connected vessels mounted between levels a and b, f(ti,l) can be imagined as the volume of the vessel assigned to ti up to the level l. Alternatively, the diameter of vessel ti at level l may be set as the left-hand side derivative of f(ti,l).
Formally, in many cases, we can simply obtain a parametric representation of F from a numerical standard r that is equitable relative to F with f(ti,2r(ti, g ))i 5g . In general,i the range ofl can be defined as follows:
(i) a5inf h2r(t, y): (t, y)[Yj and b5suph2r(t, y): (t, y)[Yj.
i i i i
The parametric representation f can be constructed in the following way:
(iii) For 2r(t,0)#l , 2r(t,max(t)), f(t,l)5suphx[dom(t): 2r(t,x)#lj.
i i i i i i
(iv) For 2r(ti,max(ti))#l #b, f(ti,l)5max(ti).
Let us check what happens when the above construction is applied outside of Young’s I
domain of claims, e.g. for T and the leximin rule L introduced in Section 4.3. Since
r(u , y)i 5 2u ( y) and max(u )i i 5 1 `, we have:
I I
(i*) a5infhu ( y): u [T and y[R j5 2 ` and b5suphu ( y): u [T and y[
i i 1 i i
R1j5 1 `.
(ii*) For 2 ` #l ,u (0), f(u ,i il)50.
21 21
(iii*) For u (0)i #l ,limy→` u ( y), f(u ,i il)5ui (l), where ui is the inverse function of u.
(iv*) For limy→` u ( y)i #l # 1 `, f(u ,l)i 5 1 `.
It is easy to check that f is a parametric representation of L according to the definition stated above. This fact suggests that Young’s result can be applied to a wider space of types. Let T be any separable space. If a continuous rule F is representable by a parametric function, then it is clearly symmetric and consistent. On the other hand, Theorem 2 implies that if F is continuous, symmetric, and a bilaterally consistent rule, then it is equitable relative to a numerical standard r. It is a mechanical exercise to check that applying (i)–(iv) to this particular standard r brings a parametric representation of
F. Therefore, the following proposition can be formulated:
Theorem 4. Let T be any separable topological space and F be a continuous rule. F
satisfies SYM and B.CONS iff it is representable by a parametric function.
Theorem 4 provides a characterization similar to Young’s (1987) Theorem 1 for a wider space of types but the family of parametric functions considered in this theorem is not necessarily continuous in the topology on T3R. When continuity is assumed, the ‘if’ part makes a weaker claim, while the ‘only if’ part makes a stronger claim than the relevant parts of Theorem 4. Whether the equivalence holds when the term ‘parametric function’ is substituted by ‘continuous parametric function’ remains an open question.
6. Conclusion
The present paper introduces rationing problems as cross-products of a space of finite vectors of types and a unidimensional Euclidean space of available resources. Working with abstract type space allowed for a unified analysis of various non-isomorphic
n rationing problems. Specific spaces that were discussed include R1 and R1 with relevant restrictions, and various sets of functions u:R1→R. Interpretations of such settings include bequest, bankruptcy, claims settlement, taxation, cost sharing, and social choice. Other non-isomorphic settings that are covered by the present setup include profit-sharing, with T5R1 and no restriction, and problems with complex types.
fundamental properties were distinguished as minimal conditions that one would like an allocation rule to obey. These properties include symmetry, continuity and consistency. Almost all rationing rules that have been suggested and used by theorists or practitioners satisfy these properties. Thus, the question of whether there exists a general procedure that can be used to generate any solution with such properties to any allocation problem defined over a separable type space was addressed. As the family of symmetric, continuous and consistent rules is quite large and covers a range of different domains, the existence of such a procedure is by no means an obvious proposition.
The main result of this paper for separable type spaces is a characterization theorem which shows that within the class of continuous rules, a rule is symmetric and consistent if and only if it is generated by a numerical standard. A standard is a general procedure of the desired kind, since from any initial distribution of resources, it specifies the direction in which resources should be redistributed in order to more closely conform to the allocation rule. Since a numerical standard can be imagined as a system of connected vessels, allocation rules that are generated by a standard were called hydraulic.
Other main results remain applicable to all spaces of types. Most notably, a universal criterion formulates necessary and sufficient conditions for the existence of a consistent extension of a bilateral rule. The criterion says that a monotonic and anonymous bilateral rule has a consistent extension if and only if it defines some standard.
The novelty of the present results is in showing that most important rationing rules are structurally similar, despite their different domains and restrictions, and can be characterized jointly with the same set of fundamental principles.
Acknowledgements
The final version of this paper was prepared while the author was a Fellow at the Central Eastern European Economic Research Centre at Warsaw University and was supported by a grant from the Open Society Institute’s Individual Project Fellowships Program. The comments of Robert Aumann, Steven Brams, Peter Coughlin, Keith Dougherty, Marc Kilgour, David Lalman, Guy Laroque, Grzegorz Lissowski, Burt
´
Monroe, Herve Moulin, Jeff Silver, Karol Soltan, Michael Tkacik, Jim Vreeland, Peyton Young, anonymous referees and, especially, Piotr Swistak, are gratefully acknowledged. The usual disclaimers apply.
Appendix A
Let T be any non-empty set of types, and max: T→R1<h1 `j any restriction. Let
Y5h(t, g ):t [T and g [dom(t)j denote all types and portions they could get. i i i i i
Two auxiliary priority functions will represent relative priorities of a type]]]]] tito various portions of a good according to the standard and according to the rule, within a specific vector t. Let operator ‘inf’ (‘sup’) assign to any non-empty set of reals its infimum (supremum). By convention, sup([)50. Functions f and r assume values int t R1<
Priority functions: For any anonymous rule F and standard R, any (t; g)[P,t [t, i
g [dom(t): i i
f (tt, g ):5suphx[ [0,max(t)): F(t;x) #gj;
i i i i
utu
r (tt, g ):5
O
suphx[dom(t):(t,x)R(t, g )j. i i j j i ij51
Function ft assigns to a type ti and his portion gi the maximal total amount that types in t get whenti gets at least g , according to F.i ]]]]]]]]]]]]]]]]]]]]
Function rt denotes a certain sum and has a more complex interpretation. The component of this sum corresponding to typetj denotes the limiting portion of a good such thattj has a priority to all smaller portions over the priority oftito g . This numberi represents how much tj must get beforeti gets g , according to R. Wheni t includes
]]]]]]]]]]]
only two types t 5(ti,tj), the corresponding functions are denoted by fij and r ,ij respectively. Finally, notice that by anonymity of F, f (tti, g ) does not depend on thei position ofti int. This fact will be assumed later in the constructions.
Consider again the example of the unconstrained equal division rule E from Section 2. utu
Obviously, f (tt, g )5utug . On the other hand, r (t, g )5o suphx[ i i i t i i j51
utu
dom(tj):(tj,x)R(ti, g )i j5oj51 gi5utug . Thus, fi t;r . It turns out that this relationshipt holds in general for all standards that satisfy CB, i.e. that;t[S,;(t, g )[Y s.t.t [t,
i i i
r (tti, g )i 5f (tti, g ), in short, ri ;f.
The plan of action is as follows. First, Lemmas 1–3 investigate the properties of f andt
r . These functions are used to construct the rule F from a standard R and vice versa,t and obtain Theorems 5 and 6. Proposition 2 asserts that these two results imply Theorem 1. Finally, Theorem 2 is proved.
Lemma 1 establishes the transitivity of f for pairwise comparisons.t
Lemma 1. For every rule F that satisfies B.SYM, B.CONS and B.MON:
(a) F satisfies MON;
(b) F(t; g) is continuous in g;
(c) For allt[S,t[t, g [dom(t), if f (t, g )5g, 1 `, then F(t; g) 5g ; i i i t i i i i (d ) For all (t, g ),(t, g )[Y, if f (t, g ), f (t, g ), 1 ` then f (t, g )#
i i j j t i i t j j t i i
f (ttj, g )j ⇔f (ijti, g )i #f (ijtj, g );j
(e) For all (t, g ),(t, g ),(t, g )[Y, [ f (t, g )# f (t, g ) and f (t, g )# i i j j k k ij i i ij j j jk j j
f (jktk, g )]k →f (ikti, g )i #f (iktk, g );k ( f ) F satisfies AN.
Proof. Ad (a): Left to the reader. From now on, I assume MON.
Ad (b): For g.0, assume that limx→g2 F(t;x)i5hi±F(t; g)i5g . From MONi
gi.h . Leti ´:5gi2h . For any c such that gi 2c,´ we have from MON F(t;c)i5
oj±i F(t;c) . This means that F(t;x) is not non-decreasing for at least one type whichj contradicts MON. Similarly, limx→g1 F(t;x)5F(t; g) for all g$0.
Ad(c): The proof follows directly from the continuity of F and the details are left to the reader. From now on, I assume this property implicitly in all constructions.
Ad(d): Since f (tt, g ), f (t, g ), 1 `, (t; f (t, g ))[P and (t; f (t, g ))[P. Consider i i t j j t i i t j j
two cases:
Case 1 : f (tt i, g )i ,f (ttj, g ). This means by MON that F(j t; f (ttj, g ))j i.gi and
F(t; f (tt j, g ))j j5g .j By B.CONS, F(ti,tj;F(t; f (ttj, g ))j i1F(t; f (tt j, g )) )j j i.gi and
F(ti,tj;F(t; f (ttj, g ))j i1F(t; f (ttj, g )) )j j j5g . Thus, by definition of fj ij and B.MON,
f (ijti, g )i ,f (ijtj, g ).j
Case2 : f (tt i, g )i 5f (t tj, g ). In this case, F(t; f (j tti, g ))i 5g and F(i t; f (tt i, g ))i j5g and,j by B.CONS, F(ti,tj; gi1g )j 5( g , g ); thus f (i j ijti, g )i $gi1g and f (j ijtj, g )j $gi1g . Ifj
gi5max(ti) and gj5(tj) then f (tij i, g )i 5f (ijtj, g )j 5gi1g . Otherwise, for a sufficientlyj small ´ .0, (t; f (tt , g )1´)[P. Let us define h :5F(t; f (t, g )1´) and h :5
i i i t i i i j
F(t; f (tt i, g )i 1´) . By assumption, hj i.g , hi j.g , and by MON hj i1hj#gi1gj1´. By B.CONS, F(ti,tj;hi1h )j i5hi.gi and F(ti,tj;hi1h )j j5hj.g , which impliesj
f (ijti, g )i #gi1g and f (j ijtj, g )j #gi1g . Thus, f (j ijti, g )i 5gi1gj5f (ijtj, g ).j
Ad(e): Let us definet 5(ti,tj,tk) and g5( g , g , g ). Consider two cases.i j k
Case1 : All values f are finite. Transitivity is a simple consequence of Lemma 1(d).t
Case 2 : At least one value of f is infinite. This implies that max(t t), 1 ` and, for some ´ .0, (t; g1´)[P. Assume that f (t, g ),f (t, g ). Consider F(t; g1´). By
ik k k ik i i
assumption, for at least one index m, F(t; g1´)m#g . Since gm 5gi1gj1g , for atk least one index m, F(t; g1´)k.g and at least one of the following three cases mustm hold: F(t; g1´)i#g and F(i t; g1´)j.g or F(j t; g1´)j#g and F(j t; g1´)k.g ork
F(t; g1´)k#g and F(k t; g1´)i.g . Let us assume that, for instance, F(i t; g1´)i#g ,i
F(t; g1´)j.g . By B.CONS and MON, F(j ti,tj;F(t; g1´)i1F(t; g1´) )j i#g andi
F(ti,tj;F(t; g1´)i1F(t; g1´) )j j.g , which implies f (j ijti, g )i .f (ijtj, g ), contrary toj our assumption that f (tij i, g )i #f (ijtj, g ). Similarly, we reject the remaining two cases.j Thus, it is not true that f (tik k, g )k ,f (ikti, g ) and f (ti ik k, g )k $f (ikti, g ).i
Ad( f): First, B.AN is established. Consider a problem ((ti,tj); g). Let us associate with this problem the following problem: ((ti,tj,ti,tj);2g). B.AN follows from B.CONS and B.SYM applied to this problem. The remaining part of the proof is left to the reader. h Lemmas 2–3 investigate the properties of r . For every standard R, the set Yt t,Y includes all pairs (t, g ) such that r (t, g ) is finite: Y 5h(t, g )[Y: r (t, g ), 1 `j.
i i t i i t i i t i i
Lemma 2. If R satisfies CB, then for all (t, g ),(t, g )[Y , r (t, g )#r (t, g ) iff i i j j t t i i t j j (ti, g )R(ti j, g ).j
Proof. if : directly from the definition of r .t
only if : Assume that (t, g )P(t, g ). By CB, B(t, g ,t)5hx[dom(t): (t, g )R(t,x)jis j j i i i i j j i i j closed. If B(ti, g ,ti j) is non-empty, let us define g05min B(ti, g ,ti j). Note that: (i)
g 5suphx[dom(t): (t,x)R(t, g )j; and (ii) g .g . Thus, the comparison of the sums
0 j j i i 0 j
utu utu
r (tt, g )5o suphx[dom(t):(t,x)R(t, g )j and r (t, g )5o suphx[ j j k51 k k j j t i i k51
dom(t):(t,x)R(t, g )j reveals that, for all k, suphx[dom(t): (t,x)R(t, g )j#suphx[
dom(t): (t,x)R(t, g )j but suphx[dom(t): (t,x)R(t, g )j2suphx[dom(t): definitions of m, n, and k , we have a following sequence of inequalities: gi ,
kn11 utu kn11 utu ki11 utu ki
Theorem 5. If a rule F satisfies B.SYM, B.CONS and B.MON, then there exists a unique
standard that satisfies CB such that r;f.
Theorem 6. For any standard R that satisfies CB, there exists a unique rule F such that
r;f. Rule F satisfies axioms B.SYM, B.CONS and B.MON.
Proof of Theorem 5. Let us define a binary relation R on Y as (ti, g )R(ti j, g )j ⇔
f (ijti, g )i #f (ijtj, g ). R is complete and transitive, by Lemma 1(e). We have to check: (a)j that R satisfies SSM and CB; (b) that r;f; and (c) that R is a unique standard with such
a property. The definition of f and MON, imply the following simple fact, which will bet used repeatedly below:
Proof of Theorem 6. Let us define rule F on the basis of a standard. For any (t; g)[P, let us find, by Lemma 3, such (t, g ) that r (t, g )5g. F(t; g) is defined as suphx[
k k t k k i
dom(ti): (ti,x)R(tk, g )k j. This construction is independent of the choice of (tk, g ) byk Lemma 2.
We have to check (a) that F is a rule that satisfies B.SYM, B.CONS and B.MON, and (b) that F is a unique rule such that r;f.
utu
Ad(a): That F is a rule, i.e. that F satisfiesoi51F(t; g)i5g, stems directly from the
definitions of F and r . By definition, F is symmetric. Next, B.MON is a consequence oft the definition of F and Lemma 2. To check B.CONS let us define g :i 5F(t; g) ,i
Proposition 2. For every standard R that satisfies CB, rule F is R-equitable if and only
if r;f.
Proof. if : For any problem (t; g), and any t,t [t, let us define g :5F(t; g) and
i j i i
f (tti, gi2´),g, and, by the fact that r;f, r (ttj, g )j .r (tti, gi2´). By definition of r ,t (ti, gi2´)P(tj, g ) and no transfer fromj ti totj is justified.
only if : By Theorem 6, for any standard R that satisfies CB, there exists a unique rule F such that r;f. By the if part of the proof, F is R-equitable. Thus, it is sufficient to
show that there exists at most one rule that is R-equitable. Suppose that for some
R-equitable rule G we have F(t; g)±G(t; g). There must exist i, j such that F(t; g) 5
i
F G F G 1 G F
]
gi ,gi 5G(t; g) and F(i t; g)j5gj .gj 5G(t; g) . Let us takej ´ 52minhgi 2g ,i F G
gj 2gjj. Since a transfer of ´from j to i is not justified in the allocation F(t; g), we
F F G F F G
have (tj, gj 2´)R(ti, g ). Thus, by SSM, we have (i tj, g )P(tj j, gj 2´)R(ti, g )P(i ti, gi 2 ´), which implies that a transfer of´from j to i is justified in the allocation G(t; g) and
G cannot be R-equitable. h
Proposition 2 allows us to write ‘F is R-equitable’ instead of ‘r;f ’ in the theorems
stated in the main body of the paper.
Proof of Theorem 2. If : Directly from Theorem 1.
Only if : Lemmas 4–5 precede the main proof:
Lemma 4 [Young]. Axioms of B.SYM, B.CONS and B.CONT imply B.MON.
Proof. See Young (1987, pp. 401–402), Lemma 1 for a specific space of claims. The
proof remains valid for any separable topological space after notational modifications. h
By Lemma 4, we can apply Theorem 5. Let us denote by R the unique standard that satisfies CB such that for F it holds that r;f. By Proposition 2, F is R-equitable. We
will show that R is numerical.
Case 1 : max(t)5 1 ` for allt [T.
i i
Since T is separable, we can find a countable subset of T that is dense in T. Let us
C
denote this subset by T and let us denote by Q1 the set of all positive rationals. A closed interval [(t, g ); (t, g )] is defined as h(t, g )[Y: (t , g )R(t, g )R(t, g )j. We
1 1 2 2 i i 1 1 i i 2 2
C
will show that a countable set T 3Q1is R-dense in Y, that is, that any interval [(t1, g );1 C
(t, g )] s.t. (t, g )P(t , g ) contains a point (t, g )[T 3Q such that
2 2 1 1 2 2 3 3 1
(t1, g )R(t1 3, g )R(t3 2, g ). This will conclude the proof by Cantor’s (1895, 1915) Theorem2
which says that, if R is an ordering over a non-empty set X, the existence of a countable
subset of X that is R-dense implies the existence of a numerical representation for R.
Lemma 5. If max(t)5 1 ` for all t[T, then for all t [T, and 0#g ,g , there
i i o 1 2
C
exists (t , g )[T 3Q s.t. (t , g )[[(t, g ); (t, g )]. m m 1 m m o 1 o 2
C
Proof. Let (ti) be a series from T converging toto. Since max(ti)5 1 `for allti, for all g.0 we have that (t,t; g)[P. By B.CONT, for any ´ .0, F(t,t; 2g 1
1
]
2´)→( g11´, g11´). Let us define ´:53( g22g ). For a sufficiently large m the1
following inequalities are satisfied:
(a) F(to,tm;2g11´)o.g and F(1 to,tm;2g11´)m,g11´;
(b) F(to,tm;2g115´)m.g112´ and F(to,tm;2g115´)o,g113´.
B.MON and inequality (a) imply that f (tmo o, g )1 ,f (motm, g11´). By a similar argument, f (tmo m, g112´),f (moto, g113´)5f (moto, g ). This, by the fact that r2 ;f and
Lemma 2, implies that (to, g )P(t1 m, g11´)P(tm, g112´)P(to, g ). To complete the proof2
of Lemma 5 note that we can find a rational number gm between ´ and 2´ such that (tm, g11´)P(tm, g )P(tm m, g112´). h
Now, let us take any interval [(t1, g ); (t1 2, g )] such that (t2 1, g )P(t1 2, g ). By Lemma 22
and the fact that f;r, f (12t1, g )1 ,f (12t2, g ). This means that F(t2 1,t2; f (t12 2, g ))2 1.g .1 1
]
Let us define g :3 52(F(t1,t2; f (t12 2, g ))2 11g ).1 Since g3,F(t1,t2; f (t12 2, g )) ,2 1
f (12t1, g )3 ,f (12t2, g ) and, by Lemma 2 and the fact that f2 ;r again, (t1, g )P(t3 2, g ).2 C
Since g .g , (t, g )P(t, g ). By Lemma 5, there exists (t , g )[T 3Q such that
3 1 1 1 1 3 m m 1
(t1, g )P(t1 m, g )P(tm 1, g ), which implies (t3 1, g )P(t1 m, g )P(tm 2, g ).2
Case2 : max(t), 1 `for at least onet [T. Let us define the following family of
i i
strictly increasing transformations:
If max(t)5 1 `, for all g [dom(t), h ( g )5g ; i i i i i i
max(ti) ]]]] If max(t), 1 `, for all g [dom(t)2hmax(t)j, h ( g )5g .
i i i i i i i max(t)2g i i
Now, let us define the following binary relation Q:
For allt,t [T, for all g , g [R , i j i j 1
21 21
(ti, g )Q(i tj, g ) if and only if (tj i,hi ( g ))R(ti j,hj ( g )).j
It is straightforward that Q is a standard and that Case 1 applies. Thus Q is numerical with a representation r. By construction of Q, r is a representation of R, except for all (t, g ) such that g 5max(t), 1 `. By CB, for all t,t[T, if max(t), 1 `,
i i i i i j i
R
max(tj), 1 `, then (ti,max(ti))I (tj,max(tj)). Thus, we can easily transform r and get a representation for the entire R. h
References
Aumann, R.J., Maschler, M., 1985. Game theoretic analysis of a bankruptcy problem from the Talmud. Journal of Economic Theory 36, 195–213.
Balinski, M.L., Young, H.P., 1978. Stability, coalitions, and schizms in proportional representation systems. American Political Science Review 72, 848–858.
Balinski, M.L., Young, H.P., 1982. Fair representation. Yale University Press, New Haven.
¨ ¨
Cantor, G., 1895. Beitrage zur Begrundnung der Transfiniten Mengenlehre. Mathematische Annalen 46, 481–512.
Cantor, G., 1915. Contributions to the Founding of the Theory of Transfinite Numbers. Dover, New York. Cowans, D.R., 1989. Bankruptcy Law and Practice. West Publishing.
Dagan, N., Volij, O., 1997. Bilateral comparisons and consistent fair division rules in the context of bankruptcy problems. International Journal of Game Theory 26, 11–25.
Debreu, G., 1954. Representation of a preference ordering by a numerical function. In: Thrall, R.M., Coombs, C.H., Davis, R.L. (Eds.), Decision Processes. Wiley, New York, pp. 159–165.
Fleurbaey, M., 1994. On fair compensation. Theory and Decision 36, 277–307.
Fleurbaey, M., 1995. Three solutions for the compensation problem. Journal of Economic Theory 65, 505–521.
Harsanyi, J.C., 1959. A bargaining model for the cooperative n-person game. In: Tucker, A.W., Luce, R.D. (Eds.). Contributions to the Theory of Games, Vol. IV. Princeton University Press, Princeton, pp. 325–355. Harsanyi, J.C., 1963. A simplified bargaining model for the n-person cooperative game. International
Economic Review 4, 194–220.
Kalai, E., 1977. Proportional solutions to bargaining situations: Interpersonal utility comparisons. Econo-metrica 45, 1623–1630.
Kalai, E., Smorodinsky, M., 1975. Other solutions to Nash’s bargaining problem. Econometrica 43, 510–518. Kaminski, M.M., 1997. A theory of hydraulic allocations, Ph.D. Thesis, University of Maryland, College Park,
MD.
Lensberg, T., 1987. Stability and collective rationality. Econometrica 55, 935–961.
Moulin, H., 1985. The separability axiom and equal-sharing methods. Journal of Economic Theory 36, 120–148.
Nash, J.F., 1950. The bargaining problem. Econometrica 18, 155–162.
O’Neill, B., 1982. A problem of rights arbitration from the Talmud. Mathematical Social Sciences 2, 345–371. Thomson, W., 1995. Axiomatic analyses of bankruptcy and taxation problems: A survey, Rochester Center for
Economic Research Working Paper No. 413, University of Rochester, Rochester, NY.
Thomson, W., 1996. Consistent allocation rules, Rochester Center for Economic Research Working Paper No. 418, University of Rochester, Rochester, NY.
Young, H.P., 1987. On dividing an amount according to individual claims or liabilities. Mathematics of Operations Research 12, 398–414.