KONDISI KARUSH-KUHN-TUCKER PADA OPTIMISASI SEPARABLE PROGRAMMING S KRIPS I MELIKA FIFANI BOHO PAKPAHAN

(1)

KONDISI KARUSH-KUHN-TUCKER PADA OPTIMISASI SEPARABLE PROGRAMMING

S K R I P S I

ME L I K A FI FANI B O H O PA K PAH AN 1 2 0 8 0 3 0 5 9

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2016

UNIVERSITAS SUMATERA UTARA

(2)

KONDISI KARUSH-KUHN-TUCKER PADA OPTIMISASI SEPARABLE PROGRAMMING

S K R I P S I

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

ME L I K A FI FANI B O H O PA K PAH AN 1 2 0 8 0 3 0 5 9

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2016

(3)

PERSETUJUAN

Judul : KONDISI KARUSH-KUHN-TUCKER PADA

OPTIMISASI SEPARABLE PROGRAMMING

Kategori : SKRIPSI

Nama : MELIKA FIFANI BOHO PAKPAHAN

Nomor Induk Mahasiswa : 120803059

Program Studi : PROGRAM (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Disetujui di Medan, Juni 2016 Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Prof. Dr. Drs. Iryanto, M.si Dr. Esther S M. Nababan, M.Sc NIP. 19460404 197107 1 001 NIP. 19610318 198711 2 001

Diketahui/Disetujui oleh

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si

NIP. 19620901 198803 1002

(4)

iii

PERNYATAAN

KONDISI KARUSH-KUHN-TUCKER PADA OPTIMISASI SEPARABLE PROGRAMMING

SKRIPSI

Saya menyatakan bahwa skripsi ini adalah hasil karya saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing – masing disebutkan sumbernya.

Medan, Juni 2016

Melika Fifani Boho Pakpahan 120803059

(5)

iv

PENGHARGAAN

Puji dan syukur penulis ucapkan kepada Tuhan Yesus Kristus atas berkat yang telah Dia berikan kepada penulis, sehingga penulis dapat menyelesaikan skripsi ini.

Penulis menyadari bahwa dalam penulisan skripsi ini tidak lepas dari dukungan, motivasi, kerjasama maupun bimbingan dari beberapa pihak. Oleh karena itu, pada kesempatan ini penulis mengucapkan terima kasih kepada :

1. Ibu Dr. Eshter S M. Nababan, M.Sc dan Bapak Prof. Dr. Drs. Iryanto, M.si, selaku pembimbing, Bapak Drs. Marihat Situmorang, M.Kom dan Ibu Asima Manurung, S.Si, M.Si selaku pembanding yang telah menyediakan waktu serta memberikan saran dan kritik yang membangun dalam penyusunan skripsi ini.

2. Bapak Prf. Dr. Tulus, M.Si dan Ibu Dra. Mardiningsih, M.Si selaku ketua dan sekretaris Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

3. Bapak Dr. Kerista Sebayang, M.S selaku dekan Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

4. Seluruh staf pengajar dan staf administrasi di lingkungan Departemen Matematika serta seluruh civitas akademika di lingkungan Fakultas Matematika dan Ilmu Pengetahuan Alam.

5. Orangtua tercinta Humala Tua Pakpahan dan Amister Silalahi yang senantiasa mendoakan, memberi semangat dan memberikan dukungan baik secara moril maupun material kepada penulis sejak awal perkuliahan hingga selesainya skripsi ini. Dan untuk adik- adik ku (Frederik, Joi, dan Josep) terkasih serta seluruh keluarga yang telah memberikan semangat dan dukungan kepada penulis.

(6)

v

6. Rekan – rekan sepelayanan di KMKS (Kebaktian Muda/i Kampung Susuk) koordinasi periode 26 dan 27, khususnya kelompok rohaniku Bang Seny, Andre, Maria, dan Janet.

7. Para sahabat (Theresia, Siska, Mei Anita dan Gracia) dan teman – teman satu kos yang telah mendukung penyusunan skripsi ini.

8. Rekan – rekan mahasiswa Matematika stambuk 2012.

9. Semua pihak yang telah membantu dan memberikan dukungan dalam penulisan skripsi ini.

Penulis juga menyadari bahwa masih banyak kekurangan dan kesalahan dalam skripsi ini. Oleh karena itu, saran dan kritik yang membangun penulis harapkan sebagai sebuah koreksi. Demikian skripsi ini penulis susun. Semoga skripsi ini dapat memberikan manfaat bagi penulis dan pembaca.

Medan, Juni 2016 Penulis

Melika Fifani Boho Pakpahan

(7)

vi

KONDISI KARUSH-KUHN-TUCKER PADA OPTIMISASI SEPARABLE PROGRAMMING

ABSTRAK

Salah satu bentuk khusus dari permasalahan pemrograman nonlinier adalah masalah separable programming. Di mana separable programming memiliki fungsi tujuan yang berbentuk kuadratis dan fungsi kendala berbentuk linier.

Dalam penelitian ini dirancang sebuah penyelesaian permasalahan separable programming dengan menggunakan kondisi Karush-Kuhn-Tucker. Kondisi yang harus dipenuhi untuk optimum adalah bahwa turunan parsial pertama dari fungsi tujuan terhadap semua variabel dan pengali Lagrange bernilai nol. ( . Contohnya adalah pengoptimalan portofolio. Pembentukan model nonlinier portofolio optimal pada investasi saham di bidang perbankan yaitu Bank Rakyat Indonesia dan Bank mandiri periode 7 Juli 2014 sampai dengan 27 April 2015.

Model nonlinear pada portofolio disusun dengan mendefinisikan variabel- variabel penyimpangan, memformulasikan fungsi tujuan dalam bentuk persamaan atau pertidaksamaan, selanjutnya fungsi tujuan utama dalam pola memaksimumkan expected return dengan tingkat risiko tertentu.

Kata kunci: Pemrograman Nonlinear, Separable Programming, Karush- Kuhn-Tucker, Portofolio

(8)

vii

KARUSH-KUHN-TUCKER CONDITIONS IN OPTIMIZATION SEPARABLE PROGRAMMING

ABSTRACT

One particular form of nonlinear programming is separable programming. This separable programming where the objective function which has a quadratic form and the constraint function is a linear. In this research we proposed a separable programming problem solving using Karush-Kuhn-Tucker condition. The condition that must be met for the optimum is that the first partial derivative of the objective function of all variables and Lagrange multiplier is zero. ( . The example is to optimise a portofolio. The model of nonlinear optimal portfolio investment in banking stocks, Bank Rakyat Indonesia and Bank Mandiri period July 7, 2014 until 27 of April 2015. Nonlinear models on a portfolio compiled by defining variables deviations, to formulate the objective function in the form of equation or inequality, then objective function in the pattern maximizes expected return with certain risk level.

Keyword : Non-linear programming, Separable Programming, Karush-Kuhn- Tucker, Portofolio

(9)

viii

DAFTAR ISI

Halaman

Penghargaan iv

Abstrak vi

Abstract vii

Daftar Isi viii

Daftar Tabel x

BAB 1. Pendahuluan

1.1 Latar Belakang 1

1.2 Perumusan Masalah

1.3 Batasan masalah 3

1.4 Tinjauan Pustaka 3

1.5 Tujuan Penelitian 6

1.6 Manfaat Penelitian 6

1.7 Metodologi Penelitian 6

BAB 2. Landasan Teori

2.1 Pemrograman Nonlinier 8

2.1.1 Pemrograman Nonlinier tak Berkendala 8 2.1.2 Pemrograman Nonlinier Berkendala 9 2.2 Separable Programming (Pemrograman Terpisah) 13

2.2.1 Permasalahan Separable Programming 14 2.2.1.1 Pemilihan Portofolio dengan Sekuritas Berisiko 14

2.2.1.1.1 Uji Normalitas 16

2.2.1.1.2 Return 17

2.2.1.1.3 Expected Return 18

2.2.1.1.4 Risiko 19

2.2.1.1.4.1 Risiko Portofolio 19

2.2.1.1.5 Operasi Perpangkatan Bentuk Aljabar 20

2.3 Konveksitas Fungsi 21

2.3.1 Fungsi Konveks atau Konkaf Satu Variabel 22 2.3.2 Fungsi Konveks dan Konkaf untuk Beberapa Variabel 23

(10)

ix

2.4 Matriks Hessian 25

2.5 Sifat Konveks dan Konkaf Berdasarkan Sifat Matriks

Hessian 26

2.5.1 Contoh Penggunaan Matriks Hessian untuk Penentuan Sifat Konveks/Konkaf suatu fungsi 26

2.6 Matriks Definit Positif 28

2.7 Persyaratan Karush-Kuhn-Tucker 29

BAB 3. Pembahasan

3.1 Kondisi Karush-Kuhn-Tucker pada Optimasi Separable

Programming 32

3.2 Penerapan Model pada Investasi Saham BRI dan Bank

Mandiri 34

3.3 Uji Normalitas Return Saham BRI dan Bank Mandiri 35 3.4 Return, Expected Return, dan Risiko Saham BRI dan

Bank Mandiri 36

3.4.1 Return 36

3.4.2 Expected Return 36

3.4.3 Risiko 36

3.4.4 Model Nonlinier portofolio optimal pada investasi

saham BRI dan Bank Mandiri 37

3.5 Pembentukan Fungsi Separable Programming 38 3.6 Separable Programming Karush-Kuhn-Tucker 38 BAB 4. Kesimpulan dan Saran

4.1 Kesimpulan 46

4.2 Saran 46

DAFTAR PUSTAKA 48

LAMPIRAN 50

(11)

x

DAFTAR TABEL

Halaman Tabel 2.1 Uji Konveksitas untuk Fungsi Dua Variabel 25

Tabel 3.1 Total Return 36

Tabel 3.2 Expected Return 36

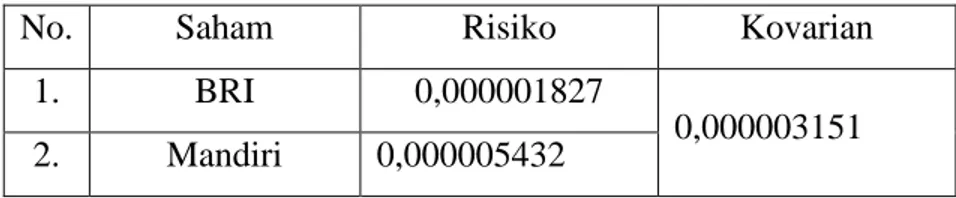
Tabel 3.3 Risiko dan Kovarian 37

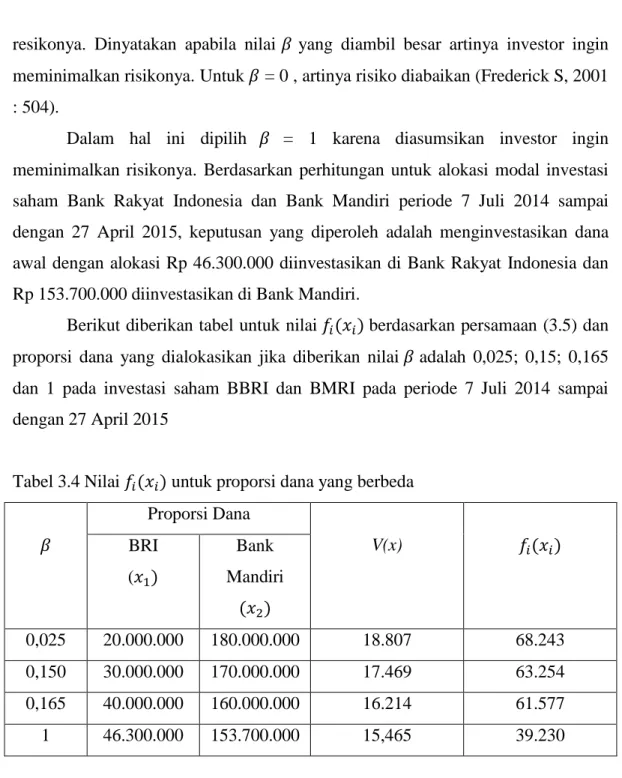
Tabel 3.4 Nilai untuk Proporsi Dana yang Berbeda 43

Tabel 3.5 Jumlah Lembar Saham yang Dibeli 44

Tabel 3.6 Keuntungan yang Diperoleh 44

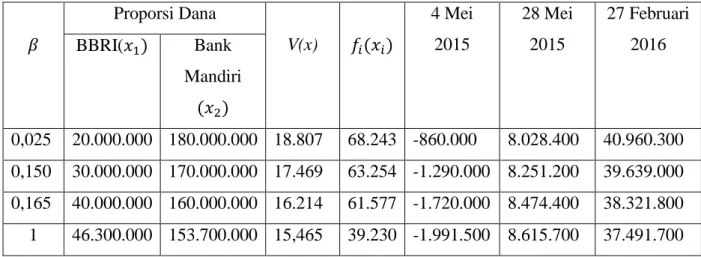
Tabel 3.7 Keuntungan yang Diperoleh pada Periode Tertentu 44

(12)

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Salah satu bidang Matematika yang dapat memecahkan masalah optimisasi adalah penelitian operasional (operation research). Penelitian operasional (operation research) berkaitan dengan masalah optimisasi yang berkaitan dengan penentuan nilai optimum (nilai maksimum atau nilai minimum) dari suatu fungsi matematik.

Optimisasi adalah suatu langkah untuk menemukan hasil terbaik dari suatu permasalahan yang dapat dicari solusi optimal sesuai dengan perumusan fungsi tujuan dan kendala yang ada (Hillier dan Gerald, 2001).

Pemecahan masalah optimisasi dapat diselesaikan dengan pemrograman linier maupun nonlinier. Dalam pemrograman linierfungsi tujuan dan fungsi kendalaadalah linier(Agustini dan Rahmadi,2004). Sedangkan, pemrograman nonlinier memiliki fungsi tujuan atau fungsi kendala yang tidak linier, atau keduanya tidak linier (Avriel, 2003). Untuk mengatasi permasalahan yang kompleks, menggunakan model linier tidak begitu efektifsehingga pemrograman nonlinier menjadi alternatifnya.

Dalam pemrograman linier, umumnya solusi berada di titik perpotongan antara 2 garis. Sedangkan dalam pemrograman nonlinier, titik solusinya tidak menentu di perpotongan garis tersebut. Dengan kata lain, solusi optimalnya tidak di penyelesaian layak yang terletak pada perpotongan antara 2 garis (corner point feasiable) (Gupta dan Hira, 2006).

Pemrograman nonlinier ada dua macam yaitu pemrograman nonlinier dengan kendala (constrained) dan pemrograman tanpa kendala (unconstrained), sehingga dapat mengakibatkan cara penyelesaian yang berbeda (Gupta and Hira, 2006). Pemrograman nonlinier dengan kendala yaitu memperhatikan faktor – faktor pembatas dalam penyelesaian optimasi. Sedangkan pemrograman nonlinier tanpa kendala hanya menyelesaikan masalah tanpa terdapat faktor – faktor

(13)

2

pembatas yang mempengaruhi proses perhitungan sampai optimasi tercapai.

Kemungkinan yang ada dalam pemrograman nonlinier yaitu fungsi tujuan dan kendala nonlinier, fungsi tujuan nonlinier dan fungsi kendala linier, fungsi tujuan linier dan kendala nonlinier. Beberapa metode penyelesaian dalam pemrograman nonlinier secara analitik antara lain Lagrange Multiplier, The Karush-Kuhn- Tucker Conditions, Quadratic Programming, Separable Programming.

Terdapat banyak jenis masalah pemrograman nonlinier, tergantung pada karakteristik fungsi tujuan dan fungsi kendala. Salah satunya adalah pemrograman terpisah (separable programming) yang merupakan bentuk khusus dari pemrograman nonlinier. Pemrograman terpisah (separable programming) menyelesaikan pemrograman nonlinier dengan mentransformasi bentuk nonlinier menjadi bentuk linier yang hanya memuat satu variabel.

Beberapa metode telah dikembangkan untuk menyelesaikan kasus pemrograman terpisah (separable programming) dengan asumsi tambahan fungsi tujuan merupakan fungsi konveks. Salah satu metode untuk megoptimalkan pemrograman terpisah (separable programming) adalah menggunakan kondisi Karush-Kuhn-Tucker. Metode ini sangat efektif untuk permasalahan optimasi nonlinier dengan kendala pertidaksamaan.

Penyelesaian masalah pemrograman linier ataupun nonlinier dapat diselesaikan dengan menggunakan kondisi Karush-Kuhn-Tucker. Kondisi Karush- Kuhn-Tucker dapat dipergunakan untuk mencari solusi yang optimum dari suatu fungsi tanpa memandang sifat dari fungsi tersebut apakah linier atau nonlinier.

Pada penelitian sebelumnya yang dilakukan oleh Amalia (2009), penerapan kondisi Karush-Kuhn-Tucker telah digunakan untuk mencari solusi optimal untuk pemrograman kuadratis. Dalam penelitian ini, penulisbertujuan mencari solusi optimal dari pemrograman yang berbeda yaitu pemrograman terpisah (separable programming) menggunakan kondisi Karush-Kuhn-Tucker juga. Dengan menerapkan persyaratan Karush-Kuhn-Tucker, dapat diketahui kapan kondisi maksimum dan minimum dari pemrograman terpisah (separable programming) dengan asumsi tambahan fungsi tujuan merupakan fungsi konveks

(14)

3 1.2 PERUMUSAN MASALAH

Permasalahan yang akan dibahas adalah mencari solusi optimal pemrograman terpisah(separable programming) dengan menerapkan kondisi Karush-Kuhn- Tucker. Dalam hal ini kondisi yang perlu diperhatikan adalah mengikuti syarat cukup agar mendapatkan nilai – nilai variabel yang optimal untuk mencapai hasil yang diinginkan. Persyaratannya adalah

= 0 (j = 1, 2 ,…, 2n + m)

= 0 (i = 1, 2 ,…, m + n) 0 (i = 1, 2 ,…, m + n)

1.3 BATASAN MASALAH

Pembahasan optimisasi separable programming pada tulisan ini hanya menerapkan kondisi Karush-Kuhn-Tucker.

1.4 TINJAUAN PUSTAKA

1. Pemrograman Terpisah (Separable Programming)

Pemrograman Terpisah (Separable Programming) merupakan suatu metode penyelesaian dalam pemrograman nonlinier dengan mentransformasi bentuk nonlinier menjadi bentuk linier yang hanya memuat satu variabel. Pemrograman Terpisah (Separable Programming) berhubungan dengan fungsi yang berbentuk nonlinier, yang selanjutnya dipisahkan menjadi fungsi dengan variabel tunggal.

Misalnya dalam kasus dua variabel fungsi f(x,y)dipisahkan menjadi h(x) + g(y).

Suatu fungsi f(x) dapat dikatakan terpisah apabila fungsi tersebut dapat dinyatakan dalam bentuk penjumlahan dari fungsi – fungsi yang hanya memuat satu variabel, didefinisikan sebagai berikut (Bazaraa et al, 2006)

f(x) = f( …, = f( ) + f ) +…+f( ) = ( ) (1.1)

(15)

4 2. Kondisi Karush-Kuhn-Tucker

Pada tahun 1951 Kuhn Tucker mengemukakan suatu teknik optimisasi yang dapat digunakan untuk pencarian titik optimum dari suatu fungsi yang berkendala.

Metode Karush-Kuhn-Tucker ini dapat dipergunakan untuk mencari solusi yang optimum dari suatu fungsi tanpa memandang sifat dari fungsi tersebut apakah linier atau nonlinier. Jadi metode Kuhn-Tucker ini bersifat teknik yang umum dalam pencarian titik optimum dari setiap fungsi. Metode Karush-Kuhn-Tucker dapat digunakan untuk memecahkan persoalan baik yang nonlinier maupun yang linier.

Jika menghadapi masalah optimasi dalam bentuk:

Maksimumkan/minimumkan :

Z = f(X) dengan X = (1.2)

dengan kendala : (X) 0 atau

(X) dengan i = 1,2,3,…,m X 0

m ≤ n (jumlah kendala lebih kecil dari variabel)

Pertama tuliskan kembali persyaratan – persyaratan yang tak negatif seperti - ≤ 0, ≤ 0,…, - ≤ 0, sehingga himpunan kendalanya adalah m+n persayaratan ketidaksamaan yang masing – masing dengan tanda lebih kecil dari pada atau sama dengan. Kemudian tambahkan variabel – variabel kurang

, ,…, berturut – turut pada ruas kiri dari kendala – kendala tadi, yang demikian merubah tiap – tiap ketidaksamaan menjadi suatu kesamaan. Slack variable yang ditambahkan di sini berbentuk suku – suku kuadrat untuk menjamin bahwa mereka tak negatif. Kemudian bentuk fungsi Lagrange :

L F(x) -

(X) -

] -

(X) -

]

Untuk , adalah pengali – pengali Lagrange. Terakhir selesaikan sistem persamaan

= 0 (j = 1,2,…,2n+m)

= 0 (i = 1,2,…, m+n) (1.3)

(16)

5 0 (i = 1,2,…,m+n)

Persamaan - persamaan tersebut membentuk persyaratan Karush-Kuhn-Tucker untuk maksimsi ataupun minimasi program linier dan nonlinier (Nering and Tucker, 1993).

3. Kondisi optimal pemrograman terpisah (separable programming)

Untuk memudahkan penulisan, masalah pemrograman terpisah (separable programming) ditulis dengan Masalah P. Jadi, bentuk umum persamaan dapat dituliskan sebagai berikut

Masalah P

Maksimalkan/Minimalkan

Z = ) (1.4)

dengan kendala

i= 1,2,…,m

0, j = 1,2,..,n

Di mana masing – masing fungsi merupakan fungsi tujuan dari merupakan fungsi kendala dengan menunjukkan nilai syarat kendala tersebut. Dalam hal ini, merupakan variabel independen.

Suatu fungsi dapat dikatakan terpisah jika fungsi tersebut dapat dinyatakan dalam bentuk penjumlahan dari fungsi – fungsi yang memuat satu variabel sebagai jumlah dari n fungsi variabel tunggal yang dituliskan sebagai berikut:

z = + +…+ (1.5)

: + +…+ ( )

+ +…+ ( )

+ +…+ ( ) dan

…, 0

Jadi, persamaan ini merupakan fungsi tujuan dan fungsi kendala yang sudah dipisahkan (Stefanov, 2001).

(17)

6 1.5 TUJUAN PENELITIAN

Adapun yang menjadi tujuan penelitian ini adalah menguraikan cara dan persyaratan Karush-Kuhn-Tucker untuk mencari solusi optimal (nilai maksimal atau nilai minimal) dari pemrograman terpisah (separable programming).

1.6 MANFAAT PENELITIAN

Selain untuk tambahan literatur dan pengetahuan pembaca mengenai metode yang dapat digunakan dalam menentukan nilai optimal dari pemrograman terpisah (separable programming), dalam bidang ekonomi penelitian ini juga bermanfaat untuk membantu memformulasikan pemrograman terpisah dalam pemilihan portofolio dan sekuritasnya yang beresiko.

1.7 METODOLOGI PENELITIAN

Langkah-langkah yang digunakan dalam penelitian ini adalah sebagai berikut : 1. Membuat formulasi model pemrograman terpisah (separable programming)

dalam kondisi Karush-Kuhn-Tucker.

2. Fungsi tujuan yang telah dimodifikasi setelah mendapatkan pemisahan program menjadi

L(x, ) = F(X) +

(X)

; harus sesuai pada titik tersebut 3. Menghitung titik - titik kritis dan menguji nilai untuk fungsi objektif pada

setiap titik – titik kritis tersebut yang membuat nilai fungsi objektif menjadi optimal.

4. Mencari semua solusi (x, ) dalam himpunan persamaan berikut

(x, )=0;

j = 1,2,…,n di mana

(x, ) 0;

⁰

(18)

7

(x, ) 0;

i=1,2.,..,l

5. Diperoleh titik – titik kritis yang salah satunya merupakan solusi optimal dari pemrograman terpisah (separable programming)

(19)

BAB 2

LANDASAN TEORI

2.1 Pemrograman Nonlinier

Model matematika dari permasalahan optimisasi dapat secara umum digambarkan oleh himpunan kendala X dan nilai fungsi f yang memetakan setiap elemen X ke bilangan riil. Himpunan bilangan X yang memenuhi nilai x dan harga f(x) berukuran skalar dari pemilihan nilai x (Bertsekas, 1999). Pemrograman nonlinier merupakan pemrograman dengan fungsi tujuan dan kendalanya mempunyai bentuk nonlinier pada salah satu atau keduanya yaitu pangkat dari variabelnya lebih dari satu. Salah satu bentuk umum masalah pemrograman non linier adalah untuk menentukan n keputusan variabel sehingga mencapai tujuan untuk:

Maksimumkan/minimiumkan :

Dengan kendala : dan

Dengan dan merupakan fungsi yang diketahui dengan variabel keputusan.

Jenis masalah pemrograman non linier tergantung pada karakteristik fungsi tujuan dan kendalanya. Pemrograman nonlinier dapat mempunyai kendala ataupun tidak mempunyai kendala.

2.1.1 Pemrograman Nonlinier tak Berkendala

Pemrograman nonlinier tak berkendala merupakan masalah optimasi yang tidak memiliki batasan-batasan, sehingga untuk mempunyai fungsi tujuan adalah

(20)

9 Maksimumkan/minimumkan :

Syarat perlu dan cukup agar suatu penyelesaian merupakan penyelesaian optimal saat merupakan fungsi yang dapat diturunkan adalah

pada untuk (2.1) Dimana merupakan fungsi konkaf, kondisi ini juga mencukupi,sehingga mencari solusi untuk tereduksi menjadi penyelesaian dari sistem persamaan yang diperoleh dengan turunan parsial sama dengan nol.

Ketika variabel memiliki kendala tidak negatif atau ,kondisi yang diperlukan dan mungkin cukup akan berubah menjadi

(2.2)

(2.3) untuk setiap .

Apabila titik kritis telah memenuhi kondisi diketahui, masing-masing titik digolongkan sebagai maksimum atau minimum lokal jika fungsi tersebut bersifat konveks ataupun konkaf disekitar titik tersebut. Maksimum dan minimum global akan ditemukan dengan membandingkan maksimum dan minimum lokal kemudian menguji nilai dari fungsi tersebut dengan sebagian variabel mendekati -∞ atau +∞. Jika fungsi diketahui konveks maupun konkaf, maka titik kritisnya pastilah merupakan minimum global maupun maksimum globalnya.

2.1.2.Pemrograman Nonlinier Berkendala

Pemrograman nonlinier berkendala merupakan masalah optimasi yang memiliki batasan-batasan , sehingga untuk maka bentuk standard untuk program-program tak linier yang mengandung hanya kendala-kendala kesamaan (equality) adalah

(21)

10

Maksimumkan/minimiumkan : dengan kendala :

Disini (jumlah kendala lebih kecil daripada variabel), jika terjadi bahwa ,maka biasanya tidak dapat diselesaiakan. Pada program minimasi dapat diubah ke dalam bentuk program maksimasi dengan mengalikan fungsi objektif - 1.

Suatu metode yang dapat dipakai untuk menyelesaikan masalah optimasi ini adalah metode pengali Lagrange. Metode penggali Lagrange dipilih karena prinsip kerjanya sederhana dan mudah dimengerti. Metode ini dimulai dengan pembentukan fungsi Lagrangean yang didefinisikan sebagai:

(2.4)

Syarat perlu bagi sebuah fungsi dengan kendala , dengan agar mempunyai minimum relatif pada titik adalah derivasi parsial pertama dari fungsi Lagrange-nya yang didefenisikan sebagai terhadap setiap argumennya mempunyai nilai nol.

Syarat harus bagi sebuah fungsi agar mempunyai minimum atau maksimum relatif pada titik adalah jika fungsi kuadrat , yang didefinisikan sebagai

(2.5)

Dievaluasi pada harus definit positif (atau negatif ) untuk setiap nilai yang memenuhi semua kendala.

Syarat perlu agar menjadi definit positif (atau negatif ) untuk setiap variasi nilai adalah setiap akar dari polinomial , yang didapat dari determinan persamaan di bawah ini harus positif (atau negatif).

(22)

11 Dengan

Pengali Lagrange mempunyai arti secara fisik yang menarik. Misalkan terdapat permasalahan optimasi dengan ssatu kendala sebagai berikut:

Maksimumkan/ Minimumkan : Dengan kendala : Fungsi Lagrange-nya adalah

(2.6) Syarat perlu untuk penyelesaian di atas adalah

untuk dan

Persamaan di atas menghasilkan

(2.7)

untuk

atau Maka:

untuk (2.8)

(23)

12

(2.9) (2.10)

Karena adalah dan adalah

Maka persamaan final dari adalah

atau (2.11) Dari persamaan ini dapat ditarik kesimpulan bahwa pada penyelesaian optimum, perubahan fungsi tujuan , berbanding lurus dengan perubahan kendala dengan faktor sebesar pengali lagrange .

Bentuk standard dari program-program tak linier yang mengandung hanya kendala-kendala ketidaksamaan adalah:

Maksimumkan/ Minimumkan :

dengan kendala : untuk

Kunci dari penanganan permasalahan tersebut adalah mengubah kendala pertidaksamaan menjadi persamaan dengan menambah variabel slack .Masalah pemrograman ini ditandai dengan adanya kendala-kendala yang sama sepenuhnya dengan pemrograman linier. Semua fungsi kendala adalah linier, tetapi fungsi tujuan berbentuk nonlinier. Masalah ini dipertimbangkan secara sederhana dengan hanya memiliki satu fungsi nonlinier yang diperhitungkan, bersama dengan daerah layak dari pemrograman linier. Sejumlah algoritma khusus yang didasari atas perluasan metode simpleks telah dikembangkan untuk memperhitungkan fungsi tujuan yang nonlinier.

(24)

13

2.2 Separable Programming (Pemrograman Terpisah )

Pemrograman Terpisah (Separable Programming) merupakan suatu metode penyelesaian dalam pemrograman nonlinier dengan mentransformasi bentuk nonlinier menjadi bentuk linier yang hanya memuat satu variabel. Pemrograman Terpisah (Separable Programming) berhubungan dengan fungsi yang berbentuk nonlinier, yang selanjutnya dipisahkan menjadi fungsi dengan variabel tunggal.

Misalnya dalam kasus dua variabel fungsi f(x,y) dipisahkan menjadi h(x) + g(y).

Suatu fungsi f(x) dapat dikatakan terpisah apabila fungsi tersebut dapat dinyatakan dalam bentuk penjumlahan dari fungsi – fungsi yang hanya memuat satu variabel, didefinisikan sebagai berikut (Bazaraadkk, 2006)

(2.12)

Untuk memudahkan penulisan, masalah pemrograman terpisah (separable programming) ditulis dengan Masalah P. Jadi, bentuk umum persamaan dapat dituliskan sebagai berikut

Masalah P

Maksimalkan/Minimalkan

Z = (2.13)

dengan kendala

i = 1,2,…,m

j = 1,2,..,n

Di mana masing – masing fungsi merupakan fungsi tujuan dari merupakan fungsi kendala dengan menunjukkan nilai syarat kendala tersebut. Dalam hal ini, merupakan variabel independen.

Suatu fungsi dapat dikatakan terpisah jika fungsi tersebut dapat dinyatakan dalam bentuk penjumlahan dari fungsi – fungsi yang memuat satu variabel sebagai jumlah dari n fungsi variabel tunggal yang dituliskan sebagai berikut:

z = + +…+ (2.14) : + +…+ ( )

(25)

14

+ +…+ ( )

+ +…+ ( ) dan

…, 0

Jadi, persamaan ini merupakan fungsi tujuan dan fungsi kendala yang sudah dipisahkan (Stefanov, 2001).

2.2.1 Permasalahan Separable Programming

Masalah pemrograman terpisah berhubungan dengan fungsi yang berbentuk nonlinier, yang selanjutnya dipisahkan menjadi fungsi dengan variabel tunggal.

Misalnya dalam kasus dua variabel fungsi f(x,y) dipisahkan menjadi h(x) + g(y).

Contoh yang akan dibahas dalam menyelesaikan masalah separable programming (pemrograman terpisah) adalah contoh kasus pemilihan portofolio dengan sekuritas berisiko.

2.2.1.1 Pemilihan Portofolio dengan Sekuritas Berisiko

Menurut Husnan (2003:45), portofolio berarti sekumpulan investasi dan menyangkut identifikasi sekuritas-sekuritas mana yang akan dipilih dan berapa proporsi dana yang akan ditanamkan pada masing-masing sekuritas tersebut.

Sekuritas dapat berupa saham, surat berharga, obligasi, sertifikat, dll. Portofolio efisien adalah portofolio memaksimalkan Expected Return dengan tingkat risiko tertentu, atau portofolio yang menawarkan risiko terendah dengan Expected Return tertentu.

Saat ini para manajer profesional dari portofolio besar biasa menggunakan model komputer berbasis pemrograman nonlinier untuk memandu pekerjaan mereka. Oleh karena itu investor harus memperhatikan baik ekspektasi pendapatan maupun resiko investasi, pemrograman nonlinier digunakan untuk menentukan portofolio yang pada asumsi tertentu dapat menghasilkan keseimbangan optimal antara kedua faktor tersebut. Pendekatan ini sebagian besar merupakan hasil riset yang dilakukan oleh Harry Markowitz dan William Sharpe,

(26)

15

pemenang hadiah nobel tahun 1990 dalam bidang ekonomi karena hasil risetnya tersebut.

Model pemrograman nonlinier untuk masalah ini dapat dirumuskan sebagai berikut. Misalkan terdapat n jenis saham/sekuritas yang sedang dipertimbangkan untuk masuk dalam portofolio, dan variabel keputusan (j = 1,2,..,n) adalah share dari saham j yang masuk dalam portofolio dan adalah (estimasi) rata – rata dan varians masing – masing untuk pendapatan setiap share dari saham j, dengan sebagai ukuran resiko dari saham ini. Untuk i = 1,2,...,n (i j), adalah kovariansi dari pendapatan setiap share antara saham i dan saham j . Oleh karena itu sulit mengestimasi seluruh nilai , langsung dari dan . Kemudian, nilai ekspektasi R(x) dari total pendapatan keseluruhan portofolio adalah

R(x) = (2.15)

V(x)=

(2.16)

Dengan V(x) mengukur resiko yang terasosiasi dengan portofolio. Salah satu cara untuk mempertimbangkan keseimbangan antara dua faktor adalah dengan menggunakan V(x) sebagai fungsi tujuan untuk diminimumkan dan mengggunakan kendala yang memastikan R(x) tidak lebih kecil dari ekspektasi pendapatan minimum yang dapat diterima. Model pemrogaman nonlinier yang lengkap adalah

Maksimumkan/Minimumkan V(x) =

(2.17)

dengan kendala

untuk j = 1,2,..., n

Dengan L adalah ekspektasi pendapatan minimum yang dapat diterima, adalah harga tiap share dari saham j dan B adalah jumlah uang yang dianggarkan untuk portofolio.

Sebuah model pemrograman nonlinier pada portofolio yang memaksimalkan Expected return dengan tingkat risiko tertentu, di mana parameter merupakan

(27)

16

konstanta tak negatif yang mengukur tingkat keinginan investor terhadap hubungan antara Expected return dan risikonya. Untuk = 0, artinya risiko diabaikan. dinyatakan apabila nilai yang diambil besar artinya sangat memperhatikan risiko dan ingin meminimalkan risikonya. Nilai untuk yaitu 0 < 1. Dalam hal ini dipilih = 1 karena diasumsikan investor ingin meminimalkan risikonya.

Untuk memilih nilai L yang sesuai agar tercapai keseimbangan terbaik antara R(x) dan V(x) relatif sulit. Pendekatan pemrograman nonlinier parametrik biasa digunakan untuk membengkitkan solusi optimal sebagai fungsi L pada kisaran nilai L yang lebar. Langkah selanjutnya adalah mengevaluasi R(x) dan V(x) untuk solusi optimal tersebut dan memilih solusi yang memberikan keseimbangan antara dua nilai itu. Prosedur ini sering disebut pembangkitan solusi pada batas efisien dari grafik dua dimensi titik – titik {R(x),V(x)} untuk nilai x yang layak.

Alasannya adalah titik {R(x),V(x)} yang optimal untuk x (pada beberapa nilai L) pasti terletak pada batas daerah layak. Setiap nilai optimal x disebut efisien karena tidak ada solusi layak lain yang sekurang-kurangnya memiliki satu nilai ukuran yang sama R atau Vdan lebih baik pada ukuran yang lain (nilai V yang lebih kecil atau nilai R yang lebih besar).

2.2.1.1.1 Uji Normalitas

Uji normalitas sering digunakan pada investasi untuk melihat apakah return saham berdistribusi normal atau tidak. Saham tersebut dapat dimasukkan dalam portofolio jika return saham berdistribusi normal. Tujuan pengujian normalitas dalam return saham adalah untuk mengantisipasi terjadinya kestabilan harga karena dikhawatirkan akan mengalami penurunan harga saham yang sangat signifikan dan merugikan investor. Uji normalitas pada SPSS menggunakan pengujian Kolmogorov-smirnov.

Berikut tahap pengujian menggunakan uji Kolmogorov-smirnov a. Hipotesis

: data dapat diasumsikan normal,

: data tidak dapat diasumsikan berdistribusi normal.

(28)

17 b. Tingkat signifikan

c. Statistik uji

Kolmogorov-smirnov T = adalah distribusi kumulatif data sampel ) adalah distribusi kumulatif yang dihipotesakan d. Kriteria Uji

ditolak jika p – value <

e. Perhitungan f. Kesimpulan

2.2.1.1.2 Return

Return merupakan hasil yang diperoleh dari investasi. Adanya hubungan positif antara return dan risiko dalam berinvestasi yang dikenal dengan high risk – high return, yang artinya semakin besar risiko yang ditanggung, semakin besar pula return yang diperoleh. Hal ini dimaksudkan harus ada pertambahan return sebagai kompensasi dari pertambahan resiko yang akan ditanggung oleh investor. Return dapat berupa realized return yang sudah terjadi atau expected return yang belum terjadi tetapi diharapkan akan diperoleh pada masa mendatang (Jogiyanto, 2003:205).

Realized return adalah return yang sudah terjadi yang dihitung berdasarkan data historis. Realized return berguna sebagai dasar perhitungan tingkat pengambilan yang diharapkan (expected return) dan risiko di masa mendatang. Realized return merupakan salah satu komponen penting dalam dunia bisnis karena merupakan salah satu alat ukur kinerja dari sebuah perusahaan.

Return ini juga merupakan dasar penentuan return ekspektasi dan risiko di masa mendatang. Menurut kegunaannya return realisasi dibagi menjadi 3 macam yaitu Return Total (Net Return), Return Relatif (Gross Return), dan Log return.

Jika seseorang menginvestasikan dananya pada saham ke-i periode dengan harga dan harga pada periode selanjutnya adalah , maka return total pada periode sampai adalah ( - )/ . Return

(29)

18

total dapat digambarkan sebagai pendapatan relatif atau tingkat keuntungan (profit rate).

Secara umum return total antara periode t – 1 sampai t adalah sebagai berikut (Jogiyanto, 2003:206)

(2.18)

dengan

= Return Capital Gain atau Capital Loss saham ke-i pada periode t

= Harga penutupan saham ke- i pada periode ke- t

= Harga penutupan saham ke-i pada periode ke- (t-1)

Jika harga investestasi sekarang lebih tinggi dari harga investasi periode lalu ini berarti terjadi keuntungan modal (Capital Gain), sebaliknya terjadi kerugian modal (Capital Loss).

Nilai return total dapat bernilai positif atau negatif, bergantung dari selisih harga sekuritas periode sekarang dan sebelumnya. Investor mendapat keuntungan jika nilai return total > 0 (positif) dan mengalami kerugian jika nilai return total <

0 (negatif).

2.2.1.1.3 Expected Return

Seorang investor mengetahui jika suatu investasi mempunyai risiko, artinya bahwa tingkat keuntungan yang akan diperoleh bersifat tidak pasti. Investor hanya akan mengharapkan tingkat keuntungan tertentu. Expected return adalah return (pengembalian) yang diharapkan akan diperoleh oleh investor pada masa mendatang dan belum terjadi. Expected return merupakan return yang penting karena dapat digunakan sebagai pengambilan keputusan investasi.

Expected return secara sederhana merupakan rata – rata tertimbang dari berbagai return. Rumus yang dapat digunakan adalah (Jogiyanto, 2003: 208)

(2.19)

dengan

= Expected return saham ke- i

(30)

19

=Return saham ke- i pada teriode t

N = Banyaknya return yang terjadi pada periode observasi

2.2.1.1.4 Risiko

Risiko didefinisikan sebagai besarnya penyimpangan antara tingkat pengembalian yang diharapkan (expected return) dengan tingkat pengembalian yang dicapai secara nyata (realized return) (Halim, 2003). Semakin besar penyimpangannya maka berarti semakin besar pula tingkat risikonya.

Jika mengacu pada definisi resiko tersebut, maka resiko keuangan didefiniskan sebagai ketidakpastian return mendatang dari suatu investasi, atau bahwa investasi mendapatkan hasil yang lebih kecil dari return yang diperkirakan dan menghasilkan suatu kerugian, yaitu return yang bernilai negatif. Jenis risiko dapat dikelompokkan menjadi dua yaitu risiko sistematis (systematic risk) dan risiko tidak sistematis (unsystematic risk). Salah satu pengukur risiko adalah standar deviasi atau varians yang merupakan kuadrat dari standar deviasi (Jogiyanto, 2003: 256)

(2.20)

dengan

= risiko saham ke- i

= return saham ke- i

= Expected return saham ke-i

2.2.1.1.4.1 Risiko Portofolio

Risiko dapat dianggap sebagai tingkat kerugian tidak terduga yang besarnya tergantung pada portofolio yang dibentuk. Salah satu pengukur risiko adalah standar deviasi atau varians yang merupakan kuadrat dari standar deviasi. Risiko portofolio dapat diukur dengan besarnya varians dari nilai – nilai return saham – saham tunggal yang ada di dalamnya (Jogiyanto, 2003:256)

(31)

20

Banyaknya saham dalam suatu portofolio juga dapat mempengaruhi nilai varians dari risiko. Untuk membentuk suatu portofolio minimal diperlukan dua sekuritas, dimana besar risiko dari kedua sekuritas tersebut dapat dihitung dengan besarnya varians dari nilai – nilai kedua sekuritas yang ada dalam portofolio.

Untuk aktiva sebanyak n maka rumus varians untuk portofolio dapat dituliskan sebagai berikut

(2.21a)

(2.21b)

dengan

= Risiko portofolio

= Risiko saham individual

= Proporsi dana yang diinvestasikan pada saham i = Proporsi dana yang diinvestasikan pada saham j

dengan rumus ( sebagai berikut

(2.22) dengan

cov( ) = kovarian return saham i dengan saham j

= return saham i pada periode t = Expected return saham i

= return saham j pada periode t E = Expected return saham j

2.2.1.1.5 Operasi Perpangkatan Bentuk Aljabar

Operasi perpangkatan diartikan sebagai perkalian berulang dengan bilangan yang sama. Hal ini juga berlaku pada perpangkatan bentuk aljabar. Pada perpangkatan bentuk aljabar suku dua, koefisien tiap suku ditentukan menurut segitiga Pascal.

Perhatikan barisan segitiga Pascal berikut,

(32)

21

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

Demikian seterusnya untuk dengan n merupakan bilangan asli.

Pangkat dari a (unsur pertama) pada dimulai dari kemudian berkurang satu demi satu dan terakhir pada suku ke- n. Sebaliknya, pangkat dari b (unsur kedua) dimulai dengan pada suku kedua yang selanjutnya bertambah satu demi satu dan berakhir pada suku ke- n+1

Berdasarkan barisan segitiga pascal, maka bentuk aljabar suku dua dapat dituliskan sebagai berikut

(2.23)

Persamaan (2.23) dapat ditulis ulang sebagai berikut

(2.24)

Untuk perkalian lebih dari dua variabel, misalkan perkalian abc. Maka perkalian tersebut dapat ditulis sebagai berikut

abc = -

- (2.25)

2.3 Konveksitas Fungsi

Dalam pemrograman nonlinier, konsep konveksitas fungsi sering digunakan dalam bidang penelitian operasional. Konsep fungsi konveks berhubungan langsung dengan himpunan konveks. Jika adalah fungsi konveks maka kumpulan titik – titik yang terletak di atas atau pada grafik f( ,..., ) membentuk himpunan konveks. Hal yang sama, kumpulan titik yang terletak di bawah atau pada grafik fungsi konkaf adalah himpunan konveks.

(33)

22

S

R

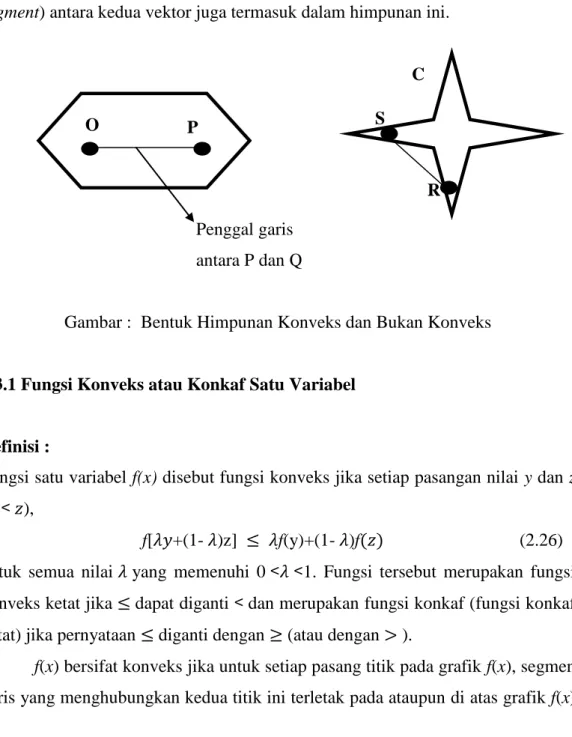
Himpunan konveks mempunyai sifat penting yaitu untuk beberapa himpunan konveks, kumpulan titik yang berada dalam semua himpunan (irisan dari himpunan konveks) juga merupakan himpunan konveks. Dengan demikian, kumpulan titik yang terletak di atas atau pada fungsi konveks dan di bawah atau pada fungsi konkaf adalah merupakan himpunan konveks juga. Jadi, himpunan konveks dapat dilihat secara intuitif sebagai kumpulan titik dengan batas atas fungsi konveks dan batas bawah fungsi konkaf.

Sebuah himpunan vektor berdimensi-m adalah konveks jika untuk dua vektor yang termasuk dalam himpunan ini berlaku bahwa penggal garis (line segment) antara kedua vektor juga termasuk dalam himpunan ini.

C C

Penggal garis antara P dan Q

Gambar : Bentuk Himpunan Konveks dan Bukan Konveks

2.3.1 Fungsi Konveks atau Konkaf Satu Variabel

Definisi :

Fungsi satu variabel f(x) disebut fungsi konveks jika setiap pasangan nilai y dan z ( ),

f[ +(1- )z] f(y)+(1- )f (2.26) untuk semua nilai yang memenuhi 0 1. Fungsi tersebut merupakan fungsi konveks ketat jika dapat diganti dan merupakan fungsi konkaf (fungsi konkaf ketat) jika pernyataan diganti dengan (atau dengan ).

f(x) bersifat konveks jika untuk setiap pasang titik pada grafik f(x), segmen garis yang menghubungkan kedua titik ini terletak pada ataupun di atas grafik f(x)

Q P

(34)

23

dan begitu juga sebaliknya untuk fungsi konkaf. Tepatnya jika memiliki turunan kedua, maka f(x) bersifat konveks jika dan hanya jika 0 untuk setiap nilai x yang mungkin.

Uji konveksitas untuk fungsi satu variabel :

Pertimbangkan fungsi satu variabel f(x) yang memiliki turunan kedua untuk setiap nilai x yang mungkin. Dengan demikian, fungsi f(x) dapat bersifat:

1. Konveks jika dan hanya jika

untuk setiap nilai x yang mungkin.

2. Konveks ketat jika dan hanya jika untuk setiap nilai x yang mungkin.

3. Konkaf jika dan hanya jika

untuk setiap nilai x yang mungkin.

4. Konkaf ketat jika dan hanya jika untuk setiap nilai x yang mungkin.

2.3.2 Fungsi Konveks dan Konkaf untuk Beberapa Variabel

Konsep fungsi konveks dan konkaf dari satu variabel dapat digeneralisasikan untuk fungsi dengan lebih dari satu variabel. Dengan demikian, saat f(x) digantikan dengan fungsi f definisi masih diterapkan apabila x digantikan oleh . Hal yang sama, penafsiran geometri yang berhubungan juga berlaku setelah generalisasi konsep titik dan segmen garis. Jadi, sama dengan nilai (x,y) tertentu ditafsirkan sebagai sebuah titik dalam ruang dua dimensi. Setiap kemungkinan nilai dari dapat diartikan sebagai titik dalam ruang m-dimensi (ruang Euclide).

Misalkan m= n+1, titik pada grafik f menjadi nilai yang mungkin dari titik [ , f ]. Kemudian dikatakan terletak di atas, tepat, atau di bawah grafik f tergantung pada nilai yang lebih besar, sama dengan atau lebih kecil daripada f

(35)

24 Definisi 1 :

Segmen garis yang menghubungkan kedua titik ( ) dan ( ) merupakan penjumlahan titik – titik

= [ + (1- ) , + (1- ,…, +(1- ) ] (2.27) Dengan 0 1. Jadi segmen garis dalam ruang m-dimensi merupakan generalisasi langsung dari segmen garis dalam ruang dua dimensi.

Definisi 2 :

f merupakn fungsi konveks jika untuk setiap pasang titik pada grafik f , segmen garis yang menghubungkan kedua titik tersebut seluruhnya terletak di atas atau tepat pada grafik fungsi f . Fungsi tersebut merupakan fungsi konveks ketat jika segmen garis tersebut seluruhnya terletak di atas grafik kecuali pada kedua titik akhirnya. Begitu juga sebaliknya untuk fungsi konkaf dan fungsi konkaf ketat.

Turunan parsial kedua dapat digunakan untuk menguji fungsi banyak variabel konveks atau tidak, meskipun dengan cara yang lebih kompleks.

Misalnya, jika terdapat dua variabel dan semua turunan parsial ada di semua tempat, uji koveksitas menilai tiga kuantitas memenuhi pertidaksamaan yang sesuai untuk semua nilai ( ) yang mungkin seperti yang ditunjukkan pada tabel berikut ini :

Tabel 2.1. Uji Konveksitas untuk Fungsi Dua Variabel

Kuantitas Konveks Konveks

Ketat

Konkaf Konkaf Ketat

-

≥ 0

0

≥ 0

0

˂ 0

(36)

25

f adalah konveks jika dan hanya jika matriks Hessian n x n – nya definit positif untuk semua nilai yang mungkin. Uji konveksitas selalu diperlukan sebagai sifat umum fungsi. Akan tetapi, beberapa fungsi nonkonveks memenuhi syarat konveksitas pada interval tertentu dari variabel. Dengan demikian, penting untuk membicarakan fungsi yang menjadi konveks pada daerah tertentu.

2.4 Matriks Hessian

Matriks Hessian adalah matriks yang setiap elemennya dibentuk dari turunan parsial kedua dari suatu fungsi. Misalkan f(x) fungsi dengan n variabel yang memiliki turunan parsial kedua dan turunan – turunannya kontinu. Matriks Hessian dari f(x) ditulis H(f ) adalah

Matriks Hessian dapat digunakan untuk melakukan uji turunan kedua fungsi lebih dari satu variabel, yaitu untuk mengidentifikasi optimum relatif dari nilai fungsi tersebut. Penggolongan titik stasioner fungsi dua variabel dengan menggunakan Matriks Hessian misalkan f(x)=F adalah fungsi bernilai real di mana semua turunan parsialnya kontinu. Misalkan adalah titik stasioner dari F dan definisikan H=H( ) dengan persamaan

= ( ) di mana H( ) adalah Hessian dari F pada Titik stasioner dapat digolongkan sebagai berikut :

1. adalah suatu minimum relative dari F jika H( ) definit positif.

2. adalah suatu maksimum relative dari F jika H( ) definit negatif.

(37)

26

3. adalah suatu titik pelana dari F jika H( ) indefinit.

Misalkan nilai eigen dari matriks adalah , , , …, yang didefinisikan oleh dengan I adalah matriks identitas ukuran n × n.

Maka :

i. H adalah definte negatif jika dan hanya jika nilai eigen dari matriks H yaitu , , , …, kesemuanya bertanda negatif.

ii. H adalah definte positif jika dan hanya jika nilai eigen dari matriks H yaitu , , , …, kesemuanya bertanda positif.

iii. H adalah semidefinte negatif jika dan hanya jika nilai eigen dari matriks H yaitu ≤ 0, I = 1,2,3,…, n

iv. H adalah semidefinte positif jika dan hanya jika nilai eigen dari matriks H yaitu ≥ 0, I = 1,2,3,…, n

2.5 Sifat Konveks dan Konkaf Berdasarkan Sifat Matriks Hessian

 Jika f(x) mempunyai turunan parsial kedua yang kontinu pada setiap x, maka f(x) adalah fungsi konveks jika seluruh minor utama dari f(x) adalah ≥ 0 (konveks ketat jika seluruh minor utama dari f(x) adalah > 0).

 Jika f(x) mempunyai turunan parsial kedua yang kontinu pada setiap x, maka f(x) adalah fungsi konkaf jika seluruh minor utama dari f(x) bertanda , i = 1,2,..,n atau sama dengan 0 (konkaf ketat jika seluruh minor utama dari f(x) bertanda , i = 1,2,..,n).

2.5.1 Contoh penggunaan Matriks Hessian untuk Penentuan Sifat Konveks/

Konkaf suatu fungsi

Fungsi : f( = + 2 +

Titik-titik ekstrim harus memenuhi syarat:

= 3 + 2

(38)

27

= 2 + 2

= 2

Matriks Hessian bagi fungsi tersebut adalah :

= 6 ,

= 2,

2

f(x) = H( ) =

Matriks Hessian tersebut mempunyai 2 minor utama.

Minor utama ke-1 adalah :

Untuk x₁≥ 0 maka minor utama ke-1:

2 >0 dan 6x₁ ≥0

Minor utama ke-2 adalah determinan dari:

Yang bernilai 12x₁– 4

Hanya akan bernilai ≥ 0 untuk x₁ ≥ 1/3

Fungsi pada contoh ini mempunyai matriks Hessian yang bersifat positif (semi) definit pada rentang x₁ ≥ 1/3

Fungsi bersifat konveks untuk x₁ ≥ 1/3

2.6 Matriks Definit Positif

Bentuk kuadrat pada X = adalah ekspresi yang dapat ditulis

sebagai A . Dengan A adalah matriks simetrik n×n. Jadi

misalkan

(39)

28

X= maka bentuk ini dapat ditulis sebagai .

Suatu bentuk kuadrat f(x) = disebut definit jika bentuk kuadrat tersebut hanya mempunyai tanda yang sama, di mana X bervariasi atas semua vektor – vektor taknol dalam

Definisi 3

Bentuk kuadrat disebut definit positif jika ≥ 0 untuk semua x ≠ 0, sedangkan matriks simetrik A disebut matriks definit positif jika adalah bentuk kuadrat definit positif.

Contoh :

Dipunyai matriks simetrik berikut :

A =

Untuk mengkaji apakah matriks A bersifat definit positif, maka :

= [

= ( ) + ( ) + ( )

= + + +

= +

Dari sini dapat disimpulkan bahwa matrik A bersifat definit positif karena memenuhi

+ > 0 kecuali jika = = = 0

(40)

29 Matrik A dan bentuk kuadrat disebut :

1. Definit negatif jika < 0, untuk semua x ≠ 0.

2. Semidefinit positif jika ≥ 0, untuk semua x.

3. Semidefinit positif jika ≤ 0, untuk semua x.

4. Indefinit bila tidak termasuk golongan di atas.

Himpunan syarat perlu dan syarat cukup untuk bentuk – bentuk definit positif dan negatif yaitu (Luknanto, 2000) :

1. Syarat perlu dan syarat cukup untuk bentuk definit positif.

Suatu himpunan syarat perlu dan syarat cukup bentuk sebagai definit positif adalah

>0,

> 0, ... , |A| > 0

Jika n minor dari A adalah positif, maka adalah definit positif. Dan hanya definit positif, jika minor-minor ini positif.

2. Syarat perlu dan syarat cukup untuk bentuk definit negatif

Suatu himpunan syarat perlu dan syarat cukup bentuk menjadi definit negatif atau setaranya untuk sebagai definit positif adalah

0,

>0,

<0, ... , |A| > 0

Jika n minor dari A adalah positif, maka adalah definit positif. Di mana adalah elemen – elemen dari A (bukan –A).

2.7 Persyaratan Karush-Kuhn-Tucker

Pada tahun 1951 Kuhn Tucker mengemukakan suatu teknik optimisasi yang dapat digunakan untuk pencarian titik optimum dari suatu fungsi yang berkendala.

Metode Karush-Kuhn-Tucker ini dapat dipergunakan untuk mencari solusi yang optimum dari suatu fungsi tanpa memandang sifat dari fungsi tersebut apakah linier atau nonlinier. Jadi metode Karush-Kuhn-Tucker ini bersifat teknik yang umum dalam pencarian titik optimum dari setiap fungsi. Metode Karush-Kuhn-

(41)

30

Tucker dapat digunakan untuk memecahkan persoalan baik yang nonlinier maupun yang linier.

Jika menghadapi masalah optimasi dalam bentuk :

Maksimumkan/minimumkan : Z = f(X) dengan X = (2.28) dengan kendala : (X ) 0 atau

(X ) dengan i = 1,2,3,…,m X 0

m ≤ n (jumlah kendala lebih kecil dari variabel) Pertama tuliskan kembali persyaratan – persyaratan yang tak negatif seperti - ≤ 0, ≤ 0,…, - ≤ 0, sehingga himpunan kendalanya adalah m+n persayaratan ketidaksamaan yang masing – masing dengan tanda lebih kecil dari pada atau sama dengan. Kemudian tambahkan variabel – variabel kurang

, ,…, berturut – turut pada ruas kiri dari kendala – kendala tadi, yang demikian merubah tiap – tiap ketidaksamaan menjadi suatu kesamaan. Slack variables yang ditambahkan di sini berbentuk suku – suku kuadrat untuk menjamin bahwa mereka tak negatif. Kemudian bentuk fungsi Lagrange :

(2.29)

Untuk, adalah pengali – pengali Lagrange. Terakhir selesaikan sistem persamaan

(j = 1,2,…,2n+m)

(i = 1,2,…, m+n) (i = 1,2,…,m+n)

Untuk fungsi konveks, syarat perlu dan cukup untuk mencapai titik minimum dapat dicari menggunakan syarat Karush-Kuhn-Tucker. Tetapi untuk fungsi nonkonvek, syarat Karush-Kuhn-Tucker merupakan syarat perlu saja, tetapi belum cukup untuk mencapai optimal. Jadi untuk masalah jenis konveks, syarat Karush-Kuhn-Tucker menjadi syarat perlu dan cukup untuk sebuah maksimum ataupun minimum global.

Misalkan f(x,y) merupakan fungsi 2 variabel f(x,y) merupakan fungsi konveks jika dan hanya jika dipenuhi ketiga syarat berikut (Hiller and Lieberman, 2005) :

(42)

31 (i)

=

(ii)

≥

0 (iii)

≥

0

Suatu fungsi 2 variabel f(x,y) merupakan fungsi konkaf jika tidak memenuhi paling tidak satu dari ketiga syarat pada teorema 1 atau dengan kata lain f(x,y) merupakan fungsi konveks.

Untuk permasalahan dengan asumsi f(x) konkaf dan (x) konveks, maka syarat perlu dan cukup keoptimalannya berdasarkan teorema berikut.

Misalkan f(x), (x), (x),…, (x)merupakan fungsi- fungsi yang dapat diturunkan maka = ( , ,…, ) merupakan penyelesaian optimal untuk masalah program nonlinier apabila terdapat sejumlah untuk i = 1,2,…, msehingga semua syarat terpenuhi :

(i)

+

= 0 i = 1,2,…,n

(ii) = 0 j = 1,2,…, m

(iii) ≤ 0 j = 1,2,…, m

(iv) ≥ 0 j = 1,2,…, m

Corollary

Diasumsikan bahwa f(x) merupakan fungsi konkaf dan merupakan fungsi konveks (misalkan saja masalah ini merupakan masalah pemrograman konveks), dengan semua fungsi ini memenuhi kondisi biasa. Lalu adalah solusi optimal jika dan hanya jika semua kondisi teorema terpenuhi

(43)

BAB 3

PEMBAHASAN

3.1 Kondisi Karush-Kuhn-Tucker pada Optimasi Separable Programming Suatu fungsi f(x) dapat dikatakan terpisah apabila fungsi tersebut dapat dinyatakan dalam bentuk penjumlahan dari fungsi – fungsi yang hanya memuat satu variabel, didefinisikan sebagai berikut (Bazaraadkk, 2006)

(3.1)

dengan kendala :

i = 1,2,…,m

j = 1,2,..,n

Diamsumsikan f(x), (x), (x),…, (x) merupakan fungsi yang dapat diturunkan maka = ( , ,…, ) menjadi solusi optimal untuk permasalahan pemrograman nonlinier hanya jika terdapat sejumlah m bilangan sehingga semua syarat kondisi Karush-Kuhn-Tucker berikut ini terpenuhi :

(i) + = 0 pada x= untuk j = 1,2,…, n (ii) = 0 pada x = untuk j = 1,2,…,n (iii) ( ) - ≤ 0 untuk j = 1,2,…, m

(iv) untuk j = 1,2,…, m (v) ≥ 0 untuk j = 1,2,…, m

(vi) ≥ 0 untuk j = 1,2,…, m

Dapat dilihat dari kondisi (ii) dan (iv) memerlukan hasil perkalian dua kuantitas sama dengan nol. Oleh karena itu, tiap kondisi ini menyatakan bahwa setidaknya salah satu dari kuantitas itu harus sama denga nol. Akibatnya, kondisi (iv) dapat digabung dengan kondisi (iii) untuk menyatakan mereka