ANALISIS BESAR GAYA DORONG TUG BOAT PADA PERFORMANSI SISTEM KENDALI AUTO TRACKING KAPAL LNG BERMUATAN PENUH DI PELABUHAN ARUN

(1)

i

TUGAS AKHIR - TF 141581

ANALISIS BESAR GAYA DORONG

TUG BOAT

PADA PERFORMANSI SISTEM KENDALI

AUTO TRACKING

KAPAL LNG BERMUATAN PENUH

DI PELABUHAN ARUN

MIMA AULIA NRP. 2413 100 003

Dosen Pembimbing :

Prof. Dr. Ir. Aulia Siti Aisjah, M.T. Dr. Ir. A. A. Masroeri, M.Eng.

DEPARTEMEN TEKNIK FISIKA Fakultas Teknologi Industri

Institut Teknologi Sepuluh Nopember Surabaya 2017

(2)

ii

(3)

iii

FINAL PROJECT - TF 141581

ANALYSIS OF FORCES TUG BOAT IN

PERFORMANCE FULL LOAD LNG SHIP

AUTO TRACKING CONTROL SYSTEM

ON ARUN PORT

MIMA AULIA NRP. 2413 100 003

Supervisors :

Prof. Dr. Ir. Aulia Siti Aisjah, M.T. Dr. Ir. A. A. Masroeri, M.Eng.

ENGINEERING PHYSICS DEPARTMENT Faculty of Industrial Technology

Sepuluh Nopember Institute of Technology Surabaya 2017

(4)

iv

(5)

PERNYATAAN BEBAS PLAGIARISME Saya yang bertanda tangan di bawah ini

Nama : Mima Aulia

NRP : 2413100003

Departemen / Prodi : Teknik Fisika / S1 Teknik Fisika Fakultas : Fakultas Teknologi Industri

Perguruan Tinggi : Institut Teknologi Sepuluh Nopember Dengan ini menyatakan bahwa Tugas Akhir dengan judul “Analisis Besar Gaya Dorong Tug Boat Pada Performansi Sistem Kendali Auto Tracking Kapal LNG Bermuatan Penuh Di Pelabuhan Arun” adalah benar karya saya sendiri dan bukan plagiat dari karya orang lain. Apabila di kemudian hari terbukti terdapat plagiat pada Tugas Akhir ini, maka saya bersedia menerima sanksi sesuai ketentuan yang berlaku.

Demikian surat pernyataan ini saya buat dengan sebenar-benarnya.

Surabaya, 11 Januari 2017 Yang membuat pernyataan,

Mima Aulia NRP. 2413 100 003

(6)

(7)

v

Lembar Pengesahan I LEMBAR PENGESAHAN

TUGAS AKHIR

ANALISIS BESAR GAYA DORONG TUG BOAT PADA PERFORMANSI SISTEM KENDALI AUTO TRACKING KAPAL LNG BERMUATAN PENUH DI PELABUHAN

ARUN Oleh : Mima Aulia NRP. 2413 100 003 Surabaya, 11 Januari 2017 Menyetujui, Dosen Pembimbing I

Prof. Dr. Ir. Aulia Siti Aisjah, M.T. NIPN. 196601161989032001

Menyetujui, Dosen Pembimbing II

Dr. Ir. A. A. Masroeri, M.Eng. NIPN. 195808071984031001 Mengetahui,

Ketua Departemen Teknik Fisika FTI-ITS

Agus Muhamad Hatta, S.T., M.Si., Ph.D. NIPN. 197809022003121002

(8)

vi

(9)

vii

Lembar Pengesahan II

ARUN TUGAS AKHIR

Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Teknik

pada

Bidang Studi Rekayasa Instrumentasi Progam Studi S-1 Departemen Teknik Fisika

Fakultas Teknologi Industri Institut Teknologi Sepuluh Nopember

Oleh: MIMA AULIA NRP. 2413 100 003

Disetujui oleh Tim Penguji Tugas Akhir:

1. Prof. Dr. Ir. Aulia Siti Aisjah, M.T. ... (Pembimbing I) 2. Dr. Ir. A. A. Masroeri, M.Eng ... (Pembimbing II) 3. Dr. Ir. Totok Soehartanto, DEA. ... (Penguji I) 4. Dr. Bambang L. Widjiantoro, S.T, M.T. ... (Penguji II) 5. Bagus Tris Atmaja, S.T., M.T. ... (Penguji III)

SURABAYA JANUARI, 2017

(10)

viii

(11)

ix Abstrak

ARUN

Nama : Mima Aulia

NRP : 2413 100 003

Departemen : Teknik Fisika FTI-ITS

Dosen Pembimbing : 1.Prof. Dr. Ir. Aulia S. Aisjah, M.T. 2.Dr. Ir. A. A. Masroeri, M.Eng. Abstrak

Bentuk dermaga Pelabuhan Arun yang sempit menyebabkan kapal LNG harus bermanuver secara mandiri. Sistem auto tracking telah banyak digunakan pada beberapa kapal. Sistem auto tracking tersebut belum sepenuhnya menggerakkan kapal LNG sesuai dengan lintasan yang diinginkan sehingga masih diperlukan tug boat dengan gaya dorong tertentu untuk membantu maneuvering kapal LNG. Tugas akhir ini melakukan analisis terhadap besar gaya dorong tug boat AHTS untuk membantu maneuvering kapal LNG pada jalur keluar Pelabuhan Arun. Model pengendali yang dirancang adalah PID dengan tunning terhadap gain pengendali menggunakan metode Ziegler-Nichols. Uji terhadap model dilakukan dengan metode root locus dan hasilnya menunjukkan bahwa sistem bersifat stabil. Pengendalian PID yang telah dirancang didapatkan nilai Kp sebesar 1484, Ki sebesar 0,004, Kd sebesar 9736 dan menghasilkan performansi respon sistem sesuai dengan standar IMO (International Maritime Organization) yaitu nilai maximum overshoot sebesar 20,62O

untuk set point 20O_{dan 30,92}O _untuk_{set point 30}O_{. Perhitungan}

yang dilakukan di setiap keadaan didapatkan hasil bahwa kapal LNG bermuatan penuh hanya membutuhkan bantuan 1 gaya dorong tug boat untuk memenuhi lintasan yang diharapkan. Kata Kunci : Gaya dorong, kapal LNG, tug boat AHTS

(12)

x

(13)

xi Abstract

ANALYSIS OF FORCES TUG BOAT IN PERFORMANCE FULL LOAD LNG SHIP AUTO TRACKING CONTROL

SYSTEM ON ARUN PORT

Name : Mima Aulia

NRP : 2413 100 003

Department : Teknik Fisika FTI-ITS

Supervisors : 1.Prof. Dr. Ir. Aulia S. Aisjah, M.T. 2.Dr. Ir. A. A. Masroeri, M.Eng. Abstract

Shape of Arun port is narrow, it makes LNG Ship must maneuvering independently. The auto tracking system has used widely on several ships. The system autotracking yet fully mobilize LNG Ship accordance with desired track, it still needed tugboat with specific thrust up to help the LNG Ship maneuvering. This final project do the analysis of forces AHTS tug boat AHTS to help the LNG ship maneuvering on desired out track in Port Arun. Model PID controller which is tunning with gain controller using the Ziegler-Nichols method. Plant model test is doing with root locus method and the results show that the stable nature. The PID control has designed, get the value of Kp, Ki, Kd i.e 1.484, 0.004, 9736 and the responses match with standards IMO (International Maritime Organization) is the maximum overshoot value i.e 20,62 And 30,92 for set point i.e 20 and 30. The calculation is done in every state and get the value that the full load LNG Ship requires only 1 forces AHTS tug boat to help the LNG ship maneuvering on desired out track in Port Arun.

(14)

xii

(15)

xiii

KATA PENGANTAR

Puji syukur kehadirat Allah SWT yang senantiasa melimpahkan rahmat serta hidayah-Nya, serta shalawat serta salam kepada Nabi Muhammad SAW, hingga terselesaikannya tugas akhir beserta laporan tugas akhir yang berjudul ANALISIS

BESAR GAYA DORONG TUG BOAT PADA

PERFORMANSI SISTEM KENDALI AUTO TRACKING KAPAL LNG BERMUATAN PENUH DI PELABUHAN ARUN.

Penulis telah banyak memperoleh bantuan dari berbagai pihak dalam penyelesaian tugas akhir dan laporan Tugas Akhir ini. Penulis mengucapkan terimakasih kepada :

1. Bapak Agus Muhamad Hatta, S.T., M.Si., Ph.D selaku Ketua Departemen Teknik Fisika yang telah memberikan petunjuk, ilmu, serta bimbingan selama menempuh pendidikan di Teknik Fisika.

2. Ibu Prof. Dr. Ir. Aulia Siti Aisjah, M.T. dan Bapak Dr. Ir. A. A. Masroeri, M.Eng. selaku dosen pembimbing yang telah dengan sabar memberikan petunjuk, ilmu, serta bimbingan yang sangat bermanfaat.

3. Bapak Totok Ruki Biyanto, S.T., M.T., Ph.D. selaku Kepala Laboratorium Rekayasa Instrumensi yang telah memberikan ilmu, petunjuk, nasihat, serta kemudahan perizinan.

4. Bapak Dr. Ir. Totok Soehartanto, DEA. selaku dosen wali yang telah membimbing penulis selama perkuliahan.

5. Kedua orang tua (Bapak Miftah dan Ibu Sri Suryani) serta saudara (Dita Aulia). Terimakasih atas segala cinta, kasih sayang, doa, perhatian, serta dukungan moril dan materiil yang telah diberikan.

6. Seluruh teman Tugas Akhir (Desty Ajeng Pawestri dan Farida Ambarwati), terima kasih untuk semuanya.

7. Seluruh teman – teman Departemen Teknik Fisika angkatan 2013, terima kasih untuk semuanya.

8. Seluruh dosen, karyawan dan civitas akademik Teknik Fisika, terimakasih atas segala bantuan dan kerjasamanya.

(16)

xiv

9. Semua pihak yang tidak dapat disebutkan satu persatu, terimakasih atas bantuannya.

Penulis sadar bahwa penulisan laporan tugas akhir ini tidak sempurna, namun semoga laporan ini dapat memberikan kontribusi yang berarti dan menambah wawasan yang bermanfaat bagi pembaca, keluarga besar Teknik Fisika khususnya, dan civitas akademik ITS pada umumnya. Semoga laporan tugas akhir ini dapat bermanfaat sebagai referensi pengerjaan laporan tugas akhir bagi mahasiswa yang lain.

Surabaya, 11 Januari 2017

(17)

xv DAFTAR ISI

Halaman

Halaman Judul ... i

Title Page ... iii

Lembar Pengesahan I ...v

Lembar Pengesahan II ... vii

Abstrak ... ix

Abstract ... xi

KATA PENGANTAR ... xiii

DAFTAR ISI ...xv

DAFTAR GAMBAR ... xvii

DAFTAR TABEL ... xix

DAFTAR NOTASI ... xxi

BAB I PENDAHULUAN ...1 1.1 Latar Belakang ...1 1.2 Rumusan Masalah ...2 1.3 Tujuan ...2 1.4 Batasan Masalah ...3 1.5 Sistematika Laporan ...3

BAB II TINJAUAN PUSTAKA ...5

2.1 Pemodelan Dinamika Kapal ...5

2.2 Kapal Tug Boat ...11

2.3 Pemodelan Dinamika Rudder ...13

2.4 Sistem Guidance ...14

2.5 Penurunan Persamaan Gaya Dorong ...14

2.6 Kestabilan Sistem Pengendalian ...17

2.7 Standar Maneuverability ...22

2.8 Indeks Stabilitas Yaw ...24

2.9 Root-Locus ...24

BAB III METODOLOGI PENELITIAN ...27

3.1 Studi Literatur ...28

3.2 Pengumpulan Data ...28

3.3 Pemodelan Dinamika Kapal ...32

3.4 Perancangan Sistem Kendali Auto Tracking Kapal LNG Bermuatan Penuh ...37

(18)

xvi

3.6 Analisis Hasil Uji ... 39

3.7 Perhitungan Gaya Dorong Kapal ... 42

3.8 Perhitungan Lintasan Kapal ... 42

3.9 Penutup ... 47

BAB IV ANALISIS HASIL DAN PEMBAHASAN ... 49

4.1 Analisis Uji Open Loop ... 49

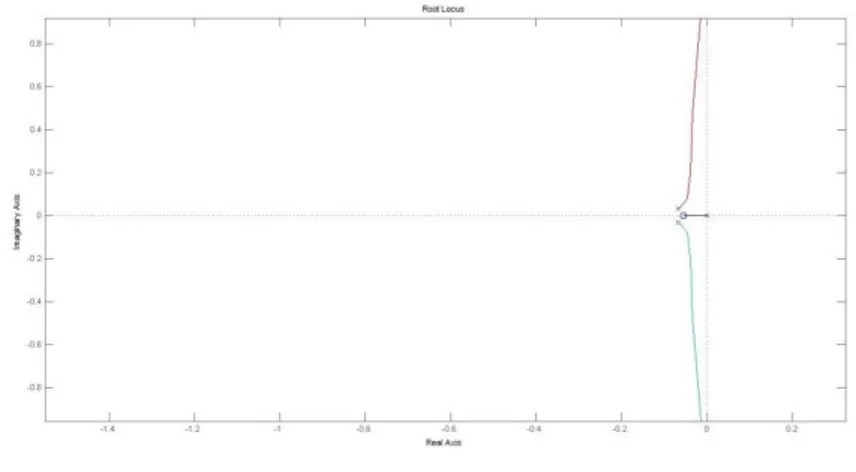
4.2 Analisis Uji Root-Locus ... 52

4.3 Analisis Uji Indeks Stabilitas ... 53

4.4 Analisis Sistem Kendali Kapal LNG... 54

4.4.1 Mode Pengendalian PI ... 54

4.4.2 Mode Pengendalian PID ... 55

4.5 Analisis Lintasan Kapal LNG Bemuatan Penuh ... 60

4.5.1 Analisis Lintasan Kapal LNG Bermuatan Penuh Tanpa Pengendali PID ... 61

4.5.2 Analisis Lintasan Kapal LNG Bermuatan Penuh Tanpa Pengendali PID Dengan Bantuan 1 Tug Boat AHTS ... 65

4.5.3 Analisis Lintasan Kapal LNG Bermuatan Penuh Tanpa Pengendali PID Dengan Bantuan 2 Tug Boat AHTS ... 68

4.5.4 Analisis Lintasan Kapal LNG Bermuatan Penuh Dengan Pengendali PID ... 71

4.5.5 Analisis Lintasan Kapal LNG Bermuatan Penuh Dengan Pengendali PID dan Bantuan 1 Tug Boat AHTS ... 74

4.5.6 Analisis Lintasan Kapal LNG Bermuatan Penuh Dengan Pengendali PID dan Bantuan 2 Tug Boat AHTS ... 77

4.6 Analisis Perhitungan Gaya Dorong ... 80

BAB V PENUTUP ... 83 5.1 Kesimpulan ... 83 5.2 Saran ... 84 DAFTAR PUSTAKA ... 85 LAMPIRAN BIODATA PENULIS

(19)

xvii

DAFTAR GAMBAR

Gambar 2.1 Notasi dan Gerakan Standar pada Kapal

(Fossen, 1994) ...6

Gambar 2.2 Kapal Tug Boat Mendorong Kapal LNG (Adiawan, 2016) ...11

Gambar 2.3 Visualisasi Kapal Tug Boat Mendorong Kapal Tongkang (Mulyanto, 2015) ...13

Gambar 2.4 Gaya yang Bekerja Pada Kapal LNG Akibat Gaya Dorong Tug boat AHTS ...14

Gambar 2.5 Diagram Blok Sistem Pengendalian Tertutup (Basilio, 2002) ...17

Gambar 2.6 Diagram Blok Pengendalian PID (Basilio, 2002) ...19

Gambar 2.7 Diagram Blok Pengendalian PID Ziegler – Nichols (Basilio, 2002) ...21

Gambar 2.8 Kurva Respon Step (Basilio, 2002) ...21

Gambar 3.1 Diagram Alir Tugas Akhir ...27

Gambar 3.2 Jalur Keluar Kapal di Pelabuhan Arun ...31

Gambar 3.3 Diagram Blok Sistem Pengendalian ...37

Gambar 3.4 Blok Diagram Simulink PID Kapal LNG Bermuatan Penuh ...38

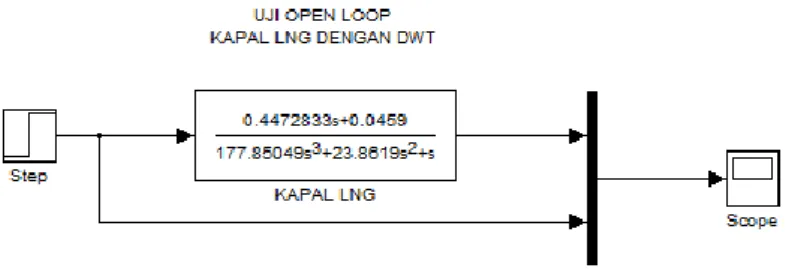
Gambar 3.5 Diagram Blok Simulink Uji Open Loop Kapal LNG Bermuatan Penuh ...40

Gambar 3.6 Diagram Blok Simulink Uji Open Loop Kapal AHTS ...40

Gambar 3.7 Simulink Uji Turning Kapal LNG Bermuatan Penuh ...41

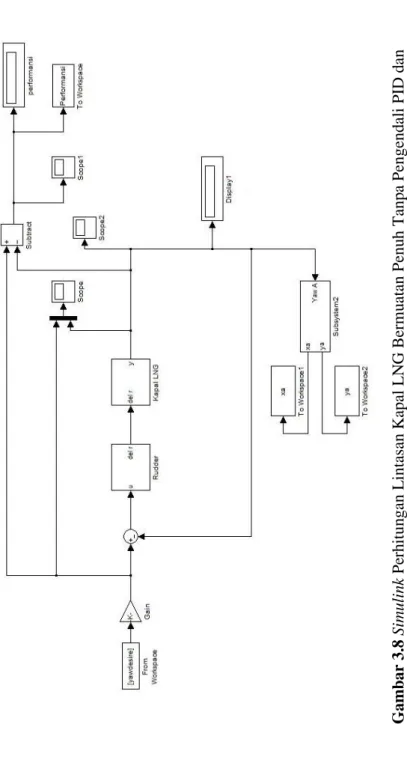
Gambar 3.8 Simulink Perhitungan Lintasan Kapal LNG Bermuatan Penuh Tanpa Pengendali PID dan ...43

Gambar 4.1 Hasil Uji Open Loop 20 Derajat Kapal LNG Bermuatan Penuh ...49

Gambar 4.2 Hasil Uji Open Loop30 Derajat Kapal LNG Bermuatan Penuh ...50

Gambar 4.3 Hasil Uji Open Loop 20 Derajat Kapal AHTS...51

(20)

xviii

Gambar 4.5 Diagram Root Locus Dari Sistem Kapal LNG Bermuatan Penuh ... 52 Gambar 4.6 Diagram Root Locus Dari Sistem Kapal AHTS .... 53 Gambar 4.7 Respon Uji Turning Mode PI Kapal LNG

Bermuatan Penuh Dengan Sudut Heading 20 Derajat ... 54 Gambar 4.8 Respon Uji Turning Mode PI Kapal LNG

Bermuatan Penuh Dengan Sudut Heading 30 Derajat ... 55 Gambar 4.9 Respon Uji Turning Kapal LNG Bermuatan

Penuh Dengan Sudut Heading 20 Derajat ... 57 Gambar 4.10 Respon Uji Turning Kapal LNG Bermuatan

Penuh Dengan Sudut Heading 30 Derajat ... 59 Gambar 4.11 Perbandingan Lintasan Desire dan Aktual

Kapal LNG Bermuatan Penuh Tanpa ... 64 Gambar 4.12 Perbandingan Lintasan Desire dan Aktual

Kapal LNG Bermuatan Penuh Tanpa

Pengendali PID Dengan Bantuan 1 Tug Boat ... 67 Gambar 4.13 Perbandingan Lintasan Desire dan Aktual

Kapal LNG Bermuatan Penuh Tanpa ... 70 Gambar 4.14 Perbandingan Lintasan Desire dan Aktual

Kapal LNG Dengan Pengendali PID ... 73 Gambar 4.15 Perbandingan Lintasan Desire dan Aktual

Kapal LNG Bermuatan Penuh Dengan ... 76 Gambar 4.16 Perbandingan Lintasan Desire dan Aktual

Kapal LNG Bermuatan Penuh Dengan ... 79 Gambar 4. 17 Perbandingan Lintasan Desire, Aktual Kapal

LNG Bermuatan Penuh Tanpa Pengendali PID dan Aktual Kapal LNG Bermuatan Penuh Dengan Pengendali PID ... 82

(21)

xix

DAFTAR TABEL

Tabel 2.1 Derajat Kebebasan Kapal (Fossen, 2002) ...5 Tabel 2.2 Pelinearan Koefisien Hidrodinamika

Menggunakan Prime System I (Fossen, 1994) ...9 Tabel 2.3 Parameter Kp, τi dan τd (Basilio, 2002) ...22 Tabel 2.4 Standar Manuverabilitas Kapal oleh

IMO(Resolution MSC 137(76), 2002) ...23 Tabel 3.1 Tabel Spesifikasi Kapal LNG ...29 Tabel 3.2 Tabel Spesifikasi Kapal AHTS ...30 Tabel 3.3 Koordinat Lintasan Kapal LNG Keluar Pelabuhan

Arun ...31 Tabel 3.4 Koefisien Hidrodinamika Kapal LNG Bermuatan

Penuh ...33 Tabel 3.5 Koefisien Hidrodinamika Tugboat AHTS ...35 Tabel 4.1 Konversi Latitude dan Longitude ...60 Tabel 4.2 Lintasan Aktual dan Error Lintasan Kapal LNG

Bermuatan Penuh Tanpa Pengendali PID dan

Tanpa Bantuan Tug Boat ...62 Tabel 4.3 Lintasan Aktual dan Error Lintasan Kapal LNG

Bermuatan Penuh Tanpa Pengendali PID Dengan Bantuan 1 Tug Boat ...65 Tabel 4.4 Lintasan Aktual dan Error Lintasan Kapal LNG

Bermuatan Penuh Tanpa Pengendali PID Dengan Bantuan 2 Tug Boat ...68 Tabel 4.5 Lintasan Aktual dan Error Lintasan Kapal LNG

Dengan Pengendali PID ...71 Tabel 4. 6 Lintasan Aktual dan Error Lintasan Kapal LNG

Dengan Pengendali PID dan Bantuan 1 Tug Boat AHTS ...74 Tabel 4. 7 Lintasan Aktual dan Error Lintasan Kapal LNG

Dengan Pengendali PID dan Bantuan 1 Tug Boat AHTS ...77 Tabel 4. 8 Analisis Error Lintasan ...80

(22)

xx

(23)

xxi

DAFTAR NOTASI X = gaya dan momen pada arah-x Y = gaya dan momen pada arah-y Z = gaya dan momen pada arah-z K = gaya dan momen pada sumbu-x M = gaya dan momen pada sumbu-y

N = gaya dan momen pada sumbu-z

u = kecepatan linier dan anguler pada arah-x v = kecepatan linier dan anguler pada arah-y w = kecepatan linier dan anguler pada arah-z

q = kecepatan linier dan anguler pada sumbu-x p = kecepatan linier dan anguler pada sumbu-y r = kecepatan linier dan anguler pada sumbu-z x = posisi dan sudut euler pada arah-x

y = posisi dan sudut euler pada arah-y z = posisi dan sudut euler pada arah-z θ = posisi dan sudut euler pada sumbu-x ϕ = posisi dan sudut euler pada sumbu-y ψ = posisi dan sudut euler pada sumbu-z M = matriks inersia

C = matriks dari coriolis dan disebut gaya sentripetal D = matriks redaman

g(η) = vektor dari gaya dan momen gravitasi τ = vektor dari input kendali

v = vektor kecepatan angular dan linear v̇ = vektor percepatan sway

ṙ = Vektor percepatan yaw

Y′_v̇̇ = turunan gaya arah sway terhadap 𝑣̇ non dimensi Y′_ṙ̇ = turunan gaya arah sway terhadap 𝑟̇ non dimensi N′_v̇̇ = turunan momen arah yaw terhadap 𝑣̇ non dimensi N′_ṙ̇ = turunan momen arah yaw terhadap 𝑟̇ non dimensi

Y_v̇̇ = turunan gaya arah sway terhadap 𝑣̇ (Ndet2_/m)

Y_ṙ̇ = turunan gaya arah sway terhadap 𝑟̇ (Ndet2_/m)

N_v̇̇ = turunan momen arah yaw terhadap 𝑣̇ (Ndet2_/m)

(24)

xxii δ_R = sudut rudder

m = massa kapal (kg) r = notasi putaran kapal xG = pusat massa

Yδ = gaya dan momen rudder pada arah-y Nδ = gaya dan momen rudder pada sumbu-z

Iz = momen inersia (kg.m2) Ir = momen inersia (kg.m2) c = command rudder a = aktuator rudder k = penguat rudder 𝜎 = time constant

w = zero-mean Gaussian white noise process

σm = nilai konstan dari intensitas gelombang

h = tinggi gelombang (m) ξ = koefisien rasio peredam ω0 = frekuensi gelombang L = panjang (m) B = lebar (m) T = sarat kapal (m) CB = block coefficient ∇ = dispacement (ton)

ρ = massa jenis air

Kp = konstanta proporsional Ki = konstanta integral Kd = konstanta derivatif

m(t) = keluaran sistem pengendali e(t) = sinyal kesalahan kendali

Ti = waktu integral Td = waktu derivatif

Kc = gain pengendali

Tc = waktu pengendali C′ = indeks stabilitas yaw

pn = Pole

zn = Zero

(25)

Rn =

Bilangan Reynold

Lwl =

length water line (m)

(26)

xxiv

(27)

1

BAB I

PENDAHULUAN

1.1 Latar Belakang

Dua pertiga wilayah Indonesia berupa perairan. Ribuan pulau berjajaran dari Sabang sampai Merauke. Posisi Indonesia sangat strategis dalam rute perdagangan. Indonesia sebagai negara kepulauan peranan pelabuhan sangat penting dalam perekonomian. Kehadiran pelabuhan yang memadai berperan penting dalam menjunjung mobilitas barang dan penumpang. Pelabuhan menjadi sarana penting untuk menghubungkan antar pulau maupun antar negara selain itu pelabuhan merupakan salah satu tempat pemberhentian kapal. Aktivitas yang dilakukan di pelabuhan adalah menerima kapal, memindahkan barang kargo ataupun memindahkan penumpang. Setiap pelabuhan menyediakan alat-alat khusus yang berfungsi untuk memuat dan membongkar muatan kapal dan setiap pelabuhan memiliki fasilitas terminal yang berbeda – beda sesuai dengan kebijakan masing-masing pelabuhan. Fasilitas tersebut berupa dermaga, crane dan gudang laut / transito. Dermaga berupa tempat kapal untuk bongkar atau menaikkan barang dan penumpang, crane merupakan alat yang membantu proses bongkar muat kapal sedangkan gudang laut / transito merupakan tempat untuk menyimpan barang yang telah dibongkar dari kapal atau barang yang akan dimuat ke kapal.

Berdasarkan letak geografi, setiap pelabuhan di Indonesia memiliki dermaga yang berbeda – beda. Salah satunya adalah Pelabuhan Arun di Lhoksumawe, Aceh Utara. Pelabuhan Arun merupakan pelabuhan milik PT Perta Arun Gas yang berfungsi sebagai terminal penerimaan dan regasifikasi LNG (Liquefied Natural Gas) yang berasal dari lapangan Tangguh di Kabupaten Teluk Bintuni Papua. Jenis kapal yang bersandar di Pelabuhan Arun berupa kapal LNG. Pelabuhan Arun memiliki bentuk dermaga yang tertutup dan sempit. Keadaan dermaga tersebut menyebabkan kapal LNG mengalami kendala dalam bersandar dan berlabuh.

(28)

Sistem sandar otomatis telah banyak digunakan di beberapa kapal (Gunawan, 2013). Sistem sandar otomatis yang telah dipasang pada kapal LNG belum sepenuhnya menggerakkan kapal LNG sesuai dengan lintasan yang diinginkan sehingga masih diperlukan tug boat dengan gaya dorong tertentu untuk membantu maneuvering kapal LNG. Tug boat adalah kapal yang berfungsi untuk menarik atau mendorong kapal-kapal lain, memandu kapal besar pada jalur yang berbahaya dan memperbaiki kapal di laut. Medan yang dilalui tug boat biasanya cukup menyulitkan seperti sungai kecil yang berliku dan laut dangkal berkarang hingga laut luas antar pulau besar, sehingga tug boat harus melakukan maneuvering yang baik (Handito, 2012). Penelitian sebelumnya telah dilakukan perancangan auto control pada kapal tug boat (Adiawan, 2016). Tugas akhir ini menganalisis besar gaya dorong yang diberikan kapal tug boat AHTS untuk membantu maneuvering kapal LNG pada jalur keluar Pelabuhan Arun.

1.2 Rumusan Masalah

Berdasarkan latar belakang di atas, rumusan masalah dari penulisan tugas akhir ini adalah :

a. Apakah sistem kendali auto tracking tetap mampu bekerja dengan adanya perubahan gaya dorong tug boat?

b. Berapa besar gaya dorong kapal tugboat yang dibutuhkan untuk membantu mengatasi error lintasan pada sistem auto tracking kapal LNG?

1.3 Tujuan

Berdasarkan pemaparan latar belakang dan permasalahan maka tujuan dari penelitian tugas akhir ini adalah sebagai berikut: a. Didapatkan sistem kendali auto tracking yang mampu

bekerja dengan adanya perubahan gaya dorong tug boat. b. Didapatkan besar gaya dorong kapal tug boat yang

dibutuhkan untuk membantu mengatasi error lintasan pada sistem auto tracking kapal LNG.

(29)

1.4 Batasan Masalah

Bedasarkan identifikasi masalah maka batasan masalah dari tugas akhir ini adalah :

a. Studi kasus pada penelitian ini dilakukan di Pelabuhan Arun Lhoksemawe, Aceh Utara.

b. Obyek yang diteliti adalah kapal LNG dan tug boat AHTS (Anchor Handling Tug Supply).

c. Variabel yang dikendalikan adalah 2 derajat kebebasan (degree of freedom) untuk gerak sway, yaw, dengan asumsi bahwa secara eksperimen gerak surge, pitch, roll dan heave tidak berpengaruh pada maneuvering kapal.

d. Model dinamika kapal menggunakan bentuk fungsi transfer dengan metode Nomoto.

e. Gangguan angin pada penelitian ini diabaikan.

f. Metode pengendalian yang digunakan pada penelitian ini yaitu pengendalian PID.

g. Penelitian dilakukan secara simulasi dengan bantuan Software MATLAB R2009a.

1.5 Sistematika Laporan

Sistematika penulisan laporan tugas akhir adalah sebagai berikut:

a. BAB I PENDAHULUAN

Pada bab I ini terdiri dari latar belakang, rumusan masalah, batasan masalah, tujuan dan sistematika laporan.

b. BAB II TEORI PENUNJANG

Pada bab II ini dibahas mengenai teori-teori yang berkaitan dengan penelitian yang akan dilakukan, seperti teori pemodelan dinamika kapal dan pengendalian PID.

c. BAB III METODOLOGI PENELITIAN

Pada bab III ini berisi mengenai rancangan dari penelitian yang dilakukan, metode dan langkah - langkah dalam penelitian.

d. BAB IV ANALISIS DATA DAN PEMBAHASAN

Pada bab IV ini berisi tentang data hasil penelitian dari simulasi kendali PID dan analisis gaya dorong kapal tug boat

(30)

yang dibutuhkan untuk membantu mengatasi error lintasan pada sistem auto tracking kapal LNG.

e. BAB V KESIMPULAN DAN SARAN

Pada bab V ini diberikan kesimpulan tentang tugas akhir yang telah dilakukan berdasarkan data-data yang diperoleh, serta diberikan saran sebagai penunjang maupun pengembangan tugas akhir selanjutnya.

(31)

5

BAB II

TINJAUAN PUSTAKA

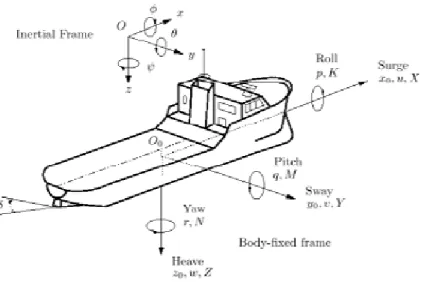
2.1 Pemodelan Dinamika Kapal

Model dinamik kapal merupakan suatu hasil dari ilmu statika dan dinamika. Ilmu statika digunakan saat kapal mempertahankan posisinya dan bergerak dengan kecepatan konstan dan dinamika saat kapal melakukan akselerasi. Model matematika ini diawali dengan penemuan Archimedes terhadap gerakan hidrostatik yang menjadi dasar statika pada suatu kendaraan laut. Ilmu dinamika dirumuskan oleh Newton mengenai dinamika gerak yang terbagi menjadi kinematika dan kinetika. Model dinamik kapal dirumuskan sebagai suatu rigid body dengan 6 derajat kebebasan. Derajat kebebasan kapal ini terdiri dari 3 derajat kebebasan terhadap sumbu x,y,z dan 3 derajat kebebasan lainnya mengacu kepada arah rotasi dan translasi dari kapal. Keenam derajat kebebasan dari kapal laut biasa disebut sebagai : Surge, Sway, Heave, Roll, Pitch, Yaw. Derajat kebebasan ini juga biasa disebut sebagai komponen gerak (Fossen, 2002). Komponen 6 gerak dari kapal diuraikan pada Tabel 2.1 dan diilustrasikan pada Gambar 2.1.

Tabel 2.1 Derajat Kebebasan Kapal (Fossen, 2002) D O F Gerakan Kapal Posisi dan Sudut Kecepatan Linier dan Angular Gaya dan Momen

1 Translasi sumbu-x (surge) X u X

2 Translasi sumbu-y (sway) Y v Y

3 Translasi sumbu-z (heave) Z w Z

4 Rotasi sumbu-x (roll) Φ p K

5 Rotasi sumbu-y (pitch) 𝜃 q M

(32)

Gambar 2.1 Notasi dan Gerakan Standar pada Kapal (Fossen, 1994)

Persamaan diferensial dari keenam gerakan kapal tersebut dituliskan dalam persamaan 2.1 sampai persamaan 2.6.

𝑚[𝑢̇ − 𝑣𝑟 + 𝑤𝑞 − 𝑥𝑔(𝑞2+ 𝑟2) + 𝑦𝑔(𝑝𝑞 − 𝑟̇) + 𝑧𝑔(𝑝𝑟 + 𝑞̇)] = 𝑋 (2.1) 𝑚[𝑣̇ − 𝑤𝑝 + 𝑢𝑟 − 𝑦𝑔(𝑟2+ 𝑝2) + 𝑧𝑔(𝑞𝑟 − 𝑝̇) + 𝑥𝑔(𝑞𝑝 + 𝑟̇)] = 𝑌 (2.2) 𝑚[𝑤̇ − 𝑢𝑞 + 𝑣𝑝 − 𝑧𝑔(𝑝2+ 𝑞2) + 𝑥𝑔(𝑟𝑝 − 𝑞̇) + 𝑦𝑔(𝑟𝑞 + 𝑝̇)] = 𝑍 (2.3) 𝐼𝑥𝑝̇ + (𝐼𝑧− 𝐼𝑦)𝑞𝑟 − (𝑟̇ + 𝑝𝑞)𝐼𝑥𝑧+ (𝑟2− 𝑞2)𝐼𝑦𝑧+ (𝑝𝑟 − 𝑞̇)𝐼𝑥𝑦+ 𝑚[𝑦𝑔(𝑤̇ − 𝑢𝑞 + 𝑝) − 𝑧𝑔(𝑣̇ − 𝑤𝑝 + 𝑢𝑟)] = 𝐾 (2.4) 𝐼𝑦𝑞̇ + (𝐼𝑥− 𝐼𝑧)𝑟𝑝 − (𝑝̇ + 𝑞𝑟)𝐼𝑥𝑦+ (𝑝2− 𝑟2)𝐼𝑧𝑥+ (𝑞𝑝 − 𝑟̇)𝐼_𝑦𝑧+ 𝑚[𝑧𝑔(𝑢̇ − 𝑣𝑟 + 𝑤𝑞) − 𝑥𝑔(𝑤̇ − 𝑢𝑞 + 𝑣𝑝)] = 𝑀 (2.5)

(33)

𝐼𝑧𝑟̇ + (𝐼𝑦− 𝐼𝑥)𝑝𝑞 − (𝑞̇ + 𝑟𝑝)𝐼𝑦𝑧+ (𝑞2− 𝑝2)𝐼𝑥𝑦+

(𝑟𝑞 − 𝑝̇)𝐼_𝑧𝑥+ 𝑚[𝑥𝑔(𝑣̇ − 𝑤𝑝 + 𝑢𝑟) − 𝑦𝑔(𝑢̇ − 𝑣𝑟 + 𝑤𝑞)] =

𝑁 (2.6)

Teori maneuvering mengasumsikan bahwa pergerakan kapal dibatasi yaitu pada air yang tenang seperti perairan yang dilindungi atau pelabuhan. Model maneuvering diturunkan untuk kapal yang bergerak dengan kecepatan U positif di bawah asumsi gelombang eksitasi frekuensi nol seperti yang ditambahkan massa dan redaman dapat direpresentasikan menggunakan penurunan hidrodinamik (parameter konstan). Asumsi frekuensi nol hanya berlaku untuk gerakan arah surge, sway dan yaw dengan periode alami dari kendali PD kapal berada di kisaran 100-150 s (Fossen, 2011). Pemodelan maneuvering kapal dirumuskan dari gerakan arah surge, sway dan yaw dengan asumsi mengabaikan gerakan arah heave, roll dan pitch (w = p = q = 0) dan distribusi massa homogen dan bidang x dan z simetris ( Ixy = Iyz= 0 ) seperti

ditunjukkan pada persamaan 2.7 sampai persamaan 2.9.

Surge : 𝑚[𝑢̇ − 𝑣𝑟 − 𝑥𝑔𝑟2− 𝑦𝑔𝑟̇] = 𝑋 (2.7)

Sway : 𝑚[𝑣̇ + 𝑢𝑟 − 𝑦𝑔𝑟2+ 𝑥𝑔𝑟̇] = 𝑌 (2.8)

Yaw : 𝐼𝑧𝑟̇ + 𝑚[𝑥𝑔(𝑣̇ + 𝑢𝑟) − 𝑦𝑔(𝑢̇ − 𝑣𝑟)] = 𝑁 (2.9)

Berdasarkan persamaan gerak kapal pada persamaan 2.7 sampai persamaan 2.9, Davidson dan Schiff (1946) mengusulkan bahwa gaya dan momen hidrodinamika dapat dimodelkan seperti pada persamaan 2.10 sampai persamaan 2.12 .

Xv̇v̇ + Xṙṙ + Xvv + Xrr + 𝑋𝛿𝛿 = 𝑋 (2.10)

Yv̇v̇ + Yṙṙ + Yvv + Yrr + 𝑌𝛿𝛿 = 𝑌 (2.11)

Nv̇v̇ + Nṙṙ + Nvv + Nrr + 𝑁𝛿𝛿 = 𝑁 (2.12)

Gaya dan momen hidrodinamika pada persamaan 2.10 sampai persamaan 2.12 digunakan untuk menurunkan persamaan

(34)

koefisien hidrodinamika kapal seperti pada persamaan 2.13 sampai persamaan 2.24 (Fossen, 1994).

-Y'_v_̇ π(T/L)2= 1+0.16 C_BB T −5.1( B L) 2 (2.13) -Y'_v_̇ π(T/L)2= 0.67( B L) −0.0033( B T) 2 (2.14) -N'_v_̇ π(T/L)2=1.1( B L)-0.041( B T) (2.15) -N'_r_̇ π(T/L)2= 1 12+0.017 C_BB T −0.33( B L) (2.16) -Y'_v_̇ π(T/L)2=1+0.14 C_BB T (2.17) -Y'_r π(T/L)2=− 1 2+2.2( B L)-0.08( B L) (2.18) -N'_v π(T/L)2= 1 2+2.4( T L) (2.19) -N'_r π(T/L)2= 1 4+ 0.039( B T)-0.56( B L) (2.20) 𝑌′𝛿 = 𝜋𝐴𝛿 4𝐿𝑇 (2.21) 𝑁′𝛿 = − 1 2𝑌 ′ 𝛿 (2.22) 𝐼′𝑟 = 𝑚′. 𝑟′2 (2.23) 𝐼′𝑧= 𝑚′. 𝑋′𝐺+ 𝐼′𝑟 (2.24)

Persamaan koefisisen hidrodinamika pada persamaan 2.13 sampai persamaan 2.24 berupa koefisien hidrodinamika yang tidak berdimensi, sehingga diperlukan perhitungan untuk mendapatkan koefisien yang berdimensi. Perubahan koefisien hidrodinamika dari yang tidak berdimensi menjadi koefisien hidrodinamika yang berdimensi membutuhkan pelinearan variabel menggunakan Prime System I. Pelinearan variabel ini disesuaikan dengan fungsi dari setiap koefisien hidrodinamika tersebut. Pelinearan koefisien hidrodinamika menggunakan Prime System I ditunjukkan pada Tabel 2.2 (Fossen, 1994).

(35)

Tabel 2.2 Pelinearan Koefisien Hidrodinamika Menggunakan Prime System I (Fossen, 1994)

Unit Prime–System I Panjang (m) L Massa (kg) 𝜌 2𝐿 3 Momen Inersia (kgm2₎ 𝜌 2𝐿 5 Waktu (s) 𝐿 𝑈 Luasan Referensi (m2₎ _L2 Posisi (m) L Sudut 1 Kecepatan Linier U Kecepatan Sudut 𝑈 𝐿 Percepatan Linier 𝑈 2 𝐿 Percepatan Sudut 𝑈 2 𝐿2 Gaya 𝜌 2𝑈 2_𝐿2 Momen 𝜌 2𝑈 2_𝐿3

Persamaan gerakan arah surge, sway dan yaw pada persamaan 2.10 sampai persamaan 2.12 dapat dinyatakan ke dalam bentuk vektorial pada persamaan 2.25 (Fossen, 1994).

𝑀𝑣̇ + 𝑁(𝑢0)𝑣 = 𝑏𝛿𝑅 (2. 25)

dimana :

v = [v, r]T_{adalah state vector}

𝛿𝑅 = sudut rudder

𝐾𝑅(1+ 𝑇3 𝑠 ) 𝑠(1+𝑇1𝑠)(1+𝑇2𝑠) (2.33) 𝜓 𝛿𝑅

(𝑠) =

𝐾𝑅+ 𝐾𝑅𝑇3 𝑠 ) 𝑇1𝑇2𝑠3+(𝑇1+𝑇2)𝑠2+𝑠 (2.34) 2.2 Kapal Tug Boat

Tug boat adalah kapal yang fungsinya menarik atau mendorong kapal - kapal lainnya. Kapal tug boat dibedakan atas beberapa jenis antara lain kapal tunda samudra, kapal tunda pelabuhan dan lain-lain. Fungsi tug boat yaitu untuk menarik dan mendorong kapal besar di pelabuhan, memandu kapal besar pada jalur yang berbahaya dan memperbaiki kapal dilaut (Prakoso, 2010). Pergerakan kapal LNG yang dipandu oleh kapal tunda atau tug boat ditunjukkan pada Gambar 2.2.

Gambar 2.2 Kapal Tug Boat Mendorong Kapal LNG (Adiawan, 2016)

Medan yang dilalui tug boat biasanya cukup menyulitkan seperti sungai kecil yang berliku dan laut dangkal berkarang hingga laut luas antar pulau besar, sehingga tug boat harus melakukan maneuvering yang baik (Handito, 2012).

(38)

a. Seagoing Tug

Fungsi dan peran dari tug boat untuk pelayaran bebas yaitu menarik atau mendorong kapal yang tidak memiliki alat penggerak sendiri.

b. Escort Tug

Kapal tug boat ini digunakan untuk mengawal kapal besar disepanjang bagian berbahaya

c. Harbours Tug

Kapal tug boat ini digunakan di pelabuhan, perairan dalam dan daerah pesisir (Perkasa, 2010).

Tug boat memiliki tenaga yang besar bila dibandingkan dengan ukurannya. Kapal tunda jaman dulu menggunakan mesin uap, saat ini menggunakan mesin diesel. Mesin induk kapal tunda biasanya berkuatan antara 750 sampai 5000 tenaga kuda (500 s.d. 3500 kW). Kebanyakan mesin yang digunakan sama dengan mesin kereta api, tetapi pada kapal menggerakkan baling-baling dan untuk keselamatan biasanya digunakan minimum dua buah mesin induk. Kapal tunda memiliki kemampuan maneuvering yang tinggi, tergantung dari unit penggerak. Kapal tunda dengan penggerak konvensional memiliki baling-baling di belakang, efisien untuk menarik kapal dari pelabuhan ke pelabuhan lainnya, jenis penggerak lainnya sering disebut schottel propulsion system (azimuth thruster/Z-peller) dimana baling-baling dibawah kapal dapat bergerak 3600 _{atau sistem propulsi Voith-Schneider yang}

menggunakan semacam pisau di bawah kapal yang dapat membuat kapal berputar 3600_{(Prakoso, 2010). Visualisasi kapal}

tug boat mendorong kapal tongkang ditunjukkan pada Gambar 2.3.

(39)

Gambar 2.3 Visualisasi Kapal Tug Boat Mendorong Kapal Tongkang (Mulyanto, 2015)

2.3 Pemodelan Dinamika Rudder

Rudder merupakan kemudi pada kapal yang berfungsi untuk menentukan arah kapal sesuai dengan perintah pengendali. Keluaran dari pengendali PID berupa command rudder (c) yang diubah menjadi aktuator rudder (a). Rudder yang digunakan memiliki spesifikasi k sebesar 0,0015789 dan time constant sebesar 0,05 (Adiawan, 2016). Pemodelan rudder didapatkan dengan menggunakan pendekatan matematis pada persamaan 2.35.

𝛿 = 𝑘

𝜎𝑠+1 (2. 35)

Spesifikasi rudder disubstitusikan pada persamaan 2.35 dan didapatkan pemodelan rudder yang ditunjukkan pada persamaan 2.36.

(40)

2.4 Sistem Guidance

Sistem guidance merupakan aksi dari sistem secara kontinyu melakukan perhitungan referensi (set point) berupa posisi, kecepatan, dan percepatan (PVA) dari kapal sebagai masukan untuk sistem pengendalian. Data PVA tersebut biasanya disediakan oleh operator dan sistem navigasi. Komponen dasar dari sistem guidance meliputi sensor (Kompas, GPS, dan Gyrocompas), eksternal data seperti data cuaca (kecepatan dan arah angiin, tinggi gelombang dan kemiringan, kecepatan arus dan arah arus). Sistem guidance ada beberapa tahapan yang diperlukan yaitu pembangkitan lintasan, database lintasan, dan perhitungan posisi kapal (Handito, 2012).

2.5 Penurunan Persamaan Gaya Dorong

Kapal LNG memiliki arah gerak surge, sway dan yaw, sedangkan kapal tug boat memiliki peranan gaya untuk mendorong kapal LNG dengan arah surge. Gaya dorong kapal tug boat ini diasumsikan sebagai gaya ekternal kapal LNG. Secara vektor, gaya-gaya yang bekerja pada kapal LNG akibat gaya dorong dari tug boat AHTS ditunjukkan pada Gambar 2.4.

Gambar 2.4 Gaya yang Bekerja Pada Kapal LNG Akibat Gaya Dorong Tug boat AHTS

(41)

Kapal yang bergerak di media air dengan kecepatan tertentu akan mengalami gaya hambat yang berlawanan dengan arah gerak kapal tersebut. Besarnya gaya hambat yang terjadi harus mampu diatasi oleh gaya dorong kapal yang dihasilkan dari kerja alat gerak kapal. Besarnya gaya dorong yang dibutuhkan pada kondisi ideal sama besar dengan gaya hambat yang terjadi dikapal. Tahanan gesek dari kapal dituliskan pada persamaan 2.37 (Wardanu, 2013).

𝑅 = 0,5 × 𝜌 × 𝑆𝑡𝑜𝑡𝑎𝑙× 𝐶𝑓× 𝑉𝑆2 (2.37)

dimana :

R = tahanan kapal (Newton) ρ = massa jenis air (Kg/m3₎

Stotal = luas total permukaan basah (m2)

Cf = kooefisien tahanan gesek

VS = kecepatan kapal (m/s)

Massa jenis fluida, koeefisien tahanan, dan nilai 0,5 merupakan suatu konstanta (k), sehingga persamaan 2.37 dapat dituliskan seperti pada persamaan 2.38 (Wardanu, 2013).

𝑅 = 𝑘 × 𝑉𝑆2 (2.38)

dimana :

R = tahanan kapal (Newton)

k = konstanta

VS = kecepatan kapal (m/s)

Persamaan luas total permukaan basah kapal yang terdapat pada persamaan 2.37 dapat diperoleh dengan menggunakan persamaan 2.39 hingga persamaan 2.41 (Waka, 2012).

𝑆𝑡𝑜𝑡𝑎𝑙 = 𝑆 + 𝑆𝑘𝑜𝑟𝑒𝑙𝑎𝑠𝑖 (2.39)

𝑆 = 1,025 × 𝐿𝑝𝑝× ((𝐶𝑏 × 𝐵) + 1,7𝑇) (2.40)

(42)

dimana :

Stotal = luas permukaan basah total (m2)

S = luas permukaan basah (m2₎

Skorelasi = luas permukaan basah korelasi (m2)

Lpp = length between perpendicullar (m)

Cb = koefisien blok kapal B = lebar kapal (m) T = tinggi kapal (m)

Konstanta koefisien gesek yang terdapat pada persamaan 2.37 dapat diperoleh dengan menggunakan persamaan 2.42 (Waka, 2012).

𝐶𝑓 =

0.075

(log(𝑅𝑛)−2)2 (2.42) dimana :

Cf = kooefisien tahanan gesek

Rn = Bilangan Reynold

Bilangan Reynold (Rn) pada persamaan 2.42 dapat diperoleh

dengan menggunakan persamaan 2.43 (Waka, 2012). 𝑅𝑛= (𝑉𝑠×𝐿𝑤𝑙) 0.000001188 (2.43) dimana : Rn = Bilangan Reynold VS = kecepatan kapal (m/s)

Lwl = length water line (m)

Tahanan kapal pada persamaan 2.37 digunakan untuk menurunkan persamaan gaya dorong kapal seperti yang ditunjukkan pada persamaan 2.44 (Saleh, 2012).

𝑇 = 𝑅

(43)

dimana :

T = gaya dorong kapal (Newton) R = tahanan kapal (Newton) t = fraksi deduksi gaya dorong

Nilai t merupakan fraksi deduksi gaya dorong dan memiliki nilai sebesar 0,05 sesuai dengan Blount (Saleh, 2012).

2.6 Kestabilan Sistem Pengendalian

Sistem pengendalian adalah gabungan dari kerja suatu komponen yang digunakan untuk mempertahankan variabel yang dikendalikan (process variable) pada suatu nilai tertentu (set point) sehingga sistem dapat dikatakan stabil. Seiring perkembangan ilmu pengetahuan dan teknologi suatu sistem pengendalian sudah memakai unit kendali otomatis seperti pada Gambar 2.5 (Basilio, 2002).

Gambar 2.5 Diagram Blok Sistem Pengendalian Tertutup (Basilio, 2002)

Suatu sistem linear (LTI/Linear Time Invariant) dikatakan stabil jika respon natural sistem tersebut mendekati nol pada waktu mendekati tak terhingga. Sistem LTI dikatakan tidak stabil jika respon natural meningkat tanpa batas jika waktu mendekati tak terhingga. Pada pengendali terdapat empat mode pengendalian, diantaranya adalah :

(44)

a. ON-OFF

Yaitu mode pengendalian yang memanipulasi sinyal error menjadi sinyal yang memiliki perintah on dan sinyal pengendalian yang bernilai off. Respon dari proses akan berosilasi membentuk grafik sinusoidal. Apabila error respon proses setelah dibandingkan dengan set point kurang dari 5% dan 2% maka mode ini dapat digunakan.

b. Proportional

Proportional merupakan mode pengendalian yang digunakan untuk memperkecil amplitudo dari osilasi respon proses. Hubungan antara keluaran pengendali m(t) dan sinyal kesalahan penggerak / error e(t) ditunjukkan pada persamaan 2.45.

𝑚(𝑡) = 𝐾𝑝. 𝑒(𝑡)

(2.45)

Dalam aplikasi-aplikasi dasar yang sederhana pengendalian P ini cukup mampu untuk memperbaiki respon transien khususnya rise time dan settling time.

c. Proportional Integral (PI)

Apabila dinginkan respon proses tidak berosilasi, maka dapat digunakan mode integral (I) karena mode pengendalian ini dapat membuat respon proses menuju ke set point secara eksponensial. Secara matematis mode pengendalian ini dapat dituliskan pada persamaan 2.46.

𝑚(𝑡) = 𝐾𝑝. 𝑒(𝑡) +

1

𝑇𝑖

∫ 𝑒(𝑡)𝑑𝑡

(2.46)

Kp menyatakan konstanta proposional dan Ti menyatakan waktu integral.

d. Proportional Integral Derivative (PID)

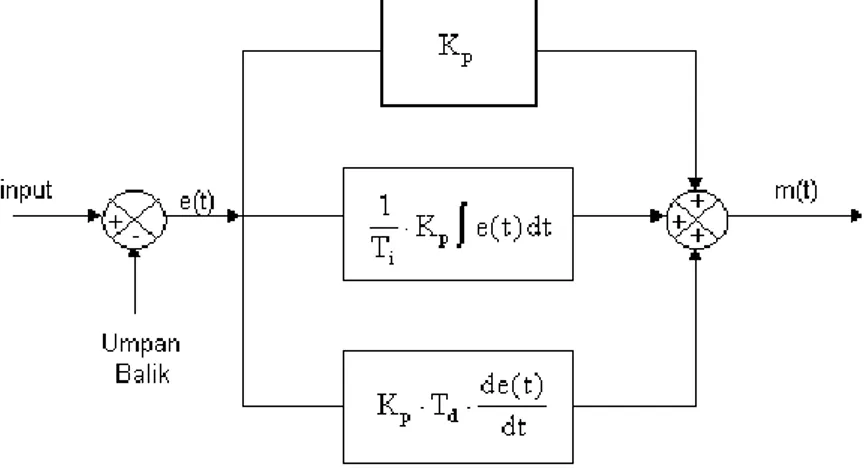
Kendali PID merupakan kombinasi dari 3 pengendali yaitu: Pengendali proporsional, pengendali integral dan pengendali derivatif yang disusun secara paralel sebagaimana ditunjukkan pada Gambar 2.6. Ketiga jenis pengendali ini

(45)

memberikan respon yang berbeda – beda pada proses orde satu, proses orde dua dan proses orde banyak. Pengendali derivatif digunakan untuk mempercepat kemampuan bereaksi, sehingga kekurangan yang ada pada pengendali integral dapat ditutupi. Ketiga mode pengendali proporsional, integral dan derivatif masing – masing berguna untuk mempercepat reaksi sistem, menghilangkan offset dan mendapatkan energi ekstra di saat – saat awal perubahan load. Keluaran dari pengendali PID merupakan penjumlahan dari keluaran pengendali P, pengendali I dan pengendali D yang ditunjukkan pada Gambar 2.6 (Basilio, 2002).

Gambar 2.6 Diagram Blok Pengendalian PID (Basilio, 2002) Pemodelan secara matematis dari pengendalian PID ditunjukkan pada persamaan 2.47.

𝐺𝑐(𝑡) = 𝐾𝑝 [𝑒(𝑡) +

1

𝑇𝑖

∫ 𝑒(𝑡)𝑑𝑡 + 𝑇𝑑

𝑑

𝑑𝑡

𝑒(𝑡)]

(

2.47) Pemodelan pengendalian PID pada persamaan 2.47 memiliki fungsi alih yang ditunjukkan pada persamaan 2.48 dan persamaan 2.49.

(46)

𝑀(𝑠) 𝐸(𝑠)

= 𝐾𝑝 (1 +

1 𝑇𝑖𝑆

+

𝑇𝑑 𝑆

)

(2.48) 𝑀(𝑠) 𝐸(𝑠)

=

𝐾𝑝(1+𝑇𝑖𝑆+𝑇𝑖 𝑇𝑑 𝑆2) 𝑇𝑖𝑆

(

2.49)

Karakteristik pengendali PID sangat dipengaruhi oleh kontribusi besaran dari ketiga parameter P, I dan D. Penyetelan konstanta Kp, Ti dan Td akan mengakibatkan penonjolan sifat dari masing – masing elemen. Satu atau dua dari ketiga konstanta tersebut dapat diatur lebih menonjol dibandingkan dengan yang lain, konstanta yang menonjol itulah yang akan memberikan pengaruh pada respon sistem secara keseluruhan (Basilio, 2002).

Penggunaan mode pengendalian baik P, PI, maupun PID disesuaikan dengan kebutuhan dan karakteristik dari proses yang dikendalikan. Mode pengendalian P digunakan apabila adanya offset masih dapat ditolerir oleh proses. Apabila tidak, maka mode pengendalian PI dapat digunakan untuk memperbaiki performasi sistem dan sedangkan mode pengendalian PID seringkali digunakan pada sistem pengendalian yang memiliki karakteristik pengendalian yang lambat seperti pengendalian temperatur. Performasi yang optimal pada algoritma pengendalian PID pada berbagai perubahan daerah operasi, disturbance dan sesuai dengan kebutuhan proses didapatkan dengan melakukan penalaan terhadap nilai parameter pengendalian PID (Kp, Ti, Td) (Basilio, 2002).

Jika pemodelan matematis sistem susah untuk dilakukan. maka perancangan pengendali PID secara analitis tidak mungkin dilakukan sehingga perancangan pengendali PID harus dilakukan secara eksperimental. Perancangan pengendali PID secara eksperimental dengan metode Ziegler –Nichols diberikan aturan untuk menentukan nilai Kp, τi dan τd yang didasarkan pada

karakteristik respon transien dari sistem (Basilio, 2002). Diagram blok pengendalian PID Ziegler – Nichols ditunjukkan pada Gambar 2.7.

(47)

Gambar 2.7 Diagram Blok Pengendalian PID Ziegler –Nichols (Basilio, 2002)

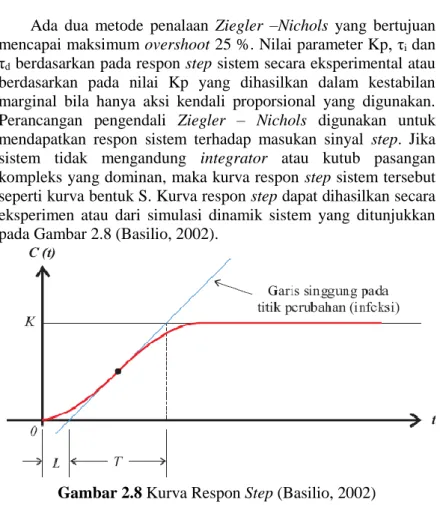
Ada dua metode penalaan Ziegler –Nichols yang bertujuan mencapai maksimum overshoot 25 %. Nilai parameter Kp, τi dan

τd berdasarkan pada respon step sistem secara eksperimental atau

berdasarkan pada nilai Kp yang dihasilkan dalam kestabilan marginal bila hanya aksi kendali proporsional yang digunakan. Perancangan pengendali Ziegler – Nichols digunakan untuk mendapatkan respon sistem terhadap masukan sinyal step. Jika sistem tidak mengandung integrator atau kutub pasangan kompleks yang dominan, maka kurva respon step sistem tersebut seperti kurva bentuk S. Kurva respon step dapat dihasilkan secara eksperimen atau dari simulasi dinamik sistem yang ditunjukkan pada Gambar 2.8 (Basilio, 2002).

Gambar 2.8 Kurva Respon Step (Basilio, 2002) Nilai parameter Kp, τi dan τd diuraikan pada Tabel 2.3.

R(s) + - 𝑲𝑷(𝟏 + 𝟏 𝝉𝒊𝒔 + 𝝉𝒅𝒔) Plant C(s) E(s) U(s)

(48)

Tabel 2.3 Parameter Kp, τi dan τd (Basilio, 2002) Tipe Pengendali Kp τi τd P T/L ∞ 0 PI 0,9 T/L L/0,3 0 PID 1,2 T/L 2L 0,5L

Pengendali PID akan mengantisipasi terjadinya error kedepan dan menerapkan aksi pengendalian yang proporsional terhadap perubahan laju error. Kombinasi dari ketiga mode pengendalian akan memiliki respon yang hampir sama dengan kombinasi pengendalian PI. Kehadiran aksi pengendalian integral akan membuat lambat respon proses. Kecepatan dapat ditingkatkan dengan memperbesar nilai gain Kc akan tetapi Kc yang terlalu besar akan membuat sistem lebih berosilasi dan berakibat terjadinya ketidakstabilan. Peran derivatif yang akan membuat sistem menjadi lebih stabil, sehingga dapat menambah kecepatan respon dengan memperbesar gain Kc yang tepat serta tetap menjaga besarnya overshoot dan rasio penurunan (Basilio, 2002). Fungsi alih pengendali PID ditunjukkan pada persamaan 2.50 dan persamaan 2.51. 𝑢(𝑡) = 𝐾𝑃[𝑒(𝑡) + 1 𝑇_𝑖∫ 𝑒(𝜏)𝑑𝜏 + 𝑇𝑑 𝑑 𝑑𝑡𝑒(𝑡) 𝑡 0 ] (2.50) 𝐾(𝑠) = 𝐾𝑃(1 + 1 𝑇𝑖𝑠+ 𝑇𝑑𝑠) (2.51) 2.7 Standar Maneuverability

Prosedur yang digunakan untuk uji maneuvering mengacu kepada peraturan standar kemampuan maneuvering kapal yang direkomendasikan oleh International Maritime Organization (IMO) yakni resolusi MSC.137 (76) annex.6 tertanggal 4 Desember 2002 dan mulai diterapkan sejak tanggal 1 Januari 2004, resolusi ini merupakan amandemen terhadap resolusi sebelumnya yakni A.751 (18) mengenai standar kemampuan maneuvering kapal (Abdullah, 2016).

(49)

Aturan standar yang dimaksud disini didasarkan atas pengertian bahwa kemampuan maneuvering kapal dapat dievaluasi berdasarkan karakteristik dari pengujian maneuvering seperti biasanya atau secara konvensional, dimana kapal yang dimaksud adalah kapal yang memiliki panjang 100 meter atau lebih dengan menggunakan sistem propulsi dan sistem kemudi (steering) konvensional yakni gaya dorong kapal dihasilkan oleh propeller yang digerakan oleh poros propeller.

IMO telah merekomendasikan beberapa kriteria standar untuk maneuverability kapal. Kriteria tersebut harus dipenuhi oleh sebuah kapal saat beroperasi di perairan yang dalam (deep water) maupun di perairan terbatas atau beroperasi di sekitar pelabuhan atau di perairan yang dangkal (restricted and shallow water). Standar pengujian yang diperlukan dalam manuver kapal disyaratkan dalam IMO Resolusi MSC 137 76 (2002) yang ditunjukkan pada Tabel 2.4 (Abdullah, 2016).

Tabel 2.4 Standar Manuverabilitas Kapal oleh IMO(Resolution MSC 137(76), 2002)

Ability Test Criteria

Turning ability Turning test with max. Rudder angle (35deg.) Advanced< 4,5 L Tactical Diameter< 5,0 L Initial turningability 10O/ 10O Z-test

Distance ship runbefore 2nd rudder execution< 2,5 L Stopping ability Stopping test with full astem Track reach<15 L Course keeping and yaw checking ability 10O/ 10O Z-test 1stOvershoot< 10O (L/U<10s)<(5+0,5(L/U))O (10s<L/U<30s)<20O (30s<L/U) 2ndOvershoot<25O (L/U<10s)<(17,5+0,75(L/U))O (10s<L/U<30s)<40O (30s<L/U)

(50)

2.8 Indeks Stabilitas Yaw

Stabilitas yaw adalah kemampuan untuk bergerak lurus maju tanpa adanya gangguan eksternal (misalnya angin) di salah satu sudut kemudi.

𝐶

′

=

𝑁𝑟 ′_−𝑚′_𝑥 𝑔′ 𝑌_𝑟′−𝑚′

−

𝑁_𝑣′ 𝑌_𝑣′ (2.52)

Nilai C’ positif menunjukkan stabilitas yaw, nilai C’ negatif menunjukkan ketidakstabilan yaw. Ketidakstabilan yaw adalah kecenderungan kapal untuk meningkatkan nilai absolut dari sudut penyimpangan yang ada. Namun, rumus numerik ini sangat sensitif dan koefisien diukur sering tidak akurat untuk memprediksi stabilitas yaw. Hal itu karena stabilitas yaw sangat sensitif terhadap perubahan kecil yang diakibatkan gaya pada badan kapal. Oleh karena itu, biasanya diperlukan analisis yang lebih rumit untuk menentukan stabilitas yaw (Abdullah, 2016). 2.9 Root-Locus

Suatu metode sederhana untuk mencari akar-akar persamaan karakteristik telah ditemukan oleh W.R. Evans sehingga digunakan secara luas dalam teknik pengendalian. Metode ini disebut metode root-locus, merupakan suatu metode dengan menggambar akar-akar persamaan karakteristik untuk semua harga dari suatu parameter sistem. Metode root-locus memungkinkan kita untuk mencari pole-pole loop tertutup dari pole dan zero loop terbuka dengan penguatan parameter. Metode ini menghilangkan kesulitan-kesulitan yang timbul pada teknik klasik dengan memberikan peragaan grafis semua pole loop tertutup untuk semua harga penguatan fungsi transfer loop terbuka.

Suatu sistem yang stabil harus memiliki pole loop tertutup yang seluruhnya terletak disebelah kiri sumbu khayal bidang s. Ringkasan aturan untuk menggambar root-locus dari sebuah sistem adalah sebagai berikut (Kemdikbud, 2010).

(51)

1 + G(s)H(s) = 0

(2.53) Maka

1 +

𝐾(𝑠+𝑧𝑛)

(𝑠+𝑝𝑛)

= 0

(2.54) b. Meletakkan pole-pole (pn) dan zero- zeronya (zn) pada

bidang s.

c. Menentukan interval terdapatnya root-locus pada sumbu nyata. Bila interval daerah sumbu nyata mempunyai jumlah pole dan atau zero di sebelah kanannya bernilai ganjil, maka daerah tersebut terdapat root locus.

d. Menentukan jumlah asimtot, sudut asimtot, dan perpotongan asimtot dengan sumbu nyata.

e. Menentukan titik pencar, temu pole-pole (break away point dan break-in point).

f. Menentukan titik potong kurva root locus dengan sumbu khayal (jika ada).

g. Menentukan sudut datang (untuk zero) dan sudut berangkat (untuk pole).

h. Sketsa root-locus dari data-data yang telah didapatkan. Penggambaran diagram root-locus juga dapat dilakukan dengan komputer menggunakan software MATLAB R2009a (Kemdikbud, 2010). Langkah-langkah yang dilakukan adalah a. Menentukan persamaan karakteristik.

b. Persamaan karakteristik diubah menjadi persamaan karakteristik software MATLAB R2009a.

1 +𝐾(𝑛𝑢𝑚)_{(𝑑𝑒𝑛)} = 0 (2.55) c. Memasukkan code program software MATLAB R2009a

(52)

>> num = [1 zn]

>> den = [1 pn]

(53)

27

BAB III

METODOLOGI PENELITIAN

Langkah-langkah dalam pengerjaan tugas akhir ini ditunjukkan pada diagram alir di bawah ini.

Mulai

Studi Literatur

Pengumpulan Data Spesifikasi Kapal LNG dan Tugboat AHTS

Pemodelan Dinamik Kapal LNG Muatan Penuh dan Tugboat AHTS

Perancangan Sistem Kendali Autotracking Kapal LNG Muatan Penuh Menggunakan Kontrol PID

Simulasi Hasil Perancangan Sistem Kendali Autotracking Kapal LNG Muatan Penuh

Analisis Hasil Simulasi Apakah respon sesuai

standar IMO?

Analisis Hasil Perhitungan Error Lintasan

Analisis Perhitungan Gaya Dorong Tugboat AHTS

Penyusunan Laporan

Selesai Ya

Tidak

(54)

3.1 Studi Literatur

Penyusunan laporan tugas akhir ini diperlukan konsep dan ide awal untuk pelaksanaannya. Studi literatur dimaksudkan untuk membangun pemahaman awal hingga detail mengenai topik tugas akhir. Oleh karena itu, diperlukan studi literatur yang berhubungan erat dengan otomasi sandar kapal dan beberapa referensi dari penelitian sebelumnya. Pendalaman materi juga dilakukan terhadap karakterisasi kapal LNG, kapal Anchor Handling Tug Supply (AHTS), maneuvering kapal, lintasan yang akan dilewati oleh kapal, dan sistem pengendalian otomatis dengan menggunakan pengendalian PID. Teori yang berdasarkan jurnal - jurnal penelitian yang sudah pernah dilakukan dan juga studi teoritis dari handbook dengan tema kendali kapal laut dan arsitektur kelautan. Penelitian ini dilakukan secara simulasi dengan menggunakan software MATLAB R2009a maka diperlukan studi pembelajaran tentang pemrograman yang akan dijalankan.

3.2 Pengumpulan Data

Data yang digunakan pada penelitian ini berupa spesifikasi kapal LNG dan AHTS, meliputi panjang, lebar kapal, ketinggian, displacement, kecepatan, coefficient block, center of gravity, rudder area dan jari-jari. Data-data tersebut digunakan sebagai masukan untuk mendapatkan koefisien hidrodinamika. Koefisien hidronimika inilah yang akan menjadi variabel – variabel penyusun persamaan untuk memodelkan kapal.

3.2.1 Data Spesifikasi Kapal LNG

Berdasarkan Maneuvering Information Booklet (In According With IMO RS.A601 (15)) didapatkan data spesifikasi kapal LNG. Satuan data yang didapatkan harus dikonversikan terlebih dahulu ke dalam bentuk satuan SI (sistem internasional). Data spesifikasi kapal yang dibutuhkan untuk mendapatkan koefisien hidrodinamika ditunjukkan pada Tabel 3.1.

(55)

Tabel 3.1 Tabel Spesifikasi Kapal LNG

Besaran Besaran Data Satuan SI

LPP Panjang 274.4 m 274.4 m U Kecepatan 19.65 knot 10.1088246 m/s B Lebar 43.4 m 43.4 m T Tinggi 26 m 26 m CB koefisien blok 0.7561 0.7561 XG specific grafity 0 0 Aδ luasan rudder 63.41 m2 63.41 m2 M Displacement 118296.4 ton 118296400 kg R jari-jari girasi 0.2 Lpp 54.88 m m’ massa non dimensional 2m / ρ(LPP 3₎ _0,010036948 XG’ spesific grafity non dimensional 0 0 DWT Deadweight 87697 ton 87697000 kg Ρ massa jenis 1014 kg/m3 _{1014 kg/m}3

3.2.2 Data Spesifikasi Tug Boat AHTS

Berdasarkan Maneuvering Information Booklet (In According With IMO RS.A601 (15)) didapatkan data spesifikasi tug boat AHTS. Satuan data yang didapatkan harus dikonversikan terlebih dahulu ke dalam bentuk satuan SI (sistem internasional). Data spesifikasi kapal yang dibutuhkan untuk mendapatkan koefisien hidrodinamika ditunjukkan pada Tabel 3.2.

(56)

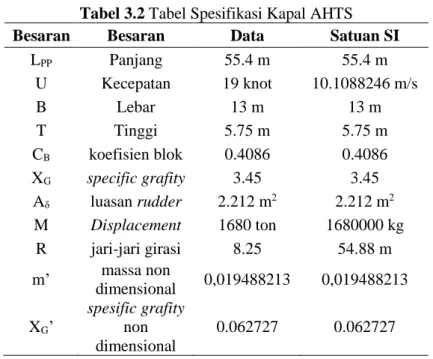
Tabel 3.2 Tabel Spesifikasi Kapal AHTS

Besaran Besaran Data Satuan SI

LPP Panjang 55.4 m 55.4 m U Kecepatan 19 knot 10.1088246 m/s B Lebar 13 m 13 m T Tinggi 5.75 m 5.75 m CB koefisien blok 0.4086 0.4086 XG specific grafity 3.45 3.45 Aδ luasan rudder 2.212 m2 2.212 m2 M Displacement 1680 ton 1680000 kg R jari-jari girasi 8.25 54.88 m m’ massa non dimensional 0,019488213 0,019488213 XG’ spesific grafity non dimensional 0.062727 0.062727

3.2.3 Data Lintasan Kapal LNG Keluar Pelabuhan Arun Lintasan jalur kapal keluar dari Pelabuhan Arun ditunjukkan pada Gambar 3.2. Data jalur pelayaran kapal keluar dari Pelabuhan Arun berupa titik koordinat latitude dan longitude dengan satuan derajat lintang dan bujur yang kemudian dikonversikan menjadi satuan kilometer (km) dengan cara dikalikan dengan 111,32 km (Fossen, 1994). Lintasan tersebut telah ditetapkan oleh pihak pelabuhan dan setiap kapal yang akan meninggalkan pelabuhan harus mengikuti lintasan yang telah ditetapkan. Oleh sebab itu, diperlukan sebuah kapal tug boat yang berfungsi untuk membantu maneuvering kapal LNG agar memenuhi lintasan yang ditetapkan.

(57)

Gambar 3.2 Jalur Keluar Kapal di Pelabuhan Arun Data jalur keluar digunakan sebagai masukan berupa kecepatan sway (v), Kecepatan anguler dalam yaw (r),dan sudut heading (ψ). Data koordinat lintasan kapal LNG keluar Pelabuhan Arun dapat ditunjukkan pada Tabel 3.3.

Tabel 3.3 Koordinat Lintasan Kapal LNG Keluar Pelabuhan Arun No Latitude Longitude 1 5,2192 97,0990 2 5,2192 97,0994 3 5,2192 97,0998 4 5,2191 97,1003 5 5,2191 97,1009 6 5,2191 97,1016 7 5,2190 97,1022 8 5,2190 97,1029 9 5,2191 97,1034 10 5,2193 97,1042 11 5,2198 97,1050 12 5,2203 97,1055 13 5,2210 97,1059 14 5,2218 97,1062 15 5,2225 97,1065

(58)

Tabel 3.3 (Lanjutan) No Latitude Longitude 16 5,2236 97,1069 17 5,2246 97,1073 18 5,2257 97,1078 19 5,2271 97,1085 20 5,2286 97,1092 21 5,2303 97,1101 22 5,2321 97,1109 23 5,2340 97,1117 24 5,2363 97,1126 25 5,2387 97,1134 26 5,2413 97,1143 27 5,2442 97,1153 28 5,2471 97,1163 29 5,2502 97,1172 30 5,2534 97,1182 31 5,2566 97,1191 32 5,2600 97,1200 33 5,2633 97,1210 34 5,2670 97,1222 35 5,2707 97,1234 36 5,2742 97,1246 37 5,2784 97,1264 38 5,2817 97,1283 39 5,2855 97,1305 40 5,2892 97,1326 41 5,2925 97,1345 3.3 Pemodelan Dinamika Kapal

Data spesifikasi kapal yang telah dikonversikan ke dalam bentuk satuan internasional akan digunakan untuk menghitung koefisien hidrodinamika. Koefisien hidrodinamika ini yang menjadi variabel – variabel penyusun persamaan dinamika kapal.

(59)

3.3.1 Pemodelan Kapal LNG Bermuatan Penuh

Berdasarkan teori persamaan maneuvering kapal yang telah dijelaskan pada Bab II, pemodelan dinamika kapal dilakukan berdasarkan data spesifikasi kapal yang telah diperoleh dan diolah dengan menggunakan pendekatan matematis Nomoto orde II (1957). Parameter yang telah diketahui tersebut di substitusukan ke dalam persamaan yang telah ada untuk mendapatkan koefisien hidrodinamika kapal. Nilai – nilai koefisien hidrodinamika kapal LNG bermuatan penuh dapat dilihat pada Tabel 3.4.

Tabel 3.4 Koefisien Hidrodinamika Kapal LNG Bermuatan Penuh Koefisien Hidrodinamika Nilai Koefisien Hidrodinamika Nilai Yvdot' -0,030287 Nvdot' -0,002975 Yrdot' -0,002728 Nrdot' -0,001482 Yv' -0,042422 Nv' -0,020506 Yr' 0,008050 Nr' -0,006386 Ydel' 0,006977 Ndel' -0,003488 Ir' 0,000786 Iz' 0,000786

Nilai-nilai koefisien hidrodinamika pada Tabel 3.4 diperoleh dari persamaan 2.13 sampai persamaan 2.24. Besarnya koefisien hidrodinamika pada Tabel 3.4 disubstitusikan ke dalam persamaan 2.26 sampai persamaan 2.28 dan diperoleh besarnya matriks yang ditunjukkan pada persamaan 3.1 sampai persamaan 3.3.

𝑀′= [0,049952 0,002728_{0,002975 0,002269}] (3. 1)

𝑁′ = [0,042423 −0,00805

0,020506 0,006386] (3. 2)

(60)

Persamaaan 3.1 sampai persamaan 3.3 merupakan persamaan tidak berdimensi sehingga diubah ke persamaan berdimensi menggunakan persamaan Prime-System I dan hasilnya ditunjukkan pada persamaan 3.5 sampai persamaan 3.7.

𝑀 = [0,134133 2,010185_{0,007989 1,672089}] (3. 4) 𝑁 = [0,004197 −0,21853_0,002029 _0,173346] (3. 5) 𝑏 = [_{−0,00348851}0,00697702 ] (3. 6) dimana : M’ = M tidak berdimensi N’ = N tidak berdimensi b’ = b tidak berdimensi M = matriks inersia

N = matriks coriolis dan redaman b = vektor dari rudder

Parameter Nomoto ini yang akan diwujudkan ke dalam model dinamika kapal. Nilai parameter – parameter Nomoto ditunjukkan pada persamaan 3.7 sampai persamaan 3.10.

𝑇1𝑇2 = det (𝑀) det (𝑁)= 177,8504 (3. 7) 𝑇1+ 𝑇2= n₁₁m₂₂+n₂₂m₁₁−n₁₂m₂₁−n₂₁m₁₂ det (𝑁) = 23,8 (3. 8) 𝐾𝑅 = n₂₁b₁−n₁₁b₂ det (𝑁) = 0,0245 (3. 9) 𝐾𝑅𝑇3 = m₂₁b₁−m₁₁b₂ det (𝑁) = 0,4472 (3. 10)

Berdasarkan pendekatan Nomoto, parameter – parameter tersebut digunakan untuk mendapatkan fungsi transfer kapal yang ditunjukkan pada persamaan 3.11.

(61)

𝜓 𝛿𝑅=

0,4472𝑠+0,0245

177,8504s3_+23,86s2_{+ 𝑠} (3. 11) 3.3.2 Pemodelan Dinamika Tugboat AHTS

Berdasarkan teori persamaan maneuvering kapal yang telah dijelaskan pada Bab II, pemodelan dinamika kapal dilakukan berdasarkan data spesifikasi kapal yang telah diperoleh dan diolah dengan menggunakan pendekatan matematis Nomoto orde II (1957). Parameter yang telah diketahui tersebut di substitusukan ke dalam persamaan yang telah ada untuk mendapatkan koefisien hidrodinamika kapal. Nilai – nilai koefisien hidrodinamika kapal LNG bermuatan penuh dapat dilihat pada Tabel 3.5.

Tabel 3.5 Koefisien Hidrodinamika Tugboat AHTS Koefisien Hidrodinamika Nilai Koefisien Hidrodinamika Nilai Yvdot' -0,029326 Nvdot' -0,005595 Yrdot' -0,004747 Nrdot' -0,000730 Yv' -0,046324 Nv' -0,025338 Yr' 0,005568 Nr' -0,006993 Ydel' 0,005451 Ndel' -0,002725 Ir' 0,000432 Iz' 0,000507

Nilai-nilai koefisien hidrodinamika pada Tabel 3.5 diperoleh dari persamaan 2.13 sampai persamaan 2.24. Besarnya koefisien hidrodinamika pada Tabel 3.5 disubstitusikan ke dalam persamaan 2.26 sampai persamaan 2.28 dan diperoleh besarnya matriks yang ditunjukkan pada persamaan 3.12 sampai persamaan 3.14.

𝑀′= [0,048814_{0,006818 0,001238}0,00597] (3. 12)

𝑁′= [0,046325 −0,00557

(62)

𝑏 = [ 0,005451012

−0,002725506] (3. 14)

Persamaaan 3.12 sampai persamaan 3.14 merupakan persamaan tidak berdimensi sehingga diubah ke persamaan berdimensi menggunakan persamaan Prime-System I dan hasilnya ditunjukkan pada persamaan 3.15 sampai persamaan 3.17.

𝑀 = [0,026464 0,179303 0,003696 0,037195] (3. 15) 𝑁 = [0,004583 −0,03052_0,002507 _0,03833 ] (3. 16) 𝑏 = [ 0,005451012 −0,002725506] (3. 17) dimana : M’ = M tidak berdimensi N’ = N tidak berdimensi b’ = b tidak berdimensi M = matriks inersia

N = matriks coriolis dan redaman b = vektor dari rudder

Parameter Nomoto ini yang akan diwujudkan ke dalam model dinamika kapal. Nilai parameter – parameter Nomoto ditunjukkan pada persamaan 3.18 sampai persamaan 3.21.

𝑇1𝑇2 = det (𝑀) det (𝑁)= 1,2753 (3. 18) 𝑇1+ 𝑇2= n11m22+n22m11−n12m21−n21m12 det (𝑁) = 3,3638 (3. 19) 𝐾𝑅 = n₂₁b₁−n₁₁b₂ det (𝑁) = 0,1037 (3. 20) 𝐾𝑅𝑇3 = m21b1−m11b2 det (𝑁) = 0,3659 (3. 21)