Pemodelan matematika pada sistem pembangkit listrik tenaga air.

vii

ABSTRAK

Sistem Pembangkit Listrik Tenaga Air pada bendungan digerakkan oleh suatu

generator. Agar generator dapat digerakkan maka diperlukan tinggi yang sesuai pada

bendungan tersebut.

Dengan mengasumsikan dua bendungan seperti dua sistem bejana, maka

model matematika pada dua sistem bejana tersebut adalah

) ( ) ( 2

) (

2 2 2 2

2 2

t h dt

t dh dt

t h d

n

n ω

ω

ξ +

+ _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ =

2 1

1 A A

K λ

D

h

, dengan

h2(t)

adalah tinggi air pada sistem bejana

yang terletak dibawahnya,

ξ

adalah rasio peredam yang baru,

hD

adalah tinggi air

yang sesuai pada sistem bejana,

ωn

adalah frekwensi alami yang baru, dan

2 1,A

A

adalah luas penampang sistem bejana.

viii

ABSTRACT

Hydroelectric Power Generation System of dam is generated by a generator.

In order to generate a generator, it’s needed a desired demand of the water level of the

dams.

By assuming two dams like two-vessel system, the mathematical model of

two-vessel system is

() 2 2() 2 ₂()

2 2 2

t h dt

t dh dt

t h d

n

n ω

ω

ξ +

+ _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ =

2 1

1 A A

K λ

D

h

, where

h2(t)

denotes the

water level of the lower vessel system,

ξ

denotes the new damping ratio,

hD

denotes

the desired demand of the water level,

ωn

denotes the new natural frequency, and

2 1,A

A

denotes the uniform cross-sectional of the two-vessel system.

i

PEMODELAN MATEMATIKA PADA SISTEM

PEMBANGKIT LISTRIK TENAGA AIR

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh

Julius Sigit Wicaksono

NIM : 993114015

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

ii

MATHEMATICAL MODELLING OF

HYDROELECTRIC POWER GENERATION SYSTEM

Thesis

Presented as Partial Fulfillment of the Requirements

to Obtain the Sarjana Sains Degree

in Mathemathics Study Program

By

Julius Sigit Wicaksono

Student Number : 993114015

STUDY PROGRAM OF MATHEMATHICS

DEPARTMENT OF MATHEMATHICS

FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY

YOGYAKARTA

v

Di Balik Setiap Batu Penghalang

Pasti Ada Hikmat Yang Tersembunyi

Dan Selalu Ada Pelajaran Yang Mematangkan Mental.

Hadapi Dengan Berani Setiap Batu Penghalang

(Wisdom to Success )

vi

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak

memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam

kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, Agustus 2007

Penulis

vii

ABSTRAK

Sistem Pembangkit Listrik Tenaga Air pada bendungan digerakkan oleh suatu

generator. Agar generator dapat digerakkan maka diperlukan tinggi yang sesuai pada

bendungan tersebut.

Dengan mengasumsikan dua bendungan seperti dua sistem bejana, maka

model matematika pada dua sistem bejana tersebut adalah

) ( ) ( 2

) (

2 2 2 2

2 2

t h dt

t dh dt

t h d

n

n ω

ω

ξ +

+ _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ =

2 1

1 A A

K λ

D

h

, dengan

h2(t)

adalah tinggi air pada sistem bejana

yang terletak dibawahnya,

ξ

adalah rasio peredam yang baru,

hD

adalah tinggi air

yang sesuai pada sistem bejana,

ωn

adalah frekwensi alami yang baru, dan

2 1,A

A

adalah luas penampang sistem bejana.

viii

ABSTRACT

Hydroelectric Power Generation System of dam is generated by a generator.

In order to generate a generator, it’s needed a desired demand of the water level of the

dams.

By assuming two dams like two-vessel system, the mathematical model of

two-vessel system is

() 2 2() 2 ₂()

2 2 2

t h dt

t dh dt

t h d

n

n ω

ω

ξ +

+ _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ =

2 1

1 A A

K λ

D

h

, where

h2(t)

denotes the

water level of the lower vessel system,

ξ

denotes the new damping ratio,

hD

denotes

the desired demand of the water level,

ωn

denotes the new natural frequency, and

2 1,A

A

denotes the uniform cross-sectional of the two-vessel system.

ix

KATA PENGANTAR

Dengan telah selesainya penulisan skripsi yang berjudul

“

Pemodelan

Matematika Pada Sistem Pembangkit Listrik Tenaga Air

”

, saya mengucapkapkan

puji dan syukur atas berkat dan rahmat yang Tuhan Yang Maha Esa.

Terutama juga saya mengucapkan terima kasih kepada dosen pembimbing

saya, Lusia Krismiyati Budiasih, S.Si, M.Si, yang dengan sabar dan penuh perhatian

membantu saya dalam penulisan ini.

Selain itu saya juga mengucapkan seluruh dosen dan staf sekretariat Fakultas

Sains Dan Teknologi dalam pelayanan membantu saya selama kuliah di Sanata

Dharma.

Tujuan dari penulisan ini adalah untuk memenuhi salah satu persyaratan

memperoleh gelar sarjana sains program studi matematika Fakultas Sains Dan

Teknologi Universitas Sanata Dharma.

Saya selaku penulis skripsi ini, menyadari masih jauh dari sempurna, oleh

sebab itu saya mengharapkan masukan dari semua pihak untuk lebih sempurnanya

tulisan skripsi ini.

Yogyakarta, Juli 2007

x

DAFTAR ISI

Halaman

HALAMAN JUDUL...

i

HALAMAN JUDUL... ii

HALAMAN PERSETUJUAN...

iii

HALAMAN PENGESAHAN...

iv

HALAMAN PERSEMBAHAN ...

v

PERNYATAAN KEASLIAN KARYA ...

vi

ABSTRAK ...

vii

ABSTRACT... viii

KATA PENGANTAR ...

ix

DAFTAR ISI...

x

DAFTAR TABEL... xiii

DAFTAR GAMBAR ... xv

BAB I PENDAHULUAN ... 1

A.

Latar Belakang ... 1

B.

Rumusan Masalah ... 2

C.

Pembatasan Masalah ... 2

D.

Manfaat Penulisan... 3

E.

Metode Penulisan ... 3

xi

G.

Sistematika Penulisan ... 4

BAB II PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERE

NTIAL DAN DERET BINOMIAL ... 6

A.

Pemodelan Matematika... 6

B.

Persamaan Diferensial... 7

1.

Persamaan Diferensial Orde Satu Terpisahkan... 11

2.

Persamaan Diferensial Linear Orde Satu ... 12

3.

Persamaan Diferensial Linear Orde Dua... 13

4.

Penerapan Persamaan Diferensial Orde Dua ... 21

C.

Deret Binomial Dan Penerapannya... 29

1. Usaha Dan Energi ... 30

2. Fluida ... 31

3. Persamaan Kontinuitas... 33

4. Persamaan Bernoulli ... 34

5.

Teorema Torricelli ... 35

BAB III PEMODELAN MATEMATIKA PADA SISTEM SATU BEJANA .. 39

A.

Sistem Satu Bejana tanpa Aliran Air ... 44

1.

Pengaruh Luas Penampang Pada Ketinggian Air Bejana ... ... 49

2.

Pengaruh Konstanta Torriceli Pada Ketinggian Air Bejana ... 50

B.

Sistem Satu Bejana dengan Aliran Air ... 51

1. Pengaruh Aliran Air Masuk Pada Ketinggian Air Bejana ... 58

xii

3.

Pengaruh Konstanta Torriceli Pada Ketinggian Air Bejana ... 60

BAB IV PEMODELAN MATEMATIKA PADA SISTEM DUA BEJANA .... 67

A.

Sistem Dua Bejana tanpa Aliran Air Masuk Pada Sistem Bejana di

Atasnya... 68

B.

Sistem Dua Bejana dengan Aliran Air Masuk Pada Sistem Bejana di

Atasnya... 79

C.

Sistem Dua Bejana dengan Aliran Air Disesuaikan ... 99

BAB V PENUTUP... 109

A.

Kesimpulan ... 109

B.

Saran... 110

xiii

DAFTAR TABEL

Tabel 2.3.1 Tabel Diferensial Metode Tak Tentu ... 20

Tabel 3.1.1 Berkurangnya Tinggi Air Untuk Aliran Air yang Masuk Sema

kin Besar ...

46

Tabel 3.1.2 Berkurangnya Tinggi Air Untuk Luas Penampang Semakin

Besar...

47

Tabel 3.1.3 Tinggi Air Untuk Luas Penampang Semakin Besar ... 49

Tabel 3.1.4 Tinggi Air Untuk Luas

( )

λ

Semakin Besar... 50

Tabel 3.2.1 Berkurangnya Tinggi Air Untuk

(q₁−q₀)

Semakin Besar...

53

Tabel 3.2.2 Berkurangnya Tinggi Air Untuk Luas Penampang Semakin

Besar...

54

Tabel 3.2.3 Bertambahnya Tinggi Air Untuk

(q₁−q₀)

Semakin Besar....

55

Tabel 3.2.4 Bertambahnya Tinggi Air Untuk Luas Penampang Semakin

Besar...

55

Tabel 3.2.5 Tinggi Air Bejana dengan Aliran Air ... 57

Tabel 3.2.6 Tinggi Air Untuk

( )

q₁

Semakin Besar... 59

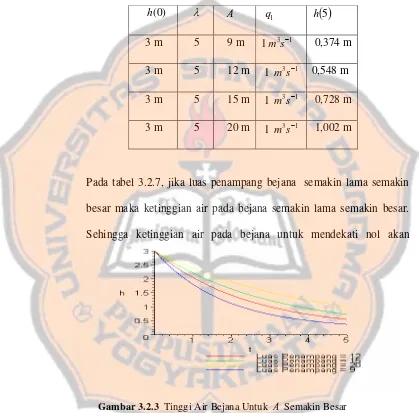
Tabel 3.2.7 Tinggi Air Untuk Luas Penampang Semakin Besar Semakin

Besar...

60

xiv

Untuk Kasus Diredam Berlebihan ... 73

Tabel 4.1.2 Tinggi Air Pada Dua Sistem Bejana tanpa Aliran Air

Untuk Kasus Diredam Kritis...

75

Tabel 4.1.3 Tinggi Air Pada Dua Sistem Bejana tanpa Aliran Air

Untuk Kasus Diredam Berkurang ... 78

Tabel 4.2.1 Tinggi Air Pada Dua Sistem Bejana dengan Aliran Air

Untuk Kasus Diredam Berlebihan ... 82

Tabel 4.2.2 Tinggi Air Pada Dua Sistem Bejana dengan Aliran Air

Untuk Kasus Diredam Kritis...

85

Tabel 4.2.3 Tinggi Air Pada Dua Sistem Bejana dengan Aliran Air

Untuk Kasus Diredam Berkurang ... 87

xv

DAFTAR GAMBAR

Gambar 2.3.4.1 Jarak Pegas Untuk Kasus Getaran Teredam ... 27

Gambar 2.3.4.2 Jarak Pegas Untuk Kasus Getaran Tak Teredam ...

29

Gambar 2.3.2.1 Tekanan Hidrostatis di Titik A, B adalah sama ...

33

Gambar 2.3.3.1 Fluida yang Mengalir Pada Luas Penampang ...

33

Gambar 2.3.5.1 Fluida yang Mengalir Pada Luas Penampang ...

35

Gambar 3.1 Fungsi Konstan...

40

Gambar 3.2 Fungsi Kecepatan ...

41

Gambar 3.3 Fungsi Percepatan ...

41

Gambar 3.4 Sistem Bendungan... 42

Gambar 3.5 Bejana tanpa Aliran Air yang Masuk...

43

Gambar 3.6 Bejana dengan Aliran Air yang Masuk ...

44

Gambar 3.1.1 Tinggi Air Bejana tanpa Aliran Air...

48

Gambar 3.1.2 Tinggi Air Untuk Luas Penampang Semakin Besar... 50

Gambar 3.1.3 Tinggi Air Bejana Untuk Kontanta Torricelli Semakin

Besar...

51

Gambar 3.2.1 Tinggi Air Bejana dengan Aliran Air...

57

Gambar 3.2.2 Tinggi Air Bejana Untuk Aliran Air yang Keluar Sema

kin Besar ...

59

Gambar 3.2.3 Tinggi Air Untuk Luas Penampang Semakin Besar ...

60

xvi

Gambar 3.2.5 Aliran Air yang Disesuaikan Pada Sistem Bejana ...

62

Gambar 4.1 Dua Bejana tanpa Aliran Air yang Masuk ...

67

Gambar 4.2 Dua Bejana dengan Aliran air yang Masuk ...

67

Gambar 4.1.1 Tinggi Air Pada Dua Sistem Bejana tanpa Aliran Air

Untuk Kasus Diredam Berlebihan ...

74

Gambar 4.1.2 Tinggi Air Pada Dua Sistem Bejana tanpa Aliran Air

Untuk Kasus Diredam Kritis...

76

Gambar 4.1.3 Tinggi Air Pada Dua Sistem Bejana tanpa Aliran Air

Untuk Kasus Diredam Berkurang ...

78

Gambar 4.2.1 Tinggi Air Pada Dua Sistem Bejana dengan Aliran Air

Untuk Kasus Diredam Berlebihan ...

83

Gambar 4.2.2 Tinggi Air Pada Dua Sistem Bejana dengan Aliran Air

Untuk Kasus Diredam Kritis ...

85

Gambar 4.2.3 Tinggi Air Pada Dua Sistem Bejana dengan Aliran Air

Untuk Kasus Diredam Kritis...

88

Gambar 4.2.4 Rasio Peredam

0<ξ<1

...

89

Gambar 4.2.5 Rasio Peredam

0,1<ξ<0,5

...

89

Gambar 4.2.6 Rasio Peredam

0,6<ξ<0,9

...

89

Gambar 4.2.7 Rasio Peredam

ξ>1

...

90

Gambar 4.2.8 Rasio Peredam

ξ=1

...

90

xvii

BAB I

PENDAHULUAN

A.

Latar Belakang Masalah

Bendungan mempunyai manfaat yang sangat berguna dalam kehidupan ini,

salah satu manfaat dari bendungan adalah untuk pembangkit tenaga listrik.

Faktor yang mempengaruhi besar atau kecilnya aliran air pada bendungan

adalah curah hujan dan besarnya aliran air sungai. Jika curah hujan tinggi dan aliran

air sungai besar, maka air pada bendungan akan besar, dan jika curah hujan rendah

dan aliran air sungai kecil, maka air pada bendungan akan kecil.

Pada umumnya bendungan yang digunakan untuk pembangkit listrik itu

terdiri dari satu bendungan, atau dua bendungan, dimana bendungan yang satu

terletak di atas bendungan yang lain.

Agar dapat menggerakkan generator pada satu bendungan, diperlukan tinggi

yang sesuai pada bendungan, sedangkan pada dua bendungan diperlukan tinggi yang

sesuai pada bendungan yang terletak di atasnya.

Dari sini muncul permasalahannya yakni bagaimana memperoleh ketinggian

yang sesuai pada satu bendungan dan dua bendungan tersebut.

B. Rumusan

Masalah

1.

Bagaimana model matematika untuk tinggi dan volume air pada

sistem satu bejana ?

2.

Bagaimana model matematika untuk tinggi dan volume air pada

sistem dua bejana ?

3.

Bagaimana model matematika agar diperoleh tinggi air yang sesuai

pada sistem satu dan dua bejana ?

C. Pembatasan

Masalah

Pembatasan masalah pada skripsi ini adalah:

1.

Bendungan yang dibahas hanya bendungan yang digunakan untuk

Pembangkit Listrik Tenaga Air.

2.

Analisa lebih dalam mengenai ketinggian air pada sistem bejana hanya

terbatas pada sistem dua bejana.

3.

Sistem yang menyerupai sistem dua bejana seperti pegas hanya

dibahas seperlunya yaitu sistem satu pegas dengan input dianggap

konstan.

5.

Sensor yang digunakan hanya terbatas untuk ketinggian air pada

bejana.

D. Manfaat

Penulisan

Manfaat yang diharapkan pada skripsi ini adalah untuk mengetahui bagaimana

tinggi air yang sesuai pada sistem bejana yang terletak di bawahnya agar dapat

membangkitkan tenaga listrik.

E.

Metode Penulisan

Metode penulisan yang digunakan dalam makalah ini adalah metode studi

pustaka yaitu mempelajari buku-buku yang berkaitan Pemodelan Matematika Pada

Sistem Pembangkit Listrik Tenaga Air.

F.

Tujuan Penulisan

G.

Sistematika Penulisan

BAB I PENDAHULUAN

A.

Latar Belakang

B.

Rumusan Masalah

C.

Pembatasan Masalah

D.

Manfaat Penulisan

E.

Metode Penulisan

F.

Tujuan Penulisan

G.

Sistematika Penulisan

BAB II PEMODELAN MATEMATIKA DENGAN PERSAMAAN

DIFERENTIAL DAN DERET BINOMIAL

A.

Pemodelan Matematika

B.

Persamaan Diferensial

2.

Persamaan Diferensial Orde Satu Terpisahkan

3.

Persamaan Diferensial Linear Orde Satu

4.

Persamaan Diferensial Linear Orde Dua

5.

Penerapan Persamaan Diferensial Orde Dua

C.

Deret Binomial Dan Penerapannya

1.

Usaha Dan Energi

2.

Fluida

4.

Persamaan Bernoulli

5.

Teorema Torricelli

BAB III PEMODELAN MATEMATIKA PADA SISTEM SATU BEJA

NA

A.

Sistem Satu Bejana tanpa Aliran Air

1.

Pengaruh Luas Penampang Pada Ketinggian Air Bejana

2.

Pengaruh Konstanta Torriceli Pada Ketinggian Air Bejana

B.

Sistem Satu Bejana dengan Aliran Air

1.

Pengaruh Aliran Air Masuk Pada Ketinggian Air Bejana

2.

Pengaruh Luas Penampang Pada Ketinggian Air Bejana

3.

Pengaruh Konstanta Torriceli Pada Ketinggian Air Bejana

BAB IV PEMODELAN MATEMATIKA PADA SISTEM DUA BEJA

NA

A.

Sistem Dua Bejana tanpa Aliran Air Masuk Pada Sistem Bejana di

Atasnya

B.

Sistem Dua Bejana dengan Aliran Air Masuk Pada Sistem Bejana

di Atasnya

C.

Sistem Dua Bejana dengan Aliran Air Disesuaikan

BAB V PENUTUP

BAB II

PEMODELAN MATEMATIKA DENGAN

PERSAMAAN DIFERENSIAL DAN DERET BINOMIAL

A. Pemodelan Matematika

Model adalah gambaran suatu objek yang disusun berdasarkan tujuan

tertentu, dan objeknya dapat berupa suatu sistem, suatu perilaku sistem, ataupun

suatu proses tertentu.

Sistem adalah suatu himpunan beserta relasi antara unsur-unsurnya yang

disusun berdasarkan tujuan tertentu. Misalnya rumah sakit, yang merupakan suatu

sistem yang bertujuan untuk merawat orang sakit, den bagian dari rumah sakit

tersebut harus mendukung tujuan merawat orang sakit.

Tujuan penyusunan model dibedakan tiga kategori yaitu :

a) Guna mengenali keadaan, sifat, atau perilaku sistem dengan cara

mencari keterkaitan antara unsur-unsurnya. Model seperti ini adalah

model keterkaitan.

b) Guna mengadakan pendugaan (prediksi) untuk memperbaiki keadaan

objek, yang disebut model pendugaan.

c) Guna mengadakan optimisasi bagi objek. Modelnya disebut model

optimisasi.

Manfaat model adalah untuk memperoleh gambaran yang lebih jelas

mengenai suatu objek tanpa merusak ataupun mengganggu objek yang aslinya,

dilihat jika dilakukan eksperimen langsung ke objeknya , maka mempunyai resiko

yang sangat merugikan.

Langkah–langkah Penyusunan Model Matematika

a) Identifikasi Masalah.

Sebelum menyusun model matematika adalah mengidentifikasi

masalahnya terlebih dahulu, yang mempunyai batasan-batasan tertentu

yang dikenal dengan penyederhanaan masalah..

b) Perumusan Masalah.

Model tersebut dirumuskan dengan simbol atau lambang yang dapat

dalam matematika baik peubahnya maupun relasi-relasinya.

c) Selesaikan Masalah.

Menyelesaikan perumusan masalah secara matematika.

d) Menafsirkan Masalah.

Model harus ditafsir lagi yakni apakah model tersebut sudah sesuai

dengan yang diharapkan atau tidak ? apakah model tersebut sudah baik

atau tidak? Jikalau tidak, kembali ke langkah semula, sehingga

diperoleh model yang sesuai atau baik seperti yang diinginkan.

e) Pelaksanaan Model.

Model dapat digunakan untuk memperoleh atau mencapai tujuan

semula.

B. Persamaan Diferensial

nya ditulis dalam bentuk

F(x,y,y',y'',...,y(n))=0

dimana (n)

y , menyatakan turunan y terhadap x yang sebanyak n kali, dan F

adalah suatu fungsi dengan peubah–peubah _{, ,} '_, ''_,..., (n)

y y y y

x .

Orde Persamaan Diferensial adalah orde derivatif tertinggi yang muncul

dalam persamaan.

Contoh 2.2.1

Bentuk persamaan diferensial orde satu adalah F(x,y,y')=0.

Persamaan Diferensial Biasa Orde n disebut linear dalam y jika

persamaan diferensial tersebut dapat ditulis dalam bentuk

a_n(x)y(n) +a_n−1(x)y(n−1) +...+a₁(x)y1+a₀(x)y= f(x)

Dengana₀,a₁,...,a_ndan f adalah fungsi yang kontinu pada suatu interval

x dan a_n(x)≠0 pada interval tersebut.

.

Contoh 2.2.2

Persamaan y''+y'+y=x2 adalah persamaan diferensial orde dua yang linear.

Untuk membuktikan suatu fungsi merupakan suatu penyelesaian

sebanyak n kali merupakan persamaan diferensial itu sendiri atau ruas kanan dan

ruas kiri dari persamaan diferensial tersebut adalah sama.

Contoh 2.2.3

Buktikan bahwa x2 +y2 =9 adalah penyelesaian persamaan diferensial

0

' =

+yy

x ?

Penyelesaian

Jika 9x2 +y2 = diturunkan terhadap x, maka diperoleh2x+2yy' =0.

0 2

2x+ yy' = dapat ditulis menjadi x+ yy' =0. Sehingga terbukti bahwa

9

2

2_{+ =}

y

x adalah penyelesaian dari persamaan diferensial x+ yy' =0.

Definisi 2.2.1

a) Suatu keluarga berparameter n dari penyelesaian persamaan diferensial

orde n disebut penyelesaian umum dari persamaan diferensial jika semua

penyelesaian persamaan diferensial dapat diperoleh dari keluarga

berparameter n.

b) Suatu penyelesaian persamaan diferensial orde n yang diperoleh dari

penyelesaian umum dengan menentukan nilai parameter n disebut dengan

penyelesaian khusus.

Contoh 2.2.4

sial y''+3y'+2y=2x−3. Untuk mendapatkan penyelesaian khusus dari

persamaan dferensial tersebut dapat dicari dengan cara memilih nilai konstanta

1

C dan C₂, yaitu dengan mengambil C₁ =10 dan C₂ =3, maka

x e e

y=10 x +3 2x +

Masalah nilai awal terdiri dari pencarian penyelesaian y dari persamaan

diferensial yang juga memenuhi persyaratan

y

( )

x₀ = y₀ y'

( )

x₀ = y₀'

Masalah nilai batas terdiri dari pencarian penyelesaian y dari persamaan

diferensial yang juga memenuhi persyaratan

y

( )

x₀ = y₀ y'

( )

x₁ = y₀'

Contoh 2.2.5

Jika persamaan diferensial y''+3y'+2y=2x−3 dengan menggunakan masalah

nilai awal di atas dan masalah nilai batas dari persamaan y''+3y'+2y=2x−3

mempunyai penyelesaian khusus yaitu y(0)=0 dan y(1)=0. Untuk

0 ,

0 =

= y

x , maka C₁+C₂ =0, dan untuk x=1,y=0 maka C₁e+C₂e2 =−1.

Sehingga diperoleh

e e C C

− = −

= 2 ₂

1

1 .

Maka penyelesaian khususnya adalah

e e x y

− +

1. Persamaan Diferensial Orde Satu Terpisahkan

Persamaan diferensial terpisahkan dari persamaan diferensial orde

satu adalah suatu persamaan diferensial orde satu dimana bentuk

dx

dy dapat difaktorkan sebagai fungsi x kali fungsi y. Dengan

perkataan lain bahwa persamaan diferensial orde satu tersebut

dapat ditulis dalam bentuk

g(x)h(y)

dx dy ₌

(2.2.1.1)

Untuk mencari penyelesaian persamaan diferensial orde tersebut,

haruslah dipisahkan sebagai antara fungsi x dan fungsi y secara

terpisah, sehingga persamaan (2.2.1.1) dapat ditulis sebagai

g x dx y

h dy

) ( )

( = (2.2.1.2)

Dengan mengintegralkan kedua ruas diperoleh

g x dx C

y h

dy _{= +}

∫

∫

( )

)

( (2.2.1.3)

Persamaan (2.2.1.3) adalah penyelesaian persamaan diferensial

orde satu yang dapat dipisahkan. Dengan menggunakan teknik

pengintergralan maka persamaan (2.2.1.3) ini dapat diselesaikan

asalkan fungsi dari g(x),h(y) diketahui.

Contoh 2.2.1

Selesaikan

y x dx dy ₌

Penyelesaian

Persamaan di atas dapat ditulis dalam bentuk persamaan diferensial

dan mengintegralkan kedua ruas , maka diperoleh

y dy= x dx

y2 = x2 +C

2 1 2 1

y=± x2 +C₁ , C ₂1C

1 =

2. Persamaan Diferensial Linear Orde Satu

Persamaan diferensial linear orde satu adalah persamaan yang

dapat ditulis dalam bentuk

P(x)y Q(x)

dx

dy_{+ =}

(2.2.2.1)

Dengan P dan Q adalah fungsi yang kontinu pada selang yang

diberikan. Untuk mencari penyelesaian persamaan diferensial

linear orde satu tersebut kedua ruas dikalikan I(x) yang sering

disebut sebagai faktor pengintergralan.

I(x)=e∫P(x)dx (2.2.2.2)

Bentuk umum penyelesaian dari persamaan diferensial linear orde

satu yang linear, yaitu

∫

⎟

⎠ ⎞ ⎜

⎝

⎛ ∫ ₊

∫

=e− Q x e C

y P(x)dx ( ) P(x)dx (2.2.2.3)

Persamaan (2.2.2.3) adalah bentuk umum penyelesaian persamaan

diselesaikan dengan teknik pengintergralan asalkan fungsi dari

) ( ),

(x Q x

P diketahui.

Contoh 2.2.2.1

Selesaikan 1 y 3x?

x dx

dy_{+ =}

Penyelesaian

Faktor pengintegralan

x x

I( )= 1, sehingga

I x =e∫xdx =elnx = x

1

) (

Dikalikan kedua ruas dengan x, maka

y 3x2 dx

dy

x + =

( )

₃ 2

x xy dx

d ₌

Dengan mengintegralkan kedua ruas diperoleh

y=x2+x−1C

Sehingga penyelesaian y x x dx dy

3

1 ₌

+ adalah

y= x2 +x−1C.

3. Persamaan Diferensial Linear Orde Dua

Persamaan Diferensial Linear Orde Dua adalah persamaan yang

( ) ( ) ( )

2

x R y x Q dx dy x P dx

y d

= +

+ (2.2.3.1)

atau

y''+P(x)y'+Q(x)y=R(x) (2.2.3.2)

dimana P(x),Q(x),R(x) adalah suatu fungsi

) (x

R terbagi atas dua yaitu R(x)=0 dan R(x)≠0, seperti yang

diuraikan berikut ini.

Persamaan diferensial linear orde dua yang homogen adalah

persamaan yang dapat ditulis dalam bentuk

( ) ( ) ( ) 0

2

= = +

+ Q x y R x

dx dy x P dx

y d

(2.2.3.3)

Persamaan diferensial linear orde dua yang nonhomogen adalah

persamaan yang dapat ditulis dalam bentuk

( ) ( ) ( ) 0

2

≠ = +

+ Q x y R x

dx dy x P dx

y d

(2.2.3.4)

Di dalam penerapan fungsi R(x) sering disebut sebagai input

(masukan). Jika R(x)=0berarti tidak ada input dan R(x)≠0

berarti ada input.

Contoh 2.2.3.1

x y x y x

xy''+ 2 '+2 3 =4 adalah persamaan diferensial linear orde dua,

4 ) (x =

R , maka persamaan tersebut adalah persamaan diferensial

yang nonhomogen.

Teorema 2.2.3.1

Jika diketahui persamaan nonhomogen y''+P(x)y'+Q(x)y= R(x)

dengan P(x),Q(x),R(x)adalah fungsi yang kontinu pada interval

] ,

[a b . Jika x₀adalah sembarang titik pada interval [a,b] , dan jika

0

0,y'

y adalah sembarang bilangan , maka persamaan homogen

mempunyai penyelesaian tunggal y(x)pada interval [a,b]

sedemikian hingga y(x₀)= y₀ dan y'(x₀)= y'₀.

Untuk membuktikan teorema ini sangatlah sukar, akan tetapi

pembuktian ini banyak dijumpai dalam buku yang lebih lanjut,

salah satunya diferential equation karangannya Shepley Ross dibab

10, yang dibuktikan dengan teorema lipschit. Didalam teorema ini

menjamin keberadaan dan keunikan suatu solusi masalah nilai

awal.

Contoh 2.2.3.2

Carilah solusi dari y''+y=0 y(0)=0 dan y'(0)=1?

Penyelesaian

Solusi dari y''+y=0 adalah y=sinx , y=cosx dan

1

c

Dari ketiga penyelesaian tersebut hanya y=sinx yang memenuhi

0 ) 0

( =

y dan y'(0)=1. Sehingga menurut teorema 1 ,

penyelesaian dari y''+y=0, jika diketahui y(0)=0 dan

1 ) 0 (

' =

y adalah y=sinx

Teorema 2.2.3.2

Jika y_g adalah penyelesaian umum yang diperoleh dari persamaan

homogen, dan y_p penyelesaian khusus yang diperoleh dari

persamaan nonhomogen, maka y_g + y_p adalah penyelesaian

umum persamaan nonhomogen yang diperoleh dari persamaan

yang homogen.

Bukti

Misalkan y adalah penyelesaian umum persamaan diferensial orde

dua yang homogen, maka y''+P(x)y'+Q(x)y=R(x) . Diketahui

bahwa y_g adalah penyelesaian umum yang diperoleh dari

persamaan diferensial orde dua yang homogen, sehingga

0 ) ( ' ) (

''+ _g + _g =

g P x y Q x y

y dan y_p penyelesaian khusus yang

diperoleh dari persamaan diferensial orde dua yang nonhomogen,

sehingga )y_p ''+P(x)y_p'+Q(x)y_p =R(x .

Akan dibuktikan y = y_g + y_p, yaitu akan dibuktikan bahwa ruas

y =(y_g +y_p)''+P(x)(y_g + y_p)'+Q(x)(y_g + y_p)

=(y_g ''+P(x)y_g'+Q(x)y_g)+(y_p ''+P(x)y_p'+Q(x)y_p)

=0+R(x)=R(x).

Teorema 2.2.3.3

Jika y₁(x) dan y₂(x)adalah penyelesaian dari persamaan yang

homogen, maka c₁ y₁(x)+c₂ y₂(x) juga merupakan penyelesaian

persamaan yang homogen untuk sembarang konstanta c₁dan c₂.

Bukti

) (

1 x

y dan y₂(x)adalah penyelesaian dari persamaan yang

homogen , maka y₁ ''+P(x)y₁'+Q(x)y₁ =0 dan

0 ) ( ' ) (

'' _{2 2}

2 +P x y +Q x y =

y .

Akan dibuktikan bahwa c₁ y₁(x)+c₂ y₂(x) juga merupakan

penyelesaian persamaan yang homogen , maka

(c₁y₁+c₂y₂)''+P(x)(c₁y₁+c₂y₂)'+Q(x)(c₁y₁+c₂y₂)=0

c₁y₁ ''+c₂y₂ ''+P(x)c₁y₁'+P(x)c₂y₂'+Q(x)c₁y₁+Q(x)c₂y₂ =0

c₁(y₁ ''+P(x)y₁'+Q(x)y₁)+ c₂(y₂ ''+P(x)y₂'+Q(x)y₂)=0

Persamaan c₁ y₁(x)+c2 y2(x) pada teorema 2.2.3.3 disebut

sebagai kombinasi linear dari persamaan y₁(x) dan y₂(x).

Sehingga teorema 2.2.3.3 menyatakan setiap kombinasi linear dari

penyelesaian y₁(x) dan y₂(x) pada persamaan yang homogen

juga merupakan penyelesaian.

Persamaan diferensial linear orde dua yang homogen yaitu

y''+P(x)y'+Q(x)y=0

misalkan )P(x),Q(x adalah p,q

maka

y''+py'+qy=0

Persamaan karakteristiknya adalah _y=_emx _{maka y'}=_memx_{, dan}

mx e m

y'' = 2 , sehingga

(m2+ pm+q)emx =0

Karena emx ≠0, maka (m2+ pm+q)=0. Dengan rumus kuadrat

diperoleh

2 4 ,

2

2 1

q p p m

m = − ± −

dimana

2 4

2

1

q p p

m = − + − dan

2 4

2

2

q p p

m = − − −

a) Akar-akar persamaan karakteristiknya m₁,m₂ real dan

berbeda

(

p2−4q>0

)

. Penyelesaian umum dari persamaan

diferensial yang homogen adalah y=c₁em1x m x

e

c 2

2

+ .

b) Akar-akar persamaan karakteristiknya m₁,m₂ real yang

berulang

(

p2−4q=0

)

. Penyelesaian umum dari persamaan

diferensial yang homogen ini adalah y=c₁em1x m x

xe

c 2

2

+ .

c) Akar–akar persamaan karakteristiknya m₁,m₂ bilangan

komplek

(

p2−4q<0

)

.. Sehingga

= − ± − − = 2 ) 4 ( , 2 2 1 q p p m m 2 ) 1 )( 4

( 2− −

±

− p p q

1 2 ) 4 ( 2 − − ± −

= p p q

= − p± p − q i=

2 ) 4 ( 2 β α i i q p P ± = − ± − = 2 ) 4 ( 2 2 maka

m₁ =α+iβ dan m₂ =α−iβ

dimana

2

P

− =

α dan

2 4

2

q p

p− −

− =

β .

Sehingga penyelesaian umumnya adalah

y=c₁em1xcosβ x

x e

c m2xsinβ

2

Untuk dapat menyelesaikan persamaan diferensial linear orde dua

yang non homogen, langkah pertama yang harus dilakukan adalah

dengan mencari penyelesaian persamaan diferensial linear orde dua

yang homogen yaitu y''+P(x)y'+Q(x)y=0.

Setelah mendapatkan penyelesaian umum tersebut, karena menurut

teorema diatas bahwa penyelesaian persamaan diferensial linear

orde dua yang nonhomogen terdiri dar I penjumlahan penyelesaian

umum dan penyelesaian khusus (y = y_g + y_p) , sehingga harus

dicari penyelesaian khusus yang sesuai.

Perhatikan ruas kanan dari persamaan y''+P(x)y'+Q(x)y= R(x),

dimana )R(x dapat berupa beberapa fungsi yaitu eksponensial,

logaritma, trigonometri, dan lain-lain, yang kadang juga

mengalami pegolahan secara aljabar, baik perkalian, penambahan,

pengurangan, pembagian dari beberapa fungsi tersebut.

Berikut ini adalah tabel yang dapat digunakan untuk penyelesaian

khusus (y_p) berdasarkan bentuk R(x).

Tabel 2.3.1 Tabel Diferensial Metode Koefisien Tak Tentu.

R(x) y_p

1 n

n t ct

P ()=

(

n=0,1,2,...

)

0 1

1 ...

)

(t C t C t Ct C

P_n = _n n+ _n− + n− + + +

2 c1sinα x x c2cosα

x C

x

3 x

ceα Ceαx

4 Pn(t)

x

ceα Pn(t)

x

Ceα

=

5 Pn(t)=

x

c₁sin

α

) (t Q_n

x c₂cosα

=

) (t

Pn C1sinα x+C2cosα x

) (t Q_n

Contoh 2.3.3

Selesaikan y''−2y'=exsinx?

Penyelesaian.

Penyelesaian umumnya adalah

x

g x c c e

y 2

2 1

)

( = + .

Penyelesaian khusus (y_p) .

y ex x

p 2 sin

1

−

= .

Jadi penyelesaian dari y''−2y'=exsinxadalah

y_g(x)+y_p(x)= c c e2x ₂1exsinx

2

1+ −

4. Penerapan Persamaan Diferensial Orde Dua

Setiap gerak yang berulang dalam waktu yang sama disebut dengan

gerak periodik. Dan setiap partikel yang bergerak secara periodik

Jika suatu partikel dalam gerak periodik bergerak bolak-balik

melalui lintasan yang sama, maka geraknya disebut dengan gerak

osilasi atau getaran.

Karena suatu partikel yang bergerak osilasi mengalami gesekan,

maka gerakan suatu partikel tersebut akan berhenti berosilasi,

dimana gerakannya disebut dengan gerakan teredam.

Salah satu partikel yang mengalami gerak osilasi dan teredam

antara lain adalah pegas, seperti yang akan dijelaskan berikut ini.

1) Getaran Tak Teredam Dan Teredam

Pada pegas terdapat dua getaran yang terjadi yakni getaran

teredam dan getaran tak teredam, seperti yang akan

diuraikan di bawah ini

Pegas menggunakan hukum hooke yakni jika pegas

demikian ditarik (diperpanjang) sejauh x, gaya pemulih

yang dilakukan pegas (juga disebut gaya pegas) adalah

F =−kx (2.2.4.1)

dimana

k: konstanta pegas (tetapan pegas) yang diukur dalam

satuan Newton meter

( )

Nm yang harganya bernilai positif

bila ditarik dan negatif bila ditekan.

Frekuensi alami pada pegas bila tidak terjadi gesekan dapat

m k v=

=2π.

ω (2 2.4.2)

Frekuensi alami yang mengalami gesekan pada pegas

dapat dirumuskan sebagai berikut

2 2 . 2 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = = m b m k v π

ω bila

m b m

k

2

> (2.2.4.3)

atau i m b m k v 2 2 . 2 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − = = π

ω bila

m b m k

2

< (2.2.4.4)

dengan

k: konstanta pegas (Newton meter).

m: massa pegas (kilogram).

b: gaya gesek pegas (Newton ).

Percepatan yang dialami massa pada pegas yang bergetar

diperoleh dari hukum Newton II, yaitu

m F

a= (2.2.4.5)

dengan m: massa pegas (kilogram)

F: gaya pegas (Newton ).

Diandaikan bahwa gaya gesekan yang terjadi pada pegas

(gaya peredam) sebanding dengan kecepatan massa dan

bekerja dalam arah berlawanan dengan arah gerak dengan

gaya gesekan lainnya diabaikan seperti yang diilustrasikan

Gambar 2.2.4.1 Pegas

Sehingga gaya peredamnya adalah

F =−cv (2.2.4.6)

dimana

c: konstanta positif, yang disebut dengan konstanta

peredam

Dari persamaan (2.2.4.5) dan (2.2.4.6), diperoleh

m F a =

dt dx c kx dt

x d

m ₂ =− −

2

.

₂ 0

2

= +

+ kx

dt dx c dt

x d

m (2.2.4.7)

Persamaan (2.2.4.7) merupakan persamaan diferensial

linear orde dua linear yang homogen, hal ini disebabkan

gaya gesekan yang lain diabaikan yang mempunyai

penyelesaian akar-akar penyelesaian sebagai berikut

m mk c

m c x

2 4

2

2 , 1

− ± −

=

c

k

⎟

⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ± − =

m k m

c m

c 2

2 (2.2.4.8)

Penyelesaian dari akar-akar pada persamaan (2.2.4.8)

tergantung dari besarnya konstanta peredam pada frekuensi

alami yang mengalami gesekan, dimana nilainya dapat

positif, negatif, dan nol. Untuk jelasnya perhatikan berikut

ini.

m k m

c ₌

2 2

4

c=2 mk

misalkan

c₁ =c

maka

c₁ =2 mk (2.2.4.9)

sehingga

mk c c

c

2

1

= =

ξ

dimana

ξ

sering disebut sebagai rasio peredam.

Dengan menggunakan istilah rasio peredam dan frekuensi

alami tanpa adanya gesekan, persamaan (2.2.4.7) dapat

ditulis

₂ 0

2

= +

+ kx

dt dx c dt

₂ 0

2

= +

+ x

m k dt dx m

c dt

x d

₂ 2 2 0

2

= +

+ x

dt dx dt

x d

ω ω

ξ

Sehingga

m mk c

m c x

2 4

2

2 , 1

− ± −

= dapat ditulis sebagai

berikut

x_1,2 =−ξ ω ±ω ξ 2−1 (2.2.4.10)

Persamaan di atas hanya berlaku untuk ξ ≥1, akan tetapi

jika 0<

ξ

<1, persamaan di atas menjadi

x_1,2 =−ξ ω ±ω 1−ξ 2 i (2.2.4.11)

Penyelesaian persamaan (2.2.1.4.7) terdiri dari tiga kasus

seperti telah dijelaskan pada bab sebelumnya.

Contoh 2.2.4.1

Misalkan diketahui bahwa konstanta pegas sebesar 625,

konstanta redaman sebesar 40 ,massa sebesar 1, diketahui

pegas pada keadaan setimbang dan kecepatan awal yang

terjadi pada pegas sebesar 100, maka

sin15)

3 20 ( )

(t e 20 t

x = − t

Waktu yang dibutuhkan agar pegas tersebut pada keadaan

sin15t =0

diperoleh 2t=0, detik dan t=0,4detik

Jarak maksimumnya pegas terjadi apabila x'(t)=0, yaitu

= − − sin15)+ 3

400 ( )

( 20

'

t e

t

x t e−20t(100cos15t)=0

diperoleh t=0,42detik

Sehingga jarak maksimum yang ditempuh oleh pegas

sejauh 1,69 meter.

Gambar 2.2.4.1 Jarak Pegas

Pada gambar 2.2.4.1 di atas, terlihat bahwa pegas

mengalami dua kali dalam keadaan stabil yaitu saat 0,2 dan

0,4 detik, dan jarak maksimum yang dilakukan oleh pegas

tersebut sejauh 1,69 meter.

Contoh 2.2.4.2

Misalkan diketahui bahwa konstanta pegas sebesar 625,

tidak ada konstanta redaman ,massa sebesar 1, diketahui

pegas pada keadaan setimbang dan kecepatan awal yang

terjadi pada pegas sebesar 100, maka

x(t)=4sin25t

Waktu yang dibutuhkan agar pegas tersebut pada keadaan

setimbang apabila x(t)=0, yaitu

sin25t =0

diperoleh t=0,125 detik dan

Jarak maksimumnya pegas terjadi apabila x'(t)=0, yaitu

x'(t)=100cos25t

diperoleh t=0,0628detik

Sehingga jarak maksimum yang ditempuh oleh pegas

sejauh 3,99 meter. Pada kasus tanpa adanya rasio peredam

pada pegas adalah hal yang unik, sebab pegas tidak akan

pernah berhenti bergetar, dan akan selalu bergetar sehingga

mencapai jarak maksimum sejauh 3,99 meter dan jarak

minimum sejauh 3,99 m dari keadaan setimbang, seperti

yang diilustrasikan pada gambar di berikut ini.

Gambar 2.2.4.2 Jarak Pegas

C. Deret Binomial Dan Penerapannya

Teorema 2.3.1 ( Deret Binomial ) Untuk bilangan real p, fungsi 2 1 ) 1 ( )

(x p

f = +

dapat dinyatakan sebagai deret Mac Laurin pada selang (-1,1) yang berbentuk

(

)

... 2 1 1 1 2 0 + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = +

∑

∞ = x p x p x n p x n n p

, x<1

dengan ! ) 1 )...( 2 )( 1 ( n n p p p p n

p − − − +

= ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛

n=0,1,2...

dimana simbol _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ n p

berlaku untuk bilangan real p , dan n bilangan bulat positif.

Dalam penulisan skripsi ini tidak diberikan bukti tentang teorema 2.3.1,

akan tetapi bukti untuk teorema 2.3.1 dapat di temukan dalam buku kalkulus lebih

lanjut.

Contoh 2.3.1

Hitung 1+x dengan menggunakan deret binomial

Dengan

2 1

=

p dan n bilangan bulat positif., maka

(

)

.... ! 2 2 2 1 1 2 1 0 2 1 ! 1 1 2 1 0 2 1 ! 0 0 2 1 1 1 2 1 + ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + = +p

( )( )

( )( )

( )

2 3

3 2 1 2 1 2 2 1 2 1 ! 3 ! 2 2 1

1+ x+ − x + − − x

= +.... ... 16 1 8 1 2 1

1+ − 2+ 3+

= x x x

Berikut ini akan dibahas bagaimana penerapan dengan deret binomial pada

bidang fisika, yaitu pada teorema Torricelli, seperti yang akan dijelaskan berikut

ini

1. Usaha Dan Energi

Usaha adalah hasil gaya dan dengan perpindahan benda, yang

biasa dirumuskan sebagai berikut

W = F.s

dimana

W : Usaha (Joule)

F :Gaya. (Newton)

s : Perpindahan Benda (meter ) .

Energi Potensial dapat dirumuskan sebagai berikut

E_P =mgh

E_P : Energi Potensial (Joule)

g : Gravitasi (ms−2)

m : Massa Benda (kg)

Energi Kinetik dapat dirumuskan sebagai berikut

_{E 2}1_mv2

k =

dimana

E_k : Energi Kinetik (Joule),

v : Kecepatan Benda (ms−1)

m : Massa Benda (kg)

Energi Mekanik dapat dirumuskan sebagai berikut

E_M = E_P +E_k

2. Fluida

Fluida adalah zat yang dapat mengalir. Tekanan adalah besarnya

gaya yang bekerja pada permukaan benda setiap satuan, yang

dirumuskan sebagai berikut

A F P=

dimana

P : Tekanan

(

Nm−2 = pascal = pa

)

A: Luas Permukaan

( )

m2

Tekanan Hidrostatis adalah tekanan di dalam zat cair yang

disebabkan oleh zat cair itu sendiri, yang dirumuskan sebagai

berikut

P_H = ρ.g.h

dimana

P_H : Tekanan Hidostatis

(

Nm−2 = pascal = pa

)

ρ: Massa Jenis Zat Cair

(

kgm−3

)

h: Kedalaman Zat Cair

( )

m

g: Gravitasi (ms−2)

Massa zat cair dapat dirumuskan sebagai berikut.

m= ρ.V = ρ.A.h

dimana

ρ: Massa Jenis Zat Cair

(

kgm−3

)

h: Kedalaman Zat Cair

( )

m

A: Luas Permukaan

( )

m2

V : Volume

Hukum Hidrostatis adalah tekanan hidrostatis semua titik pada

suatu bidang datar memiliki kedalaman yang sama adalah sama,

Gambar 2.3.2.1 Tekanan Hidrostatis di titik A, B adalah sama

Pada gambar 2.3.2.1 di atas, titik A dan B terletak pada satu bidang

datar yang memiliki kedalaman yang sama, maka tekanan

hidrostatis di A dan B adalah sama, yang dapat dirumuskan sebagai

berikut

HB HA P

P =

3. Persamaan Kontinuitas

Jika kecepatan fluida di penampang A₁ dan di penampang A₂

sebesar v₁ dan v₂, maka volume fluida yang mengalir melalui

penampang A₁ sama dengan yang mengalir melalui penampang A₂

pada saat t., seperti diilustrasikan gambar berikut ini.

Gambar 2.3.3.1 Fluida Yang Mengalir Pada Luas Penampang

A B

b h

1

h

2

h

→ 1

v

→

2

A₁ Dan A₂ Yang Memiliki Ketinggian h₁ Dan h₂

Banyaknya fluida yang mengalir melalui penampang tertentu tiap

satuan waktu disebut dengan debit

( )

Q .

Karena diketahui volume fluida yang mengalir melalui penampang

1

A = yang mengalir melalui penampang A₂, maka

V₁=V₂

A₁.∆s₁ =.A2.∆s2

A₁.∆v₁.∆t =.A₂.∆v₂.∆t

Q₁ =Q₂

Sehingga dapat dikatakan bahwa debit fluida di penampang A₁

adalah

Q = A.V

Persamaan di atas merupakan Persamaan Kontinuitas.

4. Persamaan Bernoulli

Perhatikan gambar 2.3.3.1 di atas, maka usaha total yang dilakukan

untuk mengalirkan fluida dari titik 1 ke titik 2 sama dengan

perubahan energi mekanik fluida. Sehingga dapat dirumuskan

W_total =E_m

W₁−W₂ =∆E_P +∆E_k

P₁.A₁.∆s−P₂.A₂.∆s =( 2 ₂1 ₁2)

2 2

1_mv − _{mv + ( )}

1

2 mgh

P₁.A₁.∆s+ ₂1_mv12+ 1

mgh = P₂.A₂.∆s+ ₂1_mv22

2

mgh

+

P₁.V + ₂1_mv12+ 1

mgh = P₂.V.+₂1_mv22

2

mgh

+

_⎟⎟+

⎠ ⎞ ⎜⎜ ⎝ ⎛

ρ

m

P₁. ₂1_mv12+ 1

mgh _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ =

ρ

m

P₂. ₂1_mv22

2

mgh

+

P₁.+ ₂1ρ_.v12+ 1

.gh

ρ =P₂.+ ₂1_.ρ_.v22

2

. .gh

ρ

+

Persamaan di atas dikenal dengan Persamaan Bernoulli

Berikut ini adalah salah satu kasus khusus dari Bernoulli, dimana

kecepatan awal pada pipa diabaikan dan pipa diletakkan pada

posisi mendatar seperti yang akan diuraikan berikut ini.

5. Teorema Torricelli

Teorema Torricelli adalah hubungan antara laju fluida dengan

tinggi fluida yang terdapat pada sistem bejana, seperti yang

diilustrasikan pada gambar berikut ini.

Gambar 2.3.5.1 Fluida Yang Mengalir Pada Luas Penampang Bejana

dimana

↓ ↑

H

↓ ↑

h

1

P

3

P

2

P

1

h: Tinggi Air

( )

m P₁: Tekanan Udara

H : Tinggi Air Ke Pipa. P₂: Tekanan Air Di Bawah

P₃: Tekanan Udara.

A₁: Luas Penampang Air yang Masuk Pada Pipa

A₂: Luas Penampang Air Yang Keluar Dari Pipa.

Dengan menggunakan persamaan Bernoulli

₁+ ₁2+ ₁= 2

1

h v

P ρ ρ _{2 2}2 ₂

2 1

h v

P + ρ +ρ

Karena pipa bejana dalam keadaan mendatar maka h₁ =h₂, dan

kecepatan awal pada pipa diabaikan diperoleh

∆P ( ) 2

1 2

2

v

ρ

= (2.3.5.1)

dimana

∆P : Selisih Tekanan Pada Bejana..

Karena P₁= P₃ dan P₂ =P₁+ρ.g.h maka ∆P =ρ.g.h, sehingga

diperoleh

ρ

.g.h ( ) 2

1 2

2

v

ρ

=

v₂ = 2gh (2.3.5.2)

Persamaan (2.3.5.2) menyatakan kecepatan air pada saat h. Dengan

cara yang analog, kecepatan air pada saat H yakni

Misalkan A adalah luas penampang dari pipa bejana, maka laju

rata-rata air saat h adalah

q₀

( )

h =c h (2.3.5.4)

dimana c adalah konstan 2 1

5 − −

s m

Dengan cara yang analog diperoleh laju rata-rata air saat H yaitu:

q₀

( )

H =c H (2.3.5.5)

dimana c adalah konstan 2 1

5 − −

s m

Dari persamaan (2.3.5.4), yaitu

q₀

( )

h =c h

[

(

)

]

2 1

H h H

c + −

= 2 1 1 _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ − = H H h H c 2 1 2 1 1 _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ − = H H h H

c (2.3.5.6)

Dengan memisalkan ⎟

⎠ ⎞ ⎜ ⎝ ⎛ − = H H h x

2 diperoleh

q₀

( )

h

[

(

)

]

2 1 2 1 1 x H c −

= (2.3.5.7)

Maka dengan menggunakan contoh 2.3.1, persamaan (2.3.5.7)

menjadi

q₀

( )

h 2

1 2 1 2 1 1 _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +

Karena ⎟

⎠ ⎞ ⎜

⎝ ⎛ − =

H H h x

2 , maka dari persamaan (2.3.5.8) diperoleh

q₀

( )

h _⎥

⎦ ⎤ ⎢

⎣ ⎡

⎟ ⎠ ⎞ ⎜

⎝

⎛ ₋ −

=

H H h H

c

2 1

2 1

(

h−H

)

<H

( )

(

h H

)

H

c H

q + −

=

2

0

=q₀

( )

H +λ

(

h−H

)

(2.3.5.9)

dimana

H c

2

=

λ .

Jadi untuk h semakin membesar, maka

q₀

( )

h =q₀

( )

H +λ

(

h−H

)

=c h+λ

( )

h −λ

( )

H

=c H

(

1−

( )

12 c

)

+λ

( )

h

≈λ

( )

h (2.3.5.10)

39

BAB III

PEMODELAN MATEMATIKA PADA SISTEM SATU BEJANA

Pada bab dua telah dipaparkan definisi tentang sistem. Kesalahan (error)

pada sistem adalah perbedaan antara output dan input yaitu

E =

[

output−input

]

(3.1)

Pada sistem sering sekali menggunakan sebuah alat yang disebut dengan

sensor. Sensor adalah adalah alat untuk mendeteksi sesuatu, yang bertujuan

sebagai alat perbandingan kesalahan. Berikut ini akan dibahas mengenai sensor

yang terdapat pada sistem

a) Sensor Jarak (Perpindahan).

Sensor posisi ini biasanya digunakan untuk mendeteksi posisi suatu

sistem, yang bertujuan sebagai alat perbandingan kesalahan pada

sistem tersebut.

b) Sensor Kecepatan (Laju).

Sensor posisi ini biasanya digunakan untuk mendeteksi kecepatan

atau laju suatu sistem, yang bertujuan sebagai alat perbandingan

kesalahan pada sistem tersebut.

c) Sensor Percepatan.

Sensor posisi ini biasanya digunakan untuk mendeteksi kecepatan

suatu sistem, yang bertujuan sebagai alat perbandingan kesalahan

Persamaan diferensial orde satu dan dua yaitu

P(x)y Q(x)

dx

dy_{+ =}

(3.2)

( ) ( ) ( )

2 2

x Q y x B dx dy x P dx

y

d _{+ + =}

(3.3)

Pada persamaan (3.2) dan (3.3) di atas inputnya adalah Q

( )

x , dimana

input tersebut dapat berupa fungsi konstan, fungsi periodik, fungsi ekponensial,

dan lain-lain. Berikut ini akan dijelaskan input yang terdapat pada ketiga sensor di

atas, yakni

a) Fungsi Konstan.

Misalkan K adalah konstanta, maka

Q

( )

x =K

Gambar 3.1 Fungsi Konstan

b) Fungsi Kecepatan (Laju).

Misalkan K adalah konstanta, maka

K dx

x dQ( ) ₌

atau Q(x)= Kx

) (x Q

K

x

⎪⎩ ⎪ ⎨ ⎧

< > =

0 0

0 )

(

Gambar 3.2 Fungsi Kecepatan

c) Fungsi Percepatan.

Misalkan K adalah konstanta, maka

K dx

x Q

d ₌

2 2

) (

atau _Q(x)= ₂1_Kx2

Gambar 3.3 Fungsi Percepatan

Kesalahan pada saat stabil adalah perbedaan antara input dan output

dikalikan dengan sebuah input yang baru atau dengan kata lain

E =

[

output−input

]

r(t) (3.4)

dimana )r(t adalah sebuah input yang baru adalah input

Sebelum membahas tentang Sistem Pembangkit Listrik Tenaga Air, yang

terjadi pada sistem bendungan khususnya sistem bendungan yang terdiri dari dua

bendungan, dimana bendungan yang satu terletak di bawah bendungan yang lain. )

(x Q

x

⎪⎩ ⎪ ⎨ ⎧

< > =

0 0

0 )

(

x x Kx x

Q

⎪⎩ ⎪ ⎨ ⎧

< > =

0 0

0 )

(

2 2 1

x x Kx x

Q

) (x Q

Akan dibahas terlebih dahulu bagaimana memodelkan secara matematis untuk

Sistem Pembangkit Listrik Tenaga Air

Sistem bendungan dapat digambarkan sebagai berikut.

Gambar 3.4 Sistem Bendungan

Aliran sungai dengan debit yang sangat besar ditampung dalam waduk (1)

yang ditunjang dengan sebuah bendungan (3). Air tersebut dialirkan melalui

Power Intake (2) kemudian masuk ke Pipa Pesat (Penstock) (4) untuk merubah

energi potensial menjadi energi kinetik. Pada ujung pipa pesat dipasang Katup

Utama (Main Inlet Valve) (5) untuk mengalirkan air ke turbin. Katup utama akan

ditutup otomatis apabila terjadi gangguan atau di stop atau dilakukan perbaikan /

pemeliharaan turbin.

Air yang telah mempunyai tekanan dan kecepatan tinggi (energi kinetik)

dirubah menjadi energi mekanik dengan dialirkan melalui sirip-sirip pengarah

akan mendorong sudu jalan (runner) yang terpasang pada turbin (6). Energi putar

(7) yang kemudian menghasilkan tenaga listrik yang keluar dari turbin melalui

Tail Race (8) selanjutnya kembali ke sungai (9).

Untuk memperoleh model ini, diasumsikan bahwa bendungan sebagai

bejana. Hal ini dikarenakan, tidak mudah untuk mendapatkan model matematika

untuk ketinggianair pada bendungan, jika dilakukan percobaan langsung terhadap

bendungan tersebut, karena mengandung resiko yang terlalu berbahaya