TUGAS AKHIR
ANALISIS TERMAL KABEL TANAH TEGANGAN MENENGAH
MENGGUNAKAN METODE NUMERIK
Diajukan untuk memenuhi salah satu persyaratan dalam
Menyelesaikan pendidikan sarjana (S-1) pada Departemen Teknik Elektro
Oleh :
RIZA ANSHARI 050402091
DEPARTEMEN TEKNIK ELEKTRO
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA
MEDAN
ANALISIS TERMAL KABEL TANAH TEGANGAN MENENGAH
MENGGUNAKAN METODE NUMERIK
Oleh :
RIZA ANSHARI 050402091
Disetujui oleh :
Pembimbing,
Ir.Syarifuddin Siregar
NIP: 194612081976031002
Diketahui oleh :
Pelaksana Harian
Ketua Departemen Teknik Elektro FT USU,
Prof.Dr.Ir Usman Baafai
NIP: 194610221973021001
DEPARTEMEN TEKNIK ELEKTRO
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA
MEDAN
ABSTRAK
Arus listrik yang mengalir pada konduktor suatu kabel akan menimbulkan
panas yang menaikkan suhu pada konduktor dan isolasinya, sehingga mempengaruhi
kemampuan hantar arus kabel. Kemampuan hantar arus suatu kabel yang dipasang di
dalam tanah dipengaruhi oleh desain kabel, cara pemasangan kabel, suhu keliling dan
kelembaban tanah. Untuk kabel tegangan menengah diperlukan isolasi yang tebal
untuk menahan terpaan medan listrik, tetapi sebaliknya panas yang dihasilkan
konduktor semakin sulit keluar dari kabel sehingga suhu konduktor semakin tinggi
dan mengurangi arus yang diizinkan melalui kabel.
Tugas Akhir ini membahas pengaruh resistivitas termal dan suhu tanah
terhadap arus yang diizinkan mengalir pada kabel tegangan menengah dengan
menggunakan metode numerik. Penulis menggunakan software simulasi panas
KATA PENGANTAR
Segala puji bagi Allah SWT yang telah memberikan rahmat dan karunia-Nya
sehingga penulis dapat menyelesaikan Tugas Akhir ini. Shalawat dan salam semoga
senantiasa tercurahkan kepada junjungan kita Nabi Muhammad SAW beserta
keluarga dan para sahabatnya.
Tugas akhir ini penulis persembahkan kepada yang teristimewa yaitu
ayahanda dan ibunda, serta abang dan adik tercinta yang senantiasa memberikan
do’a, semangat dan dukungannya selama ini.
Tugas Akhir ini merupakan bagian dari kurikulum yang harus diselesaikan
untuk memenuhi persyaratan menyelesaikan pendidikan Sarjana Strata Satu di
Departemen Teknik Elektro, Fakultas Teknik, Universitas Sumatera Utara. Adapun
judul Tugas Akhir ini adalah :
ANALISIS TERMAL KABEL TANAH TEGANGAN MENENGAH
MENGGUNAKAN METODE NUMERIK
Selama masa kuliah hingga diselesaikannya Tugas Akhir ini, penulis banyak
menerima bantuan, bimbingan serta dukungan dari berbagai pihak. Untuk itu dalam
kesempatan ini penulis ingin mengucapkan terima kasih kepada :
1. Bapak Ir. Syarifuddin Siregar selaku Dosen Pembimbing yang dengan sabar
dan tulus meluangkan waktu dan pikiran untuk membimbing penulis dalam
2. Bapak Ir. Masykur Sjani selaku dosen wali penulis yang senantiasa
memberikan bimbingan selama perkuliahan.
3. Bapak Prof Dr Ir Usman Baafai dan Bapak Rachmad Fauzi, ST, MT selaku
Ketua dan Sekretaris Departemen Teknik Elektro, Fakultas Teknik,
Universitas Sumatera Utara.
4. Seluruh Staf Pengajar yang telah memberi bekal ilmu kepada penulis dan
seluruh Pegawai Departemen Teknik Elektro, Fakultas Teknik, Universitas
Sumatera Utara atas bantuan administrasinya.
5. Pihak PT PLN (PERSERO) Wilayah dan Rayon Medan Kota yang telah
memberi kesempatan kepada penulis untuk melakukan penelitian.
6. Pak Ponirin, Pak Syahrul, Pak Adek, dan Pegawai Bengkel PLN Jl. Sei Batu
Gingging yang telah membantu penulis dalam pengambilan data.
7. Teman-teman stambuk 2005 : Ardhy, Harpen, Su’ib, Megi, Irpan, Prindi,
Ghifari, Reza, Harry, Rifky, Rudi, Putra, Ricky, Rizky, Luthfi, Khairil, Dedi,
Azwar, Iqri, Umar, Herman, Roy, Diana, Dewi, Muti, Ami, Anisa, Yona dan
semua teman-teman 2005 yang tidak mungkin disebutkan satu persatu.
8. Serta semua abang senior dan adik junior yang telah mau berbagi pengalaman
dan motivasi kepada penulis.
9. Teman-teman kos Citra Land 15 H : Bang Zoe, Bang Gatrick, Bang Zamir,
Bang Taufik, Bang Maulana, Bang Rasyid, Bang Iwan, Bang Arfan, Erik,
Saiful, Rahmad, Yogi, Taufik dan Fuad yang semuanya memberi motivasi
dan semangat kepada penulis.
Akhir kata penulis menyadari bahwa tulisan ini masih banyak
kekurangannya. Kritik dan saran dari pembaca untuk menyempurnakan dan
mengembangkan kajian dalam bidang ini sangat penulis harapkan. Semoga Tugas
Akhir ini dapat memberi manfaat khususnya bagi penulis maupun semua pihak yang
membutuhkannya. Dan hanya kepada Allah penulis berserah diri dan memohon
ampun.
Medan, 16 Februari 2010
Penulis
DAFTAR ISI
Abstrak ...i
Kata Pengantar ... ii
Daftar Isi ... iv
Daftar Gambar ...vii
Daftar Tabel ... viii
BAB I PENDAHULUAN ... 1
I.1 Latar Belakang ... 1
I.2 Tujuan dan Manfaat Penulisan ... 2
I.3 Batasan Masalah ... 2
I.4 Metode penulisan ... 3
I.5 Sistematika Penulisan ... 4
BAB II KABEL DAN PERPINDAHAN PANAS ... 5
II.1 Umum ... 5
II.2 Konstruksi Kabel Tegangan Menengah ... 5
II.2.1 Konduktor ... 6
II.2.2 Isolasi ... 7
II.2.3 Tabir... 8
II.2.4 Selubung ... 8
II.2.5 Bantalan ... 9
II.2.6 Perisai ... 9
II.2.7 Bahan Pengisi ... 9
II.3 Mekanisme Perpindahan Panas ... 10
II.3.1 Konduksi ... 10
II.3.1.1 Konduksi Satu Dimensi dan Tiga Dimensi...12
II.3.1.2 Konduksi pada Bidang Datar ...15
II.3.1.3 Konduksi pada Silinder...17
II.3.2 Konveksi ... 18
II.3.3 Radiasi ... 19
II.3.4 Perpindahan Panas pada Kabel ... 20
II.4 Persamaan Kesetaraaan Energi pada Kabel ... 22
II.4.1 Persamaan Perpindahan Panas ... 23
II.4.2 Pendekatan Polinomial ... 24
II.4.2 Persamaan Elemen Hingga ... 25
BAB III KEMAMPUAN HANTAR ARUS (KHA) KABEL TEGANGAN MENENGAH ... 29
III.1 Umum ... 29
III.2 Cara Menentukan Kemampuan Hantar Arus Kabel (KHA)... 29
III.3 Perhitungan Rugi-rugi Panas ... 33
III.3.1 Rugi-rugi Konduktor ... 33
III.3.2 Rugi-rugi Dielektrik ... 36
III.3.3 Rugi-rugi Selubung dan Perisai ... 38
III.4 Perhitungan Resistansi Termal ... 41
III.4.1 Resistansi Termal antara Konduktor dan Selubung ... 43
III.4.2 Resistansi Termal antara Selubung dan Perisai ... 45
III.4.4 Resistansi Termal Eksternal ... 46
III.5 Menentukan Kemampuan Hantar Arus dengan Metode Numerik ... 48
BAB IV ANALISIS TERMAL KABEL TANAH TEGANGAN MENENGAH MENGGUNAKAN METODE NUMERIK ... 53
IV.1 Umum ... 53
IV.2 Data Dimensi Kabel ... 53
IV.3 Analisis Data ... 55
IV.3.1 Analisis dengan Metode Analitik ... 55
IV.3.2 Analisis dengan Metode Numerik ... 57
IV.3.3 Perbandingan Kedua metode ... 64
KESIMPULAN DAN SARAN... 67
V.1 Kesimpulan ... 67
V.2 Saran ... 67
DAFTAR PUSTAKA ... 80
DAFTAR GAMBAR
Gambar 2.1 Bagian utama kabel berinti tunggal ... 6
Gambar 2.2 Bagian-bagian kabel berinti tiga... 6
Gambar 2.3 Konduksi pada bidang datar dan arah aliran panas ... 11
Gambar 2.4 Volume unsur untuk konduksi panas satu dimensi ... 13
Gambar 2.5 Volume unsur tiga dimensi : (a) koordinat kartesius, (b) koordinat silindris ... 15
Gambar 2.6 Perpindahan panas melalui dinding berlapis dan analogi listriknya ... 16
Gambar 2.7 Aliran panas satu dimensi melalui silinder dan analogi listriknya ... 17
Gambar 2.8 Kabel dan analogi listriknya ... 21
Gambar 2.9 Sebagian penampang kabel dan analogi listriknya ... 22
Gambar 2.10 Koordinat luas segitiga ... 24
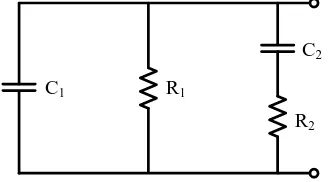
Gambar 3.1 Rangkaian ekivalen termal listrik kabel berinti tunggal ... 31
Gambar 3.2 Rangkaian ekivalen termal listrik kabel berinti tiga ... 32
Gambar 3.3 Representasi isolasi kabel ... 36
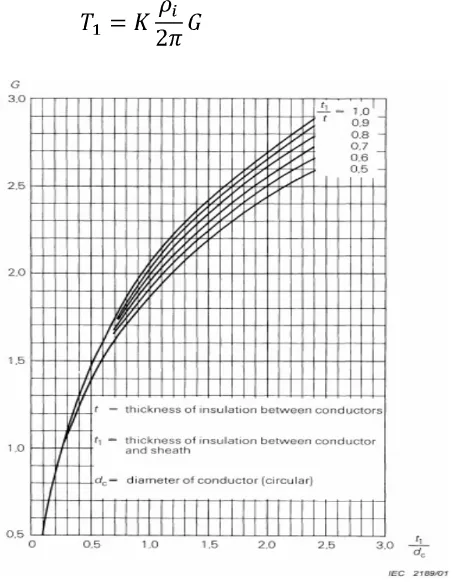
Gambar 3.4 Faktor geometrik G kabel ikat berinti tiga dengan konduktor bulat .... 44
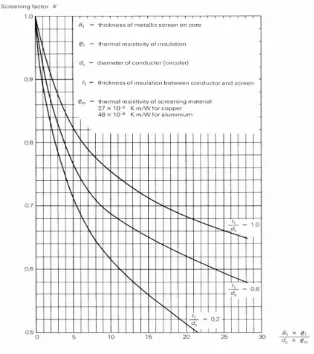
Gambar 3.5 Faktor screening kabel berinti tiga dengan konduktor bulat ... 45
Gambar 3.6 Kabel yang ditempatkan dalam backfill ... 47
Gambar 3.7 Elemen triangular dan quadrilateral ... 50
Gambar 3.8 Elemen quadratic-triangular ... 50
Gambar 3.9 Penggunaan ukuran elemen yang berbeda ... 51
Gambar 4.1 Penampang kabel NA2XSEBY 20 kV berinti tiga 240 mm2... 54
Gambar 4.3 Model kabel beserta detil instalasinya ... 59
Gambar 4.4 Model mesh kabel ... 60
Gambar 4.5 Ukuran elemen yang semakin kecil ... 61
Gambar 4.6 Distribusi suhu di sekitar kabel ... 62
Gambar 4.7 Distribusi suhu pada bagian-bagian kabel ... 62
Gambar 4.8 Grafik hubungan antara arus dengan suhu konduktor kabel ... 64
Gambar 4.9 Grafik pengaruh suhu tanah terhadap arus konduktor ... 66
DAFTAR TABEL
Tabel 2.1 Konduktivitas termal beberapa bahan ... 12
Tabel 3.1 Nilai dan ... 35
Tabel 3.2 Nilai permitivitas dan faktor rugi-rugi isolasi... 37
Tabel 3.3 Resistivitas termal bahan ... 42
Tabel 4.1 Data mekanik kabel NA2XSEBY ... 54
Tabel 4.2 Data listrik kabel NA2XSEBY ... 55
Tabel 4.3 Pengaruh suhu tanah dengan metode analitik ... 56
Tabel 4.4 Pengaruh resistivitas termal tanah dengan metode analitik ... 57
Tabel 4.5 Nilai konduktivitas bahan kabel dan medium sekitar ... 58
Tabel 4.6 Pengaruh suhu tanah dengan metode numerik ... 63
Tabel 4.7 Pengaruh resistivitas termal tanah dengan metode numerik ... 63
ABSTRAK
Arus listrik yang mengalir pada konduktor suatu kabel akan menimbulkan
panas yang menaikkan suhu pada konduktor dan isolasinya, sehingga mempengaruhi
kemampuan hantar arus kabel. Kemampuan hantar arus suatu kabel yang dipasang di
dalam tanah dipengaruhi oleh desain kabel, cara pemasangan kabel, suhu keliling dan
kelembaban tanah. Untuk kabel tegangan menengah diperlukan isolasi yang tebal
untuk menahan terpaan medan listrik, tetapi sebaliknya panas yang dihasilkan
konduktor semakin sulit keluar dari kabel sehingga suhu konduktor semakin tinggi
dan mengurangi arus yang diizinkan melalui kabel.
Tugas Akhir ini membahas pengaruh resistivitas termal dan suhu tanah
terhadap arus yang diizinkan mengalir pada kabel tegangan menengah dengan
menggunakan metode numerik. Penulis menggunakan software simulasi panas
BAB I
PENDAHULUAN
I.1 Latar Belakang
Selain saluran udara tegangan menengah dengan menggunakan konduktor
telanjang, digunakan juga kabel tanah untuk saluran kabel tegangan menengah.
Penggunaan kabel lebih handal dibanding dengan konduktor telanjang, akan tetapi
harga dan biaya instalasinya lebih mahal. Biaya yang mahal tersebut meliputi biaya
bahan dan peralatan yang digunakan, upah pekerja, dan waktu yang dibutuhkan
untuk merancang dan memasang kabel.
Oleh karena itu biaya yang mahal harus tergantikan dengan memungkinkan
kabel tersebut menghantarkan arus sesuai dengan kapasitas maksimumnya. Akan
tetapi suhu konduktor membatasi kemampuan hantar arus dari kabel tanah,
contohnya suhu yang diizinkan pada kabel dengan isolasi XLPE dibatasi hingga
90oC. Di samping itu suhu operasi sangat berpengaruh terhadap umur kabel dan suhu
yang melebihi batas operasi dapat merusak isolasi dan pelindung kabel.
Model pertama yang digunakan untuk menghitung kemampuan hantar arus
adalah model Neher-McGrath dalam tahun 1957. Model ini telah diterima secara luas
selama lebih dari 50 tahun, dan sekarang banyak perusahaan menggunakan standar
IEC 60287 yang berdasarkan pada model Neher-McGrath. Metode pada standar IEC
60287 ini sederhana dan memiliki banyak keterbatasan, sehingga tidak dapat
digunakan untuk menganalisis kabel dengan konfigurasi yang kompleks.
Metode numerik dengan metode elemen hingga (finite element method)
kompleks. Metode elemen hingga mampu memecahkan masalah yang dimodelkan
dengan persamaan diferensial parsial. Suatu region atau daerah yang dianalisis
direpresentasikan sebagai sebuah susunan elemen-elemen hingga. Fungsi-fungsi
pendekatan dalam elemen hingga didefinisikan dengan istilah nilai node dari suatu
medan fisik.
Masalah fisik yang kontinu ditransformasikan ke dalam masalah elemen
hingga yang diskrit dengan nilai-nilai node yang tidak diketahui. Kemudian solusi
masalah linier sistem persamaan aljabar linier dilakukan secara numerik. Nilai-nilai
dalam elemen hingga dapat diperoleh menggunakan solusi node.
I.2 Tujuan dan Manfaat Penulisan
Adapun tujuan dari penulisan Tugas Akhir ini adalah:
1. Menentukan kemampuan hantar arus kabel tanah tegangan menengah
menggunakan standar IEC 60287.
2. Menentukan kemampuan hantar arus kabel tanah tegangan menengah
menggunakan metode numerik dengan metode elemen hingga.
Manfaat dari penulisan Tugas Akhir ini adalah dengan mengetahui arus yang
diizinkan mengalir pada kabel tegangan menengah yang dianalisis, maka dapat
dijadikan sebagai bahan pertimbangan dalam menentukan pembebanan kabel tanah
oleh pihak PLN khususnya dan mahasiswa pada umumnya.
I.3 Batasan Masalah
Untuk membatasi masalah yang akan dibicarakan dalam Tugas Akhir ini,
maka perlu dibuat batasan agar pembahasan tidak terlalu luas. Adapun batasan
1. Kabel yang dianalisis adalah kabel tanah tegangan menengah NA2XSEBY
20 kV berinti tiga 240 mm2 dengan saluran tunggal.
2. Seluruh standar kabel yang digunakan adalah standar IEC 60287.
3. Suhu tanah dianggap isotermal dan tidak ada pengaruh dari sumber panas lain.
4. Sifat tanah dianggap seragam dan tidak ada kemungkinan perubahan
kelembaban ke bagian resistivitas termal tinggi di sekitar kabel.
5. Tidak membahas kenaikan suhu konduktor akibat sambungan (jointing).
6. Untuk simulasi panas digunakan software ANSYS 10.0.
I.4 Metode Penulisan
Metode penulisan yang digunakan dalam penulisan tugas akhir ini adalah :
1. Studi Literatur
Mempelajari buku referensi, artikel dari jurnal dan internet, dan bahan kuliah
yang mendukung topik tugas akhir.
2. Studi Lapangan
Mengumpulkan data-data yang diperlukan mengenai penanaman kabel tanah,
ukuran kabel dan detil instalasi dari pihak PLN.
3. Diskusi
Berupa konsultasi dengan dosen pembimbing, dosen-dosen lain dan rekan-rekan
mahasiswa mengenai masalah yang berhubungan dalam penulisan.
4. Analisis Data
Menentukan kemampuan hantar arus kabel dengan metode analitik
menggunakan standar IEC 60287 dan metode numerik dengan program ANSYS
I.5 Sistematika Penulisan
Untuk memberikan gambaran mengenai tulisan ini, secara singkat dapat
diuraikan sistematika penulisan sebagai berikut :
BAB I PENDAHULUAN
Bab ini mengatur tentang latar belakang masalah, tujuan penulisan,
batasan masalah, metodologi penulisan, serta sistematika penulisan.
BAB II KABEL DAN PERPINDAHAN PANAS
Bab ini membahas uraian tentang teori umum kabel dan mekanisme
perpindahan panas pada kabel.
BAB III KEMAMPUAN HANTAR ARUS (KHA) KABEL TEGANGAN
MENENGAH
Bab ini membahas tentang parameter yang mempengaruhi rating arus,
rugi-rugi kabel dan cara menentukan kemampuan hantar arus
tegangan menengah secara analitik dan numerik.
BAB IV ANALISIS TERMAL KABEL TANAH TEGANGAN
MENENGAH MENGGUNAKAN METODE NUMERIK
Bab ini membahas tentang perhitungan arus secara analitik dan
melakukan analisis termal untuk menentukan kemampuan hantar arus
secara numerik dengan program ANSYS.
BAB V PENUTUP
BAB II
KABEL DAN PERPINDAHAN PANAS
II.1 Umum
Kemampuan hantar arus kabel dipengaruhi oleh perpindahan panas yang
terjadi dari kabel ke lingkungan sekitar. Secara umum sumber panas dalam kabel
dapat dibagi menjadi dua yaitu panas yang dihasilkan oleh konduktor yang dialiri
arus dan panas yang dihasilkan oleh isolasi akibat terpaan medan listrik. Panas yang
dihasilkan oleh kabel ini harus dipindahkan ke luar dari kabel agar tidak terjadi
kenaikan suhu baik pada konduktor maupun isolasinya.
Perpindahan panas pada kabel sangat ditentukan oleh konstruksi kabel dan
keadaan lingkungan sekitarnya. Bahan penyusun kabel harus mampu menghantarkan
panas ke luar dari kabel sebesar mungkin agar kenaikan suhu yang terjadi relatif
kecil, sehingga arus yang mengalir dapat maksimal. Dalam bab ini akan dibahas
mengenai konstruksi kabel tegangan menengah dan mekanisme perpindahan panas
pada kabel.
II.2 Konstruksi Kabel Tegangan Menengah
Umumnya kabel tegangan menengah memiliki konstruksi yang sama dengan
kabel tegangan tinggi. Dalam penggunaannya kabel dirancang dengan konstruksi
yang berbeda-beda sesuai dengan kebutuhannya. Sebagai konduktor berisolasi,
konstruksi kabel dibagi menjadi bagian utama dan bagian pelengkap.
Bagian utama kabel adalah bagian yang harus dimiliki oleh kabel tenaga,
yaitu konduktor (conductor), isolasi (insulation), tabir (screen) dan selubung
kabel digunakan untuk memperbaiki sifat-sifat kabel atau untuk melindungi kabel,
bagian-bagian tersebut adalah bantalan (bedding), perisai (armor), bahan pengisi
(filler) dan sarung kabel (serving).
Gambar 2.1 dan 2.2 menunjukkan bagian utama kabel berinti tunggal dan
bagian-bagian kabel berinti tiga.
Selubung Tabir
Konduktor Isolasi
Gambar 2.1 Bagian utama kabel berinti tunggal
Sarung kabel Perisai
Bantalan Konduktor Selubung Isolasi
Bahan Pengisi (filler)
Gambar 2.2 Bagian-bagian kabel berinti tiga
II.2.1 Konduktor
Kabel tegangan menengah umumnya dibedakan menjadi kabel berinti
tunggal, berinti dua, dan berinti tiga. Setiap inti kabel merupakan konduktor dan
bentuknya dapat dirancang sesuai dengan kebutuhan. Bahan konduktor yang banyak
Adapun bentuk penampang konduktor yang digunakan dalam kabel tenaga terdiri
dari beberapa bentuk yaitu bulat tanpa rongga, sektoral dan bulat berongga.
II.2.2 Isolasi
Isolasi merupakan faktor penting pada sistem tenaga listrik dan salah satu
gangguan penyaluran tenaga listrik dengan menggunakan kabel adalah kerusakan
pada isolasinya. Dengan demikian rancangan kabel harus disesuaikan dengan
penggunaannya, sehingga bahan isolasi sesuai dengan kemampuan kabel tersebut.
Berdasarkan jenis isolasi padat yang dipakai, kabel dapat digolongkan
menjadi kabel berisolasi karet, kertas dan sintetis. Isolasi yang digunakan harus
mempunyai sifat-sifat sebagai berikut :
a. Memiliki kekuatan dielektrik yang tinggi agar diameter luar dapat dikurangi
sehingga biaya pembuatan kabel berkurang.
b. Memiliki tahanan jenis yang tinggi.
c. Dapat bekerja dalam suhu rendah atau suhu tinggi
d. Tidak mudah terbakar.
e. Tidak mengisap air (non higroskopis).
f. Mudah dibengkok-bengkokkan (fleksibel).
g. Sanggup menahan tegangan impuls listrik yang tinggi.
Suatu hal yang tidak mungkin dalam suatu jenis isolasi terdapat semua sifat-sifat di
atas. Jadi pemilihan jenis isolasi yang akan dipakai didasarkan pada pertimbangan
II.2.3 Tabir
Untuk tegangan kerja yang tinggi setiap inti kabel dilengkapi dengan suatu
lapisan yang disebut tabir (screen). Lapisan tabir dipasang diantara selubung (sheath)
dan isolasi, tapi untuk kabel sintetis dipasang juga antara isolasi dan konduktor.
Tabir ini berfungsi :
a. Untuk meratakan distribusi tegangan, sehingga tabir harus dibuat dari bahan
semikonduktor, misalnya kertas berlapis logam dan kompon grafit.
b. Untuk mendapatkan distribusi medan listrik yang radial dan seragam
sehingga tidak terjadi penumpukan tegangan.
c. Untuk melindungi dan mengamankan manusia terhadap bahaya listrik.
d. Mencegah interferensi gelombang elektromagnetik dengan kabel
telekomunikasi yang berada di dekatnya.
II.2.4 Selubung
Selubung berfungsi untuk melindungi inti kabel dari pengaruh luar yaitu
sebagai pelindung terhadap korosi, penahan gaya mekanis, dan pelindung terhadap
gaya listrik. Di samping itu selubung juga mencegah keluarnya minyak pada kabel
kertas yang diresapi minyak (impregnated paper) dan mencegah masuknya uap air
ke dalam kabel. Bahan selubung dapat dibagi menjadi tiga golongan, yaitu :
1. Selubung logam, misalnya tembaga, timbal dan aluminium.
2. Selubung karet sintetis, misalnya karet silikon (silicone rubber) dan
polychloroprene.
II.2.5 Bantalan
Bantalan adalah lapisan yang terbuat dari serat-serat baik yang diresapi
minyak ataupun tidak, dipasang bersama-sama kompon kedap air dan ditempatkan di
bawah perisai. Fungsi bantalan adalah sebagai tempat kedudukan perisai dan
mencegah proses elektrolisa sehingga tidak merusak bagian dalamnya.
Beberapa bahan dari bantalan diantaranya pita kapas (cotton tape), pita kertas
(paper tape) dan jute. Sebelum dipasang bantalan harus dikeringkan dan direndam
dalam minyak atau kompon kedap air. Bantalan dipasang lapisan demi lapisan
sehingga lapisan atas akan menutupi lapisan yang berada di bawahnya.
II.2.6 Perisai
Bahan isolasi mempunyai sifat mekanis yang kurang sempurna, sehingga
diperlukan suatu lapisan yang berfungsi melindungi bahan isolasi dari kerusakan
mekanis, lapisan ini dinamakan perisai. Secara umum perisai dapat digolongkan
menjadi dua jenis, yaitu perisai pita baja (steel tape armor) dan perisai kawat baja
(steel wire armor).
II.2.7 Bahan Pengisi
Untuk konstruksi kabel berinti tiga, bila setelah pemasangan ketiga intinya
maka masih ada ruang (celah) yang tertinggal, maka diperlukan suatu bahan yang
dapat mengisi ruangan tersebut agar didapat bentuk kabel yang bulat. Bahan yang
mengisi celah ini dinamakan bahan pengisi.
Bahan pengisi yang banyak digunakan pada bahan isolasi kertas adalah jute,
II.2.8 Sarung kabel
Sarung kabel adalah suatu lapisan bahan serat yang diresapi dengan kompon
kedap air. Pemasangan sarung kabel biasanya dipasang di atas perisai. Fungsi sarung
kabel adalah selain bantalan bagi perisai, juga sebagai komponen yang berhubungan
langsung dengan tanah, sehingga sarung kabel merupakan bagian yang pertama
sekali terkena pengaruh luar. Bahan sarung kabel yang banyak digunakan untuk
kabel tegangan menengah adalah polyethylene dan polyvinyl chloride (PVC) .
II.3 Mekanisme Perpindahan Panas pada Kabel
Perpindahan panas adalah perpindahan energi yang terjadi karena adanya
perbedaan suhu pada benda atau material. Proses perpindahan panas ini berlangsung
melalui tiga mekanisme, yaitu konduksi, konveksi dan radiasi. Perpindahan panas
pada kabel yang ditanam di dalam tanah berlangsung secara konduksi, sehingga
dalam bab ini lebih banyak dijelaskan masalah konduksi.
II.3.1 Konduksi
Jika pada suatu benda terdapat gradien suhu, maka pada benda tersebut akan
terjadi perpindahan panas dari bagian bersuhu tinggi ke bagian bersuhu rendah.
Dalam hal ini panas berpindah secara konduksi dan laju perpindahan panas itu
berbanding lurus dengan gradien suhu normal :
di mana q ialah laju perpindahan panas dan merupakan gradien suhu ke arah
perpindahan panas. Konstanta k disebut konduktivitas termal benda itu, sedangkan
tanda minus (-) diberikan agar memenuhi hukum kedua termodinamika, yaitu panas
mengalir ke tempat yang lebih rendah dalam skala suhu, sebagaimana ditunjukkan
dalam sistem koordinat pada Gambar 2.3.
Persamaan (2.1) disebut hukum Fourier tentang konduksi panas yang
ditemukan oleh seorang ahli matematika fisika bangsa Perancis, Joseph Fourier.
Persamaan (2.1) juga merupakan persamaan dasar dari konduktivitas termal dengan
satuan Watt per meter per derajat Celsius.
qx
Gambar 2.3 Konduksi pada dinding datar dan arah aliran panas
Nilai konduktivitas termal menunjukkan seberapa cepat panas mengalir dalam bahan
tertentu. Jika suatu bahan memiliki nilai konduktivitas termal yang besar, maka
bahan tersebut merupakan penghantar panas yang baik, sedangkan jika nilai
konduktivitas termalnya kecil, maka bahan itu merupakan penghantar yang buruk
Tabel 2.1 Konduktivitas termal beberapa bahan
Bahan K (W/m.oC) Bahan K (W/m.oC)
Logam Bukan Logam
Perak
Kayu mapel atau ek
Serbuk gergaji
Minyak lumas, SAE 50
Freon 12, CCl2F2
II.3.1.1 Konduksi Satu Dimensi dan Tiga Dimensi
Konduksi satu dimensi dapat dianalisis dengan mengacu pada Gambar 2.4.
Jika sistem berada pada keadaan tunak (steady state), yaitu jika suhu tidak berubah
terhadap waktu, maka penyelesaiannya hanya dengan mengintegrasikan Persamaan
(2.1) dan mensubstitusi nilai-nilai yang sesuai untuk memecahkan soal itu. Tetapi,
jika suhu zat padat itu berubah terhadap waktu, atau jika ada sumber panas dalam zat
x dx qx+dx
qx
qgen = q A dx
A
Gambar 2.4 Volume unsur untuk konduksi panas satu dimensi
Apabila suhu berubah terhadap waktu dan terdapat pula sumber panas dalam zat
padat itu, maka dapat dibuat neraca energi untuk bagian yang tebalnya dx sebagai
berikut :
Energi yang dihantarkan di muka kiri + energi yang dibangkitkan dalam unsur itu =
perubahan energi dalam atau dakhil + energi yang dihantarkan ke luar unsur itu
melalui muka kanan.
di mana = energi yang dibangkitkan per satuan volume (W/m3)
c = panas spesifik bahan (J/kg.oC)
Jika hubungan-hubungan ini digabungkan, maka kita dapatkan :
Persamaan (2.2) berlaku untuk konduksi panas satu dimensi. Untuk mendapatkan
persamaan konduksi panas tiga dimensi, maka perlu diperhatikan panas yang
dihantarkan ke dalam dan ke luar satuan volume itu dalam ketiga arah koordinat,
seperti ditunjukkan pada Gambar 2.5. Neraca energi di sini menghasilkan:
Sedangkan kuantitas energi diberikan oleh persamaan :
sehingga persamaan umum untuk konduksi panas tiga dimensi adalah :
Untuk konduktivitas termal yang konstan, Persamaan (2.3) dapat dituliskan sebagai :
di mana simbol δ = k/ρc disebut difusitas termal atau kebauran termal bahan dengan
dalam bahan itu. Persamaan (2.3a) dapat juga dialihragamkan ke dalam koordinat
silindris, dan hasilnya adalah sebagai berikut :
Sistem koordinat yang digunakan dengan Persamaan (2.3b) ditunjukkan
dalam Gambar 2.5b.
Gambar 2.5 Volume unsur tiga dimensi untuk konduksi : (a) koordinat kartesius,
(b) koordinat silinder
II.3.1.2 Konduksi pada Dinding Datar
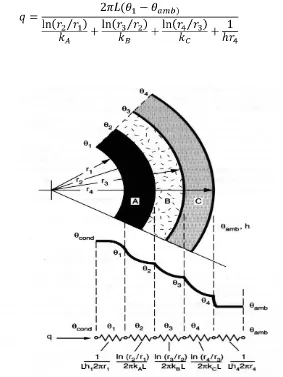
Perpindahan panas pada dinding datar yang ditunjukkan pada Gambar 2.6,
menerapkan hukum Fourier pada Persamaan 2.1. Jika persamaan tersebut
Jika konduktivitas termal dianggap tetap, tebal dinding adalah Δx, sedang dan
adalah suhu muka dinding. Jika konduktivitas termal berubah menurut hubungan
linier dengan suhu, seperti k = ko (1+βθ), maka persamaan aliran panas menjadi :
q
Gambar 2.6 Perpindahan panas melalui dinding berlapis dan analogi listriknya
Jika dalam sistem itu terdapat lebih dari satu macam bahan, seperti dinding berlapis
pada Gambar 2.6, dan gradien suhu pada ketiga bahan adalah seperti tergambar,
maka aliran panas dapat dituliskan sebagai :
Jika ketiga persamaan ini dipecahkan serentak, maka aliran panas itu dapat dituliskan
sebagai :
Laju perpindahan panas dapat dipandang sebagai aliran, sedangkan gabungan dari
Suhu merupakan fungsi potensial atau pendorong aliran itu, sehingga persamaan
Fourier dapat dituliskan sebagai berikut :
Hubungan di atas analogi dengan hukum Ohm dalam rangkaian listrik. Dalam
Persamaan (2.4), tahanan termal adalah , dan dalam Persamaan (2.6)
tahanannya adalah jumlah ketiga suku dalam pembagi. Persamaan aliran panas satu
dimensi dengan tahanan termal yang mempunyai susunan seri dan paralel adalah :
di mana merupakan penjumlahan tahanan termal yang tersusun seri atau paralel.
II.3.1.3 Konduksi pada Silinder
Suatu silinder dengan jari-jari dalam , jari-jari luar , dan panjang L,
seperti pada Gambar 2.7. Silinder ini mengalami perbedaan suhu , dan arah
aliran panas berlangsung menurut arah radial, sehingga koordinat ruang yang
diperlukan untuk menentukan sistem itu hanyalah r.
θ
iθ
oBerdasarkan hukum Fourier perpindahan panas yang terjadi pada komponen dr yang
jaraknya r dari pusat adalah :
Luas bidang aliran kalor dalam sistem silinder adalah :
sehingga hukum Fourier menjadi :
Jika Persamaan (2.11) diintegrasikan dengan batas suhu sampai , dan batas
jari-jari sampai , maka penyelesaian persamaan tersebut adalah :
Dan tahanan termal dalam hal ini adalah :
II.3.2 Konveksi
Pada kabel yang dipasang di udara akan terjadi perpindahan panas konveksi
dan radiasi dari permukaan kabel ke udara sekitar. Konveksi dapat diklasifikasikan
menurut sifat aliran menjadi konveksi paksa dan konveksi alami. Konveksi paksa
terjadi ketika aliran panas yang berpindah disebabkan oleh suatu alat penggerak
seperti angin, pompa atau kipas. Berbeda dengan konveksi alami yang timbul akibat
adanya perbedaan kerapatan udara disebabkan oleh perbedaan suhu udara. Dalam
perhitungan rating kabel dianggap hanya konveksi alami saja yang terjadi di
Dengan mengabaikan proses konveksi alami sebagian, maka persamaan
perpindahan panas konveksi dapat ditulis :
di mana q aliran panas konveksi (W/m2) yang sebanding dengan perbedaan suhu
permukaan kabel ( ) dengan suhu lingkungan ( ). Pernyataan ini dikenal
dengan hukum Newton tentang pendinginan, dengan konstanta kesebandingan h
(W/m2.K ) menunjukkan koefisien perpindahan panas konveksi. Nilai koefisien ini
bervariasi antara 2 – 25 W/m2.K untuk konveksi alami dan antara 25 – 250 W/m2.K
untuk konveksi paksa.
II.3.3 Radiasi
Radiasi termal yang terjadi pada kabel dapat berupa energi yang dipancarkan
oleh kabel atau permukaan saluran. Panas yang dipancarkan oleh permukaan kabel
diberikan oleh hukum Stefan-Boltzmann :
di mana adalah suhu mutlak dari permukaan kabel (K), disebut konstanta
Stefan-Boltzmann dengan nilai 5,67 × 10-8 W/m2.K4, dan adalah emisivitas bahan.
Nilai emisivitas bahan berada pada range , menunjukkan efisiensi suatu
permukaan memancarkan panas. Jika radiasi terjadi pada permukaan suatu benda,
maka sebagian energi akan diserap dan laju energi yang diserap persatuan luas
permukaan dapat dievaluasi dari sifat radiasi permukaan yang dikenal sebagai
di mana adalah radiasi pada permukaan, dengan nilai α berada pada 0 ≤ α ≤ 1.
Persamaan (2.15) dan (2.16) menentukan laju energi yang dipancarkan dan diserap
oleh permukaan. Dengan menganggap permukaan ini memiliki α = (permukaan
abu-abu), sehingga laju netto perubahan radiasi antara kabel dengan lingkungannya
yang dinyatakan dalam per unit luas permukaan kabel adalah :
Sehingga rugi-rugi panas pada perpindahan panas radiasi dapat diperoleh
dengan mengalikan laju perpindahan panas dengan luas daerah radiasi, dan hasilnya
adalah :
di mana (m2) adalah luas radiasi efektif per meter panjang. Pada kabel yang
dipasang di udara, panas pada permukaan kabel berpindah secara konveksi dan
radiasi. Total laju panas yang berpindah dari permukaan kabel merupakan
penjumlahan dari laju panas yang disebabkan oleh perpindahan panas konveksi dan
radiasi dan diperoleh :
di mana (m2) adalah luas kovektif per meter panjang.
II.3.4 Perpindahan Panas pada Kabel
Perpindahan panas pada kabel yang ditempatkan di udara berlangsung secara
konduksi dan konveksi. Gambar 2.8 menunjukkan suatu kabel dengan jari-jari ,
o
Gambar 2.8 Kabel dan analogi listriknya
Konduksi terjadi pada permukaan luar konduktor hingga ke permukaan luar isolasi
dengan tahanan termal yang dilalui adalah Rcond. Sedangkan secara konveksi terjadi
pada permukaan isolasi ke udara dengan tahanan termal yang dilalui Rconv. Secara
sistematis perpindahan panas pada kabel dapat ditulis sebagai :
Sedangkan untuk kabel dengan isolasi yang berlapis seperti pada Gambar 2.9, maka
laju perpindahan panas yang terjadi dapat ditulis sebagai :
L
L L L
L
Gambar 2.9 Sebagian penampang kabel dan analogi listriknya
II.4 Persamaan Kesetaraan Energi pada Kabel
Dalam analisis perpindahan panas pada sistem kabel, hukum kekekalan
energi memegang peranan penting. Hukum kekekalan energi yang berlaku di dalam
di mana adalah laju energi yang masuk ke dalam kabel, energi ini dihasilkan
oleh kabel yang lain yang berada di sekitarnya atau oleh radiasi matahari.
adalah laju energi yang dihasilkan dari rugi-rugi inti dan rugi-rugi dielektrik, dan
adalah perubahan laju energi yang tersimpan dalam kabel. Sedangkan
berhubungan dengan energi yang berpindah secara konduksi, konveksi dan radiasi.
Untuk kabel yang ditanam dalam tanah dipengaruhi juga oleh suhu tanah di sekitar.
II.4.1 Persamaan Perpindahan Panas
Perpindahan panas pada kabel yang ditanam di dalam tanah yang homogen
berlangsung secara konduksi melalui komponen-komponen kabel dan tanah. Karena
panjang dari kabel jauh lebih besar daripada diameternya, maka efeknya dapat
diabaikan sehingga masalah perpindahan panas dapat diformulasikan ke dalam dua
dimensi. Persamaan diferensial yang menjelaskan konduksi panas di dalam tanah
memiliki bentuk sebagai berikut :
di mana : θ = suhu yang tidak diketahui (oC)
δ = difusitas termal medium (m2/s)
Wint = energi panas yang berasal dari dalam kabel (W/m)
ρ = resistivitas termal bahan (K.m/W)
Persamaan (2.23) dapat diselesaikan dengan kondisi batas yang biasanya ditentukan
dari permukaan tanah. Kondisi batas ini dapat dinyatakan dalam dua bentuk, yang
di mana merupakan suhu batas yang merupakan fungsi dari panjang permukaan s.
Dan yang kedua jika panas bertambah atau hilang pada batas disebabkan oleh
konveksi atau fluks panas q, maka :
di mana n adalah arah normal permukaaan batas, h adalah koefisien konveksi, dan
adalah suhu batas yang tidak diketahui.
II.4.2 Pendekatan Polinomial
Persamaan (2.23) hingga Persamaan (2.25) dapat diselesaikan menggunakan
metode elemen hingga. Bentuk elemen dua dimensi yang paling sederhana dan
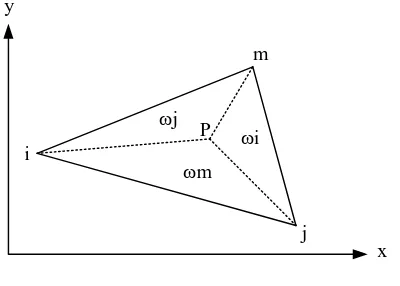
umum digunakan adalah elemen segitiga seperti ditunjukkan pada Gambar 2.10.
y
x m
i
j
ωj
ωm
ωi P
Gambar 2.10 Koordinat luas
Suhu pada beberapa titik di dalam segitiga dapat dihitung dengan persamaan aljabar
sebagai berikut :
di mana , dan adalah koordinat luas seperti yang ditunjukkan pada Gambar
maka , dengan cara yang sama untuk node j dan m diperoleh dan
, sehingga persamaan (2.27) menjadi :
Dan hubungan antara koordinat luas dan koordinat kartesius adalah :
Hasil invers dari koefisien vektor :
di mana A adalah luas segitiga. Jika dilihat Persamaan (2.28) dan (2.30) menyatakan
bahwa suhu merupakan fungsi linier dalam x dan y. Hal ini berarti gradien baik
dalam x maupun y adalah konstan.
II.4.3 Persamaan Elemen Hingga
Pada bagian sebelumnya diberikan cara menghitung suhu pada titik di dalam
sebuah elemen jika nilai suhu pada node diketahui. Untuk menghitung suhu node
dapat digunakan sifat penyederhanaan kalkulus variasi berikut :
di mana : = resistivitas termal bahan (K.m/W)
= matriks perubahan suhu =
= matriks transpos dari
h = koefisien perpindahan panas konveksi (W/m2 oC)
Persamaan (2.31) merupakan titik awal untuk menentukan suhu pada setiap node.
Dengan memperkecil Persamaan (2.31) menggunakan fungsi elemen yang
masing-masing digambarkan sebagai elemen tunggal dan ditulis dengan istilah nilai node.
Nilai node adalah nilai-nilai yang tidak diketahui di dalam formula yang diperoleh
dengan mengambil turunan , kemudian menyamakannya dengan nol. Fungsi
didefinisikan atas setiap elemen secara sendiri, dan integral dalam Persamaan (2.31)
harus dipisahkan menjadi integral pada masing-masing elemen secara sendiri dan
turunan dihitung untuk setiap elemen sehingga :
di mana adalah fungsi untuk elemen e, dan E adalah jumlah total elemen. Untuk
mempermudah menganalisisnya diambil sebuah elemen tunggal triangular. Karena
elemen tersebut menkontribusikan hanya tiga diferensial yang berhubungan dengan
Turunan dalam Persamaan (2.33) tidak dapat dievaluasi hingga integral dalam
Persamaan (2.31) ditulis dalam bentuk nilai node . Hal ini dapat dilakukan dengan
menurunkan terhadap x dan y. Hasilnya hanya ada dua koordinat luas yang terpisah
dan dianggap itu adalah dan , sehingga :
di mana Jacobian J diperoleh dengan mendiferensiasikan Persamaan (2.30). Dari
Persamaan (2.28) nilai , sehingga dapat diperoleh :
sehingga untuk elemen tunggal diperoleh :
Dengan mensubtitusikan Persamaan (2.36) ke Persamaan (2.31) dengan S dan C
yang sesuai untuk elemen tunggal dan mendiferensiasikan , setelah perhitungan
rutin Persamaan (2.33) dapat ditulis :
di mana :
Sedangkan matriks elemen kapasitas diberikan oleh :
dan elemen vektor panas yang dihasilkan sama dengan :
Tiga Persamaaan (2.38), (2.39) dan (2.40) dapat diterapkan hanya jika ada batas
sepanjang sisi elemen. Faktor menunjukkan panas total yang dihasilkan dalam
elemen (W/m). Dari Persamaan (2.37) sampai (2.40) untuk setiap elemen, akhirnya
dapat diperoleh persamaan aljabar linier untuk seluruh region :
Dalam analisis steady state Persamaan (2.41) dapat disederhanakan menjadi :
di mana : H = matriks konduktivitas panas
Q = matriks kapasitas panas
= vektor suhu node
= turunan suhu node
BAB III
KEMAMPUAN HANTAR ARUS (KHA) KABEL TEGANGAN MENENGAH
III.1 Umum
Kemampuan hantar arus suatu kabel tenaga dapat dihitung dengan metode
analitik dan metode numerik. Metode analitik menggunakan persamaan rating arus
dengan formula pendekatan yang terdapat pada standar IEC 60287. Metode numerik
membutuhkan pendekatan iteratif untuk menentukan arus konduktor pada nilai
tertentu dan menghitung suhu konduktor yang bersangkutan, kemudian arus diatur
dan perhitungan suhu diulang hingga diperoleh nilai suhu tertentu dalam toleransi
tertentu. Akan tetapi, metode numerik memberikan kemudahan dalam menganalisis
sistem kabel yang kompleks dan memberikan kondisi batas yang lebih realistis.
Dalam metode numerik, penyelesaian persamaan kemampuan hantar arus
menggunakan manipulasi matriks yang besar, sehingga akan lebih mudah jika
menggunakan program komputer untuk menyelesaikan persamaan matriks tersebut.
Dalam bab ini penulis menggunakan standar IEC 60287 untuk menjelaskan cara
menghitung kemampuan hantar arus, rugi-rugi panas yang terdapat pada kabel, dan
resistansi termal bagian-bagian kabel, sedangkan standar IEC 62095 untuk
menjelaskan metode numerik yang digunakan.
III.2 Cara Menentukan Kemampuan Hantar Arus Kabel (KHA)
Kemampuan hantar arus adalah arus maksimum yang dapat dialirkan secara
kontinu oleh penghantar pada keadaan tertentu tanpa menimbulkan kenaikan suhu
Perhitungan kemampuan hantar arus kabel mengikuti prinsip dasar bahwa
suhu pada konduktor sebagai fungsi dari panas yang dihasilkan dalam kabel (I2R)
dan jumlah panas yang dikonduksikan keluar dari kabel. Performansi termal kabel
dapat dimodelkan dengan rangkaian termal yang analogi dengan rangkaian listrik
yaitu panas analogi dengan arus, suhu analogi dengan tegangan, dan resistansi termal
analogi dengan resistansi listrik. Panas yang mengalir melalui resistansi termal akan
menaikkan suhu antara kedua sisi bahan termal. Semakin tinggi resistansi tanah atau
isolasi, maka panas akan semakin sulit keluar dari kabel dan menyebabkan suhu
konduktor semakin tinggi. Dengan menggunakan hukum Ohm perbedaan suhu antara
konduktor dengan lingkungan dapat dituliskan :
di mana : = suhu konduktor (oC)
= suhu lingkungan (oC)
= total resistansi termal antara konduktor dan udara (K.m/W)
W = panas yang dihasilkan dalam kabel (Watt/m)
I = arus listrik yang mengalir dalam konduktor (A)
R = resistansi listrik konduktor (Ω/m)
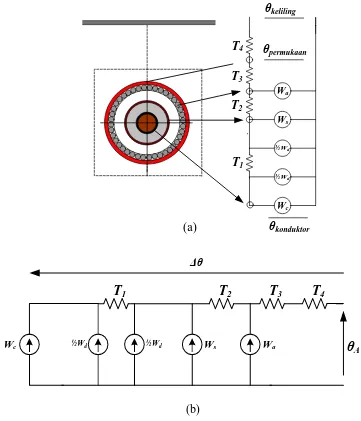
Untuk menghitung kemampuan hantar arus dianggap bahwa potensial setiap
titik dalam rangkaian adalah analogi dengan suhu antar lapisan seperti ditunjukkan
pada Gambar 3.1a. Dengan demikian perbedaan potensial antara terminal rangkaian
dengan sumber arus mewakili kenaikan suhu dari inti kabel dengan suhu keliling.
Olehkarena itu suhu inti kabel adalah suhu keliling ditambah dengan Δθ, untuk lebih
`
θkonduktor
T1
T2
T3
T4 θpermukaan θkeliling
Wc ½Wd ½Wd Ws Wa
(a)
T
1T
2T
3T
4θ
AWc ½Wd ½Wd Ws Wa
Δθ
(b)
Gambar 3.1 Rangkaian ekivalen termal listrik kabel berinti tunggal
Berdasarkan Gambar 3.1b kita dapat menghitung Δθ kabel berinti tunggal sebagai :
Untuk menurunkan persamaan kemampuan hantar arus dapat tentukan dari rumus
rugi-rugi konduktor ( ) yang dihitung dengan menggunakan resistansi ac dan arus.
Dengan mensubstitusikan Persamaan (3.3) ke Persamaan (3.2), maka diperoleh
persamaan kemampuan hantar arusnya pada Persamaan (3.4).
Untuk kabel berinti tiga rangkaian termal listriknya adalah seperti pada Gambar 3.2.
T1
T2 T3 T4
θA
3Wc 3(½Wd) 3(½Wd) Ws Wa
Δθ
T1
T1
Gambar 3.2 Rangkaian ekivalen termal listrik kabel berinti tiga
Berdasarkan Gambar 3.2 dapat dihitung Δθ kabel berinti tiga sebagai :
)
Dengan mensubstitusikan persamaan (3.3) ke persamaan (3.5), maka diperoleh
persamaan kemampuan hantar arus untuk kabel berinti tiga pada Persamaan (3.6).
di mana : I = Arus yang mengalir dalam satu konduktor (A)
= Kenaikan suhu di atas suhu keliling (oC)
= Rugi-rugi dielektrik per unit panjang (W/m)
= Resistansi termal per unit panjang antara satu konduktor dan selubung (K.m/W)
= Resistansi termal per unit panjang dari bantalan antara selubung dan perisai (K.m/W)
= Resistansi termal per unit panjang dari selubung luar kabel (K.m/W)
= Resistansi termal per unit panjang antara permukaan kabel dan medium sekitar (K.m/W)
= rasio rugi-rugi total dalam selubung logam terhadap rugi-rugi total seluruh konduktor dalam kabel
= rasio rugi-rugi total dalam perisai terhadap rugi-rugi total seluruh konduktor dalam kabel
III.3. Perhitungan Rugi-rugi Panas
Kabel tenaga tersusun dari beberapa bagian seperti dijelaskan pada bab II,
masing-masing bagian menghasilkan panas, baik yang disebabkan oleh arus, medan
listrik yang menerpa isolasinya maupun arus sirkulasi pada selubung logam atau
perisai, sehingga terjadi rugi-rugi pada bagian-bagian kabel tersebut.
III.3.1 Rugi-rugi Konduktor
Arus yang mengalir melalui suatu konduktor akan menghasilkan panas, dan
besarnya dapat dihitung dalam rugi-rugi I2R. Panas yang dihasilkan dalam inti kabel
ini harus disebarkan ke medium sekitar yang dapat berupa tanah atau udara.
Resistansi suatu konduktor ketika menghantarkan arus ac lebih besar dibandingkan
ketika menghantarkan arus dc. Hal ini disebabkan oleh dua faktor yaitu efek kulit
(skin effect) dan efek proksimiti (proximity effect). Resistansi ac per unit panjang
dimana : R = resistansi ac konduktor pada suhu maksimum (ohm/m)
R’ = resistansi dc konduktor pada suhu maksimum (ohm/m)
ys = faktor efek kulit
yp = faktor efek proksimiti
sedangkan resistansi dc per unit panjang pada suhu maksimum diberikan oleh :
di mana : = resistansi dc konduktor pada suhu 20 oC
Faktor efek kulit
Faktor efek kulit dapat ditentukan dengan rumus :
Untuk 2,8 < xs≤ 3,8
Untuk xs > 3,8
di mana :
Faktor efek proksimiti
di mana :
dc = diameter konduktor (mm)
s = adalah jarak antara sumbu konduktor (mm)
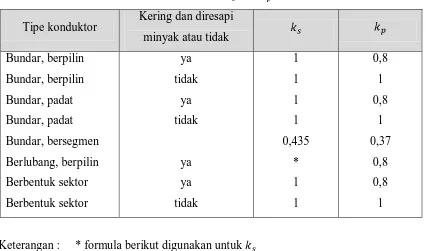
Untuk kabel dalam formasi flat, s adalah jarak antara fasa yang berdekatan. Dimana
jarak antara fasa yang berdekatan tidak sama, sehingga . Nilai dan
dapat dilihat pada tabel 3.1.
Tabel 3.1 Nilai dan
Tipe konduktor Kering dan diresapi minyak atau tidak
Bundar, berpilin
Keterangan : * formula berikut digunakan untuk
di mana : = diameter dalam konduktor (mm)
III.3.2 Rugi-rugi Dielektrik
Apabila tegangan searah diterapkan pada sebuah kapasitor sempurna, maka
arus pemuatan mengalir untuk waktu yang singkat dan memberikan kapasitor
tersebut muatan Q coulomb, sehingga timbul perbedaan potensial U antara plat-plat
kapasitor. Bila perbedaan potensial ini tercapai, maka arus berhenti mengalir. Jumlah
muatan adalah Q = C U, di mana C adalah kapasitansi yang tergantung pada
konstanta dari bahan dielektrik yang ada di plat-plat kapasitor.
Dalam kapasitor yang tidak sempurna, yaitu didapati dalam praktek, arus IC
tidak berhenti mengalir dalam waktu singkat, tetapi turun secara perlahan-lahan,
seperti pada Gambar 3.3. Arus konduksi akan mengalir dalam kapasitor praktis
karena meskipun tahanan dielektrik itu besar sekali nilainya bukan tak terhingga.
t
I
c Kapasitor tidaksempurna
Kapasitor sempurna
Gambar 3.3 Arus konduksi pada suatu dielektrik
Gejala kedua ini disebut absorpsi (penyerapan), dan bahan dielektrik yang
mempunyai sifat demikian disebut absorptif. Apabila sebuah kapasitor absorptif yang
diberi muatan (Gambar 3.4a, posisi 1), dibuang muatannya (posisi 2), lalu setelah itu
dilepaskan hubungannya (posisi 3), maka perbedaan potensial antara kapasitor naik
lagi, artinya kapasitor itu memberi dirinya muatan lagi. Hal ini dikenal sebagai efek
menganggap bahwa ada gerakan yang lamban dari molekul-molekul dielektrik
apabila plat-plat kapasitor diberi muatan. Pergerakan molekul mula-mula cepat dan
berakibat adanya arus pemuatan, lalu makin lama makin lambat dan menimbulkan
arus absorpsi.
Gambar 3.4 Kapasitor absorptif : (a) Rangkaian ekivalen (b) diagram arus dan
tegangan
Dari keterangan di atas diperoleh bahwa kapasitas sebuah kapasitor dapat dibagi
menjadi dua komponen, yaitu kapasitansi geometris dan kapasitansi absorpsi.
C1
R2
R1
C2
Gambar 3.5 Rangkaian ekivalen suatu kapasitor
Gambar 3.5 merupakan rangkaian ekivalen suatu kapasitor dengan C1 menyatakan
menyatakan efek absorpsi. Apabila dipakai arus bolak-balik, absorpsi sangat erat
hubungannya dengan rugi-rugi dielektrik dalam bahan dielektrik tersebut. Apabila
dipakai arus bolak-balik sinus dalam sebuah kapasitor sempurna maka arusnya
mendahului tegangan 90o, seperti pada Gambar 3.6. Dalam hal ini berlaku hubungan
antara arus IC dan tegangan U0 :
Akibat rugi-rugi dielektrik, maka I mendahului U0 dengan sudut kurang dari 90o,
seperti pada Gambar 3.7b. Sudut φ disebut sudut fasa dari kapasitor dan faktor
dayanya cos φ, sehingga :
Ic
U0
Gambar 3.6 Diagram fasor kapasitor sempurna
Rugi-rugi dielektrik adalah perkalian U0 dengan IR, sehingga :
Dalam kapasitor sempurna φ = 90o sehingga δ = 0, sehingga rugi-rugi dielektrik
dalam kapasitor sempurna sama dengan nol. Rangkaian ekivalen dan diagram fasor
R C I
IR Ic
Uo
Ic I
δ φ
IR
U0
(a) (b)
Gambar 3.7 Rangkaian kapasitor tidak sempurna
Menurut standar IEC, untuk isolasi yang bulat kapasitasinya adalah :
di mana : Di = diameter luar isolasi (mm)
dc = diameter konduktor termasuk tabir (mm)
= permitivitas relatif isolasi
Dari diagram fasor pada Gambar 3.7b, nilai I dapat dinyatakan dalam :
Dari substitusi Persamaan (3.16) ke Persamaan (3.20) diperoleh :
di mana : = (rad/s)
Berdasarkan Persamaan (3.22) rugi-rugi dielektrik sebanding dengan kapasitansi,
frekuensi, tegangan fasa ke netral, dan faktor rugi-rugi. Nilai permitivitas bahan
bahan isoalsi dan faktor rugi-rugi dapat dilihat pada Tabel 3.2.
Tabel 3.2 Nilai permitivitas dan faktor rugi-rugi isolasi
Tipe kabel
Kabel berisolasi dengan kertas yang diresapi
Tipe padat, fully impregnated, pre-impregnated, dan mass-impregnated nondraining
Berisi minyak, tekanan rendah
hingga = 36 kV hingga = 87 kV hingga = 160 kV
hingga = 220 kV Minyak bertekanan, tipe pipa Tekanan gas dalam
Tekanan gas luar
Kabel dengan jenis isolasi yang lain :
Karet butyl
EPR, hingga 18/30 kV EPR di atas 18/30 kV PVC
PE (HD dan LD)
XLPE meliputi dan hingga 18/30 (36) kV, tidak berisi XLPE di atas 18/30 (36) kV, tidak berisi
XLPE di atas 18/30 (36) kV, berisi Paper-polypropylene-paper (PPL)
III.3.3 Rugi-rugi Selubung dan Perisai
Medan magnet yang disebabkan oleh arus yang mengalir melalui konduktor
menginduksikan emf pada selubung logam, sehingga akan mengurangi kemampuan
melalui konduktor dan dapat dibagi menjadi dua kategori berdasarkan tipe
pembumian selubung logam. Rugi-rugi ini disebabkan oleh arus sirkulasi yang
mengalir dalam selubung logam kabel berinti tunggal jika selubung dibumikan pada
dua titik di ujung kabel dan rugi-rugi yang disebabkan oleh arus eddy yang mengalir
secara radial. Rugi-rugi arus eddy dapat terjadi baik pada kabel berinti tiga maupun
kabel berinti tunggal tidak tergantung pada metode pembumian selubung. Karena
rugi-rugi dalam selubung logam terdiri dari rugi-rugi yang disebabkan oleh arus
sirkulasi dan rugi-rugi arus eddy , maka faktor rugi-rugi pada selubung logam
dapat ditulis sebagai :
Rugi-rugi pada perisai tergantung pada tipe kabel, bahan perisai, dan metode
pemasangan. Kabel berinti tunggal dengan perisai tanpa selubung logam umumnya
memiliki perisai nonmagnetik disebabkan rugi-rugi dalam perisai kawat atau pita
baja akan sangat besar. Untuk kabel dengan perisai nonmagnetik rugi-rugi perisai
sebagaimana menghitung rugi-rugi pada selubung dan menggunakan gabungan
resistansi selubung dan diameter perisai dan selubung. Untuk kabel berinti dua atau
tiga yang memiliki perisai pita baja baik rugi-rugi arus eddy maupun rugi-rugi
histeresis harus dipertimbangkan sehingga :
a. Faktor rugi-rugi selubung logam untuk kabel berinti tiga
1. Konduktor berbentuk bundar atau oval dalam selubung, tidak ada perisai
Rs > 100 µΩ/m
di mana : c = jarak antara sumbu konduktor dengan sumbu kabel untuk
kabel berinti tiga (mm)
2. Konduktor berbentuk sektor
di mana : = jari-jari konduktor berbentuk tiga sektor kabel pada kabel
berinti tiga (mm)
= tebal isolasi antar konduktor (mm)
3. Kabel berinti tiga dengan perisai pita baja
Nilai yang dihitung dengan Persamaan (3.25) dan (3.27) harus dikalikan
dengan faktor Ft.
di mana : = ketebalan ekivalen perisai (mm)
= diameter rata-rata perisai (mm)
= permiabilitas relatif pita baja (biasanya 300)
b. Rugi-rugi perisai untuk kabel berinti tiga
• Konduktor berbentuk bulat
• Konduktor berbentuk sektor
2. Kabel berinti tiga dengan perisai pita baja
di mana : = resistansi perisai pada suhu maksimum (ohm/m)
III.4 Perhitungan Resistansi Termal
Panas yang mengalir keluar dari kabel akan terhalang oleh resistansi termal
bahan nonkonduktif di dalam kabel. Resistansi termal bagian logam dalam kabel
karena begitu kecil biasanya diabaikan dalam perhitungan rating arus kabel. Suatu
isolasi merupakan lapisan silindris dengan konstanta resistivitas termal yang
mempunyai jari-jari dalam dan jari-jari luar . Resistansi termal dari lapisan
Dalam bagian ini diberikan formula untuk menghitung resistansi termal per
unit panjang dari bagian-bagian yang berbeda dari kabel , , dan bagian luar
kabel . Resistivitas termal bahan yang digunakan sebagai isolasi diberikan pada
Tabel 3.3.
Tabel 3.3 Resistivitas termal bahan
Bahan Resistivitas Termal ( )
(K.m/W)
Bahan isolasi :
Isolasi kertas dalam kabel tipe padat Isolasi kertas dalam kabel berisi minyak Isolasi kertas dalam kabel bertekanan gas luar Isolasi kertas dalam kabel bertekanan gas dalam :
a. Pre-impregnated b. Mass-impregnated PE
XLPE
Polyvinyl chloride : hingga tegangan 3 kV
Lapisan pelindung :
Campuran jute dan bahan fiber Pelindung berlapis karet Polychroprene
PVC :
hingga tegangan 3 kV lebih dari tegangan 3 kV
III.4.1 Resistansi Termal antara Konduktor dan Selubung ( )
a. Kabel berinti tunggal
Resistansi termal antara satu konduktor dengan selubung dapat dihitung
dengan rumus :
di mana : = resistivitas termal isolasi (K.m/W)
= diameter konduktor (mm)
= ketebalan isolasi antara konduktor dan selubung (mm)
b. Kabel ikat berinti tiga
Perhitungan resistansi termal dalam dari kabel berinti tiga lebih kompleks
daripada kasus kabel berinti tunggal. Metode umum perhitungan menggunakan
faktor geometrik G sebagai ganti fungsi logaritmik pada Persamaan (3.34), sehingga
persamaan tersebut menjadi :
Nilai faktor geometrik G dapat dilihat pada Gambar 3.8.
c. Kabel berinti tiga dengan konduktor bulat
1. Kabel dengan tabir kawat logam pada setiap inti
Jika tabir yang digunakan merupakan kawat tembaga berjarak dipasang pada
di mana = tebal isolasi antara konduktor (mm)
= resistivitas termal bahan pengisi (K.m/W)
= resistivitas termal isolasi
Untuk kabel dengan isolasi kertas , maka persamaan tambahan pada sisi
sebelah kanan dapat diabaikan. Persamaan (3.36) juga dapat digunakan pada kabel
dengan tabir logam bersama yang meliputi ketiga inti.
2. Kabel dengan tabir pita logam pada setiap inti
Kabel berinti tiga dengan tabir pita logam dapat dianggap sebagai kabel ikat
dengan . Agar konduktivitas termal tabir logam tersebut dapat
diperhitungkan, maka Persamaan (3.35) harus dikalikan dengan faktor screening K
yang ditunjukkan pada Gambar 3.9, sehingga secara sistematis dapat ditulis sebagai :
Gambar 3.9 Faktor screening kabel berinti tiga dengan konduktor bulat
Rumus perhitungan faktor geometrik G dan faktor screening K secara digital dapat
diperoleh dari Lampiran A.
III.4.2 Resistansi Termal antara Selubung dan Perisai ( )
Resistansi termal antara selubung dan perisai dapat diperoleh dari Persamaan
(3.33), yang merepresentasikan resistansi termal lapisan konsentris. Dengan
menggunakan notasi untuk bagian kabel ini didapat :
= tebal bantalan (mm)
= diameter luar selubung (mm)
III.4.3 Resistansi Termal antara Selubung Luar ( )
Selubung luar umumnya berbentuk lapisan konsentris, dan resistansi
termalnya diberikan oleh :
di mana : = resistivitas termal selubung luar (K.m/W)
= tebal selubung luar (mm)
= diameter luar perisai (mm)
III.4.4 Resistansi Termal Eksternal ( )
Untuk kabel yang ditanam di dalam tanah, nilai resistansinya tidak lebih dari
70% kenaikan suhu konduktor. Resistansi termal eksternal ditentukan oleh
karakteristik termal tanah, diameter kabel, kedalaman tanah, cara pemasangan
misalnya ditanam langsung, dalam thermal backfill, dalam pipa dan lain-lain.
a. Resistansi termal eksternal kabel tunggal yang ditanam dalam tanah
di mana = resistivitas termal tanah (K.m/W)
=
= jarak dari permukaan tanah ke sumbu kabel (mm)
= diameter luar kabel (mm)
b. Resistansi termal eksternal kabel yang ditanam dalam thermal backfill
Jika kabel dipasang dalam thermal backfill, Persamaan (3.40) dapat
dimodifikasi menjadi :
di mana : = resistivitas termal backfill (K.m/W)
N = jumlah kabel yang dibebani dalam lubang
3.10b menunjukkan satu kabel dan tiga kabel yang ditempatkan dalam backfill.
h
III.5 Menentukan Kemampuan Hantar Arus dengan Metode Numerik
Masalah pada rating arus kabel biasanya menghitung arus yang diizinkan
sehingga suhu pada konduktor tidak melebihi nilai tertentu. Metode numerik
sebaliknya digunakan untuk menghitung distribusi suhu di dalam kabel dan suhu
keliling yang disebabkan oleh panas yang dihasilkan konduktor. Akan tetapi jika
metode numerik digunakan untuk menghitung rating arus kabel, maka digunakan
pendekatan iteratif dengan menentukan arus konduktor pada nilai tertentu dan
menghitung suhu konduktor yang bersangkutan. Kemudian arus diatur dan
perhitungan suhu diulang hingga diperoleh nilai suhu tertentu dalam toleransi
tertentu.
Standar IEC 62095 mengenai metode numerik berhubungan dengan metode
elemen hingga. Metode ini digunakan untuk memecahkan persamaan diferensial
parsial yang pada akhirnya membentuk persamaan perpindahan panas kabel. Konsep
dasar metode elemen hingga adalah bahwa suhu dapat dimisalkan menjadi model
diskrit yang tersusun dari beberapa fungsi kontinu yang didefinisikan sebagai
sejumlah subdomain berhingga. Prosedur umum penyelesaian metode elemen hingga
adalah :
1. Diskritisasi daerah penyelesaian menjadi elemen-elemen
2. Pemilihan fungsi-fungsi interpolasi atau fungsi bentuk
3. Membentuk persamaan-persamaan elemen
4. Menyusun persamaan elemen untuk memperoleh sistem persamaan simultan
5. Menyelesaikan sistem persamaan-persamaan elemen
Dalam penyelesaian rating arus kabel, model yang digunakan biasanya dalam
bidang dua dimensi x dan y, dan elemen yang digunakan umumnya berbentuk
triangular atau quadrilateral. Fungsi elemen dapat berupa sebuah bidang atau
permukaan kurva seperti yang telihat pada Gambar 3.11 dan 3.12. Bidang tersebut
berhubungan dengan jumlah minimum node elemen, di mana tiga untuk triangle dan
empat untuk quadrilateral.
Gambar 3.11 Elemen triangular dan quadrilateral
Ketelitian perhitungan tergantung pada kontrol pengguna yang meliputi beberapa
parameter, diantaranya adalah ukuran region yang didiskritkan, ukuran elemen yang
dibentuk oleh mesh generator, tipe dan lokasi dari batas region, adanya rugi-rugi
kabel, dan pemilihan tingkat waktu dalam analisis transien.
Ukuran region
Region merupakan daerah batas tempat menentukan nilai node. Permukaan
tanah merupakan salah satu batas, tetapi bagian bawah dan sisi kanan dan kiri harus
didefinisikan sedemikian sehingga suhu node keseluruhan mempunyai nilai yang
sama dan gradien suhu yang melalui batas sama dengan nol. Dari penelitian yang
dilakukan, sebuah medan segi empat dengan lebar 10 m dan kedalaman 5 m, dengan
kabel diletakkan di tengah, memberikan hasil yang memuaskan dalam banyak kasus
praktis (IEC 62095, p 25).
Ukuran elemen
Dengan menentukan ukuran ruang antara batas node pada berbagai bagian
dari jaringan yang dianalisis seperti kabel, thermal backfill, tanah, dan lain-lain,
maka digunakan beberapa kontrol ukuran. Ukuran elemen harus lebih kecil
mendekati bagian-bagian kabel untuk memperoleh hasil yang teliti. Penggunaan
Gambar 3.13 Penggunaan ukuran elemen yang berbeda
Kondisi batas
Metode elemen hingga menggunakan representasi kondisi batas yang berbeda
dan lokasi batas yang acak, termasuk garis lurus dan batas kurva. Untuk rating arus
kabel, tiga kondisi batas yang berbeda masih bisa digunakan. Kondisi isotermal
digunakan jika suhu diketahui sepanjang bagian batas. Suhu ini merupakan fungsi
dari panjang permukaan.
Sebuah batas konveksi ada jika panas bertambah atau hilang, dan sebaiknya
digunakan ketika kabel dengan diameter yang besar dipasang mendekati permukaan
tanah. Jika ini adalah kasus di mana pengguna harus menentukan koefisien kenveksi
panas dan suhu udara, maka nilai koefisien tersebut 2 sampai 25 W/m2.K untuk
konveksi alami dan 25 sampai 250 W/m2.K untuk konveksi paksa.
Pada kondisi ketiga, fluks yang mengalir adalah konstan, dan ini biasanya
digunakan ketika ada sumber panas lain di sekitar kabel.
Representasi rugi-rugi kabel
Rugi-rugi kabel seperti yang dijelaskan sebelumnya baik konduktor, selubung
dan dielektrik dianggap sebagai sumber panas dalam metode numerik. Rugi-rugi ini
perhitungan dalam metode analitik nilai rugi-rugi kabel harus dihitung pada setiap
langkah menggunakan prosedur yang berulang-ulang.
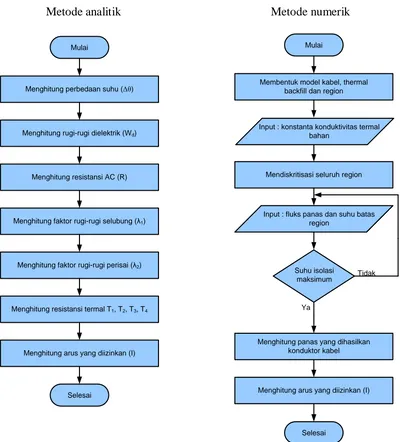
Dari penjelasan di atas, maka dapat disimpulkan cara menentukan kemampuan
hantar arus dengan metode analitik maupun numerik dalam bentuk flowchart pada
Gambar 3.14.
Metode analitik Metode numerik
Mulai
Menghitung perbedaan suhu (Δθ)
Menghitung rugi-rugi dielektrik (Wd)
Menghitung resistansi AC (R)
Menghitung faktor rugi-rugi selubung (λ1)
Menghitung faktor rugi-rugi perisai (λ2)
Menghitung resistansi termal T1, T2, T3, T4
Menghitung arus yang diizinkan (I)
Selesai
Mulai
Membentuk model kabel, thermal backfill dan region
Mendiskritisasi seluruh region
Menghitung panas yang dihasilkan konduktor kabel
Selesai
Input : fluks panas dan suhu batas region
Suhu isolasi
maksimum Tidak
Ya
Menghitung arus yang diizinkan (I) Input : konstanta konduktivitas termal
bahan
BAB IV
ANALISIS TERMAL KABEL TANAH TEGANGAN MENENGAH
MENGGUNAKAN METODE NUMERIK
IV.1 Umum
Dalam usaha melayani kebutuhan beban sistem kelistrikan di Sumatera Utara,
maka PT PLN Wilayah Sumatera Utara melakukan pembangunan yang meliputi
gardu induk dan saluran distribusi baru. Diantara saluran distribusi yang dibangun
adalah saluran kabel tanah yang bertegangan 20 kV. Kabel tanah yang umumnya
digunakan oleh PLN adalah kabel NA2XSEBY dan NA2XSEY dengan ukuran
penampang 150 mm2, 240 mm2, dan 300 mm2, disesuaikan dengan kebutuhan.
Saat ini PT PLN Rayon Medan Kota sedang merencanakan penanaman kabel
tanah bertegangan 20 kV, 240 mm2 dengan saluran tunggal. Dalam hal ini penulis
hanya mengambil data-data mengenai kabel yang akan ditanam untuk dianalisis
dengan menggunakan metode numerik berdasarkan standar IEC TR 62095.
IV.2 Data Dimensi Kabel
Untuk menganalisis kabel tanah tegangan menengah harus diketahui lebih
dahulu gambaran umum dari kabel tersebut, sehingga dengan menggunakan formula
atau suatu metode tertentu dapat dengan mudah menganalisisnya. Kabel yang
dianalisis adalah kabel NA2XSEBY 20 kV berinti tiga 240 mm2 seperti ditunjukkan
pada Gambar 4.1.
Kabel ini berinti pilinan aluminium berbentuk bulat kompak, berisolasi
XLPE, dengan tabir kawat dan pita tembaga. Agar tetap pada tempatnya ketiga inti
kabel. Untuk menahan beban mekanis kabel dipasang perisai pita baja galvanis, dan
untuk melindungi kabel dari pengaruh luar diberi selubung PVC bagian luar.
Sarung kabel
Gambar 4.1 Penampang kabel NA2XSEBY 20 kV berinti tiga 240 mm2
Sedangkan untuk analisis secara analitik dan numerik diperlukan data-data mekanik
dan listriknya dari kabel seperti yang terlihat pada Tabel 4.1 dan Tabel 4.2.
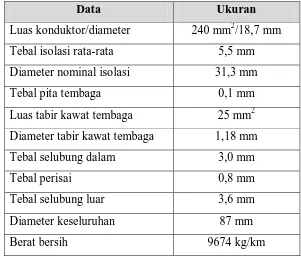
Tabel 4.1 Data mekanik kabel NA2XSEBY
Data Ukuran
Luas konduktor/diameter 240 mm2/18,7 mm Tebal isolasi rata-rata 5,5 mm
Diameter nominal isolasi 31,3 mm
Tebal pita tembaga 0,1 mm
Luas tabir kawat tembaga 25 mm2 Diameter tabir kawat tembaga 1,18 mm
Tebal selubung dalam 3,0 mm
Tebal perisai 0,8 mm
Tebal selubung luar 3,6 mm
Diameter keseluruhan 87 mm