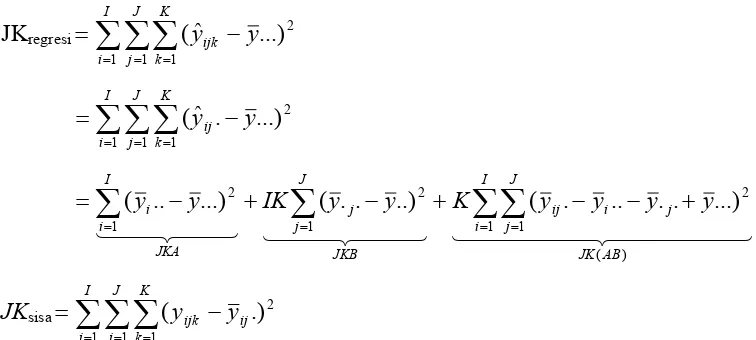Pendekatan Regresi Berganda Pada Analisis Varians Klasifikasi Dua Arah

PENDEKATAN REGRESI BERGANDA PADA ANALISIS

VARIANS KLASIFIKASI DUA ARAH

SKRIPSI

ERNI SYAHPUTRI

090823074

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

PENDEKATAN REGRESI BERGANDA PADA ANALISIS

VARIANS KLASIFIKASI DUA ARAH

SKRIPSI

ERNI SYAHPUTRI

090823074

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

PENDEKATAN REGRESI BERGANDA PADA ANALISIS

VARIANS KLASIFIKASI DUA ARAH

SKRIPSI

Diajukan untuk memenuhi tugas dan memenuhi syarat mencapai gelar Sarjan Sains

ERNI SYAHPUTRI

090823074

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

PERSETUJUAN

Judul : PENDEKATAN REGRESI BERGANDA PADA

ANALISIS VARIANS KLASIFIKASI DUA ARAH

Kategori : SKRIPSI

Nama : ERNI SYAHPUTRI

Nomor Induk Mahasiswi : 090823074

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM

(FMIPA) UNIVERSITAS SUMATERA UTARA

Disetujui

Medan, September 2011

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. Ujian Sinulingga, M.Si Drs. Pengarapen Bangun,M.Si

195603031984031004 NIP. 195608151985031005

Diketahui/Disetujui oleh

Departemen Matematika FMIPA USU

Ketua,       

     

PERNYATAAN

PENDEKATAN REGRESI BERGANDA PADA ANALISIS VARIANS KLASIFIKASI DUA ARAH

SKRIPSI

Saya mengakui bahwa Skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan ringkasan yang masing-masing disebutkan sumbernya.

Medan, September 2011

PENGHARGAAN

Bismillahirrohmanirrahim, Segala Puji dan syukur penulis panjatkan kehadirat Allah SWT atas berkat dan limpah-Nya sehingga penulis dapat menyelesaikan Skripsi ini tepat pada waktu yang telah ditentukan.

Ucapan terima kasih saya sampaikan kepada Drs. Pengarapen Bangun,M.Si dan Drs. Ujian Sinulingga, M.Si selaku pembimbing pada penyelesaian skripsi ini yang telah memberikan panduan dan penuh kepercayaan pada penulis dalam menyempurnakan kajian ini. Panduan ringkas, padat dan professional telah diberikan agar penulis dapat menyelesaikan skripsi ini. Serta Bapak Drs. Djakaria Sebayang, M.Si dan Drs. Rachmad Sitepu, M.Si yang telah bersedia menjadi dosen penguji skripsi. Terima kasih atas saran dan masukannya.

ABSTRAK

Prosedur Regresi Berganda untuk memperoleh suatu jawaban b = (XT X)-1 (XT Y) bagi

persamaan normal XT Xb = (XT Y) maka disyaratkan bahwa matriks XT X bersifat tidak

singular. Dalam praktek, ini berarti bahwa persamaan normalnya harus terdiri atas persamaan-persamaan yang bebas satu sama lain yang banyaknya sama dengan banyaknya parameter yang harus diduga. Akan tetapi kalau datanya berasal dari percobaan yang terancang, perlu diperiksa bahwa semua persamaan itu bebas, kalau ternyata tidak demikian diambil langkah-langkah yang diperlukan untuk memperoleh nilai dugaan.

Pendekatan Regresi Berganda dapat digunakan untuk memecahkan masalah Analisi Ragam, baik ANOVA klasifikasi satu arah ataupun klasifikasi dua arah. Dalam ANOVA, model adalah faktor terpenting. Disini akan dipelajari ANOVA klasifikasi dua arah dengan pendekatan regresi berganda untuk masalah model pengaruh tetap. Permasalahan ini dapat dikerjakan jika modelnya diidentifikasikan secara benar dan kalau langkah-langkah pencegahan telah diambil agar diperoleh persamaan normal yang bebas. Suatu ciri model analisis ragam adalah bahwa model terparameterisasikan secara berlebih sehingga harus dibuat kendala-kendala pada parameter-parameternya.

MULTIPLE REGRESSION APPROACH TO TWO WAYS CLASSIFICATION ANALYSIS OF VARIANCE

ABSTRACT

The procedurs for multiple regression to obtained a solution b = (XT X)-1 (XT Y), of the

normal equation XT Xb = (XT Y), it is necessary that XT X be a nonsingular mattrix. All

this means in practise is that the normal equations must involve as many independent equations as there are parameters to be estimated. If data are obtaned from a designed experiment, however, some case is needed to check that all the normal equations are independent, or if they are not, take steps to obtained stimated just the same.

Multiple Regression approach can be used for solving Analysis of Variance problem, whether of one way or two ways ANOVA. In ANOVA, model is an important factor. This study focus on two ways classifications ANOVA with regression approach for solving the fixed effect model. it can be done if the model is identified truly and if the preventive procedure have been done so an independent normal equation has been.A characteristic of ANOVA is that the analysis model is overparameterized, so have to made constraint for parameters.

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak v

Abstrack vi

Daftar Isi vii

Daftar Tabel ix

Daftar Gambar x

Bab 1 Pendahuluan 1.1Latar Belakang 1

1.2Perumusan Masalah 2

1.3Tujuan Penelitian 3

1.4Kontribusi Penelitian 3

1.5Tinjauan Pustaka 3

1.6Metode Penelitian 6

Bab 2 Landasan Teori 7

2.1 Analisis Regresi 7

2.1.1 Regresi Linier Sederhana 7

2.1.4 Pendekatan melalui Analisis Variansi 13

2.2 Pengertian Dasar Penyimpangan dan Ragam 14

2.3 Analisis Ragam (ANAVA) 16

2.3.1 Analisis Varians Klasifikasi Satu Arah 17

2.3.2 Analisis Varians Klasifikasi Dua Arah 22

2.3.3 Analisis Varians Klasifikasi Dua Arah dengan Interaksi 28

Bab 3 Pembahasan 34

3.1 Multiple Regresi 34

3.1.1 Metode Kuadrat Terkecil dengan Matriks 37

3.1.2 Analisis Ragam dalam Regresi Linier Berganda 39

3.2 Pendekatan Multiple Regresi pada Analisis Varians Klasifikasi Dua Arah 41

3.3 Pendekatan Multiple Regresi pada Analisis Varians Klasifikasi Dua Arah 46

dengan Interaksi 3.4 Pengguna Peubah Boneka 49

3.5 Contoh Kasus 50

Bab 4 Kesimpulan dan Saran 58

4.1 Kesimpulan 58

4.2 Saran 58

Daftar Pustaka 59

DAFTAR TABEL

Halaman

Tabel 2.1 Tabel Analisis Varians Regresi Sederhana 8

Tabel 2.2 k Sampel Acak 17

Tabel 2.3 Analsisi varians untuk Klasifikasi Satu Arah 22

Tabel 2.4 Klasifikasi Dua Arah 22

Tabel 2.5 Analisis Varians Klasifikasi Dua Arah 28

Tabel 2.6 Klasifikasi Dua Arah dengan Interaksi 29

Tabel 2.7 Analisis Varians Klasifikasi Dua Arah dengan Interaksi 33

Tabel 2.8 Jumlah Kuadrat ANAVA Dua Arah dengan Interaksi 41

Tabel 3.1 Tabel ANAVA untuk Sumber Varians Y 41

Tabel 3.2 Analisi Varians Klasifikasi Dua Arah tanpa Interaksi 45

Tabel 3.3 Analisi Varians Klasifikasi Dua Arah dengan Interaksi 48

Tabel 3.4 Data 24 Amatan darri Ka talisator dan Pereaksi 50

Tabel 3.5 Data Contoh 51

Tabel 3.6 Analisis Varians Klasifikasi Dua Arah 53

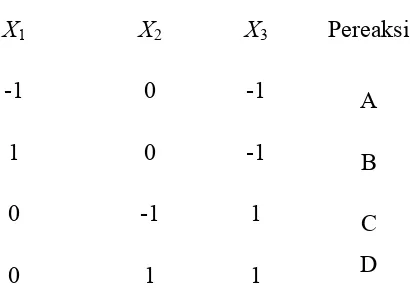
Tabel 3.7 Data Peubah Boneka X1,X2, X3 54

Tabel 3.8 Data Peubah Boneka X4,X5 54

DAFTAR GAMBAR

Halaman

Gambar 2.1 Diagram Pencar 8

Gambar 2.2 Menguraikan Variasi menurut Unsurnya 12

Gambar 2.3 Contoh Pengamatan dari Individu Pertama sampai ke N 14

ABSTRAK

Prosedur Regresi Berganda untuk memperoleh suatu jawaban b = (XT X)-1 (XT Y) bagi

persamaan normal XT Xb = (XT Y) maka disyaratkan bahwa matriks XT X bersifat tidak

singular. Dalam praktek, ini berarti bahwa persamaan normalnya harus terdiri atas persamaan-persamaan yang bebas satu sama lain yang banyaknya sama dengan banyaknya parameter yang harus diduga. Akan tetapi kalau datanya berasal dari percobaan yang terancang, perlu diperiksa bahwa semua persamaan itu bebas, kalau ternyata tidak demikian diambil langkah-langkah yang diperlukan untuk memperoleh nilai dugaan.

Pendekatan Regresi Berganda dapat digunakan untuk memecahkan masalah Analisi Ragam, baik ANOVA klasifikasi satu arah ataupun klasifikasi dua arah. Dalam ANOVA, model adalah faktor terpenting. Disini akan dipelajari ANOVA klasifikasi dua arah dengan pendekatan regresi berganda untuk masalah model pengaruh tetap. Permasalahan ini dapat dikerjakan jika modelnya diidentifikasikan secara benar dan kalau langkah-langkah pencegahan telah diambil agar diperoleh persamaan normal yang bebas. Suatu ciri model analisis ragam adalah bahwa model terparameterisasikan secara berlebih sehingga harus dibuat kendala-kendala pada parameter-parameternya.

MULTIPLE REGRESSION APPROACH TO TWO WAYS CLASSIFICATION ANALYSIS OF VARIANCE

ABSTRACT

The procedurs for multiple regression to obtained a solution b = (XT X)-1 (XT Y), of the

normal equation XT Xb = (XT Y), it is necessary that XT X be a nonsingular mattrix. All

this means in practise is that the normal equations must involve as many independent equations as there are parameters to be estimated. If data are obtaned from a designed experiment, however, some case is needed to check that all the normal equations are independent, or if they are not, take steps to obtained stimated just the same.

Multiple Regression approach can be used for solving Analysis of Variance problem, whether of one way or two ways ANOVA. In ANOVA, model is an important factor. This study focus on two ways classifications ANOVA with regression approach for solving the fixed effect model. it can be done if the model is identified truly and if the preventive procedure have been done so an independent normal equation has been.A characteristic of ANOVA is that the analysis model is overparameterized, so have to made constraint for parameters.

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Sampai saat ini, model Regresi dan model Analisis Variansi telah dipandang sebagai dua hal yang tidak berkaitan. Meskipun ini merupakan pendekatan yang umum dalam menerangkan kedua cara ini pada taraf permulaan, model Analisis Variansi dapat dipandang sebagai hal khusus model Regresi Linear.

Dalam penelitian menggunakan eksperimen, analisisnya dilakukan menggunakan Analisis Variansi (ANAVA) berdasarkan model dan desain eksperimen yang cocok untuk permasalahannya. Desain dan analisis eksperimen yang berpedoman pada pengetahuan dasar inilah yang akan dibicarakan hubungannya dengan Analisis Regresi. Analisis Regresi pada dasarnya adalah studi mengenai ketergantungan variable tak terbatas dengan satu atau lebih variabel bebas, dengan tujuan untuk mengestimasi dan/atau memprediksi rata-rata populasi atau nilai rata-rata variabel tak bebas berdasarkan nilai variabel bebas. Hasil Analisis Regresi adalah berupa koefisien (parameter) untuk masing-masing variabel

bebas. Produsen Regresi berganda untuk memperoleh parameternya, b = (XT X)-1 (XT Y)

yaitu, disyaratkan bahwa matriks (XT Y) bersifat tidak singular, ini berarti bahwa

persamaan itu bebas, kalau ternyata tidak demikian, maka harus diambil langkah-langkah yang diperlukan untuk memperoleh nilai dugaan.

Metode yang banyak digunakan untuk menganalisis data dari suatu percobaan yang terancang adalah teknik analisis variansi. Seringkali teknik ini dipandang sama sekali berbeda dari regresi secara umum, belum banyak peneliti yang menyadari bahwa setiap masalah analisis variansi dengan pengaruh tetap dapat ditangani melalui teknik regresi secara umum kalau modelnya diidentifikasi secara benar dan langkah-langkah pencegahan telah diambil agar diperoleh persamaan model yang bebas. Suatu ciri analisis variansi adalah model ini terparameterisasikan secara berlebih, artinya model ini mengandung lebih banyak parameter dari pada yang dibutuhkan untuk memprestasikan pengaruh-pengaruh yang diinginkan. Parameterisasi berlebihan ini biasanya dikompensasi dengan membuat kendala terhadap parameter-parameternya. Kendala pada

percobaan untuk klasifikasi 2 arah tanpa interaksi diambil 



I i 1i

= 



J

j 1j= 0 dan dengan

interaksi 



I

i 1i=  J

i 1j=  I

i 1yij =  J

j 1yij= 0. Seringkali tanpa disadari bahwa semua

situasi analisis variansi mempunyai model, dan bahwa model itulah yang menjadi dasar bagi pembuatan table analisis variansi.

1.2 Perumusan Masalah

Yang menjadi masalah dalam penelitian ini adalah bagaimana teknik analisis variansi klasifikasi dua arah dapat diselesaikan melalui pendekatan regresi berganada.

1.3 Tujuan Penelitian

Menguraikan cara untuk menyelesaikan persoalan analisis variansi klasifikasi dua arah dengan pendekatan regresi berganda dengan membuat peubah yang bersifat pengelompokkan.

1.4 Konstribusi Penelitian

a. Dapat diketahui bahwa Analisis Regresi merupakan model linear yang sangat umum

dan sampai batas tertentu dapat digunakan menangani permasalahan dalam Analisis Variansi.

b. Menambah wawasan dan memperkaya literature dalam bidang statistika yang

berhubungan dengan Analisis Variansi (ANOVA) dengan pendekatan regresi.

c. Mengkaji lebih dalam lagi hubungan antara Analisis Variansi dan Analisis Regresi.

1.5 TinjauanPustaka

umumnya, hubungan antara k variabel yaitu Y dengan X1, X2,…, Xk dengan k variabel

bebas suatu sampel dengan n obsevasi adalah

Yi = + + + … + +

Dengan :

Xi = variabel independen ke-i

Yi = variabel dependen ke-i

, , ,… = parameter model yang akan ditaksir

= nilai kesalahan berdistribusi N (0, ).

Setelah menaksir persamaan regresi, pada referensi [6] yaitu masalah berikutnya menilai buruknya kecocokan model regresi yang digunakan dengan data. Perhatikan kesamaan berikut :

= +

Dengan:

= variansi Regresi Sisa

Bila ruas kiri kanan dikuadratkan dan kemudian dijumlahkan maka diperoleh







_n 

i

i y y 1

2

=





 





2

1

ˆ ˆ



_n   

i

i i

i y y y

y

=













_{i i}



n

i i n

i

i i n

i

i y y y y y y y

yˆ ˆ 2 ˆ ˆ

1 2

1 1

2

 

  









_{  }

Perkalian yang terakhir penulisan i = 1 dan n pada ∑ dihilangkan sehingga menjadi

Bagian kedua ruas kanan sama dengan nol karena

Bagian pertama ruas kanan juga sama dengan nol karena

0 + b 0

Jadi persamaan dapat ditulis kembali sebagai berikut :



























 

n

i

i n

i i n

i

i y y y y y

y

1 2

1 1

2

) ˆ (

ˆ

Dengan :









sisa kuadrat Jumlah

y y

ragam kuadrat

Jumlah y

y

total kuadrat Jumlah

y y

n

i

i i n

i i n

i i

 

 

 







  

1

2

1 1

2

) ˆ (

ˆ

Persamaan ini adalah persamaan dasar dalam analisis regresi dan analisis variansi. Jadi dengan demikian dapat pula ditulis sebagai :

Dari referensi [6] dan [12] secara matematika model klasifikasi dua arah tanpa interaksi dapat ditulis sebagai berikut :

,

dengan :

i = 1,2,…,I , j = 1,2,… J,

bila kedua faktor ada interaksi, maka banyaknya pengamatan per sel haruslah lebih besar dari satu agar interaksi dan sisa dapat dipisah. Dengan adanya interaksi maka persamaan menjadi

, dengan :

i = 1,2,…, I; j 1,2, …, J; k=1,2,…, K.

K = adalah banyaknya dalam pengamatan dalam tiap sel.

1.6 Metode Penelitian

1. Membentuk model analisa Variansi klasifikasi dua arah, yaitu Model Analisis Variansi

dapat ditulis dalam bentuk umum model Analisis Regresi dengan Xi(I = 1,2,… I)

mendapat nilai 1 dan 0.

2. Menaksir parameter pada analisis variansi klasifikasi dua arah, yaitu

parameterisasi yang berlebihan dalam Analisis Variansi dikompensasi dengan membuat kendala terhadap parameter-parameternya.

3. Membentuk tabel Analisis Variansi yaitu, Model Analisis Variansi adalah menjadi

4. Pendekatan Regresi terhadap Analisis Variansi klasifikasi dua arah, yaitu membentuk

persamaan regresi berganda dengan penggunaan peubah boneka (dummy variables)

atau peubah bebas.

BAB 2

LANDASAN TEORI

2.1 Analisis Regresi

Salah satu tujuan analisis data adalah untuk memperkirakan/memperhitungkan besarnya efek kuantitatif dari perubahan suatu kejadian terhadap kejadian lainnya. Setiap kebijakan (policy), baik dari pemerintah maupun swasta, selalu dimaksudkan untuk mengadakan

perubahan (change). Sebagai contoh, Pemerintah menambah jumlah pupuk agar produksi

padi meningkat, Pemerintah menaikkan gaji pegawai negeri agar prestasi kerja mereka meningkat dan lain sebagainya. Untuk keperluan evaluasi/penilaian suatu kebijaksanaan mungkin ingin diketahui besarnya efek kuantitatif dari perubahan suatu kejadian terhadap kejadian lainnya. Kejadian-kejadian tersebut untuk keperluan analisis bisa dinyatakan

didalam perubahan nilai variabel. Untuk analisis kedua kejadian (events) digunakan dua

variabel X dan Y. Teknik Statistika untuk memeriksa dan memodelkan hubungan diantara variabel-variabel disebut Analisis Regresi.

2.1.1 Regresi Linier Sederhana

Regresi linier sederhana adalah suatu prosedur untuk mendapatkan hubungan matematis dalam bentuk suatu persamaan antara variabel dependen tunggal dengan variabel independen tunggal. Hubungan antara dua variabel dependen dan variabel independen ini dapat dirumuskan ke dalam suatu bentuk hubungan fungsional sebagai berikut:

Dengan:

Yi = variabel terikat ke-i

Xi = variabel bebas ke-i

a = intersep (titik potong kurva terhadap sumbu Y) b = kemiringan (slope) kurva linear

Dalam membuat keputusan, selalu ada resiko yang disebabkan oleh adanya

kesalahan (error). Resiko hanya bisa diperkecil dengan memperkecil kesalahan

(minimized error →minimized risk). Dengan memperhitungkan kesalahan pengganggu , maka bentuk persamaan linear menjadi sebagai berikut:

Dengan:

a dan b adalah konstanta yang diestimasi

adalah kesalahan pengganggu (disturbance’s error)

= disebut juga sisa yang terkandung galat yang sifatnya acak dan

penyimpangan model dari keadaan sesungguhnya.

Dalam praktik, untuk melihat hubungan antara X dan Y, dikumpulkan pasangan data (X,Y) sebagai suatu observasi, misalnya sebagai berikut :

X1,X2,…,Xi,…,Xn

Y1,Y2,…Y1,…,Yn

Garis lurus yang terdapat pada diagram pencar pada gambar 2.1 yang memperlihatkan adanya hubungan antara kedua variable disebut garis regresi atau garis perkiraan, dan persamaan yang digunakan untuk mendapatkan garis regresi pada data diagram pencar disebut persamaan regresi yang merupakan suatu variable matematika yang mendefenisikan hubungan antara dua variable.

2.1.2 Metode Kuadrat Terkecil

Untuk mendapatkan garis regresi yang paling baik yaitu garis regresi yang memiliki deviasi atau kesalahan terkecil, maka digunakan metode kuadrat terkecil. Metode kuadrat

terkecil ialah suatu metode untuk menghitung dan , sedemikian sehingga kesalahan

kuadrat memiliki nilai terkecil. Dengan bahasa matematika, dinyatakan sebagai berikut:

Yi = i = 1,2, …, n

= – ( = kesalahan pengganggu

= = jumlah kesalahan kuadrat

Jadi metode kuadrat terkecil adalah metode untuk menghitung dan

turunan parsial (partial differential) dari mula-mula terhadap kemudian

terhadap kemudian menyamakannya dengan nol.

= 2 = 0 …. (2.1)

= 2 = 0 ….

(2.2)

Persamaan (2.1) dibagi dengan

Sehingga

Masukkan ke persamaan (2.2)



















  



 

 



 2

1 1

2 1 1 1 )

( _{i i i} i i _{i i}

i

i X X

n X

n Y Y

X X

X X Y Y

X    









   2

1 1

) (

i i

i i i

i X

n X

n Y X Y

X    

n Y X Y

X n

X

X i i i i

i

i





 



  

    

  

 1

2

2 ( )   

Sehingga





 

 



 





 



 2 2

1 2

2 1 1

) ( )

( _i

i i i

i

i i i

X X

n

Y X Y

X n n X X

n Y X 

Setelah menaksir persamaan regresi, masalah berikutnya adalah menilai baik buruknya model regresi dengan data. Jadi diperlukan ukuran tentang kecocokan data. Analisis regresi adalah alat statistik yang digunakan untuk mengetahui derajat hubungan linear antara satu variable dengan variabel lain. Umumnya analisis korelasi digunakan dalam hubungannya dengan analisis regresi untuk mengukur ketetapan garis regresi dalam

menjelaskan (explaining) variasi nilai variabel dependen.

Untuk statistik yang dapat menggambarkan hubungan antara suatu variabel

dengan variabel lain adalah koefisien determinasi (R2) dan koefisien korelasi (r).

koefisien determinasi adalah salah satu nilai statistik yang dapat digunakan untuk mengetahui apakah ada hubungan pengaruh antara dua variabel. Perhatikan kesamaan berikut:

) ˆ )

ˆ ( )

(y_i y  y_i y  y_i y_i

Bila ruas kiri dan kanan dikuadratkan dan kemudian dijumlahkan maka diperoleh





2

1 1

2

) ˆ ( ) ˆ ( )

(





_   _n   

i

i i i

n

i

i y y y y y

y  

           (ˆ ) ( ˆ ) 2 (ˆ )( ˆ ).

1 1

2

1

2







_   _   _  

 n

i

i i i

n

i

i i n

i

i y y y y y y y

y …(2.3)

Perkalian yang terakhir pada persamaan (2.3) penulisan I = 1 dan n pada ∑ dihilangkan

sehingga menjadi



(yˆi  y)(yi yˆi)



yˆi(yi  yˆi)y



(yi  yˆi). Bagian kedua ruas kanan sama dengan nol karena menurut (2.1)



(y_i  yˆ_i)



(y_i abx_i)0



yˆ(y_i yˆ_i)



(abx_i)(y_i yˆ_i) 

    = a



(y_i yˆ_i)b



(y_i yˆ_i)x_i  

      = 0 b



(y_i abx_i)x_i = 0

Jadi persamaan dapat ditulis kembali sebagai berikut (2.4)

) ˆ ( )

ˆ ( )

(

1 2

1 1

2

i n

i n

i n

i

i y y y y y

y

i

i   











_{  }      

      JKT JKR JKS

Persamaan (2.4) adalah persamaan dasar dalam Analisis Regresi dan Analaisis variansi. Ruas kiri disebut jumlah kuadrat total (JKT) atau jumlah variasi total dan menyatakan jumlah penyimpangan y disekitar nilai rata-ratanya. Bagian pertama ruas kanan disebut jumlah kuadrat regresi (JKR) dan ini adalah variansi respons disekitar rata-ratanya ( ). Bagian kedua ruas kanan disebut jumlah kuadrat galat (sisa) dan singkat JKS. Bagian ini mengukur sisa dari variasi total (JKT) yang tidak dapat diterangkan oleh x, atau bagian yang sifatnya acak. Jadi dengan demikian dapat pula ditulis sebagai berikut:

JKT = JKR + JKS

Variasi Total = Variasi karena Regresi + Variasi karena Sisa.

Sifat penjumlahan (aditing) seperti ini banyak dijumpai dalam statistika, dan ini tidak hanya berlaku untuk bentuk kuadrat tapi juga untuk derajat kebebasannya. Jika pengaruh X terhadap Y besar maka diharapkan JKR cukup besar dibandingkan dengan JKS. Bila JKR besar maka JKS kecil dan sebaliknya, sedangkan JKT tetap. Dengan demikian JKT dapat dijadikan pembanding untuk menentukan besar kecilnya JKR atau JKS.

Dari defenisi

R

JKS JKR y

y y y

i i

   





2 2 2

) (

Dengan:

R2 disebut koefisien korelasi dua arah atau koefesien penentu (determinasi).

Karena 0< JKR< JKT, maka tentunya 0 < R2< 1. Jadi R2 dapat mengukur kecocokan data

dengan model makin dekat R2 dengan 1 makin baik kecocokan data dengan model dan

sebaliknya, makin dekat R2 dengan 0 makin jelek kecocokan tersebut.

2.1.1 Pendekatan Melalui Analisis Variansi

Dari persamaan (2.4) dapat dilihat penguraian jumlah kudrat total atas kedua komponennya, jumlah kuadrat regresi dan jumlah kuadrat galat. Tujuan utama penguraian

bukanlah untuk menghitung R2, tetapi merupakan langkah awal yang sangat penting

dalam menelaah komponen jumlah kudrat total. Untuk menentukan apakah pengaruh suatu peubah bebas X besar atau kecil terhadap respon Y diperlukan pambanding yang baku, yang tidak dipengaruhi baik buruknya model yang digunakan. Pembanding baku

tersebut adalah penaksir tak bias dari , variansi .

Disamping JKT dapat diuraikan atas kedua komponennya, derajat kebebasannya

dapat diuraikan juga. Sifat penjumlahan (aditing) ini merupakan salah satu keunggulan

Tabel 2.1 Tabel Analisis Variansi Regresi Sederhana Sumber

Variasi

JK (Jumlah Kuadrat) dk (Derajat

Kebebasan)

RK(Rataan Kuadrat)

F Hitung

Regresi Sisa

JKR =



 2

) ˆ

(Y_i Y  

JKS =



(  ˆ )2

i Y Y_i

1 n-2

 2 1

s JKR/1

 2 2

s JKS/(n-2)

2 2 2 1

s s

Total JKT =



 2

)

(Yi Y n-1

Tabel 2.1 Memperlihatkan bentuk umum table analisis variansi (ANAVA) untuk regresi linear sederhana. Kolom keempat menunjukkan jumlah kuadrat dibagi dengan derajat kebebasannya, untuk regresi dan sisa.

Andaikan hipotesis yang akan diuji adalah

H0 : β = 0

H1 : β≠ 0

Yang pada dasarnya hipotesis nol ini mengatakan bahwa variansi dalam Y diakibatkan oleh fluktuasi acak yang tidak tergantung pada nilai X dengan kata lain X tidak mempengaruhi respons Y. bila hipotesis nol ditolak yaitu bila nilai Statistik F hitungan

melebihi nilai kritis F_α (1, n-2) maka disimpulkan bahwa terdapat jumlah variasi yang

berarti dalam respon Y yang disebabkan atau diterangkan oleh model yang dipandang benar, yaitu fungsi linear. Bila statistic F berasal dalam daerah penerimaan maka disimpulkan bahwa data tidak memberikan cukup dukungan kepada model yang dianggap benar.

Sebagai contoh misalkan dilakukan penelitian lapangan melalui survei sehingga hasil sampel yang diperoleh meliputi N individu. Individu tersebut dapat berupa perorangan, rumah tangga, industry kecil, atau wilayah dan lainnya. Masing-masing individu dinyatakan dengan huruf I yang menunjukkan individu ke-i dalam sampel. Informasi

yang diperoleh dari setiap individu memberikan nilai-nilai pengamatan Y adalah: Y1, Y2 ,

Y3 …, Yn. dapat dilihat gambar 2.3 yaitu suatu contoh mengenai berbagai hasil

pengamatan yang diperoleh dari individu pertama sampai dengan ke-N.

         y      

    

Gambar 2.3 Contoh Pengamatan dalam bentuk nilai rata-rata

[image:30.612.132.441.300.486.2]

Langkah pertama yang harus dilakukan yaitu memilih model apa yang akan digunakan. Model tersebut bisa berupa nilai rata-rata, median, modus dan lainnya ataupun yang lebih rumit mengikuti suatu pola tertentu secara linear ataupun nonlinear. Pada

gambar 2.3 diambil suatu contoh dalam bentuk nilai rata-rata hitung, , dari seluruh

Dengan demikian seberapa besar penyimpangan yang terjadi diantara nilai pengamatan dan nilai yang terkandung dalam model hitung dari nilai rata-rata digambarkan dengan menguraikan setiap nilai pengamatan menjadi

)

(Y Y

Y

Y_i   _i 

= 1,2,3,…,N

Dimana memberikan besaran nilai penyimpangan sehingga menggambarkan

naik turunnya (fluktuasi) hasil pengamatan terhadap model dan menunjukkan seberapa

jauh model yang dipakai tidak mampu menjelaskan kenyataan yang ada. Arah panah ke bawah berarti penyimpangan yang negatif sedangkan arah ke atas menunjukkan penyimpangan yang positif.

Persamaan (2.5) mempergunakan suatu model yang sederhana nilai rata-rata Dalam bentuk umumnya persamaan tersebut dapat dinyatakan sebagai berikut:

) ˆ (

ˆ _{Y Y}

Y

Y_i   _i 

= 1,2,3,…,N Pengamatan = Cocokan + Residual

merupakan model yang menggambarkan prediksi atau dugaan (estimasi) yang disebut

juga dengan fitted values. Nilai dapat berupa suatu titik fungai linier atau nonlinear,

Sedangkan menunjukkan besarnya penyimpangan atau residual.

Berdasarkan definisi dapat dilihat dengan jelas bahwa residual merupakan sisa dari hasil pengamatan yang belum dapat dijelaskan oleh suatu model tertentu. Dalam Analisis Regresi, yang menjadi tujuan utama adalah membuat jumlah kuadrat sisa atau

residu, JKS = sekecil mungkin agar dicapai suatu pemecahan

mengecil dengan kata lain semakin besar kemampuan model dalam menjelaskan keragaman peubah tak bebas.

2.3 Analisis variansi (ANAVA)

Analisis variansi (Analysis of Variance) merupakan metode yang digunakan untuk

menganalisis atau menguraikan keragaman total data menjadi komponen-komponen sumber keragaman. Dalam analisis variansi yang paling sederhana, dipergunakan satu peubah tak bebas. Persyaratan utama yang harus dipenuhi berkaitan erat dengan skala pengukuran. Peubah tak bebas paling tidak harus dapat diukur dalam bentuk skala interval. Sedangkan peubah bebas dapat berupa peubah nonmetrik (peubah yang tidak dapat diukur) atau sebagai gabungan antara peubah nonmetrik dengan peubah metrik

(peubah yang dapat diukur). Peubah bebas yang nonmetrik lebih dikenal sebagai faktor,

sementara peubah metric disebut sebagai kofaktor.

Bila keseluruhan peubah bebas tersebut hanya terdiri atas kofaktor, maka analisa

yang dipakai adalah Analisa Regresi. Analisa Regresi sederhana memecahkan

permasalahan yang hanya mengandung satu kofaktor saja. Bila lebih dari satu kofaktor,

pemecahan tersebut ditangani oleh Analisa Regresi Ganda (Multiple Regression

Analysis). Akan tetapi bila keseluruhan peubah bebas adalah factor, maka analisa yang

digunakan pada dasarnya adalah Analisa Variansi (Analysis of Variance). Jika yang

menjadi perhatian utama terletak pada apakah ada kemungkinan pengaruh satu factor

terhadap peubah tak bebas, maka pembahasan ini disebut dengan Analisa Variansi Satu

faktor analisanya dilakukan dengan Analisa Variansi Dua Arah (Two - Way Classification Analysis of Variance).

2.3.1 Analisis Variansi Klasifikasi Satu Arah

Di dalam klasifikasi satu arah melibatkan sebuah factor penentu. Populasi yang berbeda ini diklasifikasikan menurut perlakuan atau grup yang berbeda dan dianggap saling bebas

dan berdistribusi normal dengan rataan = = … = dan variansi . Istilah

perlakuan digunakan secara umum dengan arti bebagai klasifikasi, apakah itu kelompok, adukan, penganalisis, pupuk yang berbeda, atau berbagai daerah disuatu negara, dan variansi

Ingin dicari metode yang sesuai untuk menguji hipotesis:

H0 : = = … =

H1 : ≠ ≠ … ≠

Misalkan menyatakan pengamatan ke j dalam perlakuan ke i dan Ti

menyatakan jumlah semua pengamatan dalam sampel dari perlakuan ke i, menyatakan

rataan semua pengamatan dalam sampel dari perlakuan ke i, T.. jumlah semua nI

pengamatan, dan .. rataan semua nI pengamatan. Tiap pengamatan dapat ditulis dalam

bentuk

= (2.6)

Tabel 2.2 k sampel acak Perlakuan

1 2 … I

11

12

y        y_22   …    y_I2                         

n

y₁        y_{2n    …}   y_In

Jumlah _T

1. T2. … TI.

 

T…

Rataan y₁.      y_2..   _…  y_.I.  y..

Dengan menyatakan penyimpangan ke j pada sampel ke i dari rataan perlakuan

padanannya. Suku menyatakan galak acak yang peranannya sama dengan suku galat

dala model regresi. Bentuk lain dari persamaan (2.6) diperoleh dengan mengganti

, dengan kendala





I

i i 1

 = 0 dipenuhi.

Jadi dapat ditulis :

=

Bila menyatakan rataan keseluruhan dari semua ; yakni

Dengan:

disebut sebagai efek atau pengaruh perlakuan ke i.

Uji yang dipakai didasarkan pada perbandingan dua taksiran bebas dari kesamaan

variasi populasi . Kedua taksiran tersebut diperoleh dengan menguraikan total variasi

data, diusahakan oleh penjumlahan ganda





2

1 1

..



_{ }I 

i n

i

ij y

y menjadi dua komponen.

Teorema 2.1 Identitas Jumlah Kuadrat





2 1 1

..



_I _ 

i n

j

ij y

y =





2

1 1

.. .



_I _ 

i n

j

i y y

n +





2

1 1

.



_I _ 

i n j i ij y y Bukti





2 1 1

..



_I _ 

i n

j

ij y

y =







   I i n j i y y 1 1 .. .

[ + (yij - i.)]2

=





2 1 1 .. . [



_I _ 

i n

j

i y

y + 2 ( i.– )2(yij - i.) + (yij - i.)2

=





2 1 1 .. . [



_I _ 

i n

j

i y

y + 2 ( i – )2(yij - i.) +





2

1 1

.



_I _ 

i n j i ij y y

Suku yang ditengah sama dengan nol, karena

0 . .) 1 1 1 1      









    n y n y y n y y y n j ij n j ij i n j ij i n j ij

Jumlah yang pertama tidak mengandung indeks, jadi dapat ditulis



. ..



. ..)2.

1 1 1 2 y y n y y I i i I i n j

i  









2 1

1 1

2

..) . ..

. y n y y

y

I

i i I

i n

j

i  







_{  }  + 







  

I

i n

j

ij y y 1 1

2 .  

Agar memudahkan penggunaannya maka suku identitas jumlah kuadrat akan ditandai dengan lambang berikut:

JKT =







  

I

i n

j

ij y y 1 1

2

. = jumlah kuadrat total

JKA = 2

1

..) . y y n

I

i

i 



_ = jumlah kuadrat perlakuan

JKG =







  

I

i n

j

ij y y 1 1

2

. = jumlah kuadrat galat

Identitas jumlah kuadrat dapat dituliskan: JKT = JKA + JKG

Identitas jumlah kuadrat menyatakan bahwa variasi antar perlakuan dan dalam perlakuan dijumlahkan menjadi jumlah kuadrat total. Akan tetapi, pemahaman lebih mendalam dapat diperoleh dengan menyelidiki nilai harapan dari JKA dan JKG. Kemudian akan diturunkan taksiran variasi yang merumuskan rasio yang akan digunakan untuk menguji kesamaan dari rataan populasi.

Perlu dibandingkan ukuran variansi antara perlakuan yang sesuai dengan variasi dalam perlakuan agar dapat ditemukan perbedaan yang berarti dalam pengamatan akibat pengaruh perlakuan. Perhatikan nilai harapan jumlah kuadrat perlakuan.

Teorema 2.2 E(JKA) = (I-1) σ2 +





I

i n

1 2 1



Bukti

Bila JKA dipandang sebagai peubah acak yang nilai-nilainya berubah bila percobaan diulang beberapa kali, maka dapat ditulis:

   JKA = 2

1

..) . (y y I

i

i 

Dari model : y_ij = + αi + Eij

Diperoleh 

    y_i = + αi + Ei.

      yi =  +E..karena 0.

1 



_I i

i

n  Jadi

JKA = 2

1

..) . E E

n _i

I

i

i  



_ 

dan E(JKA) = ( .) ( ..) 2 ( .)

1 2

2

1 1

2

i I

i i i

I

i I

i

i n E E nIE E n E E

n







 

     

karena Eij merupakan peubah bebas dengan rataan nol dan variansi σ2, maka

diperolah E( .) ,

2 2

n

E_i  E( ..) , 2 2

nI

E_i  E(Ei .) 0

sehingga E(JKA) = 2)

1

2 2  

  



_I i

i I

n  

         = (I-I)2  





I

i i n

1 2

  

Salah satu taksiran σ2 yang didasarkan pada I-1 derajat kebebasan diberikan oleh

Rataan Kuadrat Perlakuan

1 2

1  

I JKA

s  

Bila H0 benar dan tiap αi pada teorema 2.2. sama dengan nol, maka

2 1

   

 

I JKA E

dan s₁2merupakan menaksir σ2 yang tak bias. Akan tetapi, bila H1 yang benar, maka

1 1

1 2

2

        









I n I

JKA E

I

Dan s₁2menaksir σ2 ditambah suatu suku tambahan mengukur variasi akibat pengaruh yang sistematik.

Taksiran σ2 yang kedua dan bebas dari hipotesis, didasarkan pada I(n-1) derajat

kebebasan, ialah rumus yang dikenal, yaitu Rataan Kuadrat Galat

) 1 ( 2

 

n I

JKG S

Identitas jumlah kuadrat tidak saja menguraikan keragaman total data, tetapi juga jumlah semua derajat kebebasan. Dengan perkataan lain

n (I-1) = nI - n1

bila H0 benar, rasio

f = ₂ 2 1 S S

 

merupakan suatu nilai peubah acak F yang berdistribusi F dengan derajat kebebasan I-1

dan I(n-1). Karena S₁2menaksir lebih σ2 bila H0 salah, maka diperoleh uji ekasisi dengan

daerah kritis seutuhnya terletak disebelah ujung kanan fuangsi distribusi.

Hipotesis nol ditolak pada taraf keberartian α bila

f > f_α[I-1,I(n-1)]

[image:38.612.124.530.529.682.2]

Perhitungan masalah analisis variansi diringkas dalam bentuk tabel seperti pada tabel 2.3. Tabel 2.3. Analisis Variansi untuk Klasifikasi Satu Arah

Sumber Variasi

Jumlah Kuadrat

Derajat Kebebasan

Rataan Kuadrat

f Hitungan Perlakuan

Galat

JKA

JKG

I-1

I(n-1)

1 2

 

I JKA

S  

) 1 ( 2

 

n I

JKG S

Total JKT nI-1

2.3.2. Analisis Variansi Klasifikasi Dua Arah

Analisis Variansi klasifikasi dua arah merupakan pengembangan atau perluasan dari analisa dengan satu arah. Anava klasifikasi dua arah membahas tentang keragaman dalam satu peubah tidak bebas Y yang ditimbulkan oleh keragaman dua faktor.

Seperti digambarkan dalam tabel 2.4.

Tabel 2.4. Klasifikasi Dua Arah Blok

Perlakuan

1 2 … J

Jumlah Rataan

1 2

     

I

11

y    y_12   … y1j 

21

y    y_22   … y2j   

                    

1 I

y    y_I2   … yIj

T1.

T2.

     

TI

1 y  

2 y  

        

 

I y

Jumlah T.1 T.2 … T.j T..

Rataan y.₁   y._2   … y.j  y.. 

.

i

y = rataan pengamatan untuk perlakuan ke i

j

y. = rataan pengamatan dalam blok ke j

..

y = rataan keseluruhan ij pengamatan

Ti. = jumlah pengamatan untuk perlakuan ke i

T.j = jumlah pengamatan dalam blok ke j

..

T = jumlah keseluruhan ij pengamatan

Rata-rata rataan populasi perlakuan ke i, i, didefinisikan sebagai

J J

j ij j



_

 1

 

Rata-rata rataan populasi blok ke j, ._j, didefinisikan sebagai 

   

I I

i ij j



_

 1 .



  

 

Dan rata-rata rataan keseluruhan , didefinisikan sebagai

IJ I

i J

j ij j



_{ }

 1 1 .

 

 

Untuk menentukan apakah ada bagian variasi dalam pengamatan yang diakibatkan oleh perbedaan dalam perlakuan, dilakukan uji

H0 : 1. = 2. = … = I = 

dan untuk menentukan apakah ada variasi yang diakibatkan oleh perbedaan blok dilakukan uji

H0 : .1 = .2 = … = .j = 

H1 : tidak semua j = 0

Tiap pengamatan dapat dituliskan dalam bentuk yij = ij + εij

dengan εij mengukur penyimpangan nilai amatan yij dari rataan populasi ij.

Bentuk persamaan yang lebih disukai dilperoleh dengan penggantian ij =  + α1 + j

Dengan α1 menyatakan pengaruh perlakuan ke i dan j menyatakan pengaruh blok ke j.

dianggap bahwa pengaruh perlakuan dan blok aditif. Jadi dapat ditulis yij =  + α1 + j + εij

Model ini mirip dengan klasifikasi satu arah, perbedaan utamanya adalah adanya

pengaruh blok j. Konsep dasarnya mirip sekali dengan klasifikasi satu arah kecuali disini

pengaruh tambahan akibat blok harus diperhitungkan dalam analisis karena sekarang variasi dikendalikan secara sistematis dalam dua arah.

Bila sekarang dikenakan pembatasan bahwa

  0

1 



_I i

i

  dan  0

1 



J_ j

j

  

Maka,

1 1

) (

.  

  

  

  





J J

j

j i

i  dan 1

1

) (

.  

  

 



    

I I

i

j i j

Hipotesis nol bahwa i rataan perlakuan i. sama, dan area itu sama dengan  dengan

H0 : α1 = α2 = … = αI = 0,

Hi : tidak semua αi = 0

Begitu juga hipotesis nol bahwa j rataan blok .j sama, serta dengan menguji hipotesis

H0 : 1 = 2 = … = J = 0,

H1 : tidak semua J = 0

Tiap uji pada perlakuan akan didasarkan pada perbandingan takisran-taksiran

bebas untuk variasi populasi bersama σ2. Taksiran ini diperoleh dengan memisahkan

jumlah kuadrat total data menjadi tiga bagian dengan menggunakan identitas berikut.

Teorema 2.3 Identitas Jumlah Kuadrat





2

1 1 2

1 2

1 1 1

2 ..) . . ( ..) . ( ..) . ( ..

. y J y y I y y y y y y

y _j I i i J j ij j J j I i J j I i i

ij    



 



  



_{ }



_{   }

Bukti





2

1 1 1 1 2 ..)] . . ( ..) . ( ..) . ( [ ..

. y y y y y y y y y

y _{j ij i j}

I i J j i I i J j

ij         



_{ }



_{ }

     





2

1 1 2

1 1 1 1 2 ..) . . ( ..) . ( [ ..

. y y y y y y y

y _j I i i J j ij I i J j j I i J j

i       









     







. ..



( . . ..) 2 ..) . ( .. . 2 1 1 1 1 y y y y y y y y y y j i I i J j ij i I i J j j i        





   



. ..



( . . ..) 2 1 1 y y y y y

y _{i j}

I

i J

j

ij

j   





 





2 1

2

1 1 1

2

..) .

( ..)

. ( ..

. y J y y I y y

y _j

J

j I

i J

j

I

i i

ij    







_{ }



_{ }

2

1 1

..) .

.

(y y y _j y I

i

i J

j

ij   





 

Identitas jumlah kuadrat dapat dituliskan dengan lambang persamaan JKT = JKA + JKB + JKG

Dengan :

JKT =







  

I

i J

j

ij y y 1 1

2 ..

. = jumlah kuadrat total

JKA = 2

1

..) . (y y J

I

i

i 



_ = jumlah kuadrat perlakuan

JKB = 2

1

..) . (y y

I _j

J

j





_ = jumlah kuadrat blok

JKG = 2

1 1

..) . .

(y y y _j y I

i

i J

j

ij  



_{ } = jumlah kuadrat galat

Dengan mengikuti cara kerja seperti diuraikan pada teorema 2.2 yaitu bila jumlah

kuadrat tersebut ditafsirkan sebagai fungsi peubah acak bebas, maka dapat y11, y12, …., yIJ

ditunjukkan bahwa nilai harapan jumlah kuadrat perlakuan, blok, dan galat adalah,

E(JKA) = (I-1) σ2 +





I

i i J

1 2



E(JKB) = (J-1) σ2 +





J

j j I

1 2 

Salah satu taksiran σ2 didasarkan pada I-1 derajat kebebasan, adalah

1 2

1  

I JKA s

Bila pengaruh perlakuan α1 = α2 = …= αI = 0, maka s12merupakan taksiran tak bias dari σ

2

. Akan tetapi, bila pengaruh perlakuan tidak semuanya nol, maka

1 1

1 2

2

        









I J I

JKA E

I

i i  

dan s₁2akan secara berlebihan menaksir σ2, taksiran kedua σ2, didasarkan atas J-1 derajat

kebebasan, diberikan oleh

1 2

2  

J JKB

s  

Taksiran s₂2merupakan taksiran tak bias dari σ2 bila pengaruh blok 1 = 2 =…= j = 0.

Bila pengaruh blok tidak semuanya nol, maka:

1 1

1 2

2

        









J I J

JKB E

J

j j  

Dan s₂2akan secara berlebohan menaksir σ2. Taksiran ketiga dari σ2, didasarkan pada

(I-1)(J-1) derajat kebebasan dan bebas dari s2, diberikan oleh

, ) 1 )( 1 ( 2

  

J I

JKG

s  

Yang tidak bias, terlepas apakah kedua hipotesis nol benar atau salah.

Untuk menguji hipotesis nol bahwa pengaruh perlakuan semuanya sama dengan nol, dengan menghitung rasio:

, 2 2 1 1

Yang merupakan nilai peubah acak F1 yang berdistribusi F dengan derajat kebebasan I-1

dan (I-1)(J-1) bila hipotesis nol benar. Hipotesis nol ditolak pada taraf keberartian α bila

f1 > fα [I-1,(I-1)(J-1)].

Untuk menguji hipotesis nol bahwa pengaruh blok semuanya sama dengan nol, dengan menghitung rasio:

, 2 2 2 2

s s f   

Yang merupakan nilai peubah acak F2 yang berdistribusi F dengan derajat kebebasan J-1

[image:45.612.127.522.435.681.2]

dan (I-1)(J-1) bila hipotesis nol benar. Perhitungan Anava untuk klasifikasi dua arah disajikan dalam tabel 2.5.

Tabel 2.5. Analisis Variansi Klasifikasi Dua Arah Sumber

Variasi

Jumlah Kuadrat

Derajat Kebebasan

Rataan Kuadrat

f Hitungan Perlakuan

Blok

Galat

JKA

JKB

JKG

I-1

J-1

(I-1)(J-1)

1 2

 

I JKA

S  

1 2

 

J JKB S

 

) 1 )( 1 ( 2

  

J I

JKG S

2 2 1 1

S S f 

 

2 2 2 2

S S f 

2.3.3 Analisis Variansi Klasifikasi Dua Arah dengan Interaksi

Klasifikasi dua arah dengan interaksi mencakup uji hipotesa tentang pengaruh baris, kolom dan interaksi antara baris dan kolom. Untuk menentukan rumus klasifikasi dua arah dengan pengamatan yang berulang dalam rancangan acak lengkap, pandang K sebagai replikasi pada tiap kombinasi perlakuan faktor A diamati pada I taraf dan faktor B pada J taraf. Pengamatan dapat disajikan dalam suatu matriks yang barisnya menyatakan taraf faktor A sedangkan kolomnya menyatakan faktor B. Tiap kombinasi perlakuan menentukan suatu sel dalam matriks. Jadi terdapat IJ sel, masing-masing berisi K pengamatan. Seluruh IJK pengamatan diperlihatkan pada tabel 2.6.

Tabel 2.6 Klasifikasi Dua Arah dengan Interaksi Faktor A

(baris)

Faktor B (kolom) 1 2 … J

Jumlah Rataan

1 y₁₁₁  y₁₂₁ …y_1J1 

112

y   y₁₂₂ …y_1J2                    

k

y₁₁   y_12k …y_1JK 

.. 1

y y₁..

2 y₂₁₁  y₂₂₁ …y_2J1 

212

y   y₂₂₂ …y_2J2 

                  

k

y₂₁   y_22k …y_2JK 

.. 2 y  

 

.. 2 y  

                    

I

                  

11 I

y   y_I21 …y_IJ1 

12 I

y   y_I22 …y_IJ2 

                  

k I

y₁   y_I2k …y_IJK

                 

.. 1 y

         

  .. 1 y  

Jumlah

1 .

y   y.₂. …y._J. y... Rataan

1 .

y   y.₂. …y._J. y...

Pengamatan pada sel ij membentuk sampel acak berukuran n dari populasi yang

dianggap berdistribusi normal dengan rataan ij dan variansi σ2. Semua populasi yang

banyaknya IJ dianggap mempunyai variansi yang sama. Tiap pengamatan dalam tabel 2.6

dapat ditulis dalam bentuk y_ijk  _ij _ijk,

 

Dengan _ijkmengukur penyimpangan pengamatan nilai y_ijk pada sel ke ij dari rataan

populasi _ij. Bila y_ijmenyatakan pengaruh interaksi antara faktor A taraf ke I dan faktor

B taraf ke j, α1 pengaruh faktor A, j pengaruh faktor B dan  rataan keseluruhan, maka

dapat ditulis

ij j ij  1  ()

    

Sehingga y_ijk   _i  _j ()_ij_ijk  Yang akan dikenakan pembatasan

   



0,



( ) 0,



( ) 0

 

 ij

J J

ij j I

i  

Ketiga hipotesis yang akan diuji adalah: H0 : α1 = α2 = … = αI = 0

Hi : tidak semua αi = 0

H0 : 1 = 2 = … = J = 0

H1 : tidak semua J = 0

H0 : ( )11 = ( )12 = … = ( )IJ = 0

H1 : tidak semua ( )ij = 0

Tiap uji akan didasarkan pada perbandingan taksiran σ2 yang bebas diperoleh

dengan menguraikan jumlah kuadrat data menjadi empat bagian dengan menggunakan kesamaan (identitas) berikut.

Teorema 2.4 Identitas Jumlah Kuadrat









_{ }



_  



_   J_ 

j j I

i J

j

i I

i K

k

ijk y JK y y IK y y

y

1

2 2

1 1 1 1

2

...) . . ( ...)

.. ( ..

.

   







    

 I

i J

j

j i

ij y y y y

K 1 1

2 ... . . .. .

. .) (

2 2

1 1 1

ij I

i J

j K

k

ijk y y



_{  }  

Identitas jumlah kuadrat dapat dituliskan dengan lambang persamaan JKT = JKA + JKB + JK(AB) + JKG

Derajat kebebasaanya menurut kesamaan

IJK-1 = (I-1) + (J-1) + (I-1)(J-1) + IJ(K-1)

Bila tiap jumlah kuadrat pada sebelah kanan kesamaan jumlah kuadrat dibagi dengan derajat kebebasannya, maka diperoleh keempat statistic yaitu

) 1 ( ,

) 1 )( 1 (

) ( ,

1 ,

1

2 2

3 2

2 2

1

 

   

 



K IJ

JKG s

J I

AB JK s

J JKB s

Semua taksiran variansi ini adalah taksiran σ2 yang bebas dengan syarat bahwa tidak ada pengaruh αi, j, ( )ij.

Bila jumlah kuadrat dipandang sebagai fungsi dari peubah acak bebas Y111, Y112,

…,Yijk maka

1 1 ) ( 2 1 1 2 2 1         



 I JK I JKA E s E I i         1 1 ) ( 2 1 1 2 2 2         



 J JK J JKB E s E J j     ) 1 )( 1 ( ) ! )( 1 ( ) ( )

( 1 1

2 1 2 2 3           



  J I K J I AB JK E s E I i I i      

  2 2

) 1 ( ) (        K IJ JKG E s E  

Dari rumus dengan mudah dapat dsimpulkan bahwa keempat taksiran 2 tidak bias bila

H0 (Hipotesin nol) benar.

Untuk menguji hipotesis nol bahwa pengaruh perlakuan semuanya sama dengan nol, dengan menghitung rasio:

Yang merupkan nilai peubah acak F1 yang berdistribusi F dengan derajat kebebasan I-1

dan IJ(K-1) bila hipotesis nol benar. Hipotesis nol ditolak pada taraf keberartian α bila f1 >

f_α [I-1,IJ(K-1)],

Untuk menguji hipotesis nol bahwa pengaruh blok semuanya sama dengan nol, dengan menghitung rasio:

2 2 2 2

s s f 

Yang merupkan nilai peubah acak F2 yang berdistribusi F dengan derajat kebebasan J-1

dan IJ(K-1) bila hipotesis nol benar. Hipotesis nol ditolak pada taraf keberartian α bila f2 >

fα [J-1,IJ(K-1)]. Untuk menguji hipotesis H0 bahwa pengaruh interaksi semuanya nol,

maka:

2 2 3 3

s s f 

 

Yang merupkan nilai peubah acak F3 yang berdistribusi F dengan derajat kebebasan (I-1)

(J-1) dan IJ (K-1) bila H0 benar. Adanya interaksi bila f3 > fα [I-1,(J-1),IJ(K-1)].

Perhitungan mengenai masalah anava untuk klasifikasi dua arah dengan interaksi disajikan dalam tabel 2.7

Tabel 2.7. Analisis Variansi untuk Klasifikasi Dua Arah dengan Interkasi Sumber

Variasi

Jumlah Kuadrat

Derajat Kebebasan

Rataan Kuadrat

f Hitung

Utama

A (baris)

B (kolom)

Interaksi AB

Sisa

JKA

JKB

JK(AB)

JKG

I-1

J-1

(I-1)(J-1)

IJ(K-1)

 

1 2

1  

I JKA

S  

1 2

2  

J JKB S

   

) 1 )( 1 (

) ( 2

3

  

J I

AB JK S

   

) 1 ( 2

 

K IJ

JKG S

 

2 2 1 1

S S f 

 

2 2 2 2

S S f 

   

2 2 3 3

S S f 

Jumlah JKT IJK-1

[image:51.612.124.527.147.443.2]

Jumlah kuadrat diperoleh dengan membentuk tabel jumlah kuadrat berikut: Tabel 2.8

A

B 1 2 … J

Jumlah

1 2

 

I

. 11

y   y₁₂. …y_1j.  .

21

y   y₂₂. …y_2j. 

                  

  .. 1 y  

.. 2 y  

. 1 I

y   y_I1. …y_IJ 

  y₁..

BAB 3

PEMBAHASAN DAN HASIL

3.1 Regresi Berganda

Untuk memperkirakan/meramalkan nilai dari variabel Y, akan lebih baik apabila ikut memperhitungkan variabel-variabel lain yang ikut mempengaruhi Y. dengan demikian

ada hubungan antara satu variabel tidak bebas (dependent variable) Y dengan beberapa

variabel lain yang bebas (independent variable) X1, X2, …, Xk. hubungan antara sebuah

variabel tak bebas (dependent variable) dengan dua buah atau lebih variabel bebas

(independent variable) dalam bentuk regresi disebut dengan regresi linear berganda.

Untuk meramalkan Y, apabila semua nilai variabel bebas diketahui, maka dapat

digunakan persamaan regresi linear berganda. Hubungan antara Y dan X1, X2, …, Xk yang

sebenarnya adalah :

i ki k i

i

i X X X

Y ₀ _{1 1} _{2 2} ... 

Anggapan yang diambil dalam model ini ialah bahwa X1, X2, …, Xn tidak mempunyai

distribusi sedangkan _iberdistribusi N(0,σ2)

Apabila dinyatakan dalam bentuk persamaan matriks berikut.



  XB

Y  

      Dengan Y, B, ε = vektor

Dimana Y =                                                                                       n Y Y Y Y i k i n i          . . . . . . . . . . . . . . . 2 1 1 0 2 1 X =                             11 11 11 11 11 11 11 11 11 11 11 11 . . . 1 . . . . . . . . . . . . 1 . . . . . . . . 1 . . . 1 X X X X X X X X X X X X

Koefisien harus diestimasi berdasarkan data hasil penelitian sampel acak. Prosedur

estimasi tergantung pada asumsi mengenai variabel X dan kesalahan pengganggu ε.

Beberapa asumsi yang penting adalah sebagai berikut:

1. Nilai harapan setiap kesalahan pengganggu sama dengan nol  