Bagian 1 Integral Rangkap

Bagian 1

Integral Rangkap

Bagian 1 Integral Rangkap mempelajari bagaimana teknik integrasi yang telah Anda pelajari dalam Matematika Teknik 1 dikembangkan lebih lanjut sehingga menjadi integral yang rangkap. Teknik integrasi rangkap ini dapat kita pakai untuk menghitung luas dan menghitung volume benda. Lebih jauh, teknik ini dapat digunakan untuk menghitung pusat massa suatu benda.

Pengetahuan pada Bagian 1 ini diharapkan memberikan sedikit informasi kepada Anda, bahwa ilmu matematika sebenarnya sangat mudah diterapkan untuk mengatasi persoalan. Ilmu matematika tidak hanya sebatas angka-angka perhitungan saja, tapi dapat digunakan untuk memecahkan persoalan yang terjadi di sekeliling kita.

Kompetensi yang diharapkan setelah Anda menyelesaikan Bagian 1 Integral Rangkap adalah Anda mampu:

1. Menghitung integrasi rangkap dua.

2. Menghitung luas di antara dua kurva dengan menggunakan integral rangkap. 3. Menghitung integrasi rangkap tiga.

4. Menghitung volume dengan menggunakan integral rangkap tiga. 5. Menghitung pusat massa dan pusat gravitasi.

1.1 Integrasi Rangkap Dua

Gagasan dari integrasi tertentu dapat digunakan secara luas untuk fungsi dengan dua atau lebih variable. Integrasi tertentu untuk satu variable yang dinyatakan dengan rumus dx . ) x ( f b a

∫

1.1

dibuat dari permasalahan untuk menghitung luas di bawah kurva. Integrasi fungsi dua variable dibuat dari permasalahan volume.

Secara umum integral lipat dua ditulis dalam bentuk :

∫∫

s

f (x, y) atau

∫∫

f (x, y) dx dy 1.2

s

Untuk integral lipat dua atas persegi panjang ditulis dalam bentuk

∫

2 1 y y

∫

2 1 x x f (x, y) dx dy 1.3

Integral ini juga dapat diberikan dalam bentuk

∫

2 1 x x

∫

2 1 y y f (x, y) dx dy 1.4

Masalah menentukan volume benda padat pada tiap titik yeng terletak antara bidang R dalam bidang xy dan permukaan z = f(x,y), dimana f(x,y) kontinu di atas R dan f(x,y) > 0 untuk semua (x,y) dalam R dapat dilakukan dengan langkah sebagai berikut.

1. Buat garis paralel menuju sumbu koordinat.

2. Asumsikan bidang terbagi dalam n segiempat, ambil suatu luasan tertentu yang ke pada segiempat dengan luas Δxk

3. Pilih sembarang titik pada segiempat yang diambil dan untuk segiempat ke k misalkan (xk,yk)

4. Puncak dari segiempat bidang adalah nilai fungsi pada titik (xk,yk) atau nilai

f(xk,yk), maka volume dari benda segiempat tersebut adalah :

(

)

k * k * k

,

y

.

A

x

f

Δ

5. Karena terdiri banyak segiempat, maka volume benda adalah :

(

)

∑

=

Δ

n 1 k k * k * k

,

y

.

A

x

f

≈ + → = nlim V

∑

(

)

=

Δ

n 1 k k * k * k

,

y

.

A

x

f

1.5a

Penjumlahan di atas dikenal dengan Penjumlahan Riemann (Riemann Sum). Karena sisi kanan adalah definisi integrasi tertentu, maka rumus volume :

∫∫

= R dA ). y , x ( f V 1.5b

Integrasi Yang Diulang

Turunan parsial fungsi f(x,y) dihitung dengan menurunkan salah satu variable dan variable lain dihitung selanjutnya. Sedangkan proses pembalikannya disebut integrasi parsial.

∫

b a dx ). y , x ( f ... dan ...

∫

1.6 d c dy ). y , x ( f Contoh 1.1 Hitunglah integrasi

∫

1 0 2 .dx xy Penyelesaian :

∫

= = 1 0 2 2 2 y 2 1 dx . x y dx . xy

Contoh 1.2 Hitunglah integrasi

∫

1 0 2 .dx xy Penyelesaian : x 3 1 dy . y x dx . xy 1 0 2 1 0 2 = =

∫

∫

Proses integrasi dua tahap, baik terhadap x dan terhadap y disebut Integrasi Iterasi atau Integrasi Yang Diulang

∫∫

∫ ∫

⎥

⎦

⎤

⎢

⎣

⎡

=

d c b a d c b a

dy

.

dx

).

y

,

x

(

f

dy

.

dx

).

y

,

x

(

f

∫∫

∫ ∫

⎥

⎦

⎤

⎢

⎣

⎡

=

d c b a d c b a

dx

.

dy

).

y

,

x

(

f

dx

.

dy

).

y

,

x

(

f

∫∫

=

∫∫

=

∫∫

R d c b a b a d c dy . dx ). y , x ( f dy . dx ). y , x ( f dA ). y , x ( f 1.7 Contoh 1.3 Selesaikan integrasi

∫∫

+ 3 0 2 1 . ). 8 1 ( xy dydx Penyelesaian :

∫∫

∫ ∫

⎥

⎦

⎤

⎢

⎣

⎡

+

=

+

3 0 2 1 3 0 2 1

dx

.

dy

).

xy

8

1

(

dx

.

dy

).

xy

8

1

(

Contoh 1.4 Selesaikan integrasi

∫

[

+

]

=

∫

+ = 3 0 3 0 2 1 2 57 dx ). x 12 1 ( dx . xy 4 y Penyelesaian :

[

]

∫

+ =

∫

+ = 3 0 3 0 2 1 2 57 dx ). x 12 1 ( dx . xy 4 y Contoh 1.5

Evaluasi integrasi y x.dA di atas bidang segiempat R = {(x,y) ; -3<x<2, 0<y<1}

R 2

∫

∫

∫

∫

− − −

=

=

⎥⎦

⎤

⎢⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

=

2 1 2 3 2 3 10 3 1 0 2

6

5

dx

.

x

3

1

dx

.

x

y

3

1

dx

.

dy

.

x

y

V

... sat.volume ... sat.volume Contoh 1.6 Contoh 1.6

Hitung volume benda di bawah bidang z = 4 – x – y dan di atas bidang segiempat R = { (x,y) ; 0 < x < 1, 0 < y < 2 Penyelesaian :

∫

∫

∫

∫

⎟

=

⎠

⎞

⎜

⎝

⎛ −

=

⎥⎦

⎤

⎢⎣

⎡

₋

₋

=

⎥

⎦

⎤

⎢

⎣

⎡

−

−

=

2 0 2 0 2 0 1 0 2 1 0

5

dy

.

y

2

7

dy

.

xy

x

2

1

x

4

dy

.

dx

).

y

x

4

(

V

.... sat. vol. Contoh 1.7

∫

2 0

∫

1 0 (x2 _{+ 2y) dx dy =}

∫

₍ 2 0

3

1

x 3 + 2y x )

∫

dy = [,( 1 0

∫

2 0

3

1

+ 2y) – 0 ] dy = (

3

1

x 2y + y2_{) =}

∫

2 0

3

2

+ 4 = 4

3

2

Atau dapat diselesaikan dalam bentuk

∫

1 0

∫

2 0 (x2 _{+ 2y) dx dy = (x 2y + y}2_{) dx = [ (sx}2 _{+ 4) – 0] dx}

∫

1 0

∫

2 0

∫

1 0 = (

3

2

x 3 + 4 x)

∫

= 1 0

3

2

+ 4 = 4

3

2

Integrasi Rangkap Dua dengan Alas Tidak Segiempat

Yaitu integral yang alasnya bukan persegi panjang, tapi dalam bentuk fungsi x dan t, dengan memandang bidang x y dapat digambarkan alas sebagai berikut.

Dengan memandang daerah integrasi S, maka S dibagi menjadi n bagian (elemen) oleh garis – garis yang sejajar sumbu koordinat sehingga terdapat n bagian ∆ Ai.

I = 1,2,3………..,n ; dan

∆ Ai = ∆ x, ∆y

Ambillah (xi, yi) sembarang dalam ∆ Ai dan n → MMMMM, sedemikian sehingga ∆ Ai yang terbesar → o

Maka yang dimaksud integral rangkap dua dari fungsi f (x, y) melalui perhatikan daerah S yang dibatasi oleh garis-garis sejajar sumbu koordinat, sehinga terdapat bentuk garis lengkung berikut :

B1 A1 B2 memperlihatkan x = x1 (y) → fungsi dari y

B2 A2 B2 memperlihatkan x = x2 (y) → fungsi dari y

A1 B1 B2 memperlihatkan y = y1 (x) → fungsi dari x

A2 B2 A1 memperlihatkan y = y2 (x) → fungsi dari x

Maka diperoleh bentuk integral :

∫∫

s f (x,y) dx dy

=

∫

f (x,y) dx dy 2 1 b b

∫

) ( ) ( 2 1 y x y x

=

∫ ∫

f (x,y) dx dy 1.8 2 1 a a ) ( ) ( 2 1 x y x y Definisi :

a. Bidang tipe I dibatasi garis x = a dan x = b di kiri dan kanan, dan dibatasi fungsi y = g1(x) dan y = g2(x) di bawah dan di atas, dimana g1(x) < g2(x) untuk harga a

< x < b

b. Bidang tipe II dibatasi garis y = c dan y = d di bawah dan di atas, dibatasi fungsi x = h1(y) dan x = h2(y) di kanan dan kiri, dimana h1(y) < h2(y) untuk harga c < y

Teorema :

a. Jika R tipe I, dimana f(x,y) kontinu, maka :

∫∫

=

∫ ∫

R b a ) x ( g ) x ( g 2 1

dx

.

dy

).

y

,

x

(

f

dA

).

y

,

x

(

f

1.9

b. Jika R tipe II, dimana f(x,y) kontinu, maka :

∫∫

=

∫ ∫

R d c ) x ( h ) x ( h 2 1

dy

.

dx

).

y

,

x

(

f

dA

).

y

,

x

(

f

1.10 Contoh 1.8

Evaluasi integrasi

∫∫

xy

.

dA

di atas bidang R yang dibatasi antara garis y =1/2x dan y = ½ _{serta garis x =4 dan x= 2}

Penyelesaian :

∫ ∫

∫

∫

⎟

=

⎠

⎞

⎜

⎝

⎛

₋

=

⎥⎦

⎤

⎢⎣

⎡

=

4 2 2 2 / x 4 2 4 2 3 2 x 2 / x 2

6

11

dx

.

x

8

1

x

2

1

dx

.

xy

2

1

dx

.

dy

.

xy

... sat. luas

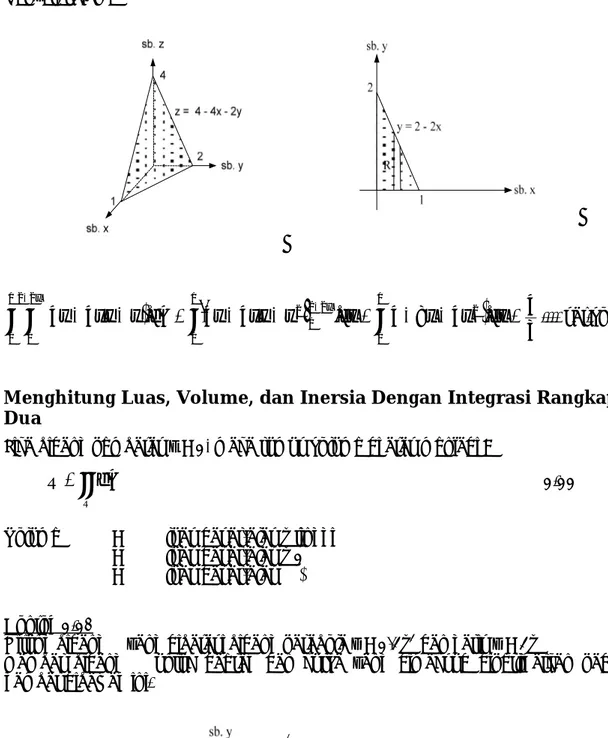
Contoh 1.9

Hitung volume benda yang dibatasi oleh bidang z = 4 – 4x – 2y dengan sumbu koordinat.

Penyelesaian :

(

)

[

]

(

)

∫ ∫

−

∫

−

∫

= − − = − − = − − 1 0 x 2 2 0 1 0 1 0 2 x 2 2 0 2 3 4 dx . x 4 x 8 4 dx . y xy 4 y 4 dA . y xy 4 y 4 .... sat.vol.

Menghitung Luas, Volume, dan Inersia Dengan Integrasi Rangkap

Dua

Jika bidang pembatas z = 1, maka rumus volume di atas menjadi :

∫∫

=

R

dA

R 1.11

Volume = luas dasar/alas x tinggi

= luas dasar/alas x 1

= luas dasar/alas (R)

Contoh 1.10

Hitung bidang R yang dibatasi bidang parabola y = 1/2x2 _{dan garis y = 2x}

Gambar bidang R untuk daerah dan kurva yang dimaksud diperlihatkan pada gambar dibawah ini.

Penyelesaian :

[ ]

∫ ∫

∫

∫

⎟

=

⎠

⎞

⎜

⎝

⎛

₋

=

=

=

4 0 x 2 x 2 / 1 4 0 4 0 2 x 2 x 2 / 1 2 2

3

16

dx

.

x

2

1

x

2

dx

.

y

dx

.

dy

R

... sat.luas Contoh 1.11

Hitunglah isi benda yang dibatasi oleh bidang z = 0, permukaan z = x2 _{+ y}2 _{+ 2 dan}

tabung x2 _{+ y}2 _{= 4.}

Penyelesaian:

Z = x2 + y2 merupakan lingkaran untuk z > 2 maka permukaan tersebut merupakan porabola putar degan poros sumbu z.

x1 = 0 → x2 = 4− y2 y1 = 0 → y2 = 2 , maka ¼ V =

∫

2 0

∫

− 2 4 0 y (x2 _{+ y}2 _{+ 2) dx dy} =

∫

( 2 0

3

1

x3 _{+ xy}2 _{+ 2x)}

∫

− 2 4 0 y dy = 4 (

3

2

) (y2 _{+ 5)}

∫

2 0 2

4

−

y

dy Substitusi : Y = s sin

θ

→ dy = 2 cos

θ

= 0 y = →

θ

= 0 y = →

θ

= ½ Maka : V =

3

8

∫

( 4 sin2 2 / 0 π

θ

+ ) (4 cos2

_θ

_{) d}

_θ

= 32₃

∫

2 / 15 0

( 4 sin2

θ

cos2

θ

) + 5 cos2

θ

) d

θ

= 32₃

∫

2 / 15 0 ( 9 cos2

_θ

_{) (4 cos}2

_θ

_{) d}

_θ

= 32_{3 9(}

[

8

3

)

8

sin

cos

3

4

sin

cos

(

4

)

2

2

sin

.

cos

θ

θ

θ

3

θ

θ

3

θ

θ

θ

+

+

−

+

]

0

2

/

15

= 32₃

⎥⎦

⎤

⎢⎣

⎡

₋

)

16

3

(

4

)

4

(

9

π

π

= 16

π

Contoh 1.12

Tentukan dan hitung letak berat, moment—momen inersia terhadap sumbu, koordinat dan terhadap titik asal 0 dari bidang datar yang dibatasi paraboa y2 _{= y}3

garis y = x kerapatan k = 1 Penyelesaian: Mx =

∫

y dy dx 1/2 y2 dx 1 0

∫

x x3/2

∫

1 0

∫

x x3/2 = ½

∫

(x2 _{– x}3_{) dx = y} 2 ( 1 0

3

4

4 3

x

x −

)

∫

= 1 0

24

1

24

10

10

/

1

21

10

10

/

1

24 21

=

=

=

=

=

Y

M

M

dan

Y

M

M

x

y x Titik berat = (

12

5

,

21

10

)

Momen inersia terhadap sumbu x : Ix =

∫

∫

y2 dy dx =

∫

1 0 x x3/2 1 0

3

1

y3 _dx

∫

x x3/2 =

3

1

∫

(x2 _{– x}912 _{) dx =} 1 0

3

1

(

11

2

4

2 / 11 4

x

x −

)

∫

1 0

44

1

Momen inersia terhadap sumbu y : Iy =

∫

∫

x2 dy dx = (x2y) dx 1 0 x x3/2

∫

x x3/2 =

∫

(x3 _{– x}712 _{) dx = (} 1 0

9

2

4

2 / 9 4

x

x −

)

∫

1 0

36

1

Latihan Soal 1.1

Setelah Anda selesai mempelajari materi di atas, kini saatnya untuk melatih diri mengerjakan soal-soal berikut. Buatlah penyelesaian setiap soal dengan sistematis untuk mendapatkan jawaban akhir yang benar. Selamat berlatih...!!!

1. Hitung integral

∫ ∫

(x,y) dx dy

1 0 1 x 2. Hitung integral

∫

1 0

∫

− 2 0 x a 2 2

1

−

x

−

y

dx dy

3. Hitunglah isi benda yang dibatasi oleh tabung x2 _{+ y}2 _{= a}2_{, z = 0 dan bidand z =}

y = 0

4. Hitunglah isi benda yang bagian atas dibatasi oleh paraboloida z = x2 _{+ 4y}2

bagian bawah dibatasi oleh bidang z = 0 dan bagan-bagian samping oleh permukaan silinder x2 _{= y dan y}2 _{= x.}

5. Hitunglah luas bidang datar yang dibatasi oleh parabola y = 4 – x2 _{dan garis Y =}

3 x.

6. Hitunglah luas bidang datar yang dibatasi oleh parabola y = x2 _{– x dan garis y +}

x = 1.

7. Tentukan letak titik berat (

x

, y

)

dari bidang datar yang dibatasi oleh parabola y2

= x dan garis x = 1, Jika Kerapatan k dititik (x,y) adalah k = x2 _{+ y}2_.

1.2 Integrasi Rangkap Tiga

Misalkan G adalah kotak segiempat yang dibatasi pertidaksamaan a ≤ x ≤ b, c ≤ y ≤ d, k ≤ z ≤ 1. Jika f adalah kontinu pada bidang G, maka :

∫∫∫

=

∫∫∫

b a f c l k dx . dy . dz ). z , y , x ( f dV ). z , y , x ( f 1.12 Contoh 1.13

Evaluasi integrasi rangkap tiga di atas kotak segiempat G yang

dibatasi pertidaksamaan : -1 ≤ x ≤ 2, 0 ≤ y ≤ 3, 0 ≤ z ≤ 2,

∫∫∫

0 3 2

dV

.

z

xy

12

Penyelesaian :

∫∫∫

G 3 2

dV

.

z

xy

12

=

∫∫∫

∫∫

[

]

− − = 2 1 3 0 2 0 2 1 3 0 2 0 4 2 3 2 dx . dy . z xy 3 dV . z xy 12 =

∫∫

∫

[

]

− − = 2 1 3 0 2 1 3 0 3 2 dx . xy 16 dx . dy . xy 48 =

∫

... sat. volume −

=

2 1

648

dx

.

x

432

Contoh 1.14

Hitunglah isi benda yang dibatasi oleh silinder x2 _{+ y}2 _{= a}2_{, bidang – bidang z = y}

dan z = o. Penyelesaian:

Satu per empat bagian dari benda tersebut maka batas :

z1 = 0 → z2 = y y1 = 0 → y2 = a2 −x2 x1 = 0 → x2 = a I = 4

∫

a o

∫

−_x2 o o

∫

y o dz dy dx = 4

∫

a o

∫

−_x2 o o = 2

∫

y2 a o

∫

−_x2 o o dx = 2

∫

(a2 – x2) dx a o = s ( a2 _{x -}

3

1

x 3)

∫

= a o

3

4

a3 Contoh 1.15

Hitunglah isi benda yang berada di dalam (dibatasi oleh) bola x2 _{+ y}2 _{+ z}2 _{= 8 dan}

paraboloida putaran x2 _{+ y}2 _{= 2 z}

Penyelesaian:

Dari kedua persamaan diperoleh : Z2 _{+ 2 z – 8 = o → (z +4) ( z – 2) = o}

Karena z =

2

1

(x2 _{+ y}2_{) selalu positif maka dibidang potongnya pada z = 2 dengan}

penyusunan koordinat silinder, maka batas menjadi :

z = ½ r2 _{→ z} 2 = 8−r2 r1 = 0 → r2 = 2 a sin

θ

θ

= 0 →

θ

2 = ½

π

I = 4

∫

π 2 / 1 o

∫

2 o =

∫

− = 2 8 2 / 1 r r z r a dr d

θ

=

∫

r.z π 2 o

∫

2 o

∫

− 2 2 / 2 8 r r - dr d

θ

π π

= 4

∫

π 2 / 1 o

3

2

( 8 2 - 7) d

θ

=

3

4

π

3

2

( 8 2 - 7)

Integrasi Rangkap Tiga dengan Banyak Bidang

Pembatas

Teorema :

Misalkan G adalah benda solid dengan permukaan atas z = g2(x,y) dan bidang alas

z = g1(x,y) dan misalkan R adalah proyeksi benda G pada bidang xy. Jika f(x,y,z)

adalah kontinu pada G, maka :

∫∫∫

∫∫ ∫

_⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

=

G R ) y , x ( g ) y , x ( g

dA

.

dz

).

z

,

y

,

x

(

f

dV

).

z

,

y

,

x

(

f

2 1 1.13 Contoh 1.16

Misalkan G adalah lempengan dalam oktan pertama yang terbuat dari benda bulat padat y2 _{+ x}2 _{≤ 1 yang dipotong oleh bidang y = x dan x = 0. Hitunglah volume G.}

Penyelesaian :

∫∫

∫

−

=

∫∫

_⎢⎣

⎡

_⎥⎦

⎤

−

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

R 1 0 y 0 y 1 0 2 y 1 0

dy

.

dx

z

2

1

dy

.

dx

.

dz

.

z

2 2

∫∫∫

G

dV

.

z

= =

∫∫

(

)

∫

(

)

⎥⎦

⎤

⎢⎣

⎡

₋

=

−

1 0 y 0 1 0 y 0 2 2

dy

.

x

.

y

1

2

1

dy

.

dx

.

y

1

2

1

=

∫

(

−

)

= 1 0 3 volume . sat ... 8 1 dy . y y 2 1

Contoh 1.17

Hitung volume benda yang dibatasi x2 _{+ y}2 _{= 9 dan bidang z =1, x + z = 5}

Penyelesaian : V = 36π sat. volume

Latihan Soal 1.2

Setelah Anda selesai mempelajari materi di atas, kini saatnya untuk melatih diri mengerjakan soal-soal berikut. Buatlah penyelesaian setiap soal dengan sistematis untuk mendapatkan jawaban akhir yang benar. Selamat berlatih...!!!

1. Evaluasi integral

∫∫∫

− + + 1 1 2 0 1 0 2 2 2 ) (x y z dxdydz 2. Evaluasi integral

∫ ∫

∫

2 / 1 3 / 1 0 1 0 sin π dx dy dz xy zx 3. Evaluasi integral

∫ ∫ ∫

− 3 0 9 0 0 2 z x dz dx dy xy

4. Evaluasi integral bidang G , dimana G adalah bidang solid pada oktan pertama yang dibatasi oleh silinder paragbola z = 2 – x2 _{dan bidang z = 0,}

y = x, dan y = 0

∫∫∫

xyz

dV

5. Evaluasi integral bidang G , dimana G adalah segiempat

yang dibatasi pertidaksamaan 0

∫ ∫∫

/2 1 3 / 1 0 1 0 sin π dx dy dz xy zx < x < π, 0 < y < 1, dan 0 < z < π/6

1.3 Pusat Gravitasi dan Teorema Pappus

Massa Benda

Massa sebuah benda dapat dihitung dengan menggunakan persamaan :

( )

x,y.dA M R

∫∫

δ =

1.14

Contoh 1.13

Sebuah segitiga dengan koordinat (0,0), (0,1), (1,0) mempunyai fungsi kepadatan δ(x,y) = xy. Tentukan massa benda.

Penyelesaian :

M =

∫∫

δ

( )

=

R dA . y , x

∫ ∫

+ − 1 0 1 x 0 dx . dy . xy

=

∫

∫

⎟

⎠

⎞

⎜

⎝

⎛

₋

₊

=

⎥⎦

⎤

⎢⎣

⎡

− + 1 0 1 0 2 3 1 x 0 2

dx

.

x

2

1

x

x

2

1

dx

.

xy

2

1

=

24

1

...sat.massa

Pusat Gravitasi

Pusat gravitasi benda dihitung dengan menggunakan persamaan :

∫∫

δ

=

=

R

dA

).

y

,

x

(

.

x

R

.

Massa

1

M

My

x

1.15

∫∫

δ

=

=

R

dA

).

y

,

x

(

.

y

R

.

Massa

1

M

Mx

y

1.16

Pusat gravitasi dan sentroid sebuah benda padat G juga dapat dihitung dengan menggunakan persamaan integrasi rangkap tiga yang diberikan dalam persamaan berikut. Untuk sebuah massa M, maka berlaku

∫∫∫

=

=

G

dV

z

y

x

G

of

mass

M

δ

(

,

,

)

1.17

Pusat gravitasi benda padat G tersebut adalah

∫∫∫

= − G dV z y x x M x 1

δ

( , , ) 1.18

∫∫∫

= − G dV z y x y M y 1

δ

( , , ) 1.19

∫∫∫

= − G dV z y x z M z 1

δ

( , , ) 1.20

Sedangkan sentroid dari benda padat G tersebut adalah

∫∫∫

= − G dV x V x 1 1.21

∫∫∫

= − G dV y V y 1 1.22

∫∫∫

= − G dV z V z 1 1.23 Contoh 1.14

Tentukan pusat gravitasi benda pada contoh 1.9 Penyelesaian:

Momen terhadap sumbu y :

∫∫

δ = =

∫ ∫

∫

+ − − +

⎤

⎡

=

` x 1 1 x 1 2 2 2

1

=

∫

(

− +

)

= 1 0 2 3 4 momen . sat .. ... 60 1 dx . x 2 1 x x 2 1

Momen terhadap sumbu x :

Mx =

∫∫

δ

=

=

R dA ). y , x ( y

∫ ∫

+ − 1 0 1 x 0 2 dx . dy . y . x

xy

.

dx

3

1

1 0 1 x 0 3

∫

_⎢⎣

⎡

_⎥⎦

⎤

− +

=

∫

⎟ = ⎠ ⎞ ⎜ ⎝ ⎛_{− − − +} 1 0 2 3 4 momen . sat ... 60 1 dx . x 3 1 x x x 3 1

sehingga pusat gravitasi :

panjang

sat

M

My

x

...

.

5

2

24

1

60

1

=

=

=

panjang

sat

M

Mx

y

...

.

5

2

24

1

60

1

=

=

=

Latihan Soal 1.3

Setelah Anda selesai mempelajari materi di atas, kini saatnya untuk melatih diri mengerjakan soal-soal berikut. Buatlah penyelesaian setiap soal dengan sistematis untuk mendapatkan jawaban akhir yang benar. Selamat berlatih...!!!

1. Sebuah lamina dengan kepadatan δ(x,y) = x + y dibatasi oleh sumbu x, garis x=1, dan kurva y = √x. Tentukan massa lamina tersebut dan pusat gravitasinya. 2. Carilah sentroid bidang yang dibatasi oleh garis y = x dan kurva y = 2 – x2

3. Carilah sentroid bidang yang dibatasi oleh kurva y= x dan garis y = 4

4. Tentukan sentroid benda pada pada oktan pertama yang dibatasi oleh bidang koordinat dan bidang x + y + z = 1

5.

Tentukan sentroid benda padat yang dibatasi oleh permukaan z = y2 dan