MODEL ASURANSI JIWA DENGAN BERBAGAI KEMUNGKINAN KEJADIAN PENGHENTIAN SKRIPSI

MODEL ASURANSI JIWA DENGAN BERBAGAI KEMUNGKINAN KEJADIAN PENGHENTIAN

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh:

Gisela Kusria NIM: 053114003

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

2009

LIFE INSURANCE MODELS WITH MULTIPLE DECREMENT

THESIS

Presented as the Partial Fulfillment of the Requirements

to Obtain The Sarjana Sains Degree

Study Program of Mathematics

by:

Gisela Kusria Student Number: 053114003

STUDY PROGRAM OF MATHEMATICS DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

2009

”Dan apa saja yang kamu minta dalam doa dengan penuh kepercayaan, kamu akan menerimanya.”

Matius 21:22

”Diri kita adalah akibat dari apa yang sudah kita pikirkan” Buddha (563-483 SM)

!

"

ABSTRAK

Terdapat dua variabel random yang membangun teori penyusutan jamak. Pertama, variabel random diskret yang menyatakan faktor yang mempengaruhi keluarnya seseorang dari asuransi, dinotasikan dengan J. Kedua, variabel random kontinu yang menyatakan waktu keluarnya seseorang dari asuransi, dinotasikan dengan T. Notasi T dan J digunakan untuk menyatakan distribusi gabungan dari T dan J serta distribusi marginal dan bersyaratnya. Skripsi ini bertujuan untuk membangun gagasan dalam menguraikan dan menggunakan distribusi dari T dan J dan distribusi bersama usia pada saat seseorang keluar dari asuransi.

Penyusutan jamak dapat dilihat dari dua kelompok survivor, yaitu kelompok survivor random dan kelompok survivor deterministik. Kelompok survivor random digunakan pada penyusutan yang terjadi pada usia yang random sedangkan kelompok survivor deterministik digunakan pada penyusutan yang terjadi pada usia tertentu.

Probabilitas seseorang akan tetap ada atau keluar pada usia tertentu dapat diperoleh pula dari penyusutan tunggal yang hanya dipengaruhi oleh sebuah penyebab.

ABSTRACT

In building multiple decrement theory there are two random variables related to it. The first is discrete random variable that refers to the cause of decrement, denoted by J. The second is continuous random variable that refers to the time-until-termination, denoted by T. T and J are used to describe the joint distribution of T and J and the related marginal and conditional distribution. This thesis developed set of ideas to describe and use the T and J distribution and the distribution of the corresponding age-at-termination.

Multiple decrement can be viewed from two group survivorship, that are, random survivorship group and deterministic survivorship group. Random survivorship group is applied for a random aged while deterministic survivorship group consider to decrement for a fixed aged.

The probability of a person will survive or leave at certain age can also be obtained from associated single decrement that depends on one decrement.

KATA PENGANTAR

Puji dan syukur penulis haturkan kepada Tuhan Yesus Kristus yang selalu menaungi dan melimpahkan rahmat kasih-Nya sehingga skripsi dengan judul ”Model Asuransi Jiwa Dengan Berbagai Kemungkinan Kejadian Penghentian” dapat terselesaikan dengan baik dan lancar.

Penulis sepenuhnya menyadari bahwa terselesaikannya skripsi ini berkat bantuan dari beberapa pihak. Pada kesempatan ini penulis mengucapkan terima kasih kepada:

1. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku Ketua Jurusan Matematika USD yang telah memberikan kesempatan kepada penulis untuk menyelesaikan skripsi ini.

2. Ibu Ch. Enny Murwaningtyas, S.Si., M.Si., selaku dosen pembimbing skripsi atas bimbingan, masukan, serta semangatnya dalam penyelesaian skripsi ini.

3. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc. dan Bapak Hongki Julie, S.Pd., M.Si. yang telah meluangkan waktu untuk menguji serta memberikan masukan yang sangat berguna bagi penulis pada tanggal 30 Juli 2009. 4. Staff dosen Jurusan Matematika USD, yang telah memberi bekal ilmu

yang berguna bagi perkembangan dan kedewasaan dalam berpikir dan bertindak.

5. Seluruh karyawan sekretariat FST yang telah membantu penulis dalam pengurusan administrasi.

6. Perpustakaan Universitas Sanata Dharma atas koleksi buku-buku serta akses internetnya sehingga penulis memperoleh bahan-bahan yang cukup lengkap dalam penulisan skripsi ini.

7. Kedua orang tua, Bapak Markus Sukarto dan Ibu Yustina Sriyatun yang telah memberikan dorongan semangat serta doa untuk keberhasilan studi penulis.

8. Petrus Eko Noviyanto yang selalu setia mendukung penulis belajar menjadi lebih baik dan memberi semangat dalam penulisan skripsi ini. 9. Adik, Katarina Kusmiyanti dan Titus Marcel Kusraynaldy yang selalu

menjadi obat serta semangat saat penulis mengalami kejenuhan dalam menulis skripsi ini.

10.Therisia Fira Hestiningsih yang mau mendengarkan pemikiran-pemikiran dan memberikan masukan yang sangat berguna bagi penulis sehingga skripsi ini dapat selesai dengan baik.

11.Semua pihak yang telah terlibat selama penyusunan skripsi ini.

Penulis menyadari bahwa tulisan ini masih terdapat keterbatasan, untuk itu penulis mengharapkan saran dan kritik yang bersifat membangun, sehingga dapat menjadi masukan dan bahan pertimbangan demi kesempurnaan tulisan ini.

Yogyakarta, 30 Juli 2009

Penulis

DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN JUDUL (INGGRIS) ... ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

HALAMAN PERSEMBAHAN ... v

PERNYATAAN KEASLIAN KARYA ... vi

ABSTRAK ... vii

ABSTACT ... viii

HALAMAN PERSETUJUAN PUBLIKASI ... ix

KATA PENGANTAR ... x

DAFTAR ISI ... xiii

DAFTAR GAMBAR ... xvi

BAB I PENDAHULUAN ... 1

A. Latar Belakang Masalah ... 1

B. Perumusan Masalah ... 4

C. Pembatasan Masalah ... 5

D. Tujuan Penulisan ... 5

E. Manfaat Penulisan ... 6

F. Metode Penulisan ... 6

G. Sistematika Penulisan ... 6

BAB II TEORI PROBABILITAS ... 8

A. Probabilitas dan Variabel Random ... 8

1. Fungsi Probabilitas dan Fungsi Distribusi Variabel Random Diskret ... 11

2. Fungsi Probabilitas dan Fungsi Distribusi Variabel Random Kontinu ... 12

B. Distribusi Probabilitas Bersama ... 14

1. Distribusi Probabilitas Diskret Bersama ... 14

2. Distribusi Probabilitas Kontinu Bersama ... 16

C. Nilai Harapan dan Variansi ... 19

D. Distribusi Probabilitas ... 24

1. Distribusi Bernoulli ... 24

2. Distribusi Binomial ... 25

3. Distribusi Seragam Kontinu ... 26

4. Distribusi Normal ... 26

5. Distribusi Normal Standar ... 27

BAB III SATU KEJADIAN PENGHENTIAN ... 28

A. Suku Bunga ... 28

B. Probabilitas Usia Pada Saat Meninggal ... 32

1. Fungsi Kelangsungan Hidup ... 32

2. Waktu Meninggal Untuk Orang yang Berusia x ... 35

3. Waktu Hidup yang Dipersingkat ... 40

C. Percepatan Mortalita ... 41

D. Tabel Kehidupan ... 47

1. Hubungan Fungsi Tabel Kehidupan dan

Fungsi Kelangsungan Hidup ... 47

2. Karakteristik ... 52

E. Asuransi Jiwa ... 68

1. Asuransi Berjangka ... 69

2. Asuransi Seumur Hidup ... 73

3. Endowmen Murni ... 74

4. Asuransi Endowmen ... 77

5. Asuransi Tertunda ... 78

BAB IV BERBAGAI KEMUNGKINAN KEJADIAN PENGHENTIAN ... 80

A. Dua Variabel Random ... 80

B. Kelompok Survivor Random ... 105

C. Kelompok survivor Deterministik ... 108

D. Faktor Penyebab Tunggal ... 114

1. Hubungan Dasar ... 116

2. Nilai Tengah Penyusutan Jamak ... 118

3. Asumsi Percepatan Konstan untuk Penyusutan Jamak ... 124

4. Asumsi Distribusi Seragam untuk Penyusutan Jamak ... 129

5. Perkiraan Hasil ... 132

E. Membuat Tabel Penyusutan Jamak ... 137

BAB V APLIKASI TEORI PENYUSUTAN JAMAK ... 148

BAB VI PENUTUP ... 159

A. Kesimpulan ... 159

B. Saran ... 161

DAFTAR PUSTAKA ... 162

LAMPIRAN ... 164

DAFTAR GAMBAR

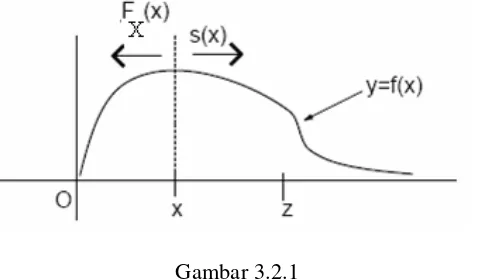
Gambar 3.2.1 Fungsi distribusi probabilitas f(x)

untuk kematin pada saat usia x ... 34 Gambar 3.2.2 Waktu hidup yang dijalani oleh x ... 36 Gambar 4.5.1 Unsur-unsur fungsi kehidupan,

( )_{, 1,2,3}

' j= p_x j

t dan

( )τ x

tp ... 144

BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Banyak permasalahan sosial yang terjadi pada masa kini. Salah satu permasalahannya yaitu masalah ketidakpastian ekonomi yang akan mempengaruhi kesejahteraan keluarga. Kesejahteraan keluarga akan terganggu bila seseorang yang bekerja dalam keluarga tersebut kehilangan penghasilannya. Sebab-sebab kehilangan penghasilan antara lain karena cacat/sakit, kecelakaan, kematian, dan mengundurkan diri dari pekerjaan. Sebagian dari jaminan kesejahteraan tersebut dapat diperoleh bila kepala keluarga mengasuransikan dirinya. Asuransi ini misalnya berupa asuransi kesehatan dan asuransi jiwa.

Orang yang mengambil asuransi berarti sepakat dengan ketentuan-ketentuan yang telah disepakati antara dirinya dengan perusahaan asuransi. Kesepakatan ini berupa kontrak antara orang yang mengasuransikan dirinya dengan perusahaan asuransi, yang biasa disebut dengan polis asuransi. Dalam polis tersebut telah diatur besarnya pembayaran serta banyaknya uang yang akan diterima. Pembayaran yang dilakukan orang yang diasuransikan biasa disebut dengan premi. Sedangkan, uang yang akan diterima disebut santunan.

Premi biasanya dihitung dengan mempertimbangkan faktor biaya (biaya pegawai, pajak, komisi, dan sebagainya). Namun pada pembahasan dalam skripsi

ini yang diperhitungkan hanya probabilitas keluarnya seseorang dari asuransi dan tingkat bunga tanpa memperhitungkan faktor biaya. Premi yang dihitung tanpa memperhatikan faktor biaya disebut premi bersih. Pembayaran premi dapat dibayarkan sekaligus, disebut premi tunggal, dapat pula seumur hidup, dan dapat pula selama jangka waktu tertentu, misalnya selama 20 tahun. Premi yang pembayarannya dilakukan sekaligus tanpa memperhitungkan faktor biaya disebut premi tunggal bersih.

Keanggotaan seseorang dalam asuransi dapat berhenti oleh beberapa faktor. Faktor-faktor tersebut antara lain meninggal dunia, keluar dari pekerjaan dan keluar dari program asuransi yang telah dijalani. Berikut ini beberapa contoh asuransi serta faktor-faktor yang mempengaruhi berhentinya keanggotaan seseorang dalam asuransi:

1. Asuransi jiwa dengan pembayaran sekali

Prinsip dari asuransi ini yaitu premi dibayarkan hanya satu kali selama mengikuti asuransi. Asuransi ini memberikan santunan kepada pewaris jika orang yang mengasuransikan dirinya meninggal dunia. Dengan kata lain, dalam asuransi ini polis akan berhenti jika orang yang mengasuransikan dirinya meninggal dunia.

2. Asuransi berjangka

mengasuransikan dirinya meninggal karena berbagai penyebab. Misalkan orang tersebut meninggal karena kecelakaan atau penyakit kronis.

3. Asuransi Pendidikan

Pembayaran premi pada asuransi pendidikan biasanya dilakukan dalam jangka waktu tertentu sebelum orang yang diasuransikan masuk sekolah atau perguruan tinggi. Santunan asuransi akan diterima bila orang yang diasuransikan sampai pada waktu yang telah ditetapkan untuk menerima santunan asuransi (telah mencapai usia sekolah). Selain itu, asuransi akan diterima jika orang yang diasuransikan meninggal dunia atau keluar dari rencana asuransi ini.

4. Dana pensiun

Pembayaran premi pada asuransi ini biasanya dilakukan sampai batas waktu sebelum pensiun. Santunan asuransi akan diterima bila orang yang diasuransikan meninggal dunia, mengalami kecacatan, pensiun, atau keluar dari pekerjaan.

Pada asuransi jiwa dengan pembayaran sekali, terdapat satu faktor penyebab sehingga seseorang keluar dari perencanaan asuransi, yaitu meninggal dunia. Pada asuransi berjangka terdapat dua faktor, yaitu orang yang diasuransikan meninggal dunia karena kecelakaan dan penyakit kronis. Untuk asuransi pendidikan terdapat tiga faktor, yaitu orang yang diasuransikan sampai pada waktu yang telah

tersebut keluar dari perencanaan asuransi. Dan faktor penyebab untuk dana pensiun yaitu orang yang diasuransikan meninggal dunia, mengalami kecacatan, pensiun, dan keluar dari pekerjaan.

Faktor yang mempengaruhi keluarnya seseorang dalam asuransi disebut penyusutan (decrement). Sedangkan keluarnya seseorang karena lebih dari satu faktor penyebab disebut sebagai penyusutan jamak ( multiple decrement).

Penyusutan jamak yang terdapat dalam permasalahan di atas sangat bergantung pula dengan dua variabel random, yaitu waktu berhentinya (time until termination) dan penyebab berhenti (cause of the termination). Variabel random

waktu berhenti merupakan variabel random kontinu dan dinotasikan dengan T(x) atau T. Sedangkan variabel random penyebab berhenti merupakan variabel random diskret dan dinotasikan dengan J(x) atau J. Distribusi serta model matematis untuk asuransi jiwa dengan berbagai kemungkinan kejadian penghentian dapat ditentukan melalui dua variabel random tersebut.

B. Perumusan Masalah

Pokok permasalahan yang akan dibahas dapat ditulis dengan beberapa pertanyaan berikut:

2. Bagaimanakah bentuk penyusutan jamak yang terdapat dalam asuransi jiwa?

3. Bagaimanakah model asuransi jiwa dengan berbagai kemungkinan kejadian penghentian?

4. Bagaimanakah aplikasi dalam asuransi jiwa yang menggunakan penyusutan jamak?

C. Pembatasan Masalah

Dalam penulisan skripsi ini diberikan beberapa batasan sebagai berikut:

1. Hanya akan dibahas untuk single life.

2. Aplikasi yang akan dibahas yaitu hanya untuk asuransi berjangka dengan dua penyebab pada kematian serta asuransi seumur hidup.

3. Premi yang digunakan pada asuransi adalah premi tunggal bersih.

D. Tujuan Penulisan

Penulisan ini memiliki tujuan sebagai berikut:

1. Mengetahui cara menentukan probabilitas dari dua variabel random yaitu waktu berhenti (time until termination) dan penyebab berhenti (cause of the termination) pada single life.

3. Mengetahui model asuransi jiwa untuk berbagai kemungkinan kejadian penghentian.

4. Mengetahui aplikasi dalam asuransi jiwa yang menggunakan penyusutan jamak.

E. Manfaat Penulisan

Penulisan ini mempunyai manfaat yaitu dapat menganalisis kemungkinan kejadian penghentian yang berasal dari dua variabel random yaitu waktu berhenti (time until termination) dan penyebab berhenti (cause of the termination) pada single life.

F. Metode Penulisan

Metode penulisan yang digunakan yaitu metode studi pustaka atau studi literatur. Studi pustaka ini dilakukan dengan cara mempelajari serta mengolah materi dari buku-buku dan informasi yang diperoleh dari internet yang berkaitan dengan permasalahan yang akan dibahas. Dalam penulisan ini tidak ditemukan sesuatu yang baru.

G. Sistematika Penulisan

masalah, perumusan masalah, pembatasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan, dan sistematika penulisan.

Bab II membahas tentang teori probabilitas yang berisi tentang probabilitas dan variabel random, distribusi probabilitas bersama, nilai harapan dan variansi, distribusi binomial, distribusi seragam, dan distribusi normal.

Bab III akan membahas tentang satu kejadian penghentian, yaitu kematian. Bab ini berisi tentang suku bunga, probabilitas usia pada saat meninggal, percepatan mortalita, tabel kehidupan, dan asuransi jiwa.

Bab IV membahas tentang berbagai kemungkinan kejadian penghentian dalam perencanaan asuransi. Pada bab ini berisi tentang dua variabel random yang mempengaruhi penyusutan jamak, kelompok survivor random, kelompok survivor deterministik, faktor penyebab tunggal, dan membuat tabel penyusutan jamak.

Bab V akan membahas aplikasi untuk asuransi berjangka dan seumur hidup.

BAB II

TEORI PROBABILITAS

A. Probabilitas dan Variabel Random

Percobaan (eksperimen) dalam statistika merupakan proses yang akan menghasilkan data. Hasil percobaan yang diperoleh bergantung pada faktor kebetulan sehingga hasilnya tidak dapat diperkirakan secara pasti. Contohnya yaitu pada pelemparan sebuah dadu yang dilemparkan berulang kali. Pada pelemparan dadu ini tidak dapat dipastikan pada pelemparan tertentu akan diperoleh sisi bernomor 6. Namun yang dapat diketahui secara pasti yaitu semua kemungkinan hasil untuk setiap pelemparan.

Himpunan semua hasil yang mungkin dari suatu percobaan disebut ruang sampel. Ruang sampel dinyatakan dengan lambang S. Setiap kemungkinan hasil yang terdapat dalam ruang sampel disebut titik sampel.

Dalam melakukan percobaan yang ingin diketahui yaitu munculnya kejadian tertentu. Setiap kejadian tersebut berkaitan dengan sekumpulan titik sampel yang terdapat dalam ruang sampel. Sekumpulan titik sampel ini akan membentuk himpunan bagian di dalam ruang sampelnya. Himpunan bagian tersebut akan mewakili semua anggota sehingga kejadian tertentu dapat terjadi.

Misalkan A adalah kejadian. Probabilitas kejadian A diperoleh dengan menjumlahkan probabilitas semua titik sampel yang terdapat dalam kejadian A. Jumlahan ini disebut probabilitas kejadian A dan dilambangkan dengan P(A).

Definisi 2.1.1

Misalkan S merupakan ruang sampel, A merupakan kejadian, dan P merupakan suatu fungsi yang didefinisikan pada A, maka P disebut fungsi probabilitas dan P(A) disebut probabilitas kejadian A jika memenuhi aksioma-aksioma berikut: a. 0≤P

( )

A ≤1

b. P

( )

φ =0

c. P

( )

S =1

d. Bersifat aditif, yaitu

( )

i n

i i n

i A P A

P

∑

= = _=

   

∪

1

1 jika Ai∩Aj=φ, i≠ j

Misalkan kejadian A menjadi syarat terjadinya kejadian B. Probabilitas terjadinya kejadian B bila diketahui kejadian A telah terjadi disebut probabilitas bersyarat. Probabilitas ini disimbolkan dengan P(B|A) yang menyatakan probabilitas B dengan syarat kejadian A telah terjadi.

Definisi 2.1.2

Misalkan A dan B merupakan kejadian sehingga probabilitas kejadian B bila diketahui kejadian A telah terjadi didefinisikan sebagai berikut:

(

) (

( )

)

A

B A A

B

P P

P | = ∩ dengan P

( )

A >0

mempengaruhi terjadinya kejadian yang lain. Kejadian ini disebut kejadian saling bebas dan didefinisikan sebagai berikut:

Definisi 2.1.3

Kejadian A dan B disebut dua kejadian yang saling bebas jika

(

A B

) ( ) ( )

P A P B

P ∩ =

Definisi 2.1.4

Misalkan S adalah ruang sampel, sehingga fungsi yang didefinisikan pada ruang sampel S, yang memetakan setiap elemen b∈S ke bilangan real, X

( )

b = x disebut variabel random X.

Huruf kapital X menyatakan variabel random dan huruf kecilnya, yaitu x menyatakan nilai variabel random yang mungkin terjadi.

yang cacat, banyaknya kecelakaan per tahun di DIY. Sedangkan, variabel random kontinu biasanya digunakan untuk data yang diukur, misalnya pengukuran tinggi, bobot, suhu, jarak atau, usia.

1. Fungsi Probabilitas dan Fungsi Distribusi Variabel Random Diskret Variabel random diskret menggambarkan data cacah. Probabilitas dari variabel random X biasanya dinyatakan dalam rumusan, misalnya

( ) ( ) ( )

x g x h x

f , , .

Definisi 2.1.5

Misalkan X adalah variabel random diskret dengan kemungkinan nilainya adalah x=x₁,x₂,⋅⋅⋅,x_n maka fungsi f

( ) (

x =P X =x

)

merupakan probabilitas untuk semua kemungkinan nilai variabel random diskret X. Fungsi ini disebut sebagai fungsi probabilitas diskret dari variabel random X dan biasa disebut dengan fungsi probabilitas.

Suatu fungsi probabilitas disebut sebagai fungsi probabilitas diskret jika memenuhi syarat-syarat tertentu yang didefinisikan sebagai berikut:

Definisi 2.1.6

Fungsi f

( )

x disebut fungsi probabilitas diskret dari variabel random X jika memenuhi syarat-syarat di bawah ini:

b.

∑

( )

∀

=

x x

f 1

Fungsi distribusi kumulatif biasa disingkat dengan fungsi distribusi suatu variabel random X , didefinisikan sebagai berikut

( ) (

)

∑

( )

≤

= ≤ =

x u

u f x

X x

F P untuk −∞<x<+∞ (2.1.1)

Suatu fungsi memiliki sifat-sifat tertentu sehingga dapat disebut sebagai fungsi distribusi. Berikut ini didefinisikan sifat-sifat fungsi distribusi yang berlaku untuk variabel random kontinu dan variabel random diskret.

Definisi 2.1.7

Fungsi F(x) adalah fungsi distribusi variabel random X bila memenuhi sifat-sifat di bawah ini:

a. lim

( )

=0

−∞ → F x

x dan xlim→+∞F

( )

x =1

b. Merupakan fungsi menaik secara monoton, F

( ) ( )

x <F y untuk x < y. c. Bernilai antara 0 dan 1, 0≤F

( )

x ≤1.

Definisi 2.1.8

Fungsi f

( )

x disebut fungsi probabilitas kontinu (fungsi densitas probabilitas) untuk variabel random kontinu X bila memenuhi syarat-syarat di bawah ini: a. f

( )

x ≥0 ∀x∈R

b.

∫

( )

∞ ∞ −

=1 dx x f

c.

(

< <

)

=

∫

( )

b

a dx x f b x a P

Fungsi distribusi, F

( )

x , untuk variabel random kontinu adalah

( ) (

)

∫

( )

∞ −

= ≤ =

x dt t f x X x

F P dengan −∞<x<+∞ (2.1.2)

Jika Persamaan (2.1.2) didiferensialkan kedua ruasnya maka diperoleh

( )

( )

( )

(

)

( )

( )

(

)

( )

( )

( ) ( )

− −∞ =

∞ − −

=

∞ − − =

= =

∞ − ∞ −

∫

f x f

f dx

d x f dx

d

f x f dx

d t f dx

d

dt t f dx

d x F dx

d

x x

' '

' '

'

Berdasarkan Definisi (2.1.8) bagian (a) maka

( ) ( )

x f x

F dx

d

= (2.1.3)

B. Distribusi Probabilitas Bersama

Pada sebuah kejadian biasanya terdapat lebih dari satu variabel random, misalnya X1,X2,...,Xn. Variabel-variabel random ini dapat dipandang sebagai komponen dari sebuah vektor berdimensi n, X=

(

X1,X2,...,Xn

)

dengan nilai

(

x1,x2,...,xn

)

=

x dalam ruang dimensi n. Vektor nilai, sebagai contoh, dapat merupakan hasil pengukuran n buah karakteristik suatu objek tertentu.

1. Distribusi Probabilitas Diskret Bersama

Distribusi probabilitas diskret bersama dapat didefinisikan sebagai berikut:

Definisi 2.2.1

Distribusi probabilitas diskret bersama dari variabel random berdimensi n,

(

X1,X2,...,Xn

)

=

X didefinisikan sebagai

(

x x xn

) (

X x X x Xn xn

)

f 1, 2,..., =P 1= 1, 2 = 2,..., = Untuk semua kemungkinan nilai x=

(

x₁,x₂,...,x_n

)

dari X.

Definisi (2.2.1) menyatakan bahwa distribusi probabilitas bersama untuk variabel random diskret merupakan suatu tabel atau rumus yang mendaftarkan semua kemungkinan nilai x=

(

x1,x2,...,xn

)

bagi variabel random diskret X dengan probabilitasnya yang sesuai.

Definisi 2.2.2

Variabel random diskret X=

(

X1,X2,...,Xn

)

memiliki probabilitas bersama

(

x x xn

)

f 1, 2,..., dengan fungsi probabilitas marginal dari X1, X2, . . ., Xn yaitu

( )

(

)

( )

(

)

( )

∑∑ ∑

(

)

∑∑ ∑

∑∑ ∑

∀ ∀ ∀ ∀ ∀ ∀ ∀ ∀ ∀

−

= = =

1 2 1

1 3

2 3

., .. , , .

. . . . .

., .. , , .

. .

., .. , , .

. .

2 1

2 1 2

2

2 1 1

1

x x x

n n

n

x x x

n x x x

n

n n n

x x x f x

f

x x x f x

f

x x x f x

f

Definisi 2.2.3

Variabel random diskret X=

(

X1,X2,...,Xn

)

didefinisikan pada ruang probabilitas sehingga fungsi distribusi bersama X1, X2, . . ., Xn didefinisikan sebagai berikut

(

n

) (

n n

)

X X

X x x x X x X x X x

F

n 1, 2,..., = 1≤ 1, 2 ≤ 2,..., ≤

. . .

2

1 P

Definisi 2.2.4

Misalkan X1 dan X2 variabel random diskret dengan fungsi probabilitas

gabungannya p(x₁,x₂) serta fungsi probabilitas marginalnya p₁(x₁) dan )

( ₂

2 x

p . Probabilitas bersyarat untuk X₁ dengan X₂ = x₂ yaitu

(

x1|x2

)

p(X1 x1|X2 x2)

(

)

) (

) , (

) (

) ,

( |

2 2

2 1

2 2

2 2 1 1 2

1

x p

x x p

x X p

x X x X p x x p

=

= = =

=

dan probabilitas bersyarat untuk X₂ jika X₁ = x₁ yaitu

(

)

) (

) , (

) (

) ,

(

) |

( |

1 1

2 1

1 1

2 2 1 1

1 1 2 2 1

2

x p

x x p

x X p

x X x X p

x X x X p x x p

=

= = =

=

= =

=

Definisi 2.2.5

Misalkan X1 dan X2 saling independen, dengan fungsi probabilitas gabungan

diskret p(x₁,x₂) serta fungsi probabilitas marginalnya p₁(x₁) dan p₂(x₂) maka

(

x₁,x₂

)

p₁(x₁)p₂(x₂)

p =

untuk semua bilangan real (x1,x2).

2. Distribusi Probabilitas Kontinu Bersama

Fungsi densitas probabilitas kontinu dapat didefinisikan sebagai berikut:

Definisi 2.2.6

Fungsi f

(

x₁,x₂,...,x_n

)

adalah fungsi densitas bersama n variabel random jika memenuhi syarat-syarat berikut ini:

dan

(

)

∫ ∫

+∞ ∞ −

+∞ ∞ −

=1 . .. ,

.. . , .

.

. f x₁ xn dx₁ dxn

dan fungsi distribusi kumulatif variabel random kontinu dapat didefinisikan pula sebagai berikut:

Definisi 2.2.7

Variabel random berdimensi n, X=

(

X1,X2,...,Xn

)

kontinu jika terdapat fungsi f

(

x1,x2,...,xn

)

yang disebut fungsi densitas bersama dari X sedemikian rupa sehingga fungsi distribusi kumulatifnya

(

)

∫ ∫

(

)

∞ − −∞

= n

x x

n n

n f t t dt dt x

x x F

1

. .. , .. . , . . . ,

.. . ,

, 2 1 1

1

Definisi 2.2.8

Variabel random kontinu X₁ dan X₂ dengan fungsi densitas bersama

(

x1,x2

)

f memiliki fungsi densitas marginal untuk X1 dan X2 yaitu

( )

(

)

( )

∫

(

)

∫

∞ +

∞ − +∞

∞ −

= =

1 2 1 2

2

2 2 1 1

1

, ,

dx x x f x f

dx x x f x f

Definisi 2.2.9

bersama f

(

x1,x2,...,xn

)

dengan fungsi probabilitas marginal dari X1, X2, . .

., Xn yaitu

( )

(

)

( )

∫ ∫ ∫

(

)

∫ ∫ ∫

∞ + ∞ − ∞ + ∞ − ∞ + ∞ − +∞ ∞ − +∞ ∞ − +∞ ∞ − = = n n n n dx dx dx x x x f x f dx dx dx x x x f x f . . . ., . . , , ... . . . ., . . , , ... 3 1 2 1 2 2 3 2 2 1 1 1

( )

+

∫ ∫ ∫

∞

(

)

∞ − ∞ + ∞ − ∞ + ∞ − −

= ... 1, 2,..., 2 3... 1

. . . n n n

n x f x x x dx dx dx f

Definisi 2.2.10

Misalkan X₁ dan X₂ variabel random kontinu dengan fungsi densitas gabungannya f(x1,x2) serta fungsi probabilitas marginalnya f1(x1) dan

) ( 2 2 x

f . Probabilitas bersyarat untuk X1 dengan X2 = x2 yaitu

(

)

     > = selainnya x f x f x x f x x f 0 0 ) ( ) ( ) , (

| 2 2 2 2

2 1 2

1

dan probabilitas bersyarat untuk X2 jika X1 = x1 yaitu

(

)

     > = selainnya x f x f x x f x x f 0 0 ) ( ) ( ) , (

| 1 1 1 1

2 1 1

2

Definisi 2.2.11

) , (x₁ x₂

f serta fungsi densitas marginalnya f₁(x₁) dan f₂(x₂) maka

(

x₁,x₂

)

f₁(x₁) f₂(x₂)

f =

untuk semua bilangan real (x1,x2).

C. Nilai Harapan dan Variansi

Nilai harapan untuk variabel random X, dinotasikan dengan E

[ ]

X dan didefinisikan sebagai berikut:

Definisi 2.3.1

Misalkan X adalah variabel random diskret dengan fungsi probabilitas p

( )

x maka nilai harapan dari X, E

[ ]

X , yaitu

[ ]

∑

( )

=

= n

i

i i p x x X

E

1

Misalkan X variabel random kontinu dengan nilai x yang memiliki fungsi densitas

( )

x

f maka nilai harapan untuk X, E

[ ]

X , yaitu

[ ]

=+∞

∫

( )

−∞< <+∞

∞ −

x dx

x f x X E

Nilai harapan untuk fungsi satu variabel random didefinisikan sebagai berikut:

Definisi 2.3.2

( )

[ ]

∑

( ) ( )

=

= n

i

i i p x x g x

g E

1

Misalkan X variabel random kontinu dengan nilai x yang memiliki fungsi densitas

( )

x

f serta fungsi dari variabel random X,g

( )

x , maka nilai harapan untuk g

( )

x ,

( )

[ ]

g x E , yaitu

( )

[ ]

=+∞

∫

( ) ( )

−∞< <+∞

∞ −

x dx

x f x g x g E

Definisi 2.3.3

Jika X1 dan X2 dua variabel random diskret, nilai harapan bersyarat untuk X1

jika X₂ =x₂ didefinisikan sebagai

(

=

)

=

∑

(

)

1

2 1 1 2

2

1| |

y

y y p y y

Y Y E

Jika X₁ dan X₂ dua variabel random kontinu, nilai harapan bersyarat untuk X₁ jika X₂ =x₂ didefinisikan sebagai

(

)

+∞

∫

(

)

∞ −

=

= 2 1 1 2 1

2

1|Y y y f y | y dy

Y E

Lemma 2.3.1

Jika X adalah variabel random kontinu dengan fungsi densitas f

( )

x , a dan b konstanta, g₁

( )

x dan g₂

( )

x fungsi-fungsi variabel random bernilai real, maka

( )

( )

[

ag x bg x

]

aE

[

g

( )

x

]

bE

[

g

( )

x

]

E ₁ + ₂ = ₁ + ₂

Bukti:

Jika X adalah variabel random kontinu maka menurut definisi nilai harapan pada Definisi (2.3.1) maka

( )

( )

[

]

[

( )

( )

]

( )

( ) ( )

( ) ( )

[

]

( ) ( )

( ) ( )

( ) ( )

∫

( ) ( )

∫

∫

∫

∫

∫

∞ +

∞ − ∞

+ ∞ −

∞ +

∞ − ∞

+ ∞ −

∞ +

∞ −

+∞ ∞ −

+ =

+ =

+ =

+ =

+

dx x f x g b dx x f x g a

dx x f x g b dx x f x g a

dx x f x g b x f x g a

dx x f x g b x g a x

g b x g a E

2 1

2 1

2 1

2 1

2 1

Berdasarkan Definisi (2.3.2) maka diperoleh bahwa

( )

( )

[

ag x bg x

]

aE

[

g

( )

x

]

bE

[

g

( )

x

]

E ₁ + ₂ = ₁ + ₂

■

Berikut ini adalah nilai harapan untuk n variabel random.

Lemma 2.3.2

random yaitu

[ ]

∑

∑

= = =       n i i n i

i E X X E 1 1 Bukti:

Berdasarkan persamaan pada Definisi (2.3.1), nilai harapan jumlah untuk n variabel random kontinu adalah

[

]

(

) (

)

(

)

(

)

[

(

)

]

(

)

(

)

. . . . . . , .. . , , . . . . . . , .. . , , . . . . . . , .. . , , . . . , .. . , , , .. . , , . . . . . . , .. . , , .. . . . . .. . 2 1 2 1 2 2 1 2 1 1 2 1 2 1 2 1 2 2 1 1 2 1 2 1 2 1 2 1 1 + + = + + + = + + + = + + + =      

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∑

∞ + ∞ − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − = n n n n n n n n n n n n n n i i dx dx dx x x x f x dx dx dx x x x f x dx dx dx x x x f x x x x f x x x x f x dx dx dx x x x f x x x X X X E X E

(

n

)

n

n f x x x dx dx dx

x , ,..., ...

. .

.

∫

1 2 1 2

∫

∫

+∞ ∞ − +∞ ∞ − +∞ ∞ − +

(

)

(

)

(

n

)

n n

n n n n n dx dx dx dx x x x f x dx dx dx x x x f x dx dx dx x x x f x       + +       +       = − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − ∞ + ∞ − +∞ ∞ − +∞ ∞ − +∞ ∞ −

∫

∫

∫

∫

∫

∫

∫

∫

∫

1 2 1 2 1 2 1 2 1 2 1 2 2 1 1 . . . , .. . , , . . . . . . . . . , .. . , , . . . . . . , .. . , , . . .

( )

∫

( )

∫

( )

∫

∑

+∞ ∞ − +∞ ∞ − +∞ ∞ − = + + + =       n n n n n i

i x f x dx x f x dx x f x dx X

E _{1 1 1 1 2 2 2 2} ...

1

Dan berdasarkan persamaan pada Definisi (2.3.1) diperoleh bahwa

[ ] [ ]

[ ]

[ ]

∑

∑

= = = + + + =       n i i n n i i X E X E X E X E X E 1 2 1 1 .. . ■ Lemma 2.3.3

Misalkan terdapat n variabel random, X=

{

X1,X2,...,Xn

}

yang saling bebas dengan fungsi densitas bersama f

(

x1,x2,...,xn

)

yang probabilitas marginalnya

( )

1 1 x

f , f2

( )

x2 , . . ., fn

( )

xn maka nilai harapan hasil kali n variabel random yaitu

[ ]

∏

∏

= = =       n i i n i

i E X

X E

1 1

Bukti:

Berdasarkan persamaan pada Definisi (2.3.1) maka nilai harapan dari hasil kali n variabel random yaitu

[

]

(

n

) (

n

)

n

n n i i dx dx dx x x x f x x x X X X E X E . .. , .. . , , . .. . . . . .. 2 1 2 1 2 1 2 1 1

∫

∫

∫

∏

∞ + ∞ − ∞ + ∞ − ∞ + ∞ − = = =      

Karena X=

{

X₁,X₂,...,X_n

}

saling bebas maka

Nilai f₁

( )

x₁ , f₂

( )

x₂ , . . ., fn

( )

xn merupakan fungsi probabilitas marginal bagi

{

X1,X2,...,Xn

}

=

X maka diperoleh

(

) ( ) ( )

( )

( )

( )

n

( )

n n

n n

n n

i i

dx x f x dx

x f x dx x f x

dx dx dx x f x f x f x x x X

E

∫

∫

∫

∫

∫

∫

∏

∞ +

∞ − ∞

+ ∞ − ∞

+ ∞ −

+∞ ∞ − +∞

∞ − +∞

∞ − =

= =

     

. . .

. . . .

. . ..

. .

. .

2 2 2 1 1 1

2 1 2

1 2

1 1

Berdasarkan persamaan pada Definisi (2.3.1) maka diperoleh

[ ] [ ]

[ ]

[ ]

∏

∏

= =

= =

     

n

i i

n n

i i

X E

X E X E X E X E

1

2 1 1

. . .

■

Pembuktian untuk sifat-sifat nilai harapan pada variabel random diskret dapat dibuktikan secara analog.

Definisi 2.3.4

Variansi untuk variabel random X yaitu

( )

( )

2

[

( )

]

2

X E X E X

Var = −

D. Distribusi Probabilitas 1. Distribusi Bernoulli

dari distribusi Bernoulli. Bila sukses disimbolkan dengan 1 dan gagal dengan 0 maka fungsi distribusi Bernoulli dapat didefinisikan sebagai berikut:

Definisi 2.4.1

Bila X adalah variabel random Bernoulli maka distribusi probabilitas X adalah

( )

_{x = p q}1− _x=0,1

p x x

Persamaan pada Definisi (2.4.1) dapat pula ditulis sebagai berikut:

( )

    

= −

= =

selainnya 0

2 1

1 x p

x p

x p

2. Distribusi Binomial

Suatu percobaan biasanya seringkali terdiri dari ulangan-ulangan, dan masing-masing memiliki kemungkinan sukses dan gagal. Percobaan ini disebut sebagai percobaan binomial. Percobaan binomial memiliki ciri-ciri berikut ini:

a. Percobaan terdiri dari n ulangan.

b. Dalam setiap pengulangan, terdapat dua hasil yang mungkin yaitu sukses atau gagal.

c. Peluang sukses, dinotasikan p, untuk setiap ulangan adalah sama, tidak berubah-ubah.

Definisi 2.4.2

Variabel random X1,X2,...,Xn masing-masing saling bebas serta berdistribusi

Bernoulli maka

∑

=

= n

i i X X

1

merupakan variabel random yang berdistribusi

Binomial yaitu

(

)

p q x n

x n p n x

b ; , _ x n x =0,1,...,

    

= −

3. Distribusi Seragam Kontinu Definisi 2.4.3

X merupakan variabel random kontinu yang berdistribusi seragam bila fungsi

densitasnya

( )

   

≤ ≤ −

=

selainnya 0

1

b x a a

b x f

4. Distribusi Normal Definisi 2.4.3

Variabel random X berdistribusi normal dengan mean µ dan simpangan baku

σ

bila fungsi densitasnya berbentuk

(

)

2

2 1

2 1 ,

;

      − −

= σ

µ πσ

σ µ

x e x

5. Distribusi Normal Standar

Distribusi normal memenuhi sifat-sifat fungsi densitas jika disubstitusikan

σ µ

−

= x

z dan dx=σdz pada persamaan pada Definisi (2.4.3) serta

diintegralkan dengan batas bawah −∞ dan batas atas +∞. Pada skripsi ini tidak akan dibuktikan bahwa distribusi normal memenuhi sifat tersebut namun akan langsung digunakan untuk menentukan distribusi normal standar. Fungsi densitas hasil transformasi dari X ke Z disebut sebagai distribusi normal standar, yang fungsinya

( )

z = e− z −∞<z<+∞ 2

2 1

BAB III

SATU KEJADIAN PENGHENTIAN

A. Suku Bunga

Bunga merupakan pertambahan jumlah uang yang telah diinvestasikan. Berdasarkan perhitungannya, bunga dibagi menjadi dua yaitu bunga tunggal dan bunga majemuk. Bunga tunggal adalah bunga yang diperhitung dari pembayaran awal dan ditambahkan pada setiap akhir jangka waktu tertentu. Sedangkan bunga majemuk adalah bunga yang dihitung dari besarnya pokok pada permulaan periode sebelumnya sehingga untuk setiap periode akan menghasilkan nilai bunga yang berbeda-beda.

Investasi dana yang dilakukan oleh seseorang memiliki periode tertentu. Pada akhir periode, besarnya dana yang telah diinvestasikan dipengaruhi oleh besarnya pembayaran awal, tingkat bunga, serta jenis bunga yang digunakan.

Untuk pembayaran awal sebesar P dengan suku bunga tahunan i, perhitungan jumlah bunga dengan pokoknya pada akhir jangka waktu t tahun, dinotasikan Pt. Berdasarkan pengertian bunga tunggal, secara matematis dapat didefinisikan jumlah bunga dan pokoknya sebagai berikut:

Definisi 3.1.1

Untuk P menyatakan uang pokok, yaitu besarnya pembayaran awal dan i menyatakan suku bunga setahun dengan bunga tunggal maka jumlah bunga dengan pokoknya pada akhir jangka waktu t tahun, Pt, yaitu:

) 1 ( ti P

tiP P P_t

+ =

+ =

Untuk pembayaran awal sebesar P dengan suku bunga setahun i, perhitungan jumlah bunga dengan pokoknya pada akhir jangka waktu t tahun, Pt, berdasarkan perhitungan bunga majemuk didefinisikan sebagai berikut:

Definisi 3.1.2

Misalkan P menyatakan uang pokok, yaitu besarnya pembayaran awal dan i menyatakan tingkat bunga setahun dengan bunga majemuk maka jumlah bunga dengan pokoknya pada akhir jangka waktu t tahun, Pt, yaitu:

t t P i P = (1+ )

Nilai (1+i) disebut sebagai faktor akumulatif untuk satu tahun.

Definisi 3.1.3

Faktor bunga dapat didefinisikan sebagai berikut

i v

+ =

1 1

Sehingga persamaan pada Definisi (3.1.2) dapat pula ditulis menjadi t

t Pv

P = −

waktu dikenakannya bunga selama m kali dalam setahun, perhitungan jumlah bunga dengan pokoknya pada akhir jangka waktu t tahun berdasarkan perhitungan bunga majemuk didefinisikan sebagai berikut:

Definisi 3.1.4

Misalkan P menyatakan uang pokok, yaitu besarnya pembayaran awal dan bunga majemuk selama m kali dalam setahun dengan tingkat bunga _i( )m _{maka jumlah} bunga dengan pokoknya pada akhir jangka waktu t tahun, Pt, yaitu

( )_m tm t

m i P

P _

  

 

+

= 1

Jika persamaan pada Definisi (3.1.4) diperhitungkan untuk satu tahun maka faktor akumulatif m kali dalam setahun ekivalen dengan faktor akumulatif untuk satu tahun sehingga diperoleh

( )

( )

i m

im m

+ =

   

 

+ 1

1

Persamaan tersebut dapat pula ditulis menjadi

( )

( )

( )

( )

m m

m m

m m

i m

i

i m

i

1 1

1 1

1 1

+ =

   

 

+

+ =

   

 

+

Sehingga bila dinyatakan untuk _i( )m _{diperoleh bahwa}

( )

( )

  



− +

= 1 m1 1

m

( )

( )

m i

im m

1 1 1+ 1 −

= (3.1.1)

Jika bunga diperhitungkan setiap waktu (misalnya dihitung per hari atau per menit) maka m→∞. Nilai limit m→∞ ini disimbolkan dengan δ , sehingga diperoleh bahwa δ = ∞ → m

mlimi (3.1.2) Untuk selanjutnya nilai δ akan disebut sebagai percepatan bunga. Jika m→∞ maka limit m→∞ untuk Persamaan (3.1.1) yaitu

( )

( )

( )

( )

m i m m i m i i m m m m m m m 1 1 1 ln 1 exp lim 1 1 1 ln exp lim 1 1 1 lim lim 1 1 −       +       = −     + = − + = ∞ → ∞ → ∞ → ∞ → δ

Dengan aturan l’Hôpital diperoleh bahwa

( )

( )

( )

( )

( )

( )

1 (3.1.3)

eδ =1+i=v−1 (3.1.4)

B. Probabilitas Usia Pada Saat Meninggal

Seseorang yang baru lahir akan hidup dalam jangka waktu tertentu. Setelah mencapai akhir jangka waktu tersebut, dia akan sampai pada batas usia hidupnya dan akhirnya meninggal. Pada umumnya, tidak dapat diketahui secara pasti usia meninggalnya seseorang. Walaupun demikian, probabilitas meninggalnya seseorang tetap dapat diperhitungkan.

1. Fungsi Kelangsungan Hidup

Misalkan seseorang yang baru lahir akan meninggal pada usia tertentu. Usia meninggalnya seseorang yang baru lahir dinotasikan dengan X merupakan variabel random kontinu. Fungsi distribusi dari X dinyatakan dengan F_X(x), yaitu:

) ( )

(x X x

F_X =P ≤ x≥0 (3.2.1) Ini merupakan probabilitas kematian akan terjadi sebelum (atau pada saat) usia x. Notasi F_X(x) memiliki komplemen yang menyatakan fungsi kelangsungan hidup seseorang (survival function). Komplemen dari F_X(x) dinotasikan dengan s(x).

Definisi 3.2.1

0 )

(

) ( 1

) ( 1 ) (

≥ >

=

≤ − =

− =

x x

X x X

x F x

s _X

P P

Fungsi kelangsungan hidup s(x) merupakan probabilitas kematian yang akan terjadi setelah usia x. Fungsi F_X(x) dan fungsi s(x) dapat digunakan untuk memperoleh distribusi variabel random X.

Karena s(x) adalah komplemen dari F_X(x), jika persamaan pada Definisi (3.2.1) diturunkan terhadap x maka diperoleh

( )

[ ]

[

( )

]

( )

[ ]

[ ]

[

( )

]

( )

[ ]

[

( )

]

( )

x F

( )

x s

x F dx

d x

s dx

d

x F dx

d dx

d x s dx

d

x F dx

d x s dx

d

X X

X X

' '

0 1 1

− =

− =

− =

− =

Berdasarkan Persamaan (2.1.3) maka F'X

( )

x = fX

( )

x , sehingga

( )

x f

( )

x

s' =− _X (3.2.2) Diasumsikan bahwa seseorang yang baru lahir akan hidup pada saat dia lahir (x=0), dinotasikan dengan FX(0)=0. Berdasarkan persamaan pada Definisi (3.2.1), asumsi tersebut berakibat s

( )

0 =1. Sebaliknya, bila diasumsikan

ω

menyatakan usia maksimal yang dilalui seseorang yang baru lahir, maka

( )

ω =0

Probabilitas seseorang yang baru lahir akan meninggal sebelum usia x telah ditentukan dengan Persamaan (3.2.1). Selain itu, dapat ditentukan pula probabilitas meninggalnya seseorang di antara usia tertentu, misalnya di antara usia x dan z. Probabilitas seseorang akan meninggal di antara usia x dan z merupakan selisih probabilitas di antara x dan z, yaitu

] [ ] [ ]

[x< X ≤z =P X ≤z −P X <x P

Berdasarkan Persamaan (3.2.1) maka diperoleh ) ( ) ( ]

[x<X ≤z =F_X z −F_X x P

Dengan menggunakan persamaan pada Definisi (3.2.1) diperoleh )

( ) ( ]

[x< X ≤z =s x −s z

P (3.2.3) Secara sederhana, F_X(x) dan s(x) dapat diperlihatkan dengan gambar berikut:

Gambar 3.2.1

Fungsi distribusi probabilitas f(x) untuk kematian pada saat usia x.

2. Waktu Meninggal Untuk Orang Yang Berusia x

Pada pembahasan sebelumnya, waktu meninggal diperhitungkan pada saat seseorang lahir. Untuk pembahasan berikut ini, waktu meninggal diperhitungkan untuk orang yang berusia x. Probabilitas orang tersebut akan meninggal di antara usia x dan z yaitu P(x< X ≤z|X >x). Probabilitas ini merupakan probabilitas bersyarat seseorang yang mencapai usia x akan meninggal di antara usia x dan z.

Berdasarkan definisi probabilitas bersyarat dalam persamaan pada Definisi (2.1.2) diperoleh

(

)

[

]

) (

) (

) (

) (

) |

(

x X

z X x

x X

x X z X x x

X z X x

> ≤ < =

> > ∩ ≤ < = > ≤

<

P P

P P

P

Substitusikan Persamaan (3.2.3) dan persamaan pada Definisi (3.2.1) sehingga diperoleh :

) ( 1

) ( ) ( ) | (

x F

x F z F x X z X x

X X X

− − =

> ≤ <

P

) (

) ( ) ( ) | (

x s

z s x s x X z X

x< ≤ > = −

P (3.2.4)

Definisi 3.2.2

Misalkan T(x) menyatakan waktu hidup yang dijalani oleh (x) sebelum meninggal maka probabilitas (x) akan meninggal dalam jangka waktu t tahun dan probabilitas (x) akan hidup paling sedikit t tahun yaitu

( )

[

T x t

]

q_x

t =P ≤ t≥0 (3.2.5)

( )

[

T x t

]

q

p_{x t x}

t =1− =P > t≥0 (3.2.6)

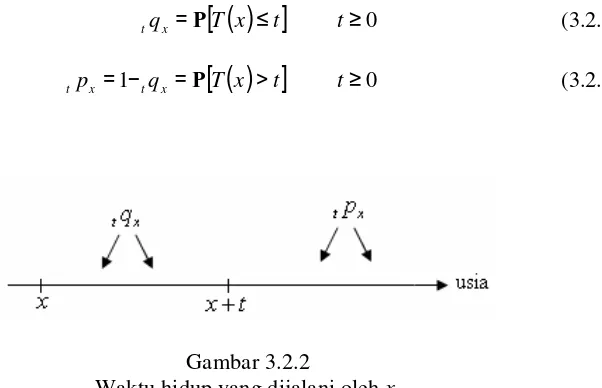
Gambar 3.2.2

Waktu hidup yang dijalani oleh x.

Dari gambar tersebut, tqx merupakan probabilitas (x) akan meninggal dalam interval (x, x+t), dan _tp_x merupakan probabilitas (x) akan meninggal dalam interval (x+t,ω). Dengan ω menyatakan usia terakhir x.

Dari Persamaan (3.2.5) pada Definisi (3.2.2) tampak bahwa tqx merupakan fungsi distribusi untuk T(x) dan _tp_x dalam Persamaan (3.2.6) pada Definisi (3.2.2) merupakan fungsi kelangsungan hidup untuk T(x).

Karena setiap orang akan meninggal maka nilai

∞ →

t

lim untuk tpx yaitu

( )

[

]

0 lim

=

∞ > =

∞

→ tpx T x

t P _(3.2.7)

baru lahir dengan fungsi kelangsungan hidupnya. Pertama-tama untuk seseorang yang baru lahir (berusia 0 tahun), hidup yang dijalani oleh (0) sebelum meninggal yaituX −0, sehingga T

( )

0 = X. Oleh karena itu, berdasarkan Persamaan (3.2.6) pada Definisi (3.2.2) diperoleh bahwa

( )

[

0

]

(

)

0

0 = T >x = X >x x≥

p

x P P

Berdasarkan persamaan pada Definisi (3.2.1) maka diperoleh

( )

0

0=s x x≥

p

x (3.2.8) Dari Persamaan (3.2.8) tampak bahwa probabilitas (0) akan hidup paling sedikit x tahun merupakan fungsi kelangsungan hidup s(x).

Andaikan (x) hidup mencapai t tahun dan diperkirakan akan meninggal dalam u tahun kemudian. Ini merupakan perkiraan (x) akan meninggal di antara usia x+t dan x+t+u. Probabilitas (x) hidup sampai t tahun dan akan meninggal dalam u tahun kemudian dinotasikan dengan t|uqx. Notasi "t|" menyatakan bahwa kematian (x) ditunda selama t tahun. Notasi t|uqx merupakan probabilitas (x) akan meninggal di antara usia x+t dan x+t+u sehingga

( )

[

]

( )

[

T x t u

]

[

T

( )

x t

]

u t x T t q_x u t

≤ −

+ ≤ =

+ ≤ < =

P P

P

|

Berdasarkan Persamaan (3.2.5) dan (3.2.6) pada Definisi (3.2.2) maka diperoleh

(

) (

)

x u t x t

x t x u t

x t x u t x u t

p p

p p

q q q

+ + +

− =

− − − =

− =

1 1

|

Probabilitas (x) akan hidup t tahun tetapi meninggal dalam u tahun kemudian dapat pula diperoleh melalui fungsi kelangsungan hidupnya. Pertama-tama, akan dinyatakan tpx dan tqx dalam bentuk fungsi kelangsungan hidup untuk seseorang yang baru lahir.

Lemma 3.2.1

Jika _tp_x adalah probabilitas (x) hidup paling sedikit t tahun dan _tq_x adalah probabilitas (x) meninggal dalam jangka waktu t tahun maka

0 0

) (

) (

p p x

s t x s p

x t x x

t = +

+

= (3.2.10)

dan

) (

) ( 1

1

x s

t x s

p

q_{x t x}

t

+ − =

− =

(3.2.11)

Bukti:

Karena T(x) adalah X −x maka tpx dalam Persamaan (3.2.6) pada Definisi (3.2.2) menjadi

(

)

(

X t x

)

t x X p_x t

+ > =

> − =

P P

Probabilitas tersebut merupakan probabilitas kematian akan terjadi setelah usia x+t untuk (x). Probabilitas ini dapat dipahami pula sebagai probabilitas bersyarat (x) akan mencapai usia x+t. Oleh karena itu, berdasarkan persamaan pada Definisi (2.1.2) maka probabilitas tersebut menjadi

] |

[X x t X x

p_x

) (

) (

) (

) ( ) (

x X

t x X

x X

x X t

x X p_x

t

> + > =

>

> ∩ + > =

P P

P P P

Dengan menggunakan persamaan pada Definisi (3.2.1) maka diperoleh

) (

) (

x s

t x s p_x

t

+ =

Berdasarkan Persamaan (3.2.8) diperoleh bahwa probabilitas (x) mencapai usia x+t yaitu

0 0

p p p

x t x x t

+

=

Berdasarkan Persamaan (3.2.6) pada definisi (3.2.2) dan hasil tpx di atas diperoleh probabilitas (x) meninggal dalam jangka waktu t tahun yaitu

) (

) ( 1

1

x s

t x s

p

q_{x t x}

t

+ − =

− =

■

Dengan menggunakan Lemma (3.2.1) dapat ditentukan _t|uq_x melalui fungsi kelangsungan hidupnya. Berdasarkan Persamaan (3.2.9),

x u t x t x u

t| q = p −+ p

Substitusikan Persamaan (3.2.10) pada Lemma (3.2.1) ke dalam persamaan di atas maka diperoleh

(

)

( )

(

s

( )

x

)

u t x s x s

t x s q_x

u t

+ + − + =

(

) (

)

( )

x

s

u t x s t x s q_x u t

+ + − + =

|

Kalikan kedua ruas dengan s

(

x+t

)

, diperoleh

(

) (

)

( )

(

(

)

)

(

) (

)

(

)

(

( )

)

(

)

(

)

(

s

( )

x

)

t x s t x s

u t x s

x s

t x s t

x s

u t x s t x s

t x s

t x s x

s

u t x s t x s q_x u t

+

   

 

+ + + − =

+ +

+ + − + =

+ + +

+ − + =

1

|

Sehingga dengan Persamaan (3.2.10) dan (3.2.11) pada Lemma (3.2.1) maka diperoleh probabilitas (x) akan meninggal di antara usia x+t dan x+t+u yaitu

x t t x u x u

t| q = q + p (3.2.12)

3. Waktu Hidup Yang Dipersingkat

Misalkan terdapat seseorang yang lahir pada tanggal 1 Januari 1980. Jika dia meninggal pada tanggal 30 September 2009 maka dia meninggal pada usia 29.8 tahun. Nilai 0.8 merupakan pecahan tahun yang dilalui sebelum meninggal. Dalam perhitungan waktu hidup yang dipersingkat, pecahan ini tidak diperhitungkan sehingga dia dianggap meninggal pada usia 29 tahun. Waktu hidup yang dipersingkat dapat dipahami pula sebagai jumlah ulang tahun (x) yang sempat dirayakan sebelum meninggal, dinotasikan dengan K(x). Dengan kata lain, K(x) menyatakan bilangan bulat terbesar untuk T(x).

] ) ( [ ] 1 ) ( [

] 1 ) ( [ ] ) ( [

k x T k

x T

k x T k k x K

< −

+ ≤ =

+ ≤ < = =

P P

P P

Dengan menggunakan Persamaan (3.2.5) pada Definisi (3.2.2) maka persamaan di atas akan menjadi

x k x k q q k

x

K( )= ]= ₊₁ − [

P

Berdasarkan Persamaan (3.2.6) pada Definisi (3.2.2) maka persamaannya akan menjadi

(

) (

)

x k x k

x k x k

x k x k

p p

p p

p p

k x K

1 1

1

1 1

1 1

] ) ( [

+ +

+

− =

+ − − =

− − − = =

P

Berdasarkan persamaan (3.2.9) maka diperoleh

x kq k x

K( ) ] _|

[ = =

P

Dan berdasarkan persamaan (3.2.12), diperoleh pula

k x x kp q k

x

K( )= ]= ₊

[

P k =0,1,2,.... (3.2.13)

C. Percepatan Mortalita

Persamaan (3.2.4) menunjukkan bahwa dengan bentuk fungsi distribusi dan fungsi kelangsungan hidupnya, dapat ditentukan probabilitas bersyarat (0) akan mencapai usia x dan meninggal di antara usia x dan z. Jika z−x=c, sebagai fungsi dari x, probabilitas bersyarat ini menggambarkan distribusi probabilitas kematian dalam selang waktu 0 dan c untuk seseorang yang