BAB VI ATOM HIDROGEN 6.1 Persamaan Schrodinger Untuk Kasus Gaya Pusat

BAB VI ATOM HIDROGEN

6.1 Persamaan Schrodinger Untuk Kasus Gaya Pusat

 Kasus elektron dalam atom hidrogen adalah kasus gaya pusat yang bersifat

spherically symetric.

 Kasus gaya pusat adalah kasus-kasus yang melibatkan partikel yang energi

potensialnya hanya merupakan fungsi jarak, artinya energi potensial hanya ditentukan oleh jarak partikel itu dari titik pusat peredaran, atau V = V( r).

Persamaan Schrodinger bebas waktu adalah

H = E     (6-1)

dengan H adalah

H = T +V =  (2/2m) 2 + V( r) (6-2)

Karena sifatnya yang spherically symetric (simetris berbentuk bola), maka kita gunakan

2

 dalam koordinat spherik, yaitu:

2  = 2 2 2 2 2 2 2 _{r sin} 1 sin sin r 1 r r r r 1                   (6-3) atau : 2  =                           2 2 2 2 2 _sin 1 sin sin 1 r r r r 1 (6-4)

Dari Bab 5 kita tahu bahwa

2 L =                       2 2 2 2 sin 1 sin sin 1  Sehingga L2/ 2=                      2 2 2 sin 1 sin sin 1

2  =              2 2 2 2 1   L r r r r =              2 2 2 2 2 1   r L r r r r (6-5)

Substitusi (6-5) ke dalam operator Hamilton diperoleh:

H= m 2 2                2 2 2 2 2 1   r L r r r r + V( r) (6-6) H= 2 2 2 2 2 2 1 2 _mr L r r r r m         + V( r) (6-7)

Persamaan Schrodinger untuk kasus gaya pusat diperoleh, yaitu dengan mensubstitusi (6-7) ke dalam (6-1), jadi :

r r r r 1 m 2 2 2 2        + 2 2 2mr L  + V( r)  = E (6-8)

Telah kita ketahui dari Bab 5, bahwa nilai eigen  terhadap operator L2adalah

(+1)2 sehingga persamaan eigennya dapat ditulis:

2

L  (+ 1) 2 (6-9)

dan (6-8) dapat ditulis:

r r r r 1 m 2 2 2 2        +





₂ 2

2

1

m r 



+ V( r)  = E  (6-10)

 Harus diingat bahwa (+ 1) 2 adalah nilai eigen dari operator L2, dimana operator L2 melibatkan variabel  dan .

 Persamaan (6-9) melibatkan tiga macam variabel, yaitu r,  dan , sehingga  yang

merupakan penyelesaian (6-9) harus (r,,) yang merupakan gabungan dari ( r) ,

() dan ().

Selanjutnya ( r) kita tulis R sedang menurut bab 5, () ditulis T dan () ditulis

sehingga

Subtitusi (6-10) ke dalam (6-9) menghasilkan: r T R r r r 1 m 2 2 2 2              + 2 2 2 ) 1 ( r m     R T  + V_{( r)} R T  = E R T  (6-12) atau 1 T 2 2 2 2             r R r r r m  + 2 2 2 ) 1 ( r m     R T  + V( r) R T  = E R T 

Jika dibagi dengan R T , hasilnya:

r R r r r 1 R 1 m 2 2 2 2             + 2 2 2 ) 1 ( r m     + V( r) = E (6-13) atau r R r r r 1 m 2 2 2 2             + 2 2 2 ) 1 ( r m     R + V( r) R = E R (6-14)

Perlu diketahui bahwa

r r r r 1 ₂ 2     = r r 2 r2 2     

sehingga (6-14) boleh ditulis:

 R r 2 2 2 2 2               r r m  + 2 2 2 ) 1 ( r m     R + V( r) R = E R atau  r 2 2 2 2 2               r R r R m  + 2 2 2 ) 1 ( r m     R + V( r) R = E R atau  ' r 2 ' ' 2 2       _  R R m  + 2 2 2 ) 1 ( r m     R + V(( r) R = E R (6-15)

Perlu ditegaskan bahwa bagi sembarang problem dengan fungsi energi potensial yang

spherically symetric V( r) , maka fungsi gelombangnya adalah  = RT yang memenuhi

persamaan (6-15), dengan R = fungsi radial, T fungsi  dan  adalah fungsi . Fungsi T

 Persamaan (6-15) adalah persamaan Schrodinger sebagai fungsi radial, untuk sembarang problem yang melibatkan fungsi energi potensial yang spherically symetric V(r) .

6.2 Gerak Rotasi ( Rigid Rotor Dua Partikel )

Problem:

Sistem dua partikel yang berada pada jarak yang tetap, dan dihubungkan oleh sebuah batang kaku tanpa massa yang panjangnya d.

Dalam kasus ini, karena jarak kedua partikel tetap, maka gerak internal dalam bentuk vibrasi pasti tidak mungkin, sehingga satu-satunya gerak internal adalah gerak rotasi.

Seluruh energi dalam rotor adalah energi kinetik, jadi:

V = 0 (6-16)

sehingga operator Hamilton untuk gerak rotasinya adalah

H =  2

2 2 

(6-17)

Dalam persamaan (6-17) di atas kita gunakan  sebagai pengganti m, karena sistemnya

terdiri atas dua partikel, sehingga massa yang digunakan adalah massa tereduksi  yang

didefinisikan:  = 2 1 2 1 m m m . m  (6-18)

dengan m1 dan m2 adalah massa masing-masing partikel. Operator2 adalah operator

2

 koordinat spherik seperti pada persamaan (6-5) yaitu:

2  =                2 2 2 ^ L 2 2 _rr _{r r} r 1 

tetapi karena dalam rigid rotor, jari-jarinya konstan, maka turunan terhadap jari-jari = 0

 _2 ₌ 2 2 2 ^ L r   (6-19)

karena jarak antar partikel adalah d, maka: 2 = 2 2 2   r L

 sehingga operator Hamiltonnya

menjadi:  H = ₂ d 2 1  2 ^ L (6-20) 2 ^

L adalah operator momentum angular untuk gerak translasi yang melengkung, sedang

yang kita bicarakan adalah gerak translasi. Untuk membedakannya, maka ^_L2 diganti

2 ^

J yaitu operator momentum angular rotasi. Sehingga (6-20) ditulis:

 H = ₂ d 2 1  2 ^ J

Demikian persamaan Schrodinger untuk rigid rotor dua partikel:

 2 d 2 1  2 ^ J  = E  (6-21)

Telah kita ketahui bahwa nilai eigen untuk  terhadap ^_L2 adalah ( + 1)2, jadi seharusnya nilai eigen ^_J2 adalah j ( j + 1)2, sehingga _J^2 = j (j + 1)2 dan (6-21) ditulis:  2 d 2 1  j (j + 1) 2   = E  (6-22) sehingga E =





2 2 d 2 1 j j    (6-23)

Selanjutnya  d2 ditulis I sehingga (6-23) ditulis:

E =





I 2 1 j j  2 J = 0, 1, 2, . . . (6-24)

dengan I = momen Inertia, yang didefinisikan:

I =  d2 (6-25)

L adalah momentum angular translasi, harganya  (1 dengan  adalah bilangan kuantum momentum angular translasi. J adalah momentum angular rotasi,

harganya  j(j1) dengan j adalah bilangan kuantum momentum angular rotasi. L

mempunyai komponen Lz = m, maka J juga mempunyai komponen yang disebut Jz =

m. Jika pada gerak translasi m harganya mulai   , (+1) . . . + , maka m pada gerak rotasi mempunyai harga mulai dari j , j+1, . . . . sampai dengan +j.

Apakah Energi rotasi mengalami degenerate ?

Kita tahu bahwa energi level rotasi hanya ditentukan oleh j. Jadi jika j = 2 misalnya maka energinya

I 32

. Untuk j = 2, maka ada 5 harga m, yaitu 2 , 1, 0, 1, 2. Kita telah tahu dari bab 5 bahwa fungsi eigen untuk operator momentum angular

ditentukan oleh  dan m. Sudah barang tentu untuk gerak rotasi, fungsi eigennya

ditentukan oleh j dan m. Karena untuk j = 2 ada 5 harga m, itu artinya untuk j = 2, ada

lima macam fungsi gelombang yaitu: -2

2  ; -1 2  ; 0 2  ; 1 2  dan 2 2  , yang

kelima-limanya mempunyai energi yang sama yaitu

I 32

. Karena ada 5 fungsi gelombang berbeda yang energinya sama, maka dikatakan bahwa untuk j = 2, energi level rotasi mengalami 5th fold degenerate.

6. 3 Gerak Rotasi Molekul Diatomik

Energi level rotasi molekul diatomik dapat diaproksimasi dengan menggunakan energi level rigid rotor dua partikel (6-24). Telah diketahui bahwa ketika molekul diatomik mengabsorpsi atau mengemisi energi, ternyata transisi rotasi murni yang mungkin adalah

j = + 1 (6-26)

Perlu ditambahkan bahwa momen dipole molekul harus tidak nol untuk dapat menghasilkan spektrum rotasi murni. Transisi rotasi disebut transisi murni jika hanya

bilangan kuantum rotasi saja yang berubah. Jika terjadi transisi rotasi dari E2 ke E1 maka

E nya yaitu E2E1 berubah menjadi foton atau h, Jadi:

h = I 2 ) 1 j ( j I 2 ) 1 j ( j_{2 2} 2 _{1 1} 2   = I 8 h ) 1 j ( j ) 1 j ( j 2 2 1 1 2 2     (6-27) Jadi:  = I 8 h ) 1 j ( j ) 1 j ( j 2 1 1 2 2     (6-28) Jika dianggap j = 1, maka j2 = j1 + 1 sehingga. Jika j1 ditulis j saja, maka j2 = j + 1, jadi:

 = I 8 h ) 1 j ( j ) 2 j ( ) 1 j ( 2      = 2 ( j + 1) B (6-29)

B = h / (82I) dan j = level yang rendah = 0, 1, 2, 3, . . . B disebut tetapan rotasi molekul.

Pengukuran terhadap frekuensi absorpsi rotasi, memungkinkan kita menghitung B. Dari B, kita dapat menghitung momen inertia I, untuk selanjutnya jarak ikatan molekul d, dapat ditentukan.

Contoh:

Garis spektrum frekuensi terendah pad absorpsi rotasi murni molekul 12C32S terjadi pada

48991 MHz. Tentukan jarak ikatan.

Jawab:

Frekuensi terendah, berarti transisi dari j = 0  1, sehingga

 = 2 B jadi B =  / 2 B = h / (82I) I = h / ( 8 2 B) = h / (4 2) I =  d2  d2 = I /  = h / (42 ) d =  2 4 h

 = 2 1 2 1 m m m . m  = 12 31,97207 ) 97207 , 31 ( 12  x 1,661 . 10 24 gram = 1,44885 . 1023 gram = 1,44885 . 1026kg d = ) kg 10 x (1,44885 ) s 48991 ( (4,14) 4 s J 10 x 62608 , 6 26 1 -2 34   = 1,5377 x 1010 m = 1,5377 A 6.4 Atom Hidrogen

Atom hidrogen terdiri atas sebuah proton dan sebuah elektron. Jika e menyatakan

muatan sebuah proton ( e = + 1,6 x 1019 C ) maka muatan elektron adalah  e. Kita akan

berasumsi bahwa elektron dan proton adalah titik massa yang interaksinya mengikuti hukum Coulomb. Dalam membahas tentang atom atau molekul , kita biasanya akan memandangnya sebagai sistem terisolasi, dengan mengabaikan interaksi antar atom dan antar molekul. Pembahasan kita tentang Hidrogen ini akan kita buat lebih umum, yaitu tidak saja untuk atom hidrogen, tetapi juga untuk atom yang mirip Hidrogen (Hidrogen liked atom) yaitu misal ion He+ ; ion Li2+ dan lain-lain.

Pertama kita akan membicarakan gaya yang bekerja dalam sistem ini, yaitu gaya Coulomb: F =  2 2 o r Ze 4 1  (6-30)

yang merupakan gaya pusat. Hubungan antara energi potensial V dengan F yang bekerja adalah

F = dV/dr (6-31)

dengan demikian maka: dV/dr = 2 2 o r Ze 4 1  , jadi: V =  r Ze 4 1 2 o   (6-32)

Supaya penulisannya ringkas (¼o)1/2e diganti e', sehingga (6-32) menjadi:

V = 

r ' Ze 2

Jika kita misalkan gerak internal dalam sistem itu diwakili oleh fungsi  dengan  adalah

 = R  (6-34)

maka sebagai representasi dari kasus gaya pusat,  harus mengikuti persamaan:

' R r 2 ' ' R m 2 2       _   +





2 r m 2 2 1     R + V(( r) R = E R (6-15)

Dengan memasukkan harga V = 

r ' Ze 2

, dan m diganti  (mengapa ?) maka (6-15)

menjadi:  R' r 2 ' ' R m 2 2       _   +





2 r 2 2 1      R  r ' Ze 2 R = E R  R' r 2 ' ' R m 2 2       _   +





2 r 2 2 1      R  r ' Ze 2 R  E R = 0  R ' r 2 ' ' R   2 2  





2 r 2 2 1      R  2 2   r ' Ze 2 R  2 2   E R = 0  R ' r 2 ' ' R  





2 r 1    R  2 2   r ' Ze 2 R  2 2   E R = 0 atau

Jika 2/e' 2 diganti a maka:

 R ' r 2 ' ' R  





2 r 1    R  r a Ze2 R  2 e' a E 2 R = 0 atau ' R r 2 ' ' R   _   r a Ze2 _ 2 e' a E 2 _





    2 r 1   R = 0 (6-35)

Persamaan (6-35) adalah persamaan Schrodinger untuk atom hidrogen dinyatakan dalam

satu variabel yaitu radial. Jika (6-35) diselesaikan, maka R diperoleh. Padahal T dan 

sudah kita ketahui dari bab 5. Jadi Jika R diperoleh maka  untuk atom mirip hidrogen

Solusi Persamaan Radial

Untuk memperoleh R, sebenarnya kita dapat langsung menyelesaikan (6-35) dengan menggunakan metode deret. Tetapi relasi recursi yang diperoleh akan terlalu rumit. Agar relasi recursi yang diperoleh bentuknya sederhana maka kita akan melakukan

beberapa langkah awal yaitu dengan memasukkan r yang sangat besar. Jika r = , maka

(6-35) menjadi: R ''  2 e' a E 2 R = 0 (6-36)

dan penyelesaian-penyelesaiannya adalah

r e' a / 2E i 2 e  (6-37).

Sekarang pembahasan akan kita fokuskan jika E positif. Untuk E positif, maka bilangan dalam akar akan negatif, sehingga muncullah i sebagai faktornya r :

R



ei 2E / ae'2 r E > 0 (6-38)

atau, jika harga a dikembalikan ke asalnya maka:

R



ei( 2E)r /  E > 0 (6-39)

Simbol



pada (4-9) menunjukkan bahwa R tersebut adalah R yang hanya berlaku untuk

r yang sangat besar, dan merupakan fungsi asymtotik terhadap R yang sesungguhnya. Bentuk persamaan (6-39) tersebut mengingatkan kita kepada persamaan (6-26) pada bab III mengenai partikel bebas. Ini berarti untuk r sangat besar dan E > 0 maka elektron atom hidrogen berada dalam keadaan partikel bebas, atau dengan perkataan lain hidrogen dalam keadaan ion positif.

Persamaan (4-9) belum memberikan faktor radial yang lengkap bagi fungsi radial

dengan E positif. Studi lebih lanjut mengenai hal ini (baca literatur Quantum Mechanics

of One and Two Electron Atoms , 1957 karangan Bethe dan Salpeter halaman 21-24) menunjukkan bahwa fungsi radial dengan E positif harganya tertentu (terhingga) untuk sembarang harga r berapapun harga E positifnya. Ini berarti, bahwa sebagai partikel

bebas sembarang harga E nonnegatif diijinkan atau untuk partikel bebas, energinya kontinum nonnegatif atau tidak energi level bagi partikel bebas.

Karena kita mendapat energi positif yang kontinum, maka eigen fungsi yang

bersangkutan disebut continuum eigenfunctions. Sebagaimana lazimnya fungsi partikel

bebas, maka fungsi eigen kontinuumpun tak ternormalisasi.

Sekarang kita akan membahas bound state atom Hidrogen yaitu jika E < 0. Jika E negatif maka bilangan di bawah tanda akar dalam (6-37) adalah positif. Karena berapapun harga r, fungsi harus bernilai terhingga, maka kita pilih tanda minus untuk persamaan (6-37) tersebut sehingga

R



e 2E / ae'2 r E < 0 (6-40)

Persamaan (6-40) menunjukkan bahwa R disitu adalah fungsi asymtotik bagi R yang sesungguhnya. Karena (6-40) adalah asymtotik terhadap R sesungguhnya maka R sesungguhnya pasti mengandung (6-40). Kita boleh memisalkan R dalam bentuk apapun asal mengandung (6-40). Misal R sesungguhnya adalah

R = K e 2E / ae'2 r (6-41)

dengan K adalah fungsi r atau K(r). [ Hati-hati dengan e dan e' pada (6-30). Ingat bahwa e disitu adalah bilangan basis logaritma natural, tidak ada hubungannya dengan muatan proton sedang e' ada hubungannya dengan muatan proton ].

Jika 2E / a e'2 dengan C, maka (6-41) menjadi:

R = K eCr (6-42)

dengan

C = 2E / a e'2 (6-43)

Penggunaan R dalam (6-43) dijamin tidak hanya berlaku untuk r sangat besar, tetapi untuk sembarang harga r asal E negatif.

Proses selanjutnya, R pada (6-42), turunan pertamanya ( R') dan turunan keduanya (R'') dimasukkan pada (6-35), maka (6-35) akan menjadi:

` r2 K '' + ( 2r  Cr2 ) K ' + [ ( 2 Z a1 2 Cr )  (+1) ] R = 0 (6-44) Sekarang, kita dapat memasukkan deret pangkat berbentuk:

K =



 0 k k k .r c (6-45)

ke dalam (6-44). Jika kita benar-benar melakukannya, maka akan kita lihat bahwa beberapa koefisien pada suku-suku yang awal dari deret penyelesaian itu adalah nol. Jika

kita misalkan koefisien pertama yang tidak nol adalah koefisien suku ke s atau cs , maka

(6-45) boleh ditulis: K =



 s k k k .r c c_k  0 (6-46)

Jika k  s diganti j maka: k = s diganti j = 0 dan k diganti j + s, sehingga (6-46) menjadi:

K =



    0 j s j s j .r c =



 0  j j s j s _{c .r} r cj+s  0 (6-47)

Selanjutnya cj+s diganti bj sehingga

K =



 0 j j j s _{b .r} r bi  0 (6-48)

(Meskipun kita telah melakukan berkali-kali substitusi, tetapi substituennya adalah substituen sembarang, jadi tidak mengubah prosedur standar penyelesaian persamaan diferensial dengan metode deret). Dalam (6-47) s adalah bilangan bulat, yang nilai ditentukan pada saat menyelesaikan persamaan diferensial. Selanjutnya kita buat fungsi

radial baru yaitu M yang harganya adalah K / rs Jadi:

K = rsM bi  0 (6-49) M =



 0 j j r . bj bi  0 (6-50)

Kita cari K' dan K'' dari (6-49) dan bersama (6-49) kita masukkan ke dalam (6-44), kita peroleh:

r2M'' + [(2s + 2 ) r  2C r2 ] M' + [ s2 + s + ( 2 Z a12 C 2 C s ) r (+1)] M = 0 (6-51) Untuk mendapatkan harga s kita tempuh langkah-langkah sebagai berikut:

Masukkan r = 0 ke dalam (6-50) sehingga :

dan diperoleh:

s =  dan s =    1 (6-53)

Dari dua harga s ini, mana yang akan dipergunakan ? Untuk itu ikuti uraian berikut: Dari (6-42) , (6-49) dan (6-50) kita peroleh:

R = eCr rs



 0 j j j r b atau (6-54) R = eCr rs M (6-55)

Ingat bahwa eCr = 1  Cr + (Cr)2/ 2 !  . . . maka untuk r yang kecil, eCr = 1,

sementara itu



 0 j j jr

b = b0 + b1 r + b2 r2 . . . . sehingga untuk r yang kecil,



 0 j j jr b = b0,

akibatnya untuk r yang kecil, (4-24) menjadi:

R = b0 rs (6-56)

Untuk s =  maka R = b0 r sedang untuk s = 1 , maka R =

1 o r b   yang akan

menjadi tak terhingga untuk r = 0. Padahal yang begitu tidak boleh. Jadi s =  1

dibuang, dan s =  dipergunakan. Dengan s = , persamaan (6-51) akan menjadi:

r2M'' + [(2 + 2 ) r  2C r2 ] M' + [2 +  + ( 2 Z a12 C 2 C ) r(+1)] M = 0 r2M'' + [(2 + 2 ) r  2C r2 ] M' + ( 2 Z a12 C 2 C ) r M = 0

r2M'' + [(2 + 2 )  2C r ] r M' + ( 2 Z 12 C 2 C ) r M = 0 jadi:

rM'' + [(2 + 2 )  2C r ] M' + ( 2 Z a12 C 2 C ) M = 0 (6-57)

Sementara itu dengan s =  Persamaan (6-55) menjadi:

R = eCr r M (6-58)

dengan M adalah dinyatakan pada (6-50) yaitu:

M =



 0 j j j .r b (6-59) M' =



   0 j 1 j jr b . j =



   1 j 1 j j r b . j =



    0 k k 1 k r b . 1) k ( =



    0 j j 1 j r b . 1) j (

M'' =



    0 j 2 j j r b . j ) 1 j ( =



    1 j 2 j jr b . j ) 1 j ( =



     0 k 1 k 1 k r b . 1) k ( ) k ( = =



     0 j 1 j 1 j r b . 1) j ( ) j (

Jika M, M' dan M'' disubstitusikan ke dalam (6-57), kita peroleh:

 



 



               _{  }      0 j j j 1 j 1 j 2C 2C 2Cj b r a Z 2 b 1 j 1 2 b 1 j j   = 0 Jadi:

 



 

_            _{  }      _{j1 j1} 2C 2C 2C_j b_j a Z 2 b 1 j 1 2 b 1 j j   = 0

dan diperoleh relasi recursi:

bj + 1 =

  

 

j 1 b 1 j 1 2 1 j j Z 2 j C. 2 C 2 C 2            (6-60) Sekarang kita harus menguji sifat deret tak terhingga (6-50) untuk r yang besar. Karena untuk r yang besar sifat deret ditentukan oleh suku-suku yang besar, maka kita akan menguji rasio antara

bj + 1/ bj untuk j yang besar. Untuk j yang besar:

bj + 1/ bj = j 2C j j C 2 2  untuk j besar (6-60)

Marilah sekarang kita perhatikan seandainya kita mempunyai bentuk e2Cr. Jika bentuk

Cr 2

e ini kita nyatakan dalam bentuk deret pangkat, maka:

Cr 2 e = 1 + (2Cr) + ! 2 r ) C 2 ( 2 2 . . . + ! j r ) C 2 ( j j + ! ) 1 j ( r ) C 2 ( j 1 j 1    . . . (6-61)

Rasio koefisien r dari sebuah suku dengan suku sebelumnya dari (6-61) tersebut adalah

! ) 1 j ( ) C 2 ( j 1   / ! j ) C 2 ( j = ! ) 1 j ( ) C 2 ( j 1   . j ) C 2 ( ! j = 1 j C 2  = j 1 C 2  untuk j besar

yang ternyata sama dengan (6-60) untuk j besar. Hal ini mendorong kita untuk

menyimpulkan bahwa untuk j yang besar (6-50) sifatnya mirip e2Cr, sehingga kita boleh

M ~ e2Cr (6-62) atau



 0 j j jr b ~ e2Cr (6-63)

dan selanjutnya maka (4-24) dapat ditulis: R ~ eCr rs e2Cr atau R ~ rs eCr

Karena uraian kita ini tadi berangkat dari s = , maka:

R ~ r eCr (6-64)

Namun perlu diperhatikan bahwa (6-64) akan menjadi tak terhingga jika r tak terhingga dan ini tidak boleh karena tidak quadratically integrable. Satu-satunya cara untuk mengatasi hal ini adalah (seperti yang sudah kita kenal pada osilator harmonis) menghentikan deret (6-50) pada suku tertentu, misal suku ke k. Ini berarti relasi recursi ( 4- 27) harus menjadi nol jika j = k, jadi:



 





j 1 b 1 k 1 k 2 1 k k Za 2 k C. 2 C 2 C 2          = 0 atau 2C + 2C + 2 C k  2 Z a-1 = 0 atau 2C (1 +  + k )  2 Z a-1 k = 0 , 1 , 2 , . . . . (6-65)

karena  dan k adalah bilangan bulat maka ( 1 +  + k ) pasti adalah bilangan bulat yang baru yang untuk selanjutnya disebut bilangan kuantum utama = n, jadi:

n = ( 1 +  + k) (6-66)

Dari (6-65) maka hubungan antara  (bilangan kuantum momentum angular ) dengan n

(bilangan kuantum utama adalah

 = n  1  k atau

 < n  1 (6-67)

Catatan:

Dalam pembahasan mengenai hidrogen ini mucul bilangan kuantum utama n. Pada pembahasan mengenai momentum angular, kita telah mengenal dua bilangan kuantum

yaitu  dan m. Karena momentum angular berlaku untuk semua gerak melengkung, dan

gerak elektron dalam atom adalah gerak melengkung maka  dam m juga berlaku pada

gerak elektron dalam atom. Jadi sampai sejauh ini kita mengenal 3 macam bilangan

kuantum adalah atom yaitu n,  dan m.

Energi Level

Jika kita masukkan (6-66) ke dalam (6-65) maka diperoleh:

C n = Z a1 (6-68)

Jika harga a = 2/e' 2 dan C = 2E / a e'2 dimasukkan kembali, maka diperoleh: E =  2 2 2 2 n 2 ' e Z   atau (6-69) E =  2 2 2 2 n Z 2 ' e   atau (6-70)

jika harga e' = (4o)-1/2 e dimasukkan kembali maka:

E =  o 4 1  2 2 2 2 n Z 2 e   (6-71) Untuk atom hidrogen:

E =  o 4 1  2 2 2 n 1 2 e   (6-72) dengan  = elektrom proton elektrom proton m m m . m  = 0,9994557 melektron =9,1044318 . 10kg;

e =muatan proton=1,602177x1019 C ; Z = nomor atom dan 0 = permitivitas dalam

vakum = 8,8541878 x 1012 C / N.m2

6.5 Fungsi Gelombang Atom Hidrogen

Fungsi Radial R

Dengan memanfaatkan (4-35) maka relasi recursi (6-60) menjadi: bj + 1 = a n Z 2

 

bj ) 2 2 j ( 1 j n 1 j         (6-73)

Pada pembahasan penurunan (6-66) dinyatakan bahwa polinomial M =



0 j j jr b akan

dihentikan pada saat j = k, sehingga polinomialnya (dikenal dengan Polinomial Laguerre) menjadi: M =



 k 0 j j jr b (6-66+)

Karena menurut (6-66), n = ( 1 +  + k) maka k = n  1, sehingga (6-66+) menjadi:

M =



   1 n 0 j j jr b  (6-74)

Fungsi radialnya dinyatakan oleh (4-24 c) yaitu: R = eCr rM. jadi R = eCr r



   1 n 0 j j jr b  atau (6-75)

jika harga C dimasukkan maka diperoleh :

R = r nar Z e 



   1 n 0 j j jr b  (6-76)

R adalah salah satu bagian saja dari fungsi gelombang Hidrogen.

Perlu diketahui bahwa elektron dalam atom hidrogen bergerak spherik, artinya pasti terjadi momentum angular. Oleh karena itu selain fungsi radial, fungsi gelombang hidrogen pasti juga terdiri atas fungsi eigen momentum angular yang sudah diturunkan pada bab V.

Secara keseluruhan fungsi gelombang atom mirip hidrogen adalah:

 = R . T .  (6-77)

dengan T dan  dapat dilihat pada bab V tentang momentum angular.

 Dari persamaan (5-30) bab V, tampak bahwa  ditentukan oleh bilangan kuantum m.

 dari persamaan (5-64) bab V, tampak bahwa T ditentukan oleh  dan m, dan

 Dari persamaan (5-4) bab ini, maka tampak bahwa R ditentukan oleh n dan 

Maka dapat disimpulkan bahwa  ditentukan oleh tiga macam bilangan kuantum yaitu n,

dan m, sehingga (6-77) biasa ditulis:

Contoh

Tentukan fungsi gelombang atom hidrogen dengan n = 3,  = 1 dan m = 1.

Jawab:

Menentukan fungsi 

Dengan menggunakan persamaan (5-30) bab V:

  = 2 / 1 2 1        e i m _ 1/2 2 1        e i _ (6-79) Menentukan T

Dengan menggunakan (5-64) bab V:





_





_



2 / 1 ! m + . 2 ! m -1 + 2             m P_

Kita hitung dulu P_m :dengan menggunakan (5-63) bab V:

m P_ = ! . 2 1   (1 - cos2) m /2 m m ) (cos d d     (cos2 - 1) = ! 1 . 2 1 1 (1 - cos 2_ )1/2 2 2 ) (cos d d  (cos 2_ - 1)1 = 2 1 (1 - cos2)1/2 2 2 ) (cos d d  (cos 2_ - 1)1

Kita selesaikan dulu

2 2 ) (cos d d  (cos

2_{ - 1)dan supaya tampak sederhana cos  kita ganti}

x sehingga 2 2 ) (cos d d  (cos 2_{ - 1)} = 2 2 dx d (x2 1) = dx d 2x = 2 Jadi: P_m = 2 1 (1 - cos2)1/2. 2 = sin 

Setelah itu, T dapat ditentukan: 



_





_



2 / 1 ! m + . 2 ! m -1 + 2             m P_ =

  

_{ }

2 / 1 ! 2 . 2 ! 1 3       sin  2 / 1 4 3       sin  (6-80)

Menentukan Fungsi Radial:

Dengan menggunakan (6-76) bab ini:

R = r nar Z e  



  1 n 0 j j jr b  = r . 3ar 1 e 



 1 0 j j jr b = r . 3ar 1 e  ( bo + b1 r ) (6-81)

Koefisien b1 ditentukan dengan relasi recursi (6-73) bab ini:

bj + 1 = a n Z 2

 

bj ) 2 2 j ( 1 j n 1 j         jadi: b1 = a 3 2 o b 2) 2 (0 ) 1 0 ( 3 1 1 0       = a 6 1  b_o

Harga b1 dimasukkan ke dalam (6-81):

R = r . r a 3 1 e  ( bo a 6 1  b_o r ) = bo { r . (1 a 6 1  r ) r a 3 1 e  } bo dicari dengan normalisasi:



  0 *_Rd R = 1



  0 2 _d R =



 0 2 2_{r dr} R = b2_o r)e a 6 1 (1 r 0 2 a 3 1



 _            r2 dr = 1

r e r) a 6 1 (1 r 0 2 a 3 2 2 2



 _            = 1/b2_o r e ) r a 6 1 r a 3 1 (r 0 2 a 3 2 4 2 2 3 2



 _             = 1/b2_o e ) r a 6 1 r a 3 1 (r 0 a 3 2 6 2 2 5 4



 _             = 1/b2_o r d e r a 6 1 r d e r a 3 1 r d e r 0 a 3 2 6 2 2 0 a 3 2 5 0 a 3 2 4

_

_



     _   = 1/b2_o 4 ! 5 2 a 3       _ a 3 1 ( 5 ! ) 6 2 a 3       + 2 2_a 6 1 ( 6 ! ) 7 2 a 3       = 1/b2_o 4. 3. 2. 35 . 25 a5 5. 4. 2. 36 26 a5 + 5 .4. 37 27 a5 = 1/b2_o 36. 22 a5 5. 36 23 a5 + 5. 37 25 a5 = 1/b2_o 4 36 a5 8 3 . 5 6 a5 + 32 3 . 5 7 a5 = 1/b2_o 16 3 . 8 6 a5 32 3 . 5 . 4 6 a5 + 32 3 . 5 7 a5 = 1/b2_o ( 8  4 . 5 + 5 . 3) 32 36 a5 = 1/b2_o 3 32 36 a5 = 1/b_o2  b_o2 = 5 6_.a 3 . 3 32  bo = 2 / 1 5 6_.a 3 . 3 32       = 2 / 1 5 6_.a 3 . 6 64       bo = 2 / 1 2 _6.a 1 a 27 8       = 6 27 8 . a a 1 2 Jadi:

R = bo { r . (1 a 6 1  r ) 3ar 1 e  } R = 6 27 8 . a a 1 2 { r . (1 6a 1  r ) 3ar 1 e  }

Akhirnya  diperoleh yaitu:

(3, 1, 1) = R T  = . . . (masukkan)

Degenerasi

Apakah energi level atom hidrogen mengalami degenerate ? Untuk menjawab ini marilah kita lihat persamaan (6-72). Dari persamaan tersebut tampak bahwa energi level atom

hidrogen hanya ditentukan oleh n, padahal fungsi gelombangnya  ditentukan oleh 3

macam bilangan kuantum, ini berarti dapat saja terjadi bahwa fungsi gelombang yang n

sama mempunyai  dan m berbeda kecuali untuk n = 1. Sebab untuk n = 1, hanya ada

satu kemungkinan harga  dan m yaitu  = 0 dan m = 0, sehingga untuk n = 1 hanya

adalah satu macam fungsi gelombang yaitu (1, 0, 0 ) . Tetapi bagaimana untuk n = 2

Untuk lebih jelasnya kita buat tabel n,  dan m serta fungsi gelombangnya.

Bil. Kuantum Utama n

Bil Kuant. Angular

 Bil. Kuan. Magnetik m

Fungsi Gelombang 1 0 0 _{( 1, 0, 0 )}  2 0 0 _{( 2, 0, 0 )} 1 1 ( 2, 1,  )  ( 2, 1, 0 )  ( 2, 1, 1 )   3 0  _{( 3, 0, 0 )} 1  _{( 3, 1,  )}  ( 3, 1, 0 )

 ( 3, 1, 1 ) 2  _{( 3, 2,  )}  ( 3, 2,  )  ( 3, 2, 0 )  ( 3, 2, 1 )  ( 3, 2, 2 ) Dst   

Dari tabel di atas tampak bahwa untuk n > 2, maka diperoleh n2 fungsi gelombang berbeda. Jadi untuk n – 2 ada 4 fungsi gelombang yang berbeda yaitu ( 3, 1,  ) , ( 3, 1, 0 )

, ( 3, 1, 1 ) dan ( 3, 2,  ). Karena n nya sama, maka ke empat fungsi gelombang tersebut

mempunyai energi level yang sama. Dengan demikian maka untuk n = 2 energi level atom hidrogen mengalami degenerasi dengan derajat degenerate = 4.

Dengan penjelasan yang sama maka dapat kita ketahui bahwa ada 9 fungsi gelombang yang energinya sama untuk n = 3 yaitu: ( 3, 0, 0 ) , ( 3, 1,  ) , ( 3, 1, 0 ), ( 3, 1, 1 )

, ( 3, 2,  ) , ( 3, 2,  ) ,

( 3, 2, 0 ) , ( 3, 2, 1 ) , dan ( 3, 2, 2 ).

6.6 Bilangan Kuantum Magnetik Spin

Sejauh ini, kita telah menurunkan 3 macam bilangan kuantum, yaitu bilangan

kuantum utama n, Bilangan kuantum momentum angular translasi  dan bilangan

kuantum orbital momentum angular m. Bilangan kuantum utama menentukan energi dengan relasi: E =  o 4 1  2 2 2 n 1 2 e  

Bilangan kuantum utama juga berkorelasi dengan kulit lintas, yang hubungannya dapat dilihat dari tabel berikut:

n  1 2 3 4 5 6 7

Bilangan kuantum utama ini muncul ketika menentukan fungsi Radial

Bilangan kuantum momentum angular, menentukan momentum angular dengan relasi:

L =  (1)

Bilangan kuantum  ini juga menentukan bentuk lintasan. Bilangan  muncul ketika

kita hendak menentukan fungsi  . Dalam bahasa spektrum, bilangan  berhubungan

dengan nama-nama orbital.



 0 1 2 3 4 dst

Orbital  s p d f g h

Bilangan kuantum yang ketiga adalah bilangan kuantum orbital momentum angular yang juga disebut bilangan kuantum magnetik translasi m. Bilangan ini merupakan penentu Lz yaitu proyeksi momentum angular L pada sumbu z. Hubungan antara Lz dan m adalah

Lz = m 

Bilangan m ini juga dipandang sebagai penentu orientasi (arah) translasi elektron, karena jika kita mengetahui m kita dapat mengetahui Lz. Jika kita mengetahui Lz, maka arah momentum angular dapat diketahui, karena:

Lz = L cos 

dengan  adalah sudut arah L terhadap sumbu z. Jika arah L diketahui, maka dengan kaidah tangan kanan, arah translasi elektron dapat diketahui.

Apakah dengan 3 macam bilangan kuantum sudah cukup ? Jika mengacu kepada fenomena makroskopis, maka dapat diketahui bahwa kedudukan planet dalam tata surya ditentukan oleh 4 macam tetapan, yaitu tetapan energi, tetapan momentum angular, tetapan komponen momentum angular dan tetapan rotasi. Dua buah planet tidak pernah bertabrakan karena tidak ada dua planet yang keempat tetapannya sama. Jika fenomena mikroskopik dipandang sebagai miniatur dari fenomena makroskopik maka atom masih membutuhkan satu tetapan lagi yang berasal dari gerak rotasi elektron. Kita tahu translasi elektron dalam atom adalah lintasan sperik, oleh karena itu mempunyai momentum angular L. Karena gerak rotasi juga bersifat spherik maka gerak rotasi juga harus mempunyai momentum angular yang disebut momentum angular rotasi, notasinya S. Jika

L ditentukan oleh  dalam relasi L =  (1) Maka S ditentukan oleh s (bilangan

kuantum angular spin) dalam relasi S =  s(s1). Kita tahu bahwa L mempunyai

komponen yang disebut Lz, maka S harus mempunyai komponen yang disebut Sz. Jika

Lz ditentukan m dalam relasi Lz = m maka penentu Sz adalah ms dalam relasi:

Sz = ms 

Kita tahu banyaknya harga m adalah 2+1 mulai dari   , (+1) . . . .+. Jika

begitu banyaknya harga ms harus 2s + 1 yaitu dari s sampai + s. Kita juga tahu bahwa m

adalah penentu arah translasi, maka ms pasti penentu arah rotasi. Karena hanya ada 2

macam arah rotasi, maka tentu hanya ada dua macam harga ms. Padahal banyaknya harga

ms = 2s + 1, jadi{

2s + 1 = 2  s = ½

Karena harga ms adalah s dan + s maka harga ms = + ½

Dan harga momentum angular rotasi S adalah S =  s(s1) =  3/4 = 3

2 

Selanjutnya ms = + ½ itulah yang dijadikan sebagai bilangan kuantum ke empat.



6.7 Pengaruh Momentum Angular Translasi Terhadap Energi (Efek Zeeman)

Telah kita ketahui bahwa energi hanya ditentukan oleh bilangan kuantum utama n. Hal itu benar, manakala atom tidak berada di bawah pengaruh medan magnet eksternal. Tetapi jika ada medan magnet eksternal maka momentum angular akan mengubah besarnya energi. Berapa besar perubahan energi yang ditimbulkan oleh momentum angular jika atom berada dalam medan magnet eksternal yang kuat medannya B, itulah yang akan kita bahas sekarang.

Jika elektron dalam atom bermassa m dan bermuatan e, membentuk lintasan spherik,

maka selain momentum angular L, juga terjadi momen magnet  yang arahnya

berlawanan dengan arah L. Sedang arah L adalah arah ibu jari tangan kanan jika arah lintasan partikel (elektron) ditunjukkan oleh keempat jari yang digenggamkan. Hubungan antara  dan L adalah

 = 

m 2

e

L (6-82)

tanda negatif tersebut menunjukkan bahwa arah L dab  berlawanan. Menurut tinjauan

mekanika kuantum besarnya L =  (1), jadi :

 =  m 2 e ) 1 (   (6-83)

Jika sebuah atom dengan momen magnet  berada dalam medan magnet eksternal yang

kuat medannya B, maka perubahan energi yang dialami atom itu adalah

Em =  . B =  . B cos  (6-84)

dengan  adalah sudut antara  dan B.

Substitusi (6-82) ke dalam (6-84) menghasilkan:

Em =

m 2

e

B . L cos  (6-85)

L cos  adalah Lz jadi:

Em =

m 2

e

B . Lz (6-86)

Kita juga tahu bahwa Lz = m jadi:

Em = m

m 2

e

B (6-87)

( m yang cetak miring adalah bilangan kuantum magnetik sedang m yang cetak tegak

adalah massa partikel/elektron). Kuantitas

m 2

e

biasa ditulis , sehingga (6-87) juga boleh ditulis:

Em = m B (6-88)

 = Bohr Magneton = 9,27402 . 1024 J/T

Dari Persamaan (6-88) itu tampak bahwa bilangan kuantum magnetik akan menentukan perubahan energi orbital, manakala atom (hidrogen) berada di bawah pengaruh medan

magnet kecuali orbital-orbital yang m-nya nol.

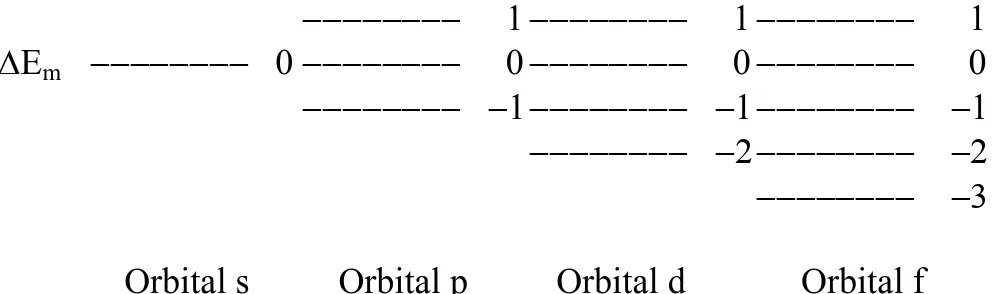
Perubahan energi orbital itu dapat digambarkan sebagai berikut:

m B

m B 3 mB 2 2

1 1 1

Em 0 0 0 0

1 1 1

  Orbital s Orbital p Orbital d Orbital f

Gambar 6.1 : Splitting Energi orbital s, p , d dan f

Dari gambar (6-82) tersebut tampak bahwa selain orbital s, semua orbital mengalami perubahan energi. Orbital p pecah menjadi 3 sub level magnetik, orbital d menjadi 5 dan orbital f menjadi 7 sub level magnetik. Banyaknya sub level dalam sebuah orbital disebut komponen Zeeman. Jadi komponen Zeeman orbital s, p, d dan f adalah 1, 3, 5 dan 7.

Secara umum dapat dinyatakan bahwa banyaknya komponen Zeeman adalah 2+1.

===000===

Soal-soal Bab 6

1. Frekuensi absorpsi terkecil untuk molekul 12C16O adalah 115271 MHz. Hitunglah:

a) Jarak ikatan 12C16O

b) Prediksilah dua frekuensi serapan terkecil berikutnya c) prediksilah frekuensi serapan terendah bagi 13C16O

2. Hitunglah panjang gelombang garis spektra yang muncul dari transisi n = 6  3 pada

atom hidrogen. Ulangi hal yang sama untuk He.

3. Hitunglah Tingkat energi dasar hidrogen dalam satuan eV.

4. Positron adalah partikel dengan massa sama dengan massa elektron tetapi bermuatan +e. Tentukan berapa eV tingkat energi dasar atom positronium (atom ini terdiri atas 1 positron dan 1 elektron.

5. Untuk atom mirip hidrogen dalam keadaan dasar, tentukan < r > 6. Tentukan < r > untuk 2p0 dari atom mirip hidrogen .

8. Tulislah fungsi radial 2s dan 2p untuk atom mirip hidrogen. Tulis pula fungsi gelombangnya.

9. Harga  untuk orbital d = 2. Berapakah harga  untuk orbital t ?

Catatan :Nama orbital adalah s, p, d, f. Setelah itu alphabetik, dengan j tidak dipergunakan.

10. Untuk atom hidrogen dalam keadaan ground state, tentukan probabilitas mendapatkan elektron pada jarak lebih dari 2a ?

11. Tentukan, berapakah jari-jari ruang 1s atom hidrogen menggunakan batas probabilitas 90 % ?

12. (a) Tentukan < T > untuk atom hidrogen keadaan dasar. (b) Dengan < T > itu, tentukan kecepatan elektron.

13. Tentukan populasi ratio gas atom hidrogen antara n = 2 dan n = 1 pada suhu: (a) 25o C (b) 1000 K (c) 10 000 K

14. Tentukan fungsi gelombang atom hidrogen 3,2,1

15. Fungsi gelombang atom hidrogen didefinisikan sebagai:

 = A r2 er / 3a sin2 e2 i  a) tentukan A b) Tentukan n c) Tentukan  d) Tentukan L e) Tentukan Lz ===000===