KAJIAN GEOMETRI ANALITIK PADA MASALAH

(1)

KAJIAN GEOMETRI ANALITIK

PADA MASALAH

CHAOS GAME

SKRIPSI

Oleh

Rere Figurani Armana 121810101052

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS JEMBER

(2)

i

KAJIAN GEOMETRI ANALITIK

PADA MASALAH

CHAOS GAME

SKRIPSI

diajukan guna melengkapi tugas akhir dan memenuhi salah satu syarat untuk menyelesaikan Program Studi Matematika (S1)

dan mencapai gelar sarjaana

Oleh

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS JEMBER

(3)

ii

PERSEMBAHAN

Dengan segala kerendahan hati dan piji syukur yang tak terhingga pada Allah SWT, skripsi ini saya persembahkan untuk:

1. Ibunda Wiwik Siti Sundari, almarhum Ayahanda Slamet Setyo Ngudi Rahardjo, Kakak Wistyarini Armana, Kakak Diah Armana Sari, serta keponakan tercinta Vania Azzalia Aftani yang memberi dukungan, doa, dan pengorbanan selama ini; 2. Guru-guruku sejak taman kanak-kanak sampai dengan Perguruan Tinggi yang terhormat, yang telah memberikan ilmu dan membimbing dengan penuh kesabaran;

(4)

iii MOTTO

Karena itu, ingatlah kamu kepada-Ku niscaya Aku ingat (pula) kepadamu, dan bersyukurlah kepada-Ku, dan janganlah

kamu mengingkari (nikmat)-Ku (Q.S. Al-Baqarah: 152)*)

Tidak pernah ada cita-cita yang terlalu tinggi, yang ada hanyalah upaya yang tak setinggi cita-cita

(Arif Rahman Lubis)**)

_______________

*)

Department Agama Republik Indonesia. 1998. Al Qur’an dan Terjemahannya. Semarang: PT Kumudasmoro Grafindo. **)

(5)

iv

PERNYATAAN

Saya yang bertanda tangan di bawah ini: Nama : Rere Figurani Armana NIM : 121810101052

menyatakan dengan sesungguhnya bahwa karya ilmiah yang berjudul: ”Kajian Geometri Analitik Pada Masalah Chaos Game” adalah benar-benar hasil karya sendiri, kecuali kutipan yang sudah saya sebutkan sumbernya, belum pernah diajukan pada institusi mana pun dan bukan karya jiplakan. Saya bertanggung jawab atas keabsahan dan kebenaran isinya sesuai dengan sikap ilmiah yang harus dijunjung tinggi.

Demikian pernyataan ini saya buat dengan sebenarnya, tanpa ada tekanan dan paksaan dari pihak mana pun serta bersedia mendapat sanksi akademik jika ternyata di kemudian hari pernyataan ini tidak benar.

Jember, Juni 2016 Yang menyatakan,

(6)

v

SKRIPSI

KAJIAN GEOMETRI ANALITIK

PADA MASALAH

CHAOS GAME

Oleh

Pembimbing

(7)

vi

PENGESAHAN

Skripsi berjudul “Kajian Geometri Analitik Pada Masalah Chaos Game” telah diuji dan disahkan pada:

Hari, tanggal :

Tempat : Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Jember

Tim Penguji Ketua,

Kosala Dwidja Purnomo, S.Si., M.Si NIP. 196908281998021001

Sekretaris,

Prof. Drs. Kusno, DEA., PhD. NIP. 196101081986021001 Anggota I,

Dr. Mohammad Fatekurohman, S.Si., M.Si NIP. 196908281998021001

Anggota II,

Ika Hesti Agustin, S.Si., M.Si NIP. 196101081986021001 Mengesahkan

Dekan,

Drs. Sujito, PhD NIP. 196102041987111001

(8)

vii RINGKASAN

Kajian Geometri Analitik Pada Masalah Chaos Game; Rere Figurani Armana; 121810101052; 2016; 50 halaman; Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Jember.

Fraktal merupakan bentuk grafik yang mengandung perulangan dirinya sendiri. Jika objek fraktal diperbesar, maka akan memperlihatkan bentuk yang sama dan sebangun dengan ukuran lebih kecil. Segitiga Sierpinski merupakan contoh dari objek fraktal. Salah satu metode untuk membangkitkan segitiga Sierpinski adalah Chaos Game. Pada penelitian ini dikaji secara geometri analitik bagaimana Chaos Game dapat membangun segitiga Sierpinski serta pengaruh titik awal terhadap pengelompokan geometri titik-titik dan running time yang dibutuhkan.

Analisis Chaos Game memanfaatkan koordinat segitiga Sierpinski pada level 3. Level segitiga menunjukkan banyaknya ukuran segitiga yang ada di dalam segitiga. Menggunakan bantuan koordinat titik tengah pada masing-masing iterasi, dapat dibuktikan bahwa apabila diambil titik sembarang yang terletak pada, di luar segitiga Sierpinski selalu ada titik serupa ke arah 3 titik sudut. Setiap percobaan Chaos Game menghasilkan segitiga Sierpinski, meskipun titik awal tidak selalu pada segitiga, yaitu di dalam ataupun di luar segitiga. Hal ini dikarenakan ketika titik awal di dalam ataupun di luar segitiga, saat sudah mencapai iterasi ke- , titik bentukan Chaos Game selanjutnya mendekati letak segitiga Sierpinski, sehingga titik awal pada, di dalam, ataupun di luar segitiga akan tetap bisa membangun segitiga Sierpinski dengan Chaos Game.

(9)

viii

(10)

ix PRAKATA

Puji dan syukur penulis kepada Allah SWT, karena atas limpahan kasih dan anugerahNya maka penulis dapat menyelesaikan penelitian dan menyusun skripsi ini dengan judul “Kajian Geometri Analitik Pada Masalah Chaos Game” yang merupakan salah satu prasyarat untuk mencapai strata satu (S1) pada Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Jember. Pada kesempatan ini penulis menyampaikan terimakasih kepada:

1. Kosala Dwidja Purnomo, S.Si., M.Si selaku dosen pembimbing utama, yang telah dengan ikhlas memberikan ilmu yang bermanfaat dan dorongan kepada penulis dalam menyelesaikan skripsi;

2. Prof. Drs. Kusno, DEA., PhD. selaku dosen pembimbing anggota yang telah bersedia meluangkan waktu dan tenaga untuk membimbing penulis dalam menyelesaikan skripsi; 3. Dr. Mohamad Fatekurohman, S.Si., M.Si dan Ika Hesti Agustin, S.Si., M.Si selaku dosen

penguji yang telah bersedia membimbing dan meluangkan waktu penulis dalam menyelesaikan skripsi;

4. Drs. Sujito, PhD selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Jember;

5. seluruh dosen Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Jember; 6. Ibunda Wiwik Siti Sundari, almarhum Ayahanda Slamet Setyo Ngudi Rahardjo, Kakak Wistyarini Armana, Kakak Diah Armana Sari, serta keponakan tercinta Vania Azzalia Aftani yang memberi dukungan, doa, dan pengorbanan selama ini; 7. teman-teman rumpik Wahyu, Anggun, Ade, Desi, Dwindah, Yuni, Ikfi, Vivie, Yasmin, Ana, Intan, dan semua anggota Poppo yang senantiasa memberikan dukungan dan menjadi keluarga kedua penulis;

(11)

x

9. HIMATIKA “Geokompstat” yang telah membantu penulis dalam berproses; 10.teman-teman “KPJ” yang memberikan pengalaman menarik bagi penulis; 11. teman-teman seangkatan Bathics’12 yang telah banyak membantu penulis selama studi; 12. adik-adikku Atlas’13, Extreme’14, Sigma’15;

13. semua pihak yang tidak dapat penulis sebutkan satu persatu, yang memberikan dorongan bagi penulis selama studi sampai penulisan skripsi.

Penulisan skripsi ini masih jauh dari kesempurnaan sehingga diharapkan adanya saran dan kritik untuk perbaikan selanjutnya. Semoga karya ilmiah ini bermanfaat bagi semua pihak.

Jember, Juni 2016

(12)

xi DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN PERSEMBAHAN ... ii

HALAMAN MOTTO ... iii

HALAMAN PERNYATAAN ... iv

HALAMAN PEMBIMBINGAN ... v

HALAMAN PENGESAHAN ... vi

RINGKASAN ... vii

PRAKATA ... ix

DAFTAR ISI ... xi

DAFTAR TABEL ... xiii

DAFTAR GAMBAR ... xiv

DAFTAR LAMPIRAN ... xv

BAB 1. PENDAHULUAN ... 1

1.1Latar Belakang ... 1

1.2Rumusan Masalah ... 2

1.3Tujuan ... 2

1.4Manfaat ... 3

BAB 2. TINJAUAN PUSTAKA ... 4

2.1Fraktal ... 4

2.2Segitiga Sierpinski ... 6

2.3Chaos Game ... 7

2.4Beberapa Konsep Geometri ... 10

2.4.1 Koordinat Titik pada Segmen Garis ... 10

(13)

xii

BAB 3. METODE PENELITIAN ... 12

BAB 4. HASIL DAN PEMBAHASAN ... 16

4.1Analisis Geometris Segitiga Sierpinski dan Chaos Game ... 16

4.2 Simulasi Program ... 31

4.2.1 Fasilitas yang Tersedia pada GUI ... 31

4.2.2 Data Awal yang Harus Ditentukan User ... 32

4.2.3 Tahapan Chaos Game ... 33

4.3 Pembahasan ... 36

BAB 5. KESIMPULAN DAN SARAN ... 43

5.1Kesimpulan ... 43

5.2Saran ... 43

DAFTAR PUSTAKA ... 44

(14)

xiii

DAFTAR TABEL

(15)

xiv

DAFTAR GAMBAR

Halaman

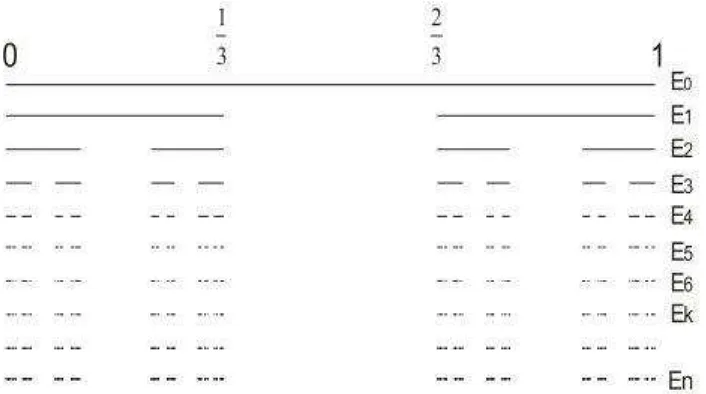
Gambar 2.1 Himpunan per-tiga tengah Cantor ... 4

Gambar 2.2 Kurva Van Koch ... 5

Gambar 2.3 Segitiga Sierpinski ... 5

Gambar 2.4 Debu Cantor ... 5

Gambar 2.5 Segitiga awal yang sudah diberi nama ketiga titik sudutnya untuk memainkan Chaos Game ... 7

Gambar 2.6 Chaos Game setelah iterasi ke-30 dalam membangkitkan Segitiga Sierpinski ... 8

Gambar 2.9 Chaos Game setelah iterasi ke-30.000 dalam membangkitkan Segitiga Sierpinski ... 9

Gambar 2.10 Titik R diantara titik P dan Q ... 10

Gambar 2.11 Segitiga dengan perbandingan segmen segmen pada garis beratnya 11 Gambar 3.1 Skema Penelitian ... 12

Gambar 3.2 Ilustrasi pembentukan titik tengah menggunakan Chaos Game ... 14

Gambar 4.1 Segitiga Sembarang ... 16

Gambar 4.2 Segitiga dengan perbandingan segmen-segmen pada garis beratnya .. 18

Gambar 4.3 Segitiga dengan diketahui koordinat titik beratnya ... 19

(16)

xv

Gambar 4.5 Segitiga Sierpinskilevel 2 ... 21

Gambar 4.6 Segitiga Sierpinskilevel 3 ... 24

Gambar 4.7 Segitiga Sierpinskidengan titik awal terletak pada segitiga ... 25

Gambar 4.8 Segitiga Sierpinskidengan titik awal di dalam segitiga ... 26

Gambar 4.9 Segitiga Sierpinskidengan titik awal di luar segitiga ... 27

Gambar 4.10 Segitiga Sierpinskidengan jarak dari titik sudut pada level 1 ... 29

(17)

xvi

DAFTAR LAMPIRAN

(18)

BAB 1. PENDAHULUAN

1.1Latar Belakang

Fraktal merupakan bentuk grafik yang mengandung perulangan dirinya sendiri. Jika objek fraktal diperbesar, maka akan memperlihatkan bentuk yang sama dan sebangun dengan ukuran lebih kecil. Terdapat beberapa karakter penting pada fraktal yaitu self similar (penjelmaan diri), self affine (penyederhaan diri), self inverse (pembalikan diri), dan self squaring (pemutaran diri). Pada fraktal terdapat istilah dimensi fraktal atau fractal dimensions yaitu bilangan-bilangan pecahan atau bilangan tak bulat (non-integer) yang mencirikan skala fraktal. Secara umum, di dalam suatu himpunan fraktal terdapat suatu himpunan bagian yang merupakan skala kecil dari keseluruhannya (Sulistiyantoko, 2008).

Beberapa teknik yang biasa digunakan untuk membuat fraktal diantaranya adalah Metode Iterated Function Systems (IFS), Metode Iterated Complex Polynomial, Metode L-system, dan Metode Strange Attractor. Iterated Function Systems atau IFS pertama kali dipopulerkan oleh Michael Barnsley dalam bukunya Fractal Everywhere. Fraktal IFS terdiri dari gabungan beberapa tiruan dirinya sendiri, yang kemudian ditransformasikan ke dalam suatu fungsi. Terdapat dua metode untuk membangun fraktal IFS, yaitu Supercopier dan Chaos Game. IFS Supercopier menerapkan konsep seperti fotocopy, dimana akan ada citra baru yang diproduksi (I1)

dari citra awal (I0). Kemudian citra I1 bertindak sebagai citra awal, yang akan

memroduksi citra baru lagi yaitu I2. Hal ini dilakukan terus berulang hingga

didapatkan citra Ik(Riyadi, 2007).

(19)

2

setengah dari titik awal ke salah satu titik sudut yang dipilih acak. Ulangi memilih titik sudut acak, kemudian tandai titik baru yang berjarak setengah dari titik sudut ke titik sebelumnya. Ulangi iterasi hingga terlihat pola segitiga Sierpinski. Semakin banyak iterasi, maka semakin terlihat jelas pola segitiga Sierpinski.

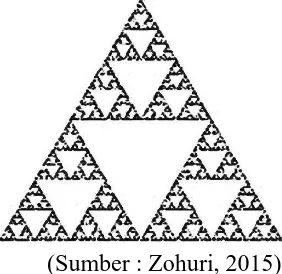
Menurut Purnomo (2014) segitiga Sierpinski adalah fraktal linier yang mempunyai keserupaan diri identik sampai iterasi tak hingga. Segitiga Sierpinski merupakan segitiga yang terdiri dari segitiga-segitiga lain yang berbentuk sama dan berulang dengan skala tertentu. Apabila bagian dari segitiga tersebut diperbesar, maka akan tampak keseluruhan dari segitiga Sierpinski.

Menurut Devaney (2003) membangun segitiga Sierpinski dengan Chaos Game menggunakan bantuan dadu berwarna dan segitiga yang telah diberi tanda warna pada masing-masing titik sudutnya. Sundbye (Tanpa Tahun) membangun segitiga Sierpinski dengan perangkat spinner untuk mendapatkan angka acak dan segitiga yang telah diberi tanda pada titik sudutnya. Titik awal acak yang digunakan oleh Devaney dan Sundbye terletak di dalam segitiga. Zohuri (2015) mengatakan bahwa bila titik awal pada Chaos Game terletak pada segitiga Sierpinski, maka titik yang ditandai berikutnya juga akan berada pada segitiga Sierpinski. Namun, sebenarnya titik yang dibentuk dari Chaos Game tidak selalu tepat terletak pada segitiga Sierpinski. Berdasarkan uraian tersebut, peneliti tertarik untuk mengkaji secara geometri analitik bagaimana Chaos Game dapat membangun segitiga Sierpinski serta pengaruh titik awal terhadap pengelompokan titik-titik dan running time yang dibutuhkan.

1.2Rumusan Masalah

Berdasarkan latar belakang yang telah dijelaskan di atas, maka rumusan masalah yang dibahas dalam tugas akhir ini adalah

(20)

3

b. bagaimana pengaruh letak titik awal terhadap pengelompokan titik-titik pada Chaos Game?

c. bagaimana pengaruh letak titik awal terhadap running time yang dibutuhkan pada Chaos Game?

1.3Tujuan

Berdasarkan rumusan masalah di atas, tujuan dari penulisan tugas akhir ini adalah

a. mengetahui analisis geometris Chaos Game sehingga dapat membentuk Segitiga Sierpinski;

b. mengetahui pengaruh letak titik awal terhadap pengelompokan titik-titik pada Chaos Game;

c. mengetahui pengaruh letak titik awal terhadap running time yang dibutuhkan terhadap Chaos Game.

1.4Manfaat

(21)

BAB 2. TINJAUAN PUSTAKA

2.1 Fraktal

Mandelbrot (dalam Riyadi, 2007) mengatakan bahwa fraktal berasal dari bahasa latin fractus yang artinya tidak teratur atau terfragmentasi dan frangere yang artinya memecah atau membuat fragmen-fragmen yang tidak beraturan. Fraktal merupakan bentuk geometri yang terfragmentasi, dapat dibagi dalam beberapa bagian, dan tiap bagian merupakan tiruan dalam ukuran yang sama besar atau lebih kecil dari bentuk asli keseluruhannya.

Menurut Sulistiyantoko (2008) terdapat beberapa bentuk fraktal yaitu himpunan per-tiga tengah Cantor, kurva Von Koch, segitiga Sierpinski, dan debu Cantor.

(22)

5

Gambar 2.2 Kurva VonKoch (Sumber: Sulistiyantoko, 2008)

Gambar 2.3 Segitiga Sierpinski (Sumber: Sulistiyantoko, 2008)

(23)

6

Riyadi (2007) mengklasifikasikan fraktal berdasarkan self-similarity menjadi tiga macam, yaitu Exact self-similarity, Quasi-self-similarity, dan Statistical self-similarity. Fraktal exact self-similarity tampak terlihat sama persis dengan ukuran dan rasio yang berbeda. Fraktal quasi-self-similarity lebih lemah jika dibandingkan dengan fraktal exact self-similarity. Fraktal quasi-self-similarity tampak mirip, namun tidak sama persis dengan ukuran dan rasio yang berbeda. Sedangkan statistical self-similarity merupakan fraktal self-similarity yang paling lemah diantara ketiganya. Pada umumnya, fraktal statistical self-similarity merupakan bentuk fraktal yang paling dasar. Hal ini dikarenakan fraktal statistical self-similarity memiliki ukuran numerik atau statistik yang dipertahankan pada ukuran dan rasio yang berbeda. Fraktal Iterated Function Systems biasanya menghasilkan jenis exact self-similarity.

2.2 Segitiga Sierpinski

Segitiga Sierpinski merupakan fraktal linier yang mempunyai bentuk geometris yang identik hingga pada iterasi tak hingga. Salah satu cara untuk membangkitkan segitiga Sierpinskiyaitu dengan menentukan terlebih dahulu segitiga sama sisi yang telah diberi warna tertentu, kemudian titik tengah masing-masing sisinya dihubungkan sehingga diperoleh segitiga baru yang berukuran setengahnya serta terletak di tengah segitiga awal. Warnai segitiga tersebut dengan warna putih untuk menandai bahwa segitiga tersebut merupakan segitiga kosong. Selanjutnya, pada ketiga segitiga berisi yang mempunyai ukuran setengah dari segitiga awal dilakukan proses yang sama agar didapatkan segitiga-segitiga baru lagi dengan ukuran setengahnya. Algoritma ini dilakukan hingga iterasi tertentu. Pada setiap iterasi didapatkan fakta bahwa satu segitiga dibagi menjadi empat segitiga (dengan ukuran sisi setengahnya) yang terdiri atas segitiga berisi warna dan satu segitiga kosong. Luas segitiga Sierpinski Sn pada iterasi ke-n adalah dari luas awalnya.

(24)

7

2.3 Chaos Game

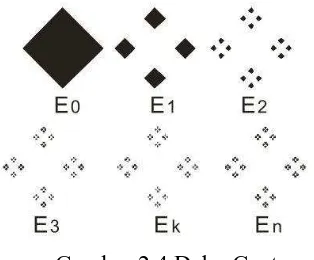
Chaos Game merupakan salah satu metode untuk membangkitkan segitiga Sierpinski. Pertama menentukan tiga titik sebagai titik pembentuk segitiga. Kemudian menentukan titik acak sebagai titik awal. Setelah itu, tandai titik baru yang berjarak setengah dari titik awal ke salah satu titik sudut yang dipilih acak. Ulangi memilih titik sudut acak, kemudian tandai titik baru yang berjarak setengah dari titik sudut ke titik sebelumnya. Ulangi iterasi hingga terlihat pola segitiga Sierpinski.

Algoritma Chaos Game: a. dibuat sebuah segitiga;

b. dipilih titik acak sebagai titik awal; c. dipilih titik sudut acak;

d. ditentukan titik baru yang berjarak setengah dari titik tersebut ke titik sudut; e. diulang (c), (d), dan (e);

f. dilakukan hingga iterasi yang diinginkan.

(Sumber : Zohuri, 2015)

(25)

8

Gambar 2.6 Chaos Game setelah iterasi ke-30 dalam membangkitkan Segitiga Sierpinski

(26)

9

Gambar 2.8 Chaos Game setelah iterasi ke-400 dalam membangkitkan Segitiga Sierpinski

Gambar 2.9 Chaos Game setelah iterasi ke-30.000 dalam membangkitkan Segitiga Sierpinski

(27)

10

2.4 Beberapa Konsep Geometri

2.4.1 Koordinat Titik pada Segmen Garis

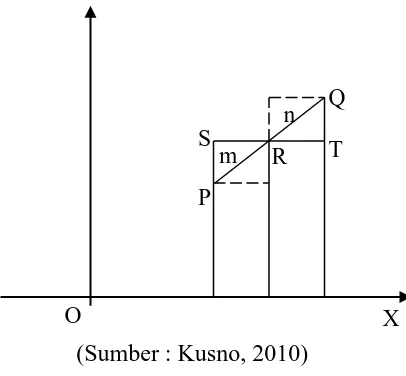
Misalkan segmen garis didefinisikan oleh titik P(x1, y1) dan Q(x2, y2),

Dengan cara yang sama untuk x, maka didapatkan hubungan

atau

(1.2)

Jika R merupakan titik tengah dari , yaitu m : n = 1: 1, maka koordinat titik R dapat dinyatakan sebagai

(28)

11

Secara umum, jika perbandingan m : n bernilai sebarang real k -1, maka posisi R dapat terletak mungkin diantara atau diperpanjangannya dan koordinat R berbentuk

R

(1.4)

Oleh karenanya terdapat beberapa kemungkinan untuk nilai k yaitu: a.) Jika , maka R diantara ;

b.) Jika , maka R pada perpanjangan ; c.) Jika , maka menunjukkan titik di tak terhingga; d.) Jika , maka R pada perpanjangan (Kusno, 2010).

2.4.2 Garis Berat pada Segitiga

Terdapat beberapa teorema tentang garis berat segitiga yang digunakan, yaitu:

a. Garis berat pada segitiga adalah suatu segmen yang ditarik dari sembarang titik sudutnya ke titik tengah sisi di hadapan sudut tadi;

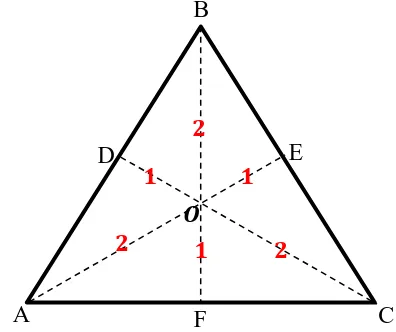
b. Ketiga garis berat segitiga melalui satu titik dan perbandingan segmen-segmennya dari titik sudut sebagai 2 dibanding 1 (Kusno, 2003).

Gambar 2.11 Segitiga dengan perbandingan segmen segmen pada garis beratnya

A C

D E

F �

(29)

BAB 3. METODE PENELITIAN

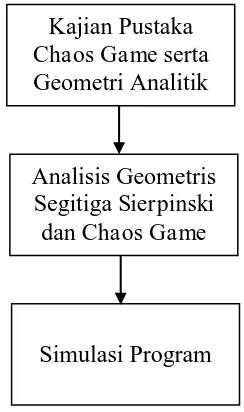
Pada bab 3 dibahas tentang prosedur yang digunakan untuk menyelesaikan penelitian ini. Secara skematik, langkah-langkah yang dilakukan dapat dilihat pada Gambar 3.1.

Gambar 3.1 Skema penelitian

Berdasarkan skema pada Gambar 3.1, langkah-langkah penelitian dapat dijelaskan sebagai berikut:

a. Kajian Pustaka Chaos Game dan Geometri Analitik

Langkah awal yaitu dengan melakukan kajian pustaka yang bertujuan untuk mendapatkan informasi dari jurnal, buku, dan skripsi yang terkait dengan Pustaka Chaos Game dan Geometri Analitik.

b. Analisis Geometris Segitiga Sierpinski dan ChaosGame

Pada tahap ini dijelaskan karakteristik segitiga Sierpinski serta dijelaskan apabila diambil titik sembarang yang terletak pada segitiga Sierpinski atau di luar segitiga Sierpinski selalu ada titik serupa ke arah 3 titik sudut.

Kajian Pustaka Chaos Game serta Geometri Analitik

Analisis Geometris Segitiga Sierpinski dan Chaos Game

(30)

13

c. Simulasi Program

Software yang digunakan untuk membuat program dalam penelitian ini adalah software MATLAB R2009. Prosedur untuk membuat program ini adalah sebagai berikut:

1) Input

Pada tahap ini diinputkan iterasi yang dilakukan pada Chaos Game, sebarang tiga titik yang membentuk segitiga, peluang terpilihnya masing-masing titik sudut, serta titik awal untuk memulai Chaos Game.

2) Proses

a) Menentukan tiga titik pada satu bidang yang membentuk segitiga. Segitiga tersebut dapat diklasifikasikan menjadi :

(1) Segitiga sama sisi (2) Segitiga sama kaki (3) Segitiga sembarang

b) Menentukan peluang terpilihnya masing-masing titik sudut. Titik sudut tersebut bisa mempunyai peluang yang sama ataupun berbeda.

c) Menentukan titik awal secara acak. Titik awal tersebut dapat diklasifikasikan menjadi :

(1) Pada segitiga Sierpinski (2) Di dalam segitiga (3) Di luar segitiga

d) Dari titik awal tersebut dihubungkan dengan salah satu titik sudut segitiga yang dipilih secara acak.

e) Kemudian beri tanda pada setengah dari jarak dua titik tersebut, sehingga membentuk titik baru.

(31)

14

3) Output

Output yang dihasilkan dari simulasi ini berupa visualisasi segitiga Sierpinski serta runningtime yang dibutuhkan. Rumus untuk menghitung running time yaitu

tic

-- run the program section to be timed -- toc

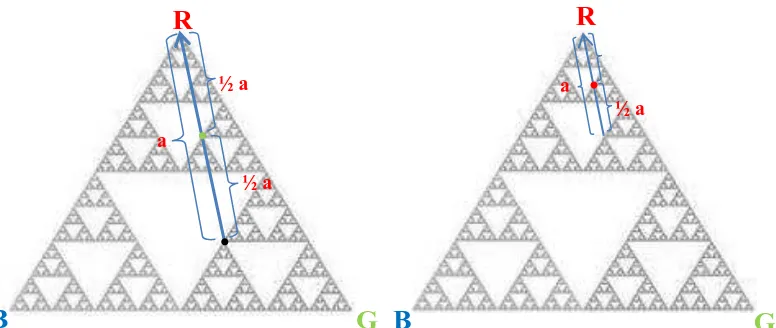
Pada Gambar 3.2 dapat diamati bahwa masing-masing titik sudut segitiga diberi tanda warna yaitu Red, Green, dan Blue. Misalkan adalah sebuah titik acak (titik berwarna hitam) dan adalah titik yang terletak setengah dari jarak ke titik sudut acak (titik berwarna biru). Maka, warna titik berdasarkan letak , yaitu sesuai dengan titik sudut terdekat dari . Hal ini bertujuan untuk membedakan pengelompokan geometri titik-titik yang dibentuk.

Gambar 3.2 Ilustrasi pembentukan titik tengah menggunakan Chaos Game

(32)

15

(33)

BAB 4. HASIL DAN PEMBAHASAN

Terdapat beberapa subbab yang dibahas pada bab ini, yaitu Analisis

Geometris Segitiga Sierpinski dan Chaos Game, dimana dipaparkan karakteristik segitiga Sierpinskiserta dijelaskan apabila diambil titik sembarang yang terletak pada segitiga Sierpinski atau di luar segitiga Sierpinski selalu ada titik serupa ke arah 3 titik sudut, Simulasi Program yang membangkitkan segitiga Sierpinski dengan variasi titik sudut, titik awal, serta peluang terpilihnya titik sudut, dan Pembahasan tentang analisis hasil simulasi yang telah dilakukan.

4.1 Analisis Geometris Segitiga Sierpinski dan Chaos Game

Pada tahap analisis geometris segitiga Sierpinski dan Chaos Game digunakan

sembarang yang diketahui garis tingginya. Setelah itu dilakukan penurunan

rumus untuk mengetahui panjang masing-masing garis beratnya. Rumus yang didapatkan selanjutnya digunakan pada segitiga sama sisi sehingga diperoleh bahwa jarak titik berat pada masing-masing titik sudut adalah sama.

Gambar 4.1 Segitiga Sembarang

A

_D

C

B

E

(34)

17

Berdasarkan Gambar 4.1, maka berlaku teorema Phytagoras, yaitu:

(4.1)

(4.2)

dengan melakukan substitusi persamaan (4.1) dan (4.2), sehingga

(4.3)

atau

kemudian substitusi persamaan (4.4) ke (4.1) sehingga diperoleh persamaan baru, yaitu:

√

apabila persamaan (4.3) disubstitusi ke persamaan (4.4), maka didapatkan persamaan (4.6)

√

Selanjutnya dilakukan penurunan rumus sehingga diperoleh panjang garis beratnya, yaitu:

√

jika menggunakan segitiga sama sisi dengan panjang sisi , maka panjang garis beratnya menjadi:

√ √

(35)

18

Menurut Kusno (2003) ketiga garis berat segitiga melalui satu titik dan perbandingan segmen-segmennya dari titik sudut sebagai 2 dibanding 1. Akibatnya titik berat pada segitiga sama sisi mempunyai jarak yang sama dengan ketiga titik sudutnya, yaitu . Hal ini dapat dilihat pada Gambar 4.2.

Gambar 4.2 Segitiga dengan perbandingan segmen-segmen pada garis beratnya

Langkah selanjutnya adalah mencari koordinat titik sudut segitiga Sierpinski dengan memanfaatkan koordinat titik berat dan perbandingan ruas garis segitiga. Diketahui bahwa koordinat A adalah dan merupakan titik berat, maka koordinat dari adalah karena proyeksi terhadap merupakan titik yang membagi sama panjang. Koordinat adalah karena perbandingan segmen-segmen garis bagi mempunyai perbandingan 2 dibanding 1.

F

A C

D E

(36)

19

Gambar 4.3 Segitiga dengan diketahui koordinat titik beratnya

Menurut Purnomo (2014) salah satu cara untuk membangkitkan segitiga Sierpinski yaitu dengan menentukan terlebih dahulu segitiga sama sisi yang telah diberi warna tertentu, kemudian titik tengah masing-masing sisinya dihubungkan sehingga diperoleh segitiga baru yang berukuran setengahnya serta terletak di tengah segitiga awal. Warnai segitiga tersebut dengan warna putih untuk menandai bahwa segitiga tersebut merupakan segitiga kosong. Selanjutnya, pada ketiga segitiga berisi yang mempunyai ukuran setengah dari segitiga awal dilakukan proses yang sama agar didapatkan segitiga-segitiga baru lagi dengan ukuran setengahnya.

Pada Gambar 4.4 disajikan segitiga Sierpinskilevel 1 dengan diketahui posisi koordinat titik beratnya. Level segitiga menunjukkan banyaknya ukuran segitiga yang ada di dalam segitiga .

Algoritma segitiga Sierpinski berdasarkan level: 1. dibuat segitiga ;

2. ditentukan titik tengah pada masing-masing ruas garis ;

3. dihubungkan masing-masing titik tengah sehingga didapatkan segitiga yang terletak di tengah dengan panjang sisi setengah dari segitiga , untuk kemudian segitiga tersebut ditandai sebagai segitiga kosong;

A C

B

(37)

20

4. dilakukan penentuan titik tengah pada masing-masing segitiga baru yang berukuran panjang sisinya setengah dari sisi segitiga ;

5. dilakukan cara yang sama hingga level yang diinginkan.

Untuk mengetahui koordinat titik-titik menggunakan perhitungan titik tengah (Gambar 4.4) , yaitu:

Koordinat titik tengah , Koordinat titik tengah Koordinat titik tengah

Gambar 4.4 Segitiga Sierpinskilevel 1

Dapat dicari koordinat pada segitiga Sierpinski level 2 (Gambar 4.5). Koordinat tersebut adalah:

Koordinat titik tengah ,

Koordinat titik tengah

A C

D E

B

(38)

21

(39)

(40)

(41)

24

Tahapan Chaos Game dimulai dengan penentuan koordinat titik awalnya secara acak dan titik sudut acak. Setelah itu menentukan titik baru yang berjarak setengah dari titik awal ke titik sudut. Selanjutnya titik baru bentukan Chaos Game berperan sebagai titik awal, sehingga didapatkan titik-titik lain bentukan Chaos Game sesuai iterasi yang ditentukan.

Koordinat titik awal acak dapat diklasifikasikan menjadi 3, yaitu: a) Pada segitiga Sierpinski

b) Di dalam segitiga Sierpinski c) Di luar segitiga Sierpinski

apabila sudah diketahui letak titik awalnya, maka dapat diketahui koordinat titik-titik bentukan Chaos Game pada iterasi selanjutnya.

(42)

25

a) Pada segitiga Sierpinski

Gambar 4.7 Segitiga Sierpinskidengan titik awal terletak pada segitiga

Apabila diambil sebarang titik awal yang terletak pada segitiga Sierpinski, misalkan koordinat titik awalnya adalah . Apabila terpilih titik sudut , maka koordinat titik yang terbentuk adalah

, dimana titik tersebut merupakan koordinat dari . Apabila terpilih titik sudut , maka koordinat titik yang terbentuk adalah

, dimana titik tersebut merupakan koordinat dari .

(43)

26

Sehingga dapat disimpulkan bahwa jika diambil sebarang titik yang terletak pada segitiga Sierpinski maka selalu ada titik serupa ke arah 3 titik sudutnya yang berjarak setengah dari titik awal, karena titik bentukan dari Chaos Game merupakan titik tengah dari titik awal dan titik sudutnya maka mempunyai setengah dari jarak awal ke titik sudut.

b) Di dalam segitiga Sierpinski

Gambar 4.8 Segitiga Sierpinskidengan titik awal di dalam segitiga

Apabila diambil sebarang titik awal yang terletak di dalam segitiga Sierpinski, misalkan koordinat titik awalnya adalah . Maka titik awal tersebut mempunyai jarak terdekat dengan titik pada . Sesuai dengan perbandingan segmen-segmen garis bagi yaitu 2 dibanding 1, maka titik awal tersebut mempunyai jarak terkecil dengan atau atau , yaitu .

(44)

27

Kemudian dilakukan lagi pemilihan acak titik sudut, misalkan terpilih titik sudut , maka koordinat titik bentukannya adalah Jarak dengan adalah .

Jika diamati terdapat suatu pola pada jarak titik awal dengan segitiga terdekatnya yaitu:

Jarak titik awal terhadap

Jarak titik pada iterasi ke-1 terhadap Jarak titik pada iterasi ke-2 terhadap

Untuk iterasi ke- jaraknya adalah dari jarak awal. Apabila dilakukan iterasi semakin banyak, maka jarak antara titik bentukan Chaos Game dengan segitiga terdekatnya adalah semakin kecil, sehingga koordinat titik tersebut mendekati segitiga. Apabila sudah mencapai koordinat segitiga, maka mengikuti aturan titik awal yang terletak pada segitiga Sierpinski.

c) Di luar segitiga Sierpinski

Gambar 4.9 Segitiga Sierpinskidengan titik awal di luar segitiga

(45)

28

Ambil sebarang titik awal yang terletak di luar segitiga, misalkan titik awalnya terletak di sisi kanan segitiga seperti pada Gambar 4.9, andaikan koordinatnya . Apabila terpilih titik sudut atau , maka titik bentukan dari Chaos Game semakin mendekati segitiga. Karena peluang terpilihnya masing-masing titik sudut adalah sama, maka titik sudut terpilih dengan peluang yang sama dengan titik sudut ataupun . Apabila terpilih titik sudut , maka titik bentukan Chaos Game masuk ke dalam segitiga, dimana jarak antara titik bentukan Chaos Game dan titik sudut kurang dari dua kali jarak titik sudut terhadap . Ketika titik bentukan tersebut sudah masuk ke dalam segitiga, maka tidak mungkin titik tersebut keluar lagi dari segitiga. Titik bentukan Chaos Game yang sudah terletak di dalam segitiga mengikuti aturan titik awal yang terletak pada segitiga Sierpinski ataupun yang terletak di dalam segitiga Sierpinski.

Untuk mengetahui pada iterasi keberapa terbentuk segitiga Sierpinski, maka ditentukan terlebih dahulu toleransi ( ). Toleransi menunjukkan jarak antara titik awal dengan segitiga terdekat agar didapatkan toleransi dari setiap nilai pendekatan jarak titik awal terhadap garis . Kemudian dilakukan perhitungan dengan rumus dari jarak awal . Iterasi dihentikan ketika .

Misalkan diketahui dan , maka dilakukan perhitungan sebagai berikut:

Iterasi 1 : Iterasi 2 : Iterasi 3 : Iterasi 4 :

(46)

29

Titik bentukan Chaos Game berjarak setengah dari titik awal ke titik sudut. Ketika jarak yang dipilih bukan , misal , maka panjang sisi segitiga baru adalah dari masing-masing ruas garis. Titik bentukan Chaos Game terletak pada jarak antara titik awal dan titik sudut, yang dihitung dari titik sudut. Hal ini dapat dilihat pada Gambar 4.10.

Gambar 4.10 Segitiga Sierpinski dengan jarak dari titik sudut pada level 1

A

(47)

30

A

B

C

A

(48)

31

Segitiga Sierpinski merupakan segitiga yang dibangun dengan jarak setengah dari titik sudut, sehingga membentuk segitiga baru pada bagian tengahnya. Ketika jaraknya diubah menjadi dari titik sudut, maka terbentuk suatu poligon segilima. Karena tidak menghasilkan segitiga Sierpinski, maka jarak Chaos Game haruslah setengah dari titik sudut agar dapat membangun segitiga Sierpinski.

4.2 Simulasi Program

4.2.1 Fasilitas yang Tersedia pada GUI

Software yang digunakan untuk menyelesaikan penelitian ini adalah MATLAB R2009a. Terdapat hal yang perlu diperhatikan pada tampilan program GUI yang disajikan pada layar untuk menghasilkan visualisasi pembentukan segitiga Sierpinski dari Chaos Game, diantaranya variasi segitiga, koordinat titik awal, serta peluang kemunculan titik sudut.

(49)

32

di luar segitiga. Sedangkan text Running Time berfungsi untuk menampilkan waktu yang dibutuhkan untuk Chaos Game.

Output dari program tersebut adalah running time yang dibutuhkan serta visualisasi segitiga Sierpinski yang dibangkitkan dari Chaos Game.

Gambar 4.13 Tampilan program GUI

4.2.2 Data Awal yang Harus Ditentukan User

(50)

33

a. Koordinat titik sudut segitiga 1) Segitiga sama sisi

2) Segitiga sama kaki 3) Segitiga sembarang b. Koordinat titik awal

1) Pada segitiga Sierpinski 2) Di dalam segitiga Sierpinski 3) Di luar segitiga Sierpinski c. Peluang munculnya titik sudut

1) Peluang semua titik sudut sama 2) Peluang semua titik sudut berbeda 4.2.3 Tahapan Chaos Game

Setelah mendapatkan variasi segitiga, koordinat titik awal, dan peluang kemunculan titik sudut, langkah selanjutnya yaitu melakukan simulasi program. Iterasi yang digunakan untuk semua simulasi adalah 1000. Banyaknya iterasi berpengaruh pada pola segitiga Sierpinski yang dihasilkan. Semakin banyak iterasi maka pola segitiga Sierpinski semakin jelas terlihat.

Langkah pertama ketika melakukan simulasi adalah menginputkan iterasi pada edit teks iterasi, kemudian menentukan letak titik awal dan titik sudut pada axes. Ketika akan memilih letak titik awal dan titik sudut, pushbutton mulai harus ditekan terlebih dahulu. Langkah selanjutnya adalah menekan enter pada keyboard dengan tujuan menampilkan titik titik pada axes. Setelah itu menginputkan peluang terpilihnnya masing-masing titik sudut pada edit teks Kemunculan Titik Sudut. Langkah terakhir yaitu menekan pushbutton proses untuk memulai Chaos Game.

(51)

34

Game, segitiga Sierpinski mempunyai daerah yang berbeda warna serta menyebar ke semua daerah titik sudut. Running time yang dibutuhkan adalah Percobaan ke-2 menggunakan segitiga dan titik awal yang sama, hanya peluang untuk masing-masing titik sudut berbeda, yaitu , , . Terdapat perbedaan daerah distribusi titik segitiga Sierpinski. Titik sudut mempunyai daerah dengan titik bentukan Chaos Game paling banyak jika dibandingkan dengan dan . Running time yang dibutuhkan pada percobaan ke-2 adalah Percobaan selanjutnya menggunakan segitiga yang sama serta peluang kemunculan titik sudutnya adalah sama yaitu , namun titik awalnya terletak di dalam segitiga. Running time yang dibutuhkan adalah Segitiga Sierpinski yang dibentuk mempunyai distribusi titik sama dan menyebar ke semua masing-masing daerah titik sudut. Percobaan ke-4 menggunakan segitiga dan titik awal yang sama, hanya peluang untuk masing-masing titik sudut berbeda, yaitu , , .Titik sudut mempunyai daerah dengan titik bentukan Chaos Game paling banyak, kemudian , baru selanjutnya . Running time yang dibutuhkan pada percobaan ke-4 adalah Setelah itu melakukan percobaan menggunakan segitiga yang sama serta peluang kemunculan titik sudutnya adalah sama yaitu

, namun titik awalnya terletak di luar segitiga. Running time yang dibutuhkan

(52)

35

Segitiga Sierpinski yang dibentuk mempunyai distribusi titik sama dan menyebar ke semua masing-masing daerah titik sudut. Percobaan ke-8 menggunakan segitiga dan titik awal yang sama, hanya peluang untuk masing-masing titik sudut berbeda, yaitu

, , . Titik sudut mempunyai daerah dengan titik

bentukan Chaos Game paling banyak, kemudian , baru selanjutnya . Running time yang dibutuhnkan pada percobaan ke-8 adalah Percobaan selanjutnya menggunakan segitiga yang sama serta peluang kemunculan titik sudutnya adalah sama yaitu , namun titik awalnya terletak di dalam segitiga. Running time yang dibutuhkan pada percobaan ke-9 adalah Segitiga Sierpinski yang dibentuk mempunyai distribusi titik sama dan menyebar ke semua masing-masing daerah titik sudut. Percobaan ke-10 menggunakan segitiga dan titik awal yang sama, hanya peluang untuk masing-masing titik sudut berbeda, yaitu , ,

. Titik sudut mempunyai daerah dengan titik bentukan Chaos Game

(53)

36

dan menyebar ke semua masing-masing daerah titik sudut. Percobaan ke-14 menggunakan segitiga dan titik awal yang sama, hanya peluang untuk masing-masing titik sudut berbeda, yaitu , , . Titik sudut mempunyai daerah dengan titik bentukan Chaos Game paling banyak jika dibandingkan dengan dan . Running time yang dibutuhkan pada percobaan ke-14 adalah Percobaan selanjutnya menggunakan segitiga yang sama serta peluang kemunculan titik sudutnya adalah sama yaitu , namun titik awalnya terletak di dalam segitiga. Running time yang dibutuhkan adalah Segitiga Sierpinski yang dibentuk mempunyai distribusi titik sama dan menyebar ke semua masing-masing daerah titik sudut. Percobaan ke-16 menggunakan segitiga dan titik awal yang sama, hanya peluang untuk masing-masing titik sudut berbeda, yaitu

, , . Titik sudut mempunyai daerah dengan titik

bentukan Chaos Game paling banyak, kemudian , baru selanjutnya . Running time yang dibutuhkan pada percobaan ke-16 adalah Setelah itu melakukan percobaan menggunakan segitiga yang sama serta peluang kemunculan titik sudutnya adalah sama yaitu , namun titik awalnya terletak di luar segitiga. Running time yang dibutuhkan adalah Segitiga Sierpinski yang dibentuk mempunyai distribusi titik sama dan menyebar ke semua masing-masing daerah titik sudut. Percobaan yang terakhir masih menggunakan segitiga dan titik awal yang sama, hanya peluang untuk masing-masing titik sudut berbeda, yaitu , ,

. Titik sudut mempunyai daerah dengan titik bentukan Chaos Game

paling banyak jika dibandingkan dengan serta daerah tidak mempunyai titik bentukan. Running time yang dibutuhkan pada percobaan ke-18 adalah

(54)

37

4.3 Pembahasan

Pada percobaan pertama menggunakan segitiga sama sisi dengan peluang terpilihnya masing-masing titik sudut adalah sama yaitu , serta titik awalnya terletak pada segitiga. Setelah itu dilakukan percobaan lagi dengan variasi koordinat titik sudut segitiga, koordinat titik awal, dan peluang terpilihnya titik sudut. Maka dibuat tabel penelitian agar lebih mudah untuk mengetahui informasi mengenai percobaan yang telah dilakukan.

Pada Tabel 4.1 dapat dilihat bahwa setiap percobaan Chaos Game menghasilkan segitiga Sierpinski, meskipun titik awal tidak selalu pada segitiga, yaitu di dalam ataupun di luar segitiga. Hal ini dikarenakan ketika titik awal di dalam ataupun di luar segitiga, saat sudah mencapai iterasi ke- , titik bentukan Chaos Game akan mendekati segitiga Sierpinski, sehingga titik awal pada, di dalam, ataupun di luar segitiga akan tetap dapat membangun segitiga Sierpinski dengan Chaos Game.

(55)

38

Peluang munculnya titik sudut berpengaruh pada distribusi pengelompokan titik yang dihasilkan. Apabila titik sudut tersebut mempunyai peluang lebih banyak, maka lebih banyak pula titik yang dihasikan dari titik sudut tersebut. Pada saat salah satu titik sudut mempunyai peluang , maka tidak terbentuk pola segitiga Sierpinski. Selain itu titik yang dihasilkan cenderung sama sehingga pada visualisasi hasil Chaos Game titik yang dihasilkan terlihat lebih sedikit meskipun iterasinya adalah 1000. Ketika titik sudut mempunyai peluang dan titik awalnya terletak berseberangan dengan titik sudut tersebut, maka Chaos Game tidak menghasilkan titik yang terletak di dalam segitiga serta tidak dihasilkan pola segitiga Sierpinski.

(56)

(57)

(58)

(59)

(60)

BAB 5. KESIMPULAN DAN SARAN

5.1 Kesimpulan

Berdasarkan hasil analisis geometri pada Chaos Game, maka dapat diambil kesimpulan sebagai berikut :

1. Pembangkitan titik tengah dari titik awal sembarang yaitu pada, di dalam, ataupun di luar segitiga, dapat membangun segitiga Sierpinski.

2. Chaos Game menghasilkan daerah segitiga Sierpinski yang berbeda dengan bantuan warna yang berbeda pada masing-masing titik sudut.

3. Letak titik awal tidak mempengaruhi running time yang dibutuhkan.

5.2 Saran

(61)

DAFTAR PUSTAKA

Devaney, Robert L. 2003. Fractal Patterns and Chaos Game. Boston: Departement of Mathematics Boston University

Hasang, S. & Supardjo, S. 2012. Geometri Fraktal dalam Rancangan Arsitektur. Media Martasain (hal.111-124). Manado: Universitas Samratulangi

Kusno. 2003. Geometri. Jember: Fakultas MIPA Universitas Jember

Kusno. 2010. Geometri Rancang Bangun Studi tentang Desain dan Pemodelan Benda dengan Kurva dan Permukaan Berbantu Komputer. Jember: Fakultas MIPA Universitas Jember

Purnomo, K. D. 2014. Pembangkitan Segitiga Sierpinski dengan Transformasi Affine Berbasis Beberapa Benda Geometris. Prosiding Seminar Nasional Matematika (hal. 365-375). Jember: Fakultas MIPA Universitas Jember Riyadi, B. 2007. Analisis dan Perancangan Perangkat Lunak Generator Gambar dan

Musik Fraktal dengan Iterated Function System. Skripsi. Jakarta: Universitas Bina Nusantara

Romadiastri, Y. 2013. Batik Fraktal. Perkembangan Aplikasi GeometriFraktal (hal. 158-164). Semarang: Jurusan Tadris Matematika Fakultas Ilmu Tarbiyah dan Keguruan IAIN Walisongo

Sulistiyantoko, D. 2008. Aplikasi Sekuensi Deret pada Perhitungan Pembentukan Geometri Fraktal Sederhana. Skripsi. Yogyakarta: Program Studi Pendidikan Matematika Fakultas Sains dan Teknologi UIN Sunan Kalijaga

Sundbye, L. Chaos and Fractals on the TI Graping Calculator. Department of Mathematical and Computer Sciences: Metropolitan State College of Denver Zohuri, B. 2015. Dimensional Analysis and Self-Similarity Methods for Engineers

(62)

LAMPIRAN

A. Lampiran Script Batas Daerah Warna Segitiga

function grslurus=grs(x,x1,x2,y1,y2) y=((y2-y1)/(x2-x1))*(x-x1)+y1; grslurus=y;

(63)

46

set(handles.axes1,'Color',[0.941 0.941 0.941],'XColor',[0 0 0],'YColor',[0 0 0],'NextPlot','add');

'YLim',[0 10],'xgrid','on','ygrid','on');

tgh1=(t3(1)+t2(1))/2;

batas1=grs(ack(1),t1(1),t2(1),t1(2),t2(2)); batas2=grs(ack(1),t1(1),t3(1),t1(2),t3(2)); batas3=grs(ack(1),t2(1),t3(1),t2(2),t3(2));

if (ack(2)<=batas1)&& (ack(2)<=batas3) && (ack(2)>=batas2) && (tanda==0) waktu=tic;

tanda=1;

plot(ack(1),ack(2),'o','markerfacecolor','m','markeredgecolor','k','markersize',8) end

(64)

47

(65)

48

{'x','y','Titik Terpilih','Segitiga'},'rowstriping','on'); set(handles.text5,'string',waktu);

wrna={' Biru',' Merah',' Hijau',' Ciyan'};

(66)

49

plot(data(i,1),data(i,2),'o','markeredgecolor','r','markerfacecolor','y','markersize',7);

end

set(handles.axes1,'Color',[1 1 1],'XColor',[0 0 0],'YColor',[0 0 0],'Xgrid','on','ygrid','on','NextPlot','add');

rownames(iter)={['A' num2str(iter)]};

end

(67)

50

for j=1:m-1 if j~=m-1

plot([data(j,1) data(j+1,1)], [data(j,2) data(j+1,2)],'k','linewidth',3); end

end

plot([data(m-1,1) data(1,1)], [data(m-1,2) data(1,2)],'k','linewidth',3);

for i=1:m-1

rname(i)={['T' num2str(i-1)]};

plot(data(i,1),data(i,2),'o','markeredgecolor','r','markerfacecolor','y','markersize',10); text(data(i,1)-0.05,data(i,2),['\color{black}T'

num2str(i-1)],'fontsize',12,'fontweight','bold','HorizontalAlignment','right')

end

rname(m)={'A0'};

set(handles.uitable1,'data',data,'rowname',rname,'columnname',{'x','y'})