MAKALAH MATEMATIKA DISKRIT II
COUNTING METHODS
INCLUSION-EXCLUSION PRINCIPLE,
DERANGEMENT,
PARITY OF INTEGER, DAN
FUNGSI PEMBANGKIT
Anggota Kelompok 2
1. Deanda Asri A (M0115012) 2. Irsalina Layalia S (M0115020) 3. Satria Adhi Wijaya (M0115038) 4. Uffi Nadzima (M0115044) 5. Zulaichah Intan P (M0115050)
PROGRAM STUDI MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SEBELAS MARET
BAB I
PENDAHULUAN
1.1
Latar Belakang
Matematika diskrit adalah satu cabang ilmu matematika yang mempelajari teori tentang himpunan, induksi matematika, graf, kombinatorial, dan lain-lain. Kombinatorial merupakan cara untuk menghitung jumlah penyusunan objek-objek tanpa harus mengenumerasi semua kemungkinan susunannya. Sebagai sa-lah satu contoh ketika melakukan perhitungan berapa banyak siswa yang mengi-kuti ekstrakurikuler basket, pecinta alam, atau futsal. Dimana 22 siswa mengimengi-kuti ekstrakurikuler basket, 12 siswa mengikuti ekstrakurikuler pecinta alam, 42 siswa mengikuti ekstrakurikuler futsal, dan 8 siswa mengikuti ekstrakurikuler untuk ke tiga pilihan ekstrakurikuler tersebut. Untuk menyelesaikan permasalahan terse-but dapat digunakan prinsip
inclusion-exclusion. Prinsip inclusion-exclusion merupakan perluasan ide dalam diagram venn beserta operasi irisan dan gabungan.
Selanjutnya, prinsip inclusion-exclusion ini akan digunakan untuk menghi-tung permutasi n objek dimana objek tersebut tidak berada pada posisi semula. Contohnya, misalkan Ani memiliki 10 bola dan 10 kotak. Setiap bola diberi label 1,2,3, . . . ,10. Begitu pula dengan kotaknya diberi label 1,2,3, . . . ,10. Ani mena-ruh masing-masing bola ke masing-masing kotak secara acak, sehingga sekarang setiap kotak berisi masing-masing satu bola. Cara menghitung peluang tidak ada satupun label bola dan kotaknya yang cocok ini dapat dikerjakan menggunakan perhitungan probabilitas biasa sehingga diperlukan cara lain untuk mempermu-dah perhitungan. Cara tepat untuk menyelesaikannya adalah menggunakan
derangement.
ba-nyak bilangan dimana salah satunya adalah bilangan integer (bulat). Dalam bilangan bulat terdapat istilah parity of integer dimana membagi bilangan bulat menjadi dua yaitu bilangan genap dan bilangan ganjil. Secara matematis dapat ditulis untuk bilangan genap dinotasikann = 2k dan bilangan ganjil dinotasikan
n= 2k+ 1.
Matematika diskrit mempunyai cabang ilmu yang dapat menyelesaikan per-masalahan dibidang matematika sepertipower series, penyelesaian relasi rekursif, dan pembuktian fungsi identitas. Ilmu tersebut adalah fungsi pembangkit. Me-nurut Rosen [2], fungsi pembangkit digunakan untuk menyajikan barisan secara ringkas dengan mengkodekan unsur dari suatu barisan sebagai koefisien dalam deret pangkat suatu variabel.
Pada makalah ini, akan dibahas mengenai prinsip - prinsip yang bisa di-gunakan untuk menyelesaikan masalah matematika yang tidak bisa diselesaikan dengan prinsip - prinsip perhitungan biasa. Adapun prinsip - prinsip tersebut, yaituinclusion-exclusion, derangement, parity of integer,dan fungsi pembangkit.
1.2
Perumusan Masalah
Berdasarkan uraian pada latar belakang masalah dapat ditulisakan lima rumusan masalah, yaitu
1. bagaimana konsep dan rumus umum prinsip inclusion-exclusion,
2. bagaimana konsep dan rumus umum derangement,
3. bagaimana konsep dan sifat parity of integer,
4. bagaimana konsep dan sifat fungsi pembangkit, dan
5. bagaimana kasus dari prinsip inclusion-exclusion, derangement, parity of integer, dan fungsi pembangkit.
1.3
Tujuan
1. mengetahui konsep dan rumus umum prinsip inclusion-exclusion,
2. mengetahui konsep dan rumus umum derangement,
3. mengetahui konsep dan sifat parity of integer,
4. mengetahui konsep dan sifat fungsi pembangkit, dan
5. dapat menerapkan kasus dari prinsip inclusion-exclusion, derangement,
BAB II
LANDASAN TEORI
2.1
Prinsip
Inclusion-Exclusion
Diberikan beberapa definisi dan teorema yang berhubungan dengan prinsip
inclusion-exclusion yang diambil dari Munir [1].
Definisi 2.1.1. Himpunan (set) adalah kumpulan objek-objek yang berbeda dan tidak berurutan.
Definisi 2.1.2. Jumlah elemen dalam A disebut kardinal dari A. Kardinalitas dari himpunan A dinotasikan |A|.
Definisi 2.1.3. Irisan (intersection) dari himpunan A dan B adalah himpunan yang setiap elemennya merupakan elemen dari himpunan A dan himpunan B.
Irisan dari himpunan A dan B dapat dinotasikan A∩B.
Definisi 2.1.4. Gabungan (union) dari himpunan A dan B adalah himpunan yang setiap anggotanya merupakan anggota himpunan A atau B. Gabungan dari
himpunan A dan B dapat dinotasikan A∪B.
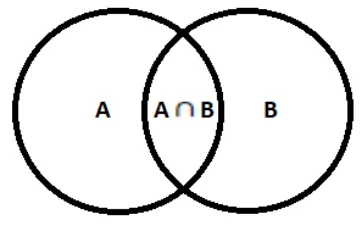
Himpunan A dan B dikatakan disjoint apabila tidak mempunyai irisan, sedangkan himpunanA dan B dikatakan nondisjoint apabila mempunyai irisan. Misal A dan B adalah sebarang himpunan nondisjoint pasti himpunan A dan himpunan B mempunyai elemen bersama. Jumlah elemen bersama antara A
dan B adalah |A∩B|. Menghitung jumlah elemen gabungan himpunan A dan
B yang nondisjoint dapat dilakukan dengan cara menjumlahkan elemen-elemen pada kedua himpunan dikurangi dengan jumlah elemen pada irisannya sehingga berlaku
Gambar 2.1. Himpunan Nondisjoint A dan B
Himpunan A dan B yang nondisjoint dapat ditunjukan pada Gambar 2.1, sedangkan untuk sebarang himpunan A dan himpunan B yang disjoint yaitu irisan dari dua himpunan atau lebihnya kosong berlaku
|A∪B|=|A|+|B|
.
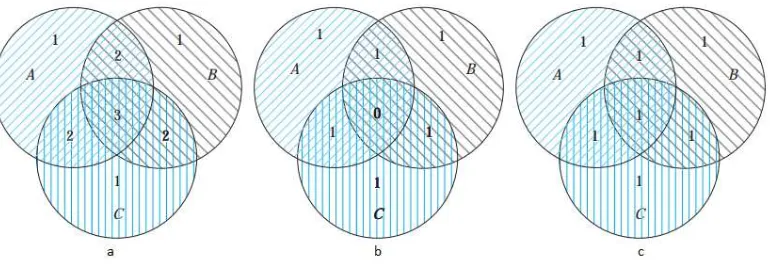
Gambar 2.2. Himpunan Nondisjoint A, B, dan C
Himpunan A,B, dan C yang nondisjoint dapat ditunjukkan pada Gambar 2.2. Dengan memperluas hasil persamaan (2.1) dapat diperoleh untuk sebarang tiga himpunan A, B, dan C berlaku persamaan (2.2) yang diilustrasikan pada Gambar 2.3.
Gambar 2.3. Jumlah Elemen dengan (a)|A|+|B|+|C|, (b)|A|+|B|+|C| − |A∩
B|−|B∩C|−|A∩C|, dan (c)|A|+|B|+|C|−|A∩B|−|B∩C|−|A∩C|+|A∩B∩C|
Menurut Rosen [2], prinsip inclusion-exclusion dinyatakan dalam Teorema 2.1.1 yang menyatakan banyaknya elemen suatu gabungan himpunan terbatas.
Teorema 2.1.1. Misalkan A1, A2, . . . An adalah himpunan berhingga maka
ben-tuk umum prinsip inclusion-exclusion dapat dinyatakan dengan
|A1∪A2∪. . .∪An| =
∑
1≤i≤n
|Ai| −
∑
1≤j≤n
|Ai∩Aj|+
∑
1<j<k≤n
|Ai∩Aj∩Ak|
+. . .+ (−1)n−1
|A1∩A2∩. . .∩An|.
Bukti. Akan dibuktikan bahwa setiap elemen dihitung tepat sekali pada sisi ka-nan persamaan. Anggap a adalah elemen dari tepat r himpunan A1, A2, . . . , An dimana 1≤r ≤n. Elemenadihitung sebanyakC(r,1) kali dari∑
|Ai|, dihitung sebanyak C(r,2) kali dari ∑
|Ai∩Aj|. Secara umum, dihitung sebanyak C(r, m) kali dari penjumlahan m himpunan Ai. Dengan demikian, elemen a dihitung dengan
C(r,1)−C(r,2) +C(r,3)−. . .+ (−1)r+1
C(r, r)
kali pada sisi kanan persamaan. Dengan menggunakan n
∑
k=0
(−1)k(n
k) = 0 maka
C(r,0)−C(r,1) +C(r,2)−. . .+ (−1)rC(r, r) = 0
oleh karena itu,
1 = C(r,0) =C(r,1)−C(r,2) +C(r,3)−. . .+ (−1)r+1
Sedemikian hingga untuk setiap elemen gabungan himpunanA1, A2, . . . , An dihitung tepat sekali pada sisi kanan persamaan. Jadi, prinsipinclusion-exclusion
terbukti.
2.2
Derangement
Diberikan definisi dan teorema yang berhubungan dengan prinsip
derangement yang diambil dari Rosen [2].
Definisi 2.2.1. Derangement adalah permutasi dari suatu objek dimana objek tersebut tidak berada pada posisi seharusnya atau telah berubah dari posisi semula.
Menurut Rosen [2], permutasi 21453 adalahderangement dari 12345 karena tidak ada angka yang berada di posisi semula. Akan tetapi, 21543 bukan meru-pakan derangement dari 12345 karena terdapat angka yang berada pada posisi semula yaitu angka 4. Dalam kasus ini akan digunakan prinsipinclusion-exclusion
untuk menghitung banyaknya derangement tersebut.
Misalkan Dn adalah notasi dari jumlah banyaknya derangement dari n ob-jek. Contohnya,D3 = 2 karena derangement dari 123 adalah 231 dan 312. Akan
ditentukan Dn, untuk semua bilangan positifn menggunakan prinsip
inclusion-exclusion
Teorema 2.2.1. Banyaknya derangement dari suatu himpunan dengann elemen adalah
Dn=n!
[
1− 1
1! + 1 2! −
1
3! +. . .+ (−1) n1
1!
]
Bukti. Misalkan permutasi Pi merupakan sifat dimana permutasi dari n objek mempunyai bilangan bulat i yang ditempatkan pada posisi ke i. Banyaknya
derangement adalah banyaknya permutasi dimana tidak terdapat sifat Pi untuk setiap i= 1,2,3, . . . , n dapat dituliskan
Dn =N(P1′, P
′
2, . . . , P
′
Dengan menggunakan prinsipinclusion-exclusion diperoleh
Diketahui N =n!, karena N adalah banyak permutasi dari n elemen. Ke-mudian, diasumsikan bahwaN(Pi) = (n−1)! karenaN(Pi) merupakan banyaknya permutasi dengan elemen i berada pada posisinya sehingga posisi ke-i dari per-mutasi telah ditentukan, tetapi untuk elemen lainnya posisi dapat disusun secara sebarang. Dengan cara yang sama diperoleh
N(PiPj) = (n−2)!
karena N(PiPj) merupakan banyaknya permutasi dengan elemen i dan j yang berada pada posisinya tetapi untuk n−2 elemen lain posisinya dapat disusun secara sebarang. Secara umum dapat dituliskan
N(P1P2. . . Pm) = (n−m)!
diketahuiN(P1P2...Pm) merupakan banyaknya permutasi dengan elemeni1, i2, . . . ,
im yang berada pada posisinya tetapi untuk n−m elemen lain posisinya dapat disusun secara sebarang. Karena C(n, m) cara untuk memlih m elemen dari n
elemen berlaku
Secara umum dapat dituliskan
∑
1≤i1<i2<...<im≤n
N(P1P2. . . Pm) = C(n, m)(n−m)!.
Persamaan (2.7) dapat disederhanakan menjadi
Dn=n!
[
1− 1
1! + 1 2! −
1
3! +. . .+ (−1) n 1
n!
]
sehingga dapat ditentukan Dn untuk setiap bilangan bulatn.
2.3
Parity of Integer
Diberikan definisi dan beberapa teorema yang berhubungan dengan prinsip
parity of integer yang diambil dari Susanna [3].
Teorema 2.3.1. Untuk sebarang bilangan bulat n dan sebarang bilangan bulat positif d, terdapat bilangan bulat q dan r sedemikian sehingga
n=dq+r dan 0≤r < d.
Bukti. Misalkan S adalah himpunan bilangan bulat nonnegatif berbentukn−dk
dengank adalah bilangan bulat. Himpunan ini mempunyai satu elemen terkecil. Jikannonnegatif makan−0.d=n ≥0 sehinggan−0.d∈S. Jikannegatif maka n−nd = n(1−d) ≥ 0 dengan n < 0 dan (1−d) ≤ 0 karena d adalah bilangan bulat positif sehingga n−nd∈S.
Menurutwell-ordering principle,Smemiliki elemen terkecil yaitursehingga untuk suatu bilangan bulat k=q, diperoleh persamaan
n−dq=r (2.8)
karena setiap bilangan bulat di dalamSdapat dituliskan dalam bentuk persama-an (2.8). Jika ditambahkan dq pada kedua ruas persamaan (2.8) maka diperoleh
n =dq+r.
Kemudian akan dibuktikan r < d. Misalkan r≥d diperoleh
n−d(q+ 1) =n−dq−d=r−d≥0,
menunjukkan bahwa pengandaian r ≥ d salah. Jadi, terbukti bahwa terdapat bilangan bulat r dan q yang memenuhi
n =dq+r dan 0≤r < d.
Definisi 2.3.1. Untuk bilangan bulat n dan bilangan bulat positif d, berlaku
ndivd = hasil bagi bilangan bulat yang diperoleh ketika n dibagi dengan d nmodd = sisa hasil bagi bilangan bulat nonnegatif yang diperoleh ketika n
dibagi dengan d.
Secara matematis, jika n dan d adalah bilangan bulat dan d >0 maka
n div d=q dan n mod d=r⇔n =dq+r.
Dimana q dan r adalah bilangan bulat dan 0≤r < d.
Diambil sebarang bilangan bulatndengann dapat dibagi 2. Menggunakan Teorema 2.3.1 (d = 2) terdapat bilangan bulat q dan r sehingga n dapat ditulis menjadi n = 2q+r untuk 0 ≤r < 2. Bilangan bulat yang memenuhi pertidak-samaan 0 ≤ r < 2 adalah r = 0 dan r = 1 sehingga untuk sebarang bilangan bulat n terdapat bilangan bulat q dengan n = 2q+ 0 atau n = 2q+ 1. Dalam permasalahan ini, n = 2q+ 0 = 2q, n adalah genap dan n = 2q+ 1, n adalah ganjil.
Menurut Susanna [3], parity of integer memuat dua kemungkinan bilangan bulat, yaitu bilangan bulat itu genap ataupun ganjil. Misalnya, 5 merupakan bilangan bulat ganjil dan 28 merupakan bilangan bulat genap.
Teorema 2.3.2. Untuk sebarang dua bilangan bulat yang saling berurutan mem-punyai paritas yang saling berlawanan.
1. Kasus 1 (m genap)
Dalam kasus ini m dapat dibentuk menjadi m = 2k untuk suatu bilangan bulatk sehingga m+ 1 = 2k+ 1. Akibatnya, m+ 1 adalah ganjil (menurut definisi bilangan ganjil). Oleh karena itu, jikamgenap maka bilangan bulat selanjutnya, m+ 1 adalah ganjil.
2. Kasus 2 (m ganjil)
Dalam kasus ini, m dapat dibentuk menjadi m = 2k + 1 untuk suatu k
bilangan bulat sehinggam+1 = (2k+1)+1 = 2k+2 = 2(k+1) dengank+1 adalah bilangan bulat (penjumalahan dua bilangan bulat adalah bilangan bulat) sehingga m+ 1 sama dengan dua kali bilangan bulat. Jadi, m+ 1 merupakan bilangan genap. Oleh karena itu, pada kasus ini berlaku salah satu dari m dan m+ 1 adalah genap serta yang lain adalah ganjil.
Dari 1 dan 2 terbukti bahwa untuk sebarang dua bilangan bulat yang saling berurutan mempunyai paritas yang saling berlawanan.
Teorema 2.3.3. Kuadrat dari sebarang bilangan bulat ganjil dapat dibentuk men-jadi 8m+ 1 untuk suatu bilangan bulat m.
Bukti. Ambil sebarang bilangan bulat ganjil n. Dengan menggunakan Teorema 2.3.1,ndapat ditulis dengan salah satu bentuk berikut, 4qatau 4q+1 atau 4q+2 atau 4q+ 3 untuk suatu bilangan bulatq. Karenan adalah bilangan bulat ganjil,
n harus merupakan salah satu dari 4q+ 1 atau 4q+ 3.
1. Kasus 1 (n= 4q+ 1 untuk suatu q bilangan bulat)
Akan dicari bilangan bulat m sedemikian sehingga n2
= 8m+ 1. Karena
n= 4q+ 1 diperoleh
n2 = (4q+ 1)2
= (4q+ 1)(4q+ 1) = 16q2 + 8q+ 1 = 8(2q2+q) + 1
dengan m = 2q2
+q, m bilangan bulat. Jadi, untuk n = 4q+ 1, kuadrat dari n dapat dibentuk menjadi n2
= 8(2q2
+q) + 1 = 8m+ 1 dengan m
adalah bilangan bulat.
2. Kasus 2 (n= 4q+ 3 untuk suatu q bilangan bulat)
Akan dicari bilangan bulat m sedemikian sehinggan2
= 8m+ 1.
n2
= (4q+ 3)2
= (4q+ 3)(4q+ 3) = 16q2
+ 24q+ 9 = 8(2q2
+ 3q+ 1) + 1
n2
= 8m+ 1
denganm = 2q2
+ 3q+ 1, m bilangan bulat.
Jadi, untuk n= 4q+ 3, kuadrat dari n dapat dibentuk menjadi
n2
= 8(2q2
+ 3q+ 1) + 1.
Dari 1 dan 2 terbukti bahwa kuadrat dari sebarang bilangan bulat ganjil dapat dibentuk menjadi 8m+ 1 untuk suatu bilangan bulat m.
2.4
Fungsi Pembangkit
Fungsi pembangkit dikembangkan untuk menyelesaikan masalah-masalah pemilihan dan penyusunan objek dengan pengulangan serta tidak memperhatikan urutan.
Definisi 2.4.1. Fungsi pembangkit dari barisan bilangan reala0, a1, a2, . . . , ak, . . .
bisa dituliskan dalam bentuk
G(x) = a0+a1x+a2x
Pada Definisi 2.4.1 tersebut, fungsi pembangkit untuk ak biasa disebut
ordinary generating function. Deret tersebut merupakan pangkat dari variabel x, dengan x adalah suatu indikator sehingga koefisien dari xk adalah harga fungsi padak. Sedangkan, sebuah fungsi dalam deret bilangan real ak dapat disederha-nakan dengan fungsi pembangkitnya.
2.4.1
Fungsi Pembangkit pada
Power Series
BAB III
PEMBAHASAN
Pada pembahasan berikut diberikan beberapa contoh soal serta penyelesa-iannya dengan menggunakan inclusion-ixclusion, derangement, parity of integer, dan fungsi pembangkit. Contoh soal diambil dari Rosen [2].
1. Terdapat 2504 mahasiswa Ilmu Komputer di sebuah kampus. Sebanyak 1876 mahasiswa mengikuti kuliah Java, 999 mahasiswa mengikuti kuliah Linux, 345 mahasiswa mengikuti kuliah C, 876 mahasiswa mengikuti kuli-ah Java dan Linux, 231 mkuli-ahasiswa mengikuti kulikuli-ah Linux dan C, dan 290 mahasiswa mengikuti kuliah Java dan C. Jika 189 mahasiswa mengambil kuliah pada ketiganya (Java, Linux, dan C) maka berapa banyak dari 2504 mahasiswa yang belum mengikuti kuliahprogramming language pada keti-ganya?
Penyelesaian: Misal dinotasikan
S = himpunan seluruh mahasiswa ilmu komputer,
X = himpunan mahasiswa yang mengikuti kuliah Java,
Y = himpunan mahasiswa yang mengikuti kuliah Linux,
Z = himpunan mahasiswa yang mengikuti kuliah C, dan
N = himpunan mahasiswa yang tidak mengambil ketiganya.
Sehingga |S| = 2504; |X| = 1876; |Y| = 999; |Z| = 345; |X ∩Y| = 876;
maka
Jadi, mahasiswa yang belum mengikuti kuliahprogramming language pada ketiganya sebanyak 492 mahasiswa.
2. Sebuah mesin yang bekerja untuk memasukkan surat ke dalam amplop tiba-tiba rusak sehingga mesin tersebut memasukkan surat secara acak ke dalam amplop. Apabila terdapat 7 surat maka berapa banyak cara agar:
a. tidak ada surat yang dimasukkan ke dalam amplop yang benar dan
b. terdapat 5 surat yang dimasukkan ke dalam amplop yang benar.
Penyelesaian: Dengan menggunakan konsepinclusion-exclusion banyaknya cara semua surat dimasukkan ke dalam amplop yang benar dapat dicari menggunakan rumus derangement
a. Tidak ada surat yang dimasukkan ke dalam amplop yang benar. Terdapat 7 surat berarti n= 7 sehingga diperoleh
Jadi, terdapat 1854 cara semua surat tidak dimasukkan ke dalam am-plop yang benar.
b. Terdapat 5 surat yang dimasukkan ke dalam amplop yang benar. Terdapat 7 surat. Jika diinginkan terdapat tepat 5 surat yang dima-sukkan ke dalam amplop yang benar berartin= 7−5 = 2.
Banyak cara memasukkan 5 surat ke dalam amplop yang benar adalah
C(7,5) = 21. Misal banyak cara adalah X1 maka diperoleh
X1 = C(7,5)D2
= 21(2!)
[
1− 1
1!+ 1 2!
]
= 21(2)
[
1− 1
1+ 1 2
]
= 21 cara.
Jadi, terdapat 21 cara semua surat dimasukkan ke dalam amplop di-mana terdapat tepat 5 surat yang dimasukkan ke dalam amplop yang benar.
3. Buktikan bahwa jika n adalah bilangan bulat dan 3n+ 2 ganjil, maka n
ganjil!
Penyelesaian:
Bukti. Pertama akan dicoba dengan menggunakan pembuktian langsung. Untuk mengkonstruksikan pembuktian langsung, diasumsikan bahwa 3n+2 adalah bilangan bulat ganjil. Berarti 3n+2 = 2k+1 untuk beberapa bilang-an bulat k, sehingga tidak dapat dilakukan dengan pembuktian langsung. Karena pembuktian langsung gagal selanjutnya akan dicoba dibuktikan de-ngan menggunakan kontraposisi.
sebarang k bilangan bulat. Subtitusi 2k sebagai n, diperoleh genap, karena merupakan kelipatan 2 dan bukan ganjil. Tetapi kontradiksi dengan yang diketahui. Sehingga asumsi salah. Dengan demikian terbukti jika n adalah bilangan bulat dan 3n+ 2 ganjil, maka n ganjil.
4. Carilah fungsi pembangkit dari barisan 1,4,16,64,256! Penyelesaian :
Menurut Definisi 2.4.1, jika terdapat barisan bilang reala0, a1, a2, . . . , ak,. . . ,
maka fungsi pembangkitnya dapat dituliskan dalam bentuk
G(x) = a0+a1x+a2x 2
+. . .+akxk+. . . .
Karena barisan bilangan tersebut terbatas, sehingga dapat dituliskan
G(x) =a0+a1x+a2x 2
+. . .+akxk.
Maka fungsi pembangkit dari barisan bilangan 1,4,16,64,256 adalah
G(x) = 1 + 4x+ 16x2+ 64x3+ 256x4.
Jadi, fungsi pembangkit dari barisan bilangan 1,4,16,64,256 adalah
G(x) =
4
∑
k=0
BAB IV
KESIMPULAN
Dari pembahasan didapatkan kesimpulan sebagai berikut.
1. Rumus umum inclusion-exclusion principle adalah
|A1∪A2∪. . .∪An| =
2. Derangement adalah permutasi dari suatu objek dimana objek tersebut tidak berada pada posisi semula. Rumus umum derangement adalah
Dn =n!
3. Parity of integer memuat dua kemungkinan yaitu apakah bilangan bulat tersebut genap atau ganjil. Rumus umum parity of integer adalah
n =dq+r dan 0≤r < d.
5. Inclusion-exclusion principle dapat diterapkan pada contoh soal nomor 1,
derangement dapat diterapkan pada contoh soal nomor 2, parity of integer
DAFTAR PUSTAKA
[1] Munir, R., Matematika Diskrit, 3rd., Informatika, Bandung, 2007.
[2] Rosen, K. H., Discrete Mathematics and Its Applications, 7th ed., McGraw-Hill, New York, 2012.
4.1
Job Description
Nama Job Description
Deanda Asri A Fungsi pembangkit dan pembahasannya, penyusunan makalah, dan proofreading
Irsalina Layalia S Derangement dan pembahasannya, penyusunan slide
presentasi, dan proofreading
Satria Adhi W Parity of integer dan pembahasannya, penyusunan makalah, dan proofreading
Uffi Nadzima Inclusion-Exclusion principle dan pembahasannya, penyusunan makalah, dan proofreading