Materi :
Menghitung nilai optimum (maksimum / minimum) dari
sistem pertidaksamaan linier.
LEMBAR KEGIATAN SISWA 4
Kelas :………
Kelompok :………..
Nama Anggota :………
Kalian telah mempelajari cara membuat grafik dari sisem
pertidaksamaan linier dua variabel, daerah penyelesaian sistem
pertidaksamaan linier dua variabel, dan model matematika. Pada
pertemuan ini kalian akan mempelajari materi program linier yaitu cara
menghitung nilai maksimum/minimum (optimum) fungsi obyektif.
Tujuan Pembelajaran :
Siswa dapat menghitung nilai maksimum/minimum (optimum) fungsi sasaran dari daerah sistem pertidaksamaan linier.
Pengantar
Dalam LKS ini kalian akan diberi suatu masalah, untuk menyelesaikan masalah
tersebut perlu kalian ikuti langkah-langkah berikut ini :
1. Ubahlah persoalan verbal ke dalam model matematika (dalam bentuk
sistem pertidaksamaan linier)
2. Buatlah grafik dari sistem petidaksamaan linier
3. Tentukan himpunan penyelesaian ( daerah penyelesaian)
4. Tentukan semua titik-titik pojok pada daerah penyelesaian tersebut
untuk mencari nilai maksimum/minimum (optimum)
5. Langkah ke 4 tidak selalu bisa digunakan, hal ini disebabkan antara lain
jika koordinat titik pojok bukan merupakan bilangan bulat.
Pada waktu SMP, kalian telah belajar cara menghitung nilai sebuah
fungsi. Masih ingatkah kalian cara menghitung nilai fungsi tersebut?
At junior higt school, you have learned about arithmetic a value of
function. Do you remember about arithmetic a value of function?
1. Perhatikan fungsi f(x , y) = 3x + 2y, dapatkah kalian mencari nilai
fungsi tersebut, jika diketahui :
a. x = 4 , y = 4
b. x = 5 , y = 1
c. x = 2 , y = 8
2. Diketaui fungsi f(x , y) = 4x + 5y, dapatkah kalian mencari nilai fungsi
tersebut untuk:
a. x = 5 , y = 2
b. x = 3 , y = 1
c. x = 1 , y = 7
Masalah 1
Unit Produksi SMK N 6 Surabaya mempunyai modal Rp 1.200.000
Pengurus unit produksi merencanakan membuat cake nanas dan angel
cake. Modal untuk membuat cake nanas Rp 30.000,00 per Loyang dan
angel cake Rp 20.000,00 per Loyang. Keuntungan dari penjualan cake
nanas Rp 6.000,00 per loyang dan keuntungan dari penjualan angel cake
Rp 4.000,00 per Loyang.
Mengingat kapasitas oven sangat terbatas, maka pengurus hanya
bisa membuat sebanyak-banyaknya 50 loyang cake.
1. Ubahlah kedalam model matematika (dalam bentuk sistem
pertidaksamaan linier) dari masalah diatas!
2. Tentukan himpunan penyelesaian (daerah penyelesaian ) dari sistem pertidaksaan linier di atas!
x y
3. Perhatikan titik-titik pojok yang ada pada daerah penyelesaian. Pilih beberapa titik dan kemudian tentukan keuntungan yang diperoleh jika banyak roti yang dibuat sesuai dengan koordinat titik-titik tersebut.
Tulislah titik pojok tersebut dengan mengecualikan titik (0,0). Tulislah titik-titik pojok tersebut!
4. Subtitusikan nilai x dan y dari masing-masing titik pada fungsi obyektif dan carilah nilai yang terbesar.
Bisakah kamu memberi alas an mengapa untuk menentukan keuntungan maksimum masalah diatas bisa dilihat dari titik pojoknya?
5. Hitunglah keuntungan maksimum Unit Produksi SMK N 6 surabaya. Diskusikan dengan teman kelompokmu.
6. Berikutnya jika diketahui keuntungan yang diperoleh dari penjualan cake gulung pelangi adalah Rp 5000,00 dan brownis kukus Rp 6000,00, maka tentukan berapa banyak cake gulung pelangi dan brownis kukus harus diproduksi agar diperoleh keuntungan maksimum! Bagaimana caramu menentukan?
Penting : Jawab :
Fungsi Obyektif : Nilai fungsi :
Untuk menyelesaikan masalah 1, cara yang digunakan adalah memanfatkan titik-titik pojok dalam mencari nilai maksimum, tetapi ingat cara tersebut tidak selalu menghasilkan jawaban yang benar, perhatikan masalah 2 berikut ini.
Masalah 2
Unit produksi SMK N 6 Surabaya bekerjasama dengan jurusan dalam melakukan kegiatan produksinya. Kegiatan produksi tersebut banyak melibatkan siswa, dan hasil produksi di jual dilingkungan sekolah. Misalnya, dalam memproduksi dua jenis roti (roti pia kacang ijo dan roti muffin). Untuk membuat roti pia kacang ijo membutuhkan 250 gram tepung terigu dan 50 gram gula putih, sedangkan untuk membuat roti muffin membutuhkan 250 gram tepung terigu dan 25 gram gula putih. Unit produksi mempunyai persediaan tepung terigu 20 kg dan gula putih 15 kg. Keuntungan dari penjualan roti pia kacang ijo Rp 750,00 dan keuntungan roti sosis keju Rp 1000,00.
Tentukan tiap-tiap jenis roti yang harus dibuat supaya didapat hasil keuntungan yang maksimum dan tentukan pula keuntungan maksimum tersebut.
1. Ubahlah kedalam model matematika (dalam bentuk sistem pertidaksamaan linier) dari masalah diatas!
2. Tentukan daerah penyelesaian dari sistem pertidaksamaan linier di atas!
3. Tunjukan fungsi obyektif dari masalah 2.
4. Tentukan keuntungan maksimum dengan menggunakan titik-titik pojok. Apa yang kalian peroleh?
Catatan :
Kalian tidak akan bisa menggunakan cara yang sama seperti pada masalah 1. Kali ini kalian bisa menggunakan titik-titik disekitar titik pojok dari fungsi obyektif, sehingga kalian menemukan koordinat yang sesuai untuk mendapatkan keuntungan maksimum.
5. Hitunglah keuntungan maksimum unit produksi SMK N 6 Surabya. Diskusikan dengan teman kelompokmu.
x y
6. Berikutnya jika diketahui keuntungan yang diperoleh dari penjualan pia kacang ijo adalah Rp 750,00 dan roti sosis keju Rp 1000,00, maka tentukan berapa banyak roti pia kacang ijo dan roti sosis keju harus diproduksi agar diperoleh keuntungan maksimum! Bagaimana caramu menentukan?
Latihan
1. Diketahui model matematika: 2x – 5y ≤10 ; x + y ≥ 5; x + y ≤ 12; -5x + 2y ≤ 10. Tentukan nilai maksimum fungsi obyektif P = 3x + 4y.
2. Tentukan nilai maksimum dan minimum P = 3x + 2y, dari daerah penyelesaian berikut.
y
0 x
3. Tentukan nilai maksimum dari fungsi obyektif P = 3x + 5y, yang memenuhi sistem petidaksamaan linier:
x + y ≤ 4 x + 2y ≤ 6 x ≥ 0 y ≥0
4. Tentukan nilai minimum dari fungsi obyektif P = 5x + 7y, yang memenuhi sistem pertidaksamaan linier: x + 2y ≥ 8 3x + 2y ≥ 12 x ≥ 0 y ≥ 0 (1,4) (6,2) (8,6) (3,8)
5. Unit Produksi SMK N 6 Surabaya mempunyai persediaan tepung terigu 9
kg dan mentega 5 kg. Dengan persediaan bahan yang ada unit produksi
tersebut akan membuat cake gulung pelagi dan brownis kukus. Untuk
membuat cake gulung pelangi membutuhkan 150 gr tepung terigu dan
50 gram mentega, sedangkan untuk brownis kukus membutuhkan 75
gram tepung terigu dan 75 gram mentega.
Keuntungan yang diperoleh dari hasil penjualan cake gulung pelagi dan
brownis kukus masing-masing Rp 5000,00 dan Rp 5000,00. Tentukan
tiap-tiap jenis roti yang harus dibuat supaya didapat hasil keuntungan
yang maksimum.
Alternatif jawaban 1. a. 20 b. 17 c. 22 2. a. 30 b. 17 c. 39 Masalah 1 1. Model matematika : 3x + 2y ≤ 120 x + y ≤ 50 x ≥ 0 y ≥ 0
2. Grafik model matematika
Daerah penyelesaian menggambarkan semua kemungkinan banyaknya cake yang bisa dibuat oleh pengurus unit produksi dengan memperhatikan semua kondisi yang dimiliki yaitu modal dan oven untuk memanggang.
x y
3. Titik-titik pojok : (0 , 50) ; ( 20 , 30) ; (40 , 0) 4. Fungsi obyeltif Z = 6000x + 4000y Z1 = 200.000 Z2 = 240.000 nilai terbesar Z3 = 16.000
Masalah 2
1. Model matematikaRoti muffin Roti pia kacang ijo Persediaan bahan
Tepung terigu 250 250 20.000 Gula putih 50 25 3400 Keuntungan 500 500 x + y ≤ 80 2x + y ≤ 136 x ≥ 0 y ≥ 0 2. Grafik penyelesaian x y
3. Fungsi obyektif : Z = 500x + 500y
4. Titik-titik pojok tidak terletak pada koordinat dengan bilangan bulat. 5. Nilai fungsi yang memenuhi
Z = 500 (50) + 500 ( 30) = 40.000
6. Dengan membuat grafik garis-garis yang sejajar fungsi objektif dan menentukan nilai maksimum pada daerah penyelesaian dari sistem pertidaksamaan.
Latihan
1. Grafik dari sistem pertidaksamaan
Nilai maksimal : P = 3x + 4y = 46 x y x + y = 5
2. Nilai maksimum : P = 3x + 2y = 36 Nilai minimum : P = 3x + 2y = 11
3. Grafik sistem pertidaksamaan
Nilai maksimum P = 3x + 5y = 16
4. Grafik sistem pertidaksamaa
x y
x y
Nilai minimum: P = 5x + 7y = 31
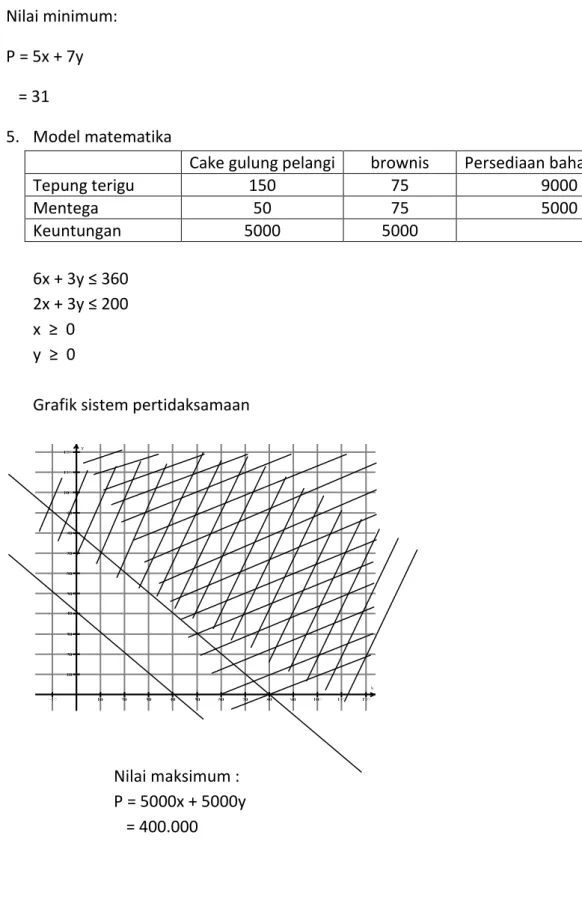
5. Model matematika
Cake gulung pelangi brownis Persediaan bahan
Tepung terigu 150 75 9000 Mentega 50 75 5000 Keuntungan 5000 5000 6x + 3y ≤ 360 2x + 3y ≤ 200 x ≥ 0 y ≥ 0
Grafik sistem pertidaksamaan
Nilai maksimum : P = 5000x + 5000y = 400.000
x y