trigonometri.docx 43KB Apr 25 2011 02:14:08 AM

TRIGONOMETRI

1

. Perbandingan Trigonometri dan Teorema Pythagoras

a. Teorema Pythagoras

Apabila diketahui panjang dua sisi suatu segitiga siku-siku, maka panjang sisi yang ketiga dapat dihitung menggunakan teorema Pythagoras.

Panjang hipotenusa sama dengan jumlah pada kedua sisi siku-siku segitiga.

AB2 _{= AC}2 _{+ BC}2

Perhatikan gambar disamping:

ABC siku-siku di C, lika besar

sudut ABC = α (alfa), maka:

sin α : sisidepan sudut

sisi miring = b

c cosec α :

sisi miring sisidepan sudut

= c_b

cos α : sisi samping sudut

sisimiring = a

c sec α :

sisimiring

sisi samping sudut = a c

tan α : _{sisi samping sudut}sisidepan sudut = b_a cotan α :

sisidepan sudut sisi miring =

b c

B

b c

c

A

contoh:

1. Di titik R (8, 15) membentuk sudut α, tentukan sec α

Jawab:

sec α : sisimiring

sisi samping sudut = r x

r2 _{= x}2 _{+ y}2

= 82 _{+ 15}2

= 64 + 225

=

√

289

r = 17

jadi, sec α : sisimiring

sisi samping sudut = r x =

17 8

2. Nilai Perbandingan Trigonometri untuk Sudut Istimewa

sudut sin cos tan

o◦ 0 1 0

30◦ 1

2

√

23

√

3 3 45◦

_√

2

2

√

2 2

1

60◦

_√

3 2

1

2

√

3

90◦ 1 0 ᷈᷈

r _{Y = 15}

Contoh:

Buktikan sin2_{45 + cos}2_{45 = 1}

jawab:

sin2_{45 + cos}2_{45 = 1}

(½

√

2 )2 _{+ (½}

_√

_{2 )}2 _{= 1}

¼ 2 + ¼ 2 = 1

2/4 + 2/4 = 1

4/4=1

Terbukti, sin2_{45 + cos}2_{45 = 1}

3. Perbandingan Trigonometri dalam Kuadran

Kuadran I

α

α α

α

y = +

y =

-Y = +

Y =

-R = +

R = +

R = +

R = + X=-

X=+

Kuadran II Kuadran I

Perbandingan

Trigonometri _{I II} Kuadran _{III IV}

Sin α + + -

-Cosα + - - +

tan α + - +

-Cosec α + + -

-sec α + - - +

cotan α + - +

-Contoh:

Cos α = -4/5 dan tan α positif, berapa nilai sin...

y2 _{= r}2 _{- x}2

= 52 _{- (-4}2₎

= 25 – 16

=

√

9

y = -3

sin α = sisidepan sudut

sisi miring = y r

= −3 5

4. Identitas Trigonometri

Perhatikan gambar berikut

y r

x y=?

r =5 X= -4

sin α : sisidepan sudut

sisi miring = y

r cosec α :

sisi miring

sisidepan sudut = r y

cos α : sisi samping sudut_sisimiring = x_r sec α :

sisimiring

sisi samping sudut = r x

tan α : _{sisi samping sudut}sisidepan sudut = y_x cotan α :

sisidepan sudut sisi miring =

x y

a. Hubungan antarpembanding

1) cosec α = 1 sinα

bukti :

cosec α = _sin1_α

cosec α = 1

y/r = r y

2) sec α = _cos1_α

Bukti:

sec α = _cos1_α

sec α = 1

x/r = r x

3) cotan α = _tan1_α

cotan α = 1 tanα

cotanα= _y1 /x =

x y

b. Identitas dari Hubungan Teorema Pythagoras (x2 _{+ y}2 _{= r}2 ₎

x2 _{+ y}2 _{= r}2 _{(sama-sama dibagi r}2₎

x2 _{/ r}2 _{+ y}2 _{/ r}2 _{= r}2 _{/ r}2

x2 _{/ r}2 _{+ y}2 _{/ r}2 _{= 1}

cos2 α + sin2 _{α = 1}

x 2 _{+ y} 2 _{= r}2 _{(sama- sama di bagi y}2₎

x2 _{/ y}2 _{+ y}2 _{/ y}2 _{= y}2 _{/ y}2

x2 _{/ y}2 _{+ y}2 _{/ y}2 _{= 1}

contoh :

1) Buktikan:

a) sinα

cosα = tan α

jawab:

sinα

cosα = y r :

x r =

y

x = tan α

b) cosα

sinα = cotan α

jawab:

cosα

sinα = x r :

y r =

y

x = cotan α

2) jika 2 sin2 _{x + 3 cos x = 0 dan 0}° _{< x < 180° maka nilai x adalah...}

Jawab :

2 sin2 _{x + 3 cos x = 0}

2(1- cos2 _{x) + 3 cos x = 0}

2cos2 _{x - - 3 cos x - 2 = 0}

(2 cos x + 1 ) ( cos x – 2 ) = 0

Cos x = - 1₂ cos x = 2 (tidak memenuhi)

= 120°

Maka nilai x = 120°

3) Dari pertidaksamaan berikut sinx . sin2 _{x + cos}2_{x < ½ berapakah nilai}

dari x

sinx . sin2 _{x + cos}2_{x < ½}

sin x .(sin2 _{x + cos}2_{x) < ½}

sin x . 1 < ½

sin x < ½

x< 30°

5. Fungsi Trigonometri

Perbandigan trigonometri dari suatu sudut tertentu terdapat tepat satu nilai dari Sinus, Cosius dan tangens dari sudut tersebut. Sehingga perbandingan trigonometri merupakan suatu pemetaan atau fungsi.

Perbandingan trigonometri sinx merupakan relasi yang memetakkan setiap

x dengan tepat satu nilai sinx yang dinyatakan dengan notasi F: x →

sinx dengan rumus fungsi f( x ) = sinx dan persamaan fungsinya Y =

sinx , demikian pula untuk Cosinus dan Tangens CONTOH :

1) Diketahui fungsi f( x )= sinx0 dengan domain (1200_,1350_,1500_,1800

)

, tentukan Rangenya ! JAWAB :

f( x )= sinx0

f( 1200 _{)= sin 120}0 ₌ 180

sin(¿¿0−600₎

¿

= sin 600 ₌

1 2

√

3

f( 1350 _{)= sin 135}0 ₌ 180

sin(¿¿0−450₎

¿

= sin 450 ₌

1 2

√

2

f( 1500 _{)= sin 150}0 ₌ 180

sin(¿¿0−300) ¿

= sin 300 ₌ 1

2

f( 1800 _{)= sin 180}0 ₌ 180

sin(¿¿0−00₎

¿

Jadi Rangenya adalah : {1 2

√

3 ,

1 2

√

2 ,

1 2,0} .

6. Nilai Maksimum Dan Minimum Fungsi

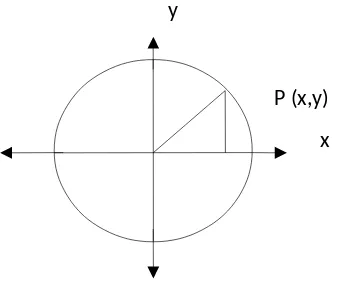
Perubahan nilai fungsi trigonometri dapat kita amati dengan menggunakan pertolongan lingkaran satuan, yaitu suatu lingkaran trigonometriyang berjari – jari samadengan satu satuan.

Gambar 1.1

Dari Gambar 1.1, kita mendapatkan

sina0=y

1=y ; nilai sina0 ditentukan oleh ordinat y .

cosa0

=x

1=x ; nilai cosa0 ditentukan oleh absis x .

tana0

=y

x ; nilai tana0 ditentukan oleh absi � ordinat y .

Misalkan titik P berputar (diawali dari titik A) berlawanan arah jarum jam pada

lingkaran satuan, sehingga sudut a0 _{= ¿ XOP bertambah secara kontinyu}

dari 00 sampai dengan 3600 .

Dengan bertambahnya sudut a0 tadi maka nilai fungsi trigonometri sina0 ,

cosa0 _{,dan tana}0 _{akan mengalami perubahan seperti berikut :}

1) (sina0

) maksimum = 1, dicapai untuk a=90+n x360

(sina0) minimum = -1, dicapai untuk a=270+n x360

P (x,y) y

Jadi, -1 ≤sina❑_{≤1 untuk tiap a∈R}

.

2) (cos¿¿0)a ¿

maksimum = 1, dicapai untuk a=n x360

(cos¿¿0)a ¿

minimum =-1, dicapai untuk a=180+n x360

Jadi, -1 ≤cosa❑

≤1 untuk tiap a∈R .

7. Kumpulan Soal-Soal

1) cos x . cosec x = cotan x

2) sin x . cos x . cosec x . sec x = 1

3) jika x memenuhi 2 (sin x)2 _{+ 3 sin x – 2 = 0 dan – ½ < x< ½ maka cos x}

adalah

4) sederhanakanlah tan (90 + α )° . sin (α – 180)° . sec (270 + α)°

5) jika diketahui tan A = p , hitunglah nilai 2 sin A coa A

6) diketahuhi segitiga ABC diketahui panjang sisi AC = 3, AB = 2 dan sudut A = 60°. Maka nilai cos C adalah...

7) jika tan x = p , maka nilai 2sin x cos x adalah..

REFERENSI

Noormadi & Sucipto, Endar. 2004. Matematika SMA. Erlangga. Jakarta

Primagama. 2008. Solusi Smart. Prima Visi Grafika.Yogyakarta

Abidin.1999.Ilmu Ukur Segitiga. Menara Pengetahuan. Yogyakarta