A. Penalaran Matematis
1. Definisi
Penalaran matematis adalah proses berfikir atau cara berfikir seseorang untuk
menarik kesimpulan, sehingga menghasilkan pernyataan baru untuk menyelesaikan
masalah matematika. Pendapat tersebut merujuk dari beberapa pendapat-pendapat
ahli. Shadiq (2004) mengartikan penalaran sebagai suatu kegiatan, suatu proses atau
suatu aktivitas berpikir untuk menarik kesimpulan atau membuat suatu pernyataan
baru yang benar, berdasarkan pada beberapa pernyataan yang kebenarannya telah
dibuktikan.
Senada dengan Shadiq, Lithner (2008) juga mendefinisikan penalaran
matematis sebagai garis pemikiran atau cara berfikir yang diadopsi untuk
menghasilkan pernyataan dan kesimpulan untuk menyelesaikan masalah. Selain
pendapat dua ahli di atas, Keraf (Shadiq, 2004) mengungkapkan penalaran sebagai
proses berfikir yang menghubung-hubungkan fakta-fakta atau evidensi-evidensi
yang diketahui menuju pada suatu kesimpulan. Misalnya persamaan kuadrat 𝑥2+ 9𝑥 − 10 = 0, dapat ditarik kesimpulan bahwa 𝑥 = 1 atau 𝑥 = −10.
Mengacu pada definisi penalaran menurut Lithner, penalaran di sini tidak
didasarkan pada logika formal selama ada argumentasi-argumentasi pendukung
yang masuk akal. Selanjutnya Lithner (2008) menyimpulkan tentang struktur
kemampuan penalaran matematis yang menjadi dasar baginya menyelesaikan suatu
a. Harus ada masalah matematika yang ditunjukkan dengan situasi matematika
untuk selanjutnya diproses.
b. Strategi pemilihan, dimana pemilihan dilihat dari pengertian yang luas seperti
memilih, mengingat, membuat, mengubah, menebak dll yang dapat didukung
oleh argumentasi prediktif. Argumentasi prediktif adalah argumentasi
perkiraan dimana dalam kriteria penalaran matematika menurut Permendikbud
(2014) yaitu poin mengajukan dugaan dan melakukan manipulasi matematis.
c. Strategi implementasi dapat didukung oleh argumentasi verifikasi.
Argumentasi verifikasi adalah argumentasi pemerikasaan tentang kebenaran
suatu solusi atau hasil pemecahan suatu masalah matematika, dimana di dalam
kriteria penalaran matematika menurut Permendikbud (2014) merupakan poin
penyusunan bukti dan penarikan kesimpulan.
d. Kesimpulan yang dimuat. Kesimpulan di sini berupa argumentasi yang
didasarkan pada pemilihan strategi dan implementasi strategi yang masuk akal
tentunya. Artinya tidak harus didukung dengan bukti langsung atau tidak
langsung.
Argumentasi adalah inti atau subtansi, bagian dari penalaran yang bertujuan
untuk menyakinkan diri sendiri atau orang lain akan kesimpulan yang disampaikan.
Berdasarkan struktur di atas, poin b dan c adalah bagian dari proses pemecahan
masalah. Maka dari itu, penalaran dan pemecahan masalah merupakan sebuah
kesatuan yang tidak dapat dipisahkan. Berdasarkan struktur penalaran di atas,
dimana struktur tersebut erat kaitannya dengan pemecahan masalah, Lithner (2006)
a. Penalaran imitatif matematis atau imitative mathematical reasoning yang
kemudian disingkat dengan IR.
b. Penalaran kreatif matematis atau creative mathematical reasoning yang
kemudian disingkat dengan CR.
2. Jenis Penalaran Matematis
Merujuk pada definisi penalaran, Lithner (2008) membagi penalaran ke
dalam dua tipe yaitu:
a. Penalaran imitatif matematis
Imitatif berasal dari bahasa inggris imitatitve yang memiliki asal kata
imitate yang berarti meniru. Dalam bahasa Indonesia imitatif memiliki arti
bersifat tiruan. Penalaran imitatif matematis adalah penalaran matematis yang
bersifat tiruan. Artinya proses berfikir peserta didik dalam membuat kesimpulan
hanya berdasarkan ingatan peserta didik dari buku ataupun contoh yang telah
mereka kerjakan. Dengan kata lain, penalaran imitatif matematis adalah
penalaran yang hanya didasarkan pada ingatan tentang apa yang telah dipelajari
dahulu.
Selaras dengan hal tersebut Lithner (2006) menyebutkan bahwa
penalaran imitatif yaitu mengikuti atau menyalin sebuah mode atau contoh tanpa
memperhatikan keasliannya. Studi empiris Lithner (2006) mengidentifikasikan
penalaran imitatif ke dalam dua jenis yaitu ingatan (memorized) dan algoritma
(algorithmic).
1) Penalaran ingatan (Memorized Reasoning)/ MR
jawaban yang telah dikerjakan sebelumnya tanpa memperhatikan langkah
penyelesaian masalah. Dengan kata lain penalaran ingatan adalah penalaran
yang menyalin jawaban pekerjaan sebelumnya dalam menyelesaikan
masalah.
Biasanya tipe soal yang terdapat di dalam penalaran ini adalah tipe
soal yang menuntut si penalar untuk mendefinisikan sebuah pernyataan,
membuat bukti, mengkonversikan satuan. Sebuah soal dapat dikatakan
memuat penalaran ingatan jika memenuhi kriteria berikut:
a) Strategi pemilihan ditentukan dengan mengingat jawaban lengkap.
Maksudnya adalah dalam menyelesaikan permasalahan matematika
(mengajukan dugaan dan manipulasi matematis) peserta didik hanya
menggunakan ingatannya untuk menjawab permasalahan tersebut.
b) Implementasi strategi terdiri hanya dengan menyalin jawaban secara
runtut. Impelemntasi tersebut didukung dengan penyusunan bukti dan
penarikan kesimpulan.
Uraian tersebut dapat ditarik kesimpulan bahwa soal yang memuat
penalaran jenis MR adalah :
a) Menanyakan definisi atau fakta dimana lebih membutuhkan kemampuan
mengingat yang tinggi.
b) Strategi pemilihan ditentukan dengan mengingat jawaban lengkap.
c) Implementasi strategi terdiri hanya dengan menyalin jawaban secara
Contoh soal tipe MR:
Tentukan jenis akar persamaan kuadrat dari 2𝑥2− 4𝑥 + 3!
Jawaban dari soal tersebut menuntut peserta didik untuk mengingat tentang
syarat akar-akar persamaan kuadrat dikatakan nyata dan berbeda, kembar,
atau imajiner.
Jika 𝐷 > 0, maka akar-akar persamaannya nyata (real) dan berbeda.
Jika 𝐷 = 0, maka akar-akar persamaannya kembar. Jika 𝐷 < 0, maka akar-akar persamaannya imajiner.
Dari soal di atas diperoleh nilai 𝐷 = (−4)2− 4 ∙ 3 ∙ 2 = −8. Sehingga nilai 𝐷 < 0.
Jadi jenis akar-akar persamaan kuadrat tersebut adalah imajiner.
2) Penalaran Algoritmik (Algorithmic Reasoning)/ AR
Penalaran algoritmik (AR) adalah salah satu jenis penalaran imitatif.
Penalaran algoritmik hampir sama dengan penalaran ingatan akan tetapi
penalaran jenis ini lebih cenderung untuk mengingat setiap langkah yang
digunakan untuk mengerjakan soal yang disediakan. Jadi penalaran
algortimik menitikberatkan kepada ingatan seseorang tentang bagaimana soal
tersebut diselesaikan berdasarkan langkah-langkah yang benar.
Penalaran jenis ini tidak membutuhkan solusi baru dalam
penyelesaiannya. Biasanya soal penalaran tipe ini terdapat di dalam buku
dengan angka yang berbeda, tetapi memiliki esensi yang sama. Sebuah soal
a) Strategi pemilihan ditentukan bukan hanya sekedar mengingat jawaban
seperti MR tetapi langkah-langkah algortima yang akan membimbing
seseorang kepada solusi yang sebenarnya. Hal tersebut didukung dengan
pengajuan dugaan yang mengandalkan ingatan.
b) Impelementasi strategi terdiri atas perhitungan–perhitungan trivial atau
tindakan-tindakan dengan aturan yang telah diberikan. Maksudnya dalam
melakukan penyelesaian masalah (manipulasi matematis, menyusun bukti
dan penarikan kesimpulan) seseorang menyerap langkah solusi seperti
yang telah dikerjakan.
Uraian di atas dapat ditarik kesimpulan bahwa soal yang mengandung
penalaran tipe AR adalah:
a) Strategi pemilihan ditentukan bukan hanya sekedar mengingat jawaban
seperti MR tetapi algortima penyelesaian.
b) Implementasi terdiri atas perhitungan trivial.
c) Tidak membutuhkan solusi baru.
Contoh soal tipe AR:
Persamaan kuadrat 𝑥2+ 4𝑝𝑥 + 4 = 0 mempunyai akar-akar 𝑥1 dan 𝑥2. Jika 𝑥1∙ (𝑥2)2+ (𝑥1)2∙ 𝑥2 = 32, maka nilai 𝑝adalah…
Jawaban dari soal tersebut adalah sebagai berikut:
Peserta didik harus memahami konsep penentuan akar-akar dengan
persamaan 𝑎𝑥2+ (𝑥1+ 𝑥2)𝑥 + (𝑥1∙ 𝑥2) = 0. Dari persamaan terakhir
secara umum diperoleh (𝑥1+ 𝑥2) =−𝑏
𝑎 dan (𝑥1∙ 𝑥2) = 𝑐
𝑎. Dengan catatan bahwa 𝑥1 dan 𝑥2 adalah akar-akar persamaan kuadrat.
Setelah mengetahui konsep tersebut maka peserta didik dapat
menemukan nilai 𝑝 setelah mengubah 𝑥1∙ (𝑥2)2+ (𝑥1)2∙ 𝑥2 = 32 menjadi 𝑥1∙ 𝑥2(𝑥1+ 𝑥2) = 32. Kemudian dengan mengetahui nilai 𝑎 = 1, 𝑏 = 4𝑝 𝑑𝑎𝑛 𝑐 = 4 sehingga diperoleh
𝑥1∙ 𝑥2 =𝑎𝑐 =41= 4
𝑥1+ 𝑥2 = −𝑏𝑎= −4𝑝1 = −4𝑝
Akan diperoleh 𝑥1∙ 𝑥2(𝑥1+ 𝑥2) = 32
4(−4𝑝) = 32
−16𝑝 = 32 → 𝑝 = −2 Jadi nilai 𝑝 = −2.
Dengan demikian seseorang tersebut hanya mengingat langkah
algortima untuk menyelesaikan masalah matematika yang disajikan. Tidak
terpaku pada jawabannya tetapi terpaku pada langkah solusi yang
dimaksudkan. Hal ini menyebabkan tipe soal untuk penalaran tipe AR sangat
beragam.
Secara sepintas kedua jenis penalaran tersebut sama, akan tetapi MR lebih
mengingat tentang fakta atau jawaban kemudian menyalinnya. Sementara AR
meskipun sama-sama mengingat, lebih mengingat prosedur dan mengerjakan
menanyakan tentang fakta atau bukti serta definisi-definisi yang membutuhkan
jawaban lengkap.
Perbedaan yang lebih mendasar adalah AR sadar benar bahwa antara
algoritma yang satu dengan algoritma selanjutnya saling berkaitan. Berbeda
dengan MR yang tidak mendasarkan algoritma satu dengan yang lain, akan tetapi
lebih mengarah kepada hafalan suatu penyelesaian.
b. Penalaran kreatif matematis (creative mathematical reasoning)
Penalaran kreatif matematis (CR) adalah proses berfikir yang
didefinisikan memiliki kebaharuan, masuk akal, fleksibel dan berdasarkan sifat
matematis. Berikut dijelaskan setiap aspek dari penalaran kreatif matematis
menurut Lithner (2006):
1) Pembaharuan
Artinya solusi pemecahan masalah tersebut baru diciptakan
berdasarkan pemahaman penalar atau solusi tersebut adalah solusi yang pernah
dilupakan kemudian dimunculkan kembali. Akan tetapi jika solusi yang
dilupakan tersebut dimunculkan kembali hanya dengan menyalin langkahnya
maka itu bukan termasuk ke dalam penalaran kreatif. Jika dikaitkan dengan
kriteria kemampuan penalaran secara umum maka penalar akan mengajukan
dugaan tentang solusi pemecahan masalah dengan menampilkan sesuatu yang
baru. Misalnya dengan menampilkan strategi penyelesaian yang berbeda.
2) Masuk akal
Adalah argumen yang disampaikan mendukung strategi pilihan atau
disampaikan benar. Berarti penalar harus membuat atau menyusun argumen
untuk membuktikan dugaan yang disampaikan benar dan masuk akal serta
dapat diterima oleh khalayak umum. Dengan kata lain menebak-nebak sebuah
jawaban atas suatu kesimpulan tidak dibenarkan.
3) Fleksibel
Menggunakan strategi dan implementasi yang berbeda dengan
menyesuaikan situasi masalah yang disediakan.
4) Berdasarkan sifat matematis
Argumen yang ditampilkan harus berdasarkan sifat instrinsik
matematis yang termuat dalam komponen penalaran. Komponen yang termuat
di dalam penalaran terdiri atas objek, transformasi dan konsep. Objek
merupakan aspek dasar, seperti angka, variabel, fungsi, grafik, diagram,
matriks dan lain sebagainya. Trasformasi adalah apa yang telah dikerjakan
terhadap objek dan menghasilkan objek yang berbeda. Misalnya seperti
menghitung apel dalam kehidupan sehari-hari kemudian ditransformasikan
menjadi angka. Konsep disini dilihat sebagai pusat dari ide matematika yang
menghubungkan antara objek, transformasi, dan unsur-unsurnya.
Berdasarkan uraian di atas dapat disimpulkan kriteria kemampuan
penalaran kreatif yaitu :
1) Pembaharuan
2) Masuk akal
3) Fleksibel
Contoh soal tipe CR di bawah ini mengutip dari hasil studi yang
dilakukan Lithner (2006).
Seorang peserta didik bernama Anne diminta untuk menyelesaikan soal berikut:
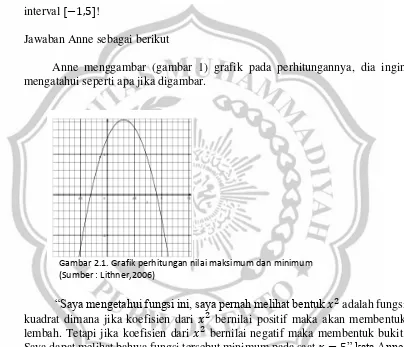
Tentukan nilai maksimum dan minimum dari fungsi 𝑦 = 7 + 3𝑥 − 𝑥2 pada interval [−1,5]!
Jawaban Anne sebagai berikut
Anne menggambar (gambar 1) grafik pada perhitungannya, dia ingin mengatahui seperti apa jika digambar.
“Saya mengetahui fungsi ini, saya pernah melihat bentuk 𝑥2 adalah fungsi kuadrat dimana jika koefisien dari 𝑥2 bernilai positif maka akan membentuk lembah. Tetapi jika koefisien dari 𝑥2 bernilai negatif maka membentuk bukit. Saya dapat melihat bahwa fungsi tersebut minimum pada saat 𝑥 = 5” kata Anne.
Dia dapat melihat bahwa nilai maksimum terjadi ketika 𝑥 = 1,5 tetapi nilai tersebut tidak dapat ditentukan menggunakan grafik. Anne menghitung beberapa nilai fungsi dengan 𝑥 = 1,5. Tetapi tidak dapat menemukannya. Dia diam selama dua menit.
“Kami telah belajar tentang turunan. Disana dikatakan tentang kemiringan.
Dan nilai maksimum hanya dapat terjadi dimana kemiringannya sama dengan nol. Saya dapat menyelesaikan itu. Saya pikir bahwa turunan dari −𝑥2 adalah – 2𝑥. Anne dengan mudah mengitung 𝑦′= 3 − 2𝑥 menemukan bahwa 𝑦′ pada saat 𝑥 = 1,5 dan menghitung 𝑦(1,5) = 9,25. Anne menyimpulkan bahwa nilai tersebut sesuai dengan grafik.
Dari contoh tersebut dapat dilihat pemikiran Anne merupakan penalaran
kreatif matematis karena memenuhi kriteria berikut:
1) Kebaharuan
Anne menggunakan konsep turunan dalam menyelesaikan soal, tetapi
belum melihat algortima untuk mendapatkan nilai maksimum yang dibangun
melalui pilihan strategi kunci: nilai maksimum terletak pada puncak dimana
nilai turunannya sama dengan nol. Dari proses terlihat Anne tidak hanya
mengikuti prosedur algoritma yang diberikan oleh orang lain.
2) Fleksibel
Anne menganalisis situasi dan mengadaptasi ke dalam kondisinya, hal
ini merupakan inisiatif yang tidak lazim diantara para peserta didik yang hanya
berfokus pada pendekatan algortimik.
3) Masuk akal
Anne mempunyai argumen berdasar matematis yang masuk akal tentang
pilihan strateginya dan kesimpulan
4) Berdasarkan matematis
Anne mengembangkan pengertian konsep yang bagus tentang fungsi dan
sifat instrinsiknya yaitu relasi antara konsep turunan gradien dan nilai
maksimum.
Pada penelitian ini, penulis mengambil dua jenis penalaran berdasarkan
kerangka kerja Lithner yaitu penalaran imitatif dan penalaran kreatif. Sementara
itu, penalaran imitatif dibagi atas dua jenis yaitu penalaran ingatan dan penalaran
penalaran ingatan (MR), penalaran algoritmik (AR) dan penalaran kreatif (CR).
Kriteria kemampuan penalaran matematis yang digunakan adalah sebagai berikut:
1. Penalaran Ingatan (MR) :
a) Strategi pemilihan ditentukan dengan mengingat jawaban lengkap. Artinya
pengajuan dugaan ditentukan dengan mengingat jawaban, definisi, atau
syarat tertentu.
b) Implementasi strategi hanya menyalin jawaban secara runtut. Peserta didik
menyimpulkan dan menyusun bukti hanya menyalin jawaban yang telah
ada. Peserta didik tidak memperhatikan keterkaitan antar langkah yang
digunakan.
2. Penalaran Algortimik (AR):
a) Strategi pemilihan ditentukan bukan hanya sekedar mengingat jawaban
tetapi langkah-langkah algortima yang akan membimbing seseorang kepada
solusi yang sebenarnya.
b) Implementasi strategi terdiri atas perhitungan-perhitungan trivial. Peserta
didik menyimpulkan dan menyusun bukti berdasarkan rumus atau langkah
awal yang dilakukan. Untuk langkah selanjutnya peserta didik hanya
mengikuti alur awal saja. Dengan demikian peserta didik memperhatikan
keterkaitan antar langkah yang dilakukan.
3. Penalaran Kreatif (CR):
a) Pembaharuan yaitu menyajikan solusi penyelesaian yang baru atau
menampilkan solusi lama tetapi tidak sekedar menyalin.
c) Masuk akal yaitu jika argumen yang ditampilkan dapat diterima oleh
khalayak umum
d) Berdasarkan sifat matematis yiatu menyusun argumen berdasarkan sifat
matematis.
B. Gaya Belajar
Peserta didik menangkap suatu materi yang disampaikan oleh guru
berbeda-beda. Mereka akan memilih cara yang paling mudah agar apa yang disampaikan
oleh guru dapat dengan mudah diterimanya dengan baik. Hal tersebut disebut
dengan gaya belajar. Gaya belajar bukan hanya berbicara mengenai bagaimana
seseorang menerima informasi dan menangkap informasi dari guru akan tetapi
memproses informasi tersebut dengan menggunakan otak kiri atau otak kanan.
Gaya belajar adalah salah satu cara seseorang untuk menyerap dan menguasi
informasi dan atau bagaimana informasi tersebut diproses. Selain itu menurut
beberapa riset yang telah dilakukan Dunn (1979) bahwa definisi gaya belajar
hampir sama yaitu mengarah kepada bagaimana seseorang memproses informasi
atau informasi tersebut disalurkan dengan persepsi dari masing masing orang. Jadi
dapat disimpulkan bahwa gaya belajar adalah cara seseorang untuk menangkap dan
mengolah informasi agar dapat dipahami dengan baik.
Dunn (1979) mengatakan ada banyak variabel yang mempengaruhi cara
belajar seseorang. Misalnya faktor fisik, lingkungan, emosional, dan sosiologi.
Tentunya jika faktor tersebut diperinci lagi maka akan banyak sekali variabel yang
mempengaruhi gaya belajar seserorang. Misalnya saja seseorang dapat belajar
diskusi kelompok, sedangkan ada lagi yang harus dibimbing oleh orang lain
misalnya guru, orang tua atau privat, dan ada pula seseorang yang memilih untuk
belajar sendiri. Terdapat banyak sekali karakter peserta didik dalam memilih cara
yang baik untuk belajar.
Faktor yang mempengaruhi gaya belajar seseorang ini memunculkan
berbagai pengelompokan gaya belajar. Ada beberapa klasifikasi gaya belajar
menurut beberapa ahli. Misalnya klasifikasi gaya belajar menurut De Porter (2003)
yang terkenal yaitu gaya belajar Visual, Audiotory, Kinestetic yang lebih dikenal
dengan VAK. Namun gaya belajar tersebut merupakan gaya belajar yang masih
umum, tidak merujuk khusus pada mata pelajaran tertentu. Meskipun gaya belajar
tersebut dapat diterapkan di dalam matematika. Akan tetapi pembagian gaya belajar
VAK didasarkan pada modalitas seseorang. Seperti kita ketahui bahwa modalitas
pasti dimiliki oleh setiap individu. Karena alasan itulah tipe gaya belajar lainnya
pun juga memiliki modalitas utama dalam setiap tipenya.
Seorang penulis bernama Gustav Carl Jung (Silver, 2010) ahli psikolog asal
Swiss mengamati tentang bagaimana seseorang mengolah informasi, berdasarkan
empat hal yaitu thinking, sensing, feeling, dan intuition. Thinking adalah fungsi
abstrak yang mengembangkan pembuktian fakta, logika, jelas, prosedur yang
konsisten dalam mengambil keputusan. Thinking menunjukan sebab-akibat, ide dan
dampak, aksi dan hasilnya sehingga dapat menentukan mana yang benar dan mana
yang salah.
Feeling adalah fungsi dasar yang digunakan dalam kehidupan, hubungan
menentukan mana yang baik dan mana yang buruk. Sensing adalah fungsi dasar
yang mengembangkan penglihatan, pendengaran, penciuman untuk menyediakan
fakta dan pengalaman langsung di lapangan. Dengan sensing dapat mengetahui
karakteristik seseorang, tempat, benda dan sebagainya. Dengan sensing pula dapat
melihat, mendengarkan, merasakan dan sebagainya. Terakhir intuition adalah
fungsi abstrak yang menggunakan firasat, pengetahuan, tebakan dan inspirasi untuk
mengelompokannya ke dalam pola atau kemungkinan-kemungkinan. Dengan
intuisi apa yang kita inginkan, mimpikan dapat kita capai (Hanson, 1996).
Silver, Strong dan Perinni membagi gaya belajar yang lebih mengarah pada
matematika menjadi 4 gaya belajar yaitu penguasaan, pemahaman, ekspresi diri,
dan antarpribadi (Silver, 2010). Gaya belajar yang muncul tersebut adalah hasil
kombinasi antara thinking dan sensing menghasilkan gaya belajar penguasaan,
thinking dan feeling menghasilkan gaya belajar antarpribadi, intuition dan feeling
menghasilkan gaya belajar ekspresi diri dan kombinasi antara intuition dan thinking
menghasilkan gaya belajar pemahaman (Silver, 2010).
Berikut klasifikasi dan ciri-ciri gaya belajar menurut Silver, dkk (2012):
1. Gaya Penguasaan
Seseorang dengan gaya belajar penguasaan akan cenderung belajar
menggunakan indra penglihatan mereka agar dapat dengan mudah menangkap
informasi. Ciri-ciri gaya belajar penguasaan:
a) Lebih senang belajar selangkah demi selangkah.
b) Lebih nyaman dengan tugas yang meminta mereka untuk mengingat tentang fakta dan prosedur.
c) Belajar dengan instruksi yang jelas.
d) Lebih cenderung ketika belajar dengan pemodelan dan praktik.
f) Senang menyelesaikan masalah matematika yang sama seperti sebelumnya dan menggunakan algoritma untuk mendapatkan jawaban tunggal.
g) Seseorang dengan gaya belajar penguasaan akan kesulitan untuk menyelesaikan masalah yang terlalu abstrak dan berhadapan dengan masalah yang bukan masalah rutin.
Moirao & Warrick(2010) menambahkan bahwa seseorang dengan tipe
penguasaan, akan mengajukan pertanyaan diawali dengan kata tanya “apa”
dimana jawabannya menuntut jawaban yang benar. Seseorang bergaya belajar
penguasaan, mereka akan termotivasi dengan sebuah kesuksesan, kompetensi
dan kejelasan. Motivasi tersebut berasal dari sebuah harapan yang jelas. Karena
motivasi tersebut maka seseorang dengan gaya belajar penguasaan harus
mengetahui kriteria untuk mengevaluasi kemampuan mereka, untuk kinerja
mereka selanjutnya.
2. Gaya Pemahaman
Seseorang dengan gaya belajar pemahaman umumnya menyukai hal
yang membutuhkan kemampuan berfikir kritis dan pembelajaran akademik.
Ciri-ciri :
a) Lebih senang kepada memahami mengapa matematika yang mereka pelajari bekerja.
b) Senang masalah matematika yang meminta untuk menjelaskan, membuktikan dan mengambil sikap.
c) Lebih senang belajar matematika dengan melihat pola dan mengidentifikasi pertanyaan terselubung.
d) Akan kesulitan ketika mereka mereka bekerja dengan lingkungan sosial/ memerlukan kerja sama atau kelompok. Hal ini dikarenakan mereka lebih senang bekerja sendiri.
e) Mereka akan senang ketika model pembelajarannya adalah sesuatu yang menantang kemampuan berfikir mereka dan membiarkan mereka untuk menjelaskan idenya. Artinya peserta didik tersebut senang dengan keadaan dimana mereka diberikan kesempatan untuk mengutarakan ide mereka. f) Peserta didik dengan gaya belajar pemahaman lebih senang menggunakan
g) Menekankan belajar mendalam. Model dan praktik dengan lebih mengarah kepada pengamatan dan memperhatikan proses adalah cara untuk menyelesaikan masalah dan mengumpulkan informasi.
Selain itu, Moirao & Warrick(2010) menambahkan bahwa tipe gaya
belajar pemahaman akan memulai pertanyaan dengan kata tanya “ mengapa”
dimana setiap pertanyaan tersebut menuntut alasan dan argumentasi. Seseorang
dengan gaya belajar pemahaman akan lebih termotivasi ketika lingkungan
menuntut sebuah pemikiran kritis dan menantang karena orang dengan gaya
belajar ini memiliki rasa ingin tahu yang tinggi.
3. Gaya Ekspresi Diri
Seseorang dengan gaya belajar ekspresi diri umumnya membutuhkan
sebuah kesempatan untuk memilih untuk mengekspresikan kreativitas mereka.
Selain itu seseorang dengan gaya belajar ini terbiasa untuk menvisualisasikan
ide mereka dalam bentuk imajinasi. Ciri-ciri gaya belajar tersebut antara lain:
a) Senang menggunakan imajinasi mereka untuk mengeksplor ide-ide matematika.
b) Senang dengan permasalahan matematika yang tidak rutin dan mengijinkan mereka untuk berfikir diluar kebiasaan.
c) Menggunakan pendekatan pemecahan masalah dengan menvisualkan masalah, menghasilkan solusi yang mungkin dan mengeksplorasi beberapa alternatif.
d) Peserta didik dengan gaya belajar ini mengalami kesulitan ketika mereka berhadapan dengan instruksi matematika yang lebih kearah sistem drill dan praktis serta pemecahan masalah yang lebih kearah hafalan.
e) Senang dengan pembelajaran yang meminta kemampuan imajinasi dan kreatif dalam memecahkan masalah di kelas.
f) Mereka senang dengan penugasan yang meminta mereka untuk menampilkan sesuatu yang baru dan langkah yang berbeda.
g) Tipe gaya belajar ini lebih senang untuk bekerja mengunakan angan-angan mereka.
Selain itu, tipe gaya belajar ini lebih sering menggunakan kata tanya
dengan kemungkinan-kemungkinan (Moirao & Warrick,2010). Seseorang
dengan gaya belajar ini termotivasi oleh keaslian dan lingkungan yang
cenderung memberikan banyak stimulasi/ rangsangan, kejutan dan memberikan
kesempatan bagi mereka untuk berfikir kreatif. Menggunakan imajinasi,
kemungkinan-kemungkinan untuk menghasilkan suatu ide baru dimana ide
tersebut dapat merubah pandangan seseorang.
4. Gaya Antarpribadi
Umumnya seseorang yang memiliki gaya belajar antarpribadi
menginginkan sebuah pengalaman belajar. Biasanya mereka akan belajar secara
berkelompok atau membutuhkan hubungan sosial yang baik selama proses
pembelajaran. Dengan demikian gaya belajar antarpribadi tidak dapat terlepas
dengan aktivitas kelompok. Ciri-ciri gaya belajar antarpribadi antara lain:
a) Senang belajar matematika melalui dialog, kolaborasi, dan kelompok belajar.
b) Senang menyelesaikan masalah matematika yang berpusat pada aplikasi matematika pada dunia nyata dan bagaimana matematika dapat membantu orang.
c) Kesulitan jika berhadapan dengan instruksi yang membebaskan jawaban pada lembar kerja atau ketika apa yang mereka pelajari kurang berkaitan dengan aplikasi pada kehidupan nyata.
d) Senang dengan pembelajaran yang memberikan perhatian pada kesuksesan mereka dan kesulitan mereka di dalam matematika.
e) Cara kerja orang yang memiliki gaya belajar ini adalah dengan feeling by feeling satu sama lain.
Berdasarkan uraian karakteristik masing-masing gaya belajar di atas, dapat
ditarik kesimpulan bahwa ada karakteristik masing-masing gaya belajar yang sesuai
dengan kemampuan penalaran matematis adalah sebagai berikut:
1. Gaya belajar penguasaan, mereka lebih cenderung untuk menganalisis setiap
penyelesaian matematika, yang membutuhkan ingatan tajam yang berkaitan
dengan jawaban sebelumnya atau algortima penyelesaian. Meskipun demikian,
gaya belajar ini sering mengalami kesalahan mengingat mereka adalah tipe
peniru yang baik.
2. Gaya belajar pemahaman, mereka mampu menarik kesimpulan dengan baik.
Hal ini dikarenakan tipe gaya belajar penguasaan lebih senang menguji
hipotesis/ dugaan-dugaan sebelum mengambil kesimpulan. Selain itu, tipe ini
tidak mengalami kesulitan ketika harus membuat dugaan, sehingga tidak heran
jika mereka akan menuliskan argumentasinya secara detail.
3. Gaya belajar ekspresi diri, mereka mampu menarik kesimpulan dengan baik
dan mampu membuat solusi baru yang berbeda. Tetapi menuntut keaslian dari
sebuah pekerjaan. Mereka juga senang dengan pekerjaan yang membutuhkan
kreativitas. Meskipun demikian, tipe gaya belajar juga mampu untuk membuat
dugaan dengan baik.
4. Gaya belajar antarpribadi, mereka cenderung menganalisis setiap masalah
dengan baik seperti gaya belajar penguasaan. Sehingga mengerti benar dengan
apa yang dilakukannya. Jadi gaya belajar ini mengerti benar setiap langkah
yang digunakan dan keterkaitan antar langkahnya.
C. Materi
KD 3.3 : Menentukan nilai persamaan kuadrat dengan satu variabel yang tidak
diketahui.
D. Penelitian Relevan
Kolopita (2015) melakukan penelitian deskriptif dengan pendekatan analisis
kualitatif dan analisis kuantitatif, terkait struktur dan kemampuan peserta didik
dalam menyelesaikan soal ujian nasioanal matematika SMP/MTs Tahun 2013/2014
menggunakan kerangka kerja Lithner. Menyebutkan bahwa dari 40 soal UN
terdapat 33 soal bertipe AR, 4 soal bertipe MR dan 3 soal bertipe CR. Selanjutnya
dari 94 peserta didik tidak ada satu peserta didik yang dapat menyelesaikan soal
tipe CR, melainkan mereka lebih menggunakan penalaran imitatif (IR) untuk
menyelesaikan soal UN tersebut.
Jonsson dkk (2014) juga melakukan penelitian yang sama tentang penalaran
algoritma dan kreatif. Penelitian deskriptif kuantitatif ini menghasilkan kesimpulan
bahwa belajar dengan mengedepankan penalaran kreatif lebih efektif dibandingkan
dengan penalaran algortima dilihat dari penyusunan konstruksi pengetahuan. Selain
itu ternyata penggunaan penalaran algortima berimbas terhadap kecakapan kognitif
dalam hal hafalan.
Meninjau dua penelitian di atas, keduanya memiliki persamaan dalam hal
penalaran. Keduanya melihat dari jenis penalaran berdasarkan kerangka kerja
Lithner. Penelitian kali ini juga akan melihat penalaran dengan kerangka Lithner
sebagai variabel utama. Akan tetapi penalaran dengan kerangka Lithner ini ditinjau
dari gaya belajar. Gaya belajar yang digunakan juga gaya belajar yang
E. Kerangka Pikir
Kemampuan penalaran matematis menjadi penting karena ketika seseorang
harus menarik kesimpulan dari sebuah masalah matematika, ia harus menggunakan
nalar untuk menyelesaikannya. Kemampuan penalaran matematis peserta didik
dikelompokan berdasarkan karakteristik dan kesulitan peserta didik dalam
menyelesaikan masalah matematika. Terdapat dua kemampuan penalaran yaitu
penalaran imitatif dan penalaran kreatif. Penalaran imitatif sendiri dibagi menjadi
dua yaitu penalaran ingatan dan penalaran algortima. Kemampuan penalaran
menurut Lithner menggunakan strategi penyelesaian dan implementasi strategi
sebagai kriteria. Strategi penyelesaian tersebut tergantung kepada setiap peserta
didik yang dipengaruhi oleh gaya belajarnya. Gaya belajar yang dikembangkan oleh
Silver dkk, mengedepankan gaya belajar yang lebih matematis. Artinya antara gaya
belajar tersebut dengan kemampuan matematis peserta didik memiliki keterkaitan.
Pemilihan strategi penyelesaian dapat didukung dengan argumentasi
prediktif. Penyusunan argumentasi prediktif inilah yang menjadi acuan
masing-masing gaya belajar, apakah akan menggunakan teori yang terdapat dalam buku,
pengembangan teori yang terdapat dalam buku, hasil diskusi atau argumentasi baru
yang dirasa masuk akal. Kemudian cara setiap peserta didik mengimplementasikan
strategi penyelesaian juga disesuaikan dengan gaya belajar. Implementasi strategi
didukung argumentasi verifikasi juga disesuaikan dengan gaya belajar
masing-masing.
Setiap gaya belajar memiliki karakteristik yang berbeda. Karakteristik yang
yang ditonjolkan kepada gaya belajar ini adalah bagaimana seseorang memandang
masalah matematika dan memahami masalah tersebut sehingga dapat diselesaikan
dengan baik. Oleh karena itu penulis tertarik untuk menganalisis kemampuan