Pembahasan Soal Tahap 2 Kalphyco 2018

Kalimantan’s Phisics Competetion 2018

KalPhiCo 2018

Olimpiade SMA

Pembahasan Soal Tahap II Number 1 : Analisa Grafik

Dua mobil A dan B bergerak melalui jalan yang sama dan berangkat dari titik awal yang sama secara bersamaan. Kurva kecepatan 𝑣 kedua mobil sebagai fungsi waktu 𝑡 diberikan pada gambar di samping.

Tentukan:

a. persamaan jarak tempuh mobil A dan B sebagai fungsi dari waktu.

b. Jika setelah menempuh jarak 60 m mobil A melambat dengan besar perlambatan yang sama dengan percepatan ketika awal perjalanan, kapan dan dimana mobil B berhasil menyusul kembali mobil A?

Pembahasan :

a. Mobil A melakukan gerak lurus berubah beraturan dengan kecepatan awal 𝑣_𝐴,0 =

2 m/s dan percepatan

𝑎 =Δ𝑣_{Δ𝑡 =} 4 − 2_{4 − 0 =}1_{2 m/s}

Kecepatan mobil A sebagai fungsi waktu adalah

𝑎 =𝑑𝑣_{𝑑𝑡 =}1₂

∫𝑣𝐴(𝑡)𝑑𝑣 𝑣𝐴,0=2

= ∫𝑡1_{2 𝑑𝑡} 0

𝑣𝐴(𝑡) − 2 =1_{2 𝑡 ⟹ 𝑣}𝐴(𝑡) = 2 +1_{2 𝑡}

Jarak tempuh mobil A sebagai fungsi waktu adalah

𝑣𝐴(𝑡) =𝑑𝑥_{𝑑𝑡 = 2 +}𝐴 1_{2 𝑡}

𝑣(m/s)

𝑡(s) 4

2 4

mobil A

∫ 𝑑𝑥𝐴 𝑥𝐴(𝑡)

0 = ∫ (2 +

1 2 𝑡) 𝑑𝑡 𝑡

0 ⟹ 𝑥𝐴(𝑡) = 2𝑡 + 1 4 𝑡2

Mobil B melakukan gerak lurus beraturan (percepatannya nol) dengan kecepatan konstan 𝑣_𝐵 = 4 m/s, maka jerak tempuh mobil B sebagai fungsi waktu adalah

𝑣𝐵= 𝑑𝑥_{𝑑𝑡 = 4}𝐵

∫ 𝑑𝑥𝐵 𝑥𝐵(𝑡)

0 = ∫ 4𝑑𝑡

𝑡

0 ⟹ 𝑥𝐵(𝑡) = 4𝑡

b. Ketika mobil A mencapai jarak 60 meter berarti 𝑡 = 12 s (silahkan buktikan) dan saat itu kecepatannya adalah 8 m/s (silahkan buktikan). Kemudian pada saat itu pula mobil B telah menempuh jarak 48 m. Posisi kedua mobil sekarang sebagai fungsi waktu akan menjadi

𝑥𝐴(𝑡) = 𝑥𝐴,0′ + 𝑣0,𝐴′ 𝑡′+1_{2 𝑎}𝐴′𝑡′2 = 60 + 8𝑡′−1_{4 𝑡}′2

𝑥𝐵(𝑡) = 𝑥𝐵,0′ + 𝑣0,𝐵′ 𝑡′+1_{2 𝑎}𝐵′𝑡′2= 48 + 4𝑡′

Saat kedua mobil bertemu, dia berada di posisi yang sama, misal terjadi saat 𝑡′= 𝜏

𝑥𝐴(𝜏) = 𝑥𝐵(𝜏)

60 + 8𝜏 −1_{4 𝜏}2 _{= 48 + 4𝜏} 1

4 𝜏2− 4𝜏 − 12 = 0 𝜏2_{− 16𝜏 − 48 = 0}

Dengan rumus kuadrat

𝜏 =−(−16) ± √(−16)₂₍₁₎2− 4(1)(−48)

𝜏 =16 ± √256 + 192₂

𝜏 =16 ± √448₂ = 16 ± 8√7₂ 𝜏 = 8 ± 4√7

𝜏 = 8 + 4√7 ≈ 18,6 s atau 𝜏 = −2,6 s

Solusi yang fisis adalah 𝜏 = 18,6 s sedangkan 𝜏 = −2,6 s bukanlah solusi yang diharapkan, nilai negatif menandakan kejadian yang terjadi sebelum acuan kondisi awal kita, yaitu 𝑡 = 12 s. Hal ini karena adanya perubahan arah percepatan pada mobil A. Kita tahu dari grafik pada c bahwa setelah bertemu untuk pertama kalinya, mobil A akan berada di depan mobil B sehingga ketika diperlambat, mobil A dan B hanya akan berpapasan satu kali.

𝑇 = 𝑡 + 𝜏 = 12 + 18,6 = 30,6 s

Posisi kedua mobil saat itu dihitung dari posisi awal adalah

𝑥𝐵(𝜏) = 𝑥𝐴(𝜏) = 48 + 4(30,6 ) = 170,4 m

Number 2 : Tangga yang Meluncur

Sebuah tangga pejal homogen dengan massa 𝑚 dan panjang 𝑙 bersandar pada dinding licin dan berada di atas lantai yang juga licin. Mula-mula tangga di sandarkan HAMPIR menempel dengan dinding dan dalam keadaan diam. Setelah di lepas tangga itu pada bagian atasnya merosot ke bawah, dan tangga bagian bawah bergerak ke kanan, seperti ditunjukkan pada gambar di bawah.

Tentukan Kecepatan pusat massa dari tangga tersebut selama bergerak! Pembahasan :

a. Kita gunakan definisi dari soal bahwa sudut antara tangga dan dinding adalah 𝜃. Kecepatan pusat tangga berubah-ubah dan kita bisa menyatakannya sebagai fungsi dari sudut 𝜃. Hal ini boleh dilakukan karena soal menanyakan kecepatan pusat massa batang selama bergerak, sedangkan nilainya berubah-ubah, maka kita bisa menyatakannya sebagai satu buah variabel yang berubah dan dalam hal ini kita pilih

𝜃. Sebenarnya bisa juga kita nyatakan dalam variabel lain seperti tinggi titik sentuh tangga dengan dinding, atau jarak titik sentuh tangga dengan lantai terhadap dinding, namun bentuk yang cukup sederhana adalah ketika kita nyatakan sebagai fungsi 𝜃. Soal ini lebih mudah kita kerjakan menggunakan Hukum Kekekalan Energi Mekanik (yap betul, energi mekanik sistem kekal karena tidak ada gaya non konservatif yang bekerja pada tangga, hal ini juga karena seluruh permukaan licin). Kita jadikan lantai sebagai acuan energi potensial sama dengan nol, energi mekanik awal sistem adalah

𝐸𝑀𝑖 = 1_{2 𝑚𝑔𝐿}

memiliki komponen kecepatan pusat massa arah horizontal 𝑣_𝑥 dan arah vertikal 𝑣_𝑦 serta batang juga berotasi terhadap pusat massanya sendiri dengan kecepatan sudut

𝜔. Sehingga energi tangga akan menjadi

𝐸𝑀𝑓 = 1_{2 𝑚𝑔𝐿 cos 𝜃 +}1_{2 𝑚(𝑣}𝑥2+ 𝑣𝑦2) +1_{2 𝐼𝜔}2

Selanjutnya kita cari dulu hubungan 𝑣_𝑥, 𝑣_𝑦, dan 𝜔.

Dapat kita lihat bahwa ujung atas tangga hanya bergerak dalam arah vertikal dan ujung bawah tangga hanya bergerak dalam arah vertikal. Kita tinjau gerak pusat massa arah horizontal relatif terhadap ujung atas tangga akan kita dapatkan

𝑣𝑥= 𝜔𝐿_{2 cos 𝜃}

Kemudian tinjau gerak pusat massa arah vertikal relatif terhadap ujung bawah tangga akan kita dapatkan pula

𝑣𝑦 =𝜔𝐿_{2 sin 𝜃}

Kita modifikasi menjadi

𝑣𝑥2 + 𝑣𝑦2 = (𝜔𝐿_{2 cos 𝜃)} 2

+ (𝜔𝐿_{2 sin 𝜃)}2 =𝜔2₄𝐿2

Juga kita tahu bahwa 𝑣_𝑥2+ 𝑣_𝑦2 = 𝑣2 adalah kecepatan pusat massa batang sehingga

𝜔2 ₌4𝑣2 𝐿2

momen inersia batang terhadap pusat massanya adalah 𝐼 =_{12 𝑚𝐿}1 2

𝐸𝑀𝑓 = 1_{2 𝑚𝑔𝐿 cos 𝜃 +}1_{2 𝑚𝑣}2+1_{2 (12 𝑚𝐿}1 2) (4𝑣 2 𝐿2 ) 𝐸𝑀𝑓 = 1_{2 𝑚𝑔𝐿 cos 𝜃 +}2_{3 𝑚𝑣}2

Hukum Kekekalan Energi mekanik

𝐸𝑀𝑖 = 𝐸𝑀𝑓

𝑣𝑥

𝑣𝑦

1

2 𝑚𝑔𝐿 = 1

2 𝑚𝑔𝐿 cos 𝜃 + 2 3 𝑚𝑣2 1

2 𝑔𝐿(1 − cos 𝜃) = 2 3 𝑣2

𝑣2 ₌ 4𝑔𝐿

3 (1 − cos 𝜃) ⟹ 𝑣 = √ 3𝑔𝐿

4 (1 − cos 𝜃)

Number 3 : Sistem Katrol dan Dua Silinder Pejal

Pada sistem di bawah ini, benda berupa silinder dengan jari-jari luar 𝑅, jari-jari dalam 𝑟 terletak pada bidang miring. Sedangkan massa yang tergantung adalah silinder yang juga berjari-jari 𝑟. Abikan massa katrol pada bidang miring. Gunakan momen inersia silinder

1/2 𝑀𝑅2_{. Tinjau kasus bidang miring licin. Tentukan percepatan 𝑚 terhadap bumi.}

Pembahasan :

Perhatikan gambar di bawah ini!

Percepatan pusat massa silinder 𝑀 terhadap tanah adalah 𝑎_𝑀 Percepatan sudut silinder 𝑀 terhadap tanah adalah 𝛼_𝑀 Percepatan pusat massa silinder 𝑚 terhadap tanah adalah 𝑎_𝑚 Percepatan sudut silinder 𝑚 terhadap tanah adalah 𝛼_𝑚

𝑀

𝑅

𝑚

𝜃 𝑟

𝑟

𝑀 𝑅

𝑚

𝜃 𝑟

𝑟

𝑚𝑔 𝑀𝑔

𝑇 𝑇

𝑎𝑚

𝑁

𝛼𝑚

Hukum II Newton Untuk gerak silinder 𝑀 Translasi

𝑀𝑔 sin 𝜃 − 𝑇 = 𝑀𝑎𝑀… (1)

Rotasi

𝑇𝑟 =1_{2 𝑀𝑅}2_𝛼

𝑀 ⟹ 𝑇 =_{2𝑟 𝑀𝑅}1 2𝛼𝑀… (2)

Hukum II Newton Untuk gerak silinder 𝑚 Translasi

𝑚𝑔 − 𝑇 = 𝑚𝑎𝑚… (3)

Rotasi

𝑇𝑟 =1_{2 𝑚𝑟}2_𝛼

𝑚 ⟹ 𝑇 =1_{2 𝑚𝑟𝛼}𝑚… (4)

Jika diperhatikan percepatan silinder 𝑚 adalah percepatan tali ditambah percepatan pusat massa silinder 𝑚 terhadap tali yang besarnya adalah 𝛼_𝑚𝑟 (silider 𝑚 dapat dianggap menggelinding tanpa silip pada tali). Sekarang berapa nilai percepatan tali. Kita amati silinder 𝑀. Tali dipercepat ke kanan bawah sejajar bidang miring dengan percepatan 𝑎_𝑀 namun juga dipercepat ke kiri atas sejajar bidang miring dengan percepatan 𝛼_𝑀𝑟. Jika kita asumsikan tali lebih cenderung bergerak ke kiri atas atau nilai 𝛼_𝑀𝑟 > 𝑎_𝑀 maka percepatannnya adalah 𝑎_{𝑡𝑎𝑙𝑖} = 𝛼_𝑀𝑟 − 𝑎_𝑀 dan jika pun sebaliknya yaitu tali lebih cenderung bergerak ke kanan bawah atau nilai 𝛼_𝑀𝑟 < 𝑎_𝑀 maka percepatannya adalah

𝑎𝑡𝑎𝑙𝑖 = 𝑎𝑀 − 𝛼𝑀𝑟. Jika kita hubungkan dengan percepatan silinder 𝑚 akan menjadi

Untuk asumsi pertama 𝛼_𝑀𝑟 > 𝑎_𝑀 (arah percepatan tali searah dengan percepatan silinder 𝑚)

𝑎𝑚 = 𝛼𝑚𝑟 + 𝑎𝑡𝑎𝑙𝑖= 𝛼𝑚𝑟 + 𝛼𝑀𝑟 − 𝑎𝑀

Untuk asumsi kedua 𝛼_𝑀𝑟 < 𝑎_𝑀 (arah percepatan tali berlawanan arah dengan percepatan silinder 𝑚)

𝑎𝑚 = 𝛼𝑚𝑟 − 𝑎𝑡𝑎𝑙𝑖= 𝛼𝑚𝑟 − (𝑎𝑀 − 𝛼𝑀𝑟) = 𝛼𝑚𝑟 + 𝛼𝑀𝑟 − 𝑎𝑀

Dan hasilnya sama saja, jadi dapat kita simpulkan hubungan antar percepatannya adalah

𝑎𝑚 = 𝛼𝑚𝑟 + 𝛼𝑀𝑟 − 𝑎𝑀… (5)

Subtitusi persamaan (4) ke (3)

Subtitusi persamaan (2) ke (3)

𝑚𝑔 −_{2𝑟 𝑀𝑅}1 2_𝛼

𝑀 = 𝑚𝑎𝑚 ⟹ 𝛼𝑀𝑟 =2𝑚𝑟

2

𝑀𝑅2 (𝑔 − 𝑎𝑚) … (7)

Kurangkan persamaan (1) dengan (3)

𝑀𝑔 sin 𝜃 − 𝑇 = 𝑀𝑎𝑀 𝑚𝑔 − 𝑇 = 𝑚𝑎𝑚

(𝑀 sin 𝜃 − 𝑚)𝑔 = 𝑀𝑎𝑀− 𝑚𝑎𝑚−

𝑎𝑀 = (𝑀 sin 𝜃 − 𝑚)𝑔 + 𝑚𝑎_𝑀 𝑚… (8)

Subtitusi persamaan (6), (7), dan (8) ke (5)

𝑎𝑚 = 2𝑔 − 2𝑎𝑚+2𝑚𝑟

Number 4 : Osilasi Sistem Dua Massa Dengan Gaya Gravitasi sebagai Gaya Pemulihnya

Tinjau sebuah sistem terisolasi yang terdiri dari 2 benda, 𝑚₁ dan 𝑚₂. Dalam sistem ini gaya gravitasi lain dari benda lain di luar sistem dapat diabaikan. Massa 𝑚₁ terpasang pada tali tak bermassa sepanjang d dan membentuk sebuah bandul yang dipasang tetap pada titik O. Massa 𝑚₁ hanya mengalami gaya gravitasi dengan bola homogen bermassa

𝑚2 berjari-jari 𝑅 yang posisinya tetap dimana pusat bola

berjarak 𝐿 dari titik O. Nilai 𝐿 hanya sedikit lebih besar dari

𝑑 + 𝑅. Sudut antara tali dan garis vertikal yang melalui titik O adalah 𝜃, dimana diasumsikan 𝜃 kecil. Tentukan periode osilasi 𝑚₁.

Petunjuk : kita bisa menyelesaikan soal ini dengan metode energi maupun metode gaya.

Pembahasan :

Cara 1 : Metode Gaya

Karena gerak massa 𝑚₁ berayun, kita akan lebih mudah menentukan persamaan geraknya dengan meninjau gerak rotasinya. Torsi pemulih yang bekerja pada massa 𝑚₁

diberikan oleh gaya gravitasi akibat adanya bola 𝑚₂ dan arah gaya ini selalu menuju pusat bola 𝑚₂. Perhatikan gambar di bawah ini!

Gaya gravitasi bekerja pada massa 𝑚₁adalah

𝐹𝑔 = 𝐺𝑚_𝑠1₂𝑚2

Menggunakan hukum dua neton tentang gerak rotasi akan kita dapatkan

𝐹𝑔sin(𝜃 + 𝜙) 𝑑 = 𝑚1𝑑2𝛼 𝐺𝑚2

𝑑𝑠2 (sin 𝜃 cos 𝜙 + sin 𝜙 cos 𝜃) = 𝛼 … (1)

Perhatikan lagi gambar di atas, kita bisa mendapatkan nilai 𝑠 dengan menggunakan phytagoras

𝑠2 _{= (𝐿 − 𝑑 cos 𝜃)}2_{+ 𝑑}2_sin2_𝜃

𝑠2 _{= 𝐿}2_{− 2𝐿𝑑 cos 𝜃 + 𝑑}2_cos2_{𝜃 + 𝑑}2_sin2_𝜃 𝑠2 _{= 𝐿}2_{− 2𝐿𝑑 cos 𝜃 + 𝑑}2_(sin2_{𝜃 + cos}2_𝜃) 𝑠2 _{= 𝐿}2_{− 2𝐿𝑑 cos 𝜃 + 𝑑}2

Dengan menggunakan aturan dasar trigonometri akan kita dapatkan

sin 𝜙 =_{𝑚𝑖𝑟𝑖𝑛𝑔 =}𝑑𝑒𝑝𝑎𝑛 𝑑 sin 𝜃_𝑠

cos 𝜙 =𝑠𝑎𝑚𝑝𝑖𝑛𝑔_{𝑚𝑖𝑟𝑖𝑛𝑔 =} 𝐿 − 𝑑 cos 𝜃_𝑠

𝐹𝑔sin(𝜃 + 𝜙) 𝐹𝑔 𝜃

𝑑 𝐿

𝑚1

𝑅 𝑚2

𝑑 cos 𝜃

𝐿 − 𝑑 cos 𝜃

𝑠 𝜙

Karena kita asumsikan simpangan sudut 𝜃 sangat kecil, kita bisa menggunakan hampiran berikut

sin 𝜃 ≈ 𝜃 dan cos 𝜃 ≈ 1, maka akan kita dapatkan

𝑠2 _{= 𝐿}2_{− 2𝐿𝑑 + 𝑑}2 _{= (𝐿 − 𝑑)}2 𝑠 = 𝐿 − 𝑑

sin 𝜙 =𝑑𝜃_𝑠

cos 𝜙 =𝐿 − 𝑑_𝑠

Subtitusi hasil ini ke persamaan (1)

𝐺𝑚2 𝑑𝑠2 (𝜃

𝐿 − 𝑑 𝑠 +

𝑑𝜃 𝑠 ) = 𝛼 𝐺𝑚2𝐿

𝑑𝑠3 𝜃 = 𝛼 𝐺𝑚2𝐿

𝑑(𝐿 − 𝑑)3𝜃 = 𝛼 … (2)

Perhatikan bahwa arah simpangan 𝜃 adalah berlawanan arah jarum jam dari titik setimbangnya sedangkan arah percepatan sudut nya searah jarum jam, berarti percepatan sudut massa 𝑚₁ adalah negatif(karena berlawanan arah) dari turunan kedua simpangan sudutnya atau

𝛼 = −𝑑_𝑑𝑡2𝜃₂ = −𝜃̈

Subtitusi hasil ini ke persamaan dua dan kita akan dapatkan persamaan gerak harmonik sederhana sistem

𝐺𝑚2𝐿

𝑑(𝐿 − 𝑑)3𝜃 = −𝜃̈

𝜃̈ +_{𝑑(𝐿 − 𝑑)}𝐺𝑚2𝐿 ₃𝜃 = 0

Persamaan terakhir analog dengan persamaan umum gerak harmonik sederhana yang berbentuk 𝜃̈ + 𝜔2𝜃 = 0, maka kecepatan sudut osilasi sistem adalah

𝜔 = √_{𝑑(𝐿 − 𝑑)}𝐺𝑚2𝐿 ₃

𝑇 = 2𝜋_{𝜔 → 𝑇 = 2𝜋}√𝑑(𝐿 − 𝑑)3 𝐺𝑚2𝐿

Cara 2 : Metode Energi

Sebenarnya menggunakan cara energi untuk sistem ini akan lebih cepat namun terkadang ada soal yang lebih mudah menggunakan cara gaya ataupun cara energi, jadi kita harus bisa keduanya dan tentunya harus bisa memilih cara mana yang paling efisien.

Untuk menggunakan cara ini kita harus tentukan energi total sistem terlebih dahulu. Karena tidak ada gaya udara dan gaya luar non-konservatif yang bekerja pada sistem, maka energi total sistem kekal. Untuk mendapatkan persamaan geraknya, kita cukup menurun persaan energinya satu kali terhadap waktu dan karena energi kekal atau konstan, turunannya ini akan sama dengan nol. Baik akan saya contohkan caranya.

𝑑

Number 5 : Roket Berpindah Orbit

Sebuah roket bermassa total 𝑚 mengelilingi bumi pada low earth orbit berbentuk lingkaran dengan jari-jari orbit

𝑅1. Roket ini akan berpindah orbit menuju orbit menuju

orbit berjari jari 𝑅₂ > 𝑅₁ dengan cara mengubah bentuk orbitnya dalam bentuk orbit elips seperti yang ditunjukkan oleh garis tebal pada gambar disamping. Manuver orbit ini dicapai dengan membuang bahan bakar sebanyak Δ𝑚₁ > 0 sehingga memberika laju Δ𝑣₁ searah kecepatan orbit pada orbit rendah. Kemudian roket membuang lagi bahan bakar sebanyak Δ𝑚₂ > 0

sehingga memberikan tambahan laju Δ𝑣₂ searah kecepatan orbit pada orbit tinggi. Laju orbit roket untuk orbit rendah adalah 𝑣_𝑅1 . Bahan bakar roket memiliki laju buang konstan 𝑣_𝑓relatif terhadap roket. Tentukan tambahan laju Δ𝑣₁ yang dibutuhkan untuk mengubah orbit dari lingkaran berjari-jari 𝑅₁ menjadi elips (nyatakan dalam 𝑣_𝑅1 , 𝑅₁, 𝑅₂). Pembahasan :

Kecepatan roket ketika berada di orbit 𝑅₁ adalah 𝑣_𝑅1. Dengan menggunakan persamaan gaya sentripetal dimana gaya gravitasilah yang berperan sabagai gaya sentripetal di sini, kita bisa menyatakan 𝑣_𝑅1 ulang sebagai berikut

𝐹𝐺 = 𝐹𝑠

𝑅2 𝑅1

𝐺𝑀𝐵𝑚

Roket kemudian membuang bahan bakarnya sehingga kecepatannya bertambah dan lintasan roket berubah menjadi elips. Ketika penambahan kecepatan ini terjadi, roket berada di perihelium atau jarak terdekatnya dengan bumi yaitu 𝑅₁ dan kecepatannya di sini adalah 𝑣_𝑝. Planet terus bergerak sampai suatu ketika dia berada di aphelium atau jarak terjauhnya dari bumi dalam lintasan elips ini yaitu 𝑅₂ dan kecepatannya di sini adalah 𝑣_𝑎. Kita bisa mencari 𝑣_𝑝 dan 𝑣_𝑎 dari hukum kekekalan momentum sudut dan hukum kekekalan energi. Pada kasus gerak melingkar terhadap dengan gaya gravitasi sebagai gaya sentripetalnya momentum sudut sistem akan kekal karena arah gaya gravitasi dan jari-jarinya sejajar, karena torsi adalah perkalian silang antara keduanya maka nilai torsi eksternal pada sistem bernilai nol. Alhasil momentum sudut sistem kekal. Kita gunakan hukum kekekalan momentum sudut untuk keadaan perihelium dan aphelium

𝐿𝑎 = 𝐿𝑝

(𝑚 − Δ𝑚1)𝑣𝑎𝑅2 = (𝑚 − Δ𝑚1)𝑣𝑝𝑅1 𝑣𝑎 =𝑅_𝑅1

2𝑣𝑝

Kemudian kita gunakan hukum kekekalan energi untuk dua keadaan seperti sebelumnya

𝑣𝑎 =𝑅_𝑅1

2𝑣𝑝 =

𝑅1 𝑅2√

2𝑅2 𝑅2+ 𝑅1𝑣𝑅1

Penambahan kecepatan Δ𝑣₁ ketika orbit planet berubah dari orbit awal berjari-jari 𝑅₁ menjadi orbit elips adalah

Δ𝑣1 = 𝑣𝑝− 𝑣𝑅1 = √_𝑅2𝑅2

2+ 𝑅1𝑣𝑅1− 𝑣𝑅1

Δ𝑣1 = 𝑣𝑅1(√_𝑅2𝑅2

2+ 𝑅1− 1)

Number 6 : Perbandingan Energi Kinetik Roda Luar dan Dalam

Sebuah mobil roda empat membelok pada suatu tikungan berbentuk lingkaran. Lintasan tengah poros roda belakang membentuk lingkaran terhadap pusat tikungan tersebut dengan jari-jari 𝑅. Panjang poros atau jarak antara kedua roda belakang adalah 𝐻. Massa masing-masing roda belakang adalah 𝑚. Roda belakang dapat diasumsikan sebagai suatu cakram dengan jari-jari 𝑏. Ambil nilai 𝑅 = 10 meter, 𝐻 = 2 meter dan 𝑏 = 0,5 meter. Jika perbandingan energi kinetik total antara roda belakang luar dengan roda belakang dalam adalah 𝑘, tentukan nilai 𝑘.

Pembahasan : Misalkan

Kecepatan pusat massa dan kecepatan sudut roda belakang dalam 𝑣₁ dan 𝜔₁ Kecepatan pusat massa dan kecepatan sudut roda belakang luar 𝑣₂ dan 𝜔₂

Kecepatan sudut bagian tengah poros kedua roda belakang terhadap pusat lintasan ω Energi kinetik roda daalam adalah

𝐸𝐾1 =1_{2 𝑚𝑣}12+1_{2 (}1_{2 𝑚𝑏}2) 𝜔12

Gerakan roda adalah menggelinding tanpa slip maka akan berlaku

𝑣1 = 𝜔1𝑏

𝐸𝐾1 =3_{4 𝑚𝑏}2𝜔12

Dengan cara yang sama energi kinetik roda luar adalah

𝐸𝐾2 = 3_{4 𝑚𝑏}2𝜔22

Hubungan 𝜔₁ dengan 𝜔

𝑣1 = 𝜔1𝑏 = 𝜔 (𝑅 −1_{2 𝐻) ⟹ 𝜔}1= 2𝑅 − 𝐻_{2𝑏 𝜔}

𝑣2 = 𝜔2𝑏 = 𝜔 (𝑅 +1_{2 𝐻) ⟹ 𝜔}2 =2𝑅 + 𝐻_{2𝑏 𝜔}

Energi kinetik kedua roda menjadi

𝐸𝐾1 =_{16 𝑚}3 (2𝑅 − 𝐻)2𝜔

𝐸𝐾2 = _{16 𝑚}3 (2𝑅 + 𝐻)2𝜔

Perbandingan energi kinetik roda luar dan dalam adalah

𝐸𝐾2 𝐸𝐾1 =

3

16 𝑚(2𝑅 + 𝐻)2𝜔 3

16 𝑚(2𝑅 − 𝐻)2𝜔 𝐸𝐾2

𝐸𝐾1 = (

2𝑅 + 𝐻 2𝑅 − 𝐻)

2

Sampai disini, menurut kamu apakah hasil ini benar? So far, sebenarnya ada hal yang lupa dipertimbangkan sehingga hasil ini tidak benar. Hasil tadi akan benar jika roda bukanlah benda tegar, namun kenyataannya di sini, ukuran roda tidak bisa kita abaikan. So mari kita tinjau ulang.

Gerakan roda belakang dalam dan luar sebenarnya adalah seperti berikut

Kita buat permisalan yang baru. Misalkan

Kecepatan sudut roda belakang luar terhadap pusat lintasan dan pusat massanya sendiri adalah Ω₁ dan 𝜔₁

Kecepatan sudut roda belakang dalam terhadap pusat lintasan dan pusat massanya sendiri adalah Ω₂ dan 𝜔₂

Kecepatan sudut bagian tengah poros kedua roda belakang terhadap pusat lintasan ω Energi kinetik roda belakang bagian luar dan dalam adalah

𝐸𝐾1 =1_{2 𝐼}pl1Ω12 +1_{2 𝐼}pm𝜔12

𝐸𝐾2 = 1_{2 𝐼}pl2Ω22+1_{2 𝐼}pm𝜔22

𝑅 𝐻

𝑧

𝑦

Dengan 𝐼_pm adalah momen inersia roda terhadap pusat massanya dan roda berputar terhadap sumbu 𝑧 sedangkan 𝐼_pl1 dan 𝐼_pl2 adalah momen inersia masing-masing roda terhadap pusat lintasan.

𝐼pm= 𝐼𝑧 = 1_{2 𝑚𝑏}2

Untuk menghitung 𝐼_pl1 dan 𝐼_pl2 kita hitung dulu momen inersia roda untuk rotasi pada sumbu 𝑦 menggunakan teorema sumbu tegak lurus

𝐼𝑧 = 𝐼𝑥+ 𝐼𝑦

Karena roda simetri 𝐼_𝑥= 𝐼_𝑦 maka

𝐼𝑦 =1_{2 𝐼}𝑧 =1_{4 𝑚𝑏}2

Momen inersia roda luar dan dalam terhadap pusat lintasan dapat kita cari menggunakan teorema sumbu sejajar

𝐼pl1 = 𝐼𝑦+ 𝑚 (𝑅 +1_{2 𝐻)} 2

= 1_{4 𝑚𝑏}2_{+ 𝑚 (𝑅 +}1 2 𝐻)

2

= 1_{4 𝑚}[𝑏2_{+ (2𝑅 + 𝐻)}2_]

𝐼pl2 = 𝐼𝑦+ 𝑚 (𝑅 −1_{2 𝐻)} 2

= 1_{4 𝑚𝑏}2_{+ 𝑚 (𝑅 −}1 2 𝐻)

2

= 1_{4 𝑚}[𝑏2_{+ (2𝑅 − 𝐻)}2_]

Hubungan 𝜔₁, Ω₁, dan 𝜔 adalah

𝜔1𝑏 = 𝜔 (𝑅 +1_{2 𝐻) ⟹ 𝜔}1 =_2𝑏1 (2𝑅 + 𝐻)𝜔

Ω1(𝑅 +1_{2 𝐻) = 𝜔 (𝑅 +}1_{2 𝐻) ⟹ Ω}1 = 𝜔

Hubungan 𝜔₂, Ω₂, dan 𝜔 adalah

𝜔2𝑏 = 𝜔 (𝑅 −1_{2 𝐻) ⟹ 𝜔}2 =_2𝑏1 (2𝑅 − 𝐻)𝜔

Ω2(𝑅 −1_{2 𝐻) = 𝜔 (𝑅 −}1_{2 𝐻) ⟹ Ω}2 = 𝜔

Energi kinetik roda belakang bagian luar akan menjadi

𝐸𝐾1 =1_{2 (}1_{4 𝑚}[𝑏2 + (2𝑅 + 𝐻)2]) 𝜔2+1_{2 (}1_{2 𝑚𝑏}2)_4𝑏1₂(2𝑅 + 𝐻)2𝜔2

𝐸𝐾1 =_{16 𝑚}1 [2𝑏2 + 3(2𝑅 + 𝐻)2]𝜔2

Dengan cara yang sama untuk roda belakang bagian dalam

𝐸𝐾2 = _{16 𝑚}1 [2𝑏2+ 3(2𝑅 − 𝐻)2]𝜔2

Maka rasio energi kinetik roda belakang bagian luar dan dalam

𝑘 =𝐸𝐾_𝐸𝐾1

2 =

1

16 𝑚[2𝑏2+ 3(2𝑅 + 𝐻)2]𝜔2 1

𝑘 =2𝑏_2𝑏2₂ + 3(2𝑅 + 𝐻)_{+ 3(2𝑅 − 𝐻)}2₂

Dengan memasukkan nilai 𝑅 = 10 m, 𝐻 = 2 m, dan 𝑏 = 0,5 m akan kita dapatkan

𝑘 =2(0,5)_2(0,5)2₂+ 3(2.10 + 2)_{+ 3(2.10 − 2)}2₂ = 1452,5_{972,5 = 1,49357326 …} 𝑘 = 1,49

Number 7 : Peluncur Barang

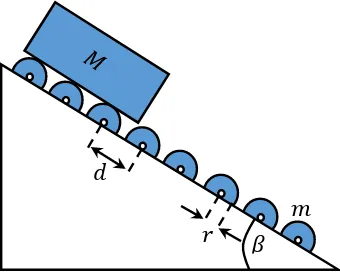
Gambar di bawah memperlihatkan sebuah peluncur barang (slipway) yang sangat panjang, dan berbentuk bidang miring yang membentuk sudut 𝛽 terhadap arah mendatar. Bidang miring tersebut dilengkapi dengan sangat banyak roda (roller) identik, dengan dua roda terdekat berada pada jarak 𝑑 satu sama lain (lihat gambar). Semua roda tersebut memiliki sumbu-sumbu rotasi mendatar dan merupakan silinder-slinder baja pejal yang permukaannya diselubungi dengan lapisan karet yang tipis dan diabaikan massanya. Masing-masing silinder tersebut bermassa 𝑚 dan berjari-jari 𝑟. Sebilah papan dengan massa 𝑀 dan panjang jauh lebih besar daripada 𝑑, mulai dilepas dari puncak peluncur barang tersebut. Abaikan gesekan udara dan gesekan pada poros-poros roda tersebut. Tentukan kelajuan akhir (terminal speed) 𝑣_max papan tersebut.

Pembahasan :

Misalkan papan sudah bergerak sejauh 𝑆 sepanjang bidang miring sampai akhirnya antara roda dan papan tidak terjadi slip lagi. Penurunan energi potensial papan sebesar

𝑀𝑔𝑆 sin 𝛽. Maka sebanyak 𝑆/𝑑 buah roda akan memiliki kecepatan linier permukaan yang sama dengan kecepatan papan, yaitu 𝑣_max. Maka kecepatan sudut tiap roda yang bergerak pada saat ini menjadi 𝜔_max = 𝑣_max/𝑟.

Momen inersia tiap roda adalah

𝐼 =1_{2 𝑚𝑟}2

Penurunan energi potensial papan ini diubah menjadi energi kinetik roda.

𝑀𝑔𝑆 sin 𝛽 =𝑆_𝑑1_{2 𝐼𝜔}max2

𝑀𝑔𝑆 sin 𝛽 =𝑆_𝑑1_{2 (}1_{2 𝑚𝑟}2_{) (}𝑣max 𝑟 )

2

𝑀𝑔𝑆 sin 𝛽 =𝑆_𝑑1_{4 𝑚𝑣}max2… (1)

𝑣max= √4𝑀𝑔𝑑 sin 𝛽_𝑚

Sebenarnya hasil di atas salah, karena kita melupakan kalor yang ditimbulkan akibat gesekan antara permukaan roda dan papan sebelum akhirnya papan mencapai kecepatan terminal. Jadi sebenarnya soal ini agak sedikit rumit, namun tidak tidak terlalu rumit juga sih. Okey kita cari dulu energi yang hilang sebagai kalor.

Misalkan 𝑓_𝑘 adalah gaya gesek kinetik antara permukaan papan dan roda. Dalam interval waktu yang singkat Δ𝑡, akan terjadi perubahan momentum sudut pada tiap roda sebesar

𝐼Δ𝜔 = 𝑓𝑘𝑟Δ𝑡

Dengan menjumlahkan semua perubahan momentum sudut roda, akan kita dapatkan momentum sudut akhir roda (kecepatannya maksimum pada saat akhir ini)

𝑟 ∑ 𝑓𝑘Δ𝑡 = 𝐼𝜔max = 𝐼𝑣max_𝑟

Usaha yang dilakukan gaya gesek kinetik ini pada selang Δ𝑡, akan memunculkan kalor sebesar Δ𝑄 dan besar usaha ini sama dengan gaya gesek kinetik di kalikan dengan besar pergeseran relatif antara kedua permukaan tersebut

Δ𝑄 = 𝑓𝑘(𝑣 − 𝑟𝜔)Δ𝑡

Dengan menjumlahkan semua kalor Δ𝑄 akan kita dapatkan kalor yang ditimbulakn oleh gesekan antara papan dengan sebuah roda

𝑄 = ∑ Δ𝑄

𝑄 = ∑ 𝑓𝑘(𝑣 − 𝑟𝜔)Δ𝑡

𝑄 = ∑ 𝑓𝑘𝑣Δ𝑡 − ∑ 𝜔𝑓𝑘𝑟Δ𝑡

𝑄 = ∑ 𝑓𝑘Δ𝑡 ∑ 𝑣 − 𝐼 ∑ 𝜔Δ𝜔

𝑄 = ∑ 𝑓𝑘Δ𝑡 ∑ 𝑟𝜔 − 𝐼 ∑ 𝜔Δ𝜔

Ingat hubungan diferensial berikut

𝑑(𝜔2_{) = 2𝜔𝑑𝜔}

Karena selang waktu Δ𝑡 sangat singkat, kita bisa lakukan pendekatan

𝑑𝜔 ≈ Δ𝜔 dan 𝑑(𝜔2_{) ≈ Δ(𝜔}2₎ Δ(𝜔2_{) = 2𝜔Δ𝜔 ⟹ 𝜔Δ𝜔 =}1

𝑄 = 𝑟 ∑ 𝑓_⏟ 𝑘Δ𝑡 𝐼𝜔max

∑ 𝜔 ⏟

𝜔max

−_{2 ∑ Δ}𝐼 (𝜔2₎ ⏟

𝜔max2

𝑄 = 𝐼𝜔max2−1_{2 𝐼𝜔}max2

𝑄 =1_{2 𝐼𝜔}max2 =1_{2 (}1_{2 𝑚𝑟}2) (𝑣max_{𝑟 )} 2

𝑄 =1_{4 𝑚𝑣}max2

Tambahkan faktor 𝑄 ini pada persamaan (1) (ingat bahwa 𝑄 adalah energi kinetik tiap roda)

𝑀𝑔𝑆 sin 𝛽 =𝑆_𝑑1_{4 𝑚𝑣}max2+_{𝑑 𝑄}𝑆

𝑀𝑔𝑆 sin 𝛽 =𝑆_𝑑1_{4 𝑚𝑣}max2+_𝑑𝑆1_{4 𝑚𝑣}max2 ⟹ 𝑣max = √2𝑀𝑔𝑑 sin 𝛽_𝑚

Number 8 : Kapasitor dan Dielektrik

Sebuah kapasitor keping sejajar mempunyai luas lempeng 𝐴 terpisah sejauh 𝑑. Serta tinggi 𝑎. Ruang di antara kapasitor berisi udara dengan permitivitas yang bisa dianggap sama dengan ruang hampa yaitu 𝜀₀. Kapasitor kemudian dihubungkan dengan sebuah baterai yang memiliki tegangan 𝑉₀. Kemudian baterai diputuskan, muatan pada kapasitor dipertahankan tetap sebesar 𝑄₀, kemudian sebuah lembaran dielektrik padat dengan luas 𝐴 dan tebal 𝑙 (dimana 𝑙 <d) serta konstanta dielektrik 𝐾₁ disisipkan tepat di tengah kapasitor. Hitung :

a. Muatan induksi pada dielektrik!

b. Medan listrik pada ruang diantara dielektrik dan plat! c. Medan listrik pada dielektrik!

d. Beda potensial kapasitor setelah dielektrik di masukkan!

Pembahasan :

a. Medan listrik awal pada kapasitor sebelum ada dielektrik adalah

𝐸0 = 𝜎_𝜀0

0 =

𝑄0 𝐴𝜀0

Ketika dielektrik dimasukkan, kapasitansi kapasitor akan meningkat namun medan listrik total di dalamnya akan berkurang menjadi 𝐸 dimana

𝐸 =_𝐾𝐸0 1

Paul. A Tipler halaman 114). Maka medan listrik pada dielektrik adalah selisih 𝐸 dan

𝐸0.

𝐸D = 𝐸0− 𝐸 𝐸D = 𝐸0(1 −_𝐾1

1) 𝜎ind

𝜀0 = 𝜎0 𝜀0(1 −

1

𝐾1) ⟹ 𝑄ind = 𝑄0(1 − 1 𝐾1)

b. Medan listrik pada ruang di antara dielektrik dan plat sama dengan medan listrik awal kapasitor

𝐸0 =_𝐴𝜀𝑄0 0

c. Medan listirk pada dielektrik adalah

𝐸D =_𝐴𝐾𝑄0 1𝜀0

d. Beda potensial pada kapasitor adalah

𝑉 = − ∫ 𝐸⃗ ̇. 𝑑𝑙 = 𝐸0(𝑑 − 𝑙) + 𝐸D𝑙

𝑉 = 𝐸0(𝑑 − 𝑙) +𝐸_𝐾0

1𝑙 ⟹ 𝑉 = 𝑄0