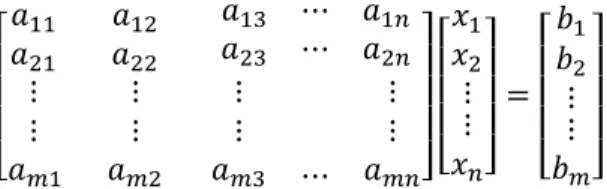BioWallacea Jurnal Ilmiah Ilmu Biologi Mei 2015 Vol. 1 No. 2, p 98-103
ISSN: 2442-2622
Analisis Diagonalisasi Matriks untuk Menentukan Individu ke
-n
Berdasarkan
Peluang Genotip Induk
M. Yakin Silmi Kaffah
1, Mamika Ujianita Romdhini
1,2 1Program Studi Matematika FMIPA Unram
Jln. Majapahit 62 Mataram 83125. Telp 0370-641724
2
Email : mamika_ur@yahoo.com
Genetika adalah salah satu cabang dari ilmu biologi yang mempelajari hereditas yaitu penurunan sifat dari satu generasi ke generasi berikutnya. Seiring perkembanagn ilmu pengetahuan para peneliti ingin mendapatkan suatu individu yang unggul dari beberapa generasi suatu individu. Penelitian ini bertujuan untuk mengetahui peluang dari suatu individu jika dilakukan perkawinan hingga generasi ke-n. Permasalahan tersebut dapat diselesaikan dengan analisis diagonalisasi matriks berdasarkan peluang dari genotip induk suatu spesies. Hal-hal yang berkaitan untuk melakukan diagonalisasi adalah nilai eigen dan vektor eigen dari matriks peluang genotip induk. Hasil yang diperoleh berupa persamaan 𝒙𝒏= 𝑨𝒏𝒙𝟎, dengan demikian dapat diketahui peluang individu pada generasi ke-n ketika
limit n menuju tak hingga dengan induk BbLL berupa 0.25 BBLL, 0.5 BbLL, dan 0.5 bbLL. Perhitungan dalam penelitian ini menggunakan aplikasi MATHEMATICA 6.
Kata-kata kunci : Diagonalisasi matriks, limit, genotip. PENDAHULUAN
Genetika adalah salah satu cabang dari ilmu biologi yang mempelajari hereditas yaitu penurunan sifat dari satu generasi ke generasi berikutnya. Sifat yang diwariskan dari suatu induk berupa sifat genotip dan fenotip. Genotip adalah bentuk atau susunan genetis suatu karakter yang dikandung individu dalam sel tubuhnya, sedangkan fenotip adalah suatu karakteristik yang dapat diukur atau sifat yang nyata pada suatu organisme. Karakteristik itu bisa tampak seperti warna dan ukuran (William.1991).
Dalam bidang biologi muncul suatu permasalahan yaitu ingin mengetahui suatu individu yang unggul dari beberapa generasi jika dilakukan perkawinan secara kontinyu terhadap individu tersebut, namun jika dilakukan secara konvensional sangat merugikan karena waktu yang cukup lama dan biaya yang tinggi jika spesiesnya tergolong langka dan mahal. Permasalahan tersebut dapat diselesaikan dengan analisis diagonalisasi matriks berdasarkan peluang dari genotip induk suatu spesies. Matriks yang digunakan berasal dari tabel peluang genotip induknya
Penelitian ini bertujuan untuk membuat sistem persamaan linear berdasarkan tabel genotip perkawinan. Berdasarkan tabel yang akan terbentuk peneliti dapat mengetahui sifat individu pada generasi ke-n dengan acara analisis
diagonalisasi matriks. Perhitungan pada penelitian ini menggunakan Mathematica versi 6 untuk mempermudah. Adapun beberapa definisi yang digunakan adalah sebagai berikut.
Definisi 1 : Suatu persamaan linear dalam n peubah (variable) adalah persamaan dengan bentuk :
𝑎1𝑥1+ 𝑎2𝑥2+ 𝑎3𝑥3+ ⋯ + 𝑎𝑛𝑥𝑛 = 𝑏
dengan 𝑎1, 𝑎2, 𝑎3… , 𝑎𝑛 dan b adalah bilangan
real dan 𝑥1, 𝑥2, 𝑥3… , 𝑥𝑛 adalah peubah. Dengan
demikian suatu sistem linear dari m persamaan dalam n peubah adalah suatu sistem berbentuk :
𝑎11𝑥1 + 𝑎12𝑥2 + ⋯ + 𝑎1𝑛𝑥𝑛 = 𝑏1
𝑎21𝑥1 + 𝑎22𝑥2 + ⋯ + 𝑎2𝑛𝑥𝑛 = 𝑏2
⋮ ⋮ ⋮ ⋮ 𝑎𝑚1𝑥1+ 𝑎𝑚2𝑥2+ ⋯ + 𝑎𝑚𝑛𝑥𝑛= 𝑏𝑚
dengan 𝑎𝑚𝑛 dan 𝑏𝑚 (𝑢𝑛𝑡𝑢𝑘 𝑚, 𝑛 = 1,2, . . . , 𝑛)
adalah bilangan real sehingga persamaan di atas sebagai sistem persamaan linear (𝑚 × 𝑛). Bentuk sistem persamaan linear tersebut dapat diubah menjadi suatu matriks, menurut Anton (2004) bentuk matriks dari suatu system persamaan linear dengan n variabel dan m persamaan secara umum adalah sebagai berikut :
[ 𝑎11 𝑎12 𝑎13 ⋯ 𝑎1𝑛 𝑎21 𝑎22 𝑎23 ⋯ 𝑎2𝑛 ⋮ ⋮ 𝑎𝑚1 ⋮ ⋮ 𝑎𝑚2 ⋮ ⋮ 𝑎𝑚3 ⋯ ⋮ ⋮ 𝑎𝑚𝑛][ 𝑥1 𝑥2 ⋮ ⋮ 𝑥𝑛] = [ 𝑏1 𝑏2 ⋮ ⋮ 𝑏𝑚]
Akibatnya berdasarkan persamaan tersebut kita dapat menuliskan berturut-turut sebagai matriks
𝐴𝑚×𝑛, 𝑥𝑛×1, dan 𝑏𝑚×1, maka sistem persamaan
linear tersebut secara umum dapat ditulis 𝐴𝒙 = 𝑏. Solusi dari persamaan linear 𝑎1𝑥1+ 𝑎2𝑥2+
𝑎3𝑥3+ ⋯ + 𝑎𝑛𝑥𝑛= 𝑏 adalah suatu urutan dari 𝑛
bilangan 𝑠1, 𝑠2, . . . , 𝑠𝑛 sedemikian rupa
sehingga persamaan tersebut akan terpenuhi jika kita menggantikan 𝑥1 = 𝑠1, 𝑥2= 𝑠2, . . . , 𝑥𝑛 =
𝑠𝑛. Kumpulan semua solusi dari persamaan itu
disebut himpunan solusi atau solusi umum. Setiap sistem persamaan linear dapat tidak memiliki solusi, memiliki tepat satu solusi, atau memiliki takterhingga banyaknya solusi. Persamaan Ax = b, dinamakan sistem persamaan linear homogen jika nilai b = 0, dan jika b ≠ 0 disebut sistem persamaan linear tidak homogen.
Definisi 2 : Misalkan 𝐴 adalah suatu matriks 𝑛 × 𝑛. Skalar 𝜆 disebut sebagai suatu nilai eigen atau nilai karakteristik dari 𝐴 jika terdapat suatu vektor takk nol 𝒙, sehingga 𝐴𝒙 = 𝜆𝒙. vektor 𝒙 disebut vektor eigen atau vektor kaarakteristik dari λ.
METODE PENELITIAN
Dalam penelitian ini metode yang dilakukan adalah studi literatur. Langkah pertama yaitu membuat tabel peluang berdasarkan genotip induk yang dipilih, dalam hal ini induk yang digunakan adalah BbLL dengan semua kemungkinannya. Langkah berikutnya yaitu melakukan proses diagonalisasi dan manipulasinya. Berikut lebih lanjut akan dibahas pada pembahasan.
HASIL PENELITIAN Proses Diagonalisasi
Proses diagonalisasi matriks adalah sebagai berikut :
Misalkan 𝐴 adalah matriks 𝑛 × 𝑛.
1. Tentukan nilai eigen dari matriks 𝐴 yaitu
𝜆1, 𝜆2, . . . , 𝜆𝑛 dengan 𝑛 = 1,2,.
2. Tentukan 𝑛 vektor eigen dari nilai eigen yang terkait matriks 𝐴 dengan syarat setiap vektor-vektor eigen 𝒑1, 𝒑𝟐, . . . , 𝒑𝑛
adalah bebas linear.
3. Dibentuk suatu matriks 𝑃 dengan
𝒑1, 𝒑𝟐, . . . , 𝒑𝑛 sebagai vektor-vektor
kolomnya.
4. Matriks 𝑃−1𝐴𝑃 adalah matriks diagonal dengan 𝜆1, 𝜆2, . . . , 𝜆𝑛 sebagai entri-entri
diagonalnya.
Berdasarkan matriks diagonalisasi 𝐷 = 𝑃−1𝐴𝑃
akan dilakukan manipulasi aljabar untuk mencari rumusan matriks 𝐷𝑛 dan 𝐴𝑛.
Misalkan 𝐷 = 𝑃−1𝐴𝑃
Untuk mencari 𝐷2 maka :
𝐷2 = 𝑃−1𝐴𝑃𝑃−1𝐴𝑃
Perhatikan 𝑃−1𝑃 = 𝑃𝑃−1= 𝐼 maka
𝐷2= 𝑃−1𝐴𝐴𝑃 𝐷2= 𝑃−1𝐴2𝑃
Untuk mencari 𝐷3 maka :
𝐷3= 𝑃−1𝐴2𝑃𝑃−1𝐴𝑃
Perhatikan 𝑃−1𝑃 = 𝑃𝑃−1= 𝐼 maka
𝐷3= 𝑃−1𝐴2𝐴𝑃 𝐷2= 𝑃−1𝐴3𝑃
Sehingga untuk 𝐷𝑛 menjadi :
𝐷𝑛= 𝑃−1𝐴(𝑃𝑃−1)𝐴(𝑃𝑃−1)𝐴𝑃 … 𝑃−1𝐴𝑃
𝐷𝑛= 𝑃−1𝐴𝑛𝑃
Berdasarkan hasil 𝐷𝑛 = 𝑃−1𝐴𝑛𝑃, akan ditentukan
matriks 𝐴𝑛 yaitu sebagai berikut :
𝐷𝑛= 𝑃−1𝐴𝑛𝑃
Kedua ruas bagian kanan dikalikan dengan 𝑃−1
sehingga menjadi :
𝐷𝑛𝑃−1= 𝑃−1𝐴𝑛𝑃𝑃−1
Perhatikan 𝑃−1𝑃 = 𝑃𝑃−1= 𝐼 maka
𝐷𝑛𝑃−1= 𝑃−1𝐴𝑛
Selanjutnya kedua ruas bagian kiri dikalikan dengan 𝑃 menjadi :
𝑃𝐷𝑛𝑃−1= 𝑃𝑃−1𝐴𝑛
Perhatikan 𝑃−1𝑃 = 𝑃𝑃−1= 𝐼 maka
𝑃𝐷𝑛𝑃−1= 𝐴𝑛 (1)
Tabel 1 Peluang genotip dari perkawinan BbLL dengan semua kemungkinannya Genoti p Genotip Induk Keturu nan BBLL-BbLL BBLl-BbLL BBll-BbLL BbLL-BbLL BbLL-BbLl BbLL-Bbll BbLL-bbLL BbLL-bbLl BbLL -bbll BBLL 0.5 0.25 0 0.25 0.125 0 0 0 0 BBLl 0 0.25 0.5 0 0.125 0.25 0 0 0 BBll 0 0 0 0 0 0 0 0 0 BbLL 0.5 0.25 0 0.5 0.25 0 0.5 0.25 0
BbLl 0 0.25 0.5 0 0.25 0.5 0 0.25 0.5
Bbll 0 0 0 0 0 0 0 0 0
bbLL 0 0 0 0.25 0.125 0 0.5 0.25 0
bbLl 0 0 0 0 0.125 0.25 0 0.25 0.5
Bbll 0 0 0 0 0 0 0 0 0
Dalam menentukan hasil keturunan pada generasi ke-n akan dimisalkan bentuk lain dari genotip-genotip keturunan sebagai berikut :
𝑎𝑛= genotip BBLL pada generasi ke-n
𝑏𝑛 = genotip BBLl pada generasi ke-n
𝑐𝑛= genotip BBll pada generasi ke-n
𝑑𝑛= genotip BbLL pada generasi ke-n
𝑒𝑛 = genotip BbLl pada generasi ke-n
𝑓𝑛= genotip Bbll pada generasi ke-n
𝑔𝑛 = genotip bbLL pada generasi ke-n
ℎ𝑛= genotip bbLl pada generasi ke-n
𝑖𝑛= genotip bbll pada generasi ke-n
𝑎𝑛+ 𝑏𝑛+ 𝑐𝑛+ 𝑑𝑛+ 𝑒𝑛+ 𝑓𝑛+ 𝑔𝑛+ ℎ𝑛+ 𝑖𝑛
= 1
Untuk 𝑛 = 0,1,2,. . .
Berdasarkan tabel (1) tersebut akan dirumuskan suatu sistem persamaan linear yaitu
𝑎𝑛= 1 2𝑎𝑛−1+ 1 4𝑏𝑛−1+ 1 4𝑑𝑛−1+ 1 8𝑒𝑛−1 𝑏𝑛= 1 4𝑏𝑛−1+ 1 2𝑐𝑛−1+ 1 8𝑒𝑛−1+ 1 4𝑓𝑛−1 𝑐𝑛= 0 𝑑𝑛= 1 2𝑎𝑛−1+ 1 4𝑏𝑛−1+ 1 2𝑑𝑛−1+ 1 4𝑒𝑛−1+ 1 2𝑔𝑛−1+ 1 4ℎ𝑛−1 𝑒𝑛 = 1 4𝑏𝑛−1+ 1 2𝑐𝑛−1+ 1 4𝑒𝑛−1+ 1 2𝑓𝑛−1+ 1 4ℎ𝑛−1+ 1 2𝑖𝑛−1 𝑓𝑛= 0 𝑔𝑛= 14𝑑𝑛−1+18𝑒𝑛−1+12𝑔𝑛−1+14ℎ𝑛−1 ℎ𝑛 = 1 8𝑒𝑛−1+ 1 4𝑓𝑛−1+ 1 4ℎ𝑛−1+ 1 2𝑖𝑛−1 𝑖𝑛 = 0
Berdasarkan sistem persamaan linear tersebut dapat diubah dalam bentuk matriks 𝑥𝑛= 𝐴𝑥𝑛−1 secara berturut-turut sebagai berikut :
[ 𝑎𝑛 𝑏𝑛 𝑐𝑛 𝑑𝑛 𝑒𝑛 𝑓𝑛 𝑔𝑛 ℎ𝑛 𝑖𝑛] [ 1 2 1 4 0 1 4 1 8 0 0 0 0 0 1 4 1 2 0 1 8 1 4 0 0 0 0 0 0 0 0 0 0 0 0 1 2 1 4 0 1 2 1 4 0 1 2 1 4 0 0 1 4 1 2 0 1 4 1 2 0 1 4 0 0 0 0 0 0 0 0 0 0 0 0 0 1 4 1 8 0 1 2 1 4 0 0 0 0 0 1 8 1 4 0 1 4 1 2 0 0 0 0 0 0 0 0 0] [ 𝑎𝑛−1 𝑏𝑛−1 𝑐𝑛−1 𝑑𝑛−1 𝑒𝑛−1 𝑓𝑛−1 𝑔𝑛−1 ℎ𝑛−1 𝑖𝑛−1] Dengan 𝑛 = 1,2,. . .
Berdasarkan persamaan 𝑥𝑛= 𝐴𝑥𝑛−1 maka akan
dilakukan manipulasi sebagai berikut :
Perhatikan 𝑥𝑛−1= 𝐴𝑥𝑛−2 dan 𝑥𝑛−2= 𝐴𝑥𝑛−3 maka 𝑥𝑛 = 𝐴𝑥𝑛−1 = 𝐴(𝐴𝑥𝑛−2) = 𝐴2(𝐴𝑥𝑛−3) = 𝐴𝑛−1(𝐴𝑥0) = 𝐴𝑛𝑥0
dengan demikian 𝑥𝑛 dapat di Definisikan sebagai :
𝑥𝑛= 𝐴𝑛𝑥0
Untuk mencari nilai 𝐴𝑛 akan dilakukan proses diagonalisasi matriks berdasarkan proses diagonalisasi.
Langkah pertama yaitu mencari nilai eigen dari matriks 𝐴. Berdasarkan Definisi (2) yaitu nilai eigen matriks 𝐴 dapat dicari dengan 𝑑𝑒𝑡(𝐴 − 𝐼𝜆) = 0 Sehingga didapatkan 𝑑𝑒𝑡(𝐴 − 𝐼𝜆) = −𝜆 5 16+ 9𝜆6 16 − 7𝜆7 4 + 9𝜆8 4 − 𝜆 9= 0
Maka diperoleh akar-akar dari polinom berderajat sembilan sebagai berikut :
𝜆1= 1, 𝜆2= 1 2, 𝜆3 = 1 2, 𝜆4= 1 4, 𝜆5 = 0, 𝜆6 = 0, 𝜆7 = 0, 𝜆8= 0, 𝜆9= 0
Sehingga matriks 𝐴𝑛 dapat di Definisikan sebagai berikut:
𝐴𝑛= 𝐶𝐷𝑛𝐶−1
Selanjutnya kita dapat menetukan bentuk dari 𝒙𝑛= 𝐴𝑛𝒙0
Dengan vektor 𝒙0= (𝑎0, 𝑏0, 𝑐0, 𝑑0, 𝑒0, 𝑓0, 𝑔0, ℎ0, 𝑖0)
Dan didefinisikan suatu bentuk :
𝑎𝑛+ 𝑏𝑛+ 𝑐𝑛+ 𝑑𝑛+ 𝑒𝑛+ 𝑓𝑛+ 𝑔𝑛+ ℎ𝑛+ 𝑖𝑛= 1 untuk 𝑛 = 0,1,2,. . . n berhingga.
0
4
2
2
2
2
2
4
2
2
2
4
4
1
2
2
4
1
2
4
1
2
4
1
2
4
1
4
1
4
2
4
1
2
3
2
4
1
2
4
1
0
2
2
2
2
2
2
2
2
1
2
2
1
2
1
2
2
1
2
2
1
2
1
2
2
1
2
2
1
2
1
0
4
2
2
2
2
2
4
2
2
2
4
2
4
1
2
2
2
4
1
2
4
1
2
2
4
1
2
2
4
1
4
1
4
4
1
2
2
3
2
4
1
2
4
1
0 1 0 2 2 1 0 1 0 2 0 1 0 2 2 1 0 0 2 2 1 0 1 0 1 0 2 0 0 0 2 2 1 0 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 1 0 0 0 1 0 0 1 0 2 2 1 0 1 0 2 0 1 0 2 2 1 0 0 1 2 2 1 0 1 0 1 0 1 2 0 0 0 1 2 2 1 0 1i
h
f
e
c
b
i
h
g
f
e
d
c
b
a
i
h
f
e
c
b
i
h
g
f
e
d
c
b
a
i
h
f
e
c
b
i
h
g
f
e
d
c
b
a
i
h
g
f
e
d
c
b
a
x
n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n nDengan demikian untuk mengetahui peluang genotip individu pada generasi ke-n maka dapat dilihat dari limit menuju tak hingga untuk matriks
𝑥𝑛. n nx
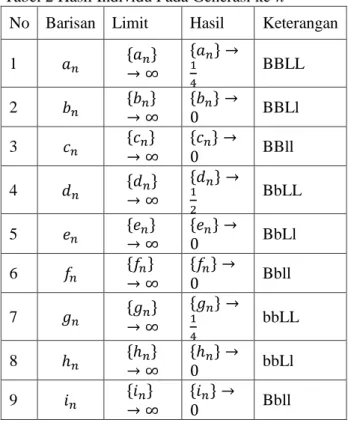
lim diperoleh hasil sebagai berikut : Tabel 2 Hasil Individu Pada Generasi ke-n
No Barisan Limit Hasil Keterangan 1 𝑎𝑛 {𝑎→ ∞𝑛} {𝑎𝑛} → 1 4 BBLL 2 𝑏𝑛 {𝑏→ ∞𝑛} {𝑏0 𝑛} → BBLl 3 𝑐𝑛 {𝑐→ ∞𝑛} {𝑐0 𝑛} → BBll 4 𝑑𝑛 {𝑑→ ∞𝑛} {𝑑𝑛} → 1 2 BbLL 5 𝑒𝑛 {𝑒→ ∞𝑛} {𝑒0 𝑛} → BbLl 6 𝑓𝑛 {𝑓→ ∞𝑛} {𝑓0 𝑛} → Bbll 7 𝑔𝑛 {𝑔→ ∞𝑛} {𝑔𝑛} → 1 4 bbLL 8 ℎ𝑛 {ℎ→ ∞𝑛} {ℎ0 𝑛} → bbLl 9 𝑖𝑛 {𝑖→ ∞𝑛} {𝑖0 𝑛} → Bbll
Berdasarkan hasil genotip yang diperoleh pada generasi ke-n, dapat diberikan suatu studi kasus terhadap biji suatu tumbuhan untuk melihat sifat fenotip yang muncul pada generasi ke-n akibat sifat genotip yang terjadi.
Tabel 3 Genotip dan Fenotip No Genotip Fenotip 1 BBLL Smooth Yellow 2 BBLl Smooth Yellow 3 BBll Smooth Green 4 BbLL Smooth Yellow 5 BbLl Smooth Yellow 6 Bbll Smooth Green 7 bbLL Wrinkled Yellow 8 bbLl Wrinkled Yellow 9 Bbll Wrinkled Yellow
Berdasarkan tabel tersebut dapat diketahui hasil individu pada generasi ke-n, yaitu individu bergenotip BBLL dengan peluang sebesar 0.25
yang memiliki sifat biji Smooth Yellow, BbLL dengan peluang sebesar 0.5 memiliki sifat Smooth Yellow dan bbLL dengan peluang sebesar 0.25
yang memiliki sifat biji Wrinkled Yellow, sedangkan tumbuhan lainnya memiliki nilai peluang genotip nol pada generasi ke-n. Hal berarti semua individu yang muncul memiliki sifat biji yang cukup baik.
KESIMPULAN
1. Suatu permasalahan genetika yaitu pewarisan sifat berdasarkan peluang genotipnya dapat disajikan dalam bentuk sistem persamaan linear
𝒙 = 𝑏 . Adapun yang mempengaruhi sistem persamaan linear tersebut adalah sifat dari induk-induknya.
2. Matriks peluang genotip dengan ukuran 9x9 memiliki vektor-vektor eigen yang bebas linear sehingga dapat dilakukan proses diagonalisasi. 3. Hasil individu yang terbentuk terhadap induk
BbLL adalah 0.25 BBLL, 0.5 BbLL, dan 0.5 bbLL.
sifat-sifat genotip yang lebih banyak dan variatif agar sifat-sifat tumbuhan yang terbentuk lebih banyak.
Berdasarkan penelitian yang telah dilakukan diharapakan dapat dijadikan sebagai acuan untuk para peneliti dibidang genetika sebelum melakukan percobaan perkawinan suatu tumbuhan dengan dua sifat beda. Diharapkan juga bagi peneliti yang ingin memperluas penelitian ini dapat melakukan modifikasi sifat-sifat genotip yang lebih banyak dan variatif agar sifat-sifat tumbuhan yang terbentuk lebih banyak.
DAFTAR PUSTAKA
Anton, H. & Rores, C., 2004, Aljabar Linear Elementer Versi Aplikasi , Edisi 8, Jilid 1. Erlangga. Jakarta.
Bartle, Robert G. & Sherbet, Donald R. 1927. Introduction to Real Analysis. John Wesley & sons. New York.
William D. 1991.Teori dan Soal-Soal Genetika.Erlangga. Jakarta.
Wijayanti, K. 1997. Penerapan Diagonalisasi
Matriks Dalam Genetika Terapan.
Cakrawala Pendidikan. XVI :93-104.
Yuliani, S. 2012. Penerapan Diagonalisasi Matriks dan Matriks Leslie Dalam Memproyeksikan Jumlah Populasi Perempuan. UNNES Journal of mathematics., 1(2):52-5