MODEL MATEMATIKA UNTUK PERUBAHAN SUHU DAN KONSENTRASI DOPANT PADA PEMBENTUKAN SERAT OPTIK MIFTAHUL JANNAH

(1)

MODEL MATEMATIKA UNTUK PERUBAHAN SUHU

DAN KONSENTRASI DOPANT

PADA PEMBENTUKAN SERAT OPTIK

MIFTAHUL JANNAH

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2009

(2)

Dengan ini saya menyatakan bahwa tesis dengan judul Model Matematika untuk Perubahan Suhu dan Konsentrasi Dopant pada Pembentukan Serat Optik adalah karya saya sendiri dengan arahan dari komisi pembimbing, dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Agustus 2009

Miftahul Jannah NIM G551070681

(3)

Dopant Concentration Changes on the Optical Fiber Drawing. Under supervision of JAHARUDDIN and SISWANDI

Optical fibers are made of transparent material (glass) with different refractive indices in the inner core and the outer cladding regions. This refractive index difference is achieved normally by adding a dopant to the inner core region. The objective of this thesis is to analyze a mathematical model for the temperature changes and dopant concentration changes during the fiber drawing process. Using a long-wave approximation, the governing equations can be reduced to a simple diffusion equation. As a result, we are able to identify key dimensionless parameters that contribute to the diffusion process. We also derive solutions for the temperature and dopant concentration. Temperature and dopant concentration depend on the viscosity and the diffusion coefficient. Some numerical simulations using Maple 12 software are carried out to explain the attitude of the solution with respect to temperature changes and dopant concentration changes during the fiber drawing.

(4)

Konsentrasi Dopant pada Pembentukan Serat Optik. Dibimbing oleh JAHARUDDIN dan SISWANDI

Serat optik merupakan serat yang terbuat dari bahan bening (transparan) yang terdiri atas teras dan selubung. Teras adalah bagian sebelah dalam dan selubung adalah lapisan di luarnya yang memiliki indeks bias, yang dapat memandu perambatan cahaya dengan pemantulan internal pada antarmuka teras-selubungnya. Indeks bias ini diperoleh dengan menambahkan sesuatu yang bersifat penghalus (dopant) di dalam teras. Masalah dalam peneitian ini adalah bagaimana menentukan hubungan antara konsentrasi dopant, suhu, dan jari-jari turbulen pada tungku pembakaran.

Tujuan penelitian ini adalah mengkaji model matematika untuk suhu, jari-jari turbulen, dan konsentrasi dopant selama pembentukan serat optik dengan menggunakan asumsi gelombang panjang. Berdasarkan solusi yang diperoleh akan ditentukan keterkaitan suhu, jari-jari turbulen dan konsentrasi dopant terhadap jarak dari input nozzle sepanjang sumbu fiber. Hasilnya disajikan dalam suatu simulasi numerik.

Model persamaan untuk suhu dan konsentrasi dopant diturunkan berdasarkan persamaan dasar fluida. Persamaan dasar fluida diturunkan dengan menggunakan hukum kekekalan massa, kekekalan momentum, kekekalan energi dan konsentrasi dopant. Model persamaan untuk suhu dan konsentrasi dopant disederhanakan dengan menggunakan asumsi gelombang panjang, rapat massa fluida yang cukup kecil, dan konduktivitas panas yang hingga, maka diperoleh persamaan difusi yang sederhana.

Kajian terhadap persamaan difusi yang telah diperoleh dilakukan dengan meninjau dua proses fisis, yaitu proses sebelum melalui pendinginan dan proses dalam keadaan pendinginan. Dari kedua proses tersebut di atas diperoleh suhu dan jari-jari turbulen. Selain kedua proses fisis tersebut, ditentukan pula konsentrasi dopant. Konsentrasi dopant diperoleh berdasarkan koefisien difusi yang bentuknya berupa fungsi Green. Karakteristik solusi dari persamaan difusi ditentukan berdasarkan suatu simulasi numerik. Simulasi numerik dilakukan dengan bantuan software Maple 12.

Hasil simulasi numerik untuk proses sebelum melalui pendinginan, diperoleh bahwa semakin besar jarak dari input nozzle sepanjang sumbu fiber, maka suhunya akan semakin besar dan jari-jari turbulennya semakin mengecil. Dalam proses pendinginan diperoleh bahwa semakin besar jarak dari input nozzle sepanjang sumbu fiber, maka suhu dan jari-jari turbulennya akan semakin mengecil. Untuk perubahan konsentrasi dopant diperoleh bahwa semakin besar jarak dari input nozzle sepanjang sumbu fiber, maka konsentrasi dopant akan semakin mengecil.

(5)

bidang, seperti di bidang kedokteran. Pada bidang kedokteran, salah satu contoh alat yang terbuat dari serat optik adalah cystoscope. Alat lain yang sangat bermanfaat dalam kehidupan sehari-hari adalah kacamata, kaca pembesar, mikroskop, kamera dan lain sebagainya. Dengan demikian hasil dari tesis ini memiliki manfaat yang cukup besar.

(6)

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Desember 2008 ini adalah serat optik, dengan judul Model Matematika untuk Perubahan Suhu dan Konsentrasi Dopant pada Pembentukan Serat Optik.

Terima kasih penulis ucapkan kepada Bapak Dr. Jaharuddin, M.S. dan Bapak Drs. Siswandi, M.Si. selaku pembimbing, serta Drs. Ali Kusnanto, M.Si. selaku penguji luar komisi yang telah membimbing dan banyak memberikan saran. Ucapan terima kasih juga disampaikan kepada Departemen Agama Republik Indonesia yang telah memberikan beasiswa kepada penulis selama menempuh pendidikan di IPB. Ucapan terima kasih yang tiada hingga kepada abeh, mamah, suami, serta seluruh keluarga, atas segala do’a dan kasih sayangnya.

Semoga karya ilmiah ini bermanfaat.

Bogor, Agustus 2009

(7)

Sobur dan ibu Aminah. Penulis merupakan anak kedua dari tiga bersaudara. Tahun 2000 penulis lulus MAN 8 jurusan Ilmu Pengetahuan Alam dan pada tahun yang sama lulus seleksi masuk Universitas Islam Negeri Syarif Hidayatullah Jakarta. Penulis memilih jurusan Pendidikan Matematika pada Fakultas Ilmu Tarbiyah dan Keguruan dan selesai pada tahun 2004.

Tahun 2005 penulis menjadi staf pengajar di MAN 8 Jakarta. Pada tahun 2007 penulis lulus seleksi masuk Program Magister Program Studi Matematika Terapan di Institut Pertanian Bogor melalui jalur Beasiswa Utusan Daerah Departemen Agama Republik Indonesia.

(8)

@ Hak Cipta Milik IPB, tahun 2009 Hak Cipta dilindungi Undang-undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber

a. Pengutipan hanya boleh untuk kepentingan pendidikan penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah,

b. Pengutipan tidak merugikan kepentingan yang wajar IPB

2. Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis dalam bentuk laporan apapun tanpa izin IPB

(9)

Nama : Miftahul Jannah NIM : G551070681

Disetujui Komisi Pembimbing

Dr. Jaharuddin, M.S. Drs. Siswandi, M.Si.

Ketua Anggota

Diketahui

Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.

(10)

(11)

Halaman DAFTAR GAMBAR... ix DAFTAR LAMPIRAN... x I PENDAHULUAN 1.1 Latar Belakang... 1 1.2 Tujuan Penelitian... 2 II LANDASAN TEORI 2.1 Persamaan Dasar... 3 2.2 Syarat Batas... 4 2.3 Penyederhanaan Model... 5

III PEMBAHASAN DAN HASIL 3.1 Suhu dan Jari-jari turbulen... 10

3.1.1 Proses Sebelum Melalui Pendinginan... 10

3.1.2 Proses Dalam Keadaan Pendinginan... 13

3.2 Difusi Dopant... 18

IV KESIMPULAN DAN SARAN 4.1 Kesimpulan... 22

4.2 Saran... 22

DAFTAR PUSTAKA... 23

LAMPIRAN... 24

(12)

Halaman

1. Skema Pemanasan dan Pendinginan... 4

2. Grafik fungsi θ dan s untuk ℋ_f = 100, α_μ = 30, dan D_r = 104_{... 13}

3. Grafik fungsi θ dan s dengan 𝒜 = 1,71 dan ℋc = 350... 17

4. Grafik fungsi θ dan s dengan 𝒜 = 0,78 dan ℋc = 1... 18

5. Grafik Konsentrasi Dopant dengan α_D = 20, ⊖= 0,15, 𝒫 = 3. 10−3_, ℋ_f = 350, α_μ = 40, dan D_r = 104_{... 21}

(13)

Halaman

1. Penurunan Persamaan (2.14) – (2.18)... 24

4. Penurunan Persamaan (3.18) dan (3.19)... 45

10. Penurunan Persamaan (3.44) – (3.46)... ... 57

12. Penurunan Persamaan (3.56)... 62

(14)

I PENDAHULUAN

1.1 Latar Belakang

Serat optik merupakan serat yang terbuat dari bahan bening (transparan) yang terdiri atas teras dan selubung. Teras adalah bagian sebelah dalam dan selubung adalah lapisan diluarnya yang memiliki indeks bias, yang dapat memandu perambatan cahaya dengan pemantulan internal pada antarmuka teras-selubungnya.

Serat optik mempunyai banyak kegunaan di berbagai bidang, seperti di bidang kedokteran. Pada bidang kedokteran, salah satu contoh alat yang terbuat dari serat optik adalah cystoscope. Alat cystoscope dipakai oleh ahli bedah untuk mengamati dan melakukan operasi dengan kendali jarak jauh. Alat lain yang sangat bermanfaat dalam kehidupan sehari-hari adalah kacamata, kaca pembesar, mikroskop, kamera dan lain sebagainya. Serat optik tersebut terbuat dari kaca yang dilelehkan kemudian direntangkan dengan menggunakan penarik mekanis. Kaca setengah jadi tersebut dibuat sebuah komponen peranti sehingga terjadi perbedaan antara indeks bias di bagian dalam inti dengan bagian lapis terluarnya. Indeks bias ini diperoleh dengan menambahkan sesuatu yang bersifat penghalus (dopant) di bagian dalam inti [3]. Umumnya material penghalus yang digunakan adalah germanium dioksida (GeO2), fosfor pentoksida (P2O5), dan boron (B) yang

tersedia dalam bentuk silika (SiO2). Selama perentangan, pemotongan, dan

penggabungan, indeks bias tersebut dapat berubah dikarenakan adanya material penghalus tersebut [6,9].

Perubahan konsentrasi material penghalus tersebut diakibatkan oleh pemotongan dan penggabungan dari serat optik. Proses perubahan konsentrasi akan menjadi lebih rumit karena adanya penyatuan material penghalus tersebut. Penyatuan material tersebut tidak hanya bergantung pada suhu, akan tetapi banyak faktor lainnya termasuk proses mekanisnya.

Beberapa peneliti telah melakukan suatu simulasi yang mengkhususkan pada pembentukan serat optik [4]. Dalam penelitiannya tersebut, suatu perentangan yang relatif perlahan, diperlihatkan bahwa semakin besar kecepatan perentangan tersebut, dan semakin rendahnya suhu material penghalus, maka akan mengurangi penyatuan material penghalus tersebut. Pada literatur lain, Yan dan

(15)

Pitchumani [9] melakukan simulasi numerik pada proses pembentukan, termasuk difusi dopant. Mereka menyederhanakan perhitungan dengan menggunakan batas permukaan fiber yang bebas. Penelitian mereka merupakan perluasan dari kajian numerik pada proses pembentukan yang diamati oleh Lee dan Jaluria [5].

Dalam tesis ini, akan dikaji model matematika untuk perubahan konsentrasi dopant selama pembentukan serat optik. Berdasarkan asumsi gelombang panjang, akan diturunkan persamaan difusi yang bergantung pada kecepatan, jari-jari turbulen, suhu dan konsentrasi dopant. Bentuk sederhana untuk koefisien dari persamaan akan diperhatikan untuk mengetahui kebergantungan semua parameter yang terlibat dalam proses difusi.

1.2 Tujuan Penelitian

Berdasarkan latar belakang di atas, maka tujuan penelitian ini adalah:

1. Mengkaji model matematika untuk perubahan suhu, jari-jari turbulen, dan konsentrasi dopant selama pembentukan serat optik.

2. Menentukan penyelesaian dari model matematika bagi perubahan suhu dan jari-jari turbulen, serta konsentrasi dopant yang telah diperoleh dengan menggunakan asumsi gelombang panjang.

3. Menentukan keterkaitan suhu, jari-jari turbulen, dan konsentrasi dopant selama pembentukan serat optik terhadap jarak dari input nozzle sepanjang sumbu fiber.

4. Melakukan simulasi numerik untuk mengetahui perilaku penyelesaian dari perubahan suhu, jari-jari turbulen, dan konsentrasi dopant selama pembentukan serat optik dengan menggunakan bantuan software Maple.

(16)

II LANDASAN TEORI

2.1 Persamaan Dasar

Persamaan dasar fluida yang digunakan dalam penelitian ini, diturunkan dengan menggunakan hukum kekekalan massa, kekekalan momentum, kekekalan energi dan konsentrasi dopant seperti dalam [9,10]. Misalkan gerak partikel fluida dinyatakan dalam dua dimensi dengan kecepatan partikel dalam arah horizontal dan arah vertikal berturut-turut adalah u dan v. Fluida mempunyai rapat massa ρ(z,r) dengan z dan r, masing-masing menyatakan jarak dari input nozzle sepanjang sumbu fiber dan jari-jari turbulen.

Berdasarkan hukum kekekalan massa, kekekalan momentum, kekekalan energi dan konsentrasi dopant diperoleh persamaan dasar sebagai berikut:

𝜕 𝜌𝑢 𝜕𝑧 + 1 𝑟 𝜕 𝑟𝜌𝑣 𝜕𝑟 = 0 (2.1) 𝜕(𝜌𝑢2₎ 𝜕𝑧 + 1 𝑟 𝜕(𝑟𝜌𝑢𝑣) 𝜕𝑟 = − 𝜕𝑝 𝜕𝑧+ 2 𝜕 𝜕𝑧 µ 𝜕𝑢 𝜕𝑧 + 1 𝑟 𝜕 𝜕𝑟 𝑟µ 𝜕𝑢 𝜕𝑟+ 𝜕𝑣 𝜕𝑧 2.2 𝜕(𝜌𝑢𝑣) 𝜕𝑧 + 1 𝑟 𝜕(𝑟𝜌𝑣2₎ 𝜕𝑟 = − 𝜕𝑝 𝜕𝑟+ 𝜕 𝜕𝑧 µ 𝜕𝑢 𝜕𝑟+ 𝜕𝑣 𝜕𝑧 + 2 𝑟 𝜕 𝜕𝑟 𝑟µ 𝜕𝑣 𝜕𝑟 − 2µ𝑣 𝑟2 (2.3) 𝜕(𝜌𝑐_𝑝𝑢𝑇) 𝜕𝑧 + 1 𝑟 𝜕(𝑟𝜌𝑐_𝑝𝑣𝑇) 𝜕𝑟 = 𝜕 𝜕𝑧 𝑘 𝜕𝑇 𝜕𝑧 + 1 𝑟 𝜕 𝜕𝑟 𝑟𝑘 𝜕𝑇 𝜕𝑟 (2.4) 𝜕 𝑢𝑐 𝜕𝑧 + 1 𝑟 𝜕 𝑟𝑣𝑐 𝜕𝑟 = 𝜕 𝜕𝑧 𝐷 𝜕𝑐 𝜕𝑧 + 1 𝑟 𝜕 𝜕𝑟 𝑟𝐷 𝜕𝑐 𝜕𝑟 , (2.5)

dengan p tekanan, T suhu, c konsentrasi dopant, µ koefisien kekentalan, 𝑐𝑝 konstanta pemanasan, 𝑘 = 𝑘𝑇 + 𝑘𝑅 konduktivitas, dan D variabel difusi dari

(17)

2.2 Syarat Batas

Tinjau domain fluida yang disajikan dalam Gambar 1.

Syarat batas diberikan pada furnace (di 𝑧 = 0 dan 𝑧 = 𝐿) dan permukaan fiber (di 𝑟 = 𝑅(𝑧)). Syarat batas pada furnace adalah

r = R0 , u = u0 , v = 0, T = To , c = co(r) pada z = 0 (2.6) dan

u = ud pada z = L. (2.7)

Syarat batas pada permukaan fiber di r = R(z) mengikuti syarat batas dinamik dan kinematik dari fluida dengan bentuk umum sebagai berikut:

𝑛𝑇𝜍 𝑛 = Г𝑘, 𝑡𝑇𝜍 𝑡 = 0, 𝑣 = 𝑅′ 𝑢

,

di 𝑟 = 𝑅(𝑧)

(2.8) dengan σ tegangan tensor, n vektor normal, t vektor ortogonal terhadap n, k lengkungan rata-rata, dan Г koefisien tegangan permukaan.

Syarat batas untuk suhu di permukaan fiber ditentukan berdasarkan Hukum Pendinginan Newton [10] yang diberikan oleh:

−𝑘𝜕𝑇

𝜕𝑛 = 𝑞 ≔

ℎ_𝑓 𝑇_𝑓 − 𝑇 , 0 ≤ 𝑧 < 𝐿_𝑓,

−ℎ𝑐 𝑇 − 𝑇𝑐 , 𝐿𝑓 ≤ 𝑧 ≤ 𝐿, (2.9)

dengan 𝑇_𝑓 suhu pada furnace, 𝑇_𝑐 suhu sekitarnya, ℎ_𝑓 koefisien penghantar panas, dan ℎ𝑐 koefisien penghantar dingin.

u0

Pemanasan Pendinginan

ud

z = 0 z = Lf z = L

(18)

Syarat batas untuk konsentrasi dopant pada permukaan fiber [8,11] di 𝑟 = 𝑅(𝑧) adalah

−𝐷𝜕𝑐_𝜕𝑛 = 0,

di 𝑟 = 𝑅(𝑧) (2.10) dan

𝜕𝑐_𝜕𝑟 = 0

di 𝑟 = 0 (2.11) Selanjutnya, koefisien kekentalan didasarkan pada rumus Arrhenius [1] yang dinyatakan oleh

𝜇 𝑇 = 𝜇₀ exp⁡(−𝐺_𝜇 𝑇 − 𝑇0 ),

(2.12)

dengan µ0 kekentalan dari T0 dan Gµ konstan.

Kemudian koefisien difusi untuk dopant didasarkan pada rumus Arrhenuis [7,11] yang dinyatakan oleh

𝐷 𝑇 = 𝐷_∞ exp⁡(−𝐺𝐷

𝑇) , (2.13)

dengan GD penjumlahan antara D∞ koefisien difusi pada suhu tinggi dan suatu konstanta.

2.3 Penyederhanaan Model

Pada bagian ini akan diawali dengan menyederhanakan model untuk perubahan suhu, jari-jari turbulen dan konsentrasi dopant selama pembentukan serat optik fiber. Persamaan dasar (2.1) - (2.5) dinondimensionalkan dengan menggunakan pengskalaan berikut:

𝑧 = 𝑧 𝐿 , 𝑟 = 𝑟 𝑅0 , 𝑅 = 𝑅 𝑅0 , 𝑢 = 𝑢 𝑢0 , 𝑣 = 𝐿𝑣 𝑅0𝑢0 , 𝑝 = 𝑅₀2_𝑝 𝜇0𝑢0𝐿 𝜇 = 𝜇 𝜇₀ , 𝜃 = 𝑇 − 𝑇0 𝑇_𝑓− 𝑇₀ , 𝐶 0 = 𝑐0 𝑐₀(0) , 𝐷 = 𝐷 𝐷_∞ .

Satuan dari variabel-variabel fisis yang muncul dalam pembahasan di atas diberikan dalam Lampiran 16.

Jika pengskalaan di atas disubstitusikan ke dalam persamaan dasar (2.1) sampai (2.5), maka diperoleh

𝜕 𝜕𝑧 𝜌𝑢 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑣 = 0, (2.14)

(19)

𝑅_𝑒 𝜕 𝜌𝑢 2 𝜕𝑧 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑢 𝑣 = − 𝜌 3𝛿2 𝜕𝑝 𝜕𝑧 + 2𝜌 3 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑧 + 𝜌 3𝛿2 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑢 𝜕𝑟 + 𝜌 3 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑣 𝜕𝑧 , (2.15) 𝜆𝐿𝑓 𝜕 𝜕𝑧 𝜌𝑢 𝑣 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑣 2 = Γ 3𝛿3 −ℓ 𝜕𝑝 𝜕𝑟 + 𝐿𝑓 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑟 + ℓ 𝜕 𝜕𝑧 𝜇 𝜕𝑣 𝜕𝑧 + 2ℓ 𝑟 𝜇 𝜕𝑣 𝜕𝑟 − 2𝐿_𝑓𝜇 𝑣 𝑟 2 (2.16) 𝛼𝜇𝛼𝐷 ℋ_𝑓 𝜕 𝜕𝑧 𝑢 𝜃 +⊖ + 1 𝑟 1 𝜕𝑟 𝑟 𝑣 𝜃 +⊖ = 1 2 𝜋 1 𝐵_𝑖 𝛿 𝜕 𝜕𝑧 𝜕 𝜕𝑧 𝜃 +⊖ + 𝛼_𝜇𝛼_𝐷 𝛿 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜕 𝜕𝑟 𝜃 +⊖ , (2.17) 𝒫 𝜕 𝜕𝑧 𝑢 𝑐 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝑣 𝑐 = 𝛿2 𝜕 𝜕𝑧 𝐷 𝜕𝑐 𝜕𝑧 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝐷 𝜕𝑐 𝜕𝑟 (2.18)

dengan syarat batas pada furnace adalah

𝑟 = 1 , 𝑢 = 1 , 𝑣 = 0 , 𝑇 = 𝑇0 , 𝑐 = 𝑐0(𝑟) pada 𝑧 = 0 (2.19)

dan

𝑢 = 𝐷𝑟 pada 𝑧 = 1. (2.20)

Penurunan persamaan (2.14) – (2.18) dapat dilihat pada Lampiran 1.

Beberapa notasi yang muncul dalam persamaan (2.14) – (2.20) diberikan sebagai berikut: 𝐷𝑟 = 𝑢_𝑑 𝑢0 , 𝛿 = 𝑅₀ 𝐿 , 𝑅𝑒 = 𝜌𝑢₀𝐿 3𝜇0 , 𝜆 = Γ𝐿 3𝜇0𝑢0𝑅0 , 𝛼_𝜇 = 𝐺_𝜇 𝑇_𝑓− 𝑇₀ , 𝛼_𝐷 = 𝐺𝐷 𝑇_𝑓 − 𝑇₀, ⊖ = 𝑇0 𝑇_𝑓 − 𝑇₀, 𝒫 = 𝑢0𝑅02 𝐿𝐷_∞ ℋ_𝑓 = 2 𝜋ℎ𝑓𝐿 𝜌𝐶_𝑝𝑢₀𝑅₀ , ℋ𝑐 = 2 𝜋ℎ𝑐𝐿 𝜌𝑐_𝑝𝑢₀𝑅₀ , ℓ = 𝐿_𝑓 𝐿 , 𝐵𝑖 = ℎ_𝑓𝑅₀ 𝑘 .

(20)

Selanjutnya dengan menggunakan pendekatan gelombang panjang 𝛿 ≪ 1 dan asumsi 𝜆 ≪ 1, 𝑅_𝑒 ≪ 1 dan 𝐵_𝑖 ≪ 1, pada persamaan (2.14) – (2.18) dengan menggunakan syarat batas (2.19) dan (2.20), kemudian membuang tanda topinya sebagai penyederhanaan penulisan, maka diperoleh

𝜕 𝜕𝑍 𝑢𝑠 = 0, (2.21) 1 𝑠 𝜕 𝜕𝑧 𝜇𝑠 𝜕𝑢 𝜕𝑧 = 0, (2.22) 𝑢𝜕𝜃 𝜕𝑧 = ℋ_𝑓 1 − 𝜃 𝐻 ℓ − 𝑧 − ℋ_𝑐𝜃𝐻(𝑧 − ℓ) 𝑠1/2 , (2.23) 𝒫 𝑢𝜕𝑐 𝜕𝑧− 𝑟 2 𝜕𝑢 𝜕𝑧 𝜕𝑐 𝜕𝑟 = 1 𝑟 𝜕 𝜕𝑟 𝑟𝐷 𝜕𝑐 𝜕𝑟 , (2.24)

dengan syarat batas

𝑠 = 1, 𝑢 = 1, 𝜃 = 0 di 𝑧 = 0, (2.25) 𝑢 = 𝐷_𝑟

di 𝑧 = 1, (2.26) 𝑐 = 𝑐₀ di 𝑧 = 0, (2.27) 𝑐𝑟 = 0 di 𝑟 = 0 dan 𝑟 = 𝑠, (2.28) dimana 𝑠 = 𝑅2_{, 𝜇 = e}−𝛼𝜇𝜃_{, 𝐷 = 𝑒}− 𝛼𝐷 𝜃+⊖_{. (2.29)}

Persamaan (2.21) - (2.23) dengan syarat batas (2.25) dan (2.26) merupakan model persamaan bagi perubahan suhu dan jari-jari turbulen. Persamaan (2.24) dengan syarat batas (2.27) dan (2.28) merupakan model persamaan bagi perubahan konsentrasi dopant.

Selanjutnya persamaan (2.21) - (2.24) dengan syarat batas (2.25) - (2.28) akan disederhanakan menjadi suatu sistem persamaan yang mudah ditentukan penyelesaiannya.

(21)

Penyelesaian persamaan (2.21) dan (2.22) dengan syarat batas (2.25) dan (2.26) adalah 𝑠𝑢 = 1 dan 𝜇𝑠𝑢_𝑧 = 2𝐹 (2.30) dengan 𝐹 = ln 𝐷𝑟 2 𝜇1 −1_𝑑𝑧 0

merupakan gaya efektif yang ditentukan dengan menggunakan syarat batas pada z = 1. Jika persamaan (2.30) digunakan untuk mengeliminasi 𝑢 dan 𝑢_𝑧 yang muncul, maka dari persamaan (2.21) dan (2.22), dan syarat batas (2.25) dan (2.26) diperoleh masalah nilai batas untuk 𝑠 dan 𝜃 berikut: 𝑠𝑧 = − 2𝐹𝑠 𝜇 , (2.31) 𝜃_𝑧 = 𝑠1/2_ℋ 𝑓 1 − 𝜃 𝐻 ℓ − 𝑧 − ℋ𝑐𝜃𝐻 𝑧 − ℓ , (2.32)

dengan syarat batas

𝑠 = 1, 𝜃 = 0 di 𝑧 = 0

dan

𝑠 = 𝐷𝑟−1 di 𝑧 = 1. (2.33)

Selanjutnya untuk menyederhanakan persamaan bagi perubahan konsentrasi dopant, didefinisikan variabel berikut:

𝜙(𝑧) ≡ 𝐷𝜃 𝑧𝑧 ′_𝑑𝑧′

0 dan 𝜙 ≡ 𝜙(1), (2.34)

dan transformasi koordinat berikut 𝜉 = 𝑟 𝑅 , 𝜏 = 𝜙(𝑧) 𝜙 . (2.35) Besaran 𝐷 = 𝜙 𝒫 (2.36) merupakan koefisien difusi dan 𝒫 bilangan peclet untuk dopant. Dengan demikian masalah nilai batas untuk konsentrasi dopant diberikan sebagai berikut:

𝑐𝜏 = 𝒟 𝜉 𝜕 𝜕𝜉 𝜉 𝜕𝑐 𝜕𝜉 , (2.37) dengan syarat batas

𝑐 = 𝑐0 𝜉 di 𝜏 = 0

dan

(22)

Solusi untuk konsentrasi dopant [2] yang diberikan pada persamaan (2.37) dengan syarat batas (2.38) adalah sebagai berikut

𝑐 𝜏, 𝜉 = 2𝜋 𝐺 𝜏, 𝜉; 𝜂 𝑐1 ₀ 𝜂 𝜂𝑑𝜂, (2.39)

0

dengan 𝐺 fungsi Green yang diberikan sebagai berikut 𝐺 𝜏, 𝜉; 𝜂 = 1 4𝜋𝒟𝜏𝑒𝑥𝑝 − 𝜉2_{+ 𝜂}2 4𝒟𝜏 𝐼0 𝜉𝜂 2𝒟𝜏 (2.40) dimana 𝐼₀ adalah fungsi Bessel jenis pertama [15].

(23)

III PEMBAHASAN DAN HASIL

Dalam bagian ini akan dibahas perilaku penyelesaian dari model persamaan bagi perubahan suhu dan jari-jari turbulen selama pembentukan serat optik berdasarkan alur yang diberikan dalam pustaka [2]. Selain itu, juga akan dibahas perubahan konsentrasi dopant selama pembentukan serat optik.

3.1 Suhu dan Jari-jari turbulen

Untuk menentukan solusi bagi suhu 𝜃 dan jari-jari turbulen 𝑠 pada pembentukan serat optik, maka ditinjau dua proses, yaitu proses sebelum melalui pendinginan (ℓ = 1) dan proses dalam keadaan pendinginan (ℓ < 1).

3.1.1 Proses Sebelum Melalui Pendinginan (𝓵 = 𝟏)

Persamaan (2.31) dan (2.32) dapat ditulis menjadi

𝑠_𝑧 = −ℱ ln 𝐷_𝑟𝑠𝑒−𝛼𝜇(1−𝜃), (3.1)

𝜃_𝑧 = ℋ_𝑓 𝑠 1 − 𝜃 , (3.2) dengan

ℱ =

2 𝐹𝑒

𝛼𝜇 ln 𝐷𝑟 .

Berdasarkan persamaan (3.1) dan (3.2) diperoleh 𝑑𝑠 𝑑𝜃= − ℱ ln 𝐷𝑟 ℋ𝑓 𝑠𝑒−𝛼𝜇(1−𝜃) 1 − 𝜃 , (3.3) sedangkan syarat batas (2.33) memberikan

𝑠 0 = 1 dan 𝜃 0 = 0. (3.4)

Jika persamaan (3.3) diintegralkan terhadap 𝜃 dan syarat batas (3.4) digunakan, maka diperoleh 𝑠 = 1 −ℱ ln 𝐷𝑟 2ℋ𝑓 𝐸1 𝛼𝜇(1 − 𝜃) − 𝐸1 𝛼𝜇 2 (3.5) dengan 𝐸₁ 𝑧 = ∞𝑒_𝑥−𝑥 𝑑𝑥 𝑧 .

(24)

Fungsi 𝐸₁ 𝑧 memenuhi

𝐸₁ 𝑧 ~𝑒−𝑧_𝑧 𝑧 → ∞, dan 𝐸₁ 𝑧 ~ − ln 𝑧 − 𝛾 𝑧 → 0.

Selanjutnya, jika persamaan (3.5) disubstitusikan ke dalam persamaan (3.2), maka diperoleh

𝜃_𝑧 = ℋ_𝑓 1 −ℱ ln 𝐷𝑟

2ℋ𝑓 𝐸1 𝛼𝜇 1 − 𝜃 − 𝐸1 𝛼𝜇 (1 − 𝜃). (3.6)

Jika 𝛼_𝜇 ≫ 1, maka 𝐸₁[𝛼_𝜇] kecil, sehingga 𝐸₁ 𝛼_𝜇 1 − 𝜃 juga kecil, jika 1 − 𝜃 ≪_𝛼1

𝜇 . Jadi dari persamaan (3.6) diperoleh

𝜃_𝑧 = ℋ_𝑓 1 − 𝜃 . (3.7) Jika persamaan (3.7) diintegralkan tarhadap z, maka diperoleh

𝜃 = 1 − 𝑒−ℋ𝑓𝑧_{. (3.8)}

Apabila z meningkat ke 1 untuk ℋ_𝑓 ≫ 1, maka 1 − 𝜃 → 0, sehingga untuk 𝑧 ≫_ℋ1

𝑓 , diperoleh

𝜃_𝑧 = ℋ_𝑓 1 +ℱ ln 𝐷𝑟

2ℋ𝑓 ln 𝛼𝜇 1 − 𝜃 + 𝛾 (1 − 𝜃). (3.9)

Untuk menentukan penyelesaian 𝜃, maka diperkenalkan variabel 𝜃 sebagai berikut

𝛼_𝜇 1 − 𝜃 = 𝑒−ℱ ln 𝐷𝑟2ℋ𝑓 𝜃 .

Dengan variabel baru ini, maka persamaan (3.9) menjadi 𝜃 _𝑧 = −ℱ ln 𝐷𝑟

2 ln 𝜃 + 𝛾 𝜃 . (3.10)

Jika persamaan (3.10) diintegralkan terhadap z, maka diperoleh

ln 𝜃 = −𝛾 + 𝐶1𝑒− ℱ ln 𝐷₂ 𝑟 𝑧, (3.11)

dengan 𝐶₁ adalah konstanta pengintegralan yang ditentukan berikut ini.

Karena untuk 𝑧 = 0, diperoleh 𝜃 = 0 dari persamaan (3.8), maka dari

persamaan (3.11) diperoleh

𝐶1 = 𝛾 + ln 𝛼𝜇 +_{ℱ ln 𝐷}2ℋ𝑓

(25)

Jika nilai 𝐶₁ pada persamaan (3.12) disubstitusikan ke dalam persamaan (3.11), maka diperoleh

𝜃 = 𝑒𝑥𝑝 −𝛾 + 𝛾 + ln 𝛼_𝜇 +_{ℱ ln 𝐷}2ℋ𝑓

𝑟 𝑒

−ℱ ln 𝐷𝑟₂ 𝑧_{. (3.13)}

Kembalikan ke variabel awal, diperoleh 𝜃 = 1 − 𝑒𝑥𝑝 − 𝛾 + ln 𝛼𝜇 +_{ℱ ln 𝐷}2ℋ𝑓

𝑟 1 − 𝑒

−ℱ ln 𝐷𝑟₂ 𝑧_.

(3.14) Selanjutnya fungsi s diperoleh dengan menggunakan persamaan (3.5), dengan 𝜃 memenuhi persamaan (3.14). Jika 𝑧 = 1 disubstitusikan ke dalam persamaan (3.14) dan (3.5) dan menggunakan syarat 𝑠 1 = 𝐷𝑟−1, maka diperoleh

nilai ℱ berikut ℱ = 1 +_{ln 𝐷}2

𝑟ln 1 +

ℱ(ln 𝛼𝜇+𝛾) ln 𝐷𝑟

2ℋ𝑓 , (3.15)

asalkan 𝛼_𝜇 ≫ 1. Secara analitik nilai ℱ sulit ditentukan dari persamaan (3.15), karena ℱ dinyatakan dalam persamaan implisit. Tetapi karena

(ln 𝛼𝜇+𝛾) ln 𝐷𝑟

2ℋ𝑓 ~10

−1 _{≪ 1,} _(3.16)

maka nilai ℱ dapat dihampiri oleh ℱ = 1 +ln 𝛼𝜇+𝛾

ℋ𝑓 . (3.17)

Dengan demikian fungsi 𝑠 dapat ditentukan berdasarkan persamaan (3.5) dengan ℱ diberikan oleh persamaan (3.17).

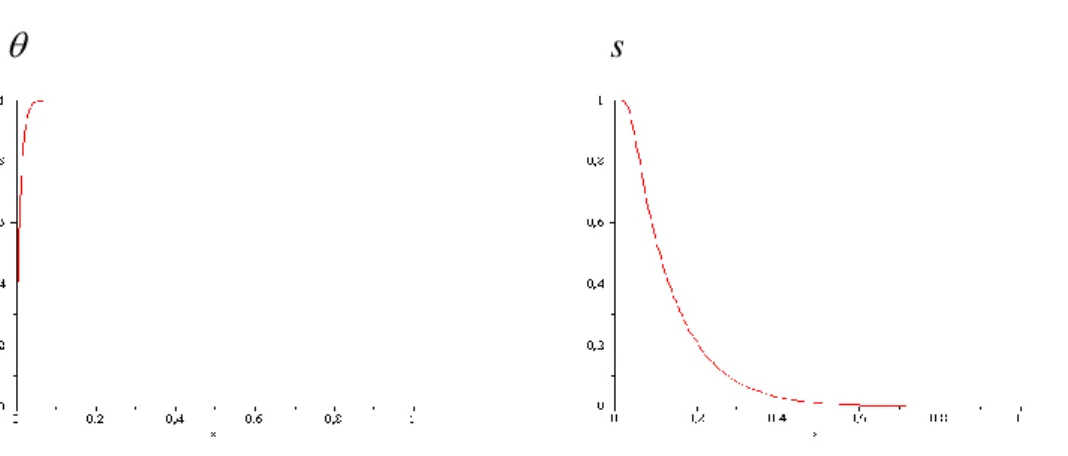
Berikut ini akan dijelaskan karakteristik dari fungsi 𝜃 dan 𝑠, masing-masing berdasarkan persamaan (3.14) dan (3.5). Untuk itu, dimisalkan ℋ_𝑓 = 100, 𝛼_𝜇 = 30, dan 𝐷_𝑟 = 104_{, sedangkan}_{ℱ = 1,039783974 diperoleh berdasarkan}

(26)

 s

Gambar 2. Grafik fungsi 𝜃 dan 𝑠 untuk ℋ_𝑓 = 100, 𝛼_𝜇 = 30, dan 𝐷_𝑟 = 104

Berdasarkan Gambar 2 diperoleh bahwa peningkatan nilai z menyebabkan nilai 𝜃 semakin besar dan nilai s semakin mengecil.

3.1.2 Proses Dalam Keadaan Pendinginan (𝓵 < 𝟏)

Kasus ini terjadi pada 𝑧 > ℓ, persamaan (2.31) dan (2.32) dapat ditulis menjadi 𝑠𝑧 = −ℱ ln 𝐷𝑟 𝑒𝛼𝜇(𝜃−1) 𝑠, (3.18)

𝜃_𝑧 = −ℋ_𝑐 𝑠 𝜃, (3.19)

dengan syarat batas

𝑠 ℓ = 𝑠ℓ dan 𝜃 ℓ = 𝜃ℓ. (3.20)

Penurunan persamaan (3.18) dan (3.19) dapat dilihat pada Lampiran 4.

Untuk menentukan penyelesaian masalah nilai batas (3.18) – (3.20), maka diperkenalkan variabel berikut:

𝜗 = 𝛼𝜇(𝜃ℓ− 𝜃), (3.21)

𝔰 = _𝑠𝑠

ℓ , (3.22)

𝒴 = ℱ ln 𝐷𝑟 𝑒𝛼𝜇 (𝜃ℓ−1)

2 𝑧 − ℓ . (3.23)

Dengan demikian berdasarkan persamaan (3.18) – (3.20) diperoleh masalah nilai batas berikut:

𝔰𝒴 = − 𝔰 𝑒−𝜗, (3.24)

(27)

dan syarat batas 𝜗 0 = 0 dan 𝔰 0 = 1 (3.26) dimana 𝒜 =2 𝑠ℓ ℋ𝑐 𝛼𝜇 𝜃ℓ 𝑒𝛼𝜇 (1−𝜃ℓ) ℱ ln 𝐷𝑟 dan ∈ = 1 𝛼𝜇𝜃ℓ ≪ 1, (3.27)

𝒜 adalah konstanta laju penurunan suhu.

Penurunan persamaan (3.24) dan (3.25) dapat dilihat pada Lampiran 5. Dari persamaan (3.24) dan (3.25), diperoleh

𝑑𝜗_𝑑𝔰 = −𝒜 1−∈ 𝜗 𝑒𝜗_. _(3.28)

Jika persamaan (3.28) diintegralkan terhadap 𝔰 dan syarat batas (3.26) digunakan, maka diperoleh

𝔰 = 1 + _𝒜1 _1−∈𝜗𝑒−𝜗 − 1 −_𝒜∈ _1−∈𝓌𝑒−𝓌 2𝑑𝓌

𝜗

0 . (3.29)

Karena ∈

1−∈𝜗 ≪ 1, maka persamaan (3.29) dapat dihampiri oleh

𝔰 = 1 + _𝒜1 _1−∈𝜗𝑒−𝜗 − 1 . (3.30) Penurunan persamaan (3.28) dan (3.29) dapat dilihat pada Lampiran 6.

Nilai 𝒜 akan mempengaruhi solusi 𝔰. Dalam hal ini akan ditinjau nilai 𝒜 dalam 3 kasus yang berbeda, yaitu: 𝒜 = 1, 𝒜 < 1, dan 𝒜 > 1.

Kasus 1. 𝓐 = 𝟏.

Berdasarkan persamaan (3.30) dan (3.25), untuk ∈ ≪ 1 diperoleh hampiran untuk 𝔰 dan 𝜗_𝒴 masing-masing sebagai berikut:

𝔰 = 𝑒−𝜗 _(3.31)

𝜗_𝒴 = 𝑒−𝜗_. _(3.32)

Jika persamaan (3.32) diintegralkan terhadap 𝒴 dengan syarat batas 𝜗 0 = 0 digunakan, maka diperoleh

𝜗 = ln 𝒴 + 1 . (3.33)

Selanjutnya, jika persamaan (3.33) disubstitusikan ke dalam persamaan (3.31), maka diperoleh

𝔰 = _𝒴+11 . (3.34)

(28)

Kasus 2. 𝓐 < 𝟏.

Karena 𝒜 < 1 dan suhu terbatas di bawah oleh 𝒜 = 1, maka dengan menggunakan kasus 1 di atas diperoleh bahwa

𝜗𝑚𝑎𝑘𝑠 = ln ℱ ln 𝐷𝑟 𝑒

𝛼𝜇 (𝜃ℓ−1)

2 1 − ℓ + 1 . (3.35)

Karena 𝜗_{𝑚𝑎𝑘𝑠} berorde satu bila ln ln 𝐷_𝑟 ≪ ∈−1, maka 𝜗 juga berorde satu 𝜗 = 𝑂 1 , sehingga dari persamaan (3.30) diperoleh hampiran sebagai berikut

𝔰 = 1 + _𝒜1 𝑒−𝜗 _{− 1 .} _(3.36)

Hal yang sama, diperoleh pula hampiran 𝜗_𝒴 sebagai berikut 𝜗_𝒴 = 𝒜 𝔰,

sehingga menurut persamaan (3.36) diperoleh

𝜗_𝒴 = 𝑒−𝜗 _{+ 𝒜 − 1.} _(3.37)

Jika persamaan (3.37) diintegralkan terhadap 𝒴 dan syarat batas 𝜗 0 = 0 digunakan, maka diperoleh

𝜗 = ln 𝒜𝑒 𝒜−1 𝒴_𝒜−1 − 1. (3.38) Jika persamaan (3.36) disubstitusikan ke dalam lim_𝒜→1𝔰, maka diperoleh

𝔰 = _𝒜−𝑒𝒜−1_{− 𝒜−1 𝒴} . (3.39) Penurunan persamaan (3.35) – (3.39) dapat dilihat pada Lampiran 8.

Kasus 3. 𝓐 > 𝟏.

Pada kasus ini, ditinjau dua kemungkinan, yaitu 𝜗 = 𝑂 1 dan 𝜗 besar. Jika 𝜗 = 𝑂 1 , maka hasil yang diperoleh sama dengan kasus 𝒜 < 1, sehingga

diperoleh persamaan (3.38) dan (3.39). Selanjutnya 𝜗 besar, misalkan 1 ≪ 𝜗 ≪ ∈−1_{, maka berdasarkan persamaan (3.30) dengan mengabaikan bentuk}

eksponensial, diperoleh hampiran 𝔰 berikut

𝔰 = 1 − _𝒜1 . (3.40)

Jika persamaan (3.40) disubstitusikan ke dalam persamaan (3.25), maka diperoleh 𝜗𝒴 = 𝒜 − 1 1−∈ 𝜗 . (3.41)

(29)

Selanjutnya, jika persamaan (3.41) diintegralkan terhadap 𝒴, maka diperoleh 𝜗 = 1− 𝐶2𝑒−∈ 𝒜−1 𝒴

∈ (3.42)

dimana 𝐶₂ adalah konstan pengintegralan yang ditentukan berikut ini. Penurunan persamaan (3.40) – (3.42) dapat dilihat pada Lampiran 9.

Karena 𝜗 besar, maka syarat batas 𝜗 0 = 0 tidak bisa digunakan. Oleh karena itu, untuk menentukan 𝐶₂, dibutuhkan bentuk 𝜗 yang diberikan oleh persamaan (3.38) dan 𝜗 besar oleh (3.42). Untuk 𝜗 → 0 dari persamaan (3.42), diperoleh

𝜗~ 1− 𝐶2 1−∈ 𝒜−1 𝒴

∈ . (3.43)

Untuk 𝜗 besar, dipilih 𝒴 → 0, maka persamaan (3.38) memberikan

𝜗~ 𝒜 − 1 𝒴 + ln_𝒜−1𝒜 . (3.44) Bandingkan persamaan (3.43) dan (3.44), diperoleh

𝐶₂ = 1− ∈ ln_𝒜−1𝒜 . (3.45)

Dengan demikian persamaan (3.42) menjadi

𝜗 = 1− 𝑒−∈ 𝒜−1 𝒴_∈ + ln_𝒜−1𝒜 𝑒−∈ 𝒜−1 𝒴_. _(3.46)

Jika 𝒜 ≫ 1 dan 𝐶₂~1, maka 𝜗 dapat dihampiri oleh

𝜗 = 1−𝑒−∈ 𝒜−1 𝒴_∈ . (3.47)

Penyelesaian 𝜗 ditentukan dengan cara mengkombinasikan nilai 𝜗 kecil dan 𝜗 besar, yaitu

𝜗 = ln𝒜𝑒 𝒜−1 𝒴_𝒜−1 − 1+ 1−𝑒−∈ 𝒜−1 𝒴_∈ + ln_𝒜−1𝒜 𝑒−∈ 𝒜−1 𝒴

− 𝒜 − 1 𝒴 − ln_𝒜−1𝒜 . (3.48) Berikut ini akan ditentukan bentuk 𝑠 berdasarkan solusi untuk 𝔰 yang

diberikan oleh persamaan (3.30). Dengan menggunakan variabel awal 𝜃 = 𝜃ℓ− _𝛼1

𝜇 𝜗, maka untuk 𝒜 ≤ 1 diperoleh

𝜃 = 𝜃ℓ− _𝛼1

𝜇 ln

𝒜𝑒 𝒜−1 𝛽 𝑧−ℓ − 1

𝒜−1 (3.49)

(30)

𝜃 = 𝜃_ℓ− _𝛼1 𝜇 ln 𝒜𝑒 𝒜−1 𝛽 𝑧−ℓ − 1 𝒜−1 − 𝜃ℓ− 1 𝛼𝜇 ln 𝒜 𝒜−1 1 − 𝑒 − 𝒜−1 𝛽 𝛼𝜇 𝜃ℓ 𝑧−ℓ ₊ _𝛼1 𝜇 𝒜 − 1 𝛽 𝑧 − ℓ , (3.50) dengan 𝛽 = ℱ ln 𝐷𝑟 𝑒𝛼𝜇 (𝜃ℓ−1) 2 .

Dengan demikian solusi untuk 𝑠 diperoleh dari persamaan (3.30) adalah 𝑠 = 𝑠ℓ 1 − _𝒜1 +𝜃ℓ 𝑒

𝛼𝜇 𝜃 −𝜃ℓ

𝒜𝜃 2

. (3.51)

Jika syarat batas 𝑠 1 = 𝐷_𝑟−1 dan 𝑧 = 1 digunakan, maka diperoleh 𝐷_𝑟−1 = 𝑠_ℓ 1 − _𝒜1 +𝜃ℓ 𝑒𝛼𝜇 𝜃 1 −𝜃ℓ

𝒜𝜃 1 2

(3.52)

Berikut ini akan dijelaskan karakteristik dari fungsi 𝜃 dan 𝑠. Persamaan (3.50) adalah solusi 𝜃 untuk 𝒜 > 1, dan persamaan (3.51) adalah solusi untuk s. Untuk itu dimisalkan ℋ_𝑓 = 350, 𝐷_𝑟 = 104, 𝛼_𝜇 = 40, ℓ = 0,2 , 𝒜 = 1,71 dan ℋ𝑐 = 350, sedangkan ℱ = 1,012188798 diperoleh berdasarkan persamaan

(3.17)

𝜃 𝑠

Gambar 3. Grafik fungsi 𝜃 dan 𝑠 untuk 𝒜 = 1,71 dan ℋ_𝑐 = 350

Berdasarkan Gambar 3 diperoleh bahwa peningkatan nilai z menyebabkan nilai 𝜃 dan s semakin mengecil.

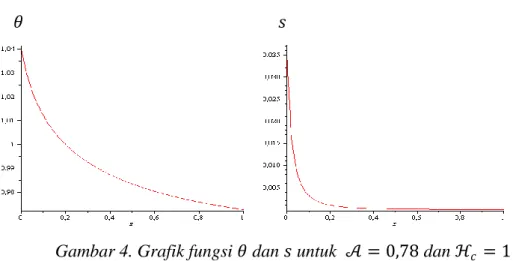
Persamaan (3.49) adalah solusi 𝜃 untuk 𝒜 ≤ 1, dan persamaan (3.51) adalah solusi untuk s. Untuk itu dimisalkan ℋ_𝑓 = 350, 𝐷_𝑟 = 104, 𝛼_𝜇 = 40, ℓ = 0,2 , 𝒜 = 0,78 dan ℋ𝑐 = 1, sedangkan ℱ = 1,012188798 diperoleh

(31)

𝜃 𝑠

Gambar 4. Grafik fungsi 𝜃 dan 𝑠 untuk 𝒜 = 0,78 dan ℋ_𝑐 = 1

Berdasarkan Gambar 4 diperoleh bahwa peningkatan nilai z menyebabkan nilai 𝜃 dan s semakin mengecil .

3.2 Difusi Dopant

Berikut ini akan ditentukan nilai 𝒟. Untuk itu tuliskan persamaan (3.14) dalam bentuk

𝜃 = 1 − 𝑒−𝐶1 1− 𝑒

− ℱ ln 𝐷𝑟 ₂ 𝑧

, (3.53)

dengan 𝐶₁ diberikan oleh (3.12). Selanjutnya, diperkenalkan variabel 𝜁 sebagai berikut

𝜁 = 1 − 𝑒− ℱ ln 𝐷𝑟 2 𝑧 _(3.54)

dan dinotasikan

𝜑 𝜁 ≡ 𝜙 𝑧 . (3.55)

Jika persamaan (3.54) dan (3.55) diturunkan terhadap z, maka diperoleh 𝑑𝜁 = ℱ ln 𝐷𝑟 2 1 − 𝜁 𝑑𝑧 dan 𝜑𝜁 = _{ℱ ln 𝐷}2 𝑟 𝑒 − 𝛼𝐷 ⊖+1−𝑒 −𝐶1𝜁 1−𝜁 𝜑 0 = 0, (3.56)

(32)

Karena 𝐶₁ ≫ 1, maka persamaan (3.56) akan ditinjau dalam dua kasus, yaitu 𝜁~𝐶1−1 dan 𝜁~1.

Kasus 1. 𝜻~𝑪_𝟏−𝟏 ≪ 𝟏.

Pada kasus ini, diperkenalkan variabel baru 𝜁 = 𝐶₁𝜁, sehingga persamaan (3.56) menjadi 𝜑_𝜁 𝑖 = 2 𝑒 − 𝛼𝐷 ⊖+1−𝑒 −𝜁 ℱ ln 𝐷𝑟 1−𝜁 , 𝜑 𝑖 _{0 = 0} _(3.57)

dengan solusi 𝜑 dinotasikan dengan 𝜑 𝑖 yang diberikan sebagai berikut: 𝜑 𝑖 𝜁 = −_𝐶 2 1ℱ ln 𝐷𝑟 𝐸1 𝑥 − 𝑒 −_⊖+1𝛼𝐷 _𝐸 1 𝑥 −_⊖+1𝛼𝐷 𝑥=𝛼𝐷_⊖ 𝑥= 𝛼𝐷 ⊖+1−𝑒 −𝜁 . (3.58) Kasus 2. 𝜻~𝟏.

Pada kasus ini, persamaan (3.56) dapat menjadi solusi outer dinotasikan dengan 𝜑 0 _{yang memenuhi}

𝜑_𝜁 0 = _{ℱ ln 𝐷}2

𝑟

𝑒 −⊖+1 𝛼𝐷

1−𝜁 , (3.59)

dengan solusi 𝜑 dinotasikan dengan 𝜑 0 yang diberikan sebagai berikut 𝜑 0 _{𝜁 =}2 𝑒 −

𝛼𝐷 ⊖+1

ℱ ln 𝐷𝑟 ln 1 − 𝜁 + 𝐶3 (3.60)

dengan 𝐶₃ adalah konstanta pengintegralan yang akan ditentukan berikut ini. Penurunan persamaan (3.60) dapat dilihat pada Lampiran 13.

Solusi 𝜑 𝑖 dan 𝜑 0 harus memenuhi lim_{𝜁 →∞}𝜑 𝑖 _{𝜁 = lim} 𝜁→0𝜑 0 𝜁 . (3.61) Untuk 𝜁 → 0, diperoleh 𝜑 0 _{𝜁 ~ 𝐶} 3+ 2 𝑒 −_⊖+𝜃𝛼𝐷 ℱ ln 𝐷𝑟 𝜁. (3.62)

Selanjutnya, untuk z yang kecil diperoleh 𝐸₁ 𝑧 ~ − 𝛾 − ln 𝑧 .

(33)

Berdasarkan persamaan (3.58) diperoleh bahwa untuk 𝜁 → ∞, 𝜑 𝑖 𝜁 ≈ −_𝐶 2 1ℱ ln 𝐷𝑟 𝐸1 𝛼𝐷 ⊖+1 − 𝐸1 𝛼𝐷 ⊖ − 𝑒 −_⊖+1𝛼𝐷 _𝐸 1 −𝛾 − ln 𝛼𝐷+ 2 ln ⊖ +1 + 𝑒 −⊖+1𝛼𝐷 𝐸₁ 𝛼𝐷 ⊖ ⊖+1 + 2 𝑒 −⊖+1 𝛼𝐷 ℱ ln 𝐷𝑟 𝜁 𝐶1 . (3.63)

Penurunan persamaan (3.63) dapat dilihat pada Lampiran 14.

Dengan demikian berdasarkan persamaan (3.62) dan (3.63) diperoleh 𝐶₃ = −_𝐶 2 1ℱ ln 𝐷𝑟 𝐸1 𝛼𝐷 ⊖+1 − 𝐸1 𝛼𝐷 ⊖ − 𝑒 −_⊖+1𝛼𝐷 _𝐸 1 −𝛾 − ln 𝛼𝐷 + 2 ln ⊖ +1 + 𝑒 −⊖+1𝛼𝐷 𝐸₁ 𝛼𝐷 ⊖ ⊖+1 . (3.64)

Dengan mengembalikan ke variabel awal, diperoleh

𝜙 0 𝑧 = 𝑒 −⊖+1𝛼𝐷 𝑧 + 𝐶₃_, _(3.65)

Jadi dari persamaan (2.32) diperoleh 𝒟 = 𝑒 −

𝛼𝐷 ⊖+1 _{+ 𝐶}₃

𝒫 . (3.66)

Penurunan persamaan (3.65) dan (3.66) dapat dilihat pada Lampiran 15.

Berikut ini akan dijelaskan tentang koefisien difusi efektif. Berdasarkan persamaan (2.36) dapat disimpulkan bahwa 𝒟 pada persamaan (3.66) adalah koefisien difusi efektif untuk 𝜃 = ⊝ untuk semua z.

Untuk itu dimisalkan 𝛼𝐷 = 20, ⊖= 0,15, 𝒫 = 3. 10−3, ℋ𝑓 = 350,

𝛼𝜇 = 40, dan 𝐷𝑟 = 104, untuk menentukan nilai 𝒟. Kemudian persamaan (2.35)

(34)

𝑐

Gambar 5. Grafik Konsentrasi Dopant dengan 𝛼𝐷 = 20, ⊖= 0,15, 𝒫 = 3. 10−3,

ℋ𝑓 = 350, 𝛼𝜇 = 40, dan 𝐷𝑟 = 104

Berdasarkan Gambar 5 diperoleh bahwa peningkatan nilai z menyebabkan nilai c semakin mengecil.

(35)

IV KESIMPULAN DAN SARAN

4.1 Kesimpulan

Model persamaan untuk suhu dan konsentrasi dopant diturunkan berdasarkan persamaan dasar fluida. Persamaan dasar fluida diturunkan dengan menggunakan hukum kekekalan massa, kekekalan momentum, kekekalan energi dan konsentrasi dopant. Kemudian model tersebut disederhanakan dengan menggunakan asumsi gelombang panjang, rapat masa yang yang cukup kecil, dan konduktivitas panas yang hingga, sehingga diperoleh persamaan difusi yang sederhana dan lebih mudah ditentukan solusinya.

Berdasarkan persamaan difusi yang diperoleh, maka ditinjau dua proses fisis yaitu proses sebelum melalui pendingnan dan proses dalam keadaan pendingnan. Dari kedua proses tersebut diperoleh solusi untuk suhu dan jari-jari turbulen. Selain kedua proses fisis tersebut, ditentukan pula konsentrasi dopant yang diperoleh berdasarkan koefisien difusi yang bentuknya berupa fungsi Green.

Perilaku solusi dari persamaan difusi ditentukan berdasarkan suatu simulasi numerik dengan menggunakan bantuan software Maple 12. Hasil simulasi numerik untuk proses sebelum melalui pendinginan, diperoleh bahwa semakin besar jarak dari input nozzle sepanjang sumbu fiber, maka suhunya akan semakin besar dan jari-jari turbulennya semakin mengecil. Dalam proses pendinginan diperoleh bahwa semakin besar jarak dari input nozzle sepanjang sumbu fiber, maka suhu dan jari-jari turbulennya akan semakin mengecil. Untuk konsentrasi dopant diperoleh bahwa semakin besar jarak dari input nozzle sepanjang sumbu fiber, maka konsentrasi dopant akan semakin mengecil.

4.2 Saran

Untuk menentukan persamaan suhu, jari-jari turbulen dan konsentrasi dopant dapat digunakan pendekatan asimtotik, sehingga dapat dengan mudah ditentukan solusinya. Pendekatan asimtotik dapat dikaji dalam sistem lain, misalkan bioteknologi.

(36)

DAFTAR PUSTAKA

[1] Huang H, Miura RM, Ireland WP, and Puil E. 2003. Heat-induced stretching of a glass tube under tension. SIAM J. Appl. Math. 63:1499-1519 [2] Huang H, Miura RM, and Wylie JJ. 2002. Optical fiber drawing and dopant

transport. http://www.math.yorku.ca.pdf. html [12 November 2008].

[3] Izawa T. 2000. Early days of VAD process. IEEE J. Selected Topics Quantum Electronics, 6:1220-1227.

[4] Lyytikainen K, Hungtington ST, Carter ALG, McNamara P, Fleming S, Abramczyk J, Kaplin I, Schotz G. 2004. Dopant diffusion during optical fiber drawing. Optical Express, 12:972-977.

[5] Lee and Jaluria Y. 1996. Effects of variable properties and viscosity dissipation during optical fiber drawing. Trans. ASME, 118:350-358. [6] Pone E, Daxhelet X, and Lacroix S. 2004. Refractive index profile of

fused-fiber couplers cross-section. Optical Express, 12:1036-1044.

[7] Rodney B. 2008. Arrhenius hukum-Arrhenius equation-van’t Hoff Hukum. http://translate.google.co.id. html [5 Januari 2009].

[8] Suchecka M, Borisovich A, and Serbinski W. Green’s functions methods for mathematical modeling of unidirectional diffusion process in isothermal metal bonding process. http://www.pg.gda.pl.pdf. html [20 Maret 2009]. [9] Yan Y and Pitchumani R. 2004. Numerical study on the dopant

consentration and refractive index profile evolution in an optical fiber manufacturing process. Int. J. Heat Mass Transfer, 49:2097-2112.

[10] Yunus A. 2003. Heat transfer a practical approach. Mc. Graw Hill companies. p. 1-335.

[11] Diffusion. p. 1-29. http://personal.cityu.edu.hk.PDF. Html [26 Maret 2009]. [12] Persamaan bessel dan fungsi-fungsi bessel jenis pertama. http://www.

(37)

(38)

Lampiran 1

Misalkan diberikan pengskalaan berikut: 𝑧 = 𝑧 𝐿 , 𝑟 = 𝑟 𝑅₀ , 𝑅 = 𝑅 𝑅₀ , 𝑢 = 𝑢 𝑢₀ , 𝑣 = 𝐿𝑣 𝑅₀𝑢₀ , 𝑝 = 𝑅₀2_𝑝 𝜇₀𝑢₀𝐿 𝜇 = 𝜇 𝜇₀ , 𝜃 = 𝑇 − 𝑇₀ 𝑇_𝑓− 𝑇₀ , 𝐶 0 = 𝑐₀ 𝑐₀(0) , 𝐷 = 𝐷 𝐷_∞ . Penurunan Persamaan (2.14)

Substitusikan pengskalaan di atas ke dalam persamaan (2.1) diperoleh bentuk berikut:

𝜕 𝜕𝑧 𝜌𝑢0𝑢 𝜕𝑧 𝜕𝑧+ 1 𝑅0𝑟 𝜕 𝜕𝑟 𝑅0𝑟 𝜌 𝑅₀𝑢₀ 𝐿 𝑣 𝜕𝑟 𝜕𝑟= 0 atau 𝑢₀ 𝜕 𝜕𝑧 𝜌𝑢 1 𝐿+ 1 𝑅0𝑟 𝑅02𝑢0 𝐿 𝜕 𝜕𝑟 𝑟 𝜌𝑣 1 𝑅0 = 0 atau 𝑢₀ 𝐿 𝜕 𝜕𝑧 𝜌𝑢 + 𝑢₀ 𝐿 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑣 = 0 atau 𝜕 𝜕𝑧 𝜌𝑢 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑣 = 0 atau 𝜕 𝜕𝑧 𝜌𝑢 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑣 = 0 Penurunan Persamaan (2.15)

Substitusikan pengskalaan di atas ke dalam ruas kiri persamaan (2.2) diperoleh bentuk berikut:

𝜕 𝜕𝑧 𝜌𝑢02𝑢 2 𝜕𝑧 𝜕𝑧+ 1 𝑅₀𝑟 𝜕 𝜕𝑟 𝑅0𝑟 𝜌𝑢0𝑢 𝑅0𝑢0 𝐿 𝑣 𝜕𝑟 𝜕𝑟 atau 𝑢02 𝜕 𝜕𝑧 𝜌𝑢 2 1 𝐿+ 1 𝑅₀𝑟 𝑅₀2𝑢₀2 𝐿 𝜕 𝜕𝑟 𝑟 𝜌𝑢 𝑣 1 𝑅₀ atau 𝑢02 𝐿 𝜕 𝜕𝑧 𝜌𝑢 2 + 𝑢02 𝐿 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑢 𝑣

(39)

atau 𝑢02 𝐿 𝜕 𝜕𝑧 𝜌𝑢 2 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑢 𝑣

Selanjutnya substitusikan pengskalaan di atas ke ruas kanan persamaan (2.2) diperoleh bentuk berikut:

− 𝜕 𝜕𝑧 𝜇0𝑢0𝐿 𝑅₀2 𝑝 𝜕𝑧 𝜕𝑧+ 2 𝜕 𝜕𝑧 𝜇0𝜇 𝜕 𝜕𝑧 𝑢0𝑢 𝜕𝑧 𝜕𝑧 𝜕𝑧 𝜕𝑧 + 1 𝑅0𝑟 𝜕 𝜕𝑟 𝑅0𝑟 𝜇0𝜇 𝜕 𝜕𝑟 𝑢0𝑢 𝜕𝑟 𝜕𝑟+ 𝜕 𝜕𝑧 𝑅₀𝑢₀ 𝐿 𝑣 𝜕𝑧 𝜕𝑧 𝜕𝑟 𝜕𝑟 atau −𝜇0𝑢0𝐿 𝑅₀2 𝜕𝑝 𝜕𝑧 1 𝐿+ 2 𝜕 𝜕𝑧 𝜇0𝑢0𝜇 𝜕𝑢 𝜕𝑧 1 𝐿 1 𝐿 + 1 𝑅₀𝑟 𝑅0𝜇0 𝜕 𝜕𝑟 𝑟 𝜇 𝑢0 𝜕𝑢 𝜕𝑟 1 𝑅₀ + 𝑅₀𝑢₀ 𝐿 𝜕𝑣 𝜕𝑧 1 𝐿 1 𝑅₀ atau −𝜇0𝑢0 𝑅₀2 𝜕𝑝 𝜕𝑧 + 2𝜇0𝑢0 𝐿2 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑧 + 𝜇0 𝑅0 1 𝑟 𝜕 𝜕𝑟 𝑢0𝑟 𝜇 1 𝑅0 𝜕𝑢 𝜕𝑟 + 𝑅0 𝐿2 𝜕𝑣 𝜕𝑧 atau −𝜇0𝑢0 𝑅02 𝜕𝑝 𝜕𝑧 + 2𝜇₀𝑢₀ 𝐿2 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑧 + 𝜇₀𝑢₀ 𝑅0 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 1 𝑅0 𝜕𝑢 𝜕𝑟 + 𝑅₀ 𝐿2 𝜕𝑣 𝜕𝑧 atau 𝜇₀𝑢₀ − 1 𝑅₀2 𝜕𝑝 𝜕𝑧 + 2 𝐿2 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑧 + 1 𝑅₀ 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 1 𝑅₀ 𝜕𝑢 𝜕𝑟 + 𝑅0 𝐿2 𝜕𝑣 𝜕𝑧

(40)

Jika ruas kiri sama dengan ruas kanan persamaan (2.2), maka diperoleh persamaan berikut: 𝑢₀2 𝐿 𝜕 𝜕𝑧 𝜌𝑢 2 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑢 𝑣 = 𝜇₀𝑢₀ − 1 𝑅₀2 𝜕𝑝 𝜕𝑧 + 2 𝐿2 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑧 + 1 𝑅0 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 1 𝑅0 𝜕𝑢 𝜕𝑟 + 𝑅₀ 𝐿2 𝜕𝑣 𝜕𝑧 atau 𝑢0 𝐿 𝜕 𝜕𝑧 𝜌𝑢 2 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑢 𝑣 = 𝜇0 − 1 𝑅02 𝜕𝑝 𝜕𝑧 + 2 𝐿2 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑧 + 1 𝑅0 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 1 𝑅0 𝜕𝑢 𝜕𝑟 + 𝑅₀ 𝐿2 𝜕𝑣 𝜕𝑧 atau 𝜌𝑢0𝐿 3𝜇₀ 𝜕 𝜕𝑧 𝜌𝑢 2 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑢 𝑣 = 𝜌𝐿 2 3 − 1 𝑅02 𝜕𝑝 𝜕𝑧 + 2 𝐿2 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑧 + 1 𝑅₀ 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 1 𝑅₀ 𝜕𝑢 𝜕𝑟 + 𝑅₀ 𝐿2 𝜕𝑣 𝜕𝑧 atau 𝑅_𝑒 𝜕 𝜕𝑧 𝜌𝑢 2 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑢 𝑣 = − 𝜌𝐿2 3𝑅₀2 𝜕𝑝 𝜕𝑧 + 2𝜌 3 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑧 + 𝜌𝐿2 3𝑅₀ 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 1 𝑅₀ 𝜕𝑢 𝜕𝑟 + 𝑅0 𝐿2 𝜕𝑣 𝜕𝑧 atau 𝑅𝑒 𝜕 𝜕𝑧 𝜌𝑢 2 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑢 𝑣 = − 𝜌 3𝛿2 𝜕𝑝 𝜕𝑧 + 2𝜌 3 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑧 + 𝜌𝐿2 3𝑅02 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑢 𝜕𝑟 +𝜌𝜌 3 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑣 𝜕𝑧 atau

(41)

𝑅𝑒 𝜕 𝜕𝑧 𝜌𝑢 2 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑢 𝑣 = − 𝜌 3𝛿2 𝜕𝑝 𝜕𝑧 + 2𝜌 3 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑧 + 𝜌 3𝛿2 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑢 𝜕𝑟 +𝜌 3 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑣 𝜕𝑧 Penurunan Persamaan (2.16)

𝜕 𝜕𝑧 𝜌𝑢0𝑢 𝑅0𝑢0 𝐿 𝑣 𝜕𝑧 𝜕𝑧+ 1 𝑅0𝑟 𝜕 𝜕𝑟 𝑅0𝑟 𝜌 𝑅₀2_𝑢 02 𝐿2 𝑣 2 𝜕𝑟 𝜕𝑟 atau 𝑢₀2_𝑅 0 𝐿 𝜕 𝜕𝑧 𝜌𝑢 𝑣 1 𝐿+ 1 𝑅₀𝑟 𝜕 𝜕𝑟 𝑅₀3_𝑢 02 𝐿2 𝑟 𝜌𝑣 2 1 𝑅₀ atau 𝑢₀2_𝑅 0 𝐿2 𝜕 𝜕𝑧 𝜌𝑢 𝑣 + 𝑢₀2_𝑅 0 𝐿2 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑣 2 atau 𝑢₀2_𝑅 0 𝐿2 𝜕 𝜕𝑧 𝜌𝑢 𝑣 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑣 2

− 𝜕 𝜕𝑟 𝜇₀𝑢₀𝐿 𝑅₀2 𝑝 𝜕𝑟 𝜕𝑟+ 𝜕 𝜕𝑧 𝜇0𝜇 𝜕 𝜕𝑟 𝑢0𝑢 𝜕𝑟 𝜕𝑟+ 𝜕 𝜕𝑧 𝑅₀𝑢₀ 𝐿 𝑣 𝜕𝑧 𝜕𝑧 𝜕𝑧 𝜕𝑧 + 2 𝑅₀𝑟 𝜕 𝜕𝑟 𝑅0𝑟 𝜇0𝜇 𝜕 𝜕𝑟 𝑅₀𝑢₀ 𝐿 𝑣 𝜕𝑟 𝜕𝑟 𝜕𝑟 𝜕𝑟− 2𝜇0𝜇 𝑅0_{𝐿 𝑣}𝑢0 𝑅₀2_𝑟2 atau −𝜇0𝑢0𝐿 𝑅₀2 𝜕𝑝 𝜕𝑟 1 𝑅0+ 𝜕 𝜕𝑧 𝜇0𝑢0𝜇 1 𝑅0 𝜕𝑢 𝜕𝑟 + 𝑅₀ 𝐿2 𝜕𝑣 𝜕𝑧 1 𝐿 + 2 𝑅0𝑟 𝜕 𝜕𝑟 𝑅₀2_𝑢 0𝜇0 𝐿 𝑟 𝜇 𝜕𝑣 𝜕𝑟 1 𝑅0 1 𝑅0− 2𝜇0𝑢0𝑅0𝜇 𝑣 𝑅₀2_𝑟2

(42)

atau −𝜇0𝑢0𝐿 𝑅₀3 𝜕𝑝 𝜕𝑟 + 𝜇₀𝑢₀ 𝐿 𝜕 𝜕𝑧 𝜇 1 𝑅₀ 𝜕𝑢 𝜕𝑟 + 𝑅₀ 𝐿2 𝜕𝑣 𝜕𝑧 + 2𝜇₀𝑢₀ 𝑅₀𝐿 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑣 𝜕𝑟 − 2𝜇₀𝑢₀ 𝑅₀ 𝜇 𝑣 𝑟 2 atau 𝜇0𝑢0 − 𝐿 𝑅₀3 𝜕𝑝 𝜕𝑟 + 1 𝐿 𝜕 𝜕𝑧 𝜇 1 𝑅0 𝜕𝑢 𝜕𝑟 + 𝑅0 𝐿2 𝜕𝑣 𝜕𝑧 + 2 𝑅0𝐿 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑣 𝜕𝑟 − 2 𝑅0 𝜇 𝑣 𝑟 2

Jika ruas kiri sama dengan ruas kanan persamaan (2.3), maka diperoleh persamaan berikut: 𝑢₀2_𝑅 0 𝐿2 𝜕 𝜕𝑧 𝜌𝑢 𝑣 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑣 2 = 𝜇0𝑢0 − 𝐿 𝑅₀3 𝜕𝑝 𝜕𝑟 + 1 𝐿 𝜕 𝜕𝑧 𝜇 1 𝑅0 𝜕𝑢 𝜕𝑟 + 𝑅₀ 𝐿2 𝜕𝑣 𝜕𝑧 + 2 𝑅0𝐿 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑣 𝜕𝑟 − 2 𝑅0 𝜇 𝑣 𝑟 2 atau Γ𝐿 𝜇₀𝑢₀𝑅₀ 𝜕 𝜕𝑧 𝜌𝑢 𝑣 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑣 2 = Γ𝐿3 3𝑅₀2 − 𝐿 𝑅₀3 𝜕𝑝 𝜕𝑟 + 1 𝐿 𝜕 𝜕𝑧 𝜇 1 𝑅₀ 𝜕𝑢 𝜕𝑟 + 𝑅₀ 𝐿2 𝜕𝑣 𝜕𝑧 + 2 𝑅₀𝐿 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑣 𝜕𝑟 − 2 𝑅₀ 𝜇 𝑣 𝑟 2 atau 𝜆 𝜕 𝜕𝑧 𝜌𝑢 𝑣 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑣 2 = ΓL 3𝛿2 − 𝐿 𝑅₀3 𝜕𝑝 𝜕𝑟 + 1 𝐿 𝜕 𝜕𝑧 𝜇 1 𝑅0 𝜕𝑢 𝜕𝑟 + 𝑅₀ 𝐿2 𝜕𝑣 𝜕𝑧 + 2 𝑅0𝐿 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑣 𝜕𝑟 − 2 𝑅0 𝜇 𝑣 𝑟 2 atau

(43)

𝜆 𝜕 𝜕𝑧 𝜌𝑢 𝑣 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑣 2 = 1 𝛿3 − Γ 3𝐿 𝜕𝑝 𝜕𝑟 + Γ 3 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑟 + Γ 3𝐿 𝜕 𝜕𝑧 𝜇 𝜕𝑣 𝜕𝑧 + 2Γ 3𝐿 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑣 𝜕𝑟 −2Γ 3 𝜇 𝑣 𝑟 2 atau 𝜆𝐿𝑓 𝜕 𝜕𝑧 𝜌𝑢 𝑣 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜌𝑣 2 = Γ 3𝛿3 −ℓ 𝜕𝑝 𝜕𝑟 + 𝐿𝑓 𝜕 𝜕𝑧 𝜇 𝜕𝑢 𝜕𝑟 + ℓ 𝜕 𝜕𝑧 𝜇 𝜕𝑣 𝜕𝑧 + 2ℓ 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜇 𝜕𝑣 𝜕𝑟 − 2𝐿_𝑓𝜇 𝑣 𝑟 2 Penurunan persamaan (2.17)

𝜕 𝜕𝑧 𝜌𝑐𝑝𝑢0𝑢 𝑇𝑓 − 𝑇0 𝜃 + 𝑇0 𝜕𝑧 𝜕𝑧 + 1 𝑅₀𝑟 𝜕 𝜕𝑟 𝑅0𝑟 𝜌𝑐𝑝 𝑅₀𝑢₀ 𝐿 𝑣 𝑇𝑓 − 𝑇0 𝜃 + 𝑇0 𝜕𝑟 𝜕𝑟 atau 𝜕 𝜕𝑧 𝜌𝑐𝑝𝑢0𝑢 𝑇𝑓 − 𝑇0 𝜃 + 𝜌𝑐𝑝𝑢0𝑢 𝑇0 1 𝐿 + 1 𝑅₀𝑟 𝜕 𝜕𝑟 𝑅02𝑢0 𝐿 𝑟 𝜌𝑐𝑝𝑣 𝑇𝑓− 𝑇0 𝜃 + 𝑅02𝑢0 𝐿 𝑟 𝜌𝑐𝑝𝑣 𝑇0 1 𝑅₀ atau 1 𝐿 𝜕 𝜕𝑧 𝜌𝑐𝑝𝑢0𝑢 𝑇𝑓 − 𝑇0 𝜃 + 𝜌𝑐𝑝𝑢0𝑢 𝑇0 +1 𝑟 𝜕 𝜕𝑟 𝑇𝑓− 𝑇0 𝜌𝑐𝑝𝑢0𝑟 𝑣 𝜃 + 𝑇0𝜌𝑐𝑝𝑢0𝑟 𝑣 𝑇0

(44)

𝜕 𝜕𝑧 𝑘 𝜕 𝜕𝑧 𝑇𝑓− 𝑇0 𝜃 + 𝑇0 𝜕𝑧 𝜕𝑧 𝜕𝑧 𝜕𝑧+ 1 𝑅₀𝑟 𝜕 𝜕𝑟 𝑅0𝑟 𝑘 𝜕 𝜕𝑟 𝑇𝑓− 𝑇0 𝜃 + 𝑇0 𝜕𝑟 𝜕𝑟 𝜕𝑟 𝜕𝑟 atau 1 𝐿2 𝜕 𝜕𝑧 𝑇𝑓 − 𝑇0 𝑘 𝜕 𝜕𝑧 𝜃 + 𝑇0𝑘 𝜕 𝜕𝑧 + 1 𝑅02 1 𝑟 𝜕 𝜕𝑟 𝑇𝑓 − 𝑇0 𝑘𝑟 𝜕 𝜕𝑟 𝜃 + 𝑇0𝑘𝑟 𝜕 𝜕𝑟

Jika ruas kiri sama dengan ruas kanan persamaan (2.4), maka diperoleh persamaan berikut: 1 𝐿 𝜕 𝜕𝑧 𝜌𝑐𝑝𝑢0𝑢 𝑇𝑓 − 𝑇0 𝜃 + 𝜌𝑐𝑝𝑢0𝑢 𝑇0 +1 𝑟 𝜕 𝜕𝑟 𝑇𝑓− 𝑇0 𝜌𝑐𝑝𝑢0𝑟 𝑣 𝜃 + 𝑇0𝜌𝑐𝑝𝑢0𝑟 𝑣 𝑇0 = 1 𝐿2 𝜕 𝜕𝑧 𝑇𝑓− 𝑇0 𝑘 𝜕 𝜕𝑧 𝜃 + 𝑇0𝑘 𝜕 𝜕𝑧 + 1 𝑅02 1 𝑟 𝜕 𝜕𝑟 𝑇𝑓 − 𝑇0 𝑘𝑟 𝜕 𝜕𝑟 𝜃 + 𝑇0𝑘𝑟 𝜕 𝜕𝑟 atau 1 𝐿 𝜕 𝜕𝑧 𝜌𝑐𝑝𝑢0𝑢 𝜃 + 𝑇0 𝑇_𝑓 − 𝑇₀ 𝜌𝑐𝑝𝑢0𝑢 +1 𝑟 𝜕 𝜕𝑟 𝜌𝑐𝑝𝑢0𝑟 𝑣 𝜃 + 𝑇0 𝑇_𝑓 − 𝑇₀ 𝜌𝑐𝑝𝑢0𝑟 𝑣 𝑇0 = 1 𝐿2 𝜕 𝜕𝑧 𝑘 𝜕 𝜕𝑧 𝜃 + 𝑇₀ 𝑇_𝑓 − 𝑇₀ 𝑘 𝜕 𝜕𝑧 + 1 𝑅02 1 𝑟 𝜕 𝜕𝑟 𝑘𝑟 𝜕 𝜕𝑟 𝜃 + 𝑇₀ 𝑇𝑓 − 𝑇0 𝑘𝑟 𝜕 𝜕𝑟 atau

(45)

1 𝐿 𝜕 𝜕𝑧 𝜌𝑐𝑝𝑢0𝑢 𝜃 +⊖ 𝜌𝑐𝑝𝑢0𝑢 + 1 𝑟 𝜕 𝜕𝑟 𝜌𝑐𝑝𝑢0𝑟 𝑣 𝜃 +⊖ 𝜌𝑐𝑝𝑢0𝑟 𝑣 𝑇0 = 1 𝐿2 𝜕 𝜕𝑧 𝑘 𝜕 𝜕𝑧 𝜃 +⊖ 𝑘 𝜕 𝜕𝑧 + 1 𝑅₀2 1 𝑟 𝜕 𝜕𝑟 𝑘𝑟 𝜕 𝜕𝑟 𝜃 +⊖ 𝑘𝑟 𝜕 𝜕𝑟 atau 𝜌𝑐_𝑝𝑢₀𝑅₀ 2 𝜋ℎ𝑓𝐿 𝜕 𝜕𝑧 𝑢 𝜃 +⊖ 𝑢 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝑣 𝜃 +⊖ 𝑟 𝑣 = 𝑅0𝑘 2 𝜋ℎ𝑓 1 𝐿2 𝜕 𝜕𝑧 𝜕𝜃 𝜕𝑧 +⊖ 𝜕 𝜕𝑧 + 𝑅₀𝑘 2 𝜋ℎ𝑓 1 𝑅₀2 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜕𝜃 𝜕𝑟 +⊖ 𝑟 𝜕 𝜕𝑟 atau 1 ℋ_𝑓 𝜕 𝜕𝑧 𝑢 𝜃 +⊖ 𝑢 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝑣 𝜃 +⊖ 𝑟 𝑣 = 𝑘 2 𝜋ℎ𝑓𝐿 𝛿 𝜕 𝜕𝑧 𝜕𝜃 𝜕𝑧 +⊖ 𝜕 𝜕𝑧 + 1 2 𝜋 1 𝐵𝑖 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜕𝜃 𝜕𝑟 +⊖ 𝑟 𝜕 𝜕𝑟 atau 𝛼_𝜇𝛼_𝐷 ℋ_𝑓 𝜕 𝜕𝑧 𝑢 𝜃 +⊖ + 1 𝑟 1 𝜕𝑟 𝑟 𝑣 𝜃 +⊖ = 1 2 𝜋 1 𝐵_𝑖 𝛿 𝜕 𝜕𝑧 𝜕 𝜕𝑧 𝜃 +⊖ + 𝛼_𝜇𝛼_𝐷 𝛿 1 𝑟 𝜕 𝜕𝑟 𝑟 𝜕 𝜕𝑟 𝜃 +⊖ Penurunan persamaan (2.18)

𝜕 𝜕𝑧 𝑢0𝑢 𝑐0 0 𝑐 𝜕𝑧 𝜕𝑧+ 1 𝑅0𝑟 𝜕 𝜕𝑟 𝑅0𝑟 𝑅₀𝑢₀ 𝐿 𝑣 𝑐0 0 𝑐 𝜕𝑟 𝜕𝑟 atau 𝑢₀𝑐₀ 0 𝐿 𝜕 𝜕𝑧 𝑢 𝑐 + 𝑢₀𝑐₀ 0 𝐿 1 𝑟 𝜕 𝜕𝑟 𝑟 𝑣 𝑐

(46)

𝜕 𝜕𝑧 𝐷∞𝐷 𝜕𝜕𝑧 𝑐0 0 𝑐 𝜕𝑧 𝜕𝑧 𝜕𝑧 𝜕𝑧+ 1 𝑅₀𝑟 𝜕 𝜕𝑟 𝑅0𝑟 𝐷∞𝐷 𝜕𝜕𝑟 𝑐0 0 𝑐 𝜕𝑟 𝜕𝑟 𝜕𝑟 𝜕𝑟 atau 𝐷∞𝑐0 0 𝐿2 𝜕 𝜕𝑧 𝐷 𝜕𝑐 𝜕𝑧 + 𝐷∞𝑐0 0 𝑅₀2 1 𝑟 𝜕 𝜕𝑟 𝑟 𝐷 𝜕𝑐 𝜕𝑟

Jika ruas kiri sama dengan ruas kanan persamaan (2.5), maka diperoleh persamaan berikut: 𝑢₀𝑐₀ 0 𝐿 𝜕 𝜕𝑧 𝑢 𝑐 + 𝑢₀𝑐₀ 0 𝐿 1 𝑟 𝜕 𝜕𝑟 𝑟 𝑣 𝑐 = 𝐷∞𝑐0 0 𝐿2 𝜕 𝜕𝑧 𝐷 𝜕𝑐 𝜕𝑧 + 𝐷_∞𝑐₀ 0 𝑅02 1 𝑟 𝜕 𝜕𝑟 𝑟 𝐷 𝜕𝑐 𝜕𝑟 atau 𝑢₀ 𝐿 𝜕 𝜕𝑧 𝑢 𝑐 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝑣 𝑐 = 𝐷_∞ 𝐿2 𝜕 𝜕𝑧 𝐷 𝜕𝑐 𝜕𝑧 + 𝐷_∞ 𝑅02 1 𝑟 𝜕 𝜕𝑟 𝑟 𝐷 𝜕𝑐 𝜕𝑟 atau 𝑢0𝑅02 𝐿𝐷∞ 𝜕 𝜕𝑧 𝑢 𝑐 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝑣 𝑐 = 𝑅02 𝐿2 𝜕 𝜕𝑧 𝐷 𝜕𝑐 𝜕𝑧 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝐷 𝜕𝑐 𝜕𝑟 atau 𝒫 𝜕 𝜕𝑧 𝑢 𝑐 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝑣 𝑐 = 𝛿2 𝜕 𝜕𝑧 𝐷 𝜕𝑐 𝜕𝑧 + 1 𝑟 𝜕 𝜕𝑟 𝑟 𝐷 𝜕𝑐 𝜕𝑟

(47)

Lampiran 2

Penurunan persamaan (3.1)

Tinjau persamaan (2.31) berikut: 𝑠_𝑧 = −2 𝐹 𝑠_𝜇 .

Karena 𝜇 = 𝑒−𝛼𝜇𝜃_{, maka persamaan (2.31) menjadi}

𝑠_𝑧 = − 2 𝐹 𝑠 𝑒−𝛼𝜇𝜃 atau 𝑠_𝑧 = −2 𝐹 𝑠 𝑒𝛼𝜇𝜃 atau 𝑠_𝑧 = −2 𝐹 𝑠 𝑒𝛼𝜇𝜃 1 atau 𝑠_𝑧 = −2 𝐹 𝑠 𝑒𝛼𝜇𝜃 𝑒−𝛼𝜇 𝑒𝛼𝜇 atau 𝑠_𝑧 = −2 𝐹 𝑠 𝑒𝛼𝜇 𝑒−𝛼𝜇(1−𝜃) atau 𝑠_𝑧 = −2 𝐹 𝑒 𝛼𝜇 ln 𝐷_𝑟 ln 𝐷𝑟 𝑠 𝑒−𝛼𝜇(1−𝜃) atau 𝑠_𝑧 = −ℱ ln 𝐷_𝑟 𝑠 𝑒−𝛼𝜇(1−𝜃). Penurunan persamaan (3.2)

Tinjau persamaan (2.32) berikut

𝜃_𝑧 = 𝑠2 1 [ ℋ_𝑓 1 − 𝜃 𝐻 𝑙 − 𝑧 − ℋ_𝑐𝜃𝐻 𝑧 − 𝑙 ],

atau

𝜃_𝑧 = 𝑠 [ ℋ𝑓 1 − 𝜃 𝐻 𝑙 − 𝑧 − ℋ𝑐𝜃𝐻 𝑧 − 𝑙 ]

Karena 𝑙 = 1, maka ℋ𝑐 = 0 sehingga diperoleh

𝜃𝑧 = 𝑠 [ ℋ𝑓 1 − 𝜃 . 1 − 0 . 𝜃. 1]

atau

(48)

Penurunan persamaan (3.3) Karena 𝑠𝑧 𝜃𝑧 = 𝑑𝑠 𝑑𝑧 𝑑𝜃 𝑑𝑧 = 𝑑𝑠 𝑑𝜃 ,

maka dengan menggunakan persamaan (3.1) dan (3.2) diperoleh 𝑑𝑠 𝑑𝜃= − ℱ ln 𝐷𝑟 𝑠 𝑒−𝛼𝜇(1−𝜃) ℋ𝑓 𝑠 1 − 𝜃 atau 𝑑𝑠 𝑑𝜃= − ℱ ln 𝐷_𝑟 ℋ_𝑓 𝑠 𝑒−𝛼𝜇 1−𝜃 (1 − 𝜃) Penurunan persamaan (3.5)

Tinjau persamaan (3.3) berikut 𝑑𝑠 𝑑𝜃= − ℱ ln 𝐷𝑟 ℋ_𝑓 𝑠 𝑒−𝛼𝜇 1−𝜃 (1 − 𝜃) atau 𝑑𝑠 𝑠= − ℱ ln 𝐷_𝑟 ℋ𝑓 𝑒−𝛼𝜇 1−𝜃 1 − 𝜃 𝑑𝜃

Jika kedua ruas persamaan di atas diintegralkan terhadap 𝜃, maka diperoleh 𝑑𝑠 𝑠12 = −ℱ ln 𝐷𝑟 ℋ_𝑓 𝑒−𝛼𝜇 1−𝜃 1 − 𝜃 𝑑𝜃 atau 2 𝑠 = −ℱ ln 𝐷_ℋ 𝑟 𝑓 𝑒−𝑥 1 − 𝜃 − 𝑑𝑥 𝛼_𝜇

Selanjutnya misalkan 𝑥 = 𝛼𝜇 1 − 𝜃 , maka 𝑑𝑥 = −𝛼𝜇 𝑑𝜃 sehingga diperoleh

2 𝑠 = ℱ ln 𝐷_ℋ 𝑟 𝑓 𝑒−𝑥 𝑥 𝑑𝑥 atau 2 𝑠 = ℱ ln 𝐷𝑟 ℋ𝑓 𝑥 −1 _{− 1 𝑒}−𝑥 _{+ 𝑐} atau

(49)

4𝑠 = −ℱ ln 𝐷𝑟 ℋ𝑓 1 − 𝑥 −1_𝑒−𝑥 _{+ 𝑐} 2 atau 4𝑠 = −ℱ ln 𝐷𝑟 ℋ_𝑓 1 − (𝛼𝜇 1 − 𝜃 )−1 𝑒−𝛼𝜇 1−𝜃 + 𝑐 2 atau 𝑠 𝜃 = −ℱ ln 𝐷𝑟 2 ℋ𝑓 1 − 𝛼𝜇 1 − 𝜃 −1 𝑒−𝛼𝜇 1−𝜃 _{+ 𝑐} 2 Jika syarat batas 𝑠 (0) = 1 digunakan, maka

𝑠 0 = −ℱ ln 𝐷𝑟 2 ℋ𝑓 1 − 𝛼𝜇 −1 𝑒−𝛼𝜇 + 𝑐 2 = 1 memberikan 𝑐 = 1 + ℱ ln 𝐷𝑟 2 ℋ𝑓 1 − 𝛼𝜇 −1 𝑒−𝛼𝜇 sehingga 𝑠 = −ℱ ln 𝐷𝑟 2 ℋ_𝑓 1 − 𝛼𝜇 1 − 𝜃 −1 𝑒−𝛼𝜇 1−𝜃 + 1 + ℱ ln 𝐷𝑟 2 ℋ𝑓 1 − 𝛼𝜇 −1 𝑒−𝛼𝜇 2 atau 𝑠 = 1 − ℱ ln 𝐷𝑟 2 ℋ_𝑓 1 − 𝛼𝜇 1 − 𝜃 −1 𝑒−𝛼𝜇 1−𝜃 − ℱ ln 𝐷𝑟 2 ℋ𝑓 1 − 𝛼𝜇 −1 𝑒−𝛼𝜇 2 atau 𝑠 = 1 − ℱ ln 𝐷𝑟 2 ℋ𝑓 𝑒−𝛼𝜇 1−𝜃 𝛼𝜇 1−𝜃 𝑑 𝛼𝜇 1 − 𝜃 − 𝑒−𝛼𝜇 𝛼𝜇 𝑑 𝛼𝜇 2 atau

(50)

𝑠 = 1 − ℱ ln 𝐷𝑟 2 ℋ_𝑓 𝑒−𝑥 𝑥 𝑑𝑥 ∞ 𝛼𝜇 1−𝜃 − 𝑒−𝑥 𝑥 𝑑𝑥 ∞ 𝛼𝜇 2 atau 𝑠 = 1 − ℱ ln 𝐷𝑟 2 ℋ_𝑓 𝐸1 𝛼𝜇 1 − 𝜃 − 𝐸1 𝛼𝜇 2 dengan 𝐸₁ 𝑧 = _𝑧∞ 𝑒_𝑥−𝑥 𝑑𝑥

(51)

Lampiran 3

Penurunan persamaan (3.6)

Dengan mensubstitusikan persamaan (3.5) ke dalam persamaan (3.2) berikut 𝜃_𝑧 = ℋ_𝑓 𝑠 1 − 𝜃 diperoleh 𝜃𝑧 = ℋ𝑓 1 − ℱ ln 𝐷_𝑟 2 ℋ𝑓 𝐸1 𝛼𝜇 1 − 𝜃 − 𝐸1 𝛼𝜇 1 − 𝜃 Penurunan persamaan (3.8)

Tinjau persamaan (3.7) berikut 𝜃𝑧 = ℋ𝑓 1 − 𝜃 atau 𝑑𝜃 𝑑𝑧 = ℋ𝑓 1 − 𝜃 atau 𝑑𝜃 1 − 𝜃 = ℋ𝑓 𝑑𝑧

Jika kedua ruas persamaan di atas diintegralkan terhadap z, maka diperoleh − ln 1 − 𝜃 = ℋ_𝑓 𝑧 atau ln 1 − 𝜃 = −ℋ𝑓 𝑧 atau 1 − 𝜃 = 𝑒−ℋ𝑓 𝑧 atau 𝜃 = 1 − 𝑒−ℋ𝑓 𝑧 Penurunan persamaan (3.9)

Tinjau persamaan (3.6) berikut 𝜃_𝑧 = ℋ_𝑓 1 − ℱ ln 𝐷𝑟

2 ℋ_𝑓 𝐸1 𝛼𝜇 1 − 𝜃 − 𝐸1 𝛼𝜇 1 − 𝜃 Karena 𝐸1 𝑧 ~ − ln 𝑧 − 𝛾, maka persamaan (3.6) menjadi

𝜃_𝑧 = ℋ_𝑓 1 − ℱ ln 𝐷𝑟

(52)

atau 𝜃𝑧 = ℋ𝑓 1 + ℱ ln 𝐷_𝑟 2 ℋ_𝑓 ln 𝛼𝜇 1 − 𝜃 + 𝛾 − ln 𝛼𝜇 − 𝛾 1 − 𝜃 atau 𝜃_𝑧 = ℋ_𝑓 1 + ℱ ln 𝐷𝑟 2 ℋ𝑓 ln 𝛼𝜇 1 − 𝜃 + 𝛾 1 − 𝜃 Penurunan persamaan (3.10)

Karena 𝛼_𝜇 1 − 𝜃 = 𝑒−ℱ ln 𝐷𝑟2 ℋ𝑓 𝜃 , maka persamaan (3.9) menjadi

𝛼𝜇𝜃 = 𝛼𝜇 − 𝑒− 2 ℋ𝑓 ℱ ln 𝐷𝑟 𝜃 atau 𝜃 = 1 − 𝑒 −_{ℱ ln 𝐷}2 ℋ𝑓 𝑟 𝜃 𝛼_𝜇

Jika persamaan di atas diturunkan terhadap z pada kedua ruas, maka diperoleh −𝑒

−_{ℱ ln 𝐷}2 ℋ𝑓

𝑟

𝛼_𝜇 𝜃 𝑧 = 𝜃𝑧

Jika persamaan (3.9) digunakan, maka diperoleh −𝑒 −_{ℱ ln 𝐷}2 ℋ𝑓 𝑟 𝛼_𝜇 𝜃 𝑧 = ℋ𝑓 1 + ℱ ln 𝐷_𝑟 2 ℋ_𝑓 𝑙𝑛 𝛼𝜇 1 − 𝜃 + 𝛾 1 − 𝜃 atau −𝑒 −_{ℱ ln 𝐷}2 ℋ𝑓 𝑟 𝛼𝜇 𝜃 𝑧 = ℋ𝑓 1 + ℱ ln 𝐷𝑟 2 ℋ𝑓 𝑙𝑛 𝑒 −_{ℱ ln 𝐷}2 ℋ𝑓 𝑟 𝜃 + 𝛾 𝑒 −_{ℱ ln 𝐷}2 ℋ𝑓 𝑟 𝛼𝜇 𝜃 atau 𝜃 𝑧 = −ℋ𝑓 1 + ℱ ln 𝐷𝑟 2 ℋ𝑓 𝑙𝑛 𝑒 −_{ℱ ln 𝐷}2 ℋ𝑓 𝑟 𝜃 + 𝛾 𝜃 atau 𝜃 𝑧 = −ℋ𝑓 1 + ℱ ln 𝐷_𝑟 2 ℋ𝑓 𝑙𝑛 𝑒 −_{ℱ ln 𝐷}2 ℋ𝑓 𝑟 + ln 𝜃 + 𝛾 𝜃 atau