APLIKASI METODE AUGMENTED LAGRANGE MULTIPLIER PADA OPTIMASI BENTUK KANTILEVER

(1)

APLIKASI METODE AUGMENTED LAGRANGE

MULTIPLIER PADA OPTIMASI BENTUK

KANTILEVER

Nasrullah

(1)

, Sir Anderson

(1)

, Yazmendra Rosa

(1) (1)

Staf Pengajar Jurusan Teknik Mesin, Politeknik Negeri Padang.

ABSTRACT

The globalization and free trade era all fields require be optimizing and working efficiently. In they are of design, optimization is used for reducing process times and production cost, increase quality, and the accuration of product design in other to produce competitive products. Optimization process also provide a systematic design procedure which can used for solving several design variables and constraints which are difficult to visualized graphically. Augmented Lagrange Multiplier (ALM) is promising optimization method because of the fast convergence rate and insensitive with penalty multiplier. Convergence rate is more influenced by the addition of Lagrange multiplier. The objective of this study is to understand ALM method and its characteristics, to create the computer program using this method and their application, to optimize the shape of a cantilever beam to get optimum design. The ALM method optimization software has already programed with several cases. This program can be applied in the other optimization cases. The optimization of a cantilever beam has applied to the program and resulted a minimum weight of 875, 56 kg in third model.

Keywords: Optimization, ALM, cantilever beam.

1. PENDAHULUAN

Ilmu tentang optimasi mandapat perhatian yang serius dari beberapa pihak. Semua ini sejalan dengan kompetisi di era globalisasi yang menuntut semua bidang untuk melakukan efisiensi dan optimasi. Pada

bidang perancangan, proses optimasi dilakukan

diantaranya untuk pengurangan waktu, biaya

produksi, jaminan kualitas, dan keakuratan hasil rancangan. Hal ini dilakukan untuk menghasilkan produk yang kompetitif dan dapat bersaing di pasaran.

Proses optimasi juga menyediakan prosedur

perancangan sistematis yang bisa menangani banyak

variabel perancangan dan kendala yang sulit

divisualisasikan secara grafik. Keberhasilan dalam

menggunakan teknik optimasi dalam prakteknya paling kurang ada 3 persyaratan yang harus dipenuhi yaitu pemodelan matematika dari problem optimasi perancangan, pengetahuan atau pengalaman dalam teknik optimasi, dan pengetahuan dalam program komputer. Untuk efisiensi dalam pemecahan problem

optimasi, banyak perangkat lunak yang bisa

digunakan, tetapi membutuhkan pengetahuan tentang

pemograman yang digunakan[1].

Pada dasarnya optimasi dapat dibagi menjadi 2 metode yaitu metode langsung (direct method) dan metode tidak langsung (indirect method).Metode langsung adalah metode optimasi meminimumkan problem optimasi tanpa mengubah fungsi objektif dan fungsi kendala. Untuk kasus masalah berkendala metode ini kurang efektif karena harus mencari syarat cukup dan perlu disemua titik di daerah

feasible, kemudian dibandingkan mana yang lebih optimum.

Metode tidak langsung adalah metode optimasi meminimumkan suatu problem berkendala yang diubah menjadi problem tanpa kendala dengan menambahkan penalti pada problem tersebut sebagai

ganti dari kendala yang dilanggar. Metode

Augmented Lagrange Multiplier (ALM) termasuk ke dalam metode ini, yang menambahkan pengali Lagrange untuk mempercepat laju konvergensi. Sehingga pengali penalti tidak berpengaruh secara signifikan dalam konvergensi. Kelebihan lain dari metode ini adalah pendekatan bisa dilakukan dari daerah feasible dan infeasible.

Perkembangan teknologi komputer yang sangat pesat dewasa ini, memudahkan kita untuk mempelajari dan

menyelesaikan masalah optimasi perancangan.

Optimasi perancangan dimodelkan dalam model

matematika dan kemudian diselesaikan dengan

program komputer. Akurasi dan ketelitian hasil

optimasi tergantung dari kesempurnaan model

matematika dan perangkat lunak yang digunakan.

Matlab adalah suatu program aplikasi dengan

kemampuan yang tinggi dalam perhitungan

matematis. Hal yang membedakan dengan program aplikasi lain adalah Matlab mempunyai komputasi, visualisasi dan pemograman dalam suatu paket tool yang mudah digunakan. Bahasa pemrograman yang digunakan pada Matlab mempunyai performa tingkat tinggi untuk memecahkan masalah yang menyangkut analisis perhitungan, baik secara analitik maupun numerik. Permasalahan dan solusi yang dihasilkan

(2)

Jurnal Teknik Mesin Vol. 8, No. 1, Juni 2011 ISSN 1829-8958

62 ditampilkan dalam ekspresi matematik yang sudah

lazim digunakan. Kelebihan Matlab terhadap bahasa

pemograman lainnya adalah kemudahan dalam

mendifinisikan matriks, penurunan persamaan

dengan fasilitas simbolik, dan fungsi-fungsi dengan jumlah cukup banyak[2].

Tujuan yang ingin dicapai dalam penulisan tesis ini adalah: Memahami metode Augmented Lagrange Multiplier untuk menyelesaikan masalah optimisasi

dengan berkendala. Membuat perangkat lunak

Augmented Lagrange Multiplier dengan program Matlab. Studi kasus, aplikasi optimasi metode ALM pada kasus beam kantilever.

Dengan adanya perangkat lunak metode ALM ini,

diharapkan membantu perancang dalam

menyelesaikan masalah-masalah optimasi, dan dapat

membuat atau merancang suatu produk yang

berkualitas, aman, dan biaya murah dalam bidang rekayasa.

2. PEMBUATAN PRANGKAT LUNAK METODE

AUGMENTED LAGRANGE MULTIPLIER

Dalam banyak kasus tidak mudah untuk

menyelesaikan problem optimasi dengan fungsi non linier secara eksak.Pencarian solusi suatu problem kadang-kadang membutuhkan formulasi matematika yang kompleks untuk memberikan solusi yang terbaik. Solusi optimum diperoleh dengan proses perhitungan yang panjang dan tidak praktis. Untuk

mengatasinya maka dikembangkanlah suatu

perangkat lunak untuk menyesaikan problem

optimasi perancangan, sehingga diperoleh solusi yang lebih baik, dalam watu cepat dan biaya lebih rendah.

Optimisasi numerik adalah salah satu alat yang diperlukan untuk menghasilkan perancangan yang optimum. Teknik optimasi numerik menawarkan

pendekatan matematika untuk mendapatkan suatu rancangan yang optimum[5].

Perangkat lunak yang akan dibuat adalah optimasi metode Augmented Langange Multiplier dengan bantuan program Matlab R2010a yang digunakan untuk perhitungan optimasi perancangan sehingga mendapatkan suatu hasil yang optimum. Pada bab ini akan dibahas mengenai diagram alir perangkat lunak, dan pembuatan perangkat lunak serta verifikasi dari perangkat lunak yang dibuat.

Perangkat lunak ini menggunakan M-file jenis

function file sehingga dapat digunakan untuk

beberapa kasus dengan input yang berbeda. Secara garis besar perangkat lunak dibagi menjadi 2 bagian besar, yaitu perangkat lunak utama Augmented Lagrange Multiplier, dan 3 sub perangkat lunak berupa function untuk fungsi objektif, fungsi kendala, fungsi pseudo-objektif

2.1. Problem dengan Kendala Kesamaan (Equality Constraint)

Problem dengan kendala kesamaan adalah problem

optimasi yang hanya mempunyai kendala

kesamaan.Fungsi kendala kesamaan (equality

constraints), disimbolkan dengan huruf h. Fungsi kendala kesamaan bisa terdiri dari satu atau lebih

dalam suatu permasalahan.Banyaknya variabel

perancangan dalam satu masalah harus lebih besar dari banyaknya kendala kesamaan yang ada. Bentuk fungsi kendala kesamaan sebagai berikut:

dengan l = banyak kendala kesamaan

Pembuatan perangkat lunak untuk persoaalan

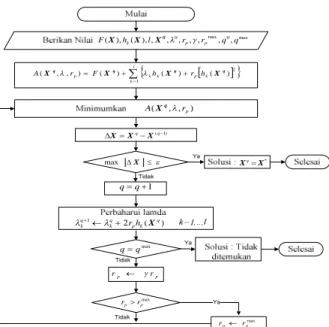
optimasi kendala kesamaan (equality constraint) mengikuti diagram alir berikut:

         l k k p k k p F h r h r A 1 2 ) ( ) ( ) ( ) , , (_Xq_ _Xq _ _Xq _Xq ) , , ( rp A q X ) ( 2 1 q k p q k q k   rh X  _  ) 1 (   _X _Xq _Xq    X max p p r r   max p p r r  max p p r r  max 0 max 0_, _, _, _, _, , , ), ( ), ( h l r r q q F k  p p 0 X X X * X Xq 1   q q max q q

(3)

63

2.2. Problem dengan Kendala Ketaksamaan

(Inequality Constraint)

Problem dengan kendala ketaksamaan adalah

problem optimasi yang hanya mempunyai kendala

ketaksamaan. Fungsi kendala ketidaksamaan

(inequality constraints), disimbolkan dengan huruf g. Fungsi kendala ketidaksamaan dapat lebih dari satu

dalam permasalahan perancangan, dan kendala sisi termasuk kedalam kendala ketaksamaan. Bentuk fungsi kendala ketidaksamaan sebagai berikut:

j= 1, ..., m Pembuatan perangakat lunak untuk problem optimasi

ketaksamaan (inequality constraint) mengikuti

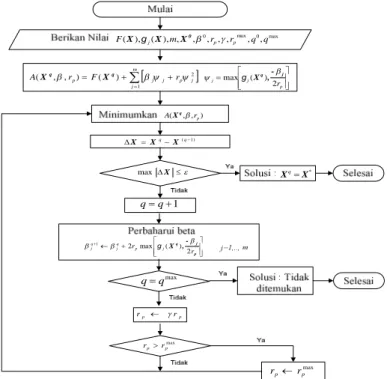
diagram alir berikut:

       m j j p j j p F r r A 1 2 ) ( ) , , ( q q   X X p p r r   max p p r r  max p p r r  ) , , ( rp A_Xq ) 1 (   _X _Xq _Xq          p j j max ( )₂_r j q_, -X   g    X max            p j q -, X r rp j q j q j 2 ) ( max 2 1 _   g max q q max 0 max 0 , , , , , , , ), ( ), ( m r r q q F j  p p 0 X X X g * X Xq 1   q q

Gambar 2 Diagram alir penyelesaian masalah optimasi dengan kendala ketaksamaan

2.3. Problem dengan Kendala Gabungan (General Constraint)

Problem optimasi yang mempunyai kendala kesamaan dan taksamaan, prmbuatan perangkat lunak mengikuti diagram alir berikut:

p p r r   max p p r r  max p p r r       _   _    l k k p k k m j j p j j p F r h r h r A 1 2 1 2 ₍ ₎ ₍ ₎ ) ( ) , , , (_Xq__ _Xq __ _ _ _Xq _Xq ) 1 (    q q X X X max 0 max 0 0_, _, _, _, _, _, , , , ), ( ), ( ), ( h lm r r q q F k j   p p 0 X X X X g ) , , , ( rp A_Xq    X max _Xq__X* 1   q q ) ( 2 1 q k p q k q k   rh X  _             p j q_, -X r rp j q j q j 2 max ( )₂ 1 _   g max q q

Gambar 3 Diagram alir penyelesaian masalah optimasi dengan kendala gabungan 0  ) ( X j g

(4)

64 3.4. Verifikasi Hasil Perangkat Lunak

Untuk menentukan apakah program yang dibuat bekerja sesuai dengan teorinya, maka dilakukan

pengecekan atau verifikasi hasil dengan cara

menyelesaikan permasalahan optimasi sederhana, kemudian membandingkan hasil yang diperoleh dengan melakukan perhitungan analitik dengan hasil yang diperoleh dari perangkat lunak yang sudah dibuat.

Perangkat lunak juga dibandingkan dengan motode lain dengan cara menyelesaikan suatu permasalahan optimasi yang sudah ada penyelesaiannya dari

referensi[5]. Permasalahan yang diambil adalah

sebagai berikut:

Sebuah beam kantilever seperti “Gambar (4)”, panjang (L) 500 cm dibagi menjadi 5 segmen sama panjang, panjang masing-masing segmen li = 100 cm, P = 50 000 N,modulus elastisitas E = 200 GPa, tegangan bending izin σizin= 14 000 N/cm2,izin= 0,5

cm, dan ρ bahan = 0,007860 kg/cm3.Variabel

rancangan adalah tinggi (ti) dan lebar(bi). Kita ingin

menentukan tinggi variabel rancangan yang

meminimumkan berat tetapi tegangan bending dan defleksi di sepanjang x harus lebih kecil atau sama dengan yang diizinkan.

Gambar 4 Beam kantilever bertingkat

Penyelesaian: Minimum berat

Kendala:

Tegangan bending maksimum yang terjadi, harus lebih kecil atau sama dengan tegangan izin yang diberikan.

izin

 max 

Momen inersia tiap segmen i adalah:

Momen bending sisi kiri dari segmen i dapat dihitung dengan:         



 i j j i i P L l l M 1 12 3 i i i t b I 

Tegangan bending maksimum dari segmen i dapat dihitung i i i i I t M 2   Kendala 1 adalah g1(t, b): 0 1izin  Kendala 2 adalah g2(t, b): 0 2izin  Kendala 3 adalah g3(t, b): 0 3izin  Kendala 4 adalah g4(t, b): 0 4izin  Kendala 5 adalah g5(t, b): 0 5izin 

Defleksi maksimum yang terjadi, harus dibawah defleksi izin yang diberikan.Defleksi maksimum terjadi pada segmen 5, jadi

izin

  5

Dengan menggunakan metode integrasi ganda,

didapatkan persamaan defleksi i sisi kanan dari

segmen i. 1 1 ' 1 1 2 ' 1 1 ' ' 0 0 3 2 2 2 0                            



i i i i j j i i i i i j j i i i i l l l L EI Pl l l L EI Pl        Kendala 6 adalah g6(t, b):

Bentuk standard dari problem di atas adalah: 0

5izin

 Variabel rancangan adalah t.

Minimum berat : ) ( ) , (t b b₁t₁l₁ b₂t₂l₂ b₃t₃l₃ b₄t₄l₄ b₅t₅l₅ W      terhadap : g1(t,b) : g2(t,b) : g3(t,b) : g4(t,b) : g5(t,b) : g6(t,b) : g7(t,b) : g6(t,b) : g9(t,b) : g10(t,b) : g11(t,b) : g12(t,b) : g13(t,b) : g14(t,b) : g15(t,b) : g16(t,b) : g17(t,b) : g18(t,b) : g19(t,b) : g20(t,b) : g21(t,b) :

Hasil optimasi yang diperoleh adalah sebagai berikut:

) ( ) , (t b b1t1l1 b2t2l2 b3t3l3 b4t4l4 b5t5l5 W      0 5izin   0 20 1 1 b  t 0 1 1   b 0 5 1   t 0 1izin  2izin0 0 3izin  4izin0 0 5izin  0 20 2 2 b  t 0 20 3 3 b  t t420b4 0 0 20 5 5 b  t 0 5 2   t  t350 0 5 4   t  t550 0 1 2   b 0 1 3   b  b410 0 1 5   b

(5)

65

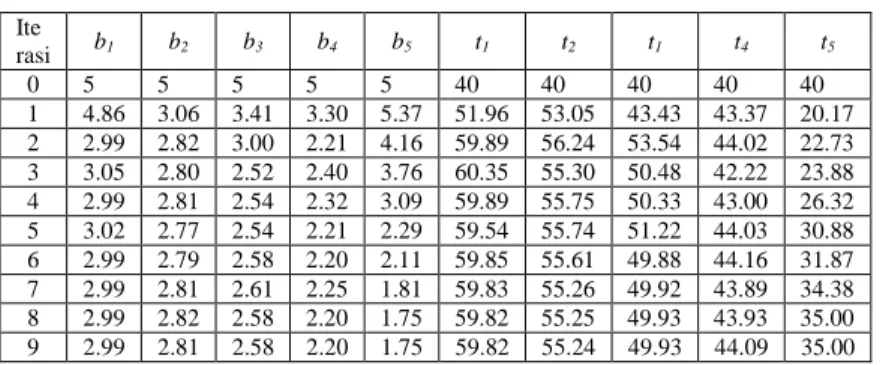
Tabel 1 Iterasi tinggi, lebar dan volume problem beam bertingkat Ite rasi b1 b2 b3 b4 b5 t1 t2 t1 t4 t5 0 5 5 5 5 5 40 40 40 40 40 1 4.86 3.06 3.41 3.30 5.37 51.96 53.05 43.43 43.37 20.17 2 2.99 2.82 3.00 2.21 4.16 59.89 56.24 53.54 44.02 22.73 3 3.05 2.80 2.52 2.40 3.76 60.35 55.30 50.48 42.22 23.88 4 2.99 2.81 2.54 2.32 3.09 59.89 55.75 50.33 43.00 26.32 5 3.02 2.77 2.54 2.21 2.29 59.54 55.74 51.22 44.03 30.88 6 2.99 2.79 2.58 2.20 2.11 59.85 55.61 49.88 44.16 31.87 7 2.99 2.81 2.61 2.25 1.81 59.83 55.26 49.92 43.89 34.38 8 2.99 2.82 2.58 2.20 1.75 59.82 55.25 49.93 43.93 35.00 9 2.99 2.81 2.58 2.20 1.75 59.82 55.24 49.93 44.09 35.00 Tabel 2 Perbandingan Iterasi volume dengan metode lain pada problem beam bertingkat

METODE ITERASI 1 2 3 4 5 program 0 100000 100000 100000 100000 100000 100000 1 17661 83824 79813 80589 50827 81499 2 25955 71806 72467 72488 64009 68964 3 30434 69033 68955 68345 64488 65748 4 34269 66574 67016 67744 65123 64427 5 39697 66065 66832 66145 65057 63264 6 43223 65760 66498 65887 65794 62745 7 49486 65736 66088 65704 65561 62434 8 51658 65746 65866 65665 65678 62215 9 57110 65866 65665 62150 10 60459 65866

Gambar 5 Grafik hubungan lebar dengan iterasi untuk problem beam bertingkat

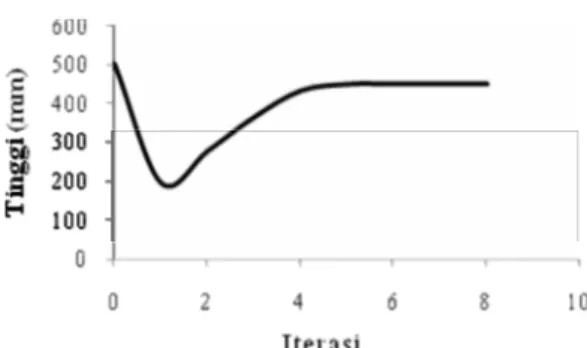
Gambar 6 Grafik hubungan tinggi dengan iterasi untuk problem beam bertingkat

Gambar 7 Grafik hubungan volume dengan iterasi untuk problem beam bertingkat

Hasil optimasi menggunakan perangkat lunak ALM, terdapat perbedaan hasil yang tidak begitu jauh dengan metode lain. Cek tegangan pada masing-masing segmen dan defleksi maksimum di peroleh

tegangan maksimum = 13999, 77 N/cm2dan defleksi

maksimum 0,374 cm. Masih di bawah tegangan izin dan defleksi izin.

3. STUDI KASUS OPTIMASI BENTUK BEAM

KANTILEVER MENGGUNAKAN METODE

AUGMENTEDLAGRANGEMULTIPLIER

3.1 Beam cantilever penampang sama

Sebuah beam kantileveryang sering digunakan pada

kontruksi “Gambar (8)”, mempunyai bentuk

penampang yang sama di sepanjang L. Beam dirancangdengan panjang L = 5000 mm, dan lebar b = 100 mm, untuk menahan beban terkosentrasi yang berada pada ujungnya sebesar P = 50 000 N.

(6)

66 Modulus elastisitas E = 200000 MPa, Tegangan

bending izin σizin = 140 MPa, izin= 13,8 mm, dan ρ

bahan = 0,000007860 kg/mm3.Variabel rancangan

adalah tinggi t. Beam harus memenuhibatasan

tegangan bending izin dan defleksiizin. Kita ingin menentukan tinggi beam (t) yang meminimumkan berat beam tetapi tegangan bending dan defleksi di sepanjang x harus lebih kecil atau sama dengan yang diizinkan.

Gambar 8 Beam kantilever dengan penampang sama sepanjang x Diketahui: L = 5000 mm σizin= 140 MPa P = 50.000 N izin= 13, 8 mm E = 200000 MPa b = 100 mm ρ = 0,000007860 kg/mm3

Tentukan nilai t yang meminimumkan berat dari beam tetapi tegangan bending dan defleksi di sepanjang x harus lebih kecil atau sama dengan yang diizinkan.

Membuat model matematika dari permasalah yang ada

Fungsi objektif: Minimum berat Kendala :

Tegangan bending maksimum yang terjadi, harus di bawah tegangan izin yang diberikan.

Kendala 1 adalah g1(t) :

Defleksi maksimum yang terjadi, harus di bawah defleksi izin yang diberikan.

Persamaan defleksi Kendala 2 adalah g2(t):

Bentuk standar dari problem di atas adalah: Variabel rancangan adalah t,

Minimum berat : terhadap : g1(t): 0 6 2        izin bt PL _ g2(t): 0 4 3 3         izin Ebt PL _

Hasil optimasi yang diperoleh adalah sebagai berikut:

Gambar 9 Grafik hubungan tinggi dengan iterasi pada problem beam kantilever

Gambar 10 Grafik hubungan berat dengan iterasi pada problem beam kantilever

Gambar 11 Grafik hubungan kendala g1(X) dengan iterasi

pada problem beam kantilever

Gambar 12 Grafik hubungan kendala g2(X) dengan iterasi

pada problem beam kantilever izin



max 0 6 2 _      Izin bt PL _ izin  max 0 maxizin  Ltb t W() 3 3 max 4 Ebt PL   

(7)

67

Gambar 13 Grafik hubungan tegangandengan panjang pada problem beam kantilever

Gambar 14 Grafik hubungan defleksi dengan panjang pada problem beam kantilever

Dari proses optimasi problem di atas diperoleh hasil yang optimum sebagai berikut:

Tinggi (t) = 449, 1 mm, Berat (W) = 1765 kg,

Tegangan max = 74, 37 MPa, Defleksi mak = 13, 8 mm.

Kita menginginkan tegangan di sepanjang xsama, defleksi yang terjadi tidak melebihi defleksi yang diizinkan dengan mengubah inersia beam yang

dipengaruhi oleh t disepanjang x. Sehingga

didapatkan berat beam yang lebih ringan lagi. Untuk itu dibuatlah beberapa bentuk beam yang lain, tetapi

tidak mengurangi fungsi dari beam tersebut,

memenuhi batasan tegangan izin dan defeksi izin.

3.2 Optimasi Bentuk Beam Kantilever

Menggunakan Metode ALM

Beberapa rancangan bentuk beam yang akan

dilakukan optimasi untuk mendapatkan berat beam yang paling minimum diberikan berikut ini :.

Bentuk Bertingkat

Beam Segitiga (Pendekatan polynomial orde 1)

Bentuk kurva (Pendekatan polynomial orde 2)

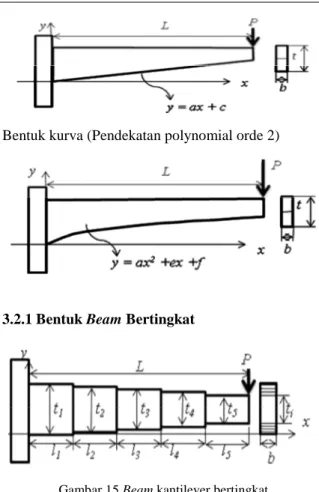
3.2.1 Bentuk Beam Bertingkat

Gambar 15 Beam kantilever bertingkat

Fungsi objektif: Minimum berat

Kendala:

Tegangan bending maksimum yang terjadi, harus lebih kecil atau sama dengan tegangan izin yang diberikan.

izin

 max

Momen bending sisi kiri dari segmen i dapat dihitung dengan:

Tegangan bending maksimum dari segmen i dapat dihitung Kendala 1 adalah g1(t, b): Kendala 2 adalah g2(t, b): Kendala 3 adalah g3(t, b): Kendala 4 adalah g4(t, b): Kendala 5 adalah g5(t, b): ) ( ) (t bt1l1 bt2l2 bt3l3 bt4l4 bt5l5 W      12 3 i i i t b I          



 i j j i i P L l l M 1 i i i i I t M 2   0 2izin   0 3izin  

0

4





izin





0 5



izin



0 1



izin 



(8)

68 Defleksi maksimum yang terjadi, harus dibawah

defleksi izin yang diberikan.Defleksi maksimum terjadi pada segmen 5, jadi

Dengan menggunakan metode integrasi ganda,

didapatkan persamaan defleksi isisi kanan segmen

i. 1 1 ' 1 1 2 ' 1 1 ' ' 0 0 3 2 2 2 0                            



i i i i j j i i i i i j j i i i i l l l L EI Pl l l L EI Pl        Kendala 6 adalah g6(t, b):

Bentuk standard dari problem di atas adalah: Variabel rancangan adalah t.

Minimum berat :

terhadap :

g1(t,b) : g2(t,b) :

g3(t,b) : g4(t,b) :

g5(t,b) : g6(t,b) :

Dari proses optimasi problem di atas diperoleh hasil yang optimum sebagai berikut:

Gambar 16 Grafik hubungan tinggi dengan iterasi pada problem beam bertingkat

Tinggi segmen 1 (t1) = 540, 36 mm Tinggi segmen 2 (t2) = 476, 87 mm Tinggi segmen 3 (t3) = 403, 68 mm Tinggi segmen 4 (t4) = 314, 50 mm Tinggi segmen 5 (t5) = 193, 35 mm Berat beam (W) = 1516 kg

Tegangan max = 80, 25 MPa

Defleksi max = 13, 80 mm

Gamba 17 Beam kantilever bertingkat hasil optimasi

3.2.2 Bentuk Beam Segitiga (polynomial orde 1)

Gambar 18 Beam kantilever segitiga

Minimum berat

Kendala:

Tegangan bending maksimum yang terjadi, harus lebih kecil atau samadengan tegangan izin yang diberikan.

izin

 max

Tegangan bending maksimum dari segmen i dapat dihitung Kendala 1 adalah g1(t,b) : Kendala 2 adalah g2(t,b) : Kendala 3 adalah g3(t,b) : Kendala 4 adalah g4(t,b) : Kendala 5 adalah g5(t,b) : Persamaan defleksi

max= pada saat x = L,

3 3 2 2 2 2 3 3 2 max ) ln( 12 6 6 . 1 2 1 12 ) ln( 12 ) ( 6 ) ( 6 Eba c Eba P c Eba PL Eb L c a c a c La P Eba c La P c La Eba Pc c La Eba PL         _  _         

Bentuk standard dari problem di atas adalah:

izin   ₅ ) ( ) , (t b b1t1l1 b2t2l2 b3t3l3 b4t4l4 b5t5l5 W 



   



a

l

c



t

₅



(

₁



₂



₃



₄



₅

)





a

l

c



t

₄



(

₁



₂



₃



₄

)





a

l

c



t

₃



(

₁



₂



₃

)



 bL t t t W 2 ) ( ) (  0 5



 



_ bL c aL c al _          2 0 0 5izin   0 3izin  4izin0 0 5izin  0 1izin  2izin0



a

l

c



t

₁



(

₁

)





a

l

c



t

₂



(

₁



₂

)



12 3 i i i t b I          



 i j j i i P L l l M 1 i i i i I t M 2   0 2izin  0 3izin   0 4izin   0 5izin  0 1izin  

(9)

69 Variabel rancangan adalah

Minimum berat :



 



_ . . . 2 ) ( ) ( ) , ( 0 L b c aL c al c a W           terhadap : g1(a, c): g2(a, c): g3(a, c): g4(a, c): g5(a, c): g6(a, c):

Dari proses optimasi dari problem di atas diperoleh hasil yang optimum sebagai berikut:

Gambar 19 Grafik hubungan tinggi terhadap iterasipada problem beam segitiga

Tinggi (t0) = 346, 67 mm Tinggi (t1) = 300, 11

mm Tinggi (t2) = 253, 55 mm Tinggi (t3)

= 207, 0 mm Tinggi (t4) = 160, 44 mm

Tinggi (t5) = 113, 88 mm

Berat beam (W) = 905, 00 kg Tegangan max= 139, 99 MPa

Defleksi max = -8, 10 mm

Gambar 20 Beam kantilever segitiga hasil optimasi

3.2.3 Bentuk Beam Kurva (polynomial orde 2)

Gambar 21 Beam kantilever kurva



al el f



t  ( )  (1) 2 1 1



a l l l l l el l l l l f



t  (     )2 (₁ ₂ ₃ ₄ ₅) 5 4 3 2 1 5



al l l l el l l l f



t  (    )2 (₁ ₂ ₃ ₄) 4 3 2 1 4



al l l el l l f



t  (   )2 (₁ ₂ ₃) 3 2 1 3



al l el l f



t  (  )  (1 2) 2 2 1 2 Minimum berat Kendala:

Tegangan bending maksimum yang terjadi, harus lebih kecil atau samadengan tegangan izin yang diberikan.

izin

 max 

12 3 i i i t b I 

Tegangan bending maksimum dari segmen i dapat dihitung Kendala 1 adalah g1 (t, b): Kendala 2 adalah g2(t, b): Kendala 3 adalah g3(t, b): Kendala 4 adalah g4(t, b): Kendala 5 adalah g5(t, b): Persamaan defleksi

max= pada saat x = L,

                                   252 2 2 2 2 5 2 2 2 2 2 2 5 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 5 2 2 2 2 2 2 2 4 . 4 4 2 arctan 144 4 . 4 2 arctan 48 4 24 4 . 4 4 2 arctan 36 4 1 4 4 2 ln 36 4 ln 36 4 24 4 1 4 4 2 ln 18 4 ln 18 4 6 4 . 4 2 arctan 12 4 6 c af Eb x c af c c af ax L Pa c af Eb c af c ax Pfa f cx ax c af Eb Pfax c af Eb c af c c af ax Pc c af Eb c af c c af ax PaL c af Eb f cx ax PaL f cx ax c af Eb PaLf c af Eb c af c c af ax Pc c af Eb f cx ax Pc f cx ax c af Eb PLc c af Eb c af c ax Pc f cx ax c af Eb x Pc                                                                                                                         0 0izin   1izin0 0 2izin   3izin0 dx f ex x a Luas



. 2  . f x x e x a Luas . 2 . 3 . 3 2     b x f x e x a Volume . . 2 . 3 . 3 2       _ _   b fL eL aL Berat _         2 3 2 3 0 4izin  _max_izin 0         



 i j j i i P L l l M 1 i i i i I t M 2   0 2izin  0 3izin   0 4izin   0 5izin  0 1izin  

(10)

Jurnal Teknik Mesin Vol. 8, No. 1, Juni 2011 ISSN 1829-8958 70                            252 2 2 5 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 5 2 2 2 2 5 2 2 2 2 5 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 5 2 2 2 4 . . 4 72 4 . 4 arctan . 48 . . 4 . . 4 . 1 4 ln 36 4 ln 36 4 24 4 1 4 ln 18 4 ln 18 4 6 4 . 4 arctan 24 . 4 4 arctan 144 4 4 arctan 72 ) 4 ( 18 ) 4 ( 36 ) 4 ( 12 ) 4 ( 6 4 . 4 4 2 arctan 72 4 . 4 4 2 arctan 72 c af Eb c c af c PaLarcta c af Eb c af c Pfa c f a a d b E c af c PaL c af Eb f PaL c af Eb PaL c af Eb c af c Pc c af Eb f Pc f c af Eb PLc c af Eb c af c Pc L c af Eb c af c L Pa c af Eb c af c ca f c af Eb Pc f c af Eb PaLc f c af Eb Pf f c af Eb PcL c af Eb ax c af c c af ax Pc c af Eb c c af c c af ax PaL                                _                                                                                                            

Dari proses optimasi dari problem di atas diperoleh hasil yang optimum sebagai berikut:

Gambar 22.Grafik hubungan tinggi dengan iterasi pada problem beam kurva Tinggi (t0) = 327, 3 mm Tinggi (t1) = 297, 5 mm Tinggi (t2) = 257, 4 mm Tinggi (t3) = 207, 0 mm Tinggi (t4) = 146, 4 mm Tinggi (t5) = 75, 5 mm Berat beam (W) = 875, 56 kg

Tegangan bending max = 139, 99 MPa

Defleksi maksimum = -8, 14 mm

Gambar 23 Beam kantilever kurva hasil optimasi

Perbandingan ketiga model bentuk beam kantilever

Gambar 24 Grafik perbandingan berat dengan iterasi pada ketiga model bentuk beam kantilever

Gambar 25 Grafik perbandingan tegangan dengan panjang pada ketiga model bentuk beam kantilever

Gambar 26 Grafik perbandingan defleksi dengan panjang pada ketiga model bentuk beam kantilever

Perbandingan tegangan maksimum, defleksi

maksimum yang terjadi pada tiap segmen beam dan berat untuk ketiga model “Tabel (3)”.

Tabel 3 Perbandingan tegangan max, defleksi max, dan berat untuk ketiga model bentuk beam kantilever

Dari ketiga optimasi bentuk beam kantilever di atas, terlihat pada kasus satu belum meratanya tegangan di sepanjang batang, dan pada tiap segmen terjadi kosentrasi tegangan. Untuk kasus dua dan tiga, tegangan sudah mulai merata di sepanjang batang, dan penurunan berat tidak terlalu signifikan. Untuk pemilihan bentuk beam yang akan digunkan perlu dilakukan perhitungan manufacturing dari beam, sehingga diperoleh proses dan biaya pembuatan yang paling minimum.

Gambar 27 Perbandingan ketiga model bentuk beam kantilever

4. KESIMPULAN DAN SARAN 4.1 Kesimpulan

1. Perangkat lunak optimasi dengan metode ALM

telah berhasil disusun dengan validasi pada beberapa kasus.

2. Dari berbagai kasus yang dibahas dapat dilihat

nilai optimal diperoleh dengan cepat (kurang dari 10 iterasi).

(11)

71

3. Perangkat lunak optimasi metode ALM yang

dibuat ini, dapat membantu perancang dalam menyelesaikan persoaalan optimasi, sehingga dapat mempercepat dan menghasilkan rancangan yang diharapkan.

4. Dari studi kasus optimasi bentuk beam

kantilever yang dilakukan, bentuk beam yang paling optimum adalah bentuk beam kantilever model kurva pendekatan orde 2, dengan berat beam 875, 56 kg.

4.2 Saran

Saran yang diajukan sehubungan dengan hasil penelitian ini adalah:

1. Karena pada penelitian ini membuat perangkat

lunak ALM dengan batuan program Matlab, mungkin kedepannya program ini dapat di gabungkan dengan program lain sehingga bisa

menyelesaikan problem optimasi yang

kompleks atau yang susah membuat model matematikanya.

2. Karena pada penelitian ini hanya dibahas studi

kasus optimasi bentuk beam kantilever dengan pendekatan sampai polinum orde 2, mungkin bisa di lanjutkan pada pilonum orde n, sehingga didapatkan hasil yang lebih bagus lagi.

3. Karena pada penelitian ini hanya ditinjau

masalah optimasi bentuk beam kantilever untuk satu penampang saja, mungkin bisa dicari dengan bentuk penampang yang lain sehingga didapatkan bentuk yang lebih ringan lagi. PUSTAKA

1. Venkataraman, P, Applied Optimization With

Matlab Programming. New York: John Wiley & Sons, Inc, 2001.

2. Sembiring, J. & Jenie, Y.I, Modul Pelatihan

Matlab, Institut Teknologi Bandung, Indonesia, 2010.

3. Wikipedia, Lagrange Multiplier. (Online),

November 2010. (http://www.wikipedia.org,

diakses November 2010).

4. Purwantara. B., Kekuatan Bahan.

(http://www.bambangpurwantana.staff.ugm.ac.id), di akses November 2010.

5. Vanderplaats, N.Garret, Numerical

Optimization Techniques for Engineering

Design With Application. McGraw-Hill Book Company. 1984.

6. Yang, W. Y.-S. Applied Numerical Methods

Using Matlab. New Jersey: A John Willey & Sons, Inc., Publication, 2005.

7. V. D. da Silva, Mechanics and Strength of

Materials. New York: Springer, 2006.

8. Louie L. Yaw. Steel Design – LRFD AISC Steel

Manual 13th Edition. Beam Limit States, 2008.

9. Hunt, B. R., Lipsman, R. L., & Jonathan M.

Rosenberg With Kevin R. Coombes, J. E. A Guide to Matlab for Beginners and Experienced Users. New York: Cambridge University Press, 2001.

10. Dong, S., Methods for Constrained

Optimization, 2006.

11. Luenberger, D. G., & Ye, Y. Linear and

Nonlinear Programming, Third Edition.

Stanford: Springer, 2008. CURRICULUM VITAE

Nasrullah, ST., MT adalah Staf Pengajar pada Jurusan Teknik Mesin Politeknik Negeri Padang. Menyelesaikan pendidikan S1 & S2 di ITB dalam bidang Teknik Mesin.

Sir Anderson, ST., MT., & Yazmendra Rosa, ST., MT. Adalah staf pengajar di Jurusan Teknik Mesin Politeknik Negeri Padang