BAB IV
ANALISIS DAN EVALUASI METODA PERHITUNGAN
DALAM MEMPREDIKSI DAYA DUKUNG AKSIAL
FONDASI TIANG
4.1 Umum
Pada bab II telah dijelaskan mengenai teori kapasitas aksial fondasi tiang tunggal dan pada bab III telah dijelaskan mengenai contoh perhitungan untuk menentukan kapasitas fondasi tiang tunggal serta mengenai contoh perhitungan interpretasi kapasitas ultimit fondasi tiang berdasarkan data tes pembebanan. Selanjutnya, pada bab ini (bab IV) dibahas mengenai evaluasi metoda perhitungan dalam memprediksi daya dukung aksial fondasi tiang terhadap kapasitas terukur berdasarkan tiga kriteria statistik yaitu analisis berdasarkan kriteria probabilitas kumulatif 50% dan 90%, analisis berdasarkan kriteria aritmetik, dan analisis berdasarkan kriteria tingkat akurasi 20%. Adapun data (data N-SPT dan data tes pembebanan statik) yang diperoleh adalah dari enam lokasi proyek di Jakarta.
Berdasarkan data SPT dilakukan perhitungan menggunakan lima metoda perhitungan yaitu metoda Meyerhoff, metoda Aoki dan Velloso, metoda Shioi dan Fukui, metoda Reese dan O’Neill serta metoda Neely. Lima metoda tersebut digunakan untuk memprediksi kapasitas aksial fondasi tiang dan hasil dari kapasitas yang dihitung disebut kapasitas prediksi (Qp). Berdasarkan data tes pembebanan dilakukan interpretasi kapasitas fondasi tiang tunggal menggunakan empat metoda interpretasi yaitu metoda Davisson, metoda Chin, metoda De Beer, dan metoda Mazurkiewics. Adapun metoda yang selanjutnya digunakan adalah metoda Davisson. Hasil kapasitas yang dihasilkan berdasarkan data tes pembebanan disebut kapasitas terukur (Qm). Berikut adalah nilai dari Qp dan Qm dari enam lokasi proyek di Jakarta :
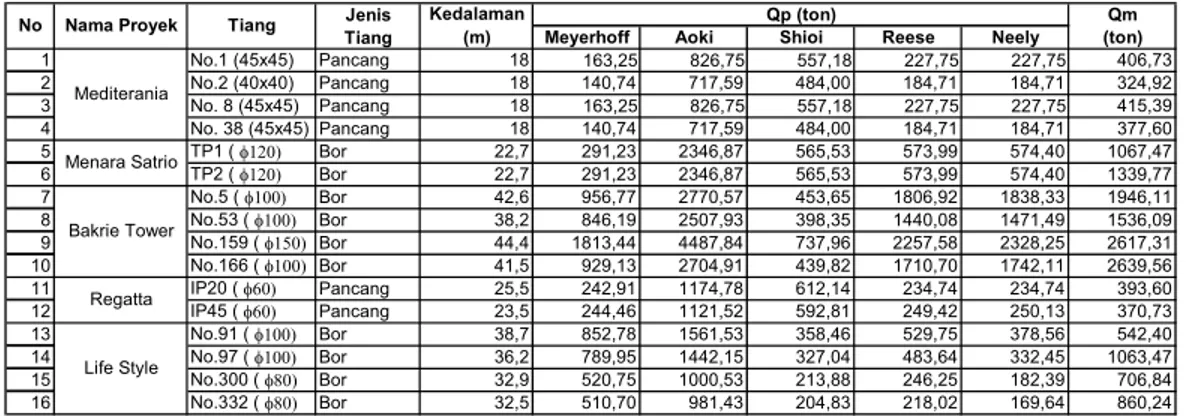
Tabel 4.1 Nilai Kapasitas Prediksi (Qp) dan Kapasitas Terukur (Qm)
Jenis Qm
Tiang Meyerhoff Aoki Shioi Reese Neely (ton)
1 No.1 (45x45) Pancang 18 163,25 826,75 557,18 227,75 227,75 406,73 2 No.2 (40x40) Pancang 18 140,74 717,59 484,00 184,71 184,71 324,92 3 No. 8 (45x45) Pancang 18 163,25 826,75 557,18 227,75 227,75 415,39 4 No. 38 (45x45) Pancang 18 140,74 717,59 484,00 184,71 184,71 377,60 5 TP1 ( I Bor 22,7 291,23 2346,87 565,53 573,99 574,40 1067,47 6 TP2 ( I Bor 22,7 291,23 2346,87 565,53 573,99 574,40 1339,77 7 No.5 ( I Bor 42,6 956,77 2770,57 453,65 1806,92 1838,33 1946,11 8 No.53 ( I Bor 38,2 846,19 2507,93 398,35 1440,08 1471,49 1536,09 9 No.159 ( I Bor 44,4 1813,44 4487,84 737,96 2257,58 2328,25 2617,31 10 No.166 ( I Bor 41,5 929,13 2704,91 439,82 1710,70 1742,11 2639,56 11 IP20 ( I Pancang 25,5 242,91 1174,78 612,14 234,74 234,74 393,60 12 IP45 ( I Pancang 23,5 244,46 1121,52 592,81 249,42 250,13 370,73 13 No.91 ( I Bor 38,7 852,78 1561,53 358,46 529,75 378,56 542,40 14 No.97 ( I Bor 36,2 789,95 1442,15 327,04 483,64 332,45 1063,47 15 No.300 ( I Bor 32,9 520,75 1000,53 213,88 246,25 182,39 706,84 16 No.332 ( I Bor 32,5 510,70 981,43 204,83 218,02 169,64 860,24 Qp (ton) No Tiang Kedalaman (m) Regatta Life Style Mediterania Nama Proyek Menara Satrio Bakrie Tower
Dari tabel 4.1 diatas terlihat kapasitas prediksi (Qp) dan kapasitas terukur (Qm) dari 16 tiang yang diuji beban (loading test). Langkah selanjutnya adalah menghitung nilai rasio Qp/Qm dari masing-masing metoda perhitungan untuk dievaluasi berdasarkan
tiga kriteria yang telah dijelaskan sebelumnya. Berikut adalah nilai Qp/Qm masing-masing metoda perhitungan tersebut :
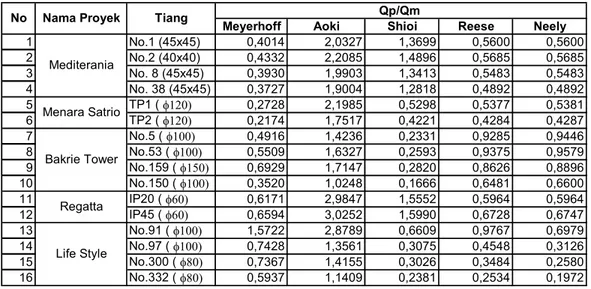
Tabel 4.2 Nilai Qp/Qm masing-masing metoda perhitungan
Meyerhoff Aoki Shioi Reese Neely
1 No.1 (45x45) 0,4014 2,0327 1,3699 0,5600 0,5600 2 No.2 (40x40) 0,4332 2,2085 1,4896 0,5685 0,5685 3 No. 8 (45x45) 0,3930 1,9903 1,3413 0,5483 0,5483 4 No. 38 (45x45) 0,3727 1,9004 1,2818 0,4892 0,4892 5 TP1 ( I 0,2728 2,1985 0,5298 0,5377 0,5381 6 TP2 ( I 0,2174 1,7517 0,4221 0,4284 0,4287 7 No.5 ( I 0,4916 1,4236 0,2331 0,9285 0,9446 8 No.53 ( I 0,5509 1,6327 0,2593 0,9375 0,9579 9 No.159 ( I 0,6929 1,7147 0,2820 0,8626 0,8896 10 No.150 ( I 0,3520 1,0248 0,1666 0,6481 0,6600 11 IP20 ( I 0,6171 2,9847 1,5552 0,5964 0,5964 12 IP45 ( I 0,6594 3,0252 1,5990 0,6728 0,6747 13 No.91 ( I 1,5722 2,8789 0,6609 0,9767 0,6979 14 No.97 ( I 0,7428 1,3561 0,3075 0,4548 0,3126 15 No.300 ( I 0,7367 1,4155 0,3026 0,3484 0,2580 16 No.332 ( I 0,5937 1,1409 0,2381 0,2534 0,1972
No Nama Proyek Tiang
Mediterania Menara Satrio Bakrie Tower Regatta Life Style Qp/Qm
Dari tabel 4.2 diatas terlihat hasil dari perhitungan Qp/Qm untuk masing-masing metoda perhitungan kapasitas aksial fondasi tiang. Dari hasil nilai Qp/Qm diatas selanjutnya adalah dilakukan analisis dan evaluasi metoda-metoda perhitungan untuk mengetahui metoda mana yang tepat yaitu mendekati nilai dari kapasitas terukur (Qm) analisis berdasarkan tiga kriteria statistik yaitu :
1. Kriteria berdasarkan analisis probabilitas kumulatif 90% dan 50 % 2. Kriteria berdasarkan analisis aritmetik
3. Kriteria berdasarkan analisis tingkat akurasi 20%.
Pada sub bab selanjutnya dibahas mengenai analisis dan evaluasi berdasarkan ketiga kriteria diatas.
4.2 ANALISIS KETEPATAN METODA-METODA PERHITUNGAN KAPASITAS FONDASI TIANG
Metoda perhitungan yang digunakan dalam perhitungan ini adalah : 1. Metoda Meyerhoff
2. Metoda Aoki dan Velloso 3. Metoda Shioi dan Fukui 4. Metoda Reese dan O’Neill 5. Metoda Neely
Masing-masing metoda diatas menghitung kapasitas aksial fondasi tiang berdasarkan data SPT (Standard Penetration Test) dan kapasitas yang didapat adalah kapasitas aksial prediksi fondasi tiang yang disebut Qp. Hasil interpretasi kapasitas aksial
Meyerhoff Aoki Shioi Reese Neely 1 100 100 100 100 100 2 75 75 75 75 75 3 50 50 50 50 50 4 25 25 25 25 25 No P(X<Qp/Qm)
Meyerhoff Aoki Shioi Reese Neely
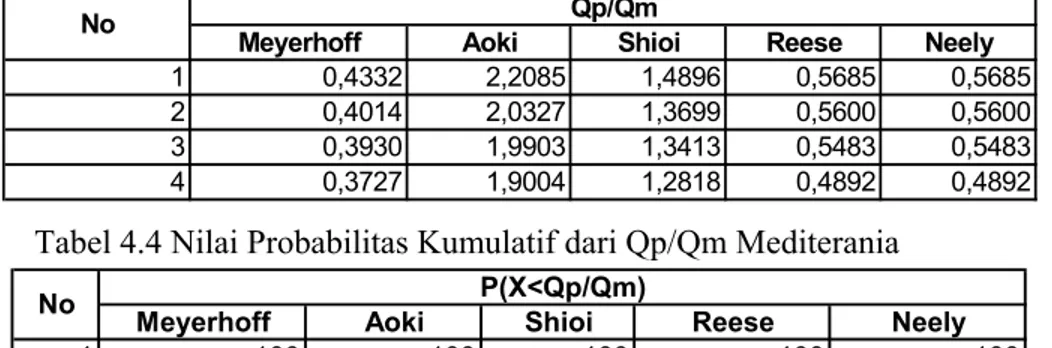
1 0,4332 2,2085 1,4896 0,5685 0,5685 2 0,4014 2,0327 1,3699 0,5600 0,5600 3 0,3930 1,9903 1,3413 0,5483 0,5483 4 0,3727 1,9004 1,2818 0,4892 0,4892 Qp/Qm No
fondasi tiang berdasarkan data tes pembebanan (Loading Test) disebut kapasitas aksial terukur yang disebut Qm. Nilai Qm ini digunakan sebagai nilai pembanding dimana nilai Qp yang paling mendekati nilai Qm menduduki nilai pertama dalam hal ketepatan metoda perhitungan.
Jumlah fondasi yang diteliti ada 16 tiang, dimana 16 tiang tersebut telah dilakukan uji pembebanan statik (loading test). Data loading test sangat diperlukan karena sebagai acuan / pembanding dari nilai-nilai kapasitas prediksi, Qp. Berikut adalah analisis dan evaluasi menggunakan tiga kriteria yang telah disebutkan sebelumnya.
4.2.1 Kriteria Berdasarkan Analisis Probabilitas Kumulatif 90% dan 50%
Untuk kriteria pertama, ada dua nilai pada probabilitas kumulatif yang dijadikan acuan analisis yaitu besarnya rasio Qp/Qm saat nilai probabilitas kumulatifnya (CP) 50% dan saat nilai probabilitas kumulatif (CP) 90%. Nilai Qp/Qm yang dianalisis adalah nilai Qp/Qm pada masing-masing proyek kontruksi dan nilai Qp/Qm gabungan dari seluruh proyek kontruksi. Hal ini dilakukan untuk mengetahui konsistensi dari metoda-metoda perhitungan.
Berikut adalah contoh dari pengolahan data di proyek Mediterania. Nilai Qp/Qm yang sudah didapat, kemudian diurutkan dari yang terbesar hingga yang terkecil.
Tabel 4.3 Nilai Qp/Qm Mediterania
Tabel 4.4 Nilai Probabilitas Kumulatif dari Qp/Qm Mediterania
Ket : P(X<Qp/Qm) adalah probabilitas dari nilai X dimana X kurang dari nilai Qp/Qm. Dimana X adalah suatu variabel acak( random varible) .
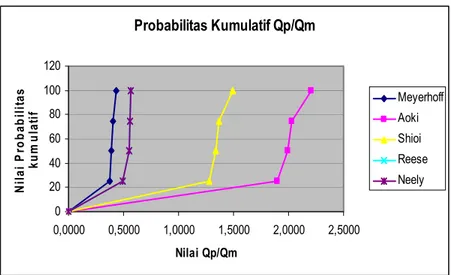
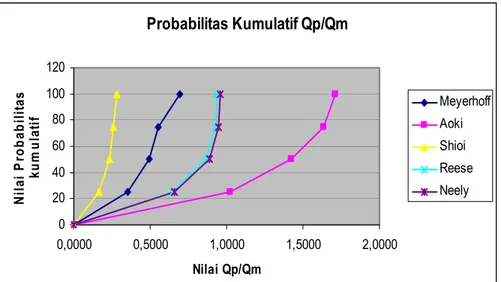
Dari hasil contoh perhitungan yang terlihat pada tabel diatas selanjutnya adalah memplot grafik probabilitas kumulatif Qp/Qm seperti yang terlihat di bawah ini. Untuk proyek-proyek lainnya juga dapat dilihat pada gambar 4.1 sd. 4.5 berikut ini :
Probabilitas Kumulatif Qp/Qm 0 20 40 60 80 100 120 0,0000 0,5000 1,0000 1,5000 2,0000 2,5000 Nilai Qp/Qm N ila i P ro b a b ili ta s ku m u la ti f Meyerhoff Aoki Shioi Reese Neely Probabilitas Kumulatif Qp/Qm 0 20 40 60 80 100 120 0,0000 0,5000 1,0000 1,5000 2,0000 2,5000 Nilai Qp/Qm N ila i P ro b a b ili ta s ku m u la ti f Meyerhoff Aoki Shioi Reese Neely Ket : Grafik Reese dan Neely Berhimpit
Gambar 4.1 Nilai Probabilitas Kumulatif Qp/Qm Mediterania
Ket : Grafik Reese, Neely dan Shioi Berhimpit
Probabilitas Kumulatif Qp/Qm 0 20 40 60 80 100 120 0,0000 0,5000 1,0000 1,5000 2,0000 Nilai Qp/Qm Ni lai P ro b a b ilit as ku m u lat if Meyerhoff Aoki Shioi Reese Neely Probabilitas Kumulatif Qp/Qm 0 20 40 60 80 100 120 0,0000 0,5000 1,0000 1,5000 2,0000 2,5000 3,0000 3,5000 Nilai Qp/Qm N il a i P ro b a b ilit a s ku m u la ti f Meyerhoff Aoki Shioi Reese Neely Probabilitas Kumulatif Qp/Qm 0 20 40 60 80 100 120 0,0000 0,5000 1,0000 1,5000 2,0000 2,5000 3,0000 3,5000 Nilai Qp/Qm N il a i P roba bi li ta s ku m u la ti f Meyerhoff Aoki Shioi Reese Neely Gambar 4.3 Nilai Probabilitas Kumulatif Qp/Qm Bakrie Tower
Keterangan : Meyerhoff, Reese dan Neely Berhimpit
Gambar 4.4 Nilai Probabilitas Kumulatif Qp/Qm Regatta
Rank Metode ' Poin
1 Reese & Neely 0,0168 1,5
2 Meyerhoff 0,0274 3
3 Shioi 0,1004 4
4 Aoki 0,1479 5
Rank Metode |L-1| Poin
1 Shioi 0,3413 1
2 Reese & Neely 0,4517 2,5
3 Meyerhoff 0,6070 4
4 Aoki 0,9903 5
Rank Metode Poin Tot.
1 Shioi, Reese, & Neely 4
2 Meyerhoff 5
3 Aoki 8
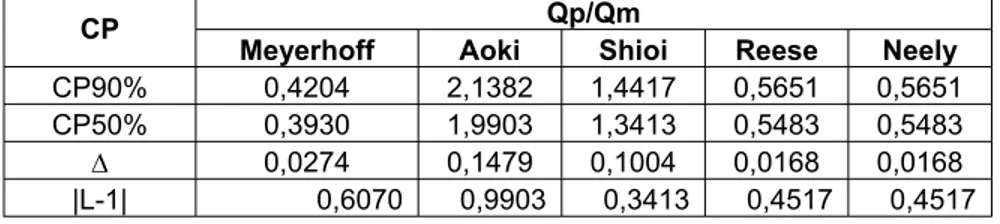
Dari tabel 4.3 dan 4.4 dapat ditentukan nilai probabilitas kumulatif Qp/Qm pada saat 50% (CP50%) dan pada saat 90% (CP90%). Berikut adalalah CP50% Qp/Qm dan CP90% Qp/Qm untuk masing-masing metoda perhitungan di proyek mediterania : Tabel 4.5 Nilai Probabilitas kumulatif Qp/Qm pada saat 50% dan 90% (Mediterania)
Qp/Qm CP
Meyerhoff Aoki Shioi Reese Neely
CP90% 0,4204 2,1382 1,4417 0,5651 0,5651
CP50% 0,3930 1,9903 1,3413 0,5483 0,5483
' 0,0274 0,1479 0,1004 0,0168 0,0168
|L-1| 0,6070 0,9903 0,3413 0,4517 0,4517
Dari tabel 4.5 dapat diketahui beda nilai CP90% Qp/Qm dan CP50% Qp/Qm yaitu ' dengan perhitungan ' = CP90% Qp/Qm - CP50% Qp/Qm. Nilai ǻ yang paling kecil dan nilai Qp/Qm pada saat CP50% mendekati satu dengan direpresentasikan |L-1| = |Qp/Qm pada saat CP50% - 1| adalah yang paling kecil menempati peringkat yang pertama.
Kemudian, setelah di setiap proyek dilakukan perangtkingan langkah berikutnya adalah memberi poin. Dimana yang mendapat rangking pertama, diberi poin satu. Ranking kedua, diberi poin dua. Ranking ketiga, diberi poin tiga. Ranking keempat, diberi poin empat, serta yang terakhir ranking kelima, diberi poin lima.
Sehingga dapat disimpulkan urutan ranking untuk metoda perhitungan di proyek mediterania adalah sebagai berikut :
Tabel 4.6 Ranking Dari Metoda Perhitungan Berdasarkan Analisis Probabilitas kumulatif (Mediterania)
Untuk hasil perhitungan urutan ranking pada proyek lainnya dapat dilihat pada tabel 4.7 sd. 4.10 di bawah ini :
Rank Metode ' Poin 1 Meyerhoff 0,0444 1 2 Shioi 0,0861 2 3 Reese 0,0874 3 4 Neely 0,0875 4 5 Aoki 0,3575 5
Rank Metode |L-1| Poin
1 Neely 0,5713 1
2 Reese 0,5716 2
3 Shioi 0,5779 3
4 Aoki 0,7517 4
5 Meyerhoff 0,7826 5
Rank Metode Poin Tot.
1 Shioi, Reese, & Neely 5
2 Meyerhoff 6
3 Aoki 9
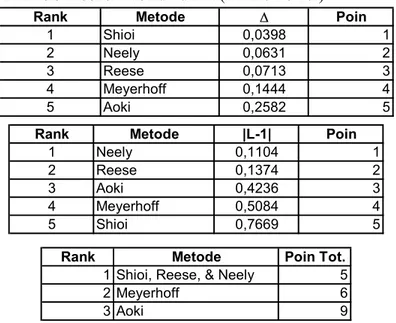
Rank Metode ' Poin
1 Shioi 0,0398 1
2 Neely 0,0631 2
3 Reese 0,0713 3
4 Meyerhoff 0,1444 4
5 Aoki 0,2582 5
Rank Metode |L-1| Poin
1 Neely 0,1104 1
2 Reese 0,1374 2
3 Aoki 0,4236 3
4 Meyerhoff 0,5084 4
5 Shioi 0,7669 5
Rank Metode Poin Tot.
1 Shioi, Reese, & Neely 5
2 Meyerhoff 6
3 Aoki 9
Tabel 4.7 Ranking Dari Metoda Perhitungan Berdasarkan Analisis Probabilitas kumulatif (Menara Satrio)
Tabel 4.8 Ranking Dari Metoda Perhitungan Berdasarkan Analisis Probabilitas kumulatif (Bakrie Tower)
Rank Metode ' Poin 1 Aoki 0,0324 1 2 Shioi 0,0350 2 3 Meyerhoff 0,0338 3 4 Reese 0,0611 4 5 Neely 0,0626 5
Rank Metode |L-1| Poin
1 Meyerhoff 0,3829 1
2 Reese & Neely 0,4036 2,5
3 Shioi 0,5552 4
4 Aoki 1,9847 5
Rank Metode Poin Tot.
1 Meyerhoff 4
2 Aoki & Shioi 6
3 Reese 6,5
4 Neely 7,5
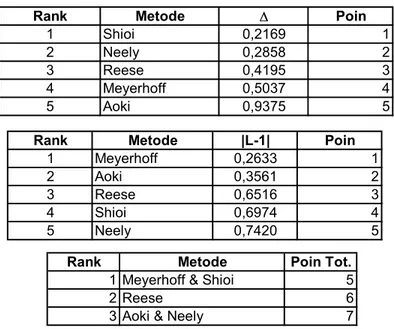
Rank Metode ' Poin
1 Shioi 0,2169 1
2 Neely 0,2858 2
3 Reese 0,4195 3
4 Meyerhoff 0,5037 4
5 Aoki 0,9375 5
Rank Metode |L-1| Poin
1 Meyerhoff 0,2633 1
2 Aoki 0,3561 2
3 Reese 0,6516 3
4 Shioi 0,6974 4
5 Neely 0,7420 5
Rank Metode Poin Tot.
1 Meyerhoff & Shioi 5
2 Reese 6
3 Aoki & Neely 7
Tabel 4.9 Ranking Dari Metoda Perhitungan Berdasarkan Analisis Probabilitas kumulatif (Regatta)
Tabel 4.10 Ranking Dari Metoda Perhitungan Berdasarkan Analisis Probabilitas kumulatif (Lifestyle)
Dari data diatas dapat dilihat bahwa masing-masing proyek, memiliki metoda yang paling tepat yang tidak sama . Tetapi dengan memberi poin pada setiap proyek maka dapat dihitung secara total metoda mana yang paling tepat. Dimana metoda yang memiliki jumlah poin terkecil adalah metoda yang paling tepat. Perhitungannya adalah sebagi berikut :
x Metoda Meyerhoff = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
x Metoda Aoki = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
= 5 + 5 + 5 + 2,5 + 4,5 = 22
x Metoda Shioi = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
= 1 + 1 + 1 + 2,5 + 1,5 = 7
x Metoda Reese = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
= 1 + 1 + 1 + 4 + 3 = 10
x Metoda Neely = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
= 1 + 1 + 1 + 5 + 4,5 = 12,5
Sehingga dari perhitungan diatas dapat kita simpulkan ranking dari metoda perhitungan berdasarkan analisis probabilitas kumulatif adalah sebgai berikut :
Tabel 4.11 Ranking Dari Metoda Perhitungan Berdasarkan Analisis Probabilitas kumulatif (R1)
Rank Metoda Poin
1 Shioi 7
2 Reese 10
3 Neely 12,5
4 Meyerhoff 14,5
5 Aoki 22
Dari tabel 4.11 dapat dilihat bahwa metoda Shioi menempati peringkat pertama secara keseluruhan proyek, metoda Reese di peringkat kedua kemudian metoda Neely dan Meyerhoff berturut-turut menduduki peringkat ketiga dan keempat, dan yang terakhir adalah metoda Aoki.
4.2.2. Kriteria Berdasarkan Analisis Nilai Rata-Rata Serta Deviasi Standar
Kriteria kedua yaitu menganalisis kemampuan prediksi tiap metoda dengan menghitung nilai rata-rata serta deviasi standar dari nilai Qp/Qm. Seperti halnya langkah sebelumnya yaitu menghitung nilai rata-rata serta deviasi standar dari nilai-nilai Qp/Qm untuk masing-masing proyek kontruksi dan dari nilai-nilai-nilai-nilai Qp/Qm yang telah digabungkan dari beberapa proyek kontruksi. Hal ini dilakukan untuk mengetahui konsistensi metoda-metoda perhitungan.
Berikut adalah contoh perhitunga analisis nilai rata-rata serta deviasi standar di proyek Mediterania. Nilai Qp/Qm untuk mediterania dapat diperoleh dari tabel 4.3. Selanjutnya dari tabel tersebut dapat dihitung nilai rata-rata dan deviasi standar dari
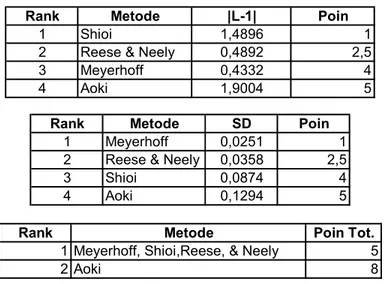
Meyerhoff Aoki Shioi Reese Neely 1 0,4014 2,0327 1,3699 0,5600 0,5600 2 0,4332 2,2085 1,4896 0,5685 0,5685 3 0,3930 1,9903 1,3413 0,5483 0,5483 4 0,3727 1,9004 1,2818 0,4892 0,4892 Rerata 0,4001 2,0330 1,3707 0,5415 0,5415 |L-1| 0,5999 1,0330 0,3707 0,4585 0,4585 SD 0,0251 0,1294 0,0874 0,0358 0,0358 No Qp/Qm
Rank Metode |L-1| Poin
1 Shioi 1,4896 1
2 Reese & Neely 0,4892 2,5
3 Meyerhoff 0,4332 4
4 Aoki 1,9004 5
Rank Metode SD Poin
1 Meyerhoff 0,0251 1
2 Reese & Neely 0,0358 2,5
3 Shioi 0,0874 4
4 Aoki 0,1294 5
Rank Metode Poin Tot.
1 Meyerhoff, Shioi,Reese, & Neely 5
2 Aoki 8
Qp/Qm. Berikut adalah tabel perhitungan dari analisis nilai rata-rata serta deviasi standar.
Tabel 4.12 Rata-Rata Serta Deviasi Standar Dari Qp/Qm Mediterania
Ket : SD adalah deviasi standar dan |L-1| adalah |1- Rerata|
Dari tabel 4.12 diatas dapat ditentukan bahwa nilai rata-rata yang mendekati satu adalah rerata Qp/Qm metoda Shioi hal ini dapat dilihat dari nilai |L-1| yang paling kecil diantara metoda-metoda yang lainnya yaitu L sama dengan 0,3707. Sedangkan nilai deviasi standar yang paling kecil diperoleh dari metoda Meyerhoff dengan SD sama dengan 0,0251.Berikut adalah ranking dari metoda-metoda perhitungan tersebut :
Tabel 4.13 Ranking Metoda Perhitungan Berdasarkan Nilai Rerata dan deviasi standar (Mediterania)
Untuk hasil dari perhitungan pada proyek lainnya, dapat dilihat pada tabel 4.14 sd. 4.17 di bawah ini :
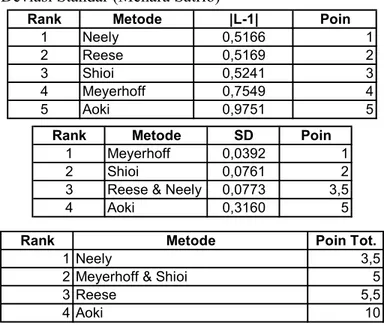
Rank Metode |L-1| Poin 1 Neely 0,5166 1 2 Reese 0,5169 2 3 Shioi 0,5241 3 4 Meyerhoff 0,7549 4 5 Aoki 0,9751 5
Rank Metode SD Poin
1 Meyerhoff 0,0392 1
2 Shioi 0,0761 2
3 Reese & Neely 0,0773 3,5
4 Aoki 0,3160 5
Rank Metode Poin Tot.
1 Neely 3,5
2 Meyerhoff & Shioi 5
3 Reese 5,5
4 Aoki 10
Rank Metode |L-1| Poin
1 Neely 0,1370 1
2 Reese 0,1558 2
3 Aoki 0,4489 3
4 Meyerhoff 0,4782 4
5 Shioi 0,7647 5
Rank Metode SD Poin
1 Shioi 0,0499 1
2 Reese 0,1349 2
3 Neely 0,1386 3
4 Meyerhoff 0,1412 4
5 Aoki 0,3082 5
Rank Metode Poin Tot.
1 Reese & Neely 4
2 Shioi 6
3 Aoki & Meyerhoff 8
Tabel 4.14 Ranking Metoda Perhitungan Berdasarkan Nilai Rerata dan Deviasi Standar (Menara Satrio)
Tabel 4.15 Ranking Metoda Perhitungan Berdasarkan Nilai Rerata dan Deviasi Standar (Bakrie Tower )
Rank Metode |L-1| Poin 1 Meyerhoff 0,3617 1 2 Neely 0,3645 2 3 Reese 0,3654 3 4 Shioi 0,5771 4 5 Aoki 2,0049 5
Rank Metode SD Poin
1 Aoki 0,0286 1
2 Meyerhoff 0,0299 2
3 Shioi 0,0310 3
4 Reese 0,0540 4
5 Neely 0,0554 5
Rank Metode Poin Tot.
1 Meyerhoff 3
2 Aoki 6
3 Shioi, Reese & Neely 7
Rank Metode |L-1| Poin
1 Meyerhoff 0,0886 1
2 Reese 0,4917 2
3 Shioi 0,6227 3
4 Neely 0,6336 4
5 Aoki 0,6978 5
Rank Metode SD Poin
1 Shioi 0,1917 1
2 Neely 0,2260 2
3 Reese 0,3229 3
4 Meyerhoff 0,4459 4
5 Aoki 0,7962 5
Rank Metode Poin Tot.
1 Shioi 4
2 Reese & Meyerhoff 5
3 Neely 6
4 Aoki 10
Tabel 4.16 Ranking Metoda Perhitungan Berdasarkan Nilai Rerata dan Deviasi Standar (Regatta)
Tabel 4.17 Ranking Metoda Perhitungan Berdasarkan Nilai Rerata (Lifestyle)
Berdasarkan tabel-tabel di atas, diperoleh lagi hasil metoda ketepatan yang berbeda-beda di setiap proyek. Sehingga harus dilakukan lagi perhitungan seperti di sub bab sebelumnya, yaitu sebagai berikut :
x Metoda Meyerhoff = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
x Metoda Aoki = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
= 5 + 5 + 4,5 + 2 + 5 = 21,5
x Metoda Shioi = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
= 1 + 2,5 + 3 + 4 + 1 = 11,5
x Metoda Reese = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
= 1 + 4 + 1,5 + 4 + 2,5 = 13
x Metoda Neely = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
= 1 + 1 + 1,5 + 4 + 4 = 11,5
Sehingga dari perhitungan diatas dapat disimpulkan ranking dari metoda perhitungan berdasarkan nilai rerata adalah sebagai berikut :
Tabel 4.18 Ranking Dari Metoda Perhitungan Berdasarkan Analisis (R2)
Rank Metoda Poin
1 Meyerhoff, Shioi, dan Neely
11,5
2 Reese 13
3 Aoki 20,5
Dari tabel diatas dapat disimpulkan bahwa metoda perhitungan dengan nilai rata-rata yang mendekati satu dan deviasi standar yang kecil diperoleh hasil yang paling tepat berdasarkan metoda Meyerhoff, Shioi, dan Neely.
4.2.3 Kriteria Berdasarkan Analisis Tingkat Akurasi 20%
Kriteria ketiga mempergunakan fungsi distribusi lognormal, dengan menilai tingkat akurasi 20%-nya, yaitu luas area dibawah kurva PDF (Probability Density Function) Qp/Qm yang diasumsikan mengikuti distribusi lognormal, antara nilai Qp/Qm sebesar 0,8 sampai 1,2. Oleh karena itu langkah awal dari analisis tingkat akurasi 20% adalah dengan memplot distribusi Qp/Qm yang mengikuti distribusi lognormal dengan kata lain nilai ln (Qp/Qm) mengikuti distribusi normal.
Berikut adalah contoh tabel hasil perhitungan ln (Qp/Qm) , nilai rata-rata (ȝ) dari distribusi ln (Qp/Qm), dan nilai deviasi standar (ı) dari distribusi ln (Qp/Qm) yang digunakan untuk memplot distribusi lognormal.
2 4 6 8 10 0 5 10 15 16.005 0 f x( ) 10 0.01 x
Nama Proyek : Mediterania
Tabel 4.19 Nilai ln (Qp/Qm) Mediterania
Meyerhoff Aoki Shioi Reese Neely
1 -0,9129 0,7094 0,3147 -0,5799 -0,5799 2 -0,8367 0,7923 0,3985 -0,5648 -0,5648 3 -0,9339 0,6883 0,2937 -0,6010 -0,6010 4 -0,9869 0,6421 0,2482 -0,7150 -0,7150 Rerata -0,9176 0,7080 0,3138 -0,6152 -0,6152 SD 0,0623 0,0628 0,0629 0,0682 0,0682 No Ln Qp/Qm
Dari Tabel diatas dapat diketahui nilai rata-rata (ȝ) distribusi ln (Qp/Qm) yaitu dan nilai deviasi standar (ı) dari distribusi ln (Qp/Qm) di setiap metoda perhitungan. Selanjutnya nilai rata-rata dan deviasi standar ini digunakan untuk memplot distribusi lognormal dari Qp/Qm. Berikut adalah grafik distribusi lognormal Qp/Qm untuk masing-masing metoda perhitungan :
x Metoda Meyerhoff
Gambar 4.6 Distribusi Lognormal Qp/Qm Meyerhoff Mediterania
Dari gambar 4.2 diatas x adalah Qp/Qm dan f(x) adalah nilai probailitas dari x (Qp/Qm). Untuk mengetahui luas dibawah kurva dimana 0,8 < Qp/Qm < 1,2 digunakan rumus : F x( ) 0.8 1.2 x 1 2 VS x exp 1 2V2 ln x( )P
2 ª « ¬ º » ¼ ´ µ µ µ ¶ dDimana nilai F(x) sama dengan luas daerah dibawah kurva dimana 0,8 < Qp/Qm < 1,2 didapat dari perhitungan nilai F(x) sama dengan 0 %.
0 2 4 6 8 10 0 1 2 3 3.135 0 f x( ) 10 0.02 x 0 2 4 6 8 10 0 2 4 4.643 0 f x( ) 10 0.02 x
x Metoda Aoki dan Velloso
Gambar 4.7 Distribusi Lognormal Qp/Qm Aoki Mediterania
Dari gambar 4.3 diatas x adalah Qp/Qm dan f(x) adalah nilai probailitas dari x (Qp/Qm). Untuk mengetahui luas dibawah kurva dimana 0,8 < Qp/Qm < 1,2 digunakan rumus : F x( ) 0.8 1.2 x 1 2 VS x exp 1 2V2 ln x( )P
2 ª « ¬ º » ¼ ´ µ µ µ ¶ dDimana nilai F(x) sama dengan luas daerah dibawah kurva dimana 0,8 < Qp/Qm < 1,2 didapat dari perhitungan nilai F(x) sama dengan 0 %.
x Metoda Shioi dan Fukui
2 4 6 8 10 0 5 10 10.831 0 f x( ) 10 0.01 x
Dari gambar 4.4 diatas x adalah Qp/Qm dan f(x) adalah nilai probailitas dari x (Qp/Qm). Untuk mengetahui luas dibawah kurva dimana 0,8 < Qp/Qm < 1,2 digunakan rumus : F x( ) 0.8 1.2 x 1 2 VS x exp 1 2V2 ln x( )P
2 ª « ¬ º » ¼ ´ µ µ µ ¶ dDimana nilai F(x) sama dengan luas daerah dibawah kurva dimana 0,8 < Qp/Qm < 1,2 didapat dari perhitungan nilai F(x) sama dengan 1,8%.
x Metoda Reese dan O’Neill
Gambar 4.9 Distribusi Lognormal Qp/Qm Reese Mediterania
Dari gambar 4.5 diatas x adalah Qp/Qm dan f(x) adalah nilai probailitas dari x (Qp/Qm). Untuk mengetahui luas dibawah kurva dimana 0,8 < Qp/Qm < 1,2 digunakan rumus : F x( ) 0.8 1.2 x 1 2 VS x exp 1 2V2 ln x( )P
2 ª « ¬ º » ¼ ´ µ µ µ ¶ dDimana nilai F(x) sama dengan luas daerah dibawah kurva dimana 0,8 < Qp/Qm < 1,2 didapat dari perhitungan nilai F(x) sama dengan 4,49 x 10-7 %.
2 4 6 8 10 0 5 10 10.831 0 f x( ) 10 0.01 x
Rank Metode Luas (%) Poin
1 Shioi 1,8 1
2 Reese & Neely 4,49 x 10-7 2,5 3 Meyerhoff & Aoki 0 4,5
x Metoda Neely
Gambar 4.10 Distribusi Lognormal Qp/Qm Reese Mediterania
Dari gambar 4.5 diatas x adalah Qp/Qm dan f(x) adalah nilai probailitas dari x (Qp/Qm). Untuk mengetahui luas dibawah kurva dimana 0,8 < Qp/Qm < 1,2 digunakan rumus : F x( ) 0.8 1.2 x 1 2 VS x exp 1 2V2 ln x( )P
2 ª « ¬ º » ¼ ´ µ µ µ ¶ dDimana nilai F(x) sama dengan luas daerah dibawah kurva dimana 0,8 < Qp/Qm < 1,2 didapat dari perhitungan nilai F(x) sama dengan 4,49 x 10-7 %.
Dari perhitungan diatas maka dapat dilihat tabel nilai metoda perhitungan berdasarkan tingkat akurasi 20% untuk proyek mediterania, yaitu :
Tabel 4.20 Ranking Metoda Perhitungan Berdasarkan Analisis Tiangkat Akurasi 20% (Mediterania)
Hasil-hasil perhitungan dari proyek-proyek lainnya dapat dilihat pada tabel 4.21 sd. 4.24 dibawah ini :
Rank Metode Luas (%) Poin 1 Aoki 1,10 x 10-1 1 2 Reese 7,39 x 10-2 2 3 Neely 7,5 x 10-2 3 4 Shioi 5,34 x 10-2 4 5 Meyerhoff 6,75 x 10-12 5
Rank Metode Luas (%) Poin
1 Neely 62 1
2 Reese 58 2
3 Aoki 22,6 3
4 Meyerhoff 5 4
5 Shioi 3,67x10-6 5
Rank Metode Luas (%) Poin
1 Reese 1,10 x 10-1 1
2 Neely 7,39 x 10-2 2
3 Meyerhoff 7,5 x 10-2 3
4 Aoki & Shioi 5,34 x 10-2 4,5
Rank Metode Luas (%) Poin
1 Meyerhoff 34,6 1
2 Aoki 20,1 2
3 Reese 11,2 3
4 Neely 4,1 4
5 Shioi 2,80 5
Tabel 4.21 Ranking Metoda Perhitungan Berdasarkan Analisis Tingkat Akurasi 20% (Menara Satrio)
Tabel 4.22 Ranking Metoda Perhitungan Berdasarkan Analisis Tingkat Akurasi 20% (Bakrie Tower)
Tabel 4.23 Ranking Metoda Perhitungan Berdasarkan Analisis Tingkat Akurasi 20% (Regatta)
Tabel 4.24 Ranking Metoda Perhitungan Berdasarkan Analisis Tingkat Akurasi 20% (Lifestyle)
Karena masing-masing proyek memiliki metoda paling tepat yang berbeda-beda, maka perlu dilakukan langkah-langkah seperti di sub bab sebelumnya. Yaitu sebagai berikut :
x Metoda Meyerhoff = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
= 4,5 + 5 + 4 + 3 + 1 = 17,5
x Metoda Aoki = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
= 4,5 + 1 + 3 + 4,5 + 2 = 15
= 1 + 4 + 5 + 4,5 + 5 = 19,5
x Metoda Reese = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
= 2,5 + 2 + 2 + 1 + 3 = 10,5
x Metoda Neely = RMediterania + RMenara Satrio + RBakrie Tower + RRegatta + RLifestyle
= 2,5 + 3 + 1 + 2 + 4 = 12,5
Sehingga dari perhitungan diatas dapat dimpulkan ranking dari metoda perhitungan berdasarkan Analisis Tingkat Akurasi 20% adalah sebagai berikut :
Tabel 4.25 Ranking Dari Metoda Perhitungan Berdasarkan Analisis Tingkat Akurasi 20% (R3)
Rank Metoda Poin
1 Reese 10,5
2 Neely 12,5
3 Aoki 15
4 Meyerhoff 17,5
5 Shioi 19,5
Dari tabel diatas dapat disimpulkan bahwa metoda perhitungan dengan nilai tingkat akurasi 20% diperoleh hasil yang paling tepat berdasarkan metoda Reese.
4.3 INDEKS RANKING
Untuk kuantitas kelaikan tiap-tiap metoda diperkenalkan parameter indeks ranking (RI), dimana RI adalah jumlah ranking dari kriteria-kriteria yang berbeda, RI = R1+R2+R3. semakin rendah nilai RI semakin baik metoda yang ditinjau dalam memprediksi kapasitas fondasi. Untuk tugas akhir ini dihitung RI untuk masing-masing lokasi proyek dan dihitung RI untuk gabungan lokasi proyek.
Sehingga perhitungan Indeks Ranking untuk masing-masing metoda perhitungan adalah sebagai berikut :
x Metoda Meyerhoff = R1 + R2 + R3 = 4 + 2 + 4 = 10 x Metoda Aoki = R1 + R2 + R3 = 5 + 5 + 3 = 13 x Metoda Shioi = R1 + R2 + R3 = 1 + 2 + 5 = 8 x Metoda Reese = R1 + R2 + R3 = 2 + 4 + 1 = 7
x Metoda Neely = R1 + R2 + R3 = 3 + 2 + 2 = 7
Sehingga dari perhitungan diatas dapat dimpulkan indeks ranking dari analisis ketepatan metoda perhitungan adalah sebagai berikut :
Tabel 4.26 Indeks Ranking Dari Metoda Perhitungan (RI)
Rank Metoda Poin
1 Reese & Neely 7 2 Shioi 8 3 Meyerhoff 10 4 Aoki 13
Setelah melakukan perhitungan yang berasal dari lima lokasi proyek di Jakarta yang mencakup 16 titik pengujian Loading Test. Dapat disimpulkan bahwa metoda Neely dan Reese & O’Neill merupakan metoda perhitungan yang paling tepat. Yang kedua adalah metoda Shioi dan Fukui. Kemudian metoda Meyerhoff menempati urutan ketiga. Sedangkan di urutan terakhir ada metoda Aoki & Velloso.