Simulasi Intensitas Difraksi Pada Celah Lingkaran (Circular Aperture) Dengan Metode Simpson.

(1)

KARYA TULIS ILMIAH

SIMULASI INTENSITAS DIFRAKSI PADA CELAH LINGKARAN (CIRCULER

APERTURE) DENGAN METODE SIMPSON

Oleh :

I Gusti Agung Widagda, S.Si, M.Kom

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS UDAYANA

(2)

ii Halaman Pengesahan

--- 1. Judul Karya Tulis : Simulasi Intensitas Difraksi pada Celah Lingkaran

(Circular Aperture) dengan metode simpson

--- 2. Penulis

a. Nama lengkap dengan gelar : I Gusti Agung Widagda, S.Si, M.Kom b. Jenis Kelamin : Laki-laki

c. Pangkat/Golongan/NIP : Penata Tk. I/III-d/197003311997021001 d. Jabatan Fungsional : Lektor

e. Fakultas/Jurusan : MIPA/Fisika

f. Universitas : Udayana

g. Bidang ilmu : Fisika Komputasi

--- 3. Jumlah Penulis : 1 (satu) orang

--- 4. Kerjasama

a. Nama Instansi : -

--- 5. Jangka Waktu Penulisan : 6 (enam) bulan

---

6. Biaya : -

--- Jimbaran, Desember 2015

Mengetahui,

Dekan FMIPA UNUD Penulis

(3)

iii

Simulasi Intensitas Difraksi Pada Celah Lingkaran (

Circular Aperture

)

dengan Metode Simpson

I G.A. Widagda

RINGKASAN

(4)

iv

Simulation of Difraction Intensity on Circular Aperture by Using

Simpson Rule

I G.A. Widagda

SUMMARY

(5)

v KATA PENGANTAR

Kami menghaturkan puji syukur kehadapan Tuhan Yang Maha Esa, karena atas berkat rahmat-Nya kami dapat menyelesaikan karya tulis ilmiah yang berjudul ”Simulasi Intesitas Difraksi Pada Celah Lingkaran (Circular Aperture) dengan Metode Simpson”.

Kami menyampaikan terima kasih kepada semua pihak yang telah membantu penyelesaian karya tulis ini antara lain :

-Bapak Dekan FMIPA, UNUD

-Bapak Ketua Jurusan Fisika, FMIPA, UNUD -Bapak Kepala Lab. Fisika Komputasi

-Rekan - rekan dosen Jurusan Fisika, FMIPA, UNUD -Istri dan anak-anakku

atas bantuan, saran dan kerjasamanya selama penulis menyelesaikan karya tulis ini. Sebagai akhir kata kami meyakini bahwa karya tulis ini masih banyak kekurangan. Sehingga kami mengharapkan kritik dan saran yang bersifat konstruktif dari semua pihak demi kesempurnaan hasil karya tulis ini.

Jimbaran, Desember 2015

(6)

vi DAFTAR ISI

Halaman

HALAMAN JUDUL i

HALAMAN PENGESAHAN ii

RINGKASAN/SUMMARY iii

KATA PENGANTAR v

DAFTAR ISI vi

DAFTAR GAMBAR vii

I PENDAHULUAN 1

II TINJAUAN PUSTAKA 3

III TUJUAN DAN MANFAAT PENELITIAN 20

IV METODE PENELITIAN 21

V HASIL DAN PEMBAHASAN 23

VI SIMPULAN DAN SARAN 26

(7)

vii DAFTAR GAMBAR

halaman Gambar 2.1 Interferensi Konstruktif dan Destruktif 3 Gambar 2.2 Percobaan Young : Interferensi pada celah ganda 4 Gambar 2.3 Interferensi Konstruktif dan Destruktif pada celah ganda 4

Gambar 2.4 Geometri celah ganda 4

Gambar 2.5 Lintasan cahaya r1,r2 sejajar 5

Gambat 2.6 Intensitas I dari Interferensi celah ganda 8

Gambar 2.7 Perambatan gelombang prinsip Huygen 8

Gambat 2.8 Perambatan cahaya pada celah sempit dan celah agak lebar 8

Gambar 2.9 Difraksi Fraunhofer 9

Gambat 2.10 Difraksi cahaya oleh celah lebar a 9

Gambar 2.11 Difraksi Fraunhofer celah tunggal 10

Gambat 2.12 Intensitas dari pola difraksi Fraunhofer celah tunggal 12

Gambar 2.13 Difraksi Fraunhofer celah lingkaran 13

Gambat 2.14 Intensitas difraksi Fraunhofer celah lingkaran 14

Gambar 2.15 Luas daerah di bawah kurva 15

Gambar 2.16 Metode Persegi Panjang 15

Gambar 2.17 Metode Trapesium 16

Gambar 2.18 Metode Simpson 17

Gambat 4.1 Diagram alir program perhitungan intensitas difraksi celah

lingkaran 20

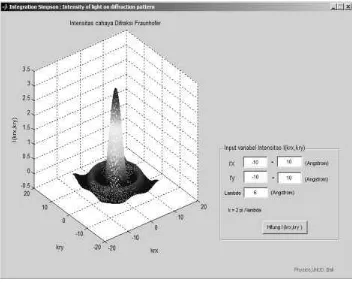
Gambar 4.2 Rancangan Gui simulasi intensitas difraksi celah lingkaran 21 Gambat 5.1 Hasil Simulasi 3 dimensi intensitas difraksi celah lingkaran,

λ = 2 Å

23 Gambar 5.2 Hasil Simulasi 3 dimensi intensitas difraksi celah lingkaran,

λ = 4Å

24 Gambat 5.3 Hasil Simulasi 3 dimensi intensitas difraksi celah lingkaran,

λ = 6Å

λ = 8Å

λ = 10Å

(8)

1 I. PENDAHULUAN

Difraksi adalah deviasi atau pembelokan arah rambat gelombang baik gelombang cahaya maupun gelombang bunyi. Pola difraksi akan teramati ketika cahaya melewati celah baik celah tunggal, celah ganda, tiga celah, celah persegi panjang, celah lingkaran (circular aperture), dan lain-lain. Pola difraksi yang teramati pada layar biasanya berupa pola terang

dan gelap. Pola terang dan gelap tersebut mengikuti fungsi tertentu yang tergantung pada variabel yaitu : panjang gelombang, lebar celah, jarak celah-layar, kuat medan listrik, dan lain-lain. Pola difraksi terang dan gelap yang teramati pada medium atau layar juga sangat bergantung pada intensitas cahaya. Semakin besar intesitas cahaya maka semakin terang pola yang teramati demikian juga sebaliknya semakin kecil intesitas maka akan menghasilkan pola yang semakin gelap pada layar. Besarnya intensitas difraksi yang teramati dapat dihitung secara analitik dengan menggunakan persamaan matematika untuk menyelesaikan model atau persamaan intensitas difraksi yang ditinjau. Penyelesaian persamaan intensitas difraksi pada celah tunggal, celah ganda, tiga celah maupun celah persegi panjang masih bisa dilakukan secara analitik mengingat masih sederhananya kasus yang ditinjau. Jika kita menyelesaikan persamaan intensitas difraksi pada celah lingkaran maka penyelesaian secara analitik menjadi sangat rumit dilakukan sebab model persamaan yang dihasilkan berupa kasus integrasi berhingga dari fungsi yang berbentuk eksponensial. Ketika penyelesaian integrasi secara analitik sudah tidak bisa atau sangat rumit dilakukan maka sebagai alternatif biasanya dipergunakan penyelesaian secara numerik. Penyelesaian integrasi secara numerik biasanya diimplementasikan dalam bentuk program komputer.

(9)

2 menghasilkan hasil yang lebih baik (lebih mendekati hasil eksak) dibanding metode Persegi Panjang dan Trapesium karena metode atau pendekatan yang dipakai dalam metode Simpson adalah dengan membagi daerah di bawah fungsi menjadi pita-pita kecil yang berbentuk fungsi kuadrat (polinom orde 2). Persamaan intensitas pada kasus difraksi celah lingkaran mengandung perhitungan integral dari fungsi non linear berupa fungsi eksponensial. Sehingga penyelesaian intensitas difraksi pada celah lingkaran sangat cocok diselesaikan dengan metode Simpson.

(10)

3 II. TINJAUAN PUSTAKA

2.1 Interferensi Gelombang

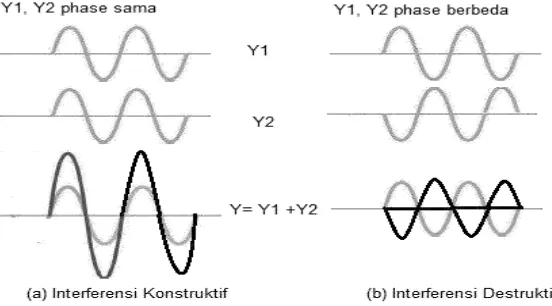
Interferensi adalah peristiwa penggabungan atau penjumlahan (combination) dua atau lebih gelombang menjadi sebuah gelombang. Apabila dua buah gelombang dengan phase yang sama dijumlahkan maka akan menghasilkan interferensi konstruktif dan jika dua buah gelombang tersebut memiliki phase yang berbeda maka akan menghasilkan interferensi destruktif seperti diperlihatkan pada Gambar 2.1. Syarat – syarat interferensi pada gelombang cahaya yaitu : cahaya bersifat koheren yaitu memiliki phase (ϕ) konstan dan cahaya bersifat monokromatis yaitu memiliki 1 panjang gelombang, λ = βπ/k.

Gambar 2.1 Interferensi konstruktif dan destruktif 2.1.1 Interferensi Celah Ganda (Double-slit Interference)

Percobaan interferensi cahaya pada celah ganda dilakukan pertama kali oleh Young seperti ditunjukkan pada Gambar 2.2. Sebuah gelombang cahaya (monokromatis) melewati layar 1 yang berisi celah tunggal S0, selanjutnya cahaya tersebut diteruskan ke layar 2 yang berisi celah ganda S1 dan S2. Celah S1 dan S2 pada layar 2 berlaku sebagai sumber cahaya koheren. Cahaya yang melewati S1 dan S2 ini

(11)

4 Gambar 2.2 Percobaan Young : interferensi pada celah ganda

Pita terang dan gelap yang terjadi di layar 3 merupakan pola interferensi yang dihasilkan oleh dua buah cahaya yang berasal dari celah S1 dan S2. Pita terang menunjukkan interferensi maximum (konstruktif) sedangkan pita gelap merupakan interferensi minimum (destruktif). Proses terjadinya interferensi konstruktif dan destruktif ini ditunjukkan pada Gambar 2.3.

Gambar 2.3 Interferensi konstruktif dan destruktif celah ganda

Proses interferensi pada celah ganda secara geometri dapat dilihat pada gambar 2.4. Jarak celah S1 dan S2 adalah d dan jarak layar ke celah adalah L. Cahaya yang merupakan hasil interferensi jatuh titik P. Jarak P ke O yaitu y.

(12)

5 Cahaya dari celah S2 akan menempuh jarak yang lebih besar jika dibandingkan dengan cahaya dari S1. Selisih jarak antara cahaya dari celah S1 dan S2 sebesar δ = r2– r1 . Jarak tambahan yang ditempuh oleh cahaya S2 ini disebut dengan Beda lintasan (path

difference). Dari hukum Cosinus maka didapatkan :

)

Dengan mencari selisih dari persamaan (2.2) dan (2.1) maka didapatkan :

)

Jika diasumsikan L ˃˃ d , yaitu jarak antara celah ke layar L jauh lebih besar dari jarak antar kedua celah d maka r1 + r2≈ 2r, sehingga :

seperti diperlihatkan oleh Gambar 2.5

Gambar 2.5 Lintasan cahaya r1,r2 sejajar

Sehingga sebuah gelombang cahaya apakah memiliki phase sama atau berbeda dengan gelombang yang lainnya dapat ditentukan dari nilai δ -nya. Interferensi konstruktif akan terjadi jika δ bernilai 0 atau kelipatan bulat dari panjang gelombang λ :

)

(13)

6

 . Jika dinyatakan dengan persamaan akan menjadi :

)

Untuk menentukan letak dari pita-pita terang dan gelap (y) dari titik pusat O, maka kita dapat menganggap bahwa jarak celah d jauh lebih besar dari panjang gelombang λ ( d ˃˃ λ ). Dengan demikian sudut θ dianggap sangat kecil dan berlaku hubungan :

)

Dengan memasukkan persamaan (2.7) ke dalam persamaan (2.5) maka akan didapatkan persamaan posisi atau letak pita terang yb yaitu :

) didapatkan persamaan posisi atau letak pita gelap yd yaitu :

)

Intensitas Interferensi

Intensitas dari cahaya hasil interferensi pada celah ganda seperti diperlihatkan pada Gambar 2.3 dapat ditentukan dengan vektor atau flux Poynting S. Jika medan

(14)

7 dengan pergeseran phase ϕ= 2π sehingga berlaku hubungan :

)

Medan listrik total E :





...(2.16)

Dari persamaan identitas trigonometri didapatkan hubungan :

)

Intensitas sebanding dengan rata-rata waktu dari medan listrik kuadrat :

)

Dengan memasukkan persamaan (2.15) ke dalam persamaan (2.19) maka didapatkan Intensitas Interferensi pada celah ganda I adalah :

)

Untuk sudut θ yang kecil maka persaman (2.20) akan menjadi :

)

(15)

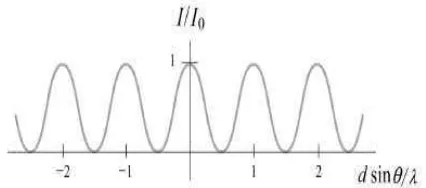
8 Gambar 2.6 Intesitas I dari interferensi celah ganda

2.2 Difraksi Gelombang

Difraksi adalah pembelokan arah rambat gelombang ketika melewati celah atau obyek. Perambatan gelombang baik pada gelombang cahaya maupun bunyi pada peristiwa difraksi mengikuti prinsip Huygen yang berbunyi : Setiap titik dari muka-muka gelombang yang tidak terganggu, pada saat tertentu bertindak sebagai sumber

muka -muka gelombang speris kedua. Permukaan gelombang yang baru adalah

merupakan tangen permukaan gelombang speris kedua. Peristiwa perambatan

gelombang ini dapat dilihat dalam Gambar 2.7.

Gambar 2.7 Perambatan gelombang prinsip Huygen

Cahaya yang melewati celah sempit akan tersebar dan mengalami pembelokan arah rambat dan akan menghasilkan pola difraksi, sedangkan jika cahaya melewati celah dengan lebar tertentu tidak akan mengalami pembelokan dan tidak akan menghasilkan pola difraksi seperti diperlihatkan dalam Gambar 2.8.

(16)

9 2.2.1 Difraksi Fraunhofer Celah Tunggal

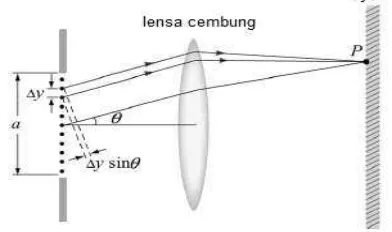
Difraksi Fraunhofer adalah peristiwa perambatan cahaya yang melewati celah dengan lebar tertentu dan tidak mengalami pembelokan. Cahaya merambat lurus dan sejajar satu sama lain. Untuk menghasilkan pola difraksi pada layar maka dipasang sebuah lensa cembung diantara celah dan layar seperti Gambar 2.9.

Gambar 2.9 Difraksi Fraunhofer

Jika dalam eksperimen Young celah ganda maka lebar celah dianggap sangat kecil maka dalam difraksi Fraunhofer celah tunggal kita menganggap celah memiliki lebar tertentu a. Jika cahaya monokromatik melewati celah tersebut maka cahaya tersebut akan merambat lurus dan sejajar seperti Gambar 2.10

Gambar 2.10 Difraksi cahaya oleh celah dengan lebar a

(17)

10 minimum pertama dapat dinyatakan dengan :

)

Jika dinyatakan dengan persamaan umum untuk difraksi minimum (destruktif) maka akan menjadi :

Jika kita membandingkan persamaan (2.24) dengan persamaan (2.5) maka didapatkan bahwa syarat difraksi minimum (destruktif) dari celah tunggal menjadi syarat terjadinya interferensi maksumum (konstruktif) dimana lebar celah tunggal a diganti dengan jarak antar celah d.

Intensitas Difraksi Fraunhofer Celah Tunggal

Intensitas cahaya hasil difraksi pada celah tunggal dapat ditentukan dengan menghitung medan listrik total hasil penjumlahan dari masing-masing sumber titik.

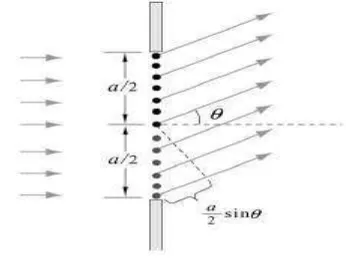
Gambar 2.11 Difraksi Fraunhofer celah tunggal

Gambar 2.11 menunjukkan celah tunggal dibagi menjadi N bagian dan masing – masing bagian merupakan sumber titik. Lebar masing – masing titik adalah : Δy = a/N. Beda lintasan antara 2 sumber titik yang berdekatan adalah δ = Δy sin θ. Beda phase Δ dinyatakan dengan perbandingan:

 

(18)

11 memiliki persamaan medan listrik :

)

Sumber titik 2 yang berdekatan dengan titik 1 memiliki pergeseran phase Δ sehingga memiliki persamaan medan listrik :

)

Jika tiap-tiap sumber titik yang berurutan mempunyai pergeseran phase yang sama maka sumber titik N akan memiliki persamaan medan listrik :

)

Medan listrik total E akan menjadi :



sin sin( ) ...sin( ( 1)



...(2.29)

Pergeseran phase total antara sumber titik N dan sumber titik 1 adalah :

)

Dari trigonometri didapatkan persamaan :

)

Jika kita menjumlahkan semua persamaan tersebut maka akan menghasilkan : ) persamaan (2.33) akan menjadi :

(19)

12 Dengan memasukkan persamaan (2.34) ke dalam persamaan (2.33) akan didapatkan :



sintsin(t)...sin(t(N1)



Sehingga medan listrik total persamaan (2.29) akan menjadi :

)

Intensitas I adalah :

)

I dinyatakan dengan :

2

Faktor N2 diperlukan untuk menjamin bahwa I0 adalah intensitas maksimum pusat = 0 (θ = 0). Jika Δ → 0 ,

Sehinga intensitas I :

) diperlihatkan pada Gambar 2.12.

(20)

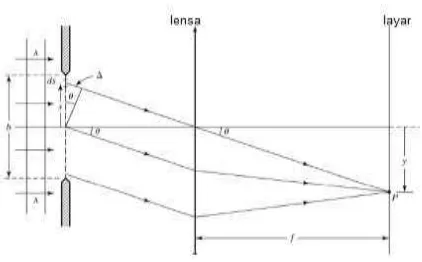
13 2.2.2 Difraksi Fraunhofer Celah Lingkaran

Difraksi pada celah berbentuk lingkaran diperlihatkan pada Gambar 2.13. Kuat medan listrik oleh elemen luas dA adalah dEp :

Gambar 2.13 Difraksi Fraunhofer celah lingkaran

)

Jika elemen luas berupa luas persegi panjang dA = x ds

2

Dari tabel integral :

(21)

14 dapat dinyatakan dengan mengambil nilai real dari rata-rata waktu Ep :

2

(22)

15 Gambar 2.15 Luas daerah di bawah kurva f(x)

Untuk menghitung integral secara numerik ada beberapa metode yaitu : metode Persegi Panjang, metode Trapesium, Metode Simpson, dan lain - lain. Pada metode Persegi panjang perhitungan integral dilakukan dengan menghitung luas di bawah kurva f(x) dengan cara membagi daerah di bawah kurva tersebut menjadi beberapa pita kecil yang berbentuk persegi panjang. Sedangkan pada metode Trapesium dengan membagi daerah di bawah kurva f(x) menjadi pita yang berbentuk trapesium. Dan metode Simpson dengan daerah di bawah kurva f(x) menjadi pita yang salah satu sisinya berbentuk fungsi kuadrat (polinom orde 2).

2.3.1 Metode Persegi Panjang (Rectangle Rule)

Dalam metode Persegi panjang untuk menghitung integral atau luas di bawah kurva f(x) adalah dengan cara membagi daerah di bawah kurva f(x) menjadi beberapa potongan pita kecil yang masing-masing berbentuk persegi panjang seperti Gambar 2.16.

Gambar 2.16 Metode Persegi Panjang

(23)

16

Masing – masing potongan pita kita beri nama dengan memberi index k dimana k = 1, 2, 3, ..., N. Misal untuk k = 1 berarti potongan pita ke-1 (pertama), k = 2 berarti pita kedua, dan seterusnya sampai potongan pita terakhir yaitu pita ke- N. Sehingga luas masing – masing potongan pita dapat dinyatakan dengan Ak. Jadi A1 menyatakan luas pita pertama, A2 menyatakan luas pita kedua, dan seterusnya sampai luas pita yang terakhir AN. Untuk potongan pita ke-k, sisi sebelah kanan akan bernilai a+ kh, sedangkan sisi sebelah kiri akan bernilai a+ kh-h atau a+ (k-1)h. Sehingga luas pita ke-k atau Ak merupakan luas persegi panjang dengan panjang h dan lebar f(a+ (k-1)h):

)

Luas seluruh daerah di bawah kurva f(x) atau integral I(a,b) adalah :

)

2.3.2 Metode Trapesium (Trapezoidal Rule)

Perhitungan integral dengan metode Trapesium adalah dengan cara membagi daerah di bawah kurva f(x) menjadi beberapa potongan pita kecil yang masing-masing berbentuk trapesium seperti diperlihatkan pada Gambar 2.17.

Gambar 2.17 Metode Trapesium

(24)

17 Luas seluruh daerah di bawah kurva f(x) atau integral I(a,b) adalah :

[ ( ( 1) ) ( )]...(2.34)

2.1.3 Metode Simpson (Simpson’s Rule)

Jika dalam 2 metode sebelumnya baik metode Persegi Panjang maupun Trapesium kita melakukan pendekatan dengan kurva berbentuk garis lurus maka dalam metode Simpson ini kita akan menggunakan kurva yang berbentuk fungsi kuadrat (polinom orde 2) seperti diperlihatkan dalam Gambar 2.18. Kurva kuadrat tersebut memiliki bentuk persamaan polinom orde 2 yaitu : f(x) = ax2 + bx + c.

Gambar 2.18 Metode Simpson

Tiap kurva kuadrat dibentuk dari 2 buah potongan pita. Jika kita mengambil nilai x yaitu x = -h, x = 0, dan x = h maka dengan melakukan kurva fitting atau interpolasi kuadrat

terhadap ketiga nilai x tersebut maka didapatkan hubungan yaitu :

Jika kita mencari solusi secara simultan dari ketiga persamaan tersebut maka kita akan dapat menentukan nilai a, b , dan c. Jika kita menjumlahkan persamaan (2.35) dengan (2.37) maka akan didapatkan :

)

(25)

18

Dan dari persaman (2.36) kita mendapatkan

) persamaan (2.41) maka didapatkan :

)

Sama seperti metode integral sebelumnya kita membagi daerah di bawah kurva f(x) dari a sampai b menjadi N buah pita dengan lebar masing – masing potongan pita yaitu h. Dalam metode Simpson ini kita memakai 2 potongan pita untuk membentuk sebuah kurva kuadrat seperti terlihat pada Gambar 2.18. Sehingga kurva kuadrat 1 akan memiliki nilai x = a, x = a+ h , dan x = a+ 2h. Kurva kuadrat 2 akan memiliki nilai x = a+ 2h, x = a+ 3h , dan x = a+ 4h, dan seterusnya sampai pita kuadrat N/2. Oleh karena

satu kurva kuadrat dibentuk oleh 2 buah potongan pita maka jumlah potongan pita N harus genap atau secara umum untuk kurva kuadrat ke-k nilai x adalah : x = a +

(2k-Luas seluruh daerah di bawah kurva f(x) atau integral I(a,b) adalah :

(26)

19 III. TUJUAN DAN MANFAAT PENELITIAN

Tujuan dari penelitian adalah untuk :

Membuat program aplikasi komputer yang dapat mensimulasikan perhitungan intensitas difraksi pada celah yang berbentuk lingkaran dengan metode Simpson serta menampilkan hasilnya dalam bentuk grafik atau kurva 3 dimensi.

Hasil dari penelitian ini diharapkan dapat memberikan manfaat yaitu :

(27)

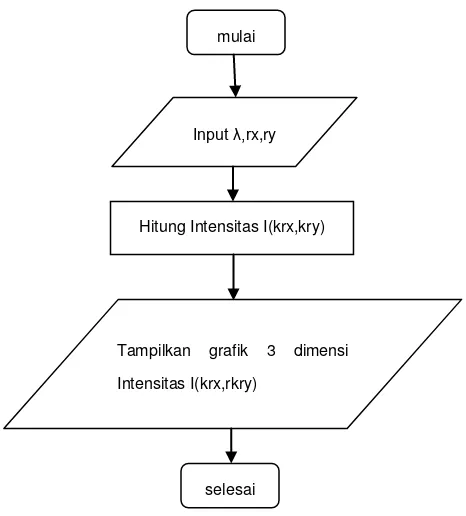
20 Hitung Intensitas I(krx,kry)

Tampilkan grafik 3 dimensi Intensitas I(krx,rkry)

Input λ,rx,ry

IV. METODE PENELITIAN

1. Tempat Penelitian : Lab. Fisika Komputasi, jurusan Fisika, FMIPA, UNUD 2. Peralatan yang digunakan dalam penelitian ini adalah :

a. Komputer NoteBook core i3, 2.30 GHz, 4 GB RAM, OS Windows 7 Ultimate b. Perangkat lunak Matlab versi 7.0

3. Pelaksanaan Penelitian

3.1 Perancangan Diagram Alir (Flow Chart)

Diagram alir dari perhitungan Intensitas Difraksi pada celah lingkaran diperlihatkan dalam Gambar 4.1.

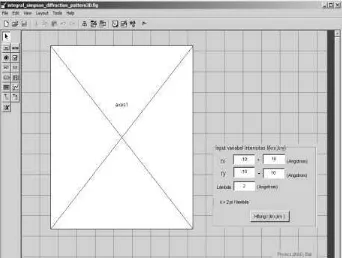
3.2 Perancangan Graphical User Interface (GUI)

Rancangan GUI dari program aplikasi simulasi intensitas difraksi celah lingkaran diperlihatkan dalam Gambar 4.2 berikut ini :

mulai

selesai

(28)

21

3.3 Implementasi kode program (source code)

Kode program dari perhitungan Intensitas Difraksi pada celah lingkaran dengan metode Simpson adalah :

function calculate_simpson_pushbutton_Callback(hObject, eventdata, handles)

rx1 = str2num(get(handles.rx1,'String'));

rx2 = str2num(get(handles.rx2,'String'));

ry1 = str2num(get(handles.ry1,'String'));

ry2 = str2num(get(handles.ry2,'String'));

%r1,r2 convert into Angstrom (10^-10 m)

rx1=rx1*1e-10;

rx2=rx2*1e-10;

ry1=ry1*1e-10;

ry2=ry2*1e-10;

num_slice=150; %number of bands

del_rx=(rx2-rx1)/num_slice; %delta r

del_ry=(ry2-ry1)/num_slice; %delta r

lambda=str2num(get(handles.lambda_edit,'String')); %wave length of light

%convert lambda into Angstrom

lambda=lambda*1e-10;

k=(2*pi)/lambda;

m=1; %orde Bessel

(29)

22

a=1;

rx=rx1:del_rx:rx2;

x=k*rx;

ry=ry1:del_ry:ry2;

y=k*ry;

axes(handles.axes1);

[rx,ry]=meshgrid(x,y);

ka=sqrt(rx.^2+ry.^2);

Gka=2*pi*a^2.*besselj(m,ka)./(ka);

mesh(x,y,Gka);

xlabel('krx'); ylabel('kry') ; zlabel('I(krx,kry)');

(30)

23 V. HASIL DAN PEMBAHASAN

Dari persamaan (2.28) didapatkan bahwa Intensitas difraksi celah lingkaran adalah :

2

J1(kr) adalah fungsi Bessel yang dapat dinyatakan dalam bentuk integral yaitu :





 0   

1(kr) cos(m krsin )d

J

Penyelesaian dari integral tersebut dapat dilakukan dengan menggunakan metode Simpson (persamaan 2.44) yang dihitung secara numerik dengan program komputer.

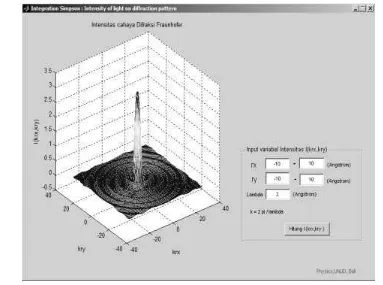
Hasil simulasi 3 dimensi perhitungan intensitas difraksi pada celah lingkaran I(krx,kry) untuk beberapa nilai panjang gelombang λ ( 2 Å, 4 Å, 6 Å, 8 Å , 10 Å) diperlihatkan pada Gambar 5.1 sampai Gambar 5.5. Plot grafik I(krx,kry) diambil dari rx = -10. 10-10 Å sampai 10.

10-10 Å dan ry = -10. 10-10 Å sampai 10. 10-10 Å.

(31)

24

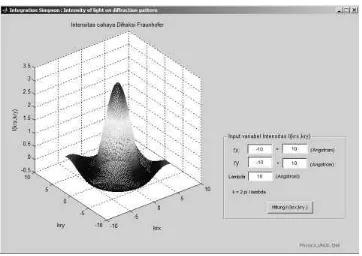
Gambar 5.2 Hasil simulasi 3 dimensi Intensitas Difraksi celah lingkaran,λ = 4 Å

(32)

25

Dari Gambar 5.1 sampai Gambar 5.5 dapat dilihat semakin besar nilai λ maka akan menghasilkan bentuk grafik atau plot I(krx,kry) yang semakin mengembang (enlarge) dan demikian sebaliknya jika nilai λ diperkecil maka akan menghasilkan bentuk plot I(krx,kry)

yang semakin menguncup (shrink).

Gambar 5.4 Hasil simulasi 3 dimensi Intensitas Difraksi celah lingkaran,λ = 8 Å

(33)

26 VI. SIMPULAN DAN SARAN

1. Simpulan

Dari penelitian didapatkan simpulan sebagai berikut :

a. Metode Simpson dapat dipakai untuk menyelesaikan persamaan Intensitas difraksi pada celah lingkaran

b. Implementasi program komputer dari metode Simpson dapat dipakai untuk menampilkan grafik 3 dimensi intensitas difraksi celah lingkaran

2. Saran

(34)

27 VII. DAFTAR PUSTAKA

Chapra Steven C., Canale Raymond P., Numerical Methods for Engineers, sixth edition ,Mc Graw-Hill Book Company, New York, 2010

E.Hechts, 2002, Optics, Addison-Wesley Publishing Company, New York.

Nayer Eradat, 2009, Fraunhofer Diffraction: lecture notes for Modern Optics, http://www.erbion.com/index_files/Modern_Optics/Ch11.pdf [diakses 2 mei 2015] ____,Integrals and Derivatives, www3.nd.edu/~newman/phys_30421/reading/ch5_int.pdf

[diakses 5 Juli 2015]

____,Interference and diffraction,

http://web.mit.edu/8.02t/www/802TEAL3D/visualizations/coursenotes/modules/guide1 4.pdf [diakses 20 Agustus 2015]