FISIKA I. OSILASI Bagian-2 MODUL PERKULIAHAN. Modul ini menjelaskan osilasi pada partikel yang bergerak secara harmonik sederhana

MODUL PERKULIAHAN

FISIKA I

OSILASI Bagian-2

Fakultas Program Studi Tatap Muka Kode MK Disusun Oleh Teknik Teknik Elektro

13

MK14008 Dian Widi Astuti, ST. MT

Abstract

Kompetensi

Modul ini menjelaskan osilasi pada partikel yang bergerak secara harmonik sederhana

Setelah membaca modul ini, mahasiswa diharapkan mampu untuk:

 Memahami dan menyelesaikan permasalahan tentang energi pada Gerak Harmonik Sederhana yang terdiri atas Energi Kinetik dan Energi Potensial

 Memahami Bandul sebagai contoh partikel yang bergerak osilasi.

Osilasi

13.1 Energi pada Gerak Harmonik Sederhana

Bila sebuah benda berosilasi pada sebuah pegas, energi kinetik benda dan energi potensial sistem benda-pegas berubah terhadap waktu, sementara jumlah kedua energi itu, yakni energi total, konstan (dengan menganggap tak ada gesekan). Energi potensial sebuah pegas dengan konstanta gaya k yang teregang sejauh x dari kesetimbangannya diberikan oleh Persamaan 9-10:

2 2 1_kx

EPelastik  (13-1)

Energi kinetik sebuah benda bermassa m yang bergerak dengan kelajuan  adalah:

2 2 1_m

EK  (13-2)

Energi total adalah jumlah energi potensial dan energi kinetik:

2 2 1 2 2 1_{kx m} EK EP Etotal     (13-3)

Ketika simpangan maksimum, x = A, kecepatan nol, dan energi total

2 2 1_kA

E_total  (13-4)

Persamaan ini memberikan sifat umum penting yang dimiliki gerak harmonik sederhana: “Energi total dalam gerak harmonik sederhana berbanding lurus dengan kuadrat amplitudo.”

Kita dapat menunjukkan bahwa energi total untuk benda yang berosilasi pada sebuah pegas bernilai konstan dengan mensubstitusi pernyataan bagi x dan  dalam Persamaan 12-5 dan 12-6 ke dalam Persamaan 13-1 dan 13-2 untuk energi potensial dan kinetik. Kita memperoleh:









2 2 1 _cos   k A t EP atau



 



 kA t EP ₂1 2_cos2 _(13-5) dan









2 2 1  _sin   m A t EK

Dengan menggunakan 2 k m dari Persamaan 12-9, energi kinetik dapat ditulis



 



 kA t

EK 2 2

2

1 _{sin (13-6)}

Dengan menjumlahkan energi potensial dan kinetik untuk memperoleh energi total, kita mendapatkan





















2 2 1 2 2 2 2 1 2 2 2 1 2 2 2 1 sin cos sin cos kA t t kA t kA t kA E_total                 

di mana kita gunakan identitas trigonometri cos2 sin2 1

Bila dinyatakan dengan energi total, energi potensial dan kinetik pada gerak harmonik sederhana adalah:

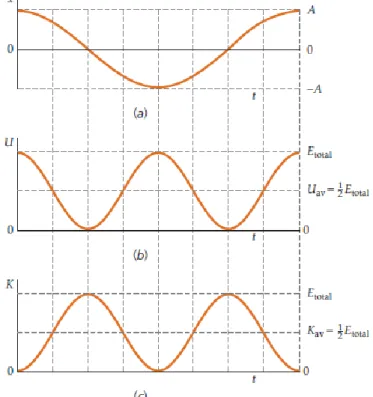
 2 cos total E EP dan  2 sin total E EK  dengan  t. Gambar 13-1b dan c memperlihatkan grafik EP dan EK sebagai fungsi t untuk  = 0. Kurva ini memiliki bentuk sama, kecuali bahwa EP

maksimum ketika EK bernilai nol dan EP bernilai nol ketika EK maksimum. Nilai rata-rata kecuali energi untuk satu atau beberapa siklus bernilai sama, dan karena

EP + EK = Etotal, nilai rata-rata ini diberikan oleh total rata rata rata rata EK E EP   ₂1   (13-7) Contoh 1:

Sebuah benda 3 kg yang dihubungkan pada sebuah pegas berosilasi dengan amplitudo 4 cm dan periode 2 s. (a) Berapakah energi total? (b) Berapakah kecepatan maksimum benda?

Jawab:

(a) Energi total adalah ₂1_kA2. _{Konstanta gaya pegas, k, berhubungan dengan periode}

melalui persamaan

k m T 2

Gambar 13-1: Ploting grafik x dari EP dan EK terhadap t.

sehingga

 

 

 

m N s kg T m k 29,6 / 4 3 4 2 2 2 2 2     

Oleh karena itu, energi totalnya adalah







J m m N kA E_total 2 2 2 1 2 2 1 10 37 , 2 04 , 0 / 6 , 29     

(b) Energi total kita gunakan untuk mencari kecepatan maksimum. Ketika kelajuannya

maksimum, energi potensial sama dengan nol dan energi total sama dengan energi kinetik saat itu:





s m kg J m E_total maks / 126 , 0 3 10 37 , 2 2 2 2      

Kita dapat mencari kelajuan maksimum dari Persamaan 12-12b:



t



A

A _maks

maks   

  sin 

Dengan menggunakan 2 T (Persamaan 12-4), kita peroleh

 



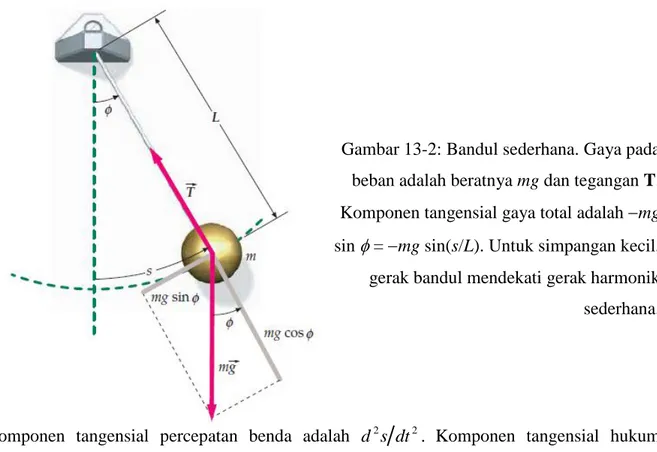
s m s cm s cm T A maks / 126 , 0 / 6 , 12 2 4 14 , 3 2 2       12.2 Bandul Bandul Sederhana

Contoh gerak osilasi yang terkenal ialah gerak osilasi bandul. Gerak bandul merupakan gerak harmonik sederhana hanya jika amplitudo geraknya kecil. Gambar 13-2 memperlihatkan bandul sederhana yang terdiri dari tali dengan panjang L dan beban bermassa m. Gaya yang bekerja pada beban adalah mg dan tegangan T pada tali. Bila tali membuat sudut  terhadap vertikal, berat memiliki komponen-komponen mg cos  sepanjang tali dan mg sin  tegak lurus tali dalam arah berkurangnya . Misalkan s sebagai panjang busur diukur dari dasar lingkaran. Pamjang busur dihubungkan ke sudut  oleh



L

Gambar 13-2: Bandul sederhana. Gaya pada beban adalah beratnya mg dan tegangan T. Komponen tangensial gaya total adalah mg

sin  = mg sin(s/L). Untuk simpangan kecil,

gerak bandul mendekati gerak harmonik sederhana.

Komponen tangensial percepatan benda adalah d2s dt2. Komponen tangensial hukum kedua Newton adalah



 sin  2₂ dt s d m mg F_t  atau L s g g dt s d sin sin 2 2      (13-9)

Jika s jauh lebih kecil daripada s L, sudut  = s L adalah kecil, dan kita dapat mendekati sin  dengan sudut . Dengan menggunakan sin

 

s L s L dalam Persamaan 13-9, kita akan memperoleh: s L g dt s d _ 2 2 (13-10a)

Kita dapat melihat bahwa untuk sudut cukup kecil sehingga sin berlaku, percepatan berbanding lurus dengan simpangan. Gerak bandul dengan demikian mendekati gerak harmonik sederhana untuk simpangan kecil. Persamaan 13-10a dapat ditulis

s dt S d 2 2 2    (13-10b) dengan

L g



2

 (13-11)

Penyelesaian Persamaan 12-10b adalah ss₀cos



t



, dengan s adalah simpangan ₀

maksimum diukur sepanjang busur lingkaran. Periode gerak harmonik tersebut adalah

g L T    2 2   (13-12)

Menurut Persamaan 13-12 makin panjang tali, makin besar periode, yang konsisten dengan pengamatan eksperimen. Perhatikan bahwa periode tidak bergantung pada massa. Hal ini berlaku karena gaya pemulih berbanding lurus dengan massa. Karena itu, percepatan

m F

a karena itu tak bergantung pada massa. Perhatikan bahwa frekuensi dan periode tak bergantung pada amplitudo osilasi, segi umum gerak harmonik sederhana.

Seringkali gerak bandul sederhana lebih mudah dinyatakan dalam bentuk simpangan sudutnya . Dengan menggunakan s = L dalam Persamaan 13-9, kita akan memperoleh

 

 _ sin 2 2 g dt L d _ atau   sin 2 2 L g dt L d _ (13-13) yang untuk  kecil menjadi

    2 2 2     L g dt d (13-14)

Penyelesaian Persamaan 13-14 adalah



 





  ₀cos t (13-15)

dengan 0 s0 L sebagai simpangan sudut maksimum. Kreteria gerak harmonik sederhana

yang dinyatakan dalam besaran-besaran sudut ini adalah bahwa percepatan sudut harus berbanding lurus dengan simpangan sudut dan berlawanan arah seperti dalam Persamaan 13-14.

Contoh 2:

(a) Perkirakan panjang pendulum pada jam besar yang bedetak sekali setiap detik. (b) Berapa periode jam dengan pendulum yang panjangnya 1,0 m?

(a) Jika kita menganggap jam “berdetak” sekali per siklus, maka periode T = 1,0 s. Kita

selesaikan dengan mempergunakan Persamaan 13-12 untuk mendapatkan L:





_

_

m s m s g T L g L T 25 , 0 / 8 , 9 4 0 , 1 4 2 2 2 2 2 2 2          

(b) Dari Persamaan 13-12, T  L. Jadi jika L empat kali lipat



40,25 m1,0 m



, maka T akan 4 = 2 kali lebih besar, atau 2,0 s.

Bandul Fisis

Sebuah benda tegas yang digantung dari suatu titik yang bukan merupakan pusat massanya akan berosilasi ketika disimpangkan dari posisi kesetimbangannya. Sistem seperti ini disebut

bandul fisis. Tinjaulah sebuah bangun datar yang

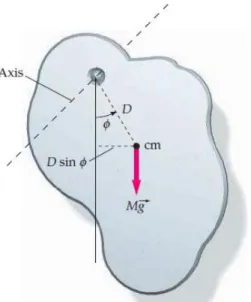
digantung pada sebuah titik berjarak D dari pusat massanya dan disimpangkan dari kesetimbangan sebesar sudut  seperti ditunjukkan dalam Gambar 13-3. Torka terhadap titik gantung bernilai MgD sin  dan cenderung mengurangi . Percepatan sudut  dihubungkan dengan torka oleh

2 2 dt d I I    

dengan I momen inersia di sekitar titik gantung. Dengan mensubstitusikan MgD sin  untuk torka total, kita memperoleh

2 2 sin dt d I MgD     atau   sin 2 2 I MgD dt d   (13-16)

Untuk bandul sederhana, I = ML2 dan D = L, sehingga Persamaan 13-16 sama seperti Persamaan 13-13. Sekali lagi, gerak mendekati gerak harmonik sederhana jika simpangan sudutnya kecil sehingga aproksimasi sin  berlaku. Dalam kasus ini, kita memperoleh

Gambar 13-3: Bandul fisis. Torka terhadap poros karena gaya gravitasi bernilai MgD sin  dan cenderung merngurangi .

    2 2 2     I MgD dt d (13-17) dengan MgD I T    2 2   (13-18) Bandul Puntir

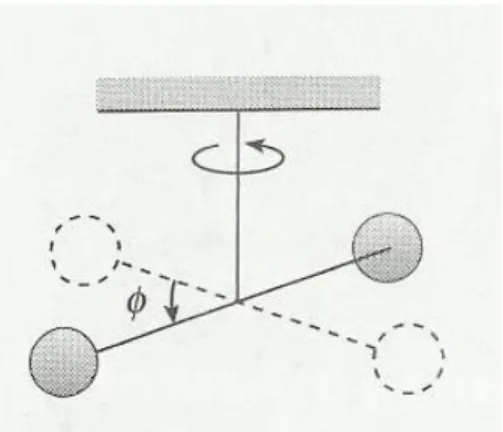
Gambar 13-4 memperlihatkan sebuah bandul puntir, yang terdiri dari benda yang digantung dengan kawat yang disangkutkan pada titik tetap. Bila dipuntir hingga sudut , kawat akan mengerjakan suatu torka pemulih yang sebanding dengan ;



  (13-19)

Konstanta kesebandingan  disebut konstanta puntir. Nilai konstanta itu dapat dicari dengan menerapkan torka yang diketahui untuk memuntir kawat dan mengukur simpangan sudut  yang terjadi. Jadi I adalah momen inersia benda terhadap sumbu sepanjang kawat, hukum kedua Newton untuk gerak rotasi memberikan 2 2 dt d I      atau      2 2 2     I dt d (13-20)

Persamaan 13-20 menjelaskan gerak harmonik sederhana dengan frekuensi sudut    I. Periode gerak tersebut adalah

  I

T 2 (13-21)

Perhatikan bahwa kita tidak melakukan aproksimasi sudut kecil. Gerak bandul puntir merupakan gerak harmonik sederhana sepanjang torka pemulih berbanding lurus dengan sudut puntiran. Hal seperti itu terjadi sepanjang batas elastik kawat untuk tegangan geser tidak terlampaui. Roda penyeimbang dalam jam merupakan bandul puntir seperti halnya timbangan puntir Cavendish.

12.3 Soal Latihan

1. Corong pengeras suara bergetar dalam Gerak Harmonik Sederhana (GHS) dengan frekuensi 262 Hz (“C tengah”). Amplitudo di pusat corong adalah A = 1,5  10-4 m, dan pada t = 0, x = A. (a) Bagaimana persamaan yang mendeskripsikan gerak di pusat corong? (b) Berapa kecepatan maksimum dan percepatan maksimumnya? (c) Bagaimana posisi corong pada t = 1,00 ms (= 1,00  10-3)?

2. Massa 400 g bergetar menurut persamaan x0,35sin



5,50t



di mana x dalam meter dan t dalam detik. Tentukan (a) Amplitudo, (b) Frekuensi, (c) Periode, (d) Energi total, dan (e) EK dan EP ketika x = 10 cm. (f) Gambarkan grarik x terhadap t yang rinci dengan menunjukkan amplitudo dan periode yang benar.

3. Sebuah benda bermassa 2 kg dihubungkan ke sebuah pegas berkonstanta gaya 40 N/m. Benda itu bergerak dengan kelajuan 25 cm/s ketika berada pada posisi kesetimbangannya. (a) Berapakah energi total benda? (b) Berapakah amplitudo gerak? [jawaban: (a) E = 0,0625 J. (b) A = 5,59 cm]

4. Sebuah pegas (Gambar 13-5a) meregang 0,150 m ketika massa 0,300 kg

digantungkan padanya (Gambar 13-5b). Pegas kemudian diregangkan 0,100 m dari titik setimbang ini, dan dilepaskan. Tentukan (a) konstanta pegas, k, (b) amplitudo osilasi A, (c) kecepatan maksimum ₀, (d) besar kecepatan , ketika massa berada 0,050 m dari

kesetimbangan, dan (e) besar percepatan maksimum massa tersebut.

5. Untuk osilator harmonis sederhana dari Soal Latihan 4, tentukan (a) Energi total, dan (b) Energi kinetik dan potensial pada setengah amplitudo



xA 2



.

6. Sebuah benda bermassa 2 kg dihubungkan ke sebuah pegas berkonstanta gaya 40 N/m. Benda itu bergerak dengan kelajuan 25 cm/s ketika berada pada posisi kesetimbangannya. (a) Berapakah energi total benda? (b) Berapakah amplitudo gerak? [Jawaban: (a) E = 0,0625 J. (b) A = 5,59 cm]

7. Benda 4 kg digantung pada sebuah pegas dengan konstanta gaya k = 200 N/m. (a) Gambar 13-5: Soal Latihan 4.

Carilah regangan y pegas ketika dalam kesetimbangan. (b) Carilah energi potensial 0

total, termasuk energi potensial gravitasi, ketika pegas diregang 12 cm dari kesetimbangan (asumsikan EP = 0 pada y y₀) (c) Carilah periode osilasi. [Jawaban: (a) 19,6 cm, (b) 1,44 J, (c) 0,889 s]

8. Pendulum jam berosilasi dengan frekuensi 2,0 Hz. Pada t = 0, pendulum dilepaskan dari keadaan diam dengan sudut 15 terhadap vertikal. Dengan mengabaikan gesekan, di mana posisi (sudut) pendulum pada (a) t = 0,25 s, (b) t = 1,60 s, dan (c) t = 500 s? [Petunjuk: Jangan kacaukan sudut ayunan  dari pendulum dengan sudut yang muncul sebagai argumen cosinus]

Daftar Pustaka

[1] David Halliday, Robert Resnick, Jearl Walker. (2010). Fundamental of Physics

Extended. Jilid 1. 9th ed. NY. John Wiley & Sons.

[2] Giancoli. (2001). Fisika. Jilid 1. 5th ed., Jakarta, Erlangga

[3] Giancoli. (2013). Physics Principles With Applications. Jilid 1. 7th ed. NY. Pearson. [4] Tripler. (2001). Fisika Untuk Sains dan Teknik. Jilid 1. 3rd ed. Jakarta: Erlangga [5] Tripler, Paul A & Gene Mosca. (2008). Physics For Scientists and Engineers. 6th ed.