TIM MATEMATIKA DASAR I

(1)

MATEMATIKA DASAR I

DIKTAT KULIAH

DISUSUN OLEH

TIM MATEMATIKA DASAR I

FAKULTAS SAIN DAN TEKNOLOGI

UNIVERSITAS JAMBI

2013

(2)

i KATA PENGANTAR

Mata kuliah Matematika Dasar merupakan mata kuliah dasar yang diwajibkan bagi mahasiswa tahun pertama di perguruan tinggi khususnya di Fakultas Sain dan Teknologi Universitas Jambi. Mata kuliah Matematika Dasar ini pada dasarnya sama dengan mata kuliah Kalkulus yang biasanya dipakai pada umumnya. Matakuliah Matematika Dasar ini terdiri dari Matematika Dasar I, Matematika Dasar II, dan Matematika Dasar Lanjut. Matematika Dasar I umumnya mempelajari tentang turunan suatu fungsi yang akan menjadi dasar ataupun pengantar bagi perkuliahan matematika dasar II dan Matematika Dasar Lanjut. Diktat ini dibuat untuk digunakan dalam perkuliahan Matematika Dasar I.

Dari segi konsep isi perkuliahan Matematika Dasar I sudah baku, tidak begitu banyak mengalami perubahan. Hanya saja perbaikan dan revisi dalam penyajian yang mungkin harus terus dipertimbangkan demi baiknya pembelajaran mata kulian ini.

Salah satu yang menjadi tujuan dalam penyusunan diktat ini adalah untuk membantu mengefektifkan pembelajaran dan menambah referensi mahasiswa. Di samping dengan pertimbangan penyeragaman pengajaran di Fakultas Sain dan teknologi, maka kami berupaya menyusun suatu bahan ajar atau diktat yang berjudul “Matematika Dasar I” sebagai acuan di lingkungan Fakultas Sain dan Teknologi dengan harapan eksistensi mutu dan hasil belajar dapat dicapai secara optimal.

Penulis mengharapkan saran dan kritik guna penyempurnaan baik dari segi isi maupun bahasa dalam bahan ajar ini. Besar harapan penulis bahwa bahan ajar ini bisa bermanfaat.

Jambi, September 2013

Tim Matematika Dasar I FST Universitas Jambi

(3)

ii DAFTAR ISI KATA PENGANTAR ________________________________________________________________________________ I DAFTAR ISI ________________________________________________________________________________________ II BAB 1 _______________________________________________________________________________________________ 1 PENDAHULUAN ___________________________________________________________________________________ 1 1.1 SISTEM BILANGAN REAL ______________________________________________________________ 1 1.2 PERTAKSAMAAN ______________________________________________________________________ 2 1.3 NILAI MUTLAK _______________________________________________________________________ 4 1.4 AKAR KUADRAT ______________________________________________________________________ 5 1.5 SISTEM KOORDINAT DAN GARIS LURUS ________________________________________________ 5 1.5.1 Sistem Koordinat _____________________________________________________________ 5 1.5.2 Persamaan Garis Lurus ______________________________________________________ 7 1.6 TEKNIK MENGGAMBAR GRAFIK SUATU PERSAMAAN GARIS _____________________________ 9 1.7 LATIHAN SOAL _____________________________________________________________________ 10 BAB 2 _____________________________________________________________________________________________ 13 FUNGSI DAN LIMIT _____________________________________________________________________________ 13 2.1 FUNGSI DAN GRAFIKNYA ____________________________________________________________ 13 2.1.1 Definisi Fungsi dan Grafiknya _____________________________________________ 13 2.1.2 Fungsi Genap dan Fungsi Ganjil ___________________________________________ 15 2.1.3 Fungsi Nilai Mutlak dan Fungsi Bilangan Bulat Terbesar _______________ 16 2.1.4 Beberapa Jenis Fungsi Lainnya di dalam Kalkulus ______________________ 17 2.2 OPERASI FUNGSI ____________________________________________________________________ 18 2.2.1 Operasi Jumlah, Selisih, Hasil Kali, Hasil Bagi, Pangkat _________________ 18 2.2.2 Komposisi Fungsi __________________________________________________________ 19 2.2.3 Invers Fungsi _______________________________________________________________ 20 2.2.4 Translasi Fungsi ____________________________________________________________ 20 2.3 FUNGSI TRIGONOMETRI _____________________________________________________________ 21 2.3.1 Definisi Fungsi Trigonometri _____________________________________________ 21 2.3.2 Empat Fungsi Trigonometri Lainnya _____________________________________ 22 2.3.3 Kesamaan Trigonometri ___________________________________________________ 22 2.4 KONSEP LIMIT ______________________________________________________________________ 23 2.5 PENGKAJIAN MENDALAM TENTANG LIMIT ___________________________________________ 25 2.5.1 Definisi Limit _______________________________________________________________ 25

(4)

iii 2.5.2 Definisi Limit Limit Sepihak _______________________________________________ 25 2.6 TEOREMA LIMIT ____________________________________________________________________ 26 2.6.1 Teorema Limit Utama _____________________________________________________ 26 2.6.2 Teorema Penggantian _____________________________________________________ 27 2.6.3 Teorema Apit _______________________________________________________________ 27 2.6.4 Limit Trigonometri ________________________________________________________ 27 2.7 KEKONTINUAN FUNGSI ______________________________________________________________ 27 2.7.1 Kekontinuan di Satu Titik _________________________________________________ 27 2.7.2 Kekontinuan Sepihak ______________________________________________________ 28 2.7.3 Kekontinuan pada Interval ________________________________________________ 28 2.8 TEOREMA KEKONTINUAN FUNGSI ___________________________________________________ 29 2.8.1 Teorema A (Kekontinuan pada fungsi polynomial dan fungsi rasional)29 2.8.2 Teorema B (Kekontinuan pada fungsi nilai mutlak dan fungsi akar ke‐n) 29 2.8.3 Teorema C (Kekontinuan pada operasi fungsi) __________________________ 29 2.8.4 Teorema D (Kekontinuan pada limit komposisi) ________________________ 29 2.8.5 Teorema E ( Teorema Nilai Antara) ______________________________________ 29 2.9 LATIHAN SOAL _____________________________________________________________________ 30 BAB 3 _____________________________________________________________________________________________ 33 TURUNAN ________________________________________________________________________________________ 33 3.1 KONSEP DASAR TURUNAN __________________________________________________________ 33 3.1.1 Permasalahan Garis Singgung ____________________________________________ 33 3.1.2 Permasalahan Kecepatan Sesaat __________________________________________ 34 3.2 TURUNAN __________________________________________________________________________ 35 3.2.1 Definisi Turunan ___________________________________________________________ 35 3.2.2 Beberapa Bentuk Setara Turunan ________________________________________ 36 3.2.3 Keterdiferensialan dan Kekontinuan Fungsi ____________________________ 36 3.3 ATURAN TURUNAN _________________________________________________________________ 37 3.4 ATURAN TURUNAN FUNGSI TRIGONOMETRI _________________________________________ 38 3.5 ATURAN RANTAI ___________________________________________________________________ 38 3.6 PENULISAN LEIBNIZ ________________________________________________________________ 39 3.7 TURUNAN TINGKAT TINGGI _________________________________________________________ 40 3.8 PENDIFERENSIALAN IMPLISIT _______________________________________________________ 41 3.9 LAJU YANG BERKAITAN _____________________________________________________________ 41 3.10 DIFERENSIAL DAN HAMPIRAN ____________________________________________________ 43 3.10.1 Turunan dan Diferensial __________________________________________________ 43

(5)

iv 3.10.2 Hampiran ___________________________________________________________________ 44 3.10.3 Penaksiran Galat (Error) __________________________________________________ 45 3.11 SOAL LATIHAN ___________________________________________________________________ 45 BAB 4 _____________________________________________________________________________________________ 48 APLIKASI TURUNAN ___________________________________________________________________________ 48 4.1 MAKSIMUM DAN MINIMUM _________________________________________________________ 48 4.2 KEMONOTONAN FUNGSI DAN TITIK EKSTRIM ________________________________________ 50 4.2.1 Kemonotonan Fungsi ______________________________________________________ 50 4.2.2 Titik Ekstrim _______________________________________________________________ 51 4.2.3 Uji Turunan untuk Kemonotonan dan Titik Ekstrim ____________________ 52 4.3 KECEKUNGAN FUNGSI DAN TITIK BELOK _____________________________________________ 54 4.3.1 Kecekungan Fungsi ________________________________________________________ 54 4.3.2 Titik Belok __________________________________________________________________ 54 4.3.3 Uji Turunan untuk Kecekungan dan Titik Belok _________________________ 54 4.4 BEBERAPA MASALAH MAKSIMUM DAN MINIMUM ____________________________________ 55 4.5 LIMIT DI TAK HINGGA DAN LIMIT TAK HINGGA ______________________________________ 56 4.5.1 Limit Tak Hingga ___________________________________________________________ 56 4.5.2 Limit di Tak Hingga ________________________________________________________ 57 4.5.3 Limit Tak Hingga di Tak Hingga __________________________________________ 57 4.6 MENGGAMBAR GRAFIK CANGGIH ____________________________________________________ 58 4.6.1 Asimtot ______________________________________________________________________ 58 4.7 TEOREMA NILAI RATA‐RATA _______________________________________________________ 61 4.8 LATIHAN SOAL _____________________________________________________________________ 62 DAFTAR PUSTAKA _____________________________________________________________________________ 65

(6)

BAB 1 PENDAHULUAN 1.1 Sistem Bilangan Real

Kalkulus sangat bergantung pada sistem bilangan real dan sifat‐sifat yang terkandung di dalamnya. Untuk memahami sistem bilangan real, kita akan memulai dengan beberapa sistem bilangan yang sederhana.

Himpunan bilangan asli, 1,2,3,4,5, . . . . Di dalam himpunan bilangan asli terdapat himpunan bilangan genap 2 | dan himpunan bilangan ganjil 2 1|

. Selain itu terdapat pula himpunan bilangan prima dan komposit. Gabungan antara himpunan bilangan asli, nol, dan himpunan negatif bilangan asli disebut sebagai himpunan bilangan bulat, . . . , 3, 2, 1,0,1,2,3, . . . . Himpunan bilangan rasional didefinisikan dengan | , , 0 . Karena 1 0 , maka , . Bilangan yang tidak bisa dituliskan dalam bentuk dengan , dikategorikan dalam himpunan bilangan irasional. Gabungan himpunan bilangan rasional dan bilangan irasional disebut sebagai himpunan bilangan real, .

Contoh 1.1:

1. , √2, dan π adalah bilangan irasional, sedangkan , √2, π . 2. Buktikan bahwa jika k genap, maka k genap.

Bukti:

Kontraposisi dari pernyataan tersebut adalah jika bukan merupakan bilangan genap, maka bukan bilangan genap. Hal ini sama artinya dengan mengatakan bahwa jika ganjil, maka ganjil. Kita akan membuktikan kontraposisinya. Misalkan 2 1, maka

2 1 4 4 1 2 2 2 1.

Terlihat bahwa jika bilangan ganjil, maka adalah bilangan ganjil. Dengan demikian terbukti bahwa jika genap, maka genap.

(7)

Bab 1 Pendahuluan |

2

Contoh 1.2:

Sistem bilangan real bisa diperluas menjadi sistem bilangan kompleks, yaitu bilangan yang berbentuk a bi, dengan a, b , dan i √ 1.

1.2 Pertaksamaan

Menyelesaikan suatu persamaan seperti 2 7 15 atau 2 3 5 0 adalah suatu hal yang mudah. Namun, dalam kalkulus kita akan lebih sering menemui permasalah menyelesaikan suatu pertaksamaan. Berikut ini akan dibahas mengenai beberapa hal yang terkait dengan penyelesaian suatu pertaksamaan.

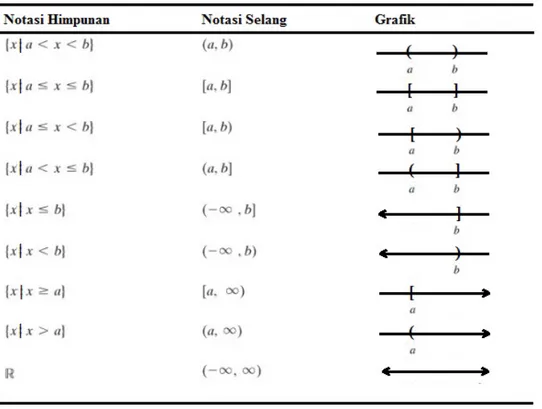
Perhatikan suatu pertaksamaan . Pertaksamaan tersebut dapat dibagi menjadi dua, yaitu dan yang keduanya menyatakan suatu selang buka yang memuat semua bilangan antara dan namun tidak memuat dan . Dalam hal ini, selang buka dinotasikan sebagai , . Berbeda dengan , pertaksamaan ini menyatakan suatu selang tutup yang memuat semua bilangan dari dan . Pertaksamaan ini dinotasikan dengan , . Terdapat pula selang setengah buka dan yang masing‐masing dinotasikan oleh , dan , . Notasi selang lainnya dapat dilihat pada Tabel 1.

Tabel 1. Notasi selang

(8)

Matematika Dasar I/FST/UNJA/2013

3

Menyelesaikan suatu Pertaksamaan

Sebagaimana menyelesaikan masalah persamaan, prosedur penyelesaian suatu pertidaksamaan juga memuat suatu transformasi sehingga diperoleh suatu himpunan penyelesaian. Kita bisa mengenakan suatu operasi yang tidak mempengaruhi solusinya, antara lain: 1. Menambahkan suatu bilangan yang sama pada kedua sisi pertaksamaan. 2. Mengalikan kedua sisi pertaksamaan dengan bilangan positif yang sama. 3. Mengalikan kedua sisi pertaksamaan dengan bilangan negatif yang sama, tetapi kita harus membalik arahnya. Contoh 1.3:

1. Selesaikan pertaksamaan 5 2 6 8 dan tunjukkan grafik himpunan penyelesaiannya. Solusi 5 2 6 8 5 6 10 (menambahkan 2) 10 (menambahkan ‐6x) 10 (mengalikan ‐1)

Himpunan penyelesaian, ∞, 10 dengan grafik yang ditunjukkan pada Gambar 1.1 a.

2. Selesaikan pertaksamaan 2 6 8 1 dan tunjukkan grafik himpunan penyelesaiannya.

Solusi

2 6 8 1

10 6 7 (menambahkan ‐8) (mengalikan ) H

Himpunan penyelesaian, , dengan grafik yang ditunjukkan pada Gambar 1.1b.

Gambar 1.1 Notasi selang sebagai himpunan penyelesaian

(9)

4

1.3 Nilai Mutlak

Konsep nilai mutlak sangatlah berguna dalam kalkulus. Nilai mutlak dari suatu bilangan , dinotasikan dengan | |, dan didefinisikan sebagai berikut

| | 0;_0. Berikut adalah sifatsifat nilai mutlak: 1. | | | || | 2. | | | || | 3. | | | | | | Ketaksamaan segitiga 4. | | || | | || 5. | | dan | | √ 6. | || | | | 7. | | | | Sifatsifat pertaksamaan yang memuat nilai mutlak: 1. | | 2. | | atau

Sifat‐sifat ini berlaku juga untuk tanda pertaksamaan lebih kecil dari atau sama dengan ( ) dan lebih besar dari atau sama dengan ( ). Contoh 1.4: 1. Tentukan himpunan penyelesaian dari |3 7| 8 Solusi |3 7| 8 8 3 7 8 1 3 15 1 3 5 Himpunan penyelesaian , 5 . 2. Tentukan himpunan penyelesaian dari |8x| 5 2. Solusi 8 5 2

(10)

Matematika Dasar I/FST/UNJA/2013 Bab 1 Pendahuluan |

5

8 5 2 13 2 2 13 atau 8 5 2 3 2 2 3 Himpunan penyelesaian: ∞, , ∞ 1.4 Akar Kuadrat Solusi dari persamaan kuadrat 0 diberikan oleh: √ 4 2

dengan 4 disebut sebagai diskriminan dari persamaan kuadrat. Suatu persamaan 0 memiliki dua solusi real jika 0, satu solusi real jika 0, dan tidak memiliki solusi real jika 0. Dengan formula kuadrat itu, kita bisa menentukan solusi persamaan kuadrat dengan mudah tanpa harus memfaktorkan atau melengkapkan kuadrat sempurna. Contoh 1.5: Dua buah solusi dari 5 4 0 adalah 5 √25 16 2 5 √41 2 dan 5 √25 16 2 5 √41 2 1.5 Sistem Koordinat dan Garis Lurus 1.5.1 Sistem Koordinat Pada suatu bidang datar, kita bisa membuat dua buah garis, yaitu garis horizontal dan garis vertikal yang berpotongan saling tegak lurus. Titik potong dari kedua garis tersebut dinamakan titik asal dan diberi label . Garis horizontal disebut sumbu‐ ,

(11)

6

sedangkan garis vertikal disebut sumbu‐ . Bagian positif dari sumbu‐ berada di sebelah kanan titik asal, sedangkan bagian positif dari sumbu‐ berada di sebelah atas titik asal. Sumbu koordinat tersebut membagi bidang datar menjadi empat daerah yang disebut kuadran, yaitu kuadaran , , , dan . Lihat Gambar 1.2.

Gambar 1.2 Koordinat kartesius

Rumus Jarak

Pada koordinat kartesius, misalkan titik , dan adalah jarak dari titik asal ke titik . Panjang adalah

atau

.

Persamaan di atas sering kita sebut sebagai rumus Phytagoras.

Misalkan pada suatu bidang koordinat terdapat dua titik, , dan , . Jarak antara titik dan adalah

,

(12)

7

Lingkaran adalah himpunan titik yang berada pada suatu jarak yang tetap terhadap suatu titik pusat. Jarak tetap tersebut dinamakan jari‐jari(radius). Suatu lingkaran dengan jari‐jari dan titik pusat , dapat dituliskan dalam sebuah persamaan lingkaran

Contoh 1.6:

Tunjukkan bahwa 2 6 6 merupakan suatu lingkaran. Tentukan pula titik pusat dan jari‐jarinya.

Solusi

Dengan melengkapkan kuadrat sempurna, kita peroleh 1 3 4. Dengan demikian, lingkaran 2 6 6 berpusat di titik 1, 3 dengan radius 2.

Rumus Titik Tengah

Titik tengah dari suatu garis yang menghubungkan , dan , adalah

2 , 2

1.5.2 Persamaan Garis Lurus

Perhatikan Gambar 1.3. Dari titik , ke titik , , terdapat rise (perubahan arah vertikal) sebesar dan run (perubahan arah horizontal) sebesar . Kita katakan garis memiliki kemiringan sebesar dengan syarat . Kemiringan ini disebut gradien dan dinotasikan dengan yaitu

Lebih jauh, persamaan garis antara dua titik , dan , adalah

(13)

8

Gambar 1.3 Kemiringan garis Apabila kita telah memperoleh titik potong suatu garis terhadap sumbu‐ pada titik 0, , persamaan garis dapat pula dituliskan sebagai 0 atau Misalkan adalah suatu konstanta. Persamaan garis yang sejajar dengan sumbu‐ dan memotong titik di sumbu‐y adalah dan memiliki kemiringan . Persamaan garis yang sejajar dengan sumbu‐ dan memotong titik di sumbu‐ adalah

dengan kemiringan yang tak terdefinisi.

Persamaan garis dapat pula berbentuk 0 dengan dan keduanya tidak bernilai 0. Misalkan dan adalah dua buah garis dengan kemiringan masing‐ masing dan . Apabila dan sejajar, maka keduanya memiliki kemiringan yang sama, yaitu . Apabila tegak lurus terhadap , maka berlaku · . Contoh 1.7:

Dapatkan persamaan garis yang melalui titik potong dari dua buah garis 3 4 8 dan 6 10 7 yang tegak lurus terhadap garis 6 10 7. Solusi

Dengan menggunakan teknik eliminasi dan substitusi, titik potong dari 3 4 8 dan 6 10 7 adalah 2, . Kemiringan garis 6 10 7 adalah . Karena persamaan garis yang kita cari tegak lurus terhadap 6 10 7, maka kemiringannya adalah .

(14)

9

Dengan demikian, persamaan garis tersebut memenuhi: 1 2 5 3 2 5 3 23 6 6 10 23 10 6 23 0 1.6 Teknik Menggambar Grafik suatu Persamaan Garis

Untuk menggambar suatu persamaan garis dengan menggunakan tangan, ikuti langkah‐langkah berikut: 1. Dapatkan koordinat dari beberapa titik yang memenuhi persamaan garis yang diberikan; 2. Plot titik‐titik tersebut dalam suatu bidang; 3. Hubungkan titik‐titik tersebut dengan kurva yang halus. Contoh 1.8: Gambarkan kurva dari 3. Solusi Ketiga langkah di atas ditunjukkan pada Gambar 1.4. Gambar 1.4. Plot Grafik

(15)

10

Sifat Simetri pada Suatu Grafik

Perhatikan sebarang grafik dengan , adalah koordinat yang terdapat pada grafik tersebut.

1. Suatu grafik simetri terhadap sumbu‐ jika disubstitusikan oleh , maka akan diperoleh persamaan garis yang sama. Contoh, .

2. Suatu grafik simetri terhadap sumbu‐ jika disubstitusikan oleh , maka akan diperoleh persamaan garis yang sama. Contoh, .

3. Suatu grafik simetri terhadap titik asal jika disubstitusikan oleh dan disubstitusikan oleh , maka akan diperoleh persamaan garis yang sama. Contoh, .

Contoh 1.9:

Periksa, apakah 3 7 simetri terhadap titik asal, sumbu‐ , atau sumbu‐ . Solusi

Dengan mensubstitusikan ke dan ke pada persamaan 3 7, kita peroleh bahwa 3 7 tidak simetri terhadap titik asal, sumbu‐ , maupun sumbu‐ . 1.7 Latihan Soal A. Sistem Bilangan Real 1. Tuliskan dalam bentuk yang paling sederhana: a 3 2 4 7 12 ; b ; c 2 ; d √5 √3 √5 √3 ; e √5 √3 ; f 2x 4 x 1 ; g 3t t 1 ; h ; i ; j

(16)

11

2. Periksa apakah pernyataan berikut ini benar. "Untuk setiap x, x x 1." 3. Buktikan pernyataan berikut: Jika n ganjil, maka n ganjil. (Buktikan dengan kontraposisi) B. Pertaksamaan dan Nilai Mutlak 1. Dapatkan solusi dari pertaksamaan berikut dalam notasi selang. a) 7x 2 9x 3; b) 3 4x 9 11; c) 0; d) 2x 3 x 1 x 3 0 2. Manakah pernyataan berikut yang benar jika a b. a a ab; b a a b; c a 3 b 3; d – a b 3. Selesaikan pertaksamaan berikut a |x 1| 2| 3|; b |2x 1|\geq |x 1|; c 2|2x 3| | 10|; d |3x 1| 2| 6|

4. Gunakan sifat‐sifat nilai mutlak untuk menunjukkan bahwa setiap pernyataan berikut ini benar. a |a b| |a| |b|; b) |a b| |a| |b|; c) |a b c| |a| |b| |c| 5. Tunjukkan bahwa |x| 2 x 2x 7 x 1 C. Akar Kuadrat dan Sistem Koordinat 1. Hitunglah jarak dari a 3,1 , 1,1 ; b 4,5 , 5, 8 ; c 3,5 , 2, 2 ; d 1,5 , 6,3

(17)

12

2. Hitunglah jarak antara 2,3 dengan titik tengah suatu garis yang menghubungkan 2, 2 dan 4,3 . 3. Dapatkan titik pusat dari jari‐jari lingkaran dari: a x 2x 10 y 6y 10 0; b 4x 16x 15 4y 6y 0 4. Tuliskan persamaan garis yang melalui 3, 3 yang a sejajar terhadap garis y 3x 6; b tegak lurus terhadap garis 4y 2x 5; c tegak lurus terhadap garis yang menghubungkan 1,2 dan 3,‐1 ; d sejajar terhadap garis x 8; e tegak lurus terhadap garis x 8 5. Dapatkan nilai c pada garis 3x cy 5 yang a melalui titik 3,1 ; b sejajar terhadap sumbu‐y; c sejajar terhadap garis 2x y 1; d memiliki titik potong yang sama pada sumbu‐x dan sumbu‐y; e tegak lurus terhadap garis y 2 3 x 3 6. Dapatkan nilai k sedemikian sehingga kx 3y 10 a sejajar terhadap garis y 2x 4; b tegak lurus terhadap y 2x 4 D. Menggambar Grafik

1. Plot grafik dari setiap persamaan berikut. Mulailah dengan memeriksa sifat‐sifat simetrinya a y x 1 b y x 2x c x y 4 d x 9 y 2 36 e 2x 4x 3y 12y 2

(18)

BAB 2 FUNGSI DAN LIMIT 2.1 Fungsi dan Grafiknya Subbab 2.1 menjelaskan beberapa hal berkenaan dengan fungsi, antara lain: definisi fungsi dan grafiknya, serta beberapa jenis fungsi yang umum digunakan dalam kalkulus. 2.1.1 Definisi Fungsi dan Grafiknya Sebuah fungsi f didefinisikan sebagai suatu aturan padanan yang menghubungkan tiap obyek x dalam suatu himpunan, yang disebut daerah asal, dengan sebuah nilai unik f(x) dari himpunan kedua yang disebut daerah nilai. Contoh 2.1: Gambar 2.1 Deskripsi Fungsi Tabel 2.1 Nilai Fungsi x ‐2 4 ‐1 1 0 0 1 1 2 4 Dari gambar 2.1 dan tabel 2.1 dapat dilihat bahwa fungsi memadankan setiap elemen x di A dengan suatu elemen y di B. Sebagai contoh, fungsi memadankan elemen x = ‐2 di A dengan elemen y = 4 di B; elemen x = ‐1 di A dengan elemen y = 1 di B; dst. ‐2 ‐1 0 1 2 0 1 2

(19)

Bab 2 Fungsi dan Limit|

14

Daerah Asal (Daerah Definisi/ Wilayah/ Domain)

Daerah asal adalah himpunan semua bilangan Riil yang menyebabkan aturan fungsi berlaku/ terdefinisi. Pada contoh 2.1, daerah asal dari f(x), yang dinotasikan dengan adalah himpunan bilangan {‐2,‐1,0,1,2}.

Jika himpunan daerah asal tidak dirinci, maka kita akan selalu menganggap bahwa himpunan daerah asalnya adalah himpunan semua bilangan Riil sedemikian sehingga aturan fungsi memberikan makna/ terdefinisi. Ini disebut daerah asal alamiah. Pada contoh 2.1, daerah asal alamiahnya adalah {R}.

Daerah Hasil (Daerah Nilai/ Jelajah/ Range)

Daerah hasil adalah himpunan nilai‐nilai yang diperoleh yang merupakan padanan semua elemen dari daerah asal. Pada contoh 2.1 untuk daerah asal {‐2,‐1,0,1,2}, maka daerah nilai ( ) adalah himpunan bilangan {0,1,4}. Contoh 2.2: Tentukan daerah asal alamiah, daerah hasil dan gambarkan grafik dari fungsi a √9 b Solusi

a) Fungsi √9 akan terdefinisi bila nilai 9 0 . Hal ini akan tercapai bila | | 3, sehingga daerah asal alamiahnya adalah [‐3,3]. Grafik fungsi ditunjukkan oleh gambar berikut. Dari grafik dapat diketahui bahwa daerah nilai adalah pada selang [0,3].

(20)

15

b) Fungsi akan terdefinisi bila nilai 1 0, artinya 1. Dengan

demikian daerah asal alamiahnya adalah (‐∞,1) (1,∞). Grafik fungsi ditunjukkan oleh gambar berikut. Dari grafik dapat diketahui bahwa daerah nilai adalah pada selang ∞, ∞ .

2.1.2 Fungsi Genap dan Fungsi Ganjil

Fungsi genap dan fungsi ganjil didefinisikan sebagai berikut:

1. Fungsi f dikatakan fungsi genap bila memenuhi f ‐a f a . Grafik fungsi genap simetri terhadap sumbu y.

2. Fungsi f dikatakan fungsi ganjil bila memenuhi f ‐a ‐f a . Grafik fungsi ganjil simetri terhadap titik asal koordinat. Gambar 2.2 Grafik fungsi genap dan fungsi ganjil a ‐a f(‐a) f(a) y = f(x) (b)Fungsi Ganjil a ‐a f(‐a) f(a) y = f(x) (a)Fungsi Genap

(21)

16

Contoh 2.3:

Tentukan apakah fungsi berikut termasuk fungsi genap, ganjil atau bukan keduanya: a 2; b ; c 2 1 ! Solusi a) 2 (fungsi genap) Bukti: 2 2 b) (fungsi ganjil) Bukti: 2 x x 2 x c) 2 1 (bukan keduanya) Bukti: 2 x 1 2x 1 2.1.3 Fungsi Nilai Mutlak dan Fungsi Bilangan Bulat Terbesar

Fungsi Nilai Mutlak dan Fungsi Bilangan Bulat Terbesar didefinisikan sebagai berikut:

1. Fungsi Nilai Mutlak didefinisikan sebagai:

(22)

17

2. Fungsi Bilangan Bulat Terbesar adalah bilangan bulat terbesar yang lebih

kecil atau sama dengan x.

Contoh 2.4:

Fungsi nilai mutlak dan fungsi bilangan bulat terbesar, termasuk ke dalam fungsi genap, ganjil, atau bukan keduanya? Gambarkan grafiknya!

Solusi

• Fungsi nilai mutlak adalah fungsi genap

• Fungsi bilangan bulat terbesar adalah bukan merupakan fungsi genap atau ganjil 2.1.4 Beberapa Jenis Fungsi Lainnya di dalam Kalkulus Beberapa jenis fungsi lainnya yang dikenal di dalam kalkulus antara lain: 1. Fungsi Konstanta 2. Fungsi Identitas 3. Fungsi Polinom 4. Fungsi Linear (fungsi derajat satu)

(23)

18

5. Fungsi Kuadat (fungsi derajat dua) 6. Fungsi Rasional 7. Fungsi Aljabar Eksplisit 8. Fungsi Trigonometri 9. Fungsi Balikan Trigonometri 10. Fungsi Eksponen 11. Fungsi Logaritma 2.2 Operasi Fungsi

Beberapa operasi fungsi yang dibahas pada subbab ini antara lain: operasi aritmatika fungsi (Jumlah, Selisih, Hasil Kali, Hasil Bagi, Pangkat), komposisi fungsi, invers fungsi, dan translasi fungsi. 2.2.1 Operasi Jumlah, Selisih, Hasil Kali, Hasil Bagi, Pangkat Misalkan f(x) dan g(x) adalah fungsi‐fungsi real dengan daerah asal Df dan Dg , maka berlaku aturan operasi fungsi seperti pada Tabel 2.2 Tabel 2.2 Operasi aritmatika fungsi Rumus Operasi Fungsi Daerah Asal . . | 0 Contoh 2.5:

Andaikan √ 1 dan √9 , dengan daerah asal alamiah Df ‐1,∞ dan Dg ‐3,3 . Cari rumus f g, f‐g, f.g, f/g, f5_{, dan tentukan daerah asal almiahnya!}

(24)

Matematika Dasar I/FST/UNJA/2013 Bab 2 Fungsi dan Limit|

19

Solusi 2.2.2 Komposisi Fungsi

Andaikan dan √3 , maka dapat dibentuk suatu fungsi baru dari kedua fungsi tersebut yang dinamakan fungsi komposisi, yaitu: 3 2√3₃ 6 9 3 6 9 Perhatikan kedua fungsi komposis di atas. Terlihat bahwa susunan komposisi fungsi tidak komutatif karena . Contoh 2.6: Tentukan daerah asal untuk kedua fungsi komposisi di atas! Solusi

a) √ akan terdefinisi jika 3 0 dan √3 0. Dengan demikian

daerah asal alamiahnya adalah : 3 : 0 , yaitu

0: 3 . Dalam bentuk selang, daerah asal alamiah adalah [0,3) (3,∞). b) 3 akan terdefinisi jika: 1) 9 0 Æ daerah asal alamiah = : | | 3 atau ∞, 3 3,3 3, ∞ 2) 0

o Pada selang ∞, 3 , 0 karena menghasilkan nilai negatif, sehingga tidak terdefinisi pada selang ∞, 3

(25)

20

o Selang 3,3 dipecah menjadi 3,0 0,3 .

Pada selang 3,0 , 0 karena menghasilkan nilai positif, sehingga terdefinisi pada selang , .

Pada selang 0,3 , 0 karena menghasilkan nilai negatif, sehingga tidak terdefinisi pada selang 0,3

o Pada selang 3, ∞ , 0 karena

menghasilkan nilai positif, sehingga terdefinisi pada selang 3, ∞ , .

Dengan demikian mempunyai daerah asal alamiah pada

selang , , ∞ , atau 0 3

2.2.3 Invers Fungsi

Jika f(x) adalah sebuah fungsi, maka f‐1_{(x) adalah fungsi invers dari f(x) yang}

memenuhi: . Contoh 2.7: Jika , buktikan bahwa ! Solusi (subsitusikan x = pada ) (kurangkan ruas kanan dan ruas kiri dengan b) 2.2.4 Translasi Fungsi Misalkan sebuah fungsi awal f(x) ditranslasi menjadi f(x+h). Jika h>0, maka grafik fungsi akan bergeser ke kiri sebesar h satuan. Sebaliknya jika h<0, maka grafik fungsi akan bergeser ke kanan sebesar h satuan. Misalkan sebuah fungsi awal f(x) ditranslasi menjadi f(x)+k. Jika k>0, maka grafik fungsi akan bergeser ke atas sebesar h satuan.Sebaliknya jika k<0, maka grafik fungsi akan bergeser ke bawah sebesar k satuan.

(26)

21

Contoh 2.8:

Jika f x |x|, sketsa grafik f x 3 , f x‐3 ,f x 2,f x ‐2, dan f x‐3 2 ! Solusi 2.3 Fungsi Trigonometri Subbab 2.3 membahas tentang fungsi trigonometri dan beberapa kesamaan fungsi trigonometri. 2.3.1 Definisi Fungsi Trigonometri

Andaikan lingkaran C pada gambar 2.3 adalah lingkaran satuan, yaitu lingkaran dengan jari‐jari, r = 1 dan berpusat di titik asal. t‐positif adalah sudut yang dihitung berdasarkan arah yang berlawanan dengan jarum jam dengan satuan radian (2π rad = 360° . Andaikan posisi titik P memiliki sudut t, maka:

(27)

22

Gambar 2.3 Ilustrasi fungsi trigonometri (Ingat kembali nilai‐nilai sudut istimewa pada fungsi trigonometri !) 2.3.2 Empat Fungsi Trigonometri Lainnya tan sin cos cot cos sin sec 1 cos csc 1 sin 2.3.3 Kesamaan Trigonometri Kesamaan ganjil‐genap Kesamaan fungsi ko

sin sin sin cos

cos cos cos sin

tan tan tan cot

Kesamaan Pythagoras

sin cos 1 1 cot csc 1 tan sec

Kesamaan Penambahan

sin x y sin x cos y cos x sin y tan x y

cos x y cos x cos y sin x sin y

t A(1,0) P(x,y) y r = 1 x

(28)

23

Kesamaan Sudut Ganda

sin 2x 2 sin x cos x

cos 2x cos x sin x 2 cos x 1 1 2 sin x

Kesamaan Jumlah Kesamaan Setengah Sudut

sin x sin y 2 sin cos sin x

cos x cos y 2 cos cos cos x

Kesamaan Hasil Kali sin x sin y 1 2 cos x y cos x y cos x cos y 1 2 cos x y cos x y sin x cos y 1 2 sin x y sin x y 2.4 Konsep Limit Misalkan I = (a,b) adalah suatu interval terbuka di R dan c R sehingga limit fungsi f di titik c mempunyai arti bahwa fungsi f(x) terdefinisi di semua titik pada I/{c} dan di c boleh terdefinisi dan boleh juga tidak.

Konsep limit digunakan untuk menentukan nilai f(x) pada x mendekati c, tetapi bukan di c. Jika dikatakan , berarti bahwa bila x mendekati c tetapi bukan di c, maka f(x) dekat ke L. Limit Kanan lim berarti bahwa bila x dekat tetapi pada sebelah kanan c, maka f(x) adalah dekat ke L. Limit Kiri

lim berarti bahwa bila x dekat tetapi pada sebelah kiri c, maka f(x) adalah dekat ke L.

(29)

24

Teorema

Limit fungsi mendekati suatu titik dikatakan ada jika nilai limit kiri sama dengan nilai limit kanan, yaitu:

lim jika lim dan lim

Contoh 2.9:

Pada keempat grafik berikut, andaikan f x terdefinisi di semua titik pada interval I, kecuali mungkin di c. Tentukan apakah f x terdefinisi pada x c? Tentukan pula limit f x bila x mendekati c! Solusi a) f(c) = L, limit x mendekati c = L b) f(c) = tidak terdefinisi, limit x mendekati c = L c) f(c) = L, limit kiri x mendekati c = M, limit kanan x mendekati c=L d) f(c) = M, limit kiri x mendekati c = M, limit kanan x mendekati c=L f(x) a c _b L f(x) a c _b L f(x) a c _b L M f(x) a c _b L M (a) (b) (c) (d)

(30)

25

2.5 Pengkajian Mendalam tentang Limit 2.5.1 Definisi Limit

lim berarti bahwa untuk tiap 0 yang diberikan (betapapun kecilnya), terdapat 0 yang berpadanan sedemikian sehingga | | asalkan bahwa 0 | | ; yakni: 0 | | | | Contoh 2.10: Dengan menggunakan definisi limit, buktikan bahwa lim 4 5 7! Solusi

Andaikan untuk sembarang bil positif kecil , | 4 5 7| bila

| 3| .

Padahal | 4 5 7| 4| 3| , dan diinginkan | 4 5 7| . Karena diketahui | 3| , maka | 4 5 7| 4 , sehingga kita dapat memilih

Bukti

Diberikan sembarang 0, pilih . Sehingga bila | 3| , maka

| 4 5 7| 4| 3| 4

Karena | 4 5 7| bila | 3| , jadi terbukti:

lim 4 5 7

2.5.2 Definisi Limit Limit Sepihak

lim berarti bahwa untuk tiap 0, terdapat 0 yang berpadanan sedemikian sehingga:

0 | |

lim berarti bahwa untuk tiap 0, terdapat 0 yang berpadanan sedemikian sehingga:

(31)

26

2.6 Teorema Limit 2.6.1 Teorema Limit Utama Andaikan n bilangan bulat positif, k konstanta, dan f dan g adalah fungsi‐fungsi yang mempunyai limit di c. Maka: 1. lim 2. lim 3. lim lim

4. lim lim lim

5. lim lim lim

6. lim . lim . lim

7. lim lim

lim , lim 0

8. lim lim

9. lim lim lim 0

Contoh 2.11:

Dengan menggunakan teorema limit utama , tentukan lim 3 2 ! Solusi

(32)

27

2.6.2 Teorema Penggantian Jika f suatu fungsi polinom atau fungsi rasional, maka: lim asalkan dalam kasus rasional nilai penyebutnya tidak nol di c. 2.6.3 Teorema Apit Andaikan f, g, dan h adalah fungsi‐fungsi yang memenuhi untuk semua x dekat c, kecuali mungkin di c. Jika lim lim maka

lim L.

2.6.4 Limit Trigonometri

1. lim sin sin lim cos x cos

2. limsin 1 lim

sin 1

3. limtan 1 lim

tan 1 Catatan:Bila lim 0 lim 1 2.7 Kekontinuan Fungsi 2.7.1 Kekontinuan di Satu Titik Misalkan f(x) terdefinisi pada interval terbuka I dan . Fungsi f disebut kontinu di titik c bila:

lim lim lim

Ini berarti bahwa f kontinu di c bila memenuhi 3 syarat, yaitu:

1) f(c) ada atau terdefinisi 2) lim ada 3) f c lim

(33)

28

Contoh 2.12: Perhatikan keempat grafik pada contoh 2.9. Pada grafik yang manakah kurva f x kontinu di c? berikan alasan! Solusi • Grafik a kontinu • Grafik b diskontinu karena f(c) tidak terdefinisi, • Grafik c tidak kotinu karena lim tidak ada (limit kiri≠limit kanan) • Grafik d tidak kotinu karena lim tidak ada (limit kiri≠limit kanan) 2.7.2 Kekontinuan Sepihak Fungsi f disebut kontinu kiri di x=c bila lim Fungsi f disebut kontinu kanan di x=c bila lim Contoh 2.12:

Pada keempat grafik contoh 2.9, kurva manakah yang menunjukkan fungsi f kontinu sepihak? Solusi Grafik c dan d kontinu sepihak Grafik c kontinu kanan di x=c karena lim Grafik d kontinu kiri di x=c karena lim 2.7.3 Kekontinuan pada Interval

1. Fungsi f disebut kontinu pada interval terbuka (a,b) bila f kontinu di setiap titik pada (a,b). 2. Fungsi f disebut kontinu pada interval tetutup [a,b] bila f kontinu di setiap titik pada (a,b) dan kontinu kanan di a dan kontinu kiri di b.

(34)

29

2.8 Teorema Kekontinuan Fungsi 2.8.1 Teorema A (Kekontinuan pada fungsi polynomial dan fungsi rasional) 1. Suatu polinom P(c) kontinu pada setiap bilangan riil c.

2. Suatu fungsi rasional , kontinu pada setiap bilangan riil c dalam daerah asalnya, kecuali pada bilangan riil c dimana penyebutnya (polinom Q(c)) menjadi 0.

2.8.2 Teorema B (Kekontinuan pada fungsi nilai mutlak dan fungsi akar ken)

1. Fungsi nilai mutlak f(c)=|c| kontinu pada setiap bilangan riil c.

2. Jika n bilangan ganjil, fungsi akar ke n, f(c)= √ , kontinu di setiap bilangan riil c. 3. Jika n bilangan ganjil, fungsi akar ke n, f(c)= √ , kontinu di setiap bilangan riil c

positif. 2.8.3 Teorema C (Kekontinuan pada operasi fungsi) Jika f dan g kontinu di c, dan k R, maka: ; ; ; . ; ; ; 0 adalah kontinu di c. 2.8.4 Teorema D (Kekontinuan pada limit komposisi) Jika lim dan jika f kontinu di L, maka : lim lim Dengan kata lain, jika g kontinu pada c dan f kontinu pada g(c), maka kontinu pada c. 2.8.5 Teorema E ( Teorema Nilai Antara)

Jika f kontinu pada [a,b] dan jikanW sebuah bilangan antara f(a) dan f(b), maka terdapat paling tidak sebuah bilangan c di antara a dan b sedemikian sehingga f(c) = W.

(35)

30

Contoh 2.13: Tentukan kekontinuan fungsi berikut: a) pada x=2; b) 2 12 2 pada t=2; Solusi a) g(x) tidak kontinu karena g(2) tidak terdefinisi. b) h(2) = 12

lim lim lim lim 2 4 = 12

h(2) = lim = 12 Æ h(x) kontinu di x=2 2.9 Latihan Soal A. Fungsi dan Grafik 1. Mana dari yang berikut menentukan suatu fungsi f dengan rumus y f x ? a 4 b 3 4 c 3 1 d 3 2. Cari daerah asal alamiah untuk masing‐masing fungsi berikut: a √2 3 b c 4 3. Nyatakan apakah fungsi berikut merupakan fungsi genap, ganjil, atau bukan keduanya! a 4 b 3 2 1 c

(36)

31

B. Operasi fungsi

1. Jika 2 dan 2/ 1 , cari rumus untuk masing‐masing berikut dan nyatakan daerah asalnya!

a

b) /

c)

d)

2. Setelah berkecimpung dalam bisnis selama x tahun, seorang pengusaha traktor membuat 100 x 2x buah tiap tahun. Harga penjualan dalam ribuan rupiah tiap buahnya telah meningkat sesuai dengan rumus P 500 6x. Tuliskan rumus untuk pendapatan tahunan pengusaha tersebut R x setelah x tahun. C. Fungsi Trigonometri 1. Hitung tanpa memakai kalkulator: a tan b sec 2. Periksa kebenaran kesamaan berikut: a 1 sin 1 sin

b sec 1 sec 1 tan

c sec sin tan cos

D. Kajian Mendalam tentang Limit 1. Berikan suatu bukti ε , δ dari tiap fakta limit berikut: a lim 2 4 8 b lim E. Teorema Limit 1. Dengan menggunakan teorema limit, tentukan: a lim 4 3 7 2 b lim

(37)

32

F. Kekontinuan Fungsi 1. Tentukan kekontinuan fungsi berikut: a b 3, 2 1, 2

2. Fungsi berikut tidak terdefinisi di suatu titik tertentu. Bagaimana seharusnya mendefinisikannya agar kontinu pada titik itu?

a

b

(38)

BAB 3 TURUNAN 3.1 Konsep Dasar Turunan

Dalam sejarah kalkulus, terdapat dua permasalahan terapan kalkulus yang sulit untuk didefinisikan secara jelas, yaitu permasalahan garis singgung (bidang geometri) dan permasalahan kecepatan sesaat (bidang mekanik). Hal ini mengimplikasikan lahirnya konsep dasar turunan (yang berasal dari konsep limit) yang berhasil memberikan uraian matematis terbaik untuk kedua permasalahan tersebut.

3.1.1 Permasalahan Garis Singgung

Perhatikan gambar 3.1. Andaikan P adalah suatu titik tetap pada kurva dengan koordinat (c,f(c)). Garis m1 merupakan tali busur yang menghubungkan titik P dan Q1. Bila titik Q1 kita geser mendekati titik P, maka ketika mencapai posisi Q2 garis singgungnya menjadi m2. Bila titik Q terus kita geser hingga ‘berimpit’ dengan titik P, maka garis talibusur PQ akan berubah menjadi garis singgung m.

Gambar 3.1 Garis Singgung

(39)

Bab 3 Turunan|

34

Secara matematis kemiringan garis singgung yang melalui PQ (perhatikan garis singgung m2) adalah:

Jika titik Q bergeser dekat ke P, maka h 0, sehingga garis singgung m pada titik P(c,(f(c)) akan memiliki kemiringan:

lim lim

3.1.2 Permasalahan Kecepatan Sesaat

Untuk menguraikan masalah kecepatan sesaat, kita ambil sebuah contoh percobaan benda jatuh bebas di ruang hampa udara. Percobaan menyimpulkan bahwa bila benda bergerak dari posisi diam, maka posisi benda pada t detik adalah S(t) = 16t2. Dengan demikian posisi benda pada detik ke t dapat digambarkan sebagai berikut:

(Gambar 3.2: Ilustrasi Jarak Tempuh)

Kecepatan rata‐rata benda dapat dihitung dengan membagi jarak tempuh dengan selang waktu. Hal ini diilustrasikan dalam tabel 3.1: Tabel 3.1 Kecepatan rata‐rata t1 t2 s(t1) s(t2) Vrata-rata = s(t2)-s(t1)/(t2-t1) 0 1 0 16 16 1 2 16 64 48 2 3 64 144 80

(40)

Bab 3 Turunan|

35

Tabel 3.1 telah menunjukkan kecepatan rata‐rata benda jatuh pada selang waktu antara t1 dan t2 atau t1+∆t. Tetapi kita tidak dapat mengetahui kecepatan sesaat benda, misalnya pada t=2. Untuk memperkirakan nilai kecepatan sesaat pada saat t=2, dapat dilakukan dengan menghitung kecepatan rata‐rata antara pada selang waktu yang sempit di dekat t=2. Hal ini diilustrasikan dalam tabel 3.2. Tabel 3.2 Kecepatan Rata‐rata t 2 t1 t2 s(t1) s(t2) Vrata-rata = s(t2)-s(t1)/(t2-t1) 1.999 2.000 63.936 64.000 63.984 2.000 2.001 64.000 64.064 64.016

Dari tabel 3.2 dapat dilihat bahwa kecepatan sesaat pada t 2 berada di antara 63,984 dan 64,016. Untuk mendapat nilai yang persis untuk kecepatan sesaat pada t=2, selang waktu perhitungan harus dipersempit hingga ∆t 0. Dengan menggunakan konsep limit, nilai keepatan sesaat dapat dihitung sebagai berikut: ∆ ∆ ∆ ∆ (Dengan menggunakan konsep limit coba hitung kecepatan sesaat pada t=2)

Kesimpulan: Dapat dilihat bahwa permasalahan garis singgung dan kecepatan sesaat

memiliki konsep penyelesaian yang sama (Konsep Limit).

3.2 Turunan

Pada subbab sebelumnya telah diberikan pemahaman tentang konsep limit untuk turunan. Pada subbab berikutnya akan diberikan pemahaman tentang turunan. 3.2.1 Definisi Turunan Jika f adalah sebuah fungsi real dengan c є Df, dapat dikatakan bahwa turunan fungsi f adalah fungsi lain f’ (dibaca “f aksen”) yang nilainya pada sebarang bilangan c adalah: lim , asalkan nilai limit ini ada. (Ingat kembali kapan nilai limit dikatakan ada?)

(41)

Bab 3 Turunan|

36

3.2.2 Beberapa Bentuk Setara Turunan

Beberapa bentuk setara turunan diantaranya adalah:

1 Berdasarkan gambar 3.3, lim tidak ada keharusan menggunakan huruf h dalam mendefinisikan f’ c , sehingga f’ c dapat juga dituliskan sebagai:

a lim atau

b lim

2 Berdasarkan gambar 3.4, lim (Sekali lagi tidak ada keharusan menggunakan huruf tertentu). (Gambar 3.3) (Gambar 3.4) 3.2.3 Keterdiferensialan dan Kekontinuan Fungsi Teorema keterdiferensialan dan kekontinuan fungsi adalah: “Jika f’(c) ada (fungsi terdiferensialkan), maka f kontinu di c”. Teorema ini menyiratkan 2 hal: • Bila fungsi f terdiferesialkan di titik c, maka fungsi f kontinu di c. • Bila fungsi f kontinu di titik c, belum tentu fungsi f terdiferensialkan di c. Contoh 3.1

1 Apakah fungsi mutlak f x |x| kontinu dan terdiferensialkan di x 0? Beri alasan! Solusi Kontinu di x=0, tetapi tidak terdiferensialkan karena pada limit diferensial, limit kiri tidak sama limit kanan. x (c,f(c)) (x,f(x)) f(x)‐f(c) x‐c c x x (c,f(c)) (c+h,f(c+h)) f(c+h)‐f(c) h c c+h

(42)

Bab 3 Turunan|

37

2 Kurva berikut menunjukkan beberapa kemungkinan kekontinuan dan

keterdiferensialan fungsi. Apaka kurva kontinu dan terdiferensialkan di titik a,b,c, dan d?

Solusi

a Titik a tidak kontinu , oleh karena itu tidak terdiferensialkan.

b Titik b kontinu tapi tidak terdiferensialkan karena pada sudut lancip, limit kiri limit untuk pembagian delta y/delta x, sesuai definisi turunan tidak sama limit kanan.

c Titik c kontinu tapi tidak terdiferensialkan karena garis singgung tegak lurus menyebabkan nilai pembilang menurut definisi diferensial mendekati tak hingga.

d Titik d kontinu dan terdiferensialkan.

3.3 Aturan Turunan

Menghitung turunan suatu fungsi menurut definisi turunan (seperti yang dijelaskan pada subbab 3.1.3 poin A ) akan memakan waktu dan membosankan. Dengan adanya teorema aturan turunan, kita dapat menentukan turunan suatu fungsi dengan lebih cepat dan mudah. Berikut adalah aturan‐aturan turunan yang dituliskan dalam bentuk penulisan operator D. 1. Aturan Fungsi Konstanta , 0 ; dimana k adalah suatu konstanta 2. Aturan Fungsi Identitas , 1 3. Aturan Pangkat , , 4. D sebagai sebuah operator linear a b c d

(43)

Bab 3 Turunan|

38

5. Aturan Penjumlahan dan Pengurangan 6. Aturan Perkalian 7. Aturan Pembagian 3.4 Aturan Turunan Fungsi Trigonometri Berikut ini beberapa aturan penting berkaitan dengan turunan fungsi trigonometri. 1. D sin x cos x 2. D cos x sin x 3. D tan x sec x 4. D csc x csc x cot x 5. D sec x sec x tan x 6. D cot x csc x

3.5 Aturan Rantai

Andaikan dan menentukan fungsi komposit

, jika g terdiferensialkan di x dan f terdiferensialkan di u = g(x), maka fog

terdiferensialkan di x dan Dalam aturan rantai dapat dituliskan D y D y . D u Aturan rantai berguna untuk mencari turunan fungsi komposisi. Agar lebih mudah memahami aturan rantai, perhatikan contoh berikut: Contoh 3.2 Jika 2 4 1 , tentukan !

(44)

Bab 3 Turunan|

39

Solusi

Andaikan y adalah sebuah fungsi komposisi dimana y=f(u) = u60_{, dan}

2 4 1. Jadi, . . 2 4 1 60 4 4 60 2 4 1 4 4 Aturan Rantai Bersusun Andaikan y=f(u) dan u=g(v) dan v=h(x), maka . . Contoh 3.3 jika 4 , tentukan ! Solusi

Andaikan ; sin ; dan 4 , sehingga

. . . sin . 4 3 – cos 4 12 cos 12 cos 12 4 cos 4 3.6 Penulisan Leibniz

Penulisan Leibniz menggunakan notasi dy/dx untuk menyatakan turunan. Leibniz menyebut dy/dx sebagai suatu hasil bagi dari dua bilangan yang sangat kecil, yakni: lim ∆ ∆ ∆ ∆lim ∆ ∆ Penulisan Leibniz juga berlaku pada aturan rantai. Sebagai contoh, andaikan y = f(u) dan u = g(x), maka:

(45)

Bab 3 Turunan|

40

Contoh 3.4 1 Tentukan dy/dx jika 3 7 ! Solusi 3 7 3 7 3 3 2 7 1 3 6 7 2 Tentukan dy/dx jika x 2x ! Solusi

Misalkan u x 2x , maka y u dan .

. 2

12 3 2

12 2 3 2

3.7 Turunan Tingkat Tinggi

Turunan sebuah fungsi dapat dituliskan dalam beberapa bentuk seperti yang dicontohkan pada Tabel 3.3. Misalkan sebuah fungsi y=f(x), maka turunan pertamanya adalah . Jika turunan pertama ini diturunkan lagi,

maka akan menghasilkan turunan kedua, yaitu

. Notasi yang sama diberikan untuk turunan ketiga, keempat, dst.

Tabel 3.3 Bentuk Penulisan Turunan

Derivatif Penulisan f' Penulisan y' Penulisan Operator D Penulisan Leibniz

Pertama f'(x) y'

Kedua f''(x) y''

Kedua f'’'(x) y''’

(46)

Bab 3 Turunan|

41

Salah satu penggunaan turunan tingkat tinggi adalah pada masalah gerak partikel. Bila S(t) merupakan posis sebuah partikel, maka kecepatan partikel adalah v(t) = S’(t). Sedangkan percepatan gerak partikel adalah a(t) = v’(t) = S”(t).

3.8 Pendiferensialan Implisit

Sebuah fungsi dikatakan berbentuk implisit bila berbentuk F(x,y) = 0. Pada bentuk ini, variabel x dan y tercampur dalam suatu ekspresi. Pendiferensialan implisit adalah mencari dy/dx tanpa terlebih dahulu mengubah bentuk persamaan menjadi y = f(x). Prinsip pendiferensialan implisit adalah sebagai berikut: untuk suatu bentuk fungsi implisit F(x,y) = 0. Untuk mencari dy/dx, kumpulkan semua variable y di ruas sebelah kiri dan variabel x di ruas sebelah kanan. Kemudian turunkan kedua ruas terhadap x dengan mengingat variabel y di sebelah kiri merupakan fungsi dari x. Contoh 3.5

Jika y3 _7y‐x3 _{0, tentukan garis singgung di titik 2,1 !} Solusi 7 3 7 3 3 7 3 3 3 7 3 2 3 1 7 12 10 6 5 3.9 Laju yang Berkaitan

Berikut ini adalah prosedur sistematis untuk menyelesaikan permasalahan laju‐laju yang berkaitan:

1. Andaikan t menyatakan waktu. Gambarlah diagram yang berlaku untuk semua t>0. Identifikasi besaran‐besaran yang nilainya tidak berubah (konstanta) bila t

(47)

Bab 3 Turunan|

42

berubah terhadap waktu), dan tandai garis‐garis pada gambar dengan peubah yang sesuai. 2. Nyatakan apa yang diketahui dan informasi yang diinginkan tentang peubah‐ peubah. Informasi ini akan berbentuk turunan‐turunan terhadap t. 3. Tulislah sebuah persamaan yang menghubungkan peubah‐peubah yang sahih untuk semua t>0, bukan hanya pada beberapa saat tertentu. 4. Diferensialkan persamaan yang ditemukan dalam langkah 3 secara implisit terhadap t. Persamaan yang dihasilkan memuat turunan‐turunan terhadap t dan sahih untuk semua t>0. 5. Gantikan persamaan yang ditemukan dalam langkah 4 untuk semua data yang sahih pada saat tertentu untuk mana jawaban atas masalah yang diisyaratkan. Selesaikan turunan yang diinginkan. Contoh 3.6

Sebuah balon dilepas pada jarak 150 kaki dari seorang pengamat yang berdiri di tanah. Jika balom maik secara lurus ke atas dengan laju 8 kaki/detik, seberapa cepat jarak antara pengamat dan balon bertambah pada waktu balon pada ketinggian 50 kaki? Solusi Penyelesaian masalah menurut prosedur sistematis: 1.

Andaikan t menyatakan detik setelah balon dilepas, h menyatakan ketinggian balon, dan s jarak balon dari pengamat. Peubah h dan s keduanya bergantung pada t. tetapi jarak antara pengamat dan titik pelepasan konstan dan tidak berubah dengan bertambahnya t. kita tekankan bahwa gambar ini sahih untuk semua t 0.

2. Diketahui laju balon naik ke atas dh/dt 8 kaki/detik.

Ditanya laju perubahan jarak antara pengamat dan balon ds/dt pada saat h 50 kaki. 3. Peubah s dan h berubah tehadap waktu mereka adalah fungsi implisit dari t , tetapi selalu dihubungkan dengan persamaan Pythagoras: s 150 h

(48)

Matematika Dasar I/FST/UNJA/2013 Bab 3 Turunan|

43

s h 150 4. Jika persamaan Pythagoras di atas kita diferensialkan secara implisit terhadap t dan memakai aturan rantai, maka akan diperoleh: 2 2 0 5. Bila h 50 kaki, maka berdasarkan persamaan Pythagoras pada poin 3, s adalah 50 150 50√10 Dengan mengguanakn persamaan turunan pada poin 4, maka diperoleh: 50√10 50 8 400 50√10 8 √10 2,53 / . 3.10 Diferensial dan Hampiran 3.10.1 Turunan dan Diferensial

Turunan adalah hasil bagi dua diferensial, biasa dilambangkan dengan f’(x) atau dy/dx. Andaikan y=f(x), maka turunan f yaitu: lim ∆ ∆ ∆ lim ∆ ∆ ∆

Andaikan bahwa dx adalah diferensial dari peubah bebas x yang menyatakan pertambahan sebarang dari x. Maka diferensial yang bersesuaian dengan dy dari peubah tak bebas y didefinisikan oleh: Dari definisi di atas dapat diartikan bahwa diferensial dari peubah tak bebas adalah hasil kali turunan dengan diferensial peubah bebas. Diferensial biasa dilambangkan dengan dy.

Tabel 3.4 berikut menunjukkan perbandingan beberapa aturan turunan dan diferensial. Ingat kembali bahwa diferensial diperoleh dengan mengalikan f’(x) dengan dx.

(49)

Bab 3 Turunan|

44

Tabel 3.4 Perbandingan aturan turunan dan aturan diferensial Aturan Turunan Aturan Diferensial 1. 0 2. 3. 4. 1. 0 2. 3. 4. 3.10.2 Hampiran Andaikan y=f(x) seperti gambar 3.5. Jika x diberi tambahan ∆x, maka y menerima tambahan yang berpadanan ∆y yang dapat dihampiri oleh dy. Gambar 3.5 Ilustrasi hampiran Dengan demikian f(x+∆x) dapat dihampiri oleh: ∆ ∆ Contoh 3.7: Dengan menggunakan metode hampiran, hitung √4,6 ! Solusi Andaikan fungsi akar adalah √ , maka _√ . Kita mengetahui bahwa nilai √4,6 berada di antara √4 dan √9. Jika kita ambil nilai x=4 dan ∆x=0,6; Menurut rumus hampiran: 4,6 4 0,6 4 √4 2 Untuk menghitung dy, ∆ y=f(x) f(x) f(x+∆x) dy ∆y x y

(50)

45

1 2√ ∆ 1 2√4 0,6 0.15 ∆ 1 2√ ∆ 1 2√4 0,6 0.15 Sehingga 4,6 2 2 0,15 2,15 3.10.3 Penaksiran Galat (Error) Penaksiran galat merupakan masalah yang khas dalam sains. Prosedur baku untuk menaksir galat adalah dengan memakai sarana diferensial. Untuk memahami cara penaksiran galat, perhatikan contoh berikut.

Contoh 3.8

Rusuk kubus memiliki panjang 11,4 cm dengan kemungkinan galat panjang rusuk 0,05 cm. HIiung volume kubus dan berikan suatu taksiran galat untuk nilai volume tersebut! Solusi Volume kubus V yang panjang rusuknya x adalah . Jadi 3 . Jika x = 11,4 cm dan dx = 0,015 cm, maka 11,4 1482 dan 3 11,4 0,015 19

Dengan demikian volume kubus adalah 1482 19 dengan taksiran galat volume adalah 19 . 3.11 Soal Latihan A. Konsep Dasar Turunan 1. Tentukan kemiringan garis singgung kurva y = 2 / (x‐2) pada titik (0,‐1). Tuliskan juga persamaan garis singgungnya! 2. Sebuah benda menjelajahi garis sehingga posisi s nya adalah 2 2 meter setelah t detik. Tentukan: a) Kecepatan rata‐rata selang 2 ≤ t ≤ 3? b) Kecepatan sesaat pada t=2 detik?

(51)

Bab 3 Turunan|

46

B. Turunan 1. Dengan menggunakan konsep limit, tentukan turunan dari: a) b) √ 4 C. Aturan Turunan dan Turunan fungsi Trigonometri 1. Tentukan turunan dari: a) b)

2. Tunjukkan kurva y √2 sin x dan y √2 cos x berpotongan tegak lurus pada 0≤x ≤π/2!(dua kurva berpotongan tegak lurus bila m1/m2 = ‐1) 3. Pada saat t detik, pusat sebuah pelampung gabus berada sejauh 2 sin t sentimeter di atas (atau di bawah) permukaan air. Berapa kecepatan pelampung pada saat t = 0, π/2, dan π? D. Aturan Rantai 1. Tentukan Dxy bila: a) 3 5 11 b)

2. Hitung Dt sin t · tan t 1

E. Turunan Tingkat Tinggi 1. Sebuah pelek berpusat di titik asal dan berjari‐jari 10 sentimeter berputar berlawanan arah perputaran jarum jam pada laju 4 putaran/detik. Sebuah titik P pada pelek berada di 10,0 pada t=0. a) Berapa koordinat P pada saat t detik? b) Pada laju berapa P naik (atau turun) pada saat t=1? 2. Sebuah benda dilempar langsung ke atas pada ketinggian s=‐16t2 + 48t + 256 kaki setelah t detik. a) Berapa kecepatan awalnya? b) Kapan ia mencapai ketinggian maksimum? c) Berapa ketinggian maksimumnya? d) Kapan ia membentur tanah?

(52)

47

e) Dengan laju berapa ia membentur tanah? F. Pendiferensialan Implisit 1. Cari persamaan garis normal (garis tegak lurus terhadap garis singgung) pada kurva 8(x2+y2)2 = 100(x2‐y2) di 3,1 . (Gunakan metode pendiferensialan implisit). G. Laju yang Berkaitan 1. Rusuk kubus yang berubah bertambah panjang dengan laju 3cm/detik. Berapa kecepatan pertambahan volume kubus pada saat panjang rusuk 10 cm? 2. Sebuah cakram baja memuai selama dipanaskan. Jika jari‐jarinya bertambah dengan laju 0,02 cm/detik, seberapa cepat luas salah satu mukanya bertambah pada saat jari‐jarinya adalah 8,1 cm? H. Diferensial dan Hampiran 1. Hitung √402 dan √26,91 dengan metode hampiran! 2. Hampiri nilai volume material dalam tempurung bola yang jari‐jari dalamnya 5 cm dan jari‐jari luarnya 5,125cm. 3. Garis tengah sebuah bola diukur sebagai 20 0,1 cm. hitung volumenya dengan suatu taksiran untuk galat.

(53)

BAB 4 APLIKASI TURUNAN

Konsep turunan dapat digunakan sebagai alat bantu untuk menyelesaikan banyak masalah, seperti: menyelesaikan masalah maksimum dan minimum serta membuat grafik fungsi secara canggih. Untuk dapat membuat grafik suatu fungsi secara canggih, perlu ditentukan kemonotonan, kecekungan dan garis asimtotik fungsi tersebut. Kemonotonan suatu fungsi dapat ditentukan dari turunan pertama fungsi tersebut, sedangkan kecekungan dapat ditentukan dari turunan keduanya.

Selanjutnya pada bab ini akan dibahas aplikasi yang dapat diterapkan menggunakan turunan.

4.1 Maksimum dan Minimum

Misalkan diberikan suatu fungsi dan daerah definisi . Maka akan timbul pertanyaan apakah memiliki nilai maksimum atau minimum pada ? Jika memiliki nilai maksimum atau minimum, dimana terjadinya? Jika ada, berapa nilainya? Pertanyaan ini adalah tujuan utama dari sub bab ini. Perhatikan gambar 4.1 berikut. Apakah maksimum? Apakah minimum?

Gambar 4.1 Kurva maksimum minimum

(54)

Bab 4 Aplikasi Turunan|

49

Teorema 1 [Definisi]

Misalkan , daerah definisi dari fungsi , memuat .

1. dikatakan mencapai maksimum di bila . disebut nilai maksimum;

2. dikatakan mencapai minimum di bila . disebut nilai minimum;

3. disebut nilai ekstrim dari pada jika merupakan nilai maksimum\minimum. Titik dimana mencapai maksimum\minimum disebut titik ekstrim;

4. fungsi yang akan dimaksimumkan atau diminimumkan disebut fungsi objektif.

Teorema 2 [Eksistensi MaksimumMinimum]

Jika kontinu dan berupa interval tutup , , maka memiliki titik minimum dan maksimum.

Teorema 3 [Titik Kritis]

Misalkan terdefinisikan pada interval yang memuat titik . Jika merupakan nilai ekstrim, maka merupakan titik kritis; yaitu, merupakan salah satu dari: 1. Titik stasioner (titik dengan sifat 0); 2. Titik ujung ; atau 3. Titik singular (titik di mana tidak mempunyai turunan). Contoh 4.1: Tentukan nilai maksmimum dan minimum dari pada 2,2 . Solusi Langkah 1 Tentukan titik kritis dari pada 2,2 . 1. Cek titik stasioner

3 , yang terdefinisikan pada 2,2 dan 0 hanya jika 0. Jadi, titik stasionernya adalah 0;

(55)

Bab 4 Aplikasi Turunan|

50

2. Cek titik ujung Titik ujung dari interval yang diberikan adalah 2 dan 2. 3. Cek titik singulir Karena memiliki turunan, maka titik singulir tidak ada. Jadi, titik kritis nya: 2, 0, 2. Langkah 2 Evalusi tiap titik kritis

2 8, 0 0, dan 2 8. Diperoleh nilai maksimum dari pada 2,2 adalah 8 (dicapai saat 2), sedangkan nilai minimumnya adalah 8 (dicapai saat 2).

4.2 Kemonotonan Fungsi dan Titik Ekstrim

4.2.1 Kemonotonan Fungsi

Misalkan terdefinisi pada interval (buka, tutup, atau lainnya).

1. disebut monoton naik pada bila: 2. disebut monoton turun pada bila: 3. disebut monoton tak turun pada bila: 4. f disebut monoton tak naik pada I bila: x x f x f x Ilustrasi fungsi monoton dapat dilihat pada Gambar 4.2 berikut: Gambar 4.2 Ilustrasi fungsi monoton