VOLUME 6, NO. 1 DECEMBER 2016 ISSN 2089-4716
Southeast Asian Ministers of Education Organization (SEAMEO)
Regional Centre for Quality Improvement of Teachers and Education Personnel (QITEP) in Mathematics Yogyakarta Indonesia
Southeast Asian Mathematics Education Journal – SEAMEJ Description of South East Asian Mathematics Education Journal
(SEAMEJ)
Southeast Asia Mathematics Education Journal (SEAMEJ) is an academic journal devoted to reflect a variety of research ideas and methods in the field of mathematics education. SEAMEJ aims to stimulate discussions at all levels of mathematics education through significant and innovative research studies. The Journal welcomes articles highlighting empirical as well as theoretical research studies, which have a perspective wider than local or national interest. All contributions are peer reviewed.
SEAMEO QITEP in Mathematics aims to publish SEAMEJ twice a year, in June and December.
Contact Information: Professor Subanar, PhD.
The Director of SEAMEO Regional Centre for QITEP In Mathematics
Jl. Kaliurang Km. 6, Sambisari, Condongcatur, Depok Sleman, Yogyakarta, Indonesia.
Phone: +62(274)889955 Fax: +62(274)887222 Email: [email protected]
v External Advisory Panel
Professor Mohan Chinnappan University of South Australia
Professor Lim Chap Sam Universiti Sains Malaysia
Associate Professor Cathy Attard Western Sydney University
Dr. S. Kanageswari a/p Suppiah Shanmugam Universitas Utara Malaysia
Dr. Ida Karnasih Universitas Muslim Nusantara Al-Washiliyah
Chair
Subanar SEAMEO Regional Centre for QITEP in Mathematics
Chief Editor
Allan Leslie White Former lecturer at University of Western Sydney Australia
Editorial Board Members
Subanar SEAMEO Regional Centre for QITEP in Mathematics
Wahyudi SEAMEO Regional Centre for QITEP in Mathematics
Fadjar Shadiq SEAMEO Regional Centre for QITEP in Mathematics
Joel Hohn SEAMEO Regional Centre for QITEP in Mathematics
Uki Rahmawati SEAMEO Regional Centre for QITEP in Mathematics
Rachma Noviani SEAMEO Regional Centre for QITEP in Mathematics
Fina Hanifa Hidayati SEAMEO Regional Centre for QITEP in Mathematics
Manuscript Editors
Rizki Nurmaya Oktarina SEAMEO Regional Centre for QITEP in Mathematics
Wahid Yunianto SEAMEO Regional Centre for QITEP in Mathematics
Administrative Assistants
Tika Setyawati SEAMEO Regional Centre for QITEP in Mathematics
Rini Handayani SEAMEO Regional Centre for QITEP in Mathematics
Cover Design & Typesetting
Joko Setiyono SEAMEO Regional Centre for QITEP in Mathematics
Suhananto SEAMEO Regional Centre for QITEP in Mathematics
Denny Saputra SEAMEO Regional Centre for QITEP in Mathematics
Febriarto Cahyo Nugroho SEAMEO Regional Centre for QITEP in Mathematics
Allan Leslie White & Wahyudi 1-2 Editorial
Fadjar Shadiq 3-17 How Can SEAMEO QITEP in Mathematics Help Indonesian Mathematics Teachers to Help Their Students to be Independent Learners in the Case of Disaster Risk Reduction (DRR)?
Madihah Khalid,
Dk Haslinah Pg. Haji Ali 19-31 Inculcating Tsunami Awareness in a Mathematics Lesson: Improving Students’ Collaborative Problem Solving via Lesson Study
Barry Kissane 33-55 The Scientific Calculator and School Mathematics
Catherine Attard 57-67 Is Current Research Assisting the
Implementation of Contemporary ICT in the Primary Mathematics Classroom? Allan Leslie White 69-79 Impact of Brain Research upon School
Mathematics for the 21st Century
CONTENTS
1
Editorial
The South East Asian Mathematics Education Journal (SEAMEJ) is an academic journal devoted to publishing a variety of research studies and theoretical papers in the field of mathematics education. SEAMEJ seeks to stimulate discussion at all levels of the mathematics education community. SEAMEJ aims to eventually publish an edition twice a year, in June and December.
SEAMEJ is supported by the Southeast Asian Ministers of Education Organization (SEAMEO), Centre for Quality Improvement of Teachers and Education Personnel (QITEP) in Mathematics situated in Yogyakarta Indonesia. Launched on July 13, 2009, there are now three QITEP SEAMEO Centres for Quality Improvement of Teachers and Education Personnel in Indonesia. One centre is in Mathematics (Yogyakarta), one in Science (Bandung) and one in Languages (Jakarta).
In this issue we present papers that were subjected to a blind review process. This collection of papers reflects a limited thematic approach using the context of Disaster Risk Reduction involving earthquakes, landslides, tsunamis etc. This is an interesting development and its progress will be closely monitored.
Attempts at teaching mathematics via a thematic approach are claimed to be good for relating mathematics to real-life situations. However, research shows that large scale attempts at teaching mathematics thematically have not been very successful due to teacher perceived obstacles involving instructional, curricula and organisational factors. Teachers are worried that it is difficult to follow the set syllabus and that more time is spent teaching the students about the thematic context than the mathematics thus reducing precious available mathematics time. The Australian state of New South Wales in the 1990’s via the Education Department introduced one of three years 9 and 10 secondary school mathematics courses using a thematic structure. The course consisted of eight themes and ten topics. The themes included: (a) Mathematics of our Environment, (b) Mathematics involving Food, (c) Mathematics in the Workplace, (d) Building Design, (e) Mathematics involving Sports, (e) Mathematics in the Community, (f) Handcrafts, and (g) Tourism and Hospitality. It was not successful. In general, teachers opted for instructional styles that used applications of mathematics rather than using a theme as the context for overarching the development of the lesson. Teachers tended to shift among different teaching styles depending on the classroom context and would revert to teaching mathematics via topics rather than in themes. The Realistic Mathematics movement appears to be more successful at giving relevance to mathematics in context without sharing the problems of the thematic movement.
The rate of change in the field of technology is breathtaking and this includes the humble scientific calculator. The early models attracted a good deal of criticism with claims of not being suitable for schools or over fears students would become mere button pushers. It is time to review these early beliefs and the next paper argues that calculators can play a valuable role in supporting students’ learning last year the OECD (2015) issued a report that stated:
2
The author of this paper provides such a strategy through a model for the educational use of calculators consisting of four key components: representation, computation, exploration and affirmation. This paper should convince many readers that it is time to reconsider the place of scientific calculators within the classroom.
This is followed by a paper that discusses TPACK and SAMR which provide frameworks for integrating technology within the mathematics teaching and learning process with a particular focus upon Tablet technology.
The final paper highlights some of the implications of brain research for mathematics teaching and learning and has a particular focus upon the importance of understanding, compression and insight.
Since our first journal was distributed in 2011 we have continued to refine our processes although we have yet to reach perfection and we apologise if we have made errors or omissions. We always welcome feedback and suggestions for improvement, but most of all, we welcome paper contributions.
This Journal seeks articles highlighting empirical as well as theoretical research studies, particularly those that have a perspective wider than local or national interests. All contributions to SEAMEJ will be peer reviewed and we are indebted to those on the External Advisory Panel for their support.
Wahyudi and Allan L White
3
How Can SEAMEO QITEP in Mathematics Help Indonesian Mathematics
Teachers to Help Their Students to be Independent Learners in the Case of
Disaster Risk Reduction (DRR)?
Fadjar Shadiq
SEAMEO QITEP in Mathematics, Yogyakarta, Indonesia. ([email protected])
There are a number of disasters threats in Indonesia, such as earthquakes, tsunamis, volcanic eruptions, fires, landslides and floods. When a natural hazard strikes, children are among the most vulnerable population group, especially those attending school in the times of disaster. What people know is more important than what they have when it comes to saving lives and reducing loss. It implies that students should also learn DRR during the teaching and learning of mathematics. This paper reports on a number of studies conducted by SEAMEO QITEP across the years 2012 – 2015 that attempted to improve both teachers and students learning outcomes.
Keywords:Disaster awareness, meaningful learning, independent learners, problem solving approach, Lesson Study.
Introduction
On one side, there are a number of disasters threats in Indonesia, such as earthquakes,
tsunamis, volcanic eruptions, fires, landslides, typhoons, and floods. Those disasters could be
natural or as a result of man-made action. UNESCO (2010) has already differentiated between
‘hazards’ and ‘disasters’. Hazards are natural while disasters are not. Hazards such as floods,
earthquakes, and tsunamis become disasters only when society lacks the ability to cope with
them. The most important thing is how to educate people in such a way that the hazards which
are natural things do not become disasters. When a natural hazard strikes, children are among
the most vulnerable population group, especially those attending school in times of disaster.
UNESCO ISDR (2007) states that disasters such as the October 2005 earthquake in Pakistan,
where over 16,000 children died in schools that collapsed, or the recent mudslide on Leyte
Island in the Philippines, where more than 200 school children were buried alive, are just a few
tragic examples of why more needs to be done to protect our children before disasters strikes.
In Indonesia and in other countries, the lack of knowledge on disaster especially the tsunami
phenomena leads to a tremendous number of victims. People living along the coastline failed
to recognize that the receding of water quickly and unexpectedly from the coast may be the
sign of tsunami will be coming. People followed it instead of running toward higher ground
4
On another side, the ability to think and to reason is very important to everyone.
Mathematics could be seen as the language that describes patterns (De Lange, 2004; NCTM,
1999). During the mathematics teaching and learning process, students can learn to think, to
solve problem, to reason, and to communicate. Therefore, Marquis de Condorcet as quoted by
Fitzgerald and James (2007, p. ix) stated: “Mathematics … is the best training for our abilities,
as it develops both the power and the precision of our thinking.” In addition, the National
Research Council from USA (NRC, 1989, p. 1), reminds us 24 years ago that: “Communication
has created a world economy in which working smarter is more important than merely working
harder. … We need workers who can absorb new ideas, to adapt to change, to cope with ambiguity, to perceive patterns, and to solve unconventional problems.” These two statements
show the importance and relevancy of mathematics to enhance the ability of our students
thinking.
In addition, Isoda and Katagiri (2012) stated that the aim of education as follows.
“ … To develop qualifications and competencies in each individual school child, including the ability to find issues by oneself, to learn by oneself, to think by oneself, to make decisions independently and to act. So that each child or student can solve problems more skilfully, regardless of how society might change in the future.” (p. 31).
However, many mathematics educators focus on skills and offer mostly procedural
practice. This form of instruction focuses on a lot of memorization and skill-and-drill practice.
Teachers offer lecture type instruction and then students complete the pages in the texts during
class time. The conclusions of the Indonesian research conducted by the writer (Shadiq, 2010,
pp. 56-57) stated that most teachers of mathematics in their schools use or implement the
traditional ways during the learning and teaching process of mathematics. They still use the
paradigm of transferring knowledge from teachers’ brain to students’ brain.
An alternative type of mathematics program leans more toward exploration of
mathematical concepts through conceptual investigation. Students use concrete materials, such
as manipulatives both concrete and virtual, and participate in experiments and kinaesthetic
demonstrations that exhibit mathematical concepts. This type of mathematics program matches
constructivism, the current issue in mathematics education. Therefore Haylock and Thangata
5
the teacher’s teaching. In Japan, Isoda and Katagiri (2012, p.1) stated that a Problem Solving
Approach (PSA) can be implemented to help learner to develop mathematical thinking.
In Indonesia, the objectives of the compulsory mathematics program are to help and
facilitate learners’ positive attitudes and personal qualities needed to succeed in life, and
develop the knowledge and basic mathematics skills in communicating, arguing, and problem
solving through using mathematics needed in their daily life and further education. However
the results of TIMSS 2007 (Kemdikbud, 2012b, p.14) shows that only 5% of Indonesian
students could work on the problems in the high category and advance level [requires
reasoning], while 71% of Korean students could. In addition to Indonesia, only 78% of students
could work on the problems in the lower categories that require only rote learning, so it is
necessary to develop a curriculum that requires the effort to strengthen the reasoning ability.
Kemdikbud (2012a, p. 11) also stated the need for change in the process of learning from
teacher-centred to process-centred to learner-centred. It requires a change of the textbook which
contains only the subject matter to the textbook that includes the learning materials, assessment
systems and competencies expected. At the elementary level, the Government also asks
teachers to implement an integrative thematic approach to all subjects in Grade 1 to Grade 6
within 30% of chosen elementary schools in Indonesia.
However, to change and to improve the quality of teaching and learning processes from
a “typical” mathematics classroom to the new one that is more innovative is not easy. The
factors that should be taken into account are teachers’ views and beliefs. In other words, the
process of teaching and learning of mathematics in the classroom will be largely determined
by teachers’ view and beliefs about mathematics and mathematics education. Frei (2008, p. 8),
for example, stated that often teachers feel comfortable teaching the way they were taught. It is
what they remember and what they know, so it becomes the way they teach, regardless of
whether they believe it is the correct way to teach.
To change and improve the quality of teaching and learning process from a “typical” or
“traditional” mathematics classroom to the new one that is more innovative is not easy.
6
Mathematics teachers need concrete examples that can be used and implemented in
mathematics classes. Teachers are more likely to implement the new approaches in their own
classes if they have experienced it in their own learning experiences. Therefore the two
questions that can arise:
First, in the case of DRR, what should be done to find the ‘best way’ in helping and
facilitating students to learn mathematics meaningfully and joyfully, to learn to think and to
find issues by oneself, to learn by oneself, to think by oneself, to make decisions independently
and to act, so that each child or student can solve problems more skilfully, regardless of how
society might change in the future?
Second, in the case of DRR, what should be done to find the ‘best way’ in helping and
facilitating mathematics teachers in such a way that they can change their teaching and learning
processes such that they can help the learners to learn mathematics meaningfully, to learn to
think and be independent learners?
Literature Review
This literature review will briefly discuss several terms which will be implemented in
this study regarding meaningful learning, independent learners, problem solving approach
(PSA) and Lesson Study (LS).
Meaningful Learning
If learners are given three numbers: (1) 37.131.512, (2) 31.117.532, and (3) 23.571.113.
The questions that arise are: (a) Which number is the easiest to repeat? Number (1), number (2)
or number (3)? Why? (b) Based on the results, what does it mean for how to help our children
to learn mathematics easily?
The third number (23.571.113) is the easiest to learn only if the learner is successfully
able to relate to the first six prime numbers (2, 3, 5, 7, 11, 13) which has been learnt by and
known to them. In other words, a student has to learn successfully the first six prime numbers
(2, 3, 5, 7, 11, 13) before s/he can repeat the third number (23.571.113). So the task of the
7
(2, 3, 5, 7, 11, 13) and the third number (23.571.113). The second number (31.117.532) is the
second easiest to learn only if the learner successfully relates it to the third number (23.571.113)
in which the second number can be found from the third number (31.117.532) in reverse order.
Otherwise, the learner must memorize or implement a rote strategy which is difficult for the
learner. In addition students will be faced with the difficulty to memorise the third and the
second numbers if they do not have the pre-existing or prior knowledge. The first number is
the most difficult number to memorise because students do not have the pre-existing knowledge
to be related. The conclusion is, that new knowledge can be easily understood if it can be related
to the pre-existing knowledge and has been learnt by the student. The learning principle stated
by NCTM (1999) is that students must learn mathematics with understanding, actively building
new knowledge from experience and prior knowledge. Therefore Ausubel (in Orton, 1987,
p.34) states “If I had to reduce all of educational psychology to just one principle, I would say
this: The most important single factor influencing learning is what the learner already knows.
Ascertain this and teach him accordingly.” The question that arises is: How to help and facilitate
students to learn mathematics meaningfully and with understanding?
Joyful Learning
Based on brain theory, Pranoto (2011) stated that every brain consists of three main
parts: cortex, mid brain, and lower brain. The cortex always searches for novelty, the mid brain
always searches for pleasure, and the lower brain will always search for safe or non-threatening
situations. This theory implies that we have to design the activities using varied rules and
contents. Students must always find the activities new. One may also include the possibility for
the students themselves to create the newer rules. This will increase the feeling of ownership
of the students. Based on the second brain part, as our brain naturally always searches for
challenge, however, the challenge we like to do is not the one that is too high. We like to do
challenges that have a probability of success. Our brain will not like to do tasks that are too
hard and that we will feel a failure. Therefore, based on this principle, the differentiation based
on readiness makes sense. It is parallel to brain theory. Based on the brain theory, this primitive
part of our brain mostly regulates our routine tasks. Our lower brain always would like to make
8
some tasks if they show some threats. This means that if we want to satisfy the lower brain, the
activities must always involve some kind of surprise, luck, joy, and celebration. Every student
should also be able to contribute. Some traditional games like bingo or snake-ladder are
appropriate and easy to modify for various mathematics contents. Activities that involve
problem solving are also good. Our brains naturally are designed for solving problems.
However, we have to apply the same three principles. They must satisfy our three brain parts.
Thus, they must consist of novelty, generate pleasure, and provide safe environment. The
question that arises is: What should be done to help students to learn joyfully?
Thinking Skills
Bastow, Hughes, Kissane, and Mortlock (1986, p.1) stated: “Among many mathematics
educators there is a growing recognition of the need in school mathematics to increase the
emphasis placed on process objectives.” Regarding the process objectives, as an example,
Gauss (1777-1855) is known widely as one of the five best mathematicians around the world.
When he was 10 years old, his teacher asked him and his friends to find the result of: 1 + 2 + 3
+ 4 + … + 98 + 99 + 100. Gauss found the structure in his method as shown in this diagram.
Gauss found that: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, . . . .
Based on the data above, little Gauss concluded that:
a) Every number has a pair with the sum of every pair was 101.
b) There were 100 numbers to be added, so this implies that there were 50 pairs altogether.
c) So, the result of addition was 50 × 101 = 5050.
9
a. The beautifulness of pattern and thinking that Gauss discovered and performed.
b. The importance of finding the structure.
c. The importance of thinking and reasoning.
d. Learning mathematics means to help anyone to think of the best way of counting (better
and easier).
Therefore, Marquis de Condorcet (in Fitzgerald and James, 2007, p. ix) stated:
“Mathematics … is the best training for our abilities, as it develops both the power and the precision of our thinking.” Students should be facilitated to achieve their potential through the
teaching and learning of mathematics. In the information technology era, the ability to think
logically, creatively and critically is very important. Regarding the importance of thinking
abilities during the teaching and learning process, the National Research Council from USA
(NRC, 1989, p.1) states “[the economy] requires workers who are mentally fit – workers who
are prepared to absorb new ideas, to adapt to change, to cope with ambiguity, to perceive
patterns, and to solve unconventional problems.” The question that arises is: What should be
done and how to help and facilitate students to learn to think?
Independent Learners
The ultimate goal of schooling is to help and facilitate children to be independent in
their real life situation. In the introduction, the importance of helping learners to be independent
in Japan was highlighted (Isoda & Katagiri, 2012). Again, the question that arises is: “What
should be done and how to help and facilitate students to be independent after finishing their
study?”
Problem Solving Approach (PSA)
Isoda and Nakamura (2011, p. 10) proposed a Problem Solving Approach which
consists of 5 steps as follow: (1) posing problem, (2) estimating the ways of solutions (planning
and predicting the solution), (3) independent solving, (4) explanation and comparison and (5)
integration and application. The problems or activity on the first step can help and facilitate
students to think, enabling them to apply and extend what they have learned to new problem
situations. Make sure that the problem on the first step can be solved by previous knowledge
10
any ideas from the children and allow them to talk on their ideas if it has originated from what
they have already learned. On the second and third steps, students learn to formulate problems
on their own, estimating the ways of finding solutions and then solving it, finally they check
the results. Once again problems become the heart of the lesson. Therefore, those tasks,
activities, or problems should be well prepared. Based on the outline above, the PSA can
facilitate students to find issues by oneself, to learn by oneself, to think by oneself, to make
decisions independently and to act by oneself. It is clear that those tasks, activities, or problems
become important to facilitate students to be independent learners.
As stated in the introduction, traditional mathematics educators focus on skills and offer
mostly procedural practice while instead mathematics programs should have more exploration
of mathematical concepts through conceptual investigation, where the teacher focuses attention
on the pupil’s learning. The task of change is not easy. The PSA can help the learner to learn
mathematics: (1) meaningfully and with understanding, (2) joyfully, (3) to think and (4) to be
independent learners.
Lesson Study
Stacey, Tall, Isoda and Imprasitha (2012, p. v) stated that Lesson Study (LS) is a system
of planning and delivering teaching and learning that is designed to challenge teachers to
innovate their teaching approaches. It operates when teachers develop a sequence of lessons
together: to plan, to do, and to see (reflect) to improve the lesson for future presentation on a
wider scale. Lewis (2011) also stated that part of the LS process is ‘kyouzaikenkyuu’, careful
study of the teaching materials focused on both the mathematics and the pedagogy. Lewis
(2011) stated that normally, there are 3 steps of Lesson Study which are: Plan Do See.
However, Catherine Lewis proposed four steps of Lesson Study which are as follows.
1. STUDY. Teachers consider long term goals for student learning and development or study
the curriculum and the standards.
2. PLAN. Teachers select or revise research lesson, do task, anticipate student responses, plan
data collection and lesson
11
4. REFLECT. Teachers share data, ask and answer this question: What was learned about
student learning, lesson design, this content? What are implications for this lesson and
instruction more broadly?
The relationship among Lesson Study, the problem solving approach and mathematical
thinking in Japanese culture are very solid. Therefore the implementation of Lesson Study was
used to change or to innovate the teaching and learning mathematics in Japan to be more
students centred and in touch with the newest issues and current trends in the teaching and
learning of mathematics. The focus of Lesson Study in Japan was the students as learners, and
how to help them to learn mathematics meaningfully, how to help students to learn to think and
how to help students to learn mathematics by/for themselves and to be independent learners.
The Lesson Study in Japan was supported by an expert from a university and also from
mathematics teachers, such as Mr. T. Seiyama from an Elementary School attached to the
University of Tsukuba who was videotaped by JICA (Japan International Cooperation Agency).
This video gives a good and clear example of problem solving approach.
Methodology
This section will discuss the methodology that was implemented in the number of
studies. Since 2012 SEAMEO QITEP in Mathematics conducted studies related to Disaster
Risk Reduction (DRR). In 2012 the study related to earthquakes and tsunamis (Ponidi,
Setyaningrum, Dwinugrahaningsih, Shadiq, Wahyudi and Subanar, 2012), in 2013 it related to
floods (Setyaningrum, Hidayah, Dwinugrahaningsih, Wismono, Shadiq, Pujiati, Sahid,
Wahyudi, Widodo and Subanar, 2013), in 2014 it related to volcanic eruptions (Rahayu,
Anindito, Darto, Wismono, Shadiq, Pujiati, Sahid, Wahyudi, Kirbani and Subanar, 2014), and
in 2015 it related to landslides (Vikrama, Windarti, Margono,, Dwinugrahaningsih, Shadiq,
Yunianto, Fina, Sahid, Wahyudi and Subanar, 2015). Every year, SEAMEO QITEP in
Mathematics conducted a workshop to develop a proposal and instruments for the study. The
workshops were attended by practitioner mathematics teachers and specialists from SEAMEO
QITEP in Mathematics as teams. For example, in 2012 the DRR topic was earthquake and
12
Schools, Logarithm for Senior Secondary Schools and no topic suitable for Junior Secondary
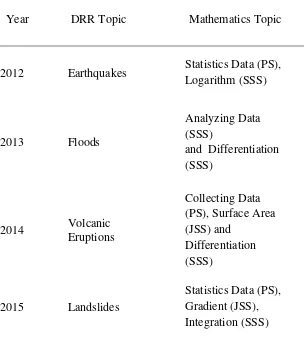
Schools. In Table 1 this information is summarised for 2012 to 2015.
Table 1
The Data of Mathematics Topic Related to DRR Topic in
SEAMEO QITEP in Mathematics
Year DRR Topic Mathematics Topic
2012 Earthquakes Statistics Data (PS),
Logarithm (SSS)
2013 Floods
Analyzing Data (SSS)
and Differentiation (SSS)
2014 Volcanic
Eruptions
Collecting Data (PS), Surface Area (JSS) and
Differentiation (SSS)
2015 Landslides
Statistics Data (PS), Gradient (JSS), Integration (SSS)
PS: Primary School, JSS: Junior Secondary School, SSS: Senior Secondary School
As mentioned earlier, the problem solving approach and Lesson Study were
implemented. Data were collected from observations of students work, student interviews,
photos of blackboard presentations, videotape of the teaching and learning processes, and
13
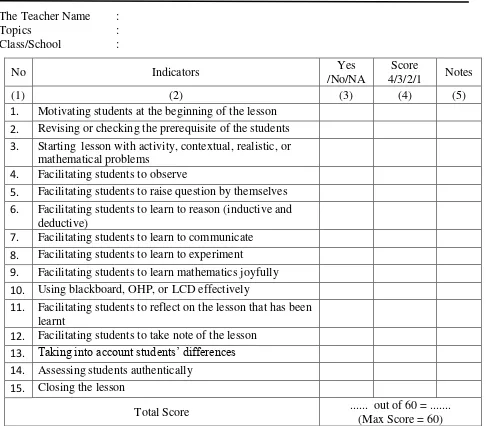
1. Motivating students at the beginning of the lesson
2. Revising or checking the prerequisite of the students 3. Starting lesson with activity, contextual, realistic, or
mathematical problems
4. Facilitating students to observe
5. Facilitating students to raise question by themselves
6. Facilitating students to learn to reason (inductive and
deductive)
7. Facilitating students to learn to communicate 8. Facilitating students to learn to experiment
9. Facilitating students to learn mathematics joyfully
10. Using blackboard, OHP, or LCD effectively
11. Facilitating students to reflect on the lesson that has been
learnt
12. Facilitating students to take note of the lesson
13. Taking into account students’ differences 14. Assessing students authentically
15. Closing the lesson
Total Score ... out of 60 = ...
(Max Score = 60)
Note: 4/3/2/1 = Very Good/Good/Fair/Poor (For observer who tick ‘Yes’ on the third column) Date: ...Observer Name:... Signature: ...
What are the interesting parts of the lesson?
What specific suggestion would you make to improve the lesson?
Note: Observer can write the teaching and learning process on the next plain pages.
The data were collected and analysed by a team to ensure reliability and to reduce bias
and the results are discussed in the next section. Readers wishing further details are directed to
the earlier listed publications (Ponidi, et al, 2012; Setyaningrum, et al, 2013; Rahayu, et al,
14
Results and Discussion
This section summarizes the specific outcomes of the research and discusses the
implication and recommendations for both the practice of teaching and learning of mathematics
in class and for further research.
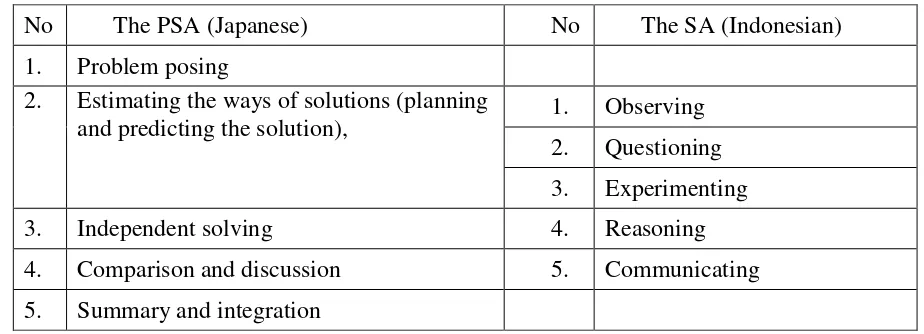
If we will consider the importance of the first step of PSA in supporting the SA. In
Japan, the PSA (Isoda & Katagiri, 2012) consist of 5 steps, while in In Indonesia, the Scientific
Approach (SA) was planned to be implemented in Indonesia under the 2013 New Curriculum.
The five steps of Scientific Approach are: (1) observing, (2) questioning, (3) experimenting,
(4) reasoning and (5) communicating, and so it is clear that the Problem-Solving Approach
(PSA) from Japan can support the Scientific Approach from Indonesia. The PSA and SA can
be compared in table 3.
Based on the table, it can be observed that the teaching and learning process should be
started with a contextual, realistic or mathematical problem which is in line with the first step
of PSA to ensure that the SA can be implemented during the teaching and learning of
mathematics.
For example, the starting problem was: How much more intense is an earthquake of
magnitude 6.5 as compared to one of magnitude 4.5? On 11 January 2012, Meulaboh Nangroe
Aceh Darussalam experienced an earthquake of Richter magnitude 7.3. Calculate the energy
associated with this earthquake!
Table 3
A comparison of the Japanese Problem Solving Approach and the Indonesian Scientific Approach
No The PSA (Japanese) No The SA (Indonesian)
1. Problem posing
2. Estimating the ways of solutions (planning
and predicting the solution), 1. Observing
2. Questioning
3. Experimenting
3. Independent solving 4. Reasoning
4. Comparison and discussion 5. Communicating
15
To change and improve the quality of the teaching and learning process from a “typical” or “traditional” mathematics classroom to a more innovative one is not easy. Goos and Vale
(2007, p. 4) stated: "Whether we are aware of it or not, all of us have our own beliefs about
what mathematics is and why it is important." Furthermore, Goos and Vale (2007, p. 4) quoted
Barkatsas and Malone (2005, p.71) who stated, “Mathematics teachers’ beliefs have an impact
on their classroom practice, on the ways they perceive teaching, learning, and assessment, and
on the ways they perceive students’ potential, abilities, dispositions, and capabilities.” The
results of this study were consistent with the conclusions of the research conducted earlier by
the author (Shadiq, 2010, pp.56-57) in that most teachers of mathematics in their schools still
use or implement the traditional ways during the learning and teaching process of mathematics.
This remained even after some experience with Lesson Study, which further points to how
strong these beliefs are. The teachers still believed in the paradigm of transferring knowledge
from teachers’ brain to students’ brain because they believed this was the best way based on
their own learning experiences. Thus, the result of this research study indicated a failure to
change the teachers’ attitudes. However, giving teachers further experience with Lesson Study
and PSA provides greater opportunities for the teachers to develop different beliefs about
teaching and learning.
The data suggests that the integration of DRR can promote students having a more
positive attitude toward mathematics.
Conclusion and Recommendations
While the author makes no claims that the findings can be generalized to all teachers in
Indonesia, nevertheless the following recommendations are made a guide for educators to
consider.
1. It is recommended that every mathematics teacher and educator be encouraged and
motivated to improve his/her competency in order to produce such high quality of teaching
and learning resource materials for teachers (including designing lesson plans that start with
activities or contextual/ realistic/ mathematical problems) as real examples for mathematics
16
2. While the initial use of Lesson Study was a failure, it is recommended that teachers still
need to experience mathematics in ways they will be expected to use in teaching.
Mathematics teachers need the experience of concrete examples that can be used and
implemented in mathematics classes. Teachers are more likely to implement the new
approaches in their own classes if they have experienced it in their own learning.
In Japan, the Lesson Study process was supported by university experts. Following this
model, it is recommended that every pre-service and in-service institution could work with and
help elementary and secondary school teachers and could focus on helping and facilitating
learners. The main focus of pre-service institution could be on how to produce mathematics
teachers who can help their students to learn mathematics meaningfully, learn to think, and to
learn mathematics by and for themselves.
It is recommended the main focus of in-service institution be upon how to maintain and
improve the quality of mathematics teachers in order to help their students to learn mathematics
meaningfully, learn to think, and to learn mathematics by and for them to anticipate the change
in technology and in society.
It is recommended that further research could be designed to find ways to influence the
Indonesian mathematics teachers’ beliefs about their classroom practice, their perceptions of
teaching, learning and assessment, and their perceptions of students’ potential abilities,
dispositions, and capabilities.
References
Bastow, B., Hughes, J., Kissane, B., & Mortlock, R. (1986). Another 20 Investigational
Works. Perth: MAWA.
De Lange, J. (2004). Mathematical Literacy for Living from OECD-PISA Perspective. Paris:
OECD-PISA.
Fitzgerald, M. & James, I. (2007). The Mind of the Mathematician. Baltimore: The Johns
Hopkins University Press.
17
Goos, M, Stillman, G, & Vale, C. (2007). Teaching Secondary School Mathematics:
Research and Practice for the 21st Century. NSW: Allen & Unwin.
Haylock, D., & Thangata, F. (2007). Key Concepts in Teaching Primary Mathematics.
London: SAGE Publications Ltd.
Isoda, M., & Nakamura, T. (2011). The theory of Problem Solving Approach on Lesson
Study for All APEC Economies. In Isoda, M., & Nakamura, T. (Chief editors):
Mathematics Education Theories for Lesson Study: Problem Solving Approach through
Extension and Integration (Special Issue of EARCOME 5) (p.83). Tokyo: Journal of
Japan Society of Mathematical Education.
Isoda, M., & Katagiri, S. (2012). Mathematical Thinking. Singapura: World Scientific.
Kemdikbud (2012a). Public Testing Materials of Curriculum 2013. Jakarta: Author.
Kemdikbud (2012b). Curriculum 2013 Development. Jakarta: Author.
Lewis, C. (2011). Lesson Study with Japanese Curriculum Materials: A Randomized
Controlled Trial. Paper presented on APEC Tsukuba International Conference V.
Tsukuba: CRICED, University of Tsukuba, Japan.
National Council of Teachers of Mathematics. (1999). Principles and standards for school
mathematics. Reston, VA: Author.
National Research Council (NRC)(1989). Everybody Counts. A Report to the Nation on the
Future of Mathematics Education. Washington DC: National Academy Press.
Orton, A. (1987). Learning Mathematics. London: Casell Educational Limited.
Ponidi, Setyaningrum, A., Dwinugrahaningsih, M., Shadiq, F., Wahyudi, & Subanar (2012).
How to Enhance the Competence in Mathematical Modelling by Implementing Lesson
Study, in the Case of Tsunami and Earthquakes? Yogyakarta: SEAMEO QITEP in
Mathematics.
Pranoto, I. (2011). Differentiating Students in Math Classroom. Yogyakarta: SEAMEO
QITEP in Mathematics.
Rahayu, P. S., Anindito, V., Darto, Wismono, A., Shadiq, F., Pujiati, Sahid, Wahyudi,
Kirbani & Subanar (2014). How to Enhance the Competence in Mathematical Modelling
by Implementing Lesson Study, in the Case of Volcanic Eruptions? Yogyakarta:
SEAMEO QITEP in Mathematics.
Setyaningrum, A., Hidayah, H. N., Dwinugrahaningsih, M., Wismono, A., Shadiq, F., Pujiati,
Sahid, Wahyudi, Widodo & Subanar (2013). How to Enhance the Competence in
Mathematical Modelling by Implementing Lesson Study, in the Case of Flood and
18
Shadiq, F. (2010). Identifikasi Kesulitan Guru Matematika SMK pada Pembelajaran
Matematika yang Mengacu pada Permendiknas No. 22 Tahun 2006. Edumat: Jurnal
Edukasi Matematika, 1(1), 49 – 60.
Stacey, K., Tall, D., Isoda, M., & Imprasitha, M. (2012). Preface to the Series: Monograph on
Lesson Study for Teaching Mathematics and Science. In Isoda, M. & Katagiri, S. (Eds).
Mathematical Thinking. Singapore: World Scientific, (pp. v – vi).
Vikrama, Windarti, Margono, A., Dwinugrahaningsih, M., Shadiq, F., Yunianto, W., Fina,
Sahid, Wahyudi & Subanar (2015). How to Enhance the Competence in Mathematical
Modelling by Implementing Lesson Study in the Case of Landslides? Yogyakarta:
SEAMEO QITEP in Mathematics.
UNESCO ISDR (2007). Disaster Risk Reduction Begins at School. Geneva: UNESCO ISDR.
UNESCO (2010). Disaster Risk Reduction (RDD). An Imperative for Education
19
Inculcating Tsunami Awareness in a Mathematics Lesson: Improving
Students’ Collaborative Problem Solving via Lesson Study
Madihah Khalid
Kulliyyah of Education, International Islamic University Malaysia
Dk Haslinah Pg. Haji Ali
SR DMW Lambak, Brunei Darussalam
Abstract
The past two cycles of PISA have reflected the demands of the skills and competencies that many countries desire their future generations to possess. Among these competencies, students’ financial literacy, problem solving, and communication skills have emerged to be as important as their reading and quantitative literacy (OECD, 2013). Problem-solving, along with other 21st century skills can be inculcated in the students by using the problem-solving
pedagogy. However, teachers who are not used to teaching mathematics via problem solving need to experience the pedagogy themselves and this can be best achieved by implementing Lesson Study. A Lesson Study research study was conducted to look at collaborative problem solving in the teaching of the topic on “rate” to year 5 students. Results showed that students benefited from their lesson in terms of increased knowledge of the problem context and the ability to apply knowledge of rates in finding the best solution that the problem posed. Consequently, Lesson Study was found to help enhance teachers’ pedagogical content knowledge. It helped them produce effective lesson plans that incorporated student-centred authentic lessons that also integrated values, use of technology and students’ creativity in problem solving.
Keywords: Lesson Study, meaningful learning, 21st century skills, problem solving approach, Higher Order
Thinking Skills,
Introduction
It was stated in the Malaysian Education Blueprint Annual Report 2013 (MOE, 2013)
that there was a concern with students’ performance on the Programme for International
Student Assessment (PISA) as well as the Trends in International Mathematics and Science
Study (TIMSS). In both assessments, Malaysian students’ mean scores were not as expected
when compared to the international average. It was also noted that both tests assess students for
higher order thinking skills (Chen, 2013; Tang, 2014). Many of the questions encountered by
the students were problem-solving types of questions which are authentic problems set in a
real-world setting, especially the problems in PISA.
The Annual Report document also highlighted the need for improving the quality of
education in Malaysia and listed the future trends that specify the goals of teaching and learning
20
should incorporate Higher Order Thinking Skills (HOTS). HOTS was defined as “the ability to
apply knowledge, skills and values while reasoning and reflecting to solve problems, make
decisions, innovate and create.” (MOE, 2013, p. 50).
The Annual Report document also stated that in a benchmarking report of 2013, Pearson
International suggested the need for “conceptual thinking of big ideas in Science and Mathematics to be integrated into the Malaysian curriculum” (pp. 50). Therefore the Ministry
will direct that HOTS and 21st century skills are highlighted explicitly in the curriculum and
learning materials of the schools. Also MOE will continue to provide Continuous Professional
Development with regards to the latest teaching and learning techniques to promote students’
active learning. All of these will be done in an attempt to also improve Science, Technology,
Engineering and Mathematics (STEM) curriculum based knowledge and skills of STEM
teachers.
As mentioned above, among the important 21st century skills that can be inculcated in
our students are collaboration, communication and technology fluency skills. So how do we
integrate and make sure that all of these aspects are present in problem-solving classes? How
do we determine that students are taught these skills in our classroom? Maybe these skills can
be inculcated by teaching through collaborative problem-solving classes (or collaborative
problem-based learning) that also practice the inquiry-learning approach. In these kind of
classes, assessment can also be accomplished concurrently.
Collaborative problem solving is defined by PISA (OECD, 2013, p. 6) as “…the
capacity of an individual to effectively engage in a process whereby two or more agents attempt
to solve a problem by sharing the understanding and effort required to come to a solution and
pooling their knowledge, skills and efforts to reach that solution.” The framework used by PISA
21
from inert information passively received from books and teachers toward dynamic
understanding that is collaboratively constructed in discussion among students”.
However, designing this kind of lesson is not easy for teachers who are not used to
teaching this way. Therefore, Lesson Study (or jugyokenkyu in Japanese) can then be employed
so that teachers, in the presence of a “knowledgeable other/s”, can collaborate to write effective
lesson plans based on the criteria selected, try out the lesson in a real setting, observe the
“research lesson” and reflect (with comment/critique from observers) accordingly to improve
the lesson plan, and repeat the process again until a satisfactory lesson is successfully executed.
The final step would be writing the report of the completed study.
Lesson Study has been practiced in Japan for more than 130 years (Shimizu, 2006) and
it was said to be the main factor that enabled teachers in Japan to teach in a manner that
incorporated most of the best practices in teaching. Japanese teaching focused on teaching for
conceptual understanding, and Japanese teachers participated in the ongoing, incremental, and
continuous improvement of their teaching (Stigler & Hiebert, 1999). Besides practicing Lesson
Study at three different levels – school, district and national levels, teachers also observe each
other on a regular basis outside Lesson Study time (Jackson, 2013). Nowadays, Lesson Study
is being practiced by more than 40 countries around the world (Burghes & Robinson, 2009). It
is being practiced in places as far away as countries in South America, North America, Asia,
Africa, Australia, Europe and even in Russia. In Malaysia, it was documented that Lesson Study
started as a research study for Master and PhD in 2004 (Cheah & Lim, 2010). Now, teachers
has started implementing Lesson Study in schools in the Penang and the Klang areas. Lesson
Study is seen as an effective continuous professional development model because teachers are
fully involved in the process as compared to traditional continuous professional development
where teachers took a more passive role.
A study by Suhaili and Khalid (2011) stated that one of the many positive outcome of
Lesson Study was as an effective alternative continuous professional development. Fernandez
and Chokshi (2002) emphasized that Lesson Study was more a process of knowledge building
22
grounded reflection about the complex activities of teaching that can be shared and discussed
with other members of the profession.
Improving something as complex and culturally embedded as teaching requires the efforts of all players, including students, parents, and politicians. But teachers must be the primary driving force behind change. They are the best positioned to understand the problems that students face and to generate possible solutions (Stigler & Hiebert, 1999, pp. 135)
The Study
This study is an attempt to examine students’ behavioural changes which includes
collaborative problem solving skills, tsunami awareness, and understanding of the topic “rate”,
while, teachers’ reactions and acceptance of “Lesson Study” were also evaluated. An intervention research study was conducted to evaluate students’ collaborative problem solving
ability via a contextual real-life problem of a tsunami, similar to what happened during the
tsunami of 2004. Many of the students were not aware of the tragedy since they were still babies
when that happened and tsunamis and earthquakes are a rare phenomenon in Malaysia. The
topic of “rate” was chosen for the mathematics lesson because when the study was
conceptualized, the researchers knew that by the time the study was implemented, the students
in Year 5 would be learning about rate. Lesson Study was used as a tool for this action research.
Lesson Study offers the teacher the chance to be directly involved in the collaborative lesson
planning under the guidance of the knowledgeable others. It also offers the opportunity for
teachers to improve their lesson planning based on critical comments and to repeat the cycle
with the improved lesson plan with other classes, in the proximity of a few weeks.
Lesson plans focusing on the student-centred approach to learning was designed with
elements like problem-posing, cooperative learning, creative thinking, use of Information
Communication Technology (ICT), contextual problem, performance assessment etc. included
in the lesson. An interactive d-book was designed so that teachers could look at the task-outline
and the suggested solution. The d-book is an interactive electronic book created using
DbookPro software. The main purpose of setting the problem in the d-book was to make sure
that students could work on the problem interactively where learning becomes more real and
23
understanding of mathematics. [The d-book can be accessed at
http://math-info.criced.tsukuba.ac.jp/ museum/dbook_site/ Burunei-pub/files/EText.html. ]
Research Questions (RQ)
In order to achieve the objectives of the study, the following research questions were
formulated to guide the research:
1. To what extent does the lessons improve students’ knowledge on Tsunami and “rate”?
2. How do students’ behave during collaborative problem solving?
3. What is the impact of Lesson Study on the school teachers?
Methodology
The sample for this research was composed of 3 classes, consisting a total of 58 Year 5
students. This study employed a mix methods research methodology, collecting both qualitative
and quantitative data, to maintain validity and reliability. Students were given a pretest one
week before the teaching started and a post-test later after one and a half month. The pre and
post- test questions tested students’ knowledge of tsunami and ‘rate’. Lessons started with class
A after lesson planning was completed. The research lesson implemented was observed by 6 –
8 teachers and officers from the Ministry of Education, followed by a discussion and reflection
session. A lesson plan was improved based on feedback given during the reflection session and
the cycle was repeated with class B and subsequently with class C.
Quantitative data was collected through using observation checklists on aspects of
teaching and learning (such as content delivery, lesson presentation, strategy and resources
used, classroom communication and assessment. These were rated on the Likert scale of 1 to 5
ranging from “not at all” to “very high” respectively), checklist for collaborative problem
solving on how they behave during collaborative problem solving (rated on a Likert scale of 1
to 5 from never to always respectively) and pre-test and post–test. The tests were made parallel
so as to make sure that students did not memorize the answers from the pre-test to answer the
24
through observations of video recordings of the lessons and the reflection stage for every cycle,
researcher’s field notes, and teachers’ interview.
SPSS was used to analyse the quantitative data collected. Paired sample t-test was used
to compare the learning outcomes of students’ achievement and behaviours among the three
lessons. Students’ performance data were also analysed using ANCOVA. This method of
analysis enabled the authors to compare students’ mathematics achievements and awareness of
tsunami based on post-test item scores by controlling the covariate (in this case, the pre-test
results). Descriptive statistics were used to compare the learning outcomes of students’
performance in problem-solving activity from the observation data. Paired t-test was also
conducted to determine the differences of students’ performance between the three classes.
Observation field notes and interviews were transcribed, and categorised into identified themes
to support the quantitative data.
Lesson Format
Set Induction: Students were first shown a very short video of a tsunami hitting the
shores of some countries. They were asked to discuss what they saw, how it occurred and what
can be learnt from it. After discussion, the students were shown a video on the cause of tsunami,
due to the movements of tectonic plates.
Main Lesson: Then the students were shown a video of a girl, named Tilly, who
managed to take prompt action and save several lives when a tsunami struck in 2004, because
she remembered the early warning signs of a tsunami that she learnt in her geography lesson.
Then, the children were asked to solve the following problem:
Problem:
Abu is standing on a beach when he heard the tsunami warning siren. He immediately decided to run to a safe place. He had 3 choices; go to a small hill or a shelter built for tsunami, which can be reached via two ways (see the diagram below). The hill is 500 metres and the shelter is 800 metres away from the beach. However, to reach the top of the hill, Abu need to climb 300 steps of staircase. Abu can run at an average rate of 5m/s and he can climb the stairs at the rate of 3 steps/s. He may also use the curved road (specially made for the shelter) which is 900 metres long, where he can run at 6m/s. In your opinion, which way should Abu take? Please explain.
The problem was made open so there were several ways to approach the solution to the
25
what they understood and some did come up with very good questions. Among the questions
posed by the students were: “To save myself, do I really need to go to the top of the hill?” “What is the normal height of the tsunami?” “What is the speed of the tsunami?”
During the problem solving process, students were made to work in groups so that their
collaborative problem solving could be assessed. Observers were asked to rate the students’
problem solving ability in terms of understanding the problem, planning and executing the
process to solve the problem, the final answer to the problem and how they communicate their
answer with their friends during the activity. Finally each group was required to present their
result.
Closure: Students were asked to state what they learnt in the lesson and the teacher
finally summarized the lesson at the end.
Results
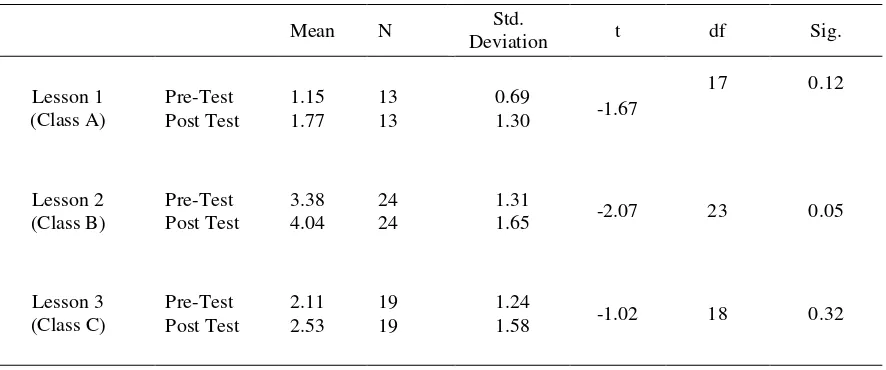
Answering RQ 1. Paired t-test on students’ achievement tests (pre-test and post-test),
found that there was improvement for every class with Class B in Lesson 2 being statistically
significant at p<0.05. Every class seemed to perform better in their post-test which suggest
students’ improved awareness of Tsunami and problem solving ability in the topic of “rate”.
Table 1
Paired t-test showing improvement from pre to post-test of the three classes
26
The ANCOVA test performed on the mean scores (to compare the effect of the lesson
on the students’ achievement when the pre-test was covariate-out) revealed near but no
significant improvement of the test results between each lesson (or class). The indication from
the qualitative data showed that students seemed to be engrossed in discussion of a tsunami and
further examination of the pre and post test showed that students answered the questions on
tsunami better than the questions on “rate”. Therefore, we consider the aim of making students
aware of tsunami as somewhat successful in terms of improved knowledge about a tsunami.
Table 2
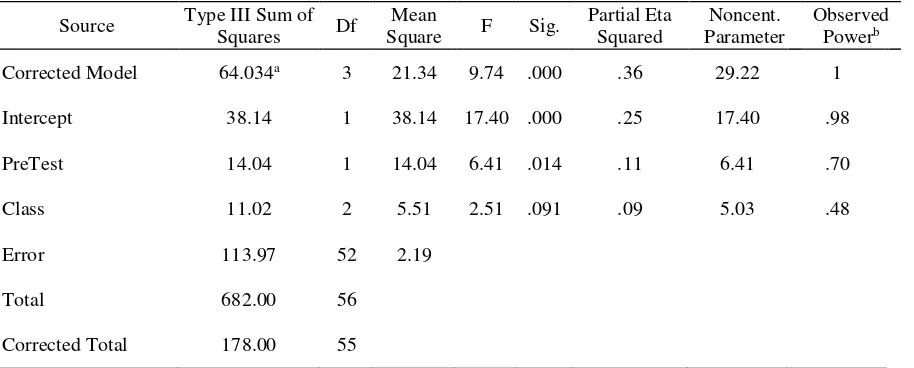
ANCOVA showing the Tests of Between-Subject Effects
Source Type III Sum of
observation checklist of the observers. It seemed to show that in most cases, lesson 2 have the
highest mean for all categories as compared to Lessons 1 and 3. It is to be reminded that lesson
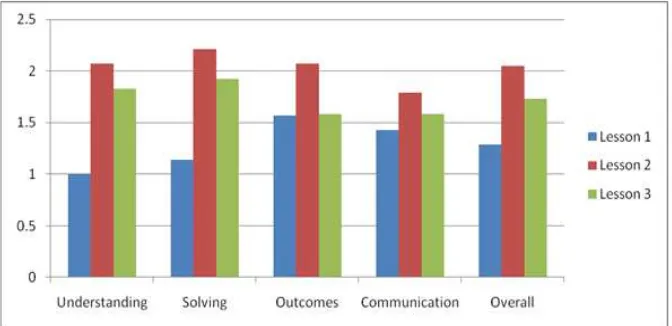
2 consist of more able students and hence is reflected in the mean scores. Figure 1 shows slight
improvements in terms of presentation and strategy of the lesson as the lesson plans were
improved. Scores on resources seemed to decrease steadily as the lesson plans were improved,
we decided to concentrate more on the problem solving part and shorten the three videos played
during the lessons. The variations exhibited for other categories of the lesson was mainly
attributed to the level of students’ ability taught in each lesson. Since lesson 2 consisted of more
able students, more content was taught, they seemed to communicate more with the teacher and
among themselves, they reacted better to the questions in the assessment part and exhibited
27
Figure 1. Mean score of all categories over the three lessons from lesson observation checklist.
For students’ problem solving abilities which were measured using a rubric in terms of
Understanding the problem; Solving the problem; Outcomes of activities and Communication
(rated from 1 to 4 for Needs Improvement, Satisfactory, Good and Excellent respectively), the
range is between needs improvement to satisfactory level which still shows weak authentic
problem solving techniques among the students. Again, in this case, students from Lesson 2
seemed to be performing better than the others.
Figure 2. Mean rubric scores in each category for all the three lessons
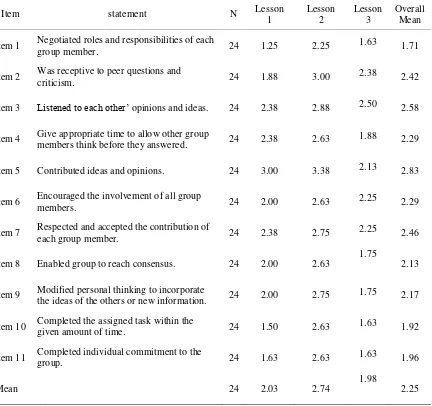
Table 3 shows the score from collaborative group work checklist rated by the observers
present during the lesson implementation part of Lesson Study. The mean score for each item is
from 1.71 to 2.83, which is between rarely to occasionally. From this result and the result from
above, it may be deduced that students’ collaborative problem solving skills is in the developing
28 Table 3
Mean scores for each item is from 1.71 to 2.83
Item statement N Lesson
Item 1 Negotiated roles and responsibilities of each
group member. 24 1.25 2.25 1.63 1.71
Item 2 Was receptive to peer questions and
criticism. 24 1.88 3.00 2.38 2.42
Item 3 Listened to each other’ opinions and ideas. 24 2.38 2.88 2.50 2.58
Item 4 Give appropriate time to allow other group
members think before they answered. 24 2.38 2.63
1.88 2.29
Item 5 Contributed ideas and opinions. 24 3.00 3.38 2.13 2.83
Item 6 Encouraged the involvement of all group
members. 24 2.00 2.63 2.25 2.29
Item 7 Respected and accepted the contribution of
each group member. 24 2.38 2.75 2.25 2.46
Item 8 Enabled group to reach consensus. 24 2.00 2.63 1.75 2.13
Item 9 Modified personal thinking to incorporate
the ideas of the others or new information. 24 2.00 2.75
1.75 2.17
Item 10 Completed the assigned task within the
given amount of time. 24 1.50 2.63
1.63 1.92
Item 11 Completed individual commitment to the
group. 24 1.63 2.63 1.63 1.96
Mean 24 2.03 2.74
1.98
2.25
RQ 3. Most teachers interviewed agreed that they learnt a great deal during the Lesson
Study process in terms of knowledge sharing especially of pedagogical content knowledge,
content and curriculum which translated in their ability to design constructivist,
student-centered instructions. A teacher involved in lesson planning remarked that working together
had broadened her knowledge of the mathematics content and subject matter. Another teacher
said that teaching and observing the research lesson made her more critical in choosing the right
teaching activities that helped students to understand and think mathematically. One teacher
also commented that the whole process of Lesson Study has been one of the most beneficial
activity she had been involved with, as she learnt about translating the curriculum into effective
29
Discussion
Students enjoyed the lesson introduction because it was made more real and interesting
with the presentation of videos. The impact of the videos made pupils feel involved in real-life
events physically and this led to motivation to discuss it. The lesson was well-linked starting
from the video on tsunami hitting Japan, followed by discussion on what causes tsunami. The
second video from UN International Strategy for Disaster Reduction was about how a girl
manage to save the lives of a few families on holiday in Thailand because she was able to recall
the early warning signs of tsunami learned from her geography class. Subsequently, students
were led to solve the “saving life” problem on mathematics. The problem was posed in a real
life context and this motivated them to solve it. The problem was made more real and interactive
using the Dbook. Students were found to discuss tsunami even after the class ended. Overall,
the lesson was successful in making students visualize, communicate, reason and think
mathematically although this were only exhibited fully by some students. Some were also able
to exhibit their computational skills and understanding of rate in obtaining the time taken for
each path and hence chose the one that required the shortest time. Students’ creativity was
evident during the lesson. They used various methods in calculating the answer, repeated
addition (proportion), multiplication, division and a mix of operations.
The teachers were also engaged in the tasks given starting from lesson planning until
the writing of the report. The collaborative nature of Lesson Study and the demand of preparing
exemplary lesson made the teachers think creatively and critically on how to design good
lessons. They claimed that the pedagogical content knowledge that they gained through Lesson
Study was more valuable than the normal professional development courses.
Conclusion
It is important to note that the findings are only applicable to the schools involved and
the writers make no claims to them being universally applicable to other Malaysian schools.
However for readers, their value lies in the possibilities of replication and adaptability. With
those qualifications, it was apparent from this research study that, Lesson Study has made it
30
Made students aware of natural disasters and learn from it.
Were more authentic by incorporating real-life events to problem-solving classes.
Incorporated the use of ICT – videos and interactive Dbook that made the activities more
interesting to the students.
Allowed students to be creative because they had the freedom to choose multiple methods in the open-ended problem presented.
Motivate students to learn because they felt the ownership of learning.
In this limited study, the Lesson Study process helped the teachers to discuss the lesson
plan and to prepare improved lessons using a constructivist approach. Teachers also
experienced how, by cooperation and collaboratively helping each other, they were able to
increase their pedagogical-content-knowledge, knowledge on curriculum and the content.
Liptak (2002) said that like most good investments, we expect that the growth and
dividends from the time we invest in Lesson Study will accrue gradually over a long period of
time. Improving our teaching in depth is hard, time-consuming work, which needs to be done
collaboratively and in a supportive setting and the researchers believe that this will happen in
our country.
References
Burghes, D., & Robinson, D. (2009). Lesson Study: Enhancing Mathematics Teaching and
Learning. London: CfBT Education Trust.
Cazden, C Cazden, C. B. & Beck, S. W. (2003). Classroom discourse. In A. C. Graesser, M.
A. Gernsbacher & S. R. Goldman (Eds.), Handbook of discourse processes (pp.
165-197). Mahwah, NJ: Lawrence Erlbaum Associates
Cheah U. H., & Lim C. S. (2010). Disseminating and Popularising Lesson Study in Malaysia and Southeast Asia. Paper delivered at the APEID Hiroshima Seminar “Current Status and Issues on Lesson Study in Asia and the Pacific Region.
Chen, K. S. (2013, December 8). Poor show in PISA ranking. Retrieved from The Star
Online:
http://www.thestar.com.my/News/Education/2013/12/08/Poor-show-in-Pisa-rankings/
Fernandez, C. & Chokshi, S. (October 2002). A practical guide to translating Lesson Study
31
Jackson, B. (2013, October 3). Why Other Countries do Better in Math. Retrieved from The
Daily Riff:
http://www.thedailyriff.com/articles/why-other-countries-do-better-in-math-520.php
Liptak, L. (2002). It's a matter of time: Scheduling Lesson Study at Paterson, NJ School 2.
Patterson, New Jersey: RBS
Ministry of Education Malaysia (MOE) (2013). Malaysia Education Blueprint Annual
Report, Ministry of Education Malaysia. Putrajaya: Author.
OECD (2013). PISA 2012 Assessment and Analytical Framework: Mathematics, Reading,
Science, Problem Solving and Financial Literacy. Bangkok: OECD Publishing.
http://dx.doi.org/10.1787/9789264190511-en
Programme for International Student Assessment (PISA) (2013). PISA 2015 Draft
collaborative problem solving framework. Retrieved 20th July, 2014 from
http://www.oecd.org/pisa/pisaproducts/Draft%20PISA%202015%20Collaborative%20Pr
oblem%20Solving%20Framework%20.pdf
Shimizu, S. (2006). Professional development through Lesson Study: A Japanese case. Paper
presented at the APEC International Symposium on Innovation and Good Practices for
Teaching and Learning Mathematics through Lesson Study, Khon Kaen, Thailand.
Stigler, J., & Hiebert, J. (1999). The Teaching Gap: Best Ideas from the World's Teachers for
Improving Education in the Classroom. New York: Free Press.
Suhaili, H. A., & Khalid, M. (2011). Mathematics Teachers Perception of Lesson Study as a
Continuous Professional Development Programme. Journal of Science and Mathematics
Education in Southeast Asia, 34, 67-89.
Tang, S. (2014, April 14). Malaysian Students Nowhere Near Top of the Class. Retrieved
from Malaysian Business Insider: