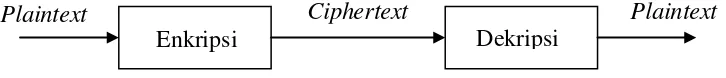BAB 2
LANDASAN TEORI
2.1. Kriptografi
Berikut ini akan dijelaskan pengertian, tujuan dan jenis kriptografi.
2.1.1. Pengertian Kriptografi
Kriptografi (cryptography) berasal dari bahasa Yunani yang terdiri dari dua suku kata yaitu kryptos yang artinya tersembunyi dan graphein yang artinya tulisan. Pesan asli disebut plaintext dan pesan yang disamarkan disebut ciphertext. Pesan yang telah disandikan dan dikirim disebut kriptogram. Proses mengubah plaintext menjadi ciphertext dosebut encryption atau enciphering atau enkripsi.Proses kebalikan dari mengubah ciphertext menjadi plaintext, yang dilakukan olehpenerima disebut dekripsi. Siapapun yang terlibat dalam kriptografi disebut cryptographer(Mollin, R. A. 2007).
Menurut Munir,R. (2006), Kriptografi (cryptography) merupakan ilmu dan seni untuk menjaga pesan agar aman. (Cryptography is the art and science of keeping messages secure) “Crypto” berarti “secret” (rahasia) dan “graphy” berarti “writing” (tulisan).
Kriptografi adalah ilmu mengenai teknik enkripsi dimana data diacak menggunakan suatu kunci enkripsi menjadi sesuatu yang sulit dibaca oleh seseorang yang tidak memiliki kunci dekripsi (Kromodimoeljo, S. 2010).
menggunakan huruf dan karakter di luar bentuk aslinya, atau dengan metode-metode lain yang hanya dapat dipahami oleh pihak-pihak yang memproses kunci, juga semua hal yang ditulis dengan cara seperti ini”(Haq, H. A. 2013).
2.1.2. Terminologi Kriptografi
Seorang pengirim (sender) ingin mengirim pesan (plaintext; kadang-kadang disebut cleartext) kepada orang yang dituju (receiver). Selain itu, pengirim ingin pesan yang dikirim tidak dapat dibaca oleh orang lain yang menyadap percakapan (eavesdropper) atau pesan tersebut. Proses menyamarkan pesan sedemikian rupa untuk menyembunyikan substansinya disebut enkripsi. Sebuah pesan yang dienkripsi disebut ciphertext. Proses untuk mengubah ciphertext kembali ke plaintext adalah dekripsi. Pada standar ISO 7498-2 menggunakan istilah encipher untuk proses enkripsi dan decipher untuk proses dekripsi. Skema rangkaian proses enkripsi dan dekripsi ditunjukkan secara umum pada Gambar 1 (Schneier, 1996).
Gambar 2.1. Skema Proses Enkripsi dan Dekripsi (Schneier, 1996)
2.1.3. Tujuan Kriptografi
Kriptografi bertujuan untuk memberikan layanan keamanan kepada pengguna sebagai berikut:
1. Kerahasiaan (Confidentiality)
Informasi dirahasiakan dari semua pihak yang tidak berwenang. 2. Keutuhan Data (Integrity)
Pesan tidak berubah dalam proses pengiriman hingga pesan diterima oleh penerima.
Enkripsi Dekripsi
3. Autentikasi (Message Authentication)
Kepastian terhadap identitas setiap entitas yang terlibat dan keaslian sumber data. 4. Nirpenyangkalan (Nonrepudiation)
Setiap entitas yang berkomunikasi tidak dapat menolak atau menyangkal atas data yang telah dikirim atau diterima.
2.1.4. Sistem Kriptografi
Sistem kriptografi terdiri dari 5 bagian yaitu sebagai berikut :
1. Plaintext: pesan atau data dalam bentuk aslinya yang dapat terbaca.
2. Secret Key: merupakan masukan bagi algoritma enkripsi yang berupa nilai bebas terhadap teks asli dan menentukan hasil keluaran algoritma enkripsi.
3. Ciphertext: keluaran algoritma enkripsi yang dianggap sebagai pesan dalam bentuk tersembunyi.
4. Algoritma Enkripsi: algoritma enkripsi memiliki 2 masukan yaitu teks asli dan teks kunci rahasia. Algoritma enkripsi melakukan transformasi terhadap teks asli sehingga menghasilkan teks sandi.
5. Algoritma Dekripsi: algoritma dekripsi memiliki 2 masukan yaitu teks sandi dan kunci rahasia. Algoritma dekripsi memulihkan kembali teks sandi menjadi teks asli bila kunci rahasia yang dipakai sesuai dengan algoritma dekripsi.
Berdasarkan kunci yang dipakai, algoritma kriptografi dibagi menjadi tiga, yaitu algoritma simetri (menggunakan satu kunci untuk enkripsi dan dekripsi), algoritma asimetri (menggunakan kunci yang berbeda untuk enkripsi dan dekripsi) dan fungsi hash (Ariyus, 2008).
2.1.5. Sistem Kriptografi Asimetris
Diffie-Hellman adalah sistem kriptografi public key yang pertama, Difie-Hellman tidak sepopuler RSA dan ElGamal karena hanya dapat digunakan untuk key agreement. Menggunakan Difie-Hellman, dua pengguna, sebut saja A dan B, dapat membuat kunci privat yang hanya diketahui oleh A dan B, meskipun komunikasi antara A dan B dapat dilihat semua orang.
Diffe-Hellman menggunakan finite field GF(q) yang sangat besar. A dan B keduanya mengetahui GF(q) dan elemen g ∈ GF(q). GF(q) dan g tidak perlu dirahasiakan, jadi boleh saja diketahui semua orang. Meskipun tidak harus, g sebaiknya merupakan generator untuk GF(q)* , atau setidaknya memiliki order yang besar agar range untuk pembuatan kunci cukup besar.
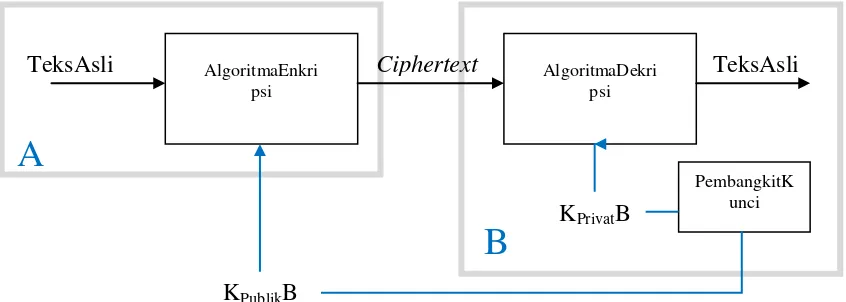
Kriptografi yang termasuk algoritma asimetris adalahDiffie-Hellman, RSA, ElGamal, DSA dan sebagainya. Skema algoritma kriptografi asimetri dengan kunci publik dapat dilihat pada Gambar 2.2. berikut ini.
Gambar 2.2. Skema Kriptografi Asimetri Kunci Publik (Sadikin, 2012)
2.1.6. Bilangan Prima
Bilangan positif p (�>1) disebut bilangan prima jika pembaginya hanya 1 dan p. Sebagai contoh bilangan 23 adalah bilangan prima karena ia hanya habis dibagi 1 dan 23. Karena bilangan prima harus lebih besar dari satu, maka barisan bilangan prima dimulai dari 2, yaitu 2, 3, 5 , 7, 11, 13, .... Seluruh bilangan prima adalah bilangan ganjil, kecuali dua yang merupakan bilangan genap.
AlgoritmaEnkri psi
AlgoritmaDekri psi
KPublikB
TeksAsli Ciphertext TeksAsli
A
B
2.1.7. Aritmatika Modulo
Aritmatika modulo merupakan sisa hasil pembagian dua bilangan. Operator yang digunakan dalam aritmatika modulo adalah mod. Misalkan, jika bilangan integer a dibagi dengan bilangan integer yang lebih besar dari nol(b> 0), maka akan menghasilkan sisa bagi r (remainder) dengan hasil bagi s (quotient). Sehingga dapat dinotasikan sebagai berikut (Harahap, A. A. 2014).
a mod b = r sedemikian sehingga a = bs + r, dengan 0 ≤ b<n ...(2.1) Sebagai contoh, jika 17 mod 3 = 2, maka 17 = (3 × 5) + 2.
Jika a negatif, maka bagi |a| dengan b mendapatkan sisa bagi r’ (Munir, 2006). Sehingga didapatkan:
a mod b = b – r’, dimana r’ ≠ 0 dan a< 0 …...……….(2.2) Sebagai contoh, jika |-25| mod 7 = 4, maka -25 mod 7 = 7 – 4 = 3.
Cormen, at al. (2009) menuliskan di dalam bukunya, untuk setiap bilangan bulat a dan setiap bilangan bulat positif b, nilai a mod b adalah sisa (residu) dari hasil bagi a / b:
a mod b = a – b (a/b), dimana 0 ≤ a mod b<b …...….(2.3) Contohnya adalah 33 mod 5 = 33 – 5(33/5) = 33 – 5(6) = 33 – 30 = 3.
2.1.8. Modulo Eksponensial
Permasalahan pada operasi modulo adalah bagaimana menghitung xy (mod z) dengan z yang sangat besar. Terdapat beberapa algoritma untuk menghitung modulo eksponensial, antara lain adalah dengan metode iterasi.
Berikur pseudocodedari modulo eksponensial dengan menggunaka metode iterasi :
Function mod exp (x, y, n) z = 1
return z }
2.1.9. Inversi Modulo
Jika a dan m relatif prima dan m> 1, maka inversi dari a mod m dapat ditemukan. Inversi dari a (mod m), juga disebut inversi perkalian, dimana bilangan bulat a-1 sedemikian sehingga
aa-1≡ 1 (mod m) ………...………(2.4) Contoh: untuk inversi dari 5 (mod 7), penyelesaiannya dapat dilihat pada Tabel 1.
Tabel 2.1 Penyelesaian contoh soal inversi modulo a-1 a-1 × 5 (mod 7)
1 5
2 3
3 1
Pada Tabel 1, iterasi berhenti ketika a-1a ≡ 1 (mod m) dan diperoleh a-1 = 3.
2.1.10.Elemen Primitif
Selain bilangan prima, dalam kriptografi ElGamal juga digunakan elemen primitif yang merupakan elemen pembangun dari grup Z
p. Untuk mencari elemen ini
digunakan p=2q+1, dimana q merupakan bilangan prima. Jika elemen α memenuhi α2 mod p ≠ 1 dan αq mod p ≠ 1, maka α merupakan elemen primitif.
Untuk mengetahui suatu bilangan merupakan elemen primitif atau tidak dapat dilakukan langkah-langkah sebagai berikut :
1. Input bilangan prima aman p ≥ 5. 2. Hitung �= �−1
2
4. Jika α 2mod p= 1, maka α bukan elemen primitif. 5. Jika αq mod p= 1, maka α bukan elemen primitif.
6. Jika tidak terpenuhi dua persyaratan di atas maka q merupakan elemen primitif.
2.1.11.Fermat’s Little Theorem
Fermat’s Little Theorem adalah suatu metode yang digunakan untuk menguji keprimaan suatu bilangan bulat. Teorema Fermat ditemukan oleh Pierre De Fermat merupakan seorang matematikawan Perancis pada tahun 1640. Meskipun dapat digunakan untuk mempermudah kalkulasi dalam kriptografi, peran terpenting dari Fermat's little theorem adalah sebagai dasar dari berbagai teknik enkripsi asimetris.
Bilangan prima jumlahnya tak terhingga banyaknya, bilangan prima terbesar yang ditemukan oleh para ahli adalah:
232.582.657-1
Salah satu perhitungan matematis yang digunakan untuk menghasilkan bilangan prima adalah metode Fermat yang dapat dirumuskan sebagai berikut:
Bila p adalah bilangan prima maka berlaku a p-1 mod p = 1 untuk
1 ≤ a < p
Di mana p adalah bilangan bulat dan a adalah urutan bilangan yang lebih kecil dari p Contoh penerapan metode Fermat adalah sebagai berikut:
a. Bila p = 4
Maka 1 ≤a< 4, didapat a = {1, 2, 3} a p-1mod p
Jadi, angka 4 bukan merupakan bilangan prima sebab dalam pengecekan menggunakan metode Fermat didapat semua hasil dari urutan bilangan yang lebih kecil dari 4 terdapat nilai yang 0.
b. Bila p = 5
Maka 1 ≤a< 5, jadi didapat a = {1, 2, 3, 4} a p-1 mod p
1 5-1 mod 5 = 14 mod 5 = 1 25-1 mod 5 = 24 mod 5 = 1 35-1 mod 5 = 34 mod 5 = 1 45-1 mod 5 = 44 mod 5 = 1
Jadi, angka 5 merupakan bilangan prima sebab dalam pengecekan menggunakan metode Fermat didapat semua hasil dari urutan bilangan yang lebih kecil dari 5 adalah 1. Untuk angka yang besar dengan jumlah nilai a yang banyak, hanya diambil beberapa angka sebagai contoh.
2.1.12.Algoritma Euclid
Algoritma Euclid dapat dikembangkan (disebut dengan algoritma Extended Euclid) agar dapat menemukan dua integer x dan y yang unik selain nilai GCD(a,b) sehingga memenuhi relasi yang ditunjukkan oleh persamaan (P14) (Harahap, A. A. 2014). x × a + y × b = GCD(a,b) ……… (2.5)
Berikut ini merupakan contoh dari algoritma Extended Euclid. Diketahui GCD(11,23) = 1, dengan mengikuti persamaan (2.3) dan (2.5) maka dapat ditemukan bilangan x dan y dari persamaan 11x + 23y = 1 (Lipschutz & Lipson, 2007). GCD(23,11) = 1 = 23 – 11(2). Dapat dilihat bahwa a = 23, b = 11, x = 1 dan y = -2. 2.2.Algoritma ElGamal
tiga proses, yaitu proses pembentukan kunci, enkripsi, dan dekripsi. Algoritma ElGamal mendasarkan kekuatannya pada fakta matematis kesulitan menghitung logaritma diskret.
Hingga saat ini belum ada yang berhasil memecahkan algoritma ElGamal. Karena kekomplesitasan algoritma ini, maka penyerangan yang dilakukan dari segala sisi tidak mampu menembus pertahanan algoritma ElGamal ini.
2.2.1. Pembangkit Kunci
Langkah-langkah dalam pembangkitan kunci
1. Pilih sembarang bilangan prima p ( p dapat di-share di antara anggota kelompok). Misalkan p = 263
2. Pilih dua buah bilangan acak, g dan x, dengan syarat g <p dan 1 ≤ x ≤ p – 2 Misalkan g = 107 dan x = 62
3. Hitung y dengan rumus
y = gxmod p ………... (2.5) y = 10762mo 263 = 39
Hasil dari algoritma ini:
1. Kunci publik: tripel (y, g, p) = (39, 107, 263) 2. Kunci privat: pasangan (p ,x) = (263,62)
2.2.2. Proses Enkripsi
Langkah-langkah dalam mengenkripsi pesan: 1. Terima kunci publik (y, g, p) = (39, 107, 263)
2. Ubah nilai blok pesan ke dalam nilai ASCII. Ekspresikan pesan P = “A” = 65 (kode ASCII) sebagai bilangan.
3. Pilih bilangan acak k, yang dalam hal ini 1 ≤ k ≤ p – 2. Misal, k = 94 4. Setiap blok m dienkripsi dengan rumus
a = 10794mod 263 = 31 b = ykm mod p
b = 3994 65mod263= 113 ………... (2.7) Pasangan a dan b adalah cipherteks untuk blok pesan m. Jadi, ukuran cipherteks dua kali ukuran plainteksnya.
5. Kirim a = 31 dan b = 113 ke pemilik kunci publik.
2.2.3. Proses Dekripsi
Langkah-langkah dalam mendekripsi pesan: 1. Gunakan kunci privatx untuk menghitung (ax)– 1
(ax)– 1 = ap – 1 – xmod p ………... (2.8) (ax)– 1 = 31263 – 1 – 94mod 263 = 96
2. Hitung plainteks m
m = b(ax)– 1 mod p ……..………... (2.9) m = 113(96)– 1 mod 263 = 65