On the strong metric dimension of antiprism graph,
king graph, and
K
m⊙
K
ngraph
Yuyun Mintarsih and Tri Atmojo Kusmayadi
Department of Mathematics, Faculty of Mathematics and Natural Sciences, Universitas Sebelas Maret, Surakarta, Indonesia
E-mail: yuyunaziz2@gmail.com, tri.atmojo.kusmayadi@gmail.com
Abstract. LetGbe a connected graph with a set of verticesV(G) and a set of edgesE(G). The interval I[u, v] between uand v to be the collection of all vertices that belong to some shortestu-v path. A vertexs∈V(G) is said to be strongly resolved for verticesu,v ∈V(G) ifv∈I[u, s] oru∈I[v, s]. A vertex setS ⊆V(G) is a strong resolving set forGif every two distinct vertices ofGare strongly resolved by some vertices ofS. The strong metric dimension ofG, denoted by sdim(G), is defined as the smallest cardinality of a strong resolving set. In this paper, we determine the strong metric dimension of an antiprismAn graph, a kingKm,n graph, and aKm⊙Kn graph. We obtain the strong metric dimension of an antiprim graph An arenfornodd andn+ 1 forn even. The strong metric dimension of King graphKm,nis m+n−1. The strong metric dimension ofKm⊙Kngraph arenform= 1,n≥1 andmn−1 form≥2,n≥1.
1. Introduction
The strong metric dimension was introduced by Seb¨o and Tannier [6] in 2004. Let G be a
connected graph with a set of vertices V(G) and a set of edges E(G). Oelermann and
Peters-Fransen [5] defined the interval I[u, v] between u and v to be the collection of all vertices that
belong to some shortest u −v path. A vertex s ∈ S is said to strongly resolve two verticesu
and vifu∈I[v, s] orv∈I[u, v]. A vertex setS ofGis a strong resolving set forGif every two
distinct vertices ofG are strongly resolved by some vertices ofS. The strong metric basis of G
is a strong resolving set with minimal cardinality. The strong metric dimension of a graphG is
defined as the cardinality of strong metric basis denoted by sdim(G).
Some authors have investigated the strong metric dimension to some graph classes. Seb¨o and
Tannier [6] observed the strong metric dimension of complete graph Kn, cycle graph Cn, and
tree. Kratica et al. [2] observed the strong metric dimension of hamming graph Hn,k. At the
same year, Kratica et al [3] determined the strong metric dimension of convex polytopeDnand
Tn. Yi [8] determined thatsdim(G) = 1 if only ifGis path graph andsdim(G) =n−1 if only if
Gis complete graph. Kusmayadi et al. [4] determined the strong metric dimension of sunflower
graph, t-fold wheel graph, helm graph, and friendship graph. In this paper, we determine the
2. Main Results
2.1. Strong Metric Dimension
Let G be a connected graph with a set of vertices V(G), a set of edges E(G), and
S={s1, s2, . . . , sk} ∈ V(G). Oelermann and Peters-Fransen [5] defined the interval I[u, v]
betweenu and v to be the collection of all vertices that belong to some shortestu −v path. A
vertexs∈S is said to strongly resolve two verticesu andvifu∈I[v, s] orv ∈I[u, s]. A vertex
setS of Gis a strong resolving set forGif every two distinct vertices of Gare strongly resolved
by some vertices of S. The strong metric basis of G is a strong resolving set with minimal
cardinality. The strong metric dimension of a graph G is defined as the cardinality of strong
metric basis denoted by sdim(G). We often make use of the following lemma and properties
about strong metric dimension given by Kratica et al. [3].
Lemma 2.1 Let u, v ∈V(G), u ̸= v,
(i) d(w,v) ≤ d(u,v) for each w such that u w∈ E(G), and (ii) d(u,w) ≤ d(u,v) for each w such that v w∈ E(G).
Then there does not exist vertex a ∈ V(G), a ̸= u,v that strongly resolves vertices u and v.
Property 2.1 If S⊂ V(G) is strong resolving set of graph G, then for every two vertices u, v
∈ V(G) satisfying conditions 1 and 2 of Lemma 2.1, obtained u ∈ S or v ∈S.
Property 2.2 If S⊂ V(G) is strong resolving set of graph G, then for every two vertices u, v
∈ V(G) satisfying d(u, v) = diam(G), obtained u ∈S or v ∈ S.
2.2. The Strong Metric Dimension of antiprism graph
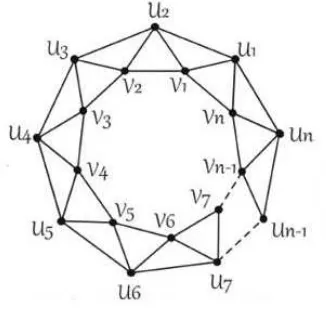
Baˇca [1] defined the antiprism graph An for n ≥ 3 is a 4-regular graph with 2n vertices and
4n edges. It consists of outer and inner Cn, while the two cycles connected by edges viui and
viu1+i(mod n) fori= 1, 2, 3, . . . ,n. The antiprism graphAn can be depicted as in Figure 1.
Figure 1. Antiprism graph An
Lemma 2.2 For every integer n≥3and n odd, if S is a strong resolving set of antiprism graph
An then|S | ≥ n.
Proof. We know that S is a strong resolving set of antiprism graph An. Suppose that S
contains at mostn - 1 vertices, then|S |< n. LetV1,V2 ⊂V(An), with V1 ={u1, u2, . . . , un}
generality, we may take |S1 | =p, p >0 and |S2 | =q,q ≥0. Clearly p +q ≥n, if not then
there are two distinct verticesva and vb whereva ∈V1\S1 and vb ∈V2\S2 such that for every
s∈S, we obtain va∈/ I[vb, s] andvb ∈/ I[va, s]. This contradicts with the supposition thatS is a
strong resolving set. Thus, |S| ≥n. ⊓⊔
Lemma 2.3 For every integer n ≥3and n odd, a set S ={u1, u2, . . . , un} is a strong resolving
set of antiprism graph An.
Proof. For every integer i, j ∈ [1, n] with 1 ≤ i < j ≤ n, a vertex ui ∈ S which strongly
resolves vi dan vj so that vj ∈ I[vi, uj]. Thus, S ={u1, u2, . . . , un} is a strong resolving set of
antiprism graphAn. ⊓⊔
Lemma 2.4 For every integer n ≥ 3 and n even, if S is a strong resolving set of antiprism graph An then |S| ≥ n+1.
Proof. We know that S is a strong resolving set of antiprism graph An. Suppose that S
contains at most nvertices, then |S|< n+ 1. LetV1,V2 ⊂V(An), withV1 ={u1, u2, . . . , un}
and V2 = {v1, v2, . . . , vn}. Now, we define S1 = V1 ∩S and S2 = V2 ∩S. Without loss of
generality, we may take|S1 |=p,p≥0 and|S2|=q,q ≥0. Clearlyp+q≥n+ 1, if not then
there are two distinct verticesvaandvb whereva∈V1\S1 andvb ∈V2\S2 such that for everys
∈S, we obtain va∈/ I[vb,s] andvb ∈/ I[va,s]. This contradicts with the supposition thatS is a
strong resolving set. Thus,|S| ≥n+1. ⊓⊔
Lemma 2.5 For every integer n≥3 and n even, a setS ={u1, u2, . . . , un 2, u
n
2+1, v1, v2, . . . , v n 2}
is a strong resolving set of antiprism graph An.
Proof. We prove that for every two distinct vertices u, v ∈ V(An)\S, u ̸= v there exists a
vertex s∈S which strongly resolvesu and v. There are three possible pairs of vertices.
(i) A pair of vertices (ui, uj) withi, j = n2 + 2,n2 + 3, . . . , n,i̸=j.
For every integer i, j ∈ [n
2 + 2, n] with i < j, we obtain the shortest ui - u1 path:
ui, ui+1, . . . , uj, . . . , un, u1. Thus,uj ∈I[ui, u1].
(ii) A pair of vertices (vi, vj) with i, j = n2 + 1,n2 + 2, . . . , n,i̸=j.
For every integer i, j ∈ [n2 + 1, n] with i < j, we obtain the shortest vi - v1 path:
vi, vi+1, . . . , vj, . . . , vn, v1. Thus, vj ∈ I[vi, v1].
(iii) A pair of vertices (ui, vj) withi= n2 + 2,n2 + 3, . . . , n dan j = n2 + 1,n2 + 2, . . . , n.
For every integeri∈ [n
2 + 2, n] and j ∈[n2 + 1, n] withi≤j, we obtain the shortestui - v1 path: ui, vi, . . . , vj,. . .,vn,v1. Thus,vj ∈I[ui, v1]. Then, for every integeri∈[n2+2, n] and j ∈[n2 + 1, n] withi > j, we obtain the shortestui -vn
2 path: ui, vi−1, . . . , vj, . . . , v n 2+1, v
n 2.
Thus,vj ∈I[ui,vn 2].
From every possible pairs of vertices, there exists a vertexs ∈S which strongly resolvesu,v ∈
V(Km,n)\S. Thus,Sis a strong resolving set of antiprism graphAn. ⊓⊔
Theorem 2.1 Let An be the antiprism graph with n ≥3, then
sdim(An) =
{
n, n odd;
n+ 1, n even.
Proof. LetAn be an antiprism graph with n≥3 and a set of vertices V(An) = {u1,u2,. . .,
un,v1,v2,. . .,vn}. We divide the proof into two cases according to the values ofn.
(i) Forn odd.
By using Lemma 2.3, a setS ={u1, u2, . . . , un} is a strong resolving set of antiprism graph
An. According to Lemma 2.2,|S |≥nso thatS is a strong metric basis of antiprism graph
(ii) Forn even.
By using Lemma 2.5, a setS ={u1, u2, . . . , un
2+1, v1, v2, . . . , v n
2}is a strong resolving set of
antiprism graphAn. According to Lemma 2.4,|S |≥nso that Sis a strong metric basis of
antiprism graphAn. Hence,sdim(An) = n+ 1. ⊓⊔
2.3. The Strong Metric Dimension of King Graph
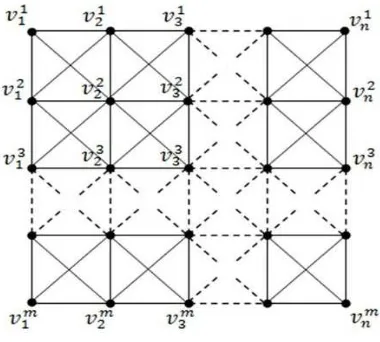
Weisstein [7] defined the king graph Km,n form, n ≥ 2 is the graph with mn vertices in which
each vertex represents a square in an m ×n chessboard, and each edge corresponds to a legal
move by king.The king graph Km,n can be depicted as in Figure 2.
Figure 2. King graph Km,n
Lemma 2.6 For every integer m,n ≥ 2, if S is a strong resolving set of king graph Km,n then
|S | ≥ m+n-1.
Proof. We know that S is a strong resolving set of king graph Km,n. Suppose that S
contains at most m+n−2 vertices, then | S | < m+n−1. Let V1, V2 ⊂ V(An), with
V1 = {v11, v21, . . . , vn1, v12, v31, . . . , vm1 } and V2 = {v22, v23, . . . , vn2, v23, v33, . . . , vn3, . . . , vm2 , vm3 , vnm}.
Now, we defineS1 =V1∩Sand S2 =V2∩S. Without loss of generality, we may take|S1 |=p,
p >0 and|S2|=q,q ≥0. Clearlyp+q≥m+n−1, if not then there are two distinct vertices
va and vb whereva ∈V1\S1 and vb ∈V2\S2 such that for everys∈S, we obtain va ∈/ I[vb, s]
and vb ∈/ I[va, s]. This contradicts with the supposition that S is a strong resolving set. Thus,
|S | ≥m+n-1. ⊓⊔
Lemma 2.7 For every integer m,n ≥ 2, a set S = {v1
1, v21, . . . , vn1, v12, v31, . . . , vm1 } is a strong
resolving set of king graph Km,n.
Proof. We prove that for every two distinct verticesu, v∈ V(Km,n)\S,u̸=v there exists a
vertex s∈S which strongly resolvesu and v. There are three possible pairs of vertices.
(i) A pair of vertices (vpk, vpl) withp= 2,3, . . . , mand k, l= 2,3, . . . , n.
For every integerp∈[2, m] andk, l∈[2, n] withk < l, we obtain the shortestvlp -v1p path:
vlp, vpl
−1, . . . , v
p k, . . . , v
p
2, v
p
1. Thus, v
p k∈I[v
p l, v
p
1].
(ii) A pair of vertices (vi
q, vjq) withi, j= 2,3, . . . , mand q= 2,3, . . . , n.
For every integer i, j ∈ [2, m], q ∈ [2, n] with i < j, we obtain the shortest vj
q - vq1 path:
vj
(iii) A pair of vertices (vi
From every possible pairs of vertices, there exists a vertex s ∈ S which strongly resolves
u, v∈V(Km,n)\S. ThusS is a strong resolving set of king graphKm,n. ⊓⊔
Theorem 2.2 Let Km,n be the king graph withm, n ≥ 2, then sdim(Km,n) = m+n−1.
Proof. By using Lemma 2.7, a setS ={v11, v12, . . . , v1n, v12, v13, . . . , vm
1 }is a strong resolving set
of king graph Km,n. According to Lemma 2.6, | S |≥ m+n−1 so that S is a strong metric
basis of king graphKm,n. Hence, sdim(Km,n) =m+n−1. ⊓⊔
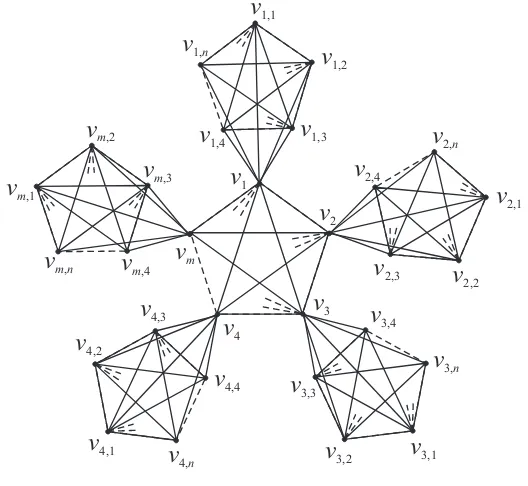
2.4. The Strong Metric Dimension of Km⊙Kn Graph
The corona product Km⊙Kn graph is graph obtained from Km and Kn by taking one copy
Proof. For every integeri∈[1, m−1], we obtain the shortestvm,n-vi,k path: vm,n, vm, vi, vi,k.
So thatvi,k strongly resolves a pair of vertices (vi, vm,n). Thus,vi ∈I[vm,n, vi,k].
For a pair of vertices (vi, vj) with i, j∈[1, m] andi̸=j, we obtain the shortestvi - vj,l path:
vi, vj, vj,l. So thatvj,l strongly resolves a pair of vertices (vi, vj). Thus,vj ∈I[vi, vj,l].
ThereforeS ={v1,1, v1,2, . . . , v1,n−1, v1,n, v2,1, v2,2, . . . , v2,n−1, v2,n, . . . , vm,1, vm,2, . . . , vm,n−1}
is a strong resolving set ofKm⊙Kngraph. ⊓⊔
Theorem 2.3 Let Km⊙Kn graph with m, n ≥ 1, then
sdim(Km⊙Kn) =
{
n, m = 1, n≥1;
mn−1, m≥2, n≥1.
Proof. SupposeKm⊙Kn graph withm, n, k≥1 and a set of verticesV(Km⊙Kn)={v1,v2,
. . .,vm,v1,1,v1,2,. . .,v1,n,v2,1,v2,2,. . .,v2,n,. . .,vm,1, vm,2, . . . , vm,n}. We divide the proof into
two cases according to the values of mand n.
(i) Form= 1 and n≥1.
By using characterization Yi [8],sdim(G) =n−1 if only ifG∼=Kn, so thatsdim(K1⊙Kn) =
n because K1 ⊙Kn ∼= Kn+1 then strong resolving set of K1 ⊙Kn graph has n element.
Hence sdim(K1⊙Kn) =n.
(ii) Form≥2 andn≥1.
By using Lemma 2.9 a setS={v1,1, v1,2, . . . , v1,n−1, v1,n, v2,1, v2,2, . . . , v2,n−1, v2,n, . . . , vm,1,
vm,2, . . . , vm,n−1}is a strong resolving set ofKm⊙Kngraph. According to Lemma 2.8,|S|≥
mn−1 so thatSis a strong metric basis ofKm⊙Kngraph. Hencesdim(Km⊙Kn) =mn−1.
⊓ ⊔
3. Conclusion
According to the discussion above, it can be concluded that the strong metric dimension of
an antiprism graph, a king graph, and a Km⊙Kngraph are as stated in Theorem 2.1, Theorem
2.2, and Theorem 2.3 respectively.
Open Problem: Determine the strong metric dimension of a Km⊙kKn graph.
4. Acknowledgement
The authors gratefully acknowledge the support from Department of Mathematics, Faculty of Mathematics and Natural Sciences, Universitas Sebelas Maret, Surakarta. Then, we wish to thank the referees for their suggestions and references, which helped to improve the paper.
References
[1] Baˇca, M., F. Bashir, and A. Semaniˇcov´a, Face Antimagic Labeling of Antiprisms, Util. Math 84 (2011), 209–224.
[2] Kratica, J., V. Kovaˇcevi´c-Vujˇci´c, and M. ˇCangalovi´c, Minimal Doubly Resolving Sets and The The Strong Metric Dimension of Hamming Graphs, Applicable Analysis and Discrete Mathematics6(2012), 63–71. [3] Kratica, J., V. Kovaˇcevi´c-Vujˇci´c, and M. ˇCangalovi´c, Minimal Doubly Resolving Sets and The The Strong
Metric Dimension of Some Comvex Polytope, Applied Mathematics and Computation218(2012), 9790– 9801.
[4] Kusmayadi, T. A., S. Kuntari, D. Rahmadi, and F. A. Lathifah,On The Strong Metric Dimension of Some Related Wheel Graph, Far East Journal of Mathematical Sciences (FJMS)99(2016), no. 9, 1325–1334. [5] Oelermann, O. and J. Peters-Fransen,The Strong Metric Dimension of Graphs and Digraphs, Discrete Applied
Mathematics155(2007), 356–364.
[6] Seb¨o, A. and E. Tannier, On Metric Generators of Graph, Mathematics and Operations Research 29(2)
(2004), 383–393.
[7] Weisstein, E. W., King Graph, From MathWorld-A Wolfram Web Resource, http://mathworld.wolfram.com/KingGraph.html.