III PEMBAHASAN. λ = 0. Ly = 0, maka solusi umum dari persamaan diferensial (3.3) adalah

(1)

III PEMBAHASAN

Pada bagian ini akan diformulasikan masalah yang akan dibahas. Solusi masalah akan diselesaikan dengan Metode Dekomposisi Adomian. Selanjutnya, metode ini akan digunakan untuk menyelesaikan model yang dinyatakan dalam bentuk Persamaan Diferensial Abelian. Agar validitas metode ini terjamin, maka pada bagian ini akan dikaji beberapa contoh kasus. Metode Dekomposisi Adomian yang diterapkan dalam tulisan ini mengikuti pustaka ( Adomian 1991).

3.1 Formulasi Masalah

Untuk mengkaji lebih lanjut Metode Dekomposisi Adomian, maka tinjau terlebih dahulu persamaan diferensial taklinear berikut

[ ( )] ( )

F y x =G x ,

(3.1) dengan F menyatakan operator turunan yang

bentuknya taklinear dan G merupakan fungsi yang diketahui, sedangkan y menyatakan fungsi yang akan ditentukan.

Misalkan bagian linear dari F dipisah menjadi dua bagian yaitu L dan R, dengan L suatu operator yang mempunyai invers dan R operator linear lainnya. Bagian taklinear dari F, dimisalkan N. Jadi, persamaan diferensial (3.1) dapat ditulis menjadi

(L+ +R N y) =G (3.2) atau dapat juga ditulis menjadi

Ly= −G Ry−Ny. (3.3) Selanjutnya, dipilih operator turunan L yang memuat turunan dengan orde tertinggi dan mempunyai invers, sedangkan R operator turunan linear lainnya yang mempunyai orde lebih kecil dari L.

Metode Dekomposisi Adomian dikonstruksi berdasarkan eksistensi dari invers L yaitu L^-1 (sebagai contoh, jika d

L= dx, maka ¹

0

( ) ( )

x

L⁻ ⋅ = ⋅

∫

ds). Jika kedua ruas pada persamaan (3.3) dikenakan operator L^-1 dari kiri, maka diperoleh solusi takhomogen dari persamaan (3.3) berbentuk

1 1 1

y=L G⁻ −L Ry⁻ −L Ny⁻ . Misalkan fungsi ( )h x merupakan solusi homogen dari persamaan (3.3) atau persamaan

0

Ly= , maka solusi umum dari persamaan diferensial (3.3) adalah

1 1 1

y= +h L G⁻ −L Ry⁻ −L Ny⁻ . (3.4) Dengan demikian solusi persamaan diferensial yang diberikan pada persamaan (3.4) bergantung pada bentuk taklinearL Ny⁻¹ . Karena adanya bentuk taklinear tersebut, maka persamaan diferensial (3.1) sulit diselesaikan secara analitik. Berdasarkan hal tersebut, maka disarankan menggunakan metode yang disebut Metode Dekomposisi Adomian, dengan bentuk taklinear Ny akan didekomposisi dengan cara yang diuraikan pada bagian selanjutnya.

3.2 Metode Dekomposisi Adomian

Pada metode ini, solusi persamaan diferensial (3.4) dimisalkan dalam bentuk uraian deret berikut

2

0 1 2

0 n

n n

y y λy λ y ^∞ λ y

=

= + + + =

∑

^,

(3.5) dengan λ suatu parameter, sedangkan

0, 1, 2,..., _n

y y y y fungsi yang akan ditentukan.

Jika operator taklinear N dikenakan pada y, maka diperoleh

2

0 1 2

( )

Ny=N y +λy +λ y + . (3.6) Dengan menggunakan uraian deret Maclaurin pada fungsi Ny dalam persamaan (3.6) terhadap λ diperoleh

2

0 1 2

0 n

n n

Ny A λA λ A ^∞ λ A

=

= + + + =

∑

^,

(3.7) dengan

0 0

1

0

1

!

n

n n

A Ny A d Ny

d

A d Ny

n d

λ

=

.

Selanjutnya, misalkan Ny= f y( ), sehingga fungsi f merupakan fungsi polinomial yang diberikan oleh persamaan (3.7) dan f juga merupakan fungsi analitik.

Fungsi polinomial ini disebut polinomial Adomian. Dengan demikian bentuk

(2)

, 0,1, 2,

A ii = … pada persamaan (3.7) dapat dinyatakan sebagai berikut

0 0

1 1 0

2 1

2 2 0 0

3 1

3 3 0 1 2 0 0

( ) '( )

'( ) ''( ) 2

'( ) ''( ) '''( )

3!

A f y A y f y

A y f y y f y

A y f y y y f y y f y

=

= +

= + +

(3.8) Penurunan persamaan (3.8) dapat dilihat pada Lampiran 2.

Selanjutnya, misalkan L Ry⁻¹ dan L Ny⁻¹ berorde λ , maka persamaan (3.4) dapat ditulis

1 1 1

y= +h L G⁻ −λL Ry⁻ −λL Ny⁻ .

(3.9) Jika y pada persamaan (3.5) dan Ny pada persamaan (3.7) disubstitusikan ke dalam persamaan (3.9), maka diperoleh

0 1

2 1 1

0 1 2 2

2

1 2

0 1 2

( ) y y y

y

A A

y h L G L R y

L A

λ λ λ λ

λ

λ λ λ

− −

−

⎛ ⎛ + ⎞⎞

+ + + ⎜⎜⎝ ⎜⎜⎝+ + ⎟⎟⎠⎟⎟⎠

− + + +

= + −

(3.10) Jika koefisien dari perpangkatan λ dari persamaan (3.10) disamakan pada kedua ruas, maka koefisien dari λ λ λ⁰, , ²,... masing- masing memberikan persamaan berikut

1 0

1 1

1 0 0

1 1

2 1 1

( ) ( )

y h L G

y L Ry L A

−

− −

= +

= − −

(3.11) Secara umum bentuk y adalah_n

1 1

-1 -1

( ) ( ), 1

n n n

y = −L⁻ Ry −L⁻ A n≥ .

Penurunan persamaan (3.11) dapat dilihat pada Lampiran 3.

Selanjutnya, berikut ini akan ditunjukkan bahwa

0 1 2

0 n n

y y y y y

∞

=

= + + + =

∑

(3.12) merupakan solusi dari persamaan diferensial (3.1) atau persamaan diferensial (3.2).

Jika y pada persamaan (3.12) disubstitusikan ke dalam ruas kiri persamaan (3.1), maka diperoleh ruas kiri persamaan (3.1) berikut

[ ]

0 1

0 1 2

2

0 1 2

( ) ( )

( ) ( ) ( )

( )

( ) ( ) ( )

R y R y L y L y L y

R y

N y N y N y

+ +

⎡ ⎤

+ + + + ⎢⎣ + ⎥⎦

+ + + +

(3.13) Berdasarkan persamaan (3.11), diperoleh

( ¹ ) ¹ ⁰

0 1 2 1

0 1

1 1

1

0 0 1 1

( ) ( ) ( )

= ( )

L y L y L y L h L G L L Ry L A L L Ry

L A

L h G Ry A Ry A

−

⎛− −⎞

+ + + = + + ⎜⎜⎝ − ⎟⎟⎠+

⎛− −⎞

⎜ ⎟+

⎜ − ⎟

⎝ ⎠

+ − − − − −

(3.14) Selain itu, dari persamaan (3.6) dan (3.7) diperoleh

2 2

0 1 2 0 1 2

( )

N y +λy +λ y + =A +λA +λ A + (3.15) atau

2 2

0 1 2 0 1 2

( ) ( ) ( )

N y +λN y +λ N y + =A +λA+λ A +

(3.16) Jika koefisien dari perpangkatan λ dari persamaan (3.16) disamakan pada kedua ruas, maka koefisien dari λ λ λ⁰, , ²,...masing- masing memberikan persamaan berikut

0 0

1 1

( ) ( ) A N y A N y

=

2 ( 2)

A =N y

(3.17) Jika persamaan (3.14) dan persamaan (3.17) disubstitusikan ke dalam persamaan (3.13), maka diperoleh persamaan berikut

[ ]

[ ] [ ]

0 1

0 1 2

2

0 1 2

0 0 1 1

0 1 2 0 1 2

( ) ( )

( ) ( ) ( )

( )

( ) ( ) ( )

( )

( ) ( ) ( )

,

R y R y L y L y L y

R y N y N y N y

L h G Ry A Ry A

R y R y R y A A

G

A

+ +

⎡ ⎤

+ + + +⎢⎣ + ⎥⎦+

+ + +

= + − − − − − +

+ + + + + + +

=

dengan L h( )=0 karena h solusi homogen dari persamaan (3.3).

3.3 Aplikasi pada Persamaan Diferensial Abelian

Bentuk umum Persamaan Diferensial Abelian adalah

2 3

0 1 2 3

' ( ) ( ) ( ) ( )

y = f x +f x y+f x y + f x y . (3.18) Persamaan (3.18) dapat ditulis menjadi

1( ) 2( ) 1( ) 3( ) 2( ) 0( )

Ly− f x y− f x N y − f x N y = f x (3.19) dengan

(3)

L d

=dx , ( )N y₁ =y², ( )N₂ y = y³. Dalam Metode Dekomposisi Adomian, dimisalkan solusi persamaan diferensial (3.18) dinyatakan dalam bentuk deret berikut

0

( ) _n( )

n

y x y x

∞

=

∑

^, (3.20) dengan y y y₀, ₁, ₂,... akan ditentukan berikut ini. Bentuk taklinear yang dipilih adalah

2 1( )

N y = y dan N y₂( )=y³ yang masing- masing memiliki polinomial Adomian sebagai berikut.

1

0

2

0

( ) ,

n n

N y A

N y B

∞

=

∞

=

∑

(3.21) dengan An dan Bn berturut-turut merupakan uraian polinomial Adomian dari fungsi N1 dan N2. Berdasarkan persamaan (3.9) diperoleh empat suku dari polinomial Adomian untuk masing-masing deret An dan Bn sebagai berikut

2,

0 0

1 0 1,

2,

2 0 2 1

3 0 3 1 2,

2 2

A y

A y y

A y y y

A y y y y

=

= +

dan

3,

0 0

2 ,

1 0 1

2 2

2 0 2 0 1,

2 3

3 0 3 0 1 2 1.

3

3 3

3 6

B y B y y B y y y y B y y y y y y

=

= +

= + +

(3.22) Selanjutnya, jika kedua ruas pada persamaan (3.19) dikenakan operator L⁻¹ dari kiri, maka diperoleh bentuk

1 2 1

1 1

0

3 2

( ) ( ) ( ) ( ) ( ) ( ) f x y f x N y

y L h L f x

f x N y

− ⎡ + ⎤ −

− ⎢⎣+ ⎥⎦= +

(3.23)

Kemudian persamaan (3.20) dan persamaan (3.21) disubstitusikan ke dalam persamaan (3.23), maka diperoleh bentuk

2

1 1 0

1

0 0

3 0 1

0

( )

( ) ( ) ( )

( ) ( )

n n

f x A y x L f x y x L

f x B h L f x

∞

∞ ∞

− − =

= = ∞

=

= −

⎡ +⎤

⎢ ⎥

− −

⎢ ⎥

⎣ ⎦

+

∑ ∑ ∑

∑

(3.24)

Jika kedua ruas dibandingkan, maka diperoleh

1

0 0

1

1 1 0 2 0 3 0

( )

( ( ) ( ) ( ) )

y h L f x

y L f x y f x A f x B

−

= +

= + +

1

2 ( ( )1 1 2( ) 1 3( ) 1) y =L⁻ f x y + f x A +f x B atau secara umum berbentuk

1

0 0

1 -1 2 -1

1

3 -1

( )

( ) ( )

, 1 ( )

n n

n

y h L f x

f x y f x A

y L n

f x B

−

= +

⎡ + ⎤

= ⎢⎣+ ⎥⎦ ≥

(3.25) Penurunan persamaan (3.22) dan (3.24) masing-masing dapat dilihat pada Lampiran 4 dan 5.

Dengan demikian solusi Persamaan Diferensial Abelian (3.18) adalah

0 1 2

( ) ( ) ( ) ( ) y x = y x +y x +y x +

dengan y y y₀, ₁, ₂,... diberikan oleh persamaan (3.25), sedangkan Ai dan Bi (i=0,1, 2,…) diberikan oleh persamaan (3.22).

Untuk memahami metode yang diberikan di atas, maka berikut ini akan diberikan dua contoh kasus. Pada contoh kasus pertama, Metode Dekomposisi Adomian akan dibandingkan dengan metode Runge-Kutta orde empat. Pada contoh kasus kedua, Metode Dekomposisi Adomian akan dibandingkan dengan solusi eksak masalah nilai awal.

Contoh 1: Misalkan diberikan Persamaan Diferensial Abelian berikut

2 2 3

' 4 4 2

y = + xy+ xy +x y , (3.26) dengan nilai awal

(0) 0 y = .

Secara analitik solusi masalah nilai awal (3.26) sulit untuk diselesaikan. Oleh karena itu, masalah nilai awal (3.26) akan diselesaikan dengan menggunakan metode numerik.

Berikut ini akan ditentukan solusi hampiran masalah nilai awal (3.26) dengan menggunakan Metode Dekomposisi Adomian yang telah diuraikan sebelumnya. Rumus untuk solusi hampiran dari masalah nilai awal (3.26) yang didasarkan pada persamaan (3.25) adalah

( )

0

1 2

-1 -1 -1

4 ,

4 2 , 1

n n n n

y x

y L⁻ xy xA x B n

=

= + + ≥

(3.27) dengan solusi homogen h= . 0

Dengan menggunakan aturan rekursif pada persamaan (3.22) diperoleh empat suku

(4)

polinomial Adomian An dan Bn yang selanjutnya digunakan untuk membentuk solusi y x . Empat suku dari solusi ( )( ) y x atau untuk n=4 diperoleh

0

3 6

4 1

5 6 7 8 9

2

11

4

16 32

3 8 3

64 176 128 112 1664

15 9 7 3 27

512 11

y x

x x

y x

x x x x x

y

x

=

= + +

= + + + +

+

7 8 9 10

3

11 12 13

14 16

256x 1144x 35072x 58592x

y 105 45 567 525

81920x 140480x 110336x

297 567 429

295936x 7424x

693 33

= + + +

+ + +

+ +

9 10 11

4

12 13

14 15

16 17

18

1024x 36496x 3424384x

y 945 1575 31185

11576864x 38692736x

42525 51975

58741120x 48458607616x

43659 30405375

75071168x 23477248x

27027 9639

19678720x 111284224x

11583

= + +

+ +

+ + ¹⁹

21

39501 7106560x

.

+ 6237

(3.28) Jadi untuk n=4 diperoleh solusi hampiran masalah nilai awal (3.26) dengan Metode Dekomposisi Adomian sebagai berikut

0 1 2 3 4

( )

y x =y +y +y +y +y .

Untuk suku-suku ke-n dapat dicari berdasarkan aturan rekursif pada persamaan (3.27). Penurunan persamaan (3.27) dan (3.28) masing-masing dapat dilihat pada Lampiran 6 dan 7.

Solusi hampiran masalah nilai awal (3.26) akan ditentukan dengan menggunakan software MATLAB untuk memperoleh solusi

n( )

y x untuk nilai n yang berbeda.

Berikut ini diberikan grafik solusi masalah nilai awal (3.26) dengan Metode Dekomposisi Adomian untuk n=5,n=10,

15

n= . Validitas metode ini diperlihatkan dengan membandingkan solusi hampiran dengan metode Runge-Kutta orde empat.

Gambar 3 Perbandingan grafik solusi masalah nilai awal (3.26) dengan metode dekomposisi Adomian untuk n=5 dan metode Runge-Kutta orde empat.

Gambar 4 Perbandingan grafik solusi masalah nilai awal (3.26) dengan metode dekomposisi Adomian untukn=10 dan metode Runge-Kutta orde empat.

Gambar 5 Perbandingan grafik solusi masalah nilai awal (3.26) dengan metode dekomposisi Adomian untukn=15 dan metode Runge-Kutta orde empat.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

0 2 4 6 8 10 12 14

metode Runge-Kutta metode dekomposisi Adomian

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

0 2 4 6 8 10 12 14

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

0 2 4 6 8 10 12 14

(5)

Dari Gambar 3, 4 dan 5 disimpulkan bahwa solusi hampiran dengan Metode Dekomposisi Adomian mendekati solusi dengan Runge-Kutta orde empat dengan ketelitian yang tinggi untuk orde yang makin besar. Ketelitian metode ini pada masalah nilai awal (3.26) diberikan pada Tabel 3.

Tabel 3 Galat hampiran solusi masalah nilai awal (3.26) untuk orde yang berbeda

xn Orde ke-n

5 10 15

0.00 0.0000 0.0000 0.0000 0.10 0.0000 0.0000 0.0000 0.15 0.0000 0.0000 0.0000 0.20 0.0000 0.0000 0.0000 0.25 0.0000 0.0000 0.0000 0.30 0.0001 0.0001 0.0001 0.35 0.0010 0.0010 0.0010 0.40 0.0080 0.0061 0.0061 0.45 0.0271 0.0254 0.0253 0.50 1.4117 0.2816 0.2072

Contoh 2: Misalkan diberikan Persamaan Diferensial Abelian berikut

2 3

' 2 2

y = − + +y y − y

(3.29) dengan nilai awal

(0) 0 y = .

Solusi eksak dari persamaan diferensial (3.29) dengan nilai awal (0)y = dinyatakan 0 dalam bentuk implisit berikut

1 1 1 1

ln 1 ln 1 ln 2 ln(2).

2 − −y 6 y+ −3 y− = −x 3 Berikut ini akan ditentukan solusi hampiran masalah nilai awal (3.29) berdasarkan Metode Dekomposisi Adomian yang telah diuraikan sebelumnya. Oleh karena itu, rumus untuk solusi hampiran dari masalah nilai awal (3.29) yang didasarkan pada persamaan (3.25) adalah

( )

0 -1

-1 -1 -1

-2

2 , 1

n n n n

y x

y L y A B n

=

= + − ≥

Dengan menggunakan aturan rekursif pada persamaan (3.22) diperoleh empat suku polinomial Adomian An dan Bn yang selanjutnya digunakan untuk membentuk solusi y x . Empat suku dari solusi ( )( ) y x atau untuk n=4 diperoleh

3

2 4

1

3 4 5 7

6 2

4 5 6 7

3

8 9 10

5 6 7 8

4

9 0 11

0

1

8 2

3

8 22 24

3 3 15 8 7

22 176 2432

12 15 45 315

517 152 228

35 7 35

26 358 514

60 45 105 315

85499 736 76204

2835 189 1155

5896 y = -2x

y x x x

x x x x

y x

x x x x

y

x x x

x x x x

y

x x x

x

= − + +

= − + − − −

= − + − −

+ + +

= − + − −

+ + −

− ¹² 5896 ¹³

105 455

− x

(3.31) Jadi untuk n=4 diperoleh solusi hampiran masalah nilai awal (3.29) dengan Metode Dekomposisi Adomian sebagai berikut

0 1 2 3 4

( )

y x =y +y +y +y +y .

n( )

Berikut ini diberikan grafik solusi masalah nilai awal (3.29) dengan Metode Dekomposisi Adomian untuk n=5, n=10 dan n=15. Validitas metode ini diperlihatkan dengan membandingkan solusi hampiran dengan Metode Dekomposisi Adomian dan solusi eksak.

Gambar 6 Perbandingan grafik solusi masalah nilai awal (3.29) metode dekomposisi Adomian untuk n= 5 dan solusi eksak.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

-1 -0.9 -0.8 -0.7 -0.6 -0.5 -0.4 -0.3 -0.2 -0.1 0

metode Runge-Kutta metode dekomposisi Adomian solusi eksak

(6)

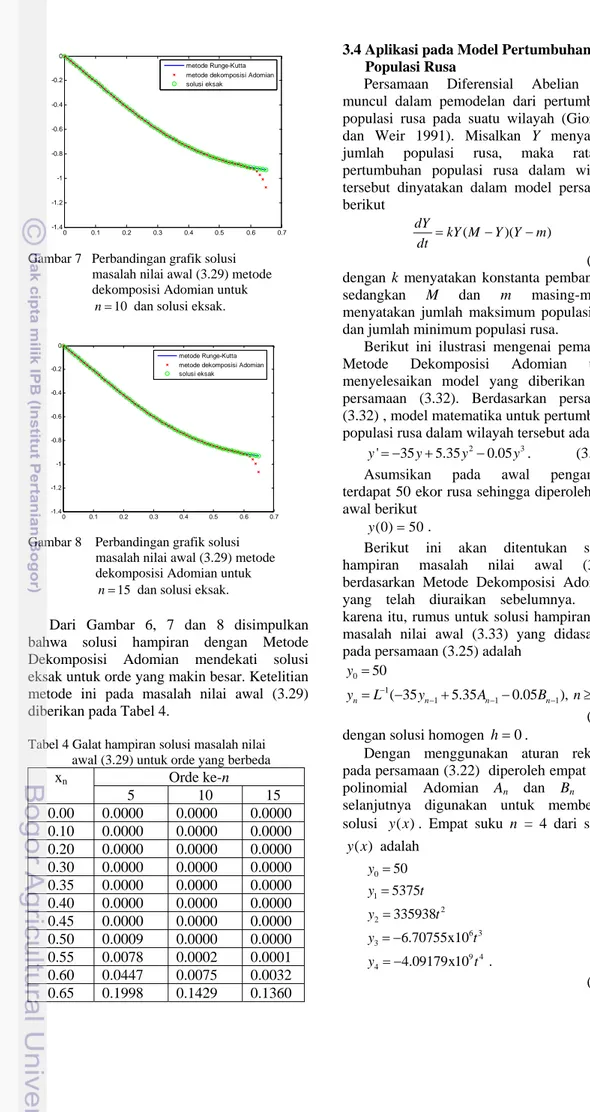
Gambar 7 Perbandingan grafik solusi

masalah nilai awal (3.29) metode dekomposisi Adomian untuk

n=10 dan solusi eksak.

Gambar 8 Perbandingan grafik solusi

masalah nilai awal (3.29) metode dekomposisi Adomian untuk

n=15 dan solusi eksak.

Dari Gambar 6, 7 dan 8 disimpulkan bahwa solusi hampiran dengan Metode Dekomposisi Adomian mendekati solusi eksak untuk orde yang makin besar. Ketelitian metode ini pada masalah nilai awal (3.29) diberikan pada Tabel 4.

Tabel 4 Galat hampiran solusi masalah nilai awal (3.29) untuk orde yang berbeda

xn Orde ke-n

5 10 15

0.00 0.0000 0.0000 0.0000 0.10 0.0000 0.0000 0.0000 0.20 0.0000 0.0000 0.0000 0.30 0.0000 0.0000 0.0000 0.35 0.0000 0.0000 0.0000 0.40 0.0000 0.0000 0.0000 0.45 0.0000 0.0000 0.0000 0.50 0.0009 0.0000 0.0000 0.55 0.0078 0.0002 0.0001 0.60 0.0447 0.0075 0.0032 0.65 0.1998 0.1429 0.1360

3.4 Aplikasi pada Model Pertumbuhan Populasi Rusa

Persamaan Diferensial Abelian juga muncul dalam pemodelan dari pertumbuhan populasi rusa pada suatu wilayah (Giordano dan Weir 1991). Misalkan Y menyatakan jumlah populasi rusa, maka rata-rata pertumbuhan populasi rusa dalam wilayah tersebut dinyatakan dalam model persamaan berikut

( )( )

dY kY M Y Y m

dt = − −

(3.32) dengan k menyatakan konstanta pembanding, sedangkan M dan m masing-masing menyatakan jumlah maksimum populasi rusa dan jumlah minimum populasi rusa.

Berikut ini ilustrasi mengenai pemakaian Metode Dekomposisi Adomian untuk menyelesaikan model yang diberikan pada persamaan (3.32). Berdasarkan persamaan (3.32) , model matematika untuk pertumbuhan populasi rusa dalam wilayah tersebut adalah

2 3

' 35 5.35 0.05

y = − y+ y − y . (3.33) Asumsikan pada awal pengamatan terdapat 50 ekor rusa sehingga diperoleh nilai awal berikut

(0) 50 y = .

Berikut ini akan ditentukan solusi hampiran masalah nilai awal (3.33) berdasarkan Metode Dekomposisi Adomian yang telah diuraikan sebelumnya. Oleh karena itu, rumus untuk solusi hampiran dari masalah nilai awal (3.33) yang didasarkan pada persamaan (3.25) adalah

0 1

1 1 1

50

( 35 5.35 0.05 ), 1

n n n n

y

y L⁻ y₋ A₋ B₋ n

=

= − + − ≥

Dengan menggunakan aturan rekursif pada persamaan (3.22) diperoleh empat suku polinomial Adomian An dan Bn yang selanjutnya digunakan untuk membentuk solusi y x . Empat suku n = 4 dari solusi ( )

( ) y x adalah

0

1

2 2

6 3 3

9 4 4

50 5375

335938 6.70755x10 4.09179x10 . y

y t

=

= −

(3.35)

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

-1.4 -1.2 -1 -0.8 -0.6 -0.4 -0.2 0

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

-1.4 -1.2 -1 -0.8 -0.6 -0.4 -0.2 0

(7)

Jadi untuk n=4 diperoleh solusi hampiran masalah nilai awal (3.33) dengan Metode Dekomposisi Adomian sebagai berikut

0 1 2 3 4

( )

y x =y +y +y +y +y .

n( )

Berikut ini diberikan grafik solusi masalah nilai awal (3.33) dengan Metode Dekomposisi Adomian untuk n=5,n=10 dan n=15. Validitas metode ini diperlihatkan dengan membandingkan solusi hampiran dengan Metode Dekomposisi Adomian dan solusi eksak.

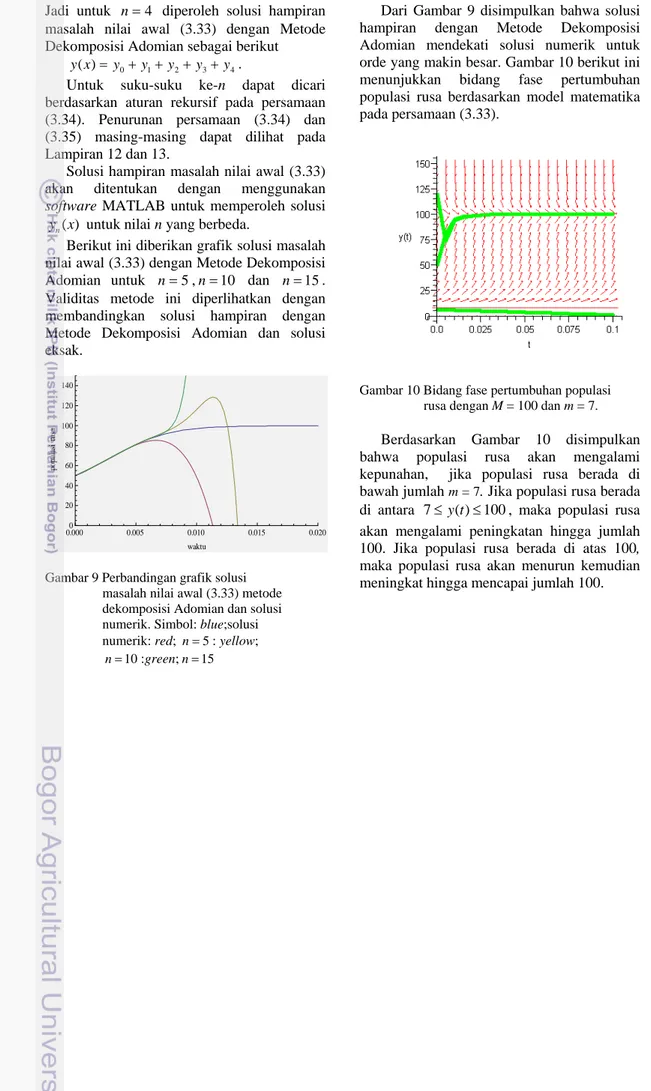
Gambar 9 Perbandingan grafik solusi masalah nilai awal (3.33) metode dekomposisi Adomian dan solusi numerik. Simbol: blue;solusi numerik: red; n= : yellow;5 n=10:green;n=15

Dari Gambar 9 disimpulkan bahwa solusi hampiran dengan Metode Dekomposisi Adomian mendekati solusi numerik untuk orde yang makin besar. Gambar 10 berikut ini menunjukkan bidang fase pertumbuhan populasi rusa berdasarkan model matematika pada persamaan (3.33).

Gambar 10 Bidang fase pertumbuhan populasi rusa dengan M = 100 dan m = 7.

Berdasarkan Gambar 10 disimpulkan bahwa populasi rusa akan mengalami kepunahan, jika populasi rusa berada di bawah jumlah m = 7. Jika populasi rusa berada di antara 7≤y t( ) 100≤ , maka populasi rusa akan mengalami peningkatan hingga jumlah 100. Jika populasi rusa berada di atas 100, maka populasi rusa akan menurun kemudian meningkat hingga mencapai jumlah 100.

0.0000 0.005 0.010 0.015 0.020

20 40 60 80 100 120 140

waktu

populasirusa