Akhir kata penulis menyadari bahwa tesis ini masih jauh dari sempurna. Untuk itu penulis mengharapkan kritik dan saran untuk penyempurnaan tesis ini. Semoga tesis ini dapat bermanfaat bagi pembaca dan pihakpihak lainnya yang memerlukannya.
Medan, Juni 2013 Penulis,
Penulis dilahirkan di Takengon Kabupaten Aceh Tengah pada Tanggal 4 Ju-ni 1988 dan merupakan anak kedua dari tiga bersaudara dari Bapak Hasanuddin dan Ibu Salmiah, S.Pd. Penulis menamatkan Sekolah Dasar di SD Negeri Buntul Kubu Takengon lulus tahun 2000, Sekolah Menengah Pertama di SMP Negeri 1 Takengon lulus tahun 2003, Sekolah Menengah Atas di SMA Negeri 2 Modal Bangsa Aceh Besar lulus Tahun 2006. Pada Tahun 2006 penulis melanjutkan pendidikan Diploma Statistika di Universitas Sumatera Utara dan lulus tahun 2009. Penulis melanjutkan pendidikan Sarjana di Universitas Sumatera Utara pa-da Fakultas Matematika pa-dan Ilmu Pengetahuan Alam jurusan Matematika lulus tahun 2011. Selanjutnya pada tahun 2011 penulis berkesempatan untuk melan-jutkan program Master pada Program Studi Magister Matematika di Universitas Sumatera Utara.
ABSTRAK
Dalam kerangka kerja penjadwalan mesin terdapat kemungkinan adanya suatu interval waktu dimana suatu unit pekerjaan tidak dapat diproses. Penelitian ini mendiskusikan model deterministik penjadwalan dalam persoalanbin packing pa-da mesin tunggal identik dengan apa-danya interval waktu pa-dalam zona terlarang. Da-lam penelitian ini ditunjukkan suatu model penjadwalan yang layak atau optimal terhadap pekerjaan dengan memperhatikan interval waktu dalam zona terlarang. Model yang diperoleh dinyatakan dalam bentuk program linier dengan objektif model adalah meminimumkan total waktu penyelesaian (makespan) sehingga di-peroleh minimum interval waktu dalam zona terlarang yang dinyatakan ke dalam bentuk program integer.
In machine scheduling of manufacturing systems there may be a certain time in-terval, during which jobs processing may not be continued. This research discuss a deterministic model of bin packing problem scheduling on a single identical ma-chine by considering a time interval in forbidden zones. This research represents a feasible or optimal scheduling of jobs by considering any time interval in forbidden zones. The model that formulated into linear programming with objective is mini-mized the completion time (makespan) in order to obtain time interval minimum in forbidden zones that represents by integer programming.
DAFTAR ISI
Halaman
KATA PENGANTAR iii
RIWAYAT HIDUP vi
ABSTRAK i
ABSTRACT ii
DAFTAR ISI iii
DAFTAR GAMBAR v DAFTAR TABEL vi BAB 1 PENDAHULUAN 1 1.1 Latar Belakang 1 1.2 Perumusan Masalah 3 1.3 Tujuan Penelitian 4 1.4 Manfaat Penelitian 4
BAB 2 KAJIAN PUSTAKA 5
2.1 Klasifikasi Persoalan Penjadwalan 5
2.1.1 Persoalan penjadwalan 5
2.1.2 Data unit pekerjaan dalam penjadwalan 7
2.1.3 Karakteristik penjadwalan 9
2.1.4 Kriteria optimalitas dalam penjadwalan 10
2.2 Penjadwalan Mesin 12
2.2.1 Definisi penjadwalan mesin 12
2.2.2 Ruang lingkup mesin 13
2.2.3 Penjadwalan mesin tunggal identik 17
2.3 PersoalanJobshop 19
2.5 Zona Terlarang dalam Penjadwalan 26
BAB 3 PROGRAM INTEGER 31
3.1 Program Linier 31
3.2 Program Integer 32
3.3 Persoalan Penjadwalan dalam Program Integer 32 BAB 4 PENJADWALAN MESIN DENGAN ADANYA
ZONA TERLARANG 35
4.1 Model Penjadwalan Mesin dengan Adanya Zona Terlarang 35
4.2 Contoh Kasus 38
BAB 5 KESIMPULAN DAN SARAN 40
5.1 Kesimpulan 40
5.2 Saran 40
5.3 Riset Lanjutan 40
DAFTAR GAMBAR
Nomor Judul Halaman
2.1 (i.) Orientasi mesin terhadap pekerjaan pada skema Gantt 1 5 2.2 (ii.) Orientasi pekerjaan terhadap mesin pada skema Gantt 2 6
2.3 IlustrasiJobshop pada satu mesin 14
2.4 Penjadwalan flowshop yang layak pada mesin 23 2.5 Ilustrasi penjadwalan yang mungkin dari Lemma 1, (a),(b) dan (c) 24 2.6 Ilustrasi interval waktu dan zona terlarang dalam penjadwalan 27 2.7 Ilustrasi penjadwalan mesin tunggal dengan waktu awal dalam zona
Nomor Judul Halaman
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Secara umum, penjadwalan didefinisikan sebagai suatu proses dalam menen-tukan penugasan suatu himpunan operasi atau pekerjaan ke pusat berdasarkan pada interval atau periode waktu. Objektif dari persoalan penjadwalan adalah un-tuk menenun-tukan suatumbarisan penjadwalan dari seluruh pekerjaanQJk yang ada pada mesin Mk, k = 1,2, . . . , mdengan nilai pada fungsi objektif yang diberikan,
φ(C1, C2, . . . , Cn) adalah minimum. Karena itu, persamaan Ci = cini dan Ci menyatakan waktu total penyelesaian pekerjaan Ji∈J.
Penjadwalan pada sejumlah mesin identik dengan tujuan untuk memini-mumkan total waktu penyelesaian pekerjaan (makespan) yang merupakan satu dari persoalan umum yang sering dikaji dalam optimisasi kombinatorial. Per-soalan penjadwalan yang telah dikembangkan oleh para peneliti banyak digunakan dalam kegiatan produksi suatu perusahaan, mesin dan sebagainya.
Dalam beberapa kasus tertentu, terdapat beberapa kebijakan tertentu yang mempengaruhi pengambilan keputusan, maka proses ini akan menambahkan su-atu kendala waktu, batas waktu operasi atau total waktu pekerjaan secara keselu-ruhan ke dalam model rancangan yang ada (Chaudhuri, 1995). Salah satu per-soalan penjadwalan yang umum dikaji merupakan perper-soalan penjadwalan mini-mummakespanyang selanjutnya disebut dengan persoalanbin packing. Andaikan terdapat batasan waktu pada rancangan operasi secara keseluruhan dengan mem-berikan batas waktu pada masing-masing pekerjaan yang ada. Dalam sistem pen-jadwalan suatu perusahaan terdapat beberapa persoalan yang menjadi kendala dalam kegiatan produksi, salah satunya berkaitan dengan informasi akurat
di-mana suatu unit pekerjaan yang akan diproses dapat diselesaikan dalam suatu interval waktu tertentu. Persoalan ini termasuk persoalan yang kompleks dimana proses pengambilan keputusan mempengaruhi penjadwalan perusahaan tersebut. Kendala waktu ini selanjutnya disebut sebagai suatu zona terlarang (forbidden zones) dalam persoalan penjadwalan.
Abdekhodaee dan Ernst (2004) juga memberikan pandangan mengenai pen-jadwalan dengan adanya kendala waktu yang selanjutnya disebut sebagai zona terlarang (forbidden zones). Asumsikan terdapat n pekerjaan yang dijadwalkan sebagai J1, J2, . . . , Jn dengan pi sebagai waktu proses Ji. Interval waktu dibagi menjadi I = {I1, . . . , Is} sehingga tiap Ij merupakan bagian dari zona terlarang yang dinotasikan sebagai Fi ⊂ Ij,∀j. Akibatnya, interval waktu Ij \Fj adalah interval waktu yang diizinkan.
Khammuang et al. (2007) menambahkan bahwa zona terlarang dalam per-soalan penjadwalan menjelaskan adanya suatu interval waktu selama suatu pe-kerjaan tertentu tidak dapat diproses. Lebih jelasnya, andaikan terdapat suatu pekerjaan yang sudah selesai tepat sebelum interval waktu yang termasuk ke da-lam zona terlarang. Selanjutnya pekerjaan tersebut akan keluar dari barisan uru-tan penjadwalan pada interval waktu berikutnya. Akibatnya, waktu penyelesaian akhir dari suatu pekerjaan pada Ij dapat dinyatakan sebagai t= 2j−1.
Dalam penelitian tesis ini mendiskusikan model deterministik dimana kendala dalam penjadwalan adalahpi, i= 1, . . . , ntotal jumlahbinyang diberikan dengan
pi mempunyai nilai rasional (0,1]. Tujuan dari persoalan ini adalah mengurut-kan penjadwalan seluruh pekerjaan dengan variasi waktu proses masing-masing pekerjaan ke total mesin yang digunakan dalam meminimumkan makespan de-ngan memperhatikan batasan atau kendala interval waktu dalam penjadwalan mesin yang termasuk dalam zona terlarang (forbidden zones). Penelitian tesis ini difokuskan pada diskusi dari model deterministik untuk penjadwalan mesin
3 tunggal identik dengan adanya interval waktu dalam zona terlarang yang direp-resentasikan ke dalam bentuk program linier. Hasil yang diperoleh merupakan model program linier dengan kendala penjadwalan yang merupakan suatu pro-gram integer yang digunakan dalam mengurutkan total pekerjaan yang tersedia
Ji ke dalam penjadwalan mesin tunggal identik yang layak.
Penulisan tesis ini disusun sebagai berikut: Bab I menjelaskan latar belakang dan masalah yang dikaji dalam penelitian tesis ini. Bab II kajian teori serta be-berapa riset yang relevan dengan penelitian tesis ini. Bab III berupa penjelasan mengenai teori program integer yang digunakan dalam model penjadwalan. Bab IV mengkaji hasil diskusi model deterministik untuk penjadwalan mesin tunggal identik dengan adanya interval waktu dalam zona terlarang (forbidden zones). Bab V memberikan kesimpulan dan saran dari hasil penelitian tesis untuk peneli-tian selanjutnya yang mungkin dapat dikembangkan.
1.2 Perumusan Masalah
Salah satu pengembangan model penjadwalan dengan adanya zona terlarang (forbidden zones) telah dilakukan sebelumnya oleh Khammuang et al. (2007). Kekurangan dari model yang telah dikembangkan oleh Khammuang et al. (2007) adalah model hanya difokuskan pada penjadwalan on-line dengan zona terlarang di waktu awal proses pekerjaan. Penelitian ini mendiskusikan model deterministik penjadwalan dalam persoalan bin packingpada mesin tunggal identik yang dapat digunakan untuk mengurutkan seluruh pekerjaan Ji(i = 1, . . . , n) dalam memi-nimumkan total waktu penyelesaian (makespan) dengan adanya kendala interval waktu yang termasuk ke dalam zona terlarang.
1.3 Tujuan Penelitian
Tujuan penelitian ini adalah mendiskusikan metode deterministik penjad-walan Ji(i = 1, . . . , n) pekerjaan pada mesin tunggal identik sehingga diperoleh suatu barisan penjadwalan yang layak. Model kemudian direpresentasikan dalam menyelesaikan persoalan bin packing dan menentukan total waktu penyelesaian (makespan) minimum penjadwalan dengan kendala interval waktu yang termasuk ke dalam zona terlarang.
1.4 Manfaat Penelitian
Manfaat dari penelitian diharapkan dapat diterapkan dalam proses penyele-saian J padan total pekerjaan sehingga model dalam penelitian ini dapat memi-nimumkan total waktu penyelesaian yang diperlukan meskipun terdapat asumsi interval waktu tertentu sebagai zona terlarang. Selanjutnya, model juga diharap-kan dapat membantu proses pengambilan keputusan dalam pengurutan dan mem-prioritaskan suatu set atau himpunan pekerjaan. Hal ini merupakan salah satu konsep literatur manajemen operasi dimana suatu metode solusi cepat, sederhana dan efektif dapat digunakan untuk menyelesaikan beberapa atau seluruh pekerja-an ypekerja-ang ada.
BAB 2
KAJIAN PUSTAKA
2.1 Klasifikasi Persoalan Penjadwalan
Teori dan beberapa istilah yang digunakan dalam penelitian ini dirujuk dari beberapa jenis persoalan penjadwalan yang telah dikaji sebelumnya. Pada bab ini, beberapa klasifikasi dasar dalam persoalan penjadwalan dikaji secara luas seperti yang telah dikaji dalam literatur (lihat Lawler et al., 1993).
2.1.1 Persoalan penjadwalan
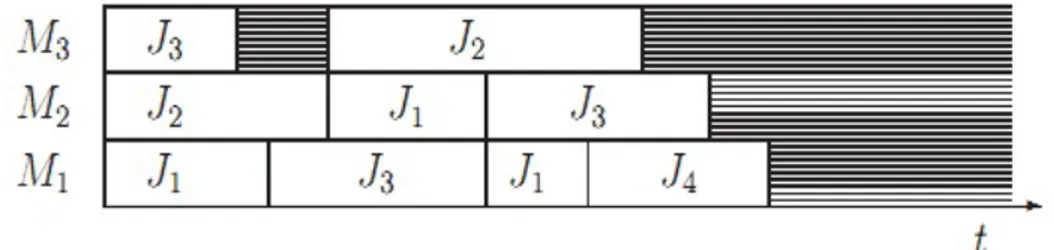
Asumsikan terdapatmmesinMj(j = 1, . . . , m) yang digunakan untuk mem-prosesn unit pekerjaanJi(i= 1, . . . , n). Suatu penjadwalan pada masing-masing unit pekerjaan yang dialokasikan pada satu atau lebih interval waktu ke satu atau lebih mesin yang ada. Penjadwalan tersebut dapat direpresentasikan dengan menggunakan skema Gantt seperi yang ditunjukkan pada Gambar 2.1 berikut.
Gambar 2.2 : (ii.) Orientasi pekerjaan terhadap mesin pada skema Gantt 2
Objektif dari persoalan penjadwalan berdasarkan skema Gantt adalah menen-tukan penjadwalan didasarkan pada orientasi jumlah mesin dan unit pekerjaan yang ada sebagai kendala dalam penjadwalan. Secara umum, persoalan pen-jadwalan dapat diklasifikasikan dengan menggunakan suatu notasi yaitu α|β|γ, dengan α merupakan total jumlah mesin yang ada, β adalah karakteristik suatu pekerjaan dan γ menyatakan kriteria optimalitas (Graham et al., 1979).
Menurut Graham et al. (1979), terdapat beberapa parameter yang relevan dalam pemodelan suatu mesin, yaitupj sebagai waktu pemrosesan suatu pekerja-an j, rj adalah waktu penyelesaian pekerjaan j yang telah ditentukan, sizej me-nyatakan total jumlah mesin atau prosesor yang dibutuhan untuk menyelesaikan pekerjaan j dan pmtn yang menyatakan preemption dalam model penjadwalan. Parameter ini menjadi gagasan untuk mengimplementasikan model ke dalam su-atu algoritma yang selanjutnya disebut dengan algoritma on-line. Algoritma ini didasarkan pada fakta bahwa suatu pekerjaan yang tersedia pada suatu rentang waktu tertentu dapat diselesaikan, dan sebaliknya. Selanjutnya, Megow et al. (2006) melakukan pengembangan terhadap model penjadwalan secara stokastik dalam menentukan suatu aturan penjadwalan stokastik online dalam memini-mumkan nilai ekspektasi pada waktu penyelesaian pekerjaan,E[PwjCj]. Dalam model terdapat asumsi adanya waktu proses distribusi Pj yang saling bebas, se-hingga diperoleh bahwa rj < rk untuk j < k. Suatu aturan penjadwalan
mem-7 berikan suatu spesifikasi tindakan terhadap pekerjaan pada waktu keputusan t
dengan waktu awal adalahtdan waktu keputusan berikutnya dinotasikan sebagai
t0 > t. Untuk suatu contoh I, dimana terdapat total jumlah mesin m, himpunan pekerjaanJ dengan masing-masing waktu penyelesaian yang ditentukanrj, bobot
wj dan waktu proses distribusi Pj, ambilSjΠ(I) dan CjΠ(I) sebagai variabel acak waktu awal dan waktu penyelesaian pekerjaan dibawah ketentuan Π. Sehingga diperoleh aturan penjadwalan secara stokastik sebagai
E[Π(I)] =E " X j∈J wjCjΠ(I) # =X j∈J wjE[CjΠ(I)]
yang kemudian disebut dengan model penjadwalan online stokastik (SoS). 2.1.2 Data unit pekerjaan dalam penjadwalan
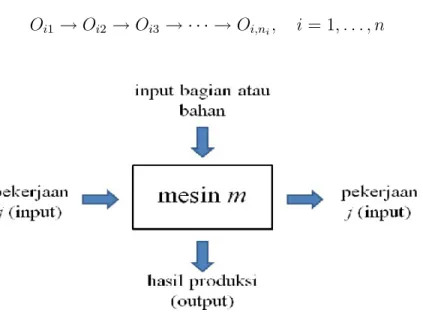
Suatu unit pekerjaan diselesaikan pada ni operasi Oi1, . . . , Oi,ni. Oij yang selanjutnya dialokasikan oleh waktu proses yang diperlukan, pij. Jika suatu unit pekerjaan Ji terdapat tepat satu operasi (ni = 1), maka dapat diidentifikasikan bahwa Ji dengan Oi1 dan denotasikan waktu proses yang diperlukan adalah pi. Lebih lanjut, terdapat waktu rilis ri suatu unit pekerjaan, dimana operasi awal
Ji tersedia untuk diproses. Alokasikan tiap operasi Oij yang merupakan suatu himpunan mesinµij ⊂ {M1, . . . , Mm} untuk diproses. Pada umumnya,µij meru-pakan himpunan satu elemen atau sama dengan himpunan jumlah mesin yang digunakan. Pada dasarnya, suatu operasi Oij dapat diproses pada sebarang me-sin yang ada. Persoalan seperti ini merupakan persoalan penjadwalan dengan Multi-Purpose Machines (MPM). Sehingga, ini memungkinkan bahwa semua me-sin pada himpunanµij digunakan secara simultan oleh Oij selama interval waktu proses berlangsung yang lebih dikenal sebagai persoalan penjadwalan multiprose-sor.
Dalam operasi Oij terdapat fungsi biaya fi(t) dalam menentukan biaya pro-ses unit pekerjaan Ji pada waktu t. Batas waktu di dan bobot unit pekerjaan
wi dapat digunakan dalam mendefinisikan fungsi fi. Secara umum, seluruh da-ta pi, pij, ri, di, wi diasumsikan dalam suatu bilangan bulat. Suatu penjadwalan adalah layak jika
• tidak terdapat dua interval waktu yang bekerja secara bersamaan pada me-sin yang sama,
• tidak terdapat dua interval waktu yang dialokasikan pada unit pekerjaan yang sama,
• dan jika, dalam perluasan, terdapat sejumlah karakteristik persoalan pen-jadwalan tertentu yang dispesifikasi
Dan suatu penjadwalan adalah optimal jika dapat meminimumkan kriteria-kriteria optimalitas yang diberikan dalam persoalan.
Teorema 2.1.1 Andaikan G = (V, E, w) merupakan suatu sistem penugasan. Terdapat suatu penjadwalan yang layak padaG jika dan hanya jikaG tidak mem-punyai cycle.
Bukti Berikut bukti pada Teorema 1:
⇒ Asumsikan G mempunyai satu cyclce v1 →v2 → · · · →vk →v1. Maka,
v1 ≺v1 dan suatu penjadwalan yang layakσ adalah σ(v1) +w(v1)≤σ(v1) haruslah benar, dimana hasil yang diperoleh adalah w(v1)>0.
⇐ Jika G merupakan asiklik, maka terdapat beberapa unit pekerjaan yang tidak dialokasikan ke mesin yang tersedia. Sehingga dapat dialokasikan terlebih dahulu. Lebih jelasnya, secara topologi verteks-verteks dan me-nentukan penjadwalan pada mesin yang sama.
9 2.1.3 Karakteristik penjadwalan
Menurut Brucker (2007), dalam persoalan penjadwalan, terdapat beberapa karakteristik pekerjaan yang dispesifikasikan oleh suatu himpunanβyang memuat paling banyak enam elemen, yaituβ1, β2, β3, β4, β5 danβ6. Beberapa karakteristik tersebut antara lain sebagai berikut:
β1 : mengindikasikan apakah preemption (atau pembagian pekerjaan) diper-bolehkan dalam suatu penjadwalan. Ini berarti bahwa proses penyelesa an pekerjaan dapat diinterupsi dan kemudian dilanjutkan, meskipun pa-da mesin yang berbepa-da dimana pekerjaan pa-dapat diinterupsi beberapa kali. Jika preemption diperbolehkan, setβ1 =pmtn.
β2 : mendeskripsikan adanya penjadwalan bersyarat pada pekerjaan ( prece-dence relations) yang direpresentasikan oleh suatu graf asiklik berarah
G= (V, A) dengan V ={1, . . . , n} dipasangkan dengan pekerjaan yang ada, dan (i, k)∈A jika dan hanya jikaJi telah selesai sebelumJk dimu-lai. Dalam kasus ini dapat dinyatakan dengan Ji →Jk dan set untuk
β2 =prec.
β3 : jikaβ3 =ri, maka waktu rilis dapat dispesifikasikan untuk tiap peker-jaan.
β4 : mendeskripsikan adanya batasan pada waktu pemrosesan atau jumlah operasi pekerjaan yang diselesaikan pada waktu tertentu. Jika β4 sama dengan pi = 1(pij = 1), maka tiap pekerjaan mempunyai ketentuan-ketentuan unit proses.
β5 : jikaβ5 =di, maka terdapat batas akhir (deadline) masing-masing pe-kerjaan Ji dengan ketentuan bahwa pekerjaanJi haruslah diselesaikan tidak lebih lama dari waktu di.
β6 : mengindikasikan total jumlah waktu maksimum penyelesaian semua pekerjaan.
Dimana terdapat suatu graf paralel yang berkaitan dengan graf pohon (tree). Suatu graf adalah seri-paralel jika memenuhi aturan sebagai berikut:
Graf dasar : Sebarang graf yang terdiri dari suatu verteks tunggal adalah seri-paralel. AmbilGi = (Vi, Ai) sebagai seri-paralel pada in-deks (i = 1,2).
Komposisi paralel : Graf G= (V1∪V2, A1∪A2) yang terbentuk dariG1 dan G2
dengan menggabungkan himpunan verteks dan arcs. Komposisi seri : Graf G= (V1∪V2, A1∪A2∪T1×S2) yang terbentuk dari
G1 dan G2 dengan menggabungkan himpunan verteks dan arcs dan menjumlahkan seluruharcs (t, s) dimana t adalah bagian himpunan T1 dan s adalah bagian dari himpunan S2.
Teorema 2.1.2 (Coffman, 1976) Asumsikan G = (V, E, w) sebagai graf asiklik berarah, p menyatakan jumlah prosesor dan σp sebagai suatu penjadwalan pada
G. Maka, M S(σp)≤ 2− 1 p M Sopt(p) (2.1)
2.1.4 Kriteria optimalitas dalam penjadwalan
Definisi 1 Penjadwalan pada suatu sistem penugasan G = (V, E, w) merupakan suatu fungsi waktu σ:V →N∗ dengan ketentuan:
∀(u, v)∈E, σ(u) +w(u)≤σ(v)
Definisi 2 (Legrand, 2004) Total jumlah waktu yang diperlukan untuk menye-lesaikan seluruh pekerjaan (makespan) pada suatu penjadwalan merupakan total jumlah waktu eksekusi yang dapat dinyatakan sebagai (Legrand, 2004) Total jum-lah waktu yang diperlukan untuk menyelesaikan seluruh pekerjaan (makespan)
11 pada suatu penjadwalan merupakan total jumlah waktu eksekusi yang dapat di-nyatakan sebagai M S(σ) = max v∈V {σ(v) +w(v)} −min v∈V {σ(v)} Makespan juga dinotasikan sebagai Cmax= max
v∈V Cv.
Terdapat dua persoalan utama dalam menentukan solusi makespan dalam per-soalan penjadwalan, yaitu:
P b(p) : menentukan penjadwalan dengan makespan minimum yang paling mungkin dengan menggunakan paling banyakp prosesor atau mesin.
M Sopt(p) menyatakanmakespan optimal dengan menggunakan p pro-sesor.
P b(∞) : menentukan penjadwalan dengan makespan paling minimum dimana jumlah prosesor yang digunakan tidak mempunyai batas. Persoalan ini dapat dinyatakan sebagai M Sopt(∞) berdasarkan pada persoalan makespan.
dengan beberapa penaksiran yang dapat ditentukan dalam jobshop antara lain sebagai berikut.
Flow time (Fj) : Total jumlah waktu yang diperlukan pekerjaan j pada sis-tem penjadwalan mesin
Makespan : Total jumlah waktu yang diperlukan untuk menyelesaikan seluruh pekerjaan
Lateness (Lj) : Total jumlah waktu dimana waktu penyelesaian pekerjaan berbeda dari waktu yang telah ditentukan
Tardiness (Tj) : Total jumlah waktu dimana waktu penyelesaian pekerjaan
j tidak sesuai dengan waktu yang ditentukan atau sama dengan 0, yaitu Tj = max{0, L}.
Dari definisi diatas diperoleh formula untuk menentukan penaksiran dalam per-soalan jobshopyaitu
Mean Flow time : ¯F = 1
n n P j=1 Fj Mean Tardiness : ¯T = 1 n n P j=1 Tj
MaksimumFlow time : Fmax= max
1≤j≤n {Fj}
MaksimumTardiness : Tmax= max
1≤j≤n {Tj}
Jumlah pekerjaan yang terkendala : NT = n
P
j=1 f(Tj)
dengan f(Tj) = 1 jika Tj >0 dan f(Tj) = 0 untuk lainnya. 2.2 Penjadwalan Mesin
2.2.1 Definisi penjadwalan mesin
Asumsikan terdapat graf bipartit lengkap G = (V1 ∪V2, V1 ×V2) dengan
V1 = {v1, . . . , vn} dan V2 = {w1, . . . , wn} dengan n ≤ m. Untuk masing-masing arc (vi, wj) terdapat suatu bilangan riil cij, sehingga diperoleh pemetaan satu-satu ϕ:V1 → V2 yang merupakan suatu persoalan penjadwalan ϕdengan fungsi objektif yaitu
minX v∈V1
cυϕ(υ) (2.2)
Persoalan penjadwalan tersebut dapat direpresentasikan oleh suatu matriks di-mensi n×m C = (cij) dan diformulasikan sebagai suatu program linier dengan
13 nilai 0-1 variabel xij yaitu
min n X i=1 m X j=1 cijxij kendala m X j=1 xij = 1, i= 1, . . . , n n X i=1 xij ≤1, j = 1, . . . , m xij ∈ {0,1}, i= 1, . . . , n;j = 1, . . . , m (2.3)
dengan xij = 1 jika dan hanya jika vi dipasangkan ke wj. Untuk masing-masing kendala yang terdapat dalam persamaan 2.5, tiap vi ∈ V1 dipasangkan ke tiap elemen di V2, dan tiap wj ∈ V2 terdapat sedikitnya pada satu penjadwalan yang ada.
2.2.2 Ruang lingkup mesin
Ambil nilai α1 ∈ {o, P, Q, R, P M P M, QM P M} dengan o didenotasikan sebagai simbol kosong (sehingga,α=α2jikaα1=o), maka tiapJi mempunyai suatu ope-rasi tunggal. Brucker (2007) mengemukakan ruang lingkup mesin diklasifikasikan oleh notasi α=α1α2 pada dua parameter yang digunakan.
Jikaα−1 = o, tiap unit pekerjaan diproses pada satu mesin identik yang dirujuk. Jikaα1 ∈ {P, Q, R}, maka terdapat mesin paralel dimana tiap unit pekerjaan da-pat diproses oleh masing-masing mesinM1, . . . , Mm. Jikaα1=P, maka terdapat mesin paralel identik. Sehingga, untuk waktu prosespij pada unit pekerjaanJi di
Mj diperolehpij =pi untuk semua mesinMj. Jikaα1 =Q, maka terdapat mesin paralel uniform dengan pij =pi/sj dengan sj adalah kecepatan kinerja mesinMj. Terakhir, jika α1 = R, maka terdapat mesin paralel yang saling bebas dengan
pij =pi/sij untuk kecepatan unit pekerjaan yang saling berkaitan sij padaMj. Jika α1 ∈ {G, X, O, J, F}, maka terdapat model suatu multi-operasi dalam pen-jadwalan yang dialokasikan ke tiap unit pekerjaanJi jika terdapat suatu himpunan operasi Oi1, . . . , Oi,ni. Mesin yang digunakan dirujuk dimana seluruh µij
meru-pakan himpunan dengan elemen 1. Persoalan ini selanjutnya disebut persoalan general shop.
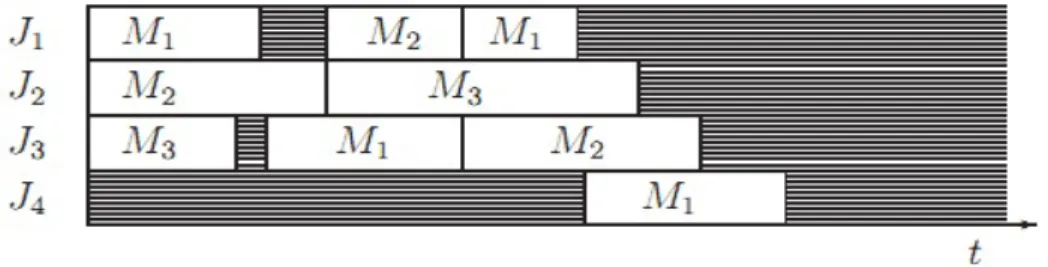
Indikasikan persoalan general shop dengan set α1 = G. Jobshop, flowshop, open shop dan mixed shop merupakan persoalan khusus dari persoalan general shop. Dalam persoalan jobshop, indikasikan α1 = J, maka diperoleh suatu relasi operasi yaitu
Oi1 →Oi2 →Oi3 → · · · →Oi,ni, i= 1, . . . , n (2.4)
Gambar 2.3 : Ilustrasi Jobshoppada satu mesin
Lebih lanjut, secara umum dapat diasumsikan bahwa µij 6=µi,j+1 untuk j = 1, . . . , ni −1. Disebut sebagai persoalan jobshop dimana µij = µi,j+1 merupakan
15 Flowshop diindikasikan oleh α1 = F dengan ni = m untuk i = 1, . . . , n dan
µij ={Mj}untuk masing-masing i = 1, . . . , ndan j = 1, . . . , m.
Open shop dinotasikan dengan α1 = O dengan definisi yang hampir sama de-ngan flowshop dengan tanpa ada relasi antara operasi tiap unit pekerjaan yang ada.
Mixed shop diindikasikan dengan α1 =X yang merupakan kombinasi dari job-shop dan open shop.
Suatu permutasi flowshop merupakan suatu flowshop dimana unit pekerja-an diproses secara bersamapekerja-an pada masing-masing mesin. Andaikpekerja-an terdapat suatu persoalanjobshop, maka setβ4 sama dengan ni ≤2. Pada kasus ini seluruh unit pekerjaan mempunyai paling banyak dua operasi dalam penjadwalan. Jika
α2 sama dengan suatu bilangan bulat positif 1,2, . . ., maka α2 didenotasikan se-bagai jumlah mesin yang tersedia. Jika α2 = k, maka k merupakan suatu nilai pendekatan pada jumlah mesin yang tersedia. Jika nilai pendekatan pada jumlah mesin, set α2=o.
Megow and Schulz (2004) mengembangkan suatu model dalam persoalan penjadwalan untuk meminimumkan waktu penyelesaian rata-rata suatu pekerjaan pada mesin paralel identik dengan menggunakan algoritma on-line. Diasumsikan bahwa terdapat suatu mesin paralel identikmdimana tiap mesinnya hanya dapat menyelesaikan satu darinpekerjaan pada rentang waktu tertentu. Masing-masing pekerjaan dari suatu himpunan J ={j1, . . . , jn} mempunyai waktu penyelesaian positifpj >0 dan suatu bobot nonnegatifwj ≥0. Sehingga fungsi objektif dalam model adalah
n
P
j=1
wjCj dimana Cj menyatakan waktu dimana pekerjaan j telah selesai pada suatu penjadwalan yang layak.
Mastrolili dan Svensson (2011) memberikan pandangan terhadap persoalan penjadwalan didasarkan pada persoalan jobshop dan flowshop. Dalam persoalan jobshop, asumsikan bahwa terdapat n pekerjaan yang dapat diselesaikan oleh m
pada himpunan M mesin yang diberikan. Tiap pekerjaan j mempunyai siklus operasi µj yaituO1j, O2j, . . . , Oµjj dimana operasi dilakukan pada unit waktu pij tanpa ada interupsi atau gangguan pada mesin mij ∈ M. Diberikan suatu pen-jadwalan yang layak dimana seluruh operasi telah dijadwalkan dengan ketentuan bahwa tiap mesin dapat bekerja paling banyak hanya satu operasi pada suatu rentang waktu tertentu. AsumsikanCj sebagai waktu dimana seluruh operasi pa-da j telah selesai, maka objektif dari model ini adalah meminimumkanmakespan
CmaxxjCj dan meminimumkan total jumlah waktu penyelesaian operasi secara
keseluruhan,PwjCj. Sedangkan persoalan penjadwalan flowshop,Fkγ, masing-masing pekerjaan diselesaikan oleh tepat satu buah mesin dan seluruh pekerjaan diselesaikan dalam waktu bersamaan yang merupakan suatu contoh kasus yang khusus pada persoalan penjadwalan jobshop yang asiklik.
Yamada (2007) memberikan notasiheaddantailpada operasi unit pekerjaan yang belum dijadwalkan. Ambil i sebagai operasi pada mesin Mk yang belum dijadwalkan. Operasi i dapat diidentifikasi sebagai suatu node i ke dalam graf untuk memilih Sp. Ambil ri sebagai panjang dari jarak terpanjang dari unit pekerjaan head ke tail dengan ri = L(0, i) dimana L(i, j) merupakan panjang dari node i ke j yang menyatakan waktu rilis unit pekerjaan. Ambil qi sebagai panjang path darii ke waktu proses yang diperlukan qi =L(I,∗)−pi dimana pi menyatakan waktu proses pada i dan qi adalah unit pekerjaan tail pada operasi
17 diformulasikan ke dalam bentuk persamaan matematika sebagai berikut:
min max i∈C {si+pi+qi} Kendala si ≥ri (i∈C) sj−si ≥pi ∨si−sj ≥ pj (i, j ∈C) (2.5)
2.2.3 Penjadwalan mesin tunggal identik
Andaikanri danpi masing-masing menyatakan jumlah pekerjaan pada him-punanOij dan waktu proses untuk tiap pekerjaan. Kemudian asumsikanfi meru-pakan fungsi monoton pada waktu penyelesaian Ci pada pekerjaan i = 1, . . . , n, dimana penjadwalan menentukan tiap pekerjaan ke n waktu proses pekerjaan. Jika waktu proses t dipasangkan ke pekerjaan i, maka fungsi monoton yang di-peroleh adalah fi(t+ 1). Selanjutnya untuk waktu proses maksimum pekerjaan
n, maka persoalan penjadwalan dapat diselesaikan dalam waktu O(n3).
Karena fungsi fi adalah monoton tak turun, maka ti waktu proses pada n peker-jaan dapat ditentukan dengan menggunakan algoritma dimana terdapat asumsi bahwa semua pekerjaan dienumerasikan sebagai berikut
r1 ≤r2 ≤ · · · ≤rn (2.6)
Algoritma Waktu Proses n Pekerjaan
1. t1 :=r1;
2. FORi:= 2 TO n DO ti:= max{ri, ti−1+ 1}
Terdapat suatu penjadwalan optimal dengan waktu proses ti(i= 1, . . . , n). Am-bil penjadwalan optimal S dengan waktu proses t1, . . . , tj dimana j < n adalah maksimum, maka tj+1 menunjukkan waktu proses selanjutnya dimana suatu
maka suatu penjadwalan di S dapat dijadwalkan dan dipindahkan ke tj+1
tan-pa adanya penambahan tan-pada nilai objektif. Oleh sebab itu, penjadwalan baru yang diperoleh juga optimal dan diperoleh suatu kontradiksi ke maksimalitas pa-da j. Graf bipartif lengkap yang menyatakan suatu penjadwalan diberikan oleh
V1 ={1, . . . , n}dan V2 ={t1, . . . , tn} dengan nilaicij ditentukan oleh
cij = fi(tj+ 1) jika ri ≤tj ∞ dan lainnya (2.7)
Teorema 2.2.1 (Brucker, 2007) Asumsikan (cij) adalah matriks berdimensi n×
m dengan n ≤ m. Selanjutnya, asumsikan bahwa cij ≤ cik untuk semua i dan
j < k. Maka, xij = 1 jika i=j 0 dan lainnya merupakan solusi optimal untuk penjadwalan.
Bukti Asumsikan y = (yij) sebagai solusi optimal dari persoalan penjadwalan dengan yvv = 1 untukv = 1, . . . , idimanai dengan nilai sebesar mungkin. Asum-sikan i < n (jika i = n). Karena yi+1,i+1 = 0, terdapat suatu indeks l > i+ 1
dengan yi+1,l= 1. Selanjutnya, perhatikan bahwa terdapat dua kasus.
1. Kasus 1. Terdapat suatu indeksj > i+ 1 dengan yj,i+1 = 1, maka ci+1,i+1+cjl ≤ci+1,l+cj,i+1
Sehingga, jika ditentukan
¯ yrs = 1 jika r=s=i+ 1 atau r =j, s =l 0 jika r=i+ 1, s =l atau r=j, s=i+ 1 yrs dan lainnya
19 maka ¯yrs adalah solusi optimal untuk persoalan penjadwalan, kontradiksi dengan maksimalitas pada i.
2. Kasus 2. yv,i+1 = 0 untuk semua v ≥ i+ 1. Terdapat l > i+ 1 dengan yi+1,l= 1. Lebih lanjut, ci+1,i+1 ≤ci+1,l, maka ¯yrs didefinisikan oleh
¯ yrs= 1 jika r=s=i+ 1 0 jika r=i+ 1, s=l yrs dan lainnya
merupakan suatu solusi optimal, kontradiksi dengan maksimalitas pada i.
2.3 Persoalan Jobshop
Dalam persoalan penjadwalan jobshop, suatu pekerjaan dapat diselesaikan oleh mesin pada sebarang urutan dimana terdapatmmesin dannpekerjaan yang akan diproses. Yamada (2007) memberikan pandangan mengenai persoalan pen-jadwalanjobshopyaitu terdapatn×mminimum-makespanyang merupakan topik umum dalam persoalan penjadwalan, yang dapat dinotasikan dengann/m/G/Cmax. Sehingga dapat dideskripsikan oleh suatu himpunan yang menyatakan n jumlah pekerjaan yang ada,{Ji}1≤j≤n, yang akan diproses olehmmesin yang dinotasikan
dengan suatu himpunan{Mr}1≤r≤m. Objek dari persoalan ini adalah menentukan
waktu minimum yang diperlukan untuk menyelesaikannpekerjaan yang ada yang juga disebut dengan makespan, yang dinotasikan sebagai Cmax = max
i≤j≤n,1≤r≤mcjr, dengan Ojr dan cjr berturut-turut menyatakan waktu awal dan waktu penyele-saian.
Definisi 3 (Definisi Jobshop) Andaikan M sebagai suatu himpunan mesin yang tersedia. Suatu pekerjaan di M merupakan suatu tripelJ = (k, µ, d) dimana
k ∈ N merupakan jumlah tahap di J, µ: {1. . . k} → M yang menunjukkan suatu mesin yang digunakan pada tiap tahap, dan d:{1. . . k} → N yang menunjukkan panjang tiap tahap. Suatu jobshop merupakan suatu himpunan J ={J1, . . . , Jn} untuk pekerjaan Ji= (ki, µi, di).
Definisi 4 (Penjadwalan layak)AsumsikanJ ={J1, . . . , Jn}sebagai pekerja-an ypekerja-ang tersedia. Suatu penjadwalpekerja-an ypekerja-ang layak untuk J merupakan suatu relasi
S ⊂ J ×K ×T sehingga (i, j, t) ∈ S menunjukkan bahwa suatu pekerjaan Ji
dalam keadaan ’sedang diproses’ pada waktu tahap ke-j untuk waktu t dan, kare-na itu, digukare-nakan mesin µi(j). Asumsikan Tji sebagai himpunan waktu dimana pekerjaan i ∈ J dieksekusi pada tahap ke-j dengan Tji ={t : (i, j, t)∈S}. Suatu penjadwalan haruslah memenuhi beberapa kondisi sebagai berikut:
1. Proses penyelesaian pekerjaan
Jika (i, j, t)∈S dan (i, j0, t0)∈S, maka j < j0 juga berakibat t < t0. 2. Covering
Untuk setiap i∈ J dan j ∈K, berlaku
Z
t∈Ti j
dt≥di(j)
untuk setiap tahap dalam penjadwalan dieksekusi. 3. Mutual eksklusi
Untuk setiap i, i0∈ J, j, j0 ∈K dan t∈T. Jika (i, j, t)∈S dan (i0, j0, t0)∈
S, maka µi(j) 6= µi0
(j0) yang menunjukkan bahwa terdapat dua tahap dari pekerjaan yang berbeda yang diproses atau dieksekusi pada waktu yang sama namun tidak menggunakan mesin yang sama.
21 Teorema 2.3.1 MisalU adalah himpunan pekerjaan yang dapat dijadwalkan ter-lebih dahulu dan misal i adalah pekerjaan yang bukan merupakan bagian dari U
dengan dj ≤di,∀j ∈U. Maka himpunan pekerjaanV =U∪{i}dapat dijadwalkan jika dan hanya jika
x(di) + dXi−m
t=1
(m−hU(t))≥m
dimana m adalah jumlah operasi dan di adalah pembagian waktu terhadap pen-jadwalan mesin.
Teorema 2.3.2 Misal I1 merupakan subhimpunan dari I ={J1, . . . , Jn}. Batas bawah dari nilai minimum makespan untuk penjadwalan satu mesin dapat diten-tukan oleh h(I1) = min i∈I1 ri+ X i∈I1 pi+ min i∈I1 qi
dengan ri, pi dan qi menyatakan waktu awal, waktu penyelesaian dan batas waktu tiap pekerjaan i secara berturut-turut.
Dalam jobshop, asumsikan terdapat suatu pekerjaan α1 = J, sehingga diperoleh suatu kondisi bersyarat (precendence relations) yang dinyatakan sebagai
Oi1 →Oi2 →Oi3 →. . . Oi, ni untuk i= 1, . . . , n
Selanjutnya, secara umum asumsikan bahwa µij 6=µi,j+1 untuk j= 1, . . . , ni−1. Akibatnya,µij =µi,j+1 merupakan suatu persoalanjobshopdengan repetisi mesin.
2.4 Penjadwalan Flowshop
Persoalan penjadwalan flowshop merupakan suatu persoalan penjadwalan umum dengan
• untuk tiap pekerjaani terdapat m pekerjaan yang dinyatakan dengan him-punanOij dimana tiap pekerjaan mempunyai waktu prosespij(j = 1, . . . , m) dan diproses pada mesinMj, dan
• terdapat kendala dengan ketentuan Oij → Oi,j+1(i = 1, . . . , m−1) untuk
tiap i = 1, . . . , n dimana tiap pekerjaan diproses dengan urutan mesin 1, mesin 2, mesin 3 dan seterusnya.
Oleh karena itu, objektif dalam persoalan ini adalah untuk menentukan urutan pekerjaanφj untuk masing-masing mesinj sehingga diperoleh suatu penjadwalan yang layak. Suatu penjadwalan flowshop disebut juga dengan suatu permutasi flowshop dimana terdapat suatu urutan pekerjaan khusus φ1, φ2, . . . , φm dengan
φ1 =φ2 =· · ·= φm. Brucker (2007) menunjukkan suatu bentuk permutasi yang dinyatakan denganL:L(1), . . . , L(n) untuk semua pekerjaan yang tersedia untuk penjadwalan flowshop dimana terdapat urutan pekerjaan yang sama pada mesin yang berbeda. Asumsikan terdapat suatu urutan optimal dengan aturan urutan kiri mesin yaituT :L(1), . . . , L(t) dan urutan kanan mesin,R:L(t+ 1), . . . , L(n) sedemikian hingga T dan R diproses oleh mesin secara bertahap.
Untuk setiap proses, asumsikan suatu pekerjaanOi∗j∗ dengan waktu proses teren-dah pi∗j∗. Jika j∗ = 1, maka ambil pekerjaan i∗ dari urutan akhir T kemudian ubah T dengan T ◦i∗. Selanjutnya yntuk yang lainnya ambili∗ dari urutan awal
R kemudian ubah R dengan i∗ ◦R. Dari asumsi diatas, Brucker (2007) menge-mukakan algoritma yang dapat digunakan dalam menentukan urutan pekerjaan sebagai berikut.
Step 1. X := 1, ..., n;T :=φ :R :=φ
Step 2. whileX 6=φ DO Step 3. BEGIN
Step 4. Tentukan i∗, j∗ dengan pi∗j∗ = min{pij|i ∈X;j = 1,2};
23 Step 6. X :=X \ {i∗}
Step 7. END; Step 8. L:=T ◦R
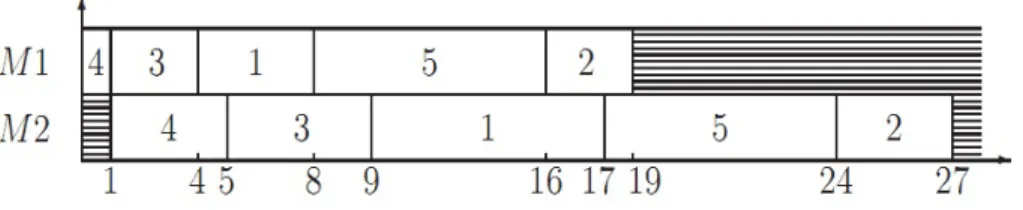
Brucker (2007) memberikan ilustrasi penjadwalan mesin untuk persoalan penjad-walan flowshop seperti pada tabel 2.1.
Tabel 2.1 : Ilustrasi Data Pekerjaani Mesin pi1 Mesinpi2
1 4 8
2 3 3
3 3 4
4 1 4
5 8 7
Dengan ketentuan algoritma yang telah diperoleh, maka penjadwalan yang layak yang mungkin dalam urutan pekerjaan yang ada diberikan pada gambar 3.1 di bawah ini.
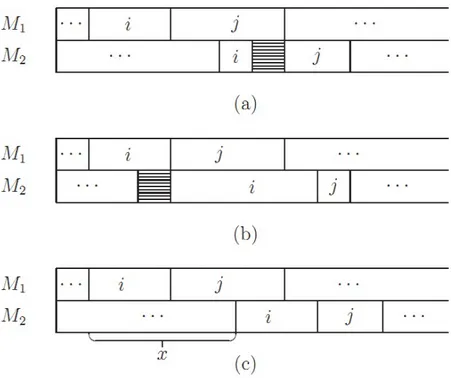
Selanjutnya, diberikan dua lemma untuk membuktikan bahwa algoritma berlaku untuk persoalan penjadwalan flowshop sebagai berikut.
Lemma 2.4.1 Asumsikan L := L(1), . . . , L(n) sebagai urutan pekerjaan yang ada, sehingga berlaku
min{pi1, pj2}<min{pj1, pi2}
yang menunjukkan bahwa pekerjaan i diproses sebelum pekerjaan j di L.
Bukti Jika pi1 < min{pj1, pi2}, maka pi1 < pi2 yang menunjukkan pekerjaan i
di T. Jika pekerjaan j ditambahkan ke urutan R, maka urutan pekerjaan di T
telah selesai. Dan selanjutnya, j diproses setelah i di T karena pi1 < pj1. Jika pj2 < min{pj1, pi2}, diperoleh penjadwalan yang sama. Penjadwalan ini dapat
diilustrasikan dengan gambar 2.2 seperti di bawah ini.
25 Lemma 2.4.2 Asumsikan terdapat suatu penjadwalan dimana pekerjaan j dijad-walkan segera setelah pekerjaan i. Maka,
min{pj1, pi2} ≤min{pi1, pj2}
menunjukkan bahwa i dan j dapat diganti tanpa mempengaruhi waktu proses pe-kerjaan.
Bukti Jikaj dijadwalkan segera setelah pekerjaan i, maka terdapat tiga kondisi penjadwalan yang mungkin. Notasikan bahwawij adalah total waktu periode dari pekerjaan i diproses hingga j, maka diperoleh
wij = max{pi1+pj1 +pj2, pi1+pi2+pj2+pi2, pj2}
= max{pi1+pj2 + max{pj1, pi2}, x+pi2 +pj2}
Kemudian untuk kondisi
max{−pi1,−pj2} ≤max{−pj1,−pi2}
ambil pi1 +pi2+pj1 +pj2 ke kedua kondisi di atas, sehingga diperoleh pj1 +pi2+ max{pi1, pj2} ≤pi1 +pj2+ max{pj1, pi2}
dimana wji < wij. Maka, terbukti bahwa pergantian urutan pekerjaan antara i dan j tidak mempengaruhi waktu proses pekerjaan.
2.4.1 Persoalan bin packing
Salah satu persoalan penjadwalan flowshop yang sering dikaji adalah per-soalanbin packingmerupakan persoalan penjadwalan minimummakespan dengan tujuan mengurutkan seluruh pekerjaan yang ada ke total mesin yang digunakan sehingga diperoleh total minimumbin yang digunakan dalam penjadwalan layak yang diperoleh.
Definisi 5 (bin packing) Diberikan pekerjaan dengan bobot s1, . . . , sn ∈ (0,1]. Alokasikan keseluruhan pekerjaan ke total jumlah minimum bin yang mungkin, dimana tiap bin berbobot 1.
2.5 Zona Terlarang dalam Penjadwalan
Asumsikan terdapat suatu penjadwalan yang layak dengan operasi atau pe-kerjaan Oij ∈ QJ dimulai pada waktu sij dengan waktu penyelesaian secara ke-seluruhan adalah cij =sij +pij, dimana pij menyatakan waktu proses pekerjaan
Oij. Asumsikan QJk sebagai himpunan yang menyatakan seluruh pekerjaan dari himpunan QJ,QJk ⊂Q
J
, yang diproses oleh mesinMk ∈M. Dalam model deter-ministik, waktu proses pij diberikan untuk semua pekerjaan Oij, Ji ∈ J dengan
j = 1,2, . . . , ni. Oleh sebab itu, suatu penjadwalan didefinisikan sebagai suatu himpunan waktu awal sij (atau waktu penyelesaian cij) pada seluruh pekerja-an QJ. Terdapat suatu himpunan waktu penyelesaian pada pekerjaan QJ yang digunakan untuk menyatakan suatu barisan penjadwalan khusus untuk waktu pe-nyelesaianQJ
k untuk setiap mesinMk, k = 1,2, . . . , m. Oleh sebab itu, pada suatu penjadwalan khusus diberikanmbarisan penjadwalan khusus untuk pekerjaanQJ k
untuk setiap mesinMk ∈M.
Objektif dari persoalan penjadwalan adalah untuk menentukan suatu m
barisan penjadwalan dari seluruh pekerjaan QJ
k yang ada pada mesin Mk, k = 1,2, . . . , m dengan nilai pada fungsi objektif yang diberikan, φ(C1, C2, . . . , Cn) adalah minimum. Karena itu, persamaan Ci = cini dan Ci menyatakan waktu total penyelesaian pekerjaanJi ∈J.
Andaikan terdapat batasan waktu pada rancangan operasi secara keselu-ruhan dengan memberikan batas waktu pada masing-masing pekerjaan yang ada. Maka proses ini akan menambahkan suatu kendala waktu, batas waktu operasi atau total waktu pekerjaan secara keseluruhan ke dalam model rancangan yang
27 ada (Chaudhuri, 1995). Kendala waktu ini selanjutnya disebut sebagai suatu zona terlarang (forbidden zones) dalam persoalan penjadwalan.
Khammuang et al. (2007) memberikan suatu kendala interval waktu yang berbeda dari model-model penjadwalan yang telah dikembangkan sebelumnya. Dalam beberapa persoalan penjadwalan, proses penyelesaian terhadap pekerjaan tetap berjalan namun tanpa adanya inisialisasi terhadap interval waktu terten-tu. Denotasikan bahwa n pekerjaan dapat dijadwalkan menjadi J1, J2, . . . , Jn. Asumsikan bahwapi sebagai waktu penyelesaian pekerjaanJi sehingga pi ≤1,∀i. Sehingga terdapat partisi waktu sebagai suatu himpunan I = {I1, I2, . . . , Is} dengan I1 = [0,2], I2 = [2,4] hingga Is = [2s − 2,2s]. Masing-masing Ij merupakan bagian dari zona terlarang (forbidden zones) Fj ⊆ Ij,∀j dimana
F1 = (1,2], F2 = (3,4], . . . , Fs = (2s−1,2s]. Akibatnya, interval waktu Is Fj merupakan interval waktu yang diperbolehkan (allowed zones) dimana pekerjaan dapat diproses oleh mesin. Lebih sederhana, interval waktu dan zona terlarang dalam penjadwalan dapat diilustrasikan sebagai berikut.
Gambar 2.6 : Ilustrasi interval waktu dan zona terlarang dalam penjadwalan
Khammuang et al. (2007) secara khusus memberikan pandangan terhadap definisi zona terlarang dalam penjadwalan sebagai suatu interval waktu dimana suatu pekerjaan atau operasi tidak dapat dilakukan, namun dapat diproses. Lebih jelasnya, andaikan suatu pekerjaan telah selesai sebelum interval waktu pada zona terlarang, maka pekerjaan tersebut akan dikeluarkan dari himpunan urutan pe-kerjaan pada interval waktu berikutnya. Sehingga, untuk pepe-kerjaan paling akhir dari suatu barisan urutan pekerjaan yang ada memerlukan waktu penyelesaian
t= 2j−1. Model ini bertujuan untuk menentukan urutan atau barisan terhadap pekerjaan yang ada sehingga diperoleh interval waktu minimum yang digunakan. Billaut dan Sourd (2001) mengembangkan model penjadwalan dengan adanya suatu kendala interval waktu menggunakan asumsi terdapat suatu himpunan wak-tu awal dalam zona terlarang (forbidden start time) yang diberikan pada persoalan jobshop. Lebih jelasnya, dalam persoalan jobshop, waktu awal dalam zona ter-larang didasarkan pada waktu yang ditentukan saat mesin akan menyelesaikan suatu pekerjaan j dengan keadaan mesin tidak dapat melakukan proses lainnya di waktu yang sama. Billaut dan Sourd (2001) memberikan ilustrasi terhadap per-soalan penjadwalan yang melibatkan multi mesin, diasumsikan seorang operator dapat melakukan pengaturan mesin. Operator tidak dapat melakukan pekerjaan lainnya dalam waktu yang bersamaan meskipun waktu yang diperlukan untuk menyelesaikan pekerjaan tersebut hanya sedikit. Oleh sebab itu, kedua pekerjaan tersebut tidak dapat diselesaikan pada waktu yang bersamaan sehingga waktu awal dalam zona terlarang menjadi parameter dalam pembagian waktu penjad-walan.
Teorema 2.5.1 (Billaut, 2001) Penjadwalan mesin tunggal dengan adanya wak-tu awal dalam zona terlarang merupakan persoalan NP-complete.
Bukti (berdasarkan Billaut, 2001) Untuk membuktikan Teorema 5, asumsikan terdapat n = 3m pekerjaan yang dibagi menjadi dua bagian, yaitu:
• 3mpekerjaan pertama dengan waktu penyelesaians(a). mpekerjaan masing-masing dinotasikan sebagai T1, T2, . . . , Tm
• m pekerjaan yang dinotasikan sebagai T1, T2, . . . , Tm dengan waktu penye-lesaian sama dengan B
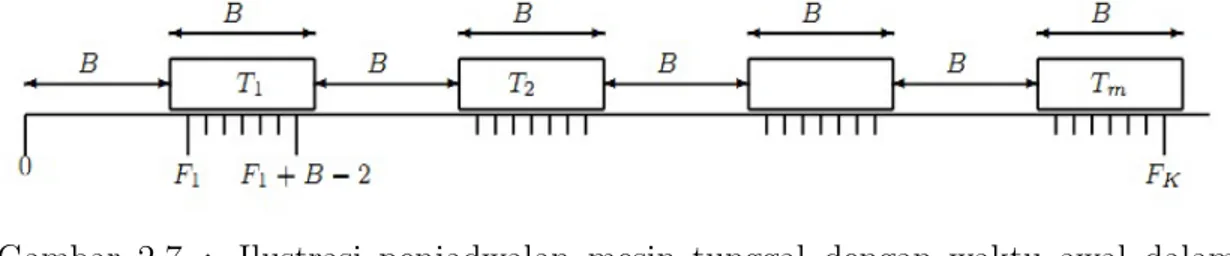
29 Total interval waktu awal dalam zona terlarang adalahK =m(B−1). Himpunan interval waktu awal dalam zona terlarang diberikan olehF =S1≤i≤m[(2i−1)B+ 1,2iB−1], sehingga secara berkala terdapatB+1 waktu awal diluar zona terlarang dan selanjutnya B − 1 interval waktu awal dalam zona terlarang seperti yang ditunjukkan pada Gambar 2.4 dengan F1 = B + 1, F2 = B + 2, . . . , FB−1 =
2B−1, FB= 3B+ 1 dan seterusnya. Persoalan ini merupakan persoalan
pseudo-Gambar 2.7 : Ilustrasi penjadwalan mesin tunggal dengan waktu awal dalam zona terlarang
polynomial dengan total waktu awal dalam zona terlarang didasarkan pada B
yang menunjukkan bahwa persoalan merupakan NP-complete.
Teorema 2.5.2 (Billaut, 2001) Persoalan 1|Sj 6∈ F, pj = p|Cmax dapat disele-saikan secara optimal dalam waktu O(K), asumsikan bahwa terdapat suatu waktu awal dalam zona terlarang.
Bukti Dalam persoalan ini, semua pekerjaan yang ada adalah indentik sehing-ga tidak terdapat suatu persoalan antrian. Persoalan yang ada adalah untuk menjadwalkan suatu waktu awal yang tidak termasuk dalamF ke tiap pekerjaan yang ada. Jika tidak terdapat suatu waktu awal yang terlarang sama dengan 0( mod p), semua pekerjaan dapat disusun tanpa adanya waktu idle. Sebaliknya, suatu waktu idle terdapat dalam persoalan dan jika terdapat suatu waktu awal terlarang sama dengan 1( mod p), pekerjaan yang ada dapat disusun tanpa ada suatu waktuidle. Proses ini membutukanK iteraksi dan kembali pada suatu ni-lai optimal makespan. Prosedur ini memberikan optimal makespan dalam O(K) waktu.
Teorema 2.5.3 (Billaut, 2001) Jika K = 1, maka terdapat suatu penjadwalan optimal mesin pada makespan adalah P dengan pi = p untuk semua pekerjaan dan F1 = kp untuk beberapa bilangan bulat k < n. Akibatnya, makespan dalam penjadwalan adalah P + 1.
Bukti (berdasarkan Billaut, 2001). Jika waktu proses semua pekerjaan adalah
p dan F1 = kp, jelas bahwa tidak terdapat suatu penjadwalan yang layak yang diselesaikan padaP =np. Andaikan suatu penjadwalan pekerjaan ke-k+1 dengan waktu awal kp yang merupakan interval dalam zona terlarang, maka diperoleh suatu penjadwalan yang diselesaikan padaP+1 dengan memulai pekerjaan ke-k+1 pada waktukp+1. Sekarang akan ditunjukkan bahwa terdapat suatu penjadwalan yang dapat diselesaikan pada P. Jika waktu pemrosesan pada seluruh pekerjaan adalah p dan F1 6=kp, maka tiap pekerjaan dimulai pada waktu kp dengan 0 ≤
k ≤ n −1 dan sebarang urutan pekerjaan adalah layak dan dapat diselesaikan pada P. Jika terdapat dua pekerjaan yang berbeda dalam suatu penjadwalan, maka dapat diasumsikan bahwa p1 6= p2 dimana p1 ≥ pi,∀i. Ambil k sebagai indeks dimana Pk−1 ≤ F1 < Pk. Sehingga, diperoleh Pk −F1 ≤ pk ≤ pi. Jika
Pk −F1 < p1, maka pekerjaan yang ada dapat dijadwalkan menjadi J2, . . . , Jk antara 0 dan Pk−p < F1 danJ1 antara Pk−p1 dan Pk. JikaPk−F1 =p1, maka pekerjaan dapat dijadwalkan sebagai J3, . . . , Jk antara 0 dan Pk −p1 −p2 < F1 dan J1 antara Pk −p1 −p2 dan Pk −p2 = F1 +p1 −p2 6= F1. Akibatnya, J2 dapat diselesaikan pada Pk −p2. Pada kedua kasus tersebut, dapat diperoleh penjadwalan untuk J1, . . . , Jk yang dapat diselesaikan sebelum Pn.