PENGOPTIMUMAN FUNGSI TAKLINEAR DENGAN METODE KUASI NEWTON: TEORI DAN APLIKASINYA MOCHAMMAD GIA PRIYANA PAJAR

PENGOPTIMUMAN FUNGSI TAKLINEAR DENGAN

METODE KUASI NEWTON: TEORI DAN APLIKASINYA

MOCHAMMAD GIA PRIYANA PAJAR

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

BOGOR 2017

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa skripsi berjudul Pengoptimuman Fungsi Taklinear dengan Metode Kuasi Newton: Teori dan Aplikasinya adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Februari 2017

Mochammad Gia Priyana Pajar

ii

ABSTRAK

MOCHAMMAD GIA PRIYANA PAJAR. Pengoptimuman Fungsi Taklinear dengan Metode Kuasi Newton: Teori dan Aplikasinya. Dibimbing oleh BIB PARUHUM SILALAHI dan SISWANDI.

Pengoptimuman fungsi taklinear tak berkendala dapat diselesaikan dengan metode kuasi Newton. Kelebihan dari metode ini adalah tidak perlu mencari invers matriks Hesse, melainkan menggantinya dengan suatu matriks yang mendekati nilai invers matriks Hesse. Untuk mendapatkan matriks penggantinya digunakan metode Davidon-Fletcher-Powell (DFP) atau Broyden-Fletcher-Golfarb-Shanno (BFGS). Karya ilmiah ini mengonstruksi invers matriks Hesse kemudian melihat sifat kedefinitan matriks yang diperoleh dari metode DFP atau BFGS. Perangkat lunak yang digunakan untuk membantu proses komputasi adalah MATLAB R2011b. Hasil numerik pada lima fungsi yang diujikan menunjukkan jumlah iterasi metode DFP dan BFGS pada umumnya sama, pada fungsi Rosenbrock.

Kata kunci: Kuasi Newton, Davidon-Fletcher-Powell (DFP), Broyden-Fletcher-Golfarb-Shanno (BFGS), Pengoptimuman

ABSTRACT

MOCHAMMAD GIA PRIYANA PAJAR. Optimization of the Nonlinear Function Using Quasi Newton Method: Theory and Application. Supervised by BIB PARUHUM SILALAHI and SISWANDI.

Unconstrained nonlinear optimization can be solved by using quasi Newton method. In this method is that finding the inverse of the Hessian matrix is unnecessary but replacing it with approximation of the Hessian matrix invers. For obtaining Hessian matrix, it is used Davidon-Fletcher-Powell (DFP) or Broyden-Fletcher-Golfarb-Shanno (BFGS). This manuscript reconstructs Hessian matrix inverse then analyze its positive definiteness property of DFP and BFGS methods. A software that used for computation is MATLAB R2011b. The numerical result in five functions that tested shows the number of iteration in DFP and BFGS method almost the same, except for the Rosenbrock function.

Keyword: Quasi Newton, Davidon-Fletcher-Powell (DFP), Broyden-Fletcher-Golfarb-Shanno (BFGS),Optimization

iii

PENGOPTIMUMAN FUNGSI TAKLINEAR DENGAN

METODE KUASI NEWTON: TEORI DAN APLIKASINYA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

BOGOR 2017

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

vi

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah Subhanahu Wa Ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan.

Terima kasih penulis ucapkan kepada:

1. Bapak Saepudin dan ibu Nurjamilah tercinta, kakak (Dian, Suci, Amir, Eko), keponakan (Nada, Naya, Raisa), dan keluarga besar yang selalu memberikan doa, kasih sayang, dukungan dan motivasi tanpa henti,

2. Dr Ir Bib Paruhum Silalahi, MKom selaku pembimbing I dan Drs Siswandi, MSi selaku pembimbing II yang telah memberikan bimbingan, ilmu, kesabaran, motivasi, dan bantuannya selama penulisan karya ilmiah ini, serta Dra Farida Hanum, MSi selaku penguji yang telah memberikan ilmu dan sarannya,

3. Alia Nisfi Jayanti, Fariz, Nala, Ria, Hesty, Fuji, Rani, Dara, Lina dan Kemal yang telah menjadi sahabat seperjuangan di IPB, yang sering mendoakan dan memberi semangat, serta keceriaan,

4. teman-teman Halal FC yang selalu memberikan semangat, sebagai penghibur diri dan tempat menyalurkan hobi dikala jenuh dengan perkuliahan,

5. teman-teman Soulmath Matematika 49 yang telah berjuang bersama dan membantu penulis dalam kegiatan belajar,

6. seluruh staf tata usaha, kakak-kakak Matematika 47, 48, adik-adik Matematika 50 dan 51, serta sahabat yang tidak bisa disebutkan satu per satu yang telah memberikan semangat, doa, dan dukungannya.

Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya Matematika dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.

Bogor, Februari 2017

vii

DAFTAR ISI

DAFTAR TABEL viii

DAFTAR GAMBAR viii

DAFTAR LAMPIRAN viii

PENDAHULUAN 1

Latar Belakang 1

Tujuan Penelitian 2

TINJAUAN PUSTAKA 2

HASIL DAN PEMBAHASAN 8

Metode Kuasi Newton 8

Metode Davidon-Fletcher-Powell (DFP) 11

Metode Broyden-Fletcher-Goldfarb-Shanno (BFGS) 15

Algoritme Kuasi Newton 20

Contoh Perhitungan Metode Kuasi Newton 21

Hasil Numerik 23

SIMPULAN 26

DAFTAR PUSTAKA 26

LAMPIRAN 28

viii

DAFTAR TABEL

1 Fungsi Kuadratik 22

2 Fungsi Variably dimensioned 23

3 Fungsi Brown badly scaled 24

4 Fungsi Beale 24

5 Fungsi Powell badly scaled 25

6 Fungsi Rosenbrock 25

DAFTAR GAMBAR

1 Plot tiga dimensi fungsi kuadratik 23

2 Plot tiga dimensi fungsi Variably dimensioned menggunakan metode

DFP (a) dan BFGS (b) 23

3 Plot tiga dimensi fungsi Brown badly scaled menggunakan metode DFP

(a) dan BFGS (b) 24

4 Plot tiga dimensi fungsi Bealemenggunakan metode DFP (a) dan BFGS

(b) 24

5 Plot tiga dimeni fungsi Powell badly scaled menggunakan metode DFP

(a) dan BFGS (b) 25

6 Plot tiga dimensi fungsi Rosenbrock menggunakan metode DFP (a) dan

BFGS (b) 25

7 Iterasi untuk metode DFP dan BFGS 26

DAFTAR LAMPIRAN

1 Sintaks program MATLAB R2011b metode kuasi Newton dalam

menyelesaikan 7 fungsi yang diujikan 28

2 Hasil komputasi program MATLAB R2011b untuk metode DFP dan metode BFGS dalam menyelesaikan fungsi Variably dimensioned 31 3 Hasil komputasi program MATLAB R2011b untuk metode DFP dan

metode BFGS dalam menyelesaikan fungsi Brown badly scaled 32 4 Hasil komputasi program MATLAB R2011b untuk metode DFP dan

metode BFGS dalam menyelesaikan fungsi Beale 33

5 Hasil komputasi program MATLAB R2011b untuk metode DFP dan metode BFGS dalam menyelesaikan fungsi Powell badly scaled 34 6 Hasil komputasi program MATLAB R2011b untuk metode DFP dan

metode BFGS dalam menyelesaikan fungsi Rosenbrock 39

PENDAHULUAN

Latar Belakang

Sekarang ini secara tidak sadar manusia sering berhadapan dengan permasalahan optimasi dalam kehidupan sehari-hari, misalnya persoalan mencari penyelesaian termurah dengan memenuhi segala kendala yang ada. Optimasi yang dilakukan oleh masyarakat awam lebih banyak dilandasi oleh intuisi daripada teori optimasi. Seiring berkembangnya teknologi dan permasalahan pengoptimuman yang semakin kompleks, banyak metode yang terus dikembangkan oleh para ilmuwan. Pengetahuan akan dasar-dasar pengoptimuman yang sederhana ataupun yang kompleks sangat diperlukan sebagai penunjang pengembangan metode baru. Permasalahan optimasi dapat berbentuk linear dan taklinear. Untuk bentuk linear, bentuk ini paling banyak diformulasikan dan diselesaikan pada masalah pengoptimuman, terutama di bidang manajemen, finansial dan aplikasi ekonomi. Untuk bentuk taklinear, secara alami muncul di bidang ilmu fisika dan tehnik kemudian mulai digunakan di bidang manajemen dan ilmu ekonomi (Nocedal & Wright 2006). Proses komputasi pada model berbentuk taklinear biasanya sulit dilakukan, oleh karena itu dibutuhkan teknik-teknik pengoptimuman dan pendekatan secara numerik dengan bantuan komputer supaya mempermudah proses komputasi.

Sebelumnya permasalahan pengoptimuman fungsi taklinear tak berkendala telah ditulis oleh Shalahuddin (2016) dengan metode conjugate gradient, Septiani (2015) dengan metode steepest descent dan metode Barzilai-Borwein dan Oktaviani (2014) dengan metode two-point stepsize gradient. Karya ilmiah ini akan membahas penggunaan metode kuasi Newton untuk menentukan solusi dari masalah pengoptimuman fungsi taklinear tak berkendala.

Metode kuasi Newton merupakan modifikasi dari metode Newton untuk menyelesaikan pemrograman taklinear. Ide dasar dari metode kuasi Newton adalah mengganti invers matriks Hesse pada metode Newton dengan suatu matriks yang mendekati nilai invers matriks Hesse yang sebenarnya. Karena tidak membutuhkan turunan kedua, terkadang metode kuasi Newton lebih efisien dari metode Newton. Secara umum algoritmenya hampir sama dengan metode Newton, yang membedakan yaitu pada pembaharuan matriks Hesse yang sudah diaproksimasi.

Terdapat beberapa formula untuk memperbaharui nilai pendekatan invers matriks Hesse pada tiap iterasinya di antaranya adalah Rank One Update, Davidon-Fletcher-Powell (DFP), Broyden-Fletcher-Golfarb-Shanno (BFGS), Powell-symmetric-Broyden (PSB).Metode BFGS merupakan pengembangan dari metode DFP, dan metode BFGS ini merupakan metode yang paling efektif untuk saat ini (Nocedal & Wright 2006), oleh karena itu pada karya ilmiah ini pembahasan akan dititikberatkan pada Metode DFP dan BFGS yang bersumber pada (Chong & Zak 2001), dengan harapan dapat menjadi landasan teori yang kuat dalam pengembangan metode baru. Kemudian penulis menerapkan metode DFP dan BFGS dalam suatu perangkat lunak MATLAB R2011b dan menentukan solusi permasalahan pengoptimuman fungsi taklinear.

2

Tujuan Penelitian Tujuan dari penelitian ini yaitu:

1. mengonstruksi pendekatan invers matriks Hesse,

2. menunjukkan sifat definit positif metode DFP dan metode BFGS,

3. menentukan solusi minimum dari beberapa masalah pengoptimuman taklinear tak berkendala dengan menggunakan algoritme kuasi Newton dan dibantu perangkat lunak MATLAB R2011b.

TINJAUAN PUSTAKA

Pada bagian ini akan dibahas teori-teori yang digunakan dalam menyusun karya ilmiah ini, yaitu meliputi fungsi kuadratik, hasil kali dalam, norma vektor, keoptimuman, fungsi konveks, kedefinitan matriks, dan metode Newton.

Fungsi Kuadratik

Suatu fungsi 𝑓 dinamakan fungsi kuadratik dalam 𝑛 variabel jika dapat dituliskan sebagai

𝑓(𝐱) =1

2𝐱𝑇𝐴𝐱 + 𝐛𝑇𝐱 + 𝑐, (1)

dengan 𝑐 ∈ ℝ, 𝐱, 𝐛 ∈ ℝn dan 𝐴 merupakan matriks berukuran 𝑛 × 𝑛 (Luenberger dan Ye 2009).

Hasil Kali Dalam

Misalkan 𝐱, 𝐲 ∈ ℝ𝑛, hasil kali dalam dari vektor 𝐱 = (𝑥1,. . . , 𝑥𝑛) dan 𝐲 = (𝑦1,. . . , 𝑦𝑛) didefinisikan dengan

〈𝐱,𝐲〉 ≡ 𝐱𝑇_{𝐲 = ∑ 𝑥} 𝑖𝑦𝑖 𝑛

𝑖=1 (2)

(Dennis dan Schnabel 1998).

Norma Vektor Definisi 1 (Norma)

Norma dari suatu vektor adalah fungsi dari ℝ𝑛 _{ke ℝ yang memunyai} beberapa sifat. Jika 𝐱 ∈ ℝ𝑛_{, maka norma dari vektor 𝐱 dinyatakan dengan ‖𝐱‖.} Berikut sifat-sifat norma vektor:

 ‖𝐱‖ ≥ 0, ∀ 𝐱 ∈ ℝ𝑛

 ‖𝛼𝐱‖ = |𝛼| ∙ ‖𝐱‖, ∀ 𝛼 ∈ ℝ, 𝐱 ∈ ℝ𝑛

 ‖𝐱 + 𝐲‖ ≤ ‖𝐱‖ + ‖𝐲‖,∀ 𝐱, 𝐲 ∈ ℝ𝑛 (Ketaksamaan segitiga) (Sauer 2012).

3 Definisi 2 (Norma Maksimum)

Norma maksimum dari vektor 𝐱 = (𝑥₁,. . . , 𝑥_𝑛) adalah ‖𝐱‖_∞= max|𝐱_𝑖| dengan 𝑖 =1,…,𝑛, merupakan nilai mutlak yang maksimum dari 𝐱 (Sauer 2012). Definisi 3 (Norma Euclid)

Norma Euclid dari vektor 𝐱 = (𝑥₁,. . . , 𝑥_𝑛) adalah ‖𝐱‖2 = (∑𝑛𝑖=1(𝑥𝑖)2)1/2 dengan 𝑖 =1,…,𝑛 (Dennis dan Schnabel 1998), atau dapat ditulis ‖𝐱‖2 =

√〈𝐱,𝐱〉 = √𝐱𝐓_{𝐲 (Chong & Zak 2001).}

Teorema 1 (Pertidaksamaan Cauchy-Schwarz )

Untuk setiap vektor 𝐱,𝐲 ∈ ℝ𝑛. Pertidaksamaan Cauchy-Schwarz yaitu

|〈𝐱,𝐲〉| ≤ ‖𝐱‖‖𝐲‖. Kemudian persamaan

|〈𝐱,𝐲〉| = ‖𝐱‖‖𝐲‖ (3)

dipenuhi jika dan hanya jika 𝐱 = 𝛼𝐲 untuk 𝛼 ∈ ℝ (Chong & Zak 2001). Matriks Simetrik

Suatu matriks 𝐴 = (𝑎_𝑖𝑗) berorde 𝑛 × 𝑛 disebut matriks simetrik jika

𝐴𝑇 = 𝐴, atau 𝑎𝑖𝑗 = 𝑎𝑗𝑖, ∀𝑖 ≠ 𝑗. Contoh: (8_{4 -2}4), ( 1 3 -7 3 2 4 -7 4 2 ) (Leon 2001). Invers Matriks Definisi 4

Matriks 𝐴 berukuran 𝑛 × 𝑛 disebut taksingular atau invertible (dapat dibalikkan) jika ada matriks 𝐵 sehingga 𝐴𝐵 = 𝐵𝐴 = 𝐼, dengan 𝐼 adalah matriks identitas. Matriks 𝐵 dikatakan sebagai invers matriks 𝐴 (Leon 2001).

Keoptimuman Definisi 5

Misalkan 𝑓(𝐱) adalah suatu fungsi dengan 𝐱 ∈ ℝ𝑛 dan 𝐱̅ ∈ ℝ𝑛 . Jika

𝑓(𝐱̅) < 𝑓(𝐱); ∀𝐱 ∈ ℝ𝑛 maka 𝐱̅ disebut minimum global. Jika ∃𝜀 sehingga

𝑓(𝐱̅) < 𝑓(𝐱);∀𝐱 ∈ 𝑁_𝜀(𝐱̅) maka 𝐱̅ disebut minimum lokal. Dan jika 𝑓(𝐱̅) < 𝑓(𝐱); ∀𝐱 ∈ 𝑁_𝜀(𝐱̅), 𝐱̅ ≠ 𝐱 maka 𝐱̅ disebut minimum lokal sejati, dengan 𝑁_𝜀(𝐱̅) = {𝐲: ‖𝐲 − 𝐱̅‖ ≤ 𝜀}, 𝐲 ∈ ℝ𝑛 (Bazaraa et al. 1993).

4

Kedefinitan Matriks Teorema 2

Misalkan 𝐴 adalah suatu matriks simetrik berukuran 𝑛 × 𝑛. Matriks 𝐴

disebut semidefinit positif jika dan hanya jika 𝐱𝑇𝐴𝐱 ≥0; ∀𝐱 ∈ ℝ𝑛 dan 𝐴 disebut definit positif jika dan hanya jika 𝐱𝑇_{𝐴𝐱 > 0; ∀𝐱 ≠ 0 di ℝ}𝑛 _{(Bazaraa et al. 1993).} Teorema 3

Misalkan 𝐴 merupakan matriks simetrik berukuran 𝑛 × 𝑛. Matriks 𝐴 definit positif jika dan hanya jika matriks 𝐴 semidefinit positif dan taksingular (Bazaraa

et al. 1993). Teorema 4

Matriks simetrik 𝐴 disebut definit positif jika dan hanya jika semua nilai eigen dari matriks 𝐴 adalah positif (Chong & Zak 2001).

Teorema ini mengindikasi bahwa melalui pendiagonalan dapat ditunjukkan matriks semidefinit positif 𝐴 memiliki matriks akar kuadrat yang semidefinit positif yang memenuhi 𝐴1/2𝐴1/2 = 𝐴,

𝐴1/2 = 𝐵𝑇 ( 𝜆₁1 /2 0 𝜆₂1/2 0 _𝜆⋱ 𝑛 1/2 ) 𝐵

dengan 𝐵 merupakan matriks yang kolom-kolomnya adalah vektor eigen dari matriks 𝐴 . Berdasarkan bentuk kuadrat 𝐱𝐓_{𝐴𝐱 dapat diekspresikan sebagai} ‖𝐴1/2𝐱‖2.

Fungsi Konveks dan Matriks Hesse Definisi 6 (Himpunan Konveks)

Himpunan 𝐶 di ℝ𝑛 adalah konveks jika untuk setiap 𝐱 dan 𝐲 di 𝐶, segmen garis yang menghubungkan 𝐱 dan 𝐲 juga berada di 𝐶 (Peressini et al. 1998). Definisi 7 (Fungsi Konveks)

Misalkan fungsi 𝑓(𝐱)terdefinisi di himpunan konveks 𝐶 di ℝ𝑛_{. Maka:} 1. fungsi 𝑓 disebut fungsi konveks di 𝐶 jika 𝑓(𝛼𝐱1+ (1− 𝛼)𝐱2) ≤ 𝛼𝑓(𝐱1) +

(1− 𝛼)𝑓(𝐱2), ∀𝐱1,𝐱2 ∈ 𝐶 dan ∀𝛼 ∈ [0,1],

2. fungsi 𝑓 disebut fungsi strictly convex di 𝐶 jika 𝑓(𝛼𝐱1+ (1− 𝛼)𝐱2) < 𝛼𝑓(𝐱1) + (1− 𝛼)𝑓(𝐱2), ∀𝐱1,𝐱2∈ 𝐶 dengan 𝐱1 ≠ 𝐱2 dan ∀𝛼 ∈ [0,1] (Peressini

et al. 1998).

Vektor Gradien dan Matriks Hesse

Misalkan 𝑓(𝐱) = 𝑓(𝑥1,𝑥2,..., 𝑥𝑛) adalah fungsi smooth, yaitu fungsi yang turunan parsial pertama dan turunan parsial keduanya kontinu. Didefinisikan vektor gradien dari suatu fungsi 𝑓 di titik 𝐱 dengan

5 ∇𝑓(𝐱) = (𝜕𝑓 𝜕𝑥1(𝐱), 𝜕𝑓 𝜕𝑥2(𝐱), …, 𝜕𝑓 𝜕𝑥_𝑛(𝐱)) 𝑇 , dan ∇2𝑓(𝐱) = {𝜕 2_𝑓(𝐱) 𝜕𝐱_𝑖𝜕𝐱_𝑗}

disebut matriks Hesse dan dinotasikan dengan

𝐻(𝐱) = ( 𝜕2𝑓(𝐱) 𝜕𝑥₁2 𝜕2𝑓(𝐱) 𝜕𝑥1𝑥2 𝜕2𝑓(𝐱) 𝜕𝑥2𝑥1 𝜕2𝑓(𝐱) 𝜕𝑥₂2 ⋯ 𝜕2𝑓(𝐱) 𝜕𝑥1𝑥𝑛 𝜕2𝑓(𝐱) 𝜕𝑥₂𝑥_𝑛 ⋮ ⋱ ⋮ 𝜕2𝑓(𝐱) 𝜕𝑥_𝑛𝑥1 𝜕2𝑓(𝐱) 𝜕𝑥_𝑛𝑥2 ⋯ 𝜕 2_𝑓(𝐱) 𝜕𝑥_𝑛𝑥_𝑛) (Peressini et al. 1998). Teorema 5

Misalkan fungsi 𝑓: ℝ𝑛 → ℝ terturunkan dua kali di 𝐱̅. Jika ∇𝑓(𝐱̅) = 𝟎 dan

𝐻(𝐱̅) semidefinit positif maka 𝐱 adalah minimum lokal (Bazaraa et al. 1993). Teorema 6 (Kekonveksan Fungsi dan Matriks Hesse)

Misalkan 𝑓(𝐱) memunyai turunan parsial kedua yang kontinu pada himpunan konveks buka 𝐶 di ℝ𝑛. Jika

1. matriks Hesse 𝐻(𝐱) dari 𝑓 adalah semidefinit positif pada 𝐶, maka 𝑓 adalah fungsi konveks pada 𝐶

2. matriks Hesse 𝐻(𝐱) dari 𝑓 adalah definit positif pada 𝐶, maka 𝑓 adalah fungsi

strictly convex pada 𝐶 (Peressini et al. 1998). Teorema 7

Misalkan 𝑓(𝐱) fungsi konveks dan 𝑓(𝐱) merupakan fungsi yang akan diminimumkan, dengan 𝐱 ∈ ℝ𝑛. Jika 𝐱̅ ∈ ℝ𝑛 merupakan minimum lokal sejati atau 𝑓 adalah fungsi strictly convex maka 𝐱̅ adalah solusi tunggal minimum global yang merupakan minimum lokal (Bazaraa et al. 1993).

Teorema Taylor

Misalkan 𝐱∗_{, 𝐱 merupakan titik di ℝ}𝑛 _{dan 𝑓(𝐱) merupakan fungsi dengan 𝑛} variabel yang turunan parsial pertama dan keduanya kontinu pada himpunan terbuka yang mengandung segmen garis [𝐱∗,𝐱] = {𝐰 ∈ ℝ𝒏: 𝐰 = 𝐱∗+ 𝑡(𝐱 − 𝐱∗);0≤ 𝑡 ≤1} yang menghubungkan 𝐱∗dan 𝐱, maka ada vektor 𝐳 ∈ [𝐱∗,𝐱]

sehingga

𝑓(𝐱) = 𝑓(𝐱∗_{) + ∇𝑓(𝐱}∗_{)(𝐱 − 𝐱}∗_{) +}1

2(𝐱 − 𝐱∗)𝐻(𝐳)(𝐱 − 𝐱∗) (Peressini et al. 1998).

6

Metode Newton

Metode Newton adalah suatu algoritme untuk menentukan nilai minimum dari fungsi taklinear. Misalkan diberikan fungsi 𝑓(𝐱) yang terturunkan di ℝ𝑛. Untuk meminimumkan 𝑓(𝐱) maka harus dipenuhi persamaan berikut

𝛻𝑓(𝐱) = 𝟎.

Berdasarkan Teorema Taylor di sekitar 𝐱 = 𝐱_𝑘 berlaku

𝑓(𝐱) = 𝑓(𝐱𝒌) + (𝐱 − 𝐱𝑘)𝑇∇𝑓(𝐱𝑘) + 1

2(𝐱 − 𝐱𝑘)

𝑇_𝐻(𝐱

𝑘)(𝐱 − 𝐱𝑘).

Jika fungsi 𝑓(𝐱) memunyai nilai minimum di 𝐱, maka 𝐱 merupakan titik kritis pada 𝑓(𝐱), yaitu

0 = ∇𝑓(𝐱) = ∇𝑓(𝐱_𝑘) + (𝐱 − 𝐱_𝑘)𝑇_∇2_𝑓(𝐱 𝑘).

Dari persamaan di atas diperoleh langkah iterasi untuk menyelesaikan masalah pengoptimuman sebagai berikut

𝐱_𝑘+1 = 𝐱_𝑘− [∇2𝑓(𝐱_𝑘)]−1_∇𝑓(𝐱 𝑘), 𝐱_𝑘+1 = 𝐱𝑘− 𝐻(𝐱𝑘)−1∇𝑓(𝐱𝑘), atau biasa ditulis

𝐱𝑘+1 = 𝐱𝑘+ 𝐝𝑘, dengan 𝐝_𝑘 = −𝐻(𝐱_𝑘)−1𝛻𝑓(𝐱_𝑘) (Peressini et al. 1998).

Exact Line Search

Exact line search adalah metode untuk menentukan ukuran langkah dari suatu proses iterasi yang akan membantu proses iterasi menuju suatu nilai yang meminimumkan fungsi.

Misalkan suatu proses iterasi untuk menyelesaikan masalah pengoptimuman tersebut sebagai berikut

𝐱𝑘+1 = 𝐱𝑘+ 𝜆𝑘𝐝𝑘.

Untuk membantu iterasi lebih cepat menuju kekonvergenan maka dicari nilai 𝜆_𝑘

yang sesuai untuk menjamin bahwa

7 Dengan formula berikut akan dipilih 𝜆_𝑘 yang meminimumkan 𝑓 dengan mencari turunan 𝑓(𝐱_𝑘+ 𝜆𝐝_𝑘) terhadap 𝜆

𝜆𝑘 = argmin{𝑓(𝐱𝑘+ 𝜆𝐝𝑘)} 𝜆_𝑘= min{𝜆 ≥ 0 | 𝛁𝒇(𝐱_𝑘+ 𝝀𝐝_𝑘)𝑻_𝐝

𝑘 = 0}.

(Sun & Yuan 2006).

Formula Sherman-Morrison-Woodbury (SMW)

Formula ini akan digunakan pada pembuktian formula BFGS untuk mendapatkan ℋ𝑘+1.

Misalkan 𝐴 adalah matriks berukuran 𝑛 × 𝑛 dan taksingular. Misalkan 𝑈,𝑉

merupakan vektor kolom di ℝ𝑛×𝑝 untuk 𝑝 =1,2,…,𝑛 dan 𝐼 + 𝑉𝑇𝐴−1𝑈 matriks taksingular maka 𝐴̂ = 𝐴 + 𝑈𝑉𝑇 _{taksingulardan}

(𝐴̂)−1 = 𝐴−1_{− 𝐴}−1_𝑈𝐶−1_𝑉𝑇_𝐴−1 dengan 𝐶 = 𝐼 + 𝑉𝑇_𝐴−1_𝑈, 𝑈 = [𝑢1, 𝑢2,…,𝑢𝑘], 𝑉 = [𝑣1,𝑣2,...,𝑣𝑘] (Householder 1975).

Contoh: misalkan diketahui matriks taksingular 𝐴 = [1 1

3 4], dengan bentuk 𝐴 = 𝐵 + 𝑈𝑉𝑇. Dengan formula SMW akan ditentukan nilai invers dari 𝐴,

𝐴−1 = (𝐵 + 𝑈𝑉𝑇)−1 _{atau dapat ditulis 𝐴}−1_{= (𝐵 + ∑ 𝐮} 𝑖𝐯𝑖𝑻 𝑛 𝑖=1 ) −1 . Berdasarkan formula SMW 𝐴−1 = 𝐵−1− 𝐵−1𝑈𝐶−1𝑉𝑇𝐵−1, atau ekuivalen dengan

(𝐵 + ∑ 𝐮_𝑖𝐯_𝑖𝑇 𝑛 𝑖=1 ) −1 = 𝐵−1_{− 𝐵}−1_𝑈𝐶−1_𝑉𝑇_𝐵−1_, dengan 𝐶_𝑖𝑗 = 𝛿_𝑖𝑗 + 𝐯_𝑖𝑇𝐵−1_𝐮 𝑗,

dan 𝛿_𝑖𝑗 merupakan elemen baris ke-𝑖 dan kolom ke-𝑗 dari matriks 𝐼 = [1 0 0 1].

Untuk kasus ini dipilih 𝑛 =2 sehingga 𝐴 = 𝐵 + ∑2_𝑖=1𝐮_𝑖𝐯_𝑖𝑇. Misalkan 𝐵 = [1 0 0 1]

maka 𝐵−1= [1 0

0 1], agar 𝐴 dipenuhi maka dipilih 𝐮1 = [ 0 1], 𝐯1 = [ 3 1], 𝐮2 = [ 1 2], dan 𝐯₂ = [0 1]. Jadi 𝐴 = [1 1 3 4] = [ 1 0 0 1] + [ 0 1] [3 1] + [ 1 2] [0 1]

8

= 𝐵 + ∑ 𝐮𝑖𝐯𝑖𝑇 2

𝑖=1

.

Kemudian akan ditentukan elemen dari matriks 𝐶 sebagai berikut

𝐶11= 𝛿11+ 𝐯1𝑇𝐵−1𝐮1 = 1 + [3 1] [1₀ 0₁] [0₁] = 2, 𝐶₂₂ = 𝛿₂₂+ 𝐯₂𝑇_𝐵−1_𝐮

2 = 3, 𝐶₁₂= 𝛿₁₂+ 𝐯₁𝑇𝐵−1𝐮₂ = 5,

𝐶21 = 𝛿21+ 𝐯2𝑇𝐵−1𝐮1 = 1.

Matriks 𝐶 dapat ditulis dalam bentuk

𝐶 = [2 5 1 3], 𝐶

−1_{= [} 3 −5

−1 2 ].

Kemudian substitusi 𝐵−1, 𝐮1, 𝐮2, 𝐯1, 𝐯2, dan 𝐶−1 ke formula SMW, sehingga 𝐴−1 = [1 0 0 1] − [ 1 0 0 1] [ 0 1 1 2] [ 3 −5 −1 2 ] [ 3 1 0 1] [ 1 0 0 1] 𝐴−1 = [ 4 −1 −3 1 ].

HASIL DAN PEMBAHASAN

Pada bagian ini akan dibahas teori metode kuasi Newton dan sifat kedefinitan pendekatan invers matriks Hesse. Selanjutnya, akan ditentukan nilai minimum dari fungsi taklinear dengan dibantu perangkat lunak MATLAB R2011b.

Metode Kuasi Newton

Metode kuasi Newton merupakan pengembangan dari metode Newton. Pada metode Newton, proses komputasi memerlukan waktu yang relatif lama karena harus mencari invers dari matriks Hesse pada tiap iterasinya. Metode kuasi Newton ini mempermudah proses komputasi dengan mendekati nilai invers matriks Hesse. Metode kuasi Newton melakukan pencarian solusi secara iteratif yang dimulai dari satu titik solusi kemudian melakukan pencarian ke arah titik solusi lain dengan menggunakan titik solusi sebelumnya. Metode kuasi Newton hanya membutuhkan gradien dari fungsi objektif sebagai informasi pada setiap iterasinya (Nocedal dan Wright 2006).

Metode kuasi Newton menyelesaikan permasalahan pengoptimuman tak berkendala. Misalkan permasalahan pengoptimuman tak berkendala sebagai berikut

9

𝐱 ∈ ℝ𝑛,

dengan 𝑓: ℝ𝑛 _{→ ℝ merupakan fungsi yang turunan parsial pertama dan turunan} parsial kedua kontinu. Suatu proses iterasi untuk menyelesaikan masalah pengoptimuman tersebut pada metode Newton yaitu

𝐱_𝑘+1 = 𝐱𝑘− 𝜆𝑘𝐻𝑘−1∇𝑓(𝐱𝑘)𝑇. (4) Jika 𝐻_𝑘−1 diganti dengan suatu matriks ℋ𝑘 yang merupakan pendekatan dari nilai 𝐻_𝑘−1 maka

𝐱_𝑘+1 = 𝐱𝑘− 𝜆𝑘ℋ𝑘∇𝑓(𝐱𝑘)𝑇,

𝐱_𝑘+1 = 𝐱𝑘+ 𝜆𝑘𝐝𝑘, (5) dengan

𝐝_𝑘 = −ℋ_𝑘𝛁𝒇(𝐱_𝑘)𝑇_,

dan ℋ_𝑘 adalah matriks simetrik definit positif berukuran 𝑛 × 𝑛. 𝑘 menunjukkan banyaknya iterasi untuk memperoleh pendekatan nilai yang optimal dari suatu fungsi, 𝜆_𝑘 adalah ukuran langkah yang diperoleh dengan exact line search dan

∇𝑓(𝐱) adalah vektor baris berdimensi 𝑛.

Teorema berikut akan menjelaskan pengonstruksian invers matriks Hesse, kemudian akan dilakukan pendekatan invers matriks Hesse oleh matriks ℋ_𝑘. Teorema 8: Misalkan 𝑓 suatu fungsi di ℝ𝑛 yang memiliki turunan parsial kedua kontinu. Misalkan terdapat dua titik yaitu 𝐱𝑘+1 dan 𝐱𝑘 . Jika𝐠_𝐤+1 = ∇𝑓(𝐱𝑘+1)𝑇, 𝐠𝑘 = 𝛁𝒇 (𝐱𝑘)𝑇, 𝐩𝑘= 𝐱𝑘+1− 𝐱𝑘 dan 𝐻(𝐱𝑘) merupakan matriks Hesse, maka

𝐪_𝑘 ≡ 𝐠_𝑘+1− 𝐠𝑘 ≈ 𝐻(𝐱𝑘)𝐩𝑘. (6) Jika nilai setiap elemen matriks Hesse 𝐻(𝐱𝑘) merupakan konstanta atau dapat disebut 𝐻 konstan maka

𝐪𝑘≡ 𝐠𝑘+1− 𝐠𝑘 = 𝐻𝐩𝑘 (7)

(Luenberger & Ye 2009).

Bukti: Berdasarkan Teorema Taylor di sekitar 𝐱 = 𝐱_𝑘 berlaku

𝑓(𝐱) = 𝑓(𝐱_𝑘) + (𝐱 − 𝐱𝑘)𝑇𝜵𝒇(𝐱𝑘) + 1

2(𝐱 − 𝐱𝑘)𝑇𝐻(𝐱𝑘)(𝐱 − 𝐱𝒌).

Kemudian turunan parsial pertama dari persamaan di atas dapat dinyatakan sebagai berikut

∇𝑓(𝐱) = ∇𝑓(𝐱_𝒌) + 𝐱𝑻_𝐻(𝐱

𝑘) − 𝐱𝑘𝑻𝐻(𝐱𝑘) (8) sehingga

10

∇𝑓(𝐱_𝑘+1) − ∇𝑓(𝐱𝑘) ≈ 𝐱𝑇𝑘+1𝐻(𝐱𝑘) − 𝐱𝑘𝑇𝐻(𝐱𝑘) = (𝐱_𝑘+1− 𝐱𝑘)𝑇𝐻(𝐱𝑘) = 𝐩_𝑘𝑇𝐻(𝐱𝑘).

Karena ∇𝑓(𝐱𝑘+1)𝑇 = 𝐠𝑘+1dan ∇𝑓 (𝐱𝑘)𝑇= 𝐠𝑘, maka diperoleh persamaan (6) yaitu

𝐠𝑘+1− 𝐠𝑘 = 𝐻(𝐱𝑘)𝐩𝑘.

Dengan cara yang sama persamaan (7) juga dapat dibuktikan.

Misalkan matriks 𝐻 konstan (setiap elemen-elemen matriksnya bernilai konstanta), seperti pada persamaan (8) maka persamaannya akan menjadi

∇𝑓(𝐱) = ∇𝑓(𝐱𝑘) + 𝐱𝑇𝐻 − 𝐱𝑘𝑇𝐻 sehingga

∇𝑓(𝐱_𝑘+1) − ∇𝑓(𝐱𝑘) = 𝐱𝑘+𝑇 1𝐻 − 𝐱𝑘𝑇𝐻 = (𝐱𝑘+1− 𝐱𝑘)𝑇𝐻 = 𝐩_𝑘𝑇𝐻.

Berdasarkan persamaan (7) diberikan 𝑘, matriks 𝐻−1 memenuhi

𝐻−1_𝐪

𝑖 = 𝐩𝑖, 0 ≤ 𝑖 ≤ 𝑘. Misalkan ℋ𝑘+1 merupakan pendekatan dari matriks 𝐻−1 maka

ℋ_𝑘+1𝐪𝑖 = 𝐩𝑖, 0 ≤ 𝑖 ≤ 𝑘. Jika terdapat 𝑛 langkah maka

ℋ𝑛q0 = 𝐩0,

ℋ_𝑛q1 = 𝐩1,

⋮

ℋ_𝑛q_𝑛−1 = 𝐩𝑛−1. Persamaan tersebut dapat ditulis sebagai

ℋ_𝑛[𝐪0, 𝐪1, … , 𝐪𝑛−1] = [𝐩0, 𝐩1, … , 𝐩𝑛−1]. Matriks 𝐻−1 memenuhi

𝐻−1_[𝐪

11

Jika [𝐪0, 𝐪1, … , 𝐪𝑛−1]nonsingular, maka 𝐻−1 akan diperoleh setelah 𝑛 langkah

𝐻−1= ℋ𝑛 = [𝐩0, 𝐩1, … , 𝐩𝑛−1][𝐪0, 𝐪1, … , 𝐪𝑛−1]−1, dengan kata lain

ℋ𝑘+1𝐪𝑘= 𝐩𝑘. (9)

Selanjutnya akan dibahas proses pembentukan formula ℋ_𝑘+1dan sifat definit positif dari formula yang digunakan pada karya ilmiah ini (DFP dan BFGS) berdasarkan informasi pada persamaan (9).

Metode Davidon-Fletcher-Powell (DFP)

Metode DFP merupakan metode kuasi Newton yang menggunakan formula DFP untuk mendekati nilai invers matriks Hesse. Pada tahun 1950 Davidon, Fletcher dan Powell adalah ilmuwan yang memelopori cara pendekatan terhadap invers matriks Hesse. Ide awalnya berasal dari Davidon, kemudian dikembangkan oleh Fletcher dan Powell.

Metode DFP juga disebut sebagai Rank Two Update dengan bentuk umum

ℋ𝑘+1 = ℋ𝑘+ 𝛼𝐮𝐮𝑇+ 𝛽𝐯𝐯𝑇, (10) dengan 𝐮,𝐯 merupakan vektor dan 𝛼,𝛽 merupakan konstanta.

Untuk mendapatkan formulanya, substitusi persamaan (10) ke persamaan (9) maka diperoleh ℋ𝑘+1𝐪𝑘 = 𝐩𝑘, (ℋ𝑘+ 𝛼𝐮𝐮𝑇+ 𝛽𝐯𝐯𝑇)𝐪𝑘 = 𝐩𝑘, ℋ_𝑘𝐪_𝑘+ 𝛼(𝐮𝑇_𝐪 𝑘)𝐮 + 𝛽(𝐯𝑇𝐪𝑘)𝐯 = 𝐩𝑘, 𝛼(𝐮𝑇_𝐪 𝑘)𝐮 + 𝛽(𝐯𝑇𝐪𝑘)𝐯 = 𝐩𝑘− ℋ𝑘𝐪𝑘. (11) Pilih 𝐮 = 𝐩𝑘 dan 𝐯 = ℋ𝑘𝐪𝑘, kemudian disubstitusi ke persamaan (11)

𝛼(𝐩_𝑘𝑇𝐪_𝑘)𝐩𝑘+ 𝛽(𝐪𝑘𝑇ℋ𝑘𝐪𝑘)ℋ𝑘𝐪𝑘 = 𝐩𝑘− ℋ𝑘𝐪𝑘, agar persamaan tersebut dapat diselesaikan, maka dipilih

𝛼 = 1

𝐩_𝑘𝑇𝐪_𝑘, 𝛽 = −

1

𝐪_𝑘𝑇ℋ_𝑘𝐪_𝑘,

12 ℋ𝑘+1 = ℋ𝑘+ 𝐩_𝑘𝐩_𝑘𝑇 𝐩_𝑘𝑇_𝐪 𝑘 −ℋ𝑘𝐪𝑘𝐪𝑘 𝑇_ℋ 𝑘 𝐪_𝑘𝑇_ℋ 𝑘𝐪𝑘 . (12) Formula ℋ𝑘+1 pada (12) merupakan formula yang digunakan untuk mendekati nilai dari invers matriks Hesse pada metode DFP. Selanjutnya akan dibahas sifat definit positif dari matriks ℋ𝑘+1 pada formula (12).

Sifat Definit Positif

Berikut ini akan diperlihatkan bahwa bila ℋ_𝑘 definit positif, maka ℋ_𝑘+1

juga definit positif. Hal ini untuk menjamin iterasi menuju suatu nilai yang meminimumkan fungsi pada metode DFP.

Lema 1: Jika ℋ𝑘merupakan matriks simetrik definit positif maka ℋ𝑘+1definit positif (𝐱𝑇ℋ𝑘+1𝐱 > 0 untuk setiap 𝐱 ≠ 𝟎 dengan 𝐱 ∈ ℝ𝑛) jika dan hanya jika 𝐩_𝑘𝑇𝐪𝑘> 0 (Griva et al. 2009).

Bukti:

Jika persamaan (12) dikalikan dengan 𝐱𝐓 dan 𝐱 diperoleh

𝐱𝑇_ℋ 𝑘+1𝐱 = 𝐱𝑇ℋ𝑘𝐱 + (𝐱𝑇_𝐩 𝑘)2 𝐩_𝑘𝑇𝐪_𝑘 − (𝐱𝑇_ℋ 𝑘𝐪𝐤)2 𝐪_𝑘𝑇ℋ_𝑘𝐪_𝑘 . (13)

Akibat dari Teorema 4 maka didefinisikan

𝐫 = ℋ_𝑘1/2𝐱 , (14)

𝐬 = ℋ_𝑘1/2𝐪_𝑘, (15)

sehingga (13) dapat ditulis kembali sebagai berikut

𝐱𝑇_ℋ 𝑘+1𝐱 = 𝐫𝑇𝐫 + (𝐱𝑇_𝐩 𝑘)2 𝐩_𝑘𝑇𝐪𝑘 −(𝐫 𝑇_𝐬)2 𝐬𝑇_𝐬 = (𝐫 𝑇_𝐫)(𝐬𝑇_{𝐬) − (𝐫}𝑇_𝐬)2 𝐬𝑇_𝐬 − (𝐱𝑇_𝐩 𝐤)2 𝐩_𝑘𝑇_𝐪 𝑘 = ‖𝐫‖ 2_‖𝐬‖2_{− (〈𝐫,𝐬〉)}2 ‖𝐬‖2 − (𝐱𝑇_𝐩 𝐤)2 𝐩_𝑘𝑇𝐪𝑘 (16) Titik minimum dari 𝑓(𝐱_k+1) relatif terhadap 𝜆 diperoleh dengan cara menurunkan fungsi tersebut terhadap 𝜆 dan 𝑑𝑓

𝑑𝜆=0. Dari persamaan (5) diperoleh 𝑓(𝐱_𝑘+1) = 𝑓(𝐱𝑘+ 𝜆𝒅𝑘)

13 𝑑𝑓 𝑑𝜆= 𝛁𝒇(𝐱𝑘+ 𝜆𝒅𝑘)𝐝𝑘 = 𝛁𝒇(𝐱_𝑘+1)𝐝𝑘 = 𝐝_𝑘𝑇∇𝑓(𝐱𝑘+1)𝑇. Karena ∇𝑓(𝐱𝑘+1)𝑇 = 𝐠(𝐱𝑘+1) maka 𝐝_𝑘𝑇𝐠(𝐱_𝑘+1) =0. Jika persamaan tersebut dikalikan dengan 𝜆_𝑘 diperoleh

𝜆𝑘𝐝𝑘𝑇𝐠(𝐱𝑘+1) =0. (17)

Karena 𝐩𝑘= 𝐱𝑘+1− 𝐱𝑘 dan dari persamaan (5) yaitu 𝐱𝑘+1 = 𝐱𝑘+ 𝜆𝑘𝐝𝑘 maka

𝐩_𝑘 = 𝜆_𝑘𝐝_𝑘, (18)

oleh karena itu berdasarkan (17) dan (18) diperoleh

𝐩_𝑘𝑇𝐠_𝑘+1 =0. (19)

Karena 𝐪_𝑘= 𝐠_𝑘+1− 𝐠_k, maka

𝐩_𝑘𝑇𝐪𝑘 = 𝐩𝑘𝑇(𝐠𝑘+1− 𝐠𝑘) = 𝐩𝑘𝑇𝐠𝑘+1− 𝐩𝑘𝑇𝐠𝑘. Dari persamaan (19), diperoleh

𝐩_𝑘𝑇𝐪_𝑘 = −𝐩_𝑘𝑇𝐠_𝑘. (20)

Dengan menggunakan persamaan (18) dan 𝐝_𝑘 = −ℋ_𝑘𝐠_𝑘 didapat

𝐩_𝑘𝑇𝐪_𝑘= −𝐩_𝑘𝑇𝐠_𝑘 = −(𝜆𝑘𝐝𝑘)𝑇𝐠𝑘

= −(𝜆_𝑘(−ℋ_𝑘𝐠_𝑘))𝑇𝐠_𝑘

= 𝜆_𝑘𝐠_𝑘𝑇ℋ_𝑘𝐠_𝑘. (21)

Kemudian persamaan (21) disubstitusi ke persamaan (16), diperoleh

𝐱𝑇_ℋ (𝑘+1)𝐱 = (𝐫𝑇_𝐫)(𝐬𝑇_{𝐬) − (𝐫}𝑇_𝐬)2 𝐬𝑇_𝐬 + (𝐱𝑇_𝐩 𝑘)2 𝜆𝑘𝐠𝑘𝑇ℋ𝑘𝐠𝑘

14 =‖𝐫‖ 2_‖𝐬‖2_{− (〈𝐫,𝐬〉)}2 ‖𝐬‖2 + (𝐱𝑇_𝐩 𝑘)2 𝜆𝑘𝐠𝑘𝑇ℋ𝑘𝐠𝑘 . (22)

Ruas kanan pada persamaan (22) memiliki nilai yang taknegatif, pada suku pertama ruas kanan, pertidaksamaan Cauchy-Schwarz menyatakan bahwa

‖𝐫‖2‖𝐬‖2− (〈𝐫,𝐬〉)2 ≥ 0 memiliki nilai yang taknegatif. Pada suku kedua ruas kanan, karena pembilangnya berbentuk kuadrat dan penyebutnya menggunakan asumsi bahwa ℋ𝑘 definit positif sehingga suku kedua pada ruas kanan memiliki nilai taknegatif. Selanjutnya untuk membuktikan 𝐱𝑇ℋ_𝑘+1𝐱 >0 untuk setiap 𝐱 ≠0, cukup menunjukkan bahwa ruas kanan pada persamaan (22) tidak bernilai nol. Berdasarkan Teorema 1, suku pertama pada ruas kanan akan bernilai nol

(‖𝐫‖2‖𝐬‖2 = (〈𝐫,𝐬〉)2) jika dan hanya jika 𝐫 = 𝛽𝐬, dengan 𝛽 ∈ ℝ . Untuk melengkapi bukti, akan ditunjukkan jika 𝐫 = 𝛽𝐬 maka

(𝐱𝑇_𝐩

𝑘)2/(𝜆𝑘 𝐠𝑘𝑇 ℋ𝑘 𝐠𝑘 ) >0. Misalkan 𝐫 = 𝛽𝐬, berdasarkan persamaan (15) maka

𝐫 = 𝛽ℋ_𝑘1/2𝐪_𝑘, (23) kemudian persamaan (14) disubstitusi ke persamaan (23), diperoleh

ℋ_𝑘1/2𝐱 = 𝛽ℋ_𝑘1/2𝐪𝑘 ℋ_𝑘1/2𝐱 = ℋ_𝑘1/2𝛽𝐪_𝑘

𝐱 = 𝛽𝐪_𝑘. (24)

lalu persamaan (24) dan 𝐫 = 𝛽𝐬 disubstitusi ke persamaan (22), diperoleh

𝐱𝑇_ℋ (𝑘+1)𝐱 = ‖𝛽𝐬‖2‖𝐬‖2− (〈𝛽s,𝐬〉)2 ‖𝐬‖2 + (𝐪_𝑘𝑇_𝛽𝐩 𝑘)2 𝜆𝑘𝐠𝑘𝑇ℋ𝑘𝐠𝑘 .

Akibat dari Teorema 1 maka ‖𝛽𝐬‖2‖𝐬‖2 = (〈𝛽s,𝐬〉)2 sehingga ‖𝛽𝐬‖2‖𝐬‖2− (〈𝛽s,𝐬〉)2 = 0, diperoleh 𝐱𝐓_ℋ (𝑘+1)𝐱 = 0 + (𝐪_𝑘𝑇_𝛽𝐩 𝑘)2 𝜆_𝑘𝐠_𝑘𝑇ℋ_𝑘𝐠_𝑘 =𝛽 2_(𝐩 𝑘 𝑇_𝐪 𝑘)2 𝜆_𝑘𝐠_𝑘𝑇_ℋ 𝑘𝐠𝑘 dari persamaan (21), diperoleh

= 𝛽 2_(𝐩 𝑘 𝑇_𝐪 𝑘)2 𝐩_𝑘𝑇𝐪𝑘 = 𝛽2𝐩_𝑘𝑇𝐪_𝑘 > 0,

Karena 𝐩_𝑘𝑇𝐪_𝑘 >0 maka 𝐱𝑇ℋ_𝑘+1𝐱 > 0 untuk setiap 𝐱 ≠ 𝟎. Jadi, ℋ_𝑘+1 definit positif (Chong & Zak 2001).

15 Metode Broyden-Fletcher-Goldfarb-Shanno (BFGS)

Algoritme kuasi Newton yang paling populer adalah metode BFGS. Pada tahun 1970 Broyden, Fletcher, Goldfarb dan Shanno mengusulkan formula alternatif untuk mendekati invers matriks Hesse pada metode Newton atau sekarang disebut sebagai metode BFGS. Metode BFGS ini adalah hasil pengembangan dari metode DFP. Konsep dasarnya yaitu dualitas atau

complementary.

Pendekatan nilai invers matriks Hesse yang diperoleh akibat dari (9) dengan persamaannya sebagai berikut

ℋ𝑘+1𝐪𝑘= 𝐩𝑘.

Untuk mendekati nilai dari matriks Hesse 𝐻−1 sama artinya mendekati nilai matriks Hesse 𝐻 itu sendiri. Misalkan 𝐵_𝑘 merupakan estimasi dari 𝐻 untuk 𝑘

langkah. Berdasarkan persamaan (7), maka

𝐪𝑘 = 𝐻𝐩𝑘.

𝐪_𝒌= 𝐵_𝑘+1𝐩_𝑘 (25)

Persamaan tersebut serupa dengan persamaan (9) untuk ℋ_𝑘+1; yang membedakannya adalah dengan menukar ℋ_𝑘 menjadi 𝐵_𝑘 dan 𝐪_𝑘 menjadi 𝐩_𝑘. Jadi nilai 𝐵𝑘pada BFGS saling bersesuaian dengan nilai ℋ𝑘 pada DFP, formula tersebut saling berhubungan dan hal ini dapat disebut dualitas atau

complementary.

Pada persamaan (12) disajikan formula DFP sebagai berikut

ℋ_𝑘+𝐷𝐹𝑃₁ = ℋ_𝑘+𝐩𝑘𝐩𝑘 𝑇 𝐩_𝑘𝑇𝐪𝑘 −ℋ𝑘𝐪𝑘𝐪𝑘 𝑇_ℋ 𝑘 𝐪_𝑘𝑇ℋ𝑘𝐪𝑘 ,

dengan menggunakan konsep complementary, maka diperoleh formula BFGS yaitu 𝐵𝑘+1= 𝐵𝑘+ 𝐪_𝑘𝐪_𝑘𝑇 𝐪_𝑘𝑇_𝐩 𝑘 −𝐵𝑘𝐩𝑘𝐩𝑘 𝑇_𝐵 𝑘 𝐩_𝑘𝑇_𝐵 𝑘𝐩𝑘 . (26)

Untuk memperoleh ℋ_𝑘+𝐵𝐹𝐺𝑆₁ maka 𝐵 dikonversi ke ℋ dengan menginverskan matriks 𝐵_𝑘+1 yaitu ℋ_𝑘+𝐵𝐹𝐺𝑆₁ = (𝐵_𝑘+1)−1 ℋ_𝑘+𝐵𝐹𝐺𝑆₁ = (𝐵_𝑘+𝐪𝑘𝐪𝑘 𝑇 𝐪_𝑘𝑇𝐩_𝑘− 𝐵𝑘𝐩𝑘𝐩𝑘𝑇𝐵𝑘 𝐩_𝑘𝑇𝐵_𝑘𝐩_𝑘 ) −1 . (27)

Nilai eksplisit dari ℋ_𝑘+1𝐵𝐹𝐺𝑆 dapat diperoleh dengan menggunakan formula Sherman-Morrison-Woodbury. Berikut adalah penurunan formula Sherman- Morrison-Woodburry.

16

Misalkan 𝐴 adalah matriks taksingular. Misalkan 𝑈,𝑉 merupakan vektor kolom dan 𝐼 + 𝑉𝑇_𝐴−1_{𝑈 ≠ 0 maka 𝐴 + 𝑈𝑉}𝑇 _{taksingulardan}

(𝐴 + 𝑈𝑉𝑇₎−1 _{= 𝐴}−1_{− 𝐴}−1_𝑈𝐶−1_𝑉𝑇_𝐴−1_{, (28)} dengan

𝐶 = 𝐼 + 𝑉𝑇𝐴−1, 𝑈 = [𝐮1,𝐮2, . . .,𝐮𝑘], dan 𝑉 = [𝐯1,𝐯2,. . . ,𝐯𝑘]. Persamaan (28) dapat ditulis sebagai berikut

(𝐴 + ∑ 𝐮_𝑖𝐯_𝑖𝑇 𝑘 𝑖=1 ) −1 = 𝐴−1 _{− 𝐴}−1_𝑈𝐶−1_𝑉𝑇_𝐴−1 ₍₂₉₎ dengan 𝐶_𝑖𝑗 = 𝛿_𝑖𝑗+ 𝐯_𝑖𝑇𝐴−1_𝐮 𝑗 𝑖, 𝑗 =1,2,…, 𝑘,

dan 𝛿_𝑖𝑗 merupakan elemen baris ke-𝑖 dan kolom ke-𝑗 dari matrik 𝐼 = [1 0

0 1]. Kemudian persamaan (26) dapat ditulis dalam bentuk

𝐵𝑘+1= 𝐵𝑘+ 𝐪_𝑘𝐪_𝑘𝑇 𝐪_𝑘𝑇_𝐩 𝑘 −𝐵𝑘𝐩𝑘𝐩𝑘 𝑇_𝐵 𝑘 𝐩_𝑘𝑇_𝐵 𝑘𝐩𝑘 , = 𝐵_𝑘+ ∑ 𝐮_𝑖𝐯_𝑖𝑇 2 𝑖=1 , (30) dengan 𝐮1 = 𝐪_𝑘 (𝐩_𝑘𝑇_𝐪 𝑘)1/2 , (31) 𝐮2 = 𝐵_𝑘𝐩_𝑘 (𝐩_𝑘𝑇_𝐵 𝑘𝐩𝑘)1/2 , (32) 𝐯1 = 𝐪_𝑘 (𝐩_𝑘𝑇_𝐪 𝑘)1/2 , (33) 𝐯₂ = − 𝐵𝑘𝐩𝑘 (𝐩_𝑘𝑇_𝐵 𝑘𝐩𝑘)1/2 . (34)

Berdasarkan persamaan (29) dan persamaan (30) diperoleh

(𝐵_𝑘+ ∑ 𝐮_𝑖𝐯_𝑖𝑇 2 𝑖=1 ) −1 = 𝐵_𝑘−1− 𝐵_𝑘−1𝑈𝐶−1_𝑉𝑇_𝐵 𝑘−1

17 Karena ℋ_𝑘 = 𝐵_𝑘−1 maka (𝐵𝑘+ ∑ 𝐮𝑖𝐯𝑖𝑇 2 𝑖=1 ) −1 = 𝐻𝑘− 𝐻𝑘𝑈𝐶−1𝑉𝑇𝐻𝑘 (35)

Kemudian akan ditentukan matriks 𝐶, dengan mencari nilai 𝐶_𝑖𝑗 diperoleh

𝐶11= 1+ 𝐯1𝑇𝐵𝑘−1𝐮1 = 1+ 𝐪_𝑘𝑇𝐻_𝑘𝐪_𝑘 𝐩_𝑘𝑇_𝐪 𝑘 , 𝐶22= 1+ 𝐯2𝑇𝐵𝑘−1𝐮2 = 1− 𝐩_𝑘𝑇𝐵𝑘𝐵𝑘−1𝐵𝑘𝐩𝑘 𝐩_𝑘𝑇𝐵𝑘𝐩𝑘 =1−1 =0, 𝐶₁₂= 𝐯₁𝑇𝐵_𝑘−1𝐮₂ = 𝐪𝑘 𝑇_𝐵 𝑘−1𝐵𝑘𝐬𝑘 (𝐩_𝑘𝑇_𝐪 𝑘)1/2(𝐩𝑘𝑇𝐵𝑘𝐩𝑘)1/2 = (𝐩𝑘 𝑇_𝐪 𝑘)1/2 (𝐩_𝑘𝑇_𝐵 𝑘𝐩𝑘)1/2 , 𝐶21= 𝐯2𝑇𝐵𝑘−1𝐮1 = −𝐶12.

Matriks 𝐶 dapat ditulis dalam bentuk

𝐶 = (𝛽 −𝛼 𝛼 0 ), 𝐶−1 = 1 𝛼2( 0 𝛼 −𝛼 𝛽), (36) dengan 𝛽 =1+𝐪𝑘 𝑇_ℋ 𝑘𝐪𝑘 𝐩_𝑘𝑇𝐪𝑘 , ₍₃₇₎ 𝛼 = (𝐩𝑘 𝑇_𝐪 𝑘)1/2 (𝐩_𝑘𝑇_𝐵 𝑘𝐩𝑘)1/2 . (38)

Kemudian substitusi persamaan (30) ke persamaan (27) diperoleh

ℋ_𝑘+𝐵𝐹𝐺𝑆₁ = (𝐵_𝑘+1)−1 = (𝐵𝑘+ ∑ 𝐮𝑖𝐯𝑖𝑇 𝑘 𝑖=1 ) −1 , Berdasarkan persamaan (31) maka

ℋ_𝑘+𝐵𝐹𝐺𝑆₁ = 𝐻_𝑘− 𝐻_𝑘𝑈𝐶−1𝑉𝑇𝐻_𝑘. (39) Misalkan 𝑈̃ = ℋ_𝑘𝑈 dan 𝑉̃ = ℋ_𝑘𝑉, dengan 𝑈̃ = [𝐮̃1 ̃]𝐮2 ,𝑉̃ = [𝐯̃1 𝐯̃ ]2 , 𝐮̃ = ℋ𝑖 𝑘𝐮𝑖 dan 𝐯̃ = ℋ_{𝑖 𝑘}𝐯_𝑖 (𝑖 =1,2), kemudian substitusi 𝑈̃ dan 𝑉̃ ke persamaan (39)

18

ℋ_𝑘+𝐵𝐹𝐺𝑆₁ = ℋ_𝑘− 𝑈̃𝐶−1_𝑉̃𝑇_{. (40)} Substitusi persamaan (36) ke persamaan (40)

ℋ_𝑘+𝐵𝐹𝐺𝑆₁ = ℋ𝑘− 1 𝛼2[𝐮̃1 𝐮̃2] [ 0 𝛼 −𝛼 𝛽] [ 𝐯̃₁𝑇 𝐯̃2𝑇 ] = ℋ𝑘− 1 𝛼2(−𝛼𝐮̃2𝐯̃1 𝑇_{+ 𝛼𝐮̃} 1𝐯̃2𝑇+ 𝛽𝐮̃2𝐯̃2𝑇) = ℋ𝑘− 1 𝛼(−𝐮̃2𝐯̃1 𝑇_{+ 𝐮̃} 1𝐯̃2𝑇) − 𝛽 𝛼2𝐮̃2𝐯̃2 𝑇_, (41) substitusi 𝐮̃_𝑖 dan 𝐯̃_𝑖 ke persamaan (41), diperoleh

ℋ_𝑘+𝐵𝐹𝐺𝑆₁ = ℋ_𝑘−1 𝛼(−ℋ𝑘𝐮2𝐯1 𝑇_ℋ 𝑘+ ℋ𝑘𝐮1𝐯2𝑇ℋ𝑘) − 𝛽 𝛼2(ℋ𝑘𝐮2𝐯2 𝑇_ℋ 𝑘) (42) Kemudian substitusi persamaan (31), (32), (33), (34), (37), dan (38) ke persamaan (42) maka diperoleh ℋ_𝑘+𝐵𝐹𝐺𝑆₁ = ℋ_𝑘− (𝐩𝑘 𝑇_𝐵 𝑘𝐩𝑘 𝐩_𝑘𝑇𝐪𝑘 ) 1/2 (−ℋ_𝑘 𝐵𝑘𝐩𝑘 (𝐩_𝑘𝑇_𝐵 𝑘𝐩𝑘)1/2 𝐪_𝑘𝑇 (𝐩_𝑘𝑇_𝐪 𝑘)1/2 ℋ_𝑘 + ℋ𝑘 𝐪_𝑘 (𝐩_𝑘𝑇_𝐪 𝑘)1/2 (− 𝐩𝑘 𝑇_𝐵 𝑘 (𝐩_𝑘𝑇_𝐵 𝑘𝐩𝑘)1/2 ) ℋ𝑘) − (1 +𝐪𝑘 𝑇_ℋ 𝑘𝐪𝑘 𝐩_𝑘𝑇𝐪_𝑘 ) 𝐩_𝑘𝑇𝐵𝑘𝐩𝑘 𝐩_𝑘𝑇𝐪_𝑘 (ℋ𝑘 𝐵𝑘𝐩𝑘 (𝐩_𝑘𝑇_𝐵 𝑘𝐩𝑘)1/2 (− 𝐩𝑘 𝑇_𝑩 𝒌 (𝐩_𝑘𝑇_𝐵 𝑘𝐩𝑘)1/2 ) ℋ_𝑘), karena ℋ_𝑘 = 𝐵_𝑘−1 maka ℋ_𝑘𝐵_𝑘 = 𝐵_𝑘ℋ_𝑘 = 𝐼, sehingga

ℋ_𝑘+1 = ℋ_𝑘−ℋ𝑘𝐪𝑘𝐩𝑘 𝑇_{+ 𝐩} 𝑘𝐪𝑘𝑇ℋ𝑘 𝐩_𝑘𝑇𝐪_𝑘 + 𝐩𝑘𝐩𝑘𝑇 𝐩_𝑘𝑇𝐪_𝑘(1+ 𝐪_𝑘𝑇ℋ𝑘𝐪𝑘 𝐩_𝑘𝑇𝐪_𝑘 )

atau ekuivalen dengan (bukti terlampir)

ℋ𝑘+1 = (𝐼 − 𝐩_𝑘𝐪_𝑘𝑇 𝐩_𝑘𝑇_𝐪 𝑘 ) ℋ𝑘(𝐼 − 𝐪_𝑘𝐩_𝑘𝑇 𝐩_𝑘𝑇_𝐪 𝑘 ) +𝐩𝑘𝐩𝑘 𝑇 𝐩_𝑘𝑇_𝐪 𝑘 . (43)

Formula pada (39) merupakan formula yang digunakan untuk mendekati nilai invers matriks Hesse pada metode BFGS, selanjutnya akan ditunjukkan sifat kedefinitan dari formula pada (39).

19 Sifat Definit Positif

Seperti pada metode DFP akan digunakan Lema 1 untuk menunjukkan sifat kedefinitan dari metode BFGS. Hal ini untuk menjamin iterasi menuju suatu nilai yang meminimumkan fungsi pada metode BFGS

Lema 1: Jika ℋ_𝑘 matriks simetrik definit positif maka ℋ_𝑘+1 definit positif (𝐱𝑇ℋ𝑘+1𝐱 > 0 untuk setiap 𝐱 ≠ 𝟎 dengan 𝐱 ∈ ℝ𝑛) jika dan hanya jika 𝐩𝑘𝑇𝐪𝑘 > 0 (Griva et al. 2006).

Bukti: Bila persamaan (43) dikalikan dengan 𝐱𝑇 _{dan 𝐱 maka} 𝐱𝐓ℋ𝑘+1𝐱 = (𝐱𝑇− 𝐱𝑇_𝐩 𝑘𝐪𝑘𝑇 𝐩_𝑘𝑇_𝐪 𝑘 ) ℋ𝑘(𝐱 − 𝐪_𝑘𝐩_𝑘𝑇𝐱 𝐩_𝑘𝑇_𝐪 𝑘 ) +𝐱 𝑇_𝐩 𝑘𝐩𝑘𝑇𝐱 𝐩_𝑘𝑇_𝐪 𝑘 atau dapat ditulis sebagai

𝐱𝑇_ℋ 𝑘+1𝐱 = 𝐰𝑇ℋ𝑘𝐰 + (𝐱𝑇𝐩𝑘)2 𝐩_𝑘𝑇𝐪_𝑘 , (44) dengan 𝐰 = (𝐱 − 𝐪_𝐤 𝐩𝑘 𝑇_𝐱 𝐩_𝑘𝑇𝐪𝑘 ).

Pertama akan dibuktikan jika 𝐩_𝑘𝑇𝐪_𝑘 > 0 maka 𝐱𝑇ℋ_𝑘+1𝐱 >0 untuk setiap 𝐱 ≠0 dengan 𝐱 ∈ ℝ𝑛_.

Jika matriks ℋ_𝑘 simetrik definit positif maka ruas kanan pada persamaan (44) memiliki nilai taknegatif untuk setiap 𝐱 ≠0 . Untuk membuktikan

𝐱𝑇ℋ𝑘+1𝐱 >0, cukup menunjukan ruas kanan pada persamaan (44) tidak bernilai nol. Suku pertama pada ruas kanan persamaan (44) akan bernilai nol jika 𝐱 = 0

dan suku kedua pada ruas kanan persamaan (44) akan bernilai nol jika 𝐱𝑇_𝐩

𝑘 = 0. Untuk 𝐱𝑇𝐩_𝑘 = 0, nilai 𝐩_𝑘 tidak mungkin bernilai nol karena diketahui 𝐩_𝑘𝑇𝐪_𝑘 > 0 sehingga 𝐱 = 𝟎, akibatnya ruas kanan persamaan (44) tidak akan bernilai nol karena 𝐱 ≠ 𝟎. Jadi 𝐱𝑇ℋ𝑘+1𝐱 >0 untuk setiap 𝐱 ≠0 dengan 𝐱 ∈ ℝ𝑛.

Kemudian akan dibuktikan jika 𝐱𝑇ℋ𝑘+1𝐱 >0 untuk setiap 𝐱 ≠0 dengan 𝐱 ∈ ℝ𝑛 maka 𝐩_𝑘𝑇𝐪𝑘 > 0.

Misalkan 𝐱𝑇ℋ_𝑘+1𝐱 >0 untuk setiap 𝐱 ≠0 dengan 𝐱 ∈ ℝ𝑛 𝐱𝑇ℋ𝑘+1𝐱 = 𝐰𝑇ℋ𝑘𝐰 +

(𝐱𝑇𝐩_𝑘)2 𝐩_𝑘𝑇_𝐪

𝑘

> 0. Pilih 𝐱 = 𝐪_𝐤∈ ℝ𝑛 _{maka diperoleh}

𝐱𝑇_ℋ 𝑘+1𝐱 = 𝐰𝑇𝐻𝑘𝐰 + (𝐱𝑇_𝐩 𝑘)2 𝐩_𝑘𝑇𝐪𝑘 > 0 = (𝐱 − 𝐪𝐤 𝐩_𝑘𝑇𝐱 𝐩_𝑘𝐓𝐪𝑘 ) 𝑇 ℋ𝑘(𝐱 − 𝐪𝑘 𝐩_𝑘𝑇𝐱 𝐩_𝑘𝑇_𝐪 𝑘 ) +(𝐱 𝑇_𝐩 𝑘)2 𝐩_𝑘𝑇_𝐪 𝑘 > 0

20 = (𝐪𝑘− 𝐪𝑘 𝐩_𝑘𝑇𝐪_𝑘 𝐩_𝑘𝑇_𝐪 𝑘 ) 𝑇 ℋ𝑘(𝐪𝑘− 𝐪𝑘 𝐩_𝑘𝑇𝐪_𝑘 𝐩_𝑘𝑇_𝐪 𝑘 ) +(𝐪𝑘 𝑇_𝐩 𝑘)2 𝐩_𝑘𝑇_𝐪 𝑘 >0 = (𝐪𝑘 𝑇_𝐩 𝑘)2 𝐩_𝑘𝑇𝐪_𝑘 > 0 = 𝐩_𝑘𝑇𝐪_𝑘> 0,

terbukti 𝐩_𝑘𝑇𝐪𝑘> 0. Oleh karena itu ℋ𝑘+1 definit positif (𝐱𝑇ℋ𝑘+1𝐱 > 0 untuk setiap 𝐱 ≠0dengan 𝐱 ∈ ℝ𝑛 jika dan hanya jika 𝐩_𝑘𝑇𝐪𝑘 > 0.

Jika pendekatan invers matriks Hesse ℋ𝑘+1 pada metode DFP dan metode BFGS memenuhi sifat definit positif, berdasarkan Teorema 6 jika matriksnya definit positif maka fungsi strictly convex. Kemudian berdasarkan Teorema 7 jika fungsi strictly convex maka akan terdapat solusi tunggal minimum global yang merupakan minimum lokal. Selanjutnya, akan ditunjukkan hasil numerik dari beberapa fungsi taklinear menggunakan algoritme metode kuasi Newton dengan menggunakan formula DFP dan BFGS. Berikut adalah algoritme yang digunakan pada metode kuasi Newton.

Algoritme Kuasi Newton

Metode kuasi Newton menggunakan algoritme sebagai berikut:

Langkah 1. Tentukan gradien dengan nilai awal 𝑥0 ∈ ℝ𝑛 dan matriks definit positif ℋ0. Misalkan 𝜀 > 0 diberikan (pada karya ilmiah ini 𝜀 = 10-6 merupakan batas toleransi yang digunakan) dan 𝑘 =0.

Langkah 2. Jika kriteria pemberhentian terpenuhi di mana norma maksimum dari

𝐠_𝑘 yaitu ‖𝐠𝑘‖∞ ≤ 𝜀 maka hentikan algoritme, jika tidak lanjutkan ke langkah selanjutnya.

Langkah 3. Hitung ukuran langkah 𝜆_𝑘;

𝜆_𝑘= argmin{𝑓(𝐱_𝑘+ 𝜆𝐝_𝑘)} atau 𝜆_𝑘= min{𝜆 ≥ 0 | 𝐝_𝑘𝑇∇𝑓(𝐱_𝑘+ 𝜆𝐝_𝑘)𝑇 _{= 0}.} Tetapkan 𝐱_𝑘+1 = 𝐱𝑘+ 𝜆𝑘𝐝𝑘, dengan 𝐝_𝑘 = −ℋ_𝑘𝐠_𝑘. Langkah 4. Hitung matriks definit positif ℋ𝑘+1.

Untuk metode DFP digunakan:

ℋ𝑘+1 = ℋ𝑘+ 𝐩_𝑘𝐩_𝑘𝑇 𝐩_𝑘𝑇_𝐪 𝑘 −ℋ𝑘𝐪𝑘𝐪𝑘 𝑇_ℋ 𝑘 𝐪_𝑘𝑇_ℋ 𝑘𝐪𝑘 .

21 Untuk metode BFGS digunakan:

ℋ_𝑘+1= (𝐼 −𝐩𝑘𝐪𝑘 𝑇 𝐩_𝑘𝑇𝐪𝑘 ) ℋ_𝑘(𝐼 −𝐪𝑘𝐩𝑘 𝑇 𝐩_𝑘𝑇𝐪𝑘 ) +𝐩𝑘𝐩𝑘 𝑇 𝐩_𝑘𝑇𝐪𝑘 dengan 𝐩𝑘 = 𝐱𝑘+1− 𝐱𝑘, 𝐪𝑘 = 𝐠𝑘+1− 𝐠𝑘.

Langkah 5. Tentukan 𝑘 = 𝑘 +1, kemudian lanjut ke langkah 2. (Wei et al. 2006).

Contoh Perhitungan Metode Kuasi Newton

Contoh fungsi yang akan digunakan adalah fungsi kuadratik pada persamaan (1) dengan vektor 𝐱 = (𝑥₁, 𝑥₂),𝐛 =0, 𝑐 = 0 dan matriks 𝐴 = [1 0

0 1]. Sehingga fungsinya 𝑓(𝑥1, 𝑥2) = 𝑥12 + 𝑥22.

Kemudian minimumkan nilai fungsi 𝑓 menggunakan metode DFP, dengan nilai awal 𝑥0 = (1,1)𝑇, ℋ0 = [1 0_{0 1}], dan toleransi 𝜀 =10-6.

Langkah 1 Iterasi = 𝑘 =0,

Tentukan vektor gradien dari 𝑓 ∇𝑓(𝐱_𝐤)𝑇 _{= 𝐠} 𝑘 = [ 𝜕𝑓 𝜕𝑥₁ 𝜕𝑓 𝜕𝑥2] = ⌊2𝑥1 2𝑥2⌋.

Substitusikan nilai awal 𝑥0 pada saat 𝑘 =0 ke vektor gradien dari 𝑓, diperoleh

𝐠0 = [2₂].

Langkah 2 ‖𝐠0‖∞= maks{|2|, |2|} =2> 𝜀 =10-6

Karena ‖𝐠0‖∞ lebih besar dari 𝜀 maka iterasi berlanjut; Langkah 3 𝐝0 = −ℋ0𝐠0 =− [1 0_{0 1}] [2₂] =[−₋2₂].

Hitung ukuran langkah 𝜆0

𝜆₀ = argmin{𝑓(𝐱0+ 𝜆𝐝0)} = argmin{𝑓 ([1 1] + 𝜆 [ −2 −2])} = argmin{(1−2𝜆)2+ (1−2𝜆)2} = argmin{8𝜆2−8𝜆 + 2}

22 𝜆0 =1₂ =0.5. Tetapkan 𝐱1 = 𝐱0+ 𝜆0𝐝𝑘 = [1 1] +0.5[ −2 −2] = [ 0 0]. Langkah 4 Hitung 𝐩_𝑘 dan 𝐪_𝑘

𝐩0 = 𝒙1− 𝒙0 = [0 0] − [ 1 1] = [ −1 −1]. Substitusi 𝐱1 ke 𝐠1, sehingga 𝐠1 = [2(0)₂₍₀₎] = [0₀]. 𝐪0 = 𝐠1− 𝐠0 = [0 0] − [ 2 2] = [ −2 −2]. Hitung matriks ℋ₁ ℋ1 = ℋ0+ 𝐩0𝐩0𝑇 𝐩₀𝑇𝐪0 −ℋ0𝐪0𝐪0 𝑇_ℋ 0 𝐪₀𝑇ℋ0𝐪0 ℋ1 = [₋0.75_0.25 −_0.750.25]. Langkah 5 Iterasi = 𝑘 +1= 1, kembali ke langkah1; Langkah 2 Iterasi = 𝑘 = 1,

‖𝐠1‖∞ =maks(|[0₀]|) =0< 𝜀 =10-6

Karena ‖𝐠1‖∞ lebih kecil dari 𝜀 maka iterasi dihentikan; Jadi nilai minimum dari 𝑓 adalah

𝐱∗ = 𝐱1 = [0₀].

Berikut adalah hasil komputasi dengan bantuan perangkat lunak MATLAB R2011b

Tabel 1 Fungsi Kuadratik

Metode Titik minimum 𝐱∗ 𝑓(𝐱∗) ‖𝑔(𝐱∗_)‖

∞ Iterasi

23

Hasil Numerik

Dalam karya ilmiah ini fungsi yang akan diujikan untuk kedua metode yaitu DFP dan BFGS, serta pemilihan titik awal didapat dari artikel yang ditulis oleh More et al (1981). 𝑓(𝐱∗) digunakan sebagai notasi untuk nilai optimal yang diperoleh dari setiap algoritme, sedangkan 𝑓(𝐱)_𝑜𝑝𝑡 merupakan nilai optimal yang sudah diketahui dari sumber yang dirujuk. Berikut ini hasil numerik dari beberapa masalah minimisasi fungsi taklinear tak berkendala dengan menggunakan metode DFP dan BFGS. Fungsi yang digunakan adalah fungsi konveks dengan 2 variabel dan memiliki nilai solusi di satu titik.

1. Fungsi Variably dimensioned

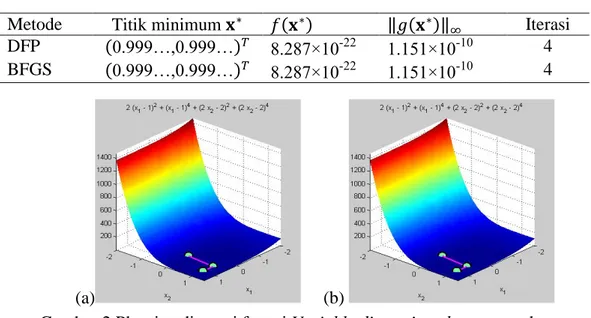
𝑓(𝑥₁, 𝑥₂) =2(𝑥1−1)2+ (𝑥1−1)4+ (2(𝑥2−1)) 2 + (2(𝑥2−1)) 4 𝑥₀ = (0.5,0)𝑇_{, 𝐱} 𝑜𝑝𝑡 = (1,1)𝑇 dan 𝑓(𝐱)𝑜𝑝𝑡 = 0. Tabel 2 Fungsi Variably dimensioned

Metode Titik minimum 𝐱∗ _𝑓(𝐱∗_{) ‖𝑔(𝐱}∗_)‖

∞ Iterasi

DFP (0.999…,0.999…)𝑇 _8.287×10-22 _1.151×10-10 ₄ BFGS (0.999…,0.999…)𝑇 _8.287×10-22 _1.151×10-10 ₄

(a) (b)

Gambar 2 Plot tiga dimensi fungsi Variably dimensioned menggunakan metode DFP (a) dan BFGS (b)

Gambar 1 Plot tiga dimensi fungsi kuadratik menggunakan metode DFP dan BFGS

24

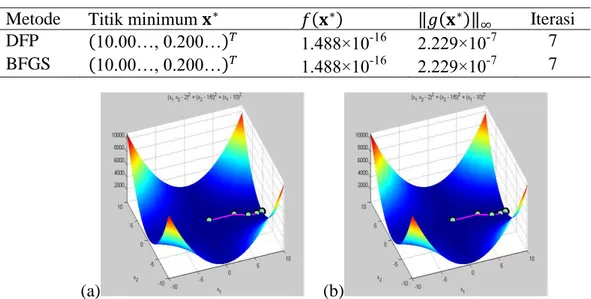
2. Fungsi Brown badly scaled

𝑓(𝑥₁, 𝑥₂) = (𝑥1−10)2+ (𝑥2−0.2)2+ (𝑥1𝑥2− 2)2 , 𝐱0 = (1,1)𝑇 , 𝐱𝑜𝑝𝑡 = (10,0.2)𝑇 _{dan 𝑓(𝐱)}

𝑜𝑝𝑡 = 0.

Tabel 3 Fungsi Brown badly scaled

Metode Titik minimum 𝐱∗ 𝑓(𝐱∗_{) ‖𝑔(𝐱}∗_)‖

∞ Iterasi DFP (10.00…, 0.200…)𝑇 _1.488×10-16 _2.229×10-7 ₇ BFGS (10.00…, 0.200…)𝑇 _1.488×10-16 _2.229×10-7 ₇ 3. Fungsi Beale 𝑓(𝑥1, 𝑥2) = (1.5− 𝑥1(1− 𝑥2)) 2 + (2.25− 𝑥1(1− 𝑥22)) 2 + (2.625− 𝑥1(1− 𝑥23)) 2 , 𝐱0 = (1,1)𝑇, 𝐱𝑜𝑝𝑡 = (3,0.5)𝑇 dan 𝑓(𝐱)𝑜𝑝𝑡 = 0. Tabel 4 Fungsi Beale

Metode Titik minimum 𝐱∗ 𝑓(𝐱∗) ‖𝑔(𝐱∗_)‖

∞ Iterasi

DFP (3.000…, 0.499…)𝑇 _7.153×10-20 _2.562×10-9 ₁₀ BFGS (3.000…, 0.499…)𝑇 _7.153×10-20 _2.562×10-9 ₁₀

(a) (b)

Gambar 3 Plot tiga dimensi fungsi Brown badly scaled menggunakan metode DFP (a) dan BFGS (b)

(a) (b)

Gambar 4 Plot tiga dimensi fungsi Bealemenggunakan metode DFP (a) dan BFGS (b)

25 4. Fungsi Powell badly scaled

𝑓(𝑥₁, 𝑥₂) = (104𝑥1𝑥2−1) 2 + (𝑒−𝑥1 _{+ 𝑒}−𝑥2₋1.0001₎2_{, 𝐱} 0 = (0,1)𝑇,𝐱𝑜𝑝𝑡 = (1.098…×10-5_{, 9.106…)}𝑇 dan 𝑓(𝐱)_𝑜𝑝𝑡 = 0. Tabel 5 Fungsi Powell badly scaled

Metode Titik minimum 𝐱∗ 𝑓(𝐱 ∗_{) ‖𝑔(𝐱}∗_)‖

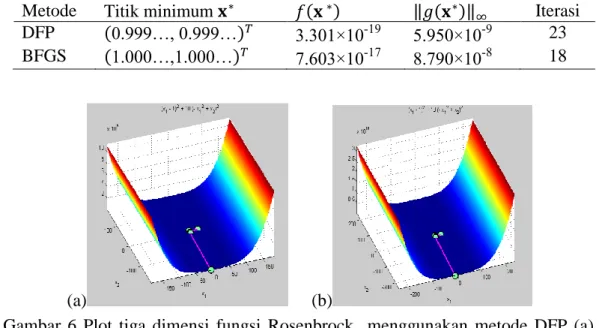
∞ Iterasi DFP _{(1.098…×10}-5_,9.106…)𝑇 _3.260×10-25 _2.414×10-8 96 BFGS _{(1.098…×10}-5_,9.106… )𝑇 1.660×10-25 1.715×10-8 96 5. Fungsi Rosenbrock 𝑓(𝑥₁, 𝑥₂) =10(𝑥2− 𝑥12) + (1− 𝑥1)2, 𝐱𝟎= (-1.2,1) 𝑇 , 𝐱_𝑜𝑝𝑡 = (1,1)𝑇 _dan 𝑓(𝐱)_𝑜𝑝𝑡 = 0.

Tabel 6 Fungsi Rosenbrock

Metode Titik minimum 𝐱∗ 𝑓(𝐱 ∗_{) ‖𝑔(𝐱}∗_)‖

∞ Iterasi DFP (0.999…, 0.999…)𝑇 _3.301×10-19 _5.950×10-9 ₂₃ BFGS (1.000…,1.000…)𝑇 _7.603×10-17 _8.790×10-8 ₁₈

a) (b)

Gambar 5 Plot tiga dimeni fungsi Powell badly scaled menggunakan metode DFP (a) dan BFGS (b)

(a) (b)

Gambar 6 Plot tiga dimensi fungsi Rosenbrock menggunakan metode DFP (a) dan BFGS (b)

26

Pada Gambar 7 dapat dilihat bahwa iterasi yang dibutuhkan metode DFP dan BFGS untuk menyelesaikan lima fungsi yang diujikan secara umum hampir sama, perbedaan hanya terletak pada saat penyelesaian fungsi Rosenbrock. Pada penyelesaian fungsi Powell badly scaled terlihat bahwa iterasi yang dibutuhkan cukup besar, hal ini terjadi jika di beberapa iterasi hasil pendekatan dari ℋ_𝑘 tidak cukup baik dari nilai invers matriks Hesse yang sesungguhnya.

Hasil lengkap untuk metode DFP dan BFGS pada tiap fungsi yang diujikan terdapat di Lampiran.

SIMPULAN

Metode kuasi Newton mengganti invers matriks Hesse pada metode Newton dengan sebuah matriks ℋ𝑘 yang mendekati invers matriks Hesse, matriks tersebut diperoleh dengan formula DFP atau BFGS. Diasumsikan ℋ_𝑘 definit positif sehingga ℋ_𝑘+1 juga definit positif, sifat ini menjamin iterasi bergerak menuju solusi minimum lokal. Metode kuasi Newton dapat menyelesaikan persamaan taklinear tak berkendala, pada umumnya metode DFP dan BFGS yang mencari 𝜆𝑘 dengan exact line search menyelesaikan persamaan taklinear dengan iterasi yang sama.

DAFTAR PUSTAKA

Bazaraa MS, Sherali HD, Shetty CM. 1993. Nonlinear Programming: Theory and Algorithms. Singapore (SG): John Willey and Sons.

Chong EKP, Zak SH. 2001. An Introduction to Optimization. 2nd Ed. New York (US): Wiley.

Gambar 7 Iterasi untuk metode DFP dan BFGS

0 20 40 60 80 100 120 DFP BFGS

27 Dennis JE, Schnabel RB. 1996. Numerical Methods for Unconstrained

Optimization and Nonlinear Equations. Philadelphia (US): SIAM.

Griva I, Nash SG, Sofer A. Linear and Nonlinear Optimization. Philadelphia. 2009.

Householder AS. 1975. The Theory of Matrices in Numerical Analysis. New York (US): Dover Publications.

Leon SJ. 2001. Aljabar Linear dan Aplikasinya. Ed ke-5. Bondan A, Penerjemah; Hardani HW, editor. Jakarta (ID): Penerbit Erlangga. Terjemahan dari:

Linear Algebra with Applications.

Luenberger DG, Ye Y. 2009. Linear and Nonlinear Programming. 3rd Ed.

Stanford (US): Springer.

More JJ, Garbow BS, Hillstrom KE. 1981. Testing unconstrained optimization software. ACM Transaction on Mathematical Software. 7:17-41.doi:10.1145/355934.355936.

Nocedal J, Wright SJ. 2006. Numerical Optimization. 2nd Ed. New York (US): Springer.

Oktaviani R. 2014. Metode two-point stepsize grradient dan metode modifikasi

two-point stepsize gradient untuk menyelesaikan optimalisasi tanpa kendala. Bogor (ID): Institut Pertanian Bogor.

Peressini AL, Sullivian FE, Uhl JJ. 1998. The Mathematics of Nonlinear Programming. New York (US) : Springer-Verlag.

Sauer T. 2012. Numerical Analysis. 2ndEd. Boston (US): Pearson.

Septiani K. 2015. Perbandingan waktu eksekusi metode steepest descent dan metode Barzilai-Borwein menggunakan perangkat lunak MATLAB. Bogor (ID): Institut Pertanian Bogor.

Shalahudin I. 2016. Pengoptimuman fungsi kuadratik dengan metode conjugate garadient dan penerapannya menggunakan aplikasi android. Bogor (ID): Institut Pertanian Bogor.

Sun W, Yuan Y. 2006. Optimization Theory and Methods Nonlinear Programming.

Wei Z, Li G, Qi L. 2006. New quasi-Newton methods for unconstrained optimization problems. Applied Mathematics and Computation. 175:1156-1188.doi:10.1016/j.amc.2005.08.027.

28

LAMPIRAN

Lampiran 1 Sintaks program MATLAB R2011b metode kuasi Newton dalam menyelesaikan 7 fungsi yang diujikan

clc;clear %Hapus semua input/output

count=0;syms b alpha;u=[];P=[];R=[];O=[];Q=[];Hs=[];Ha=[];warning off all n = 2; %dimensi fungsi

%Mendefinisikan x1, x2, ....xn for i=1:n

syms (['x' num2str(i)]); end

%Fungsi yang diujikan

%f=(x1-1)^2+(x1-1)^2+(x1-1)^4+(2*(x2-1))^2+(2*(x2-1))^4; %variablydimensioned %f=(x1-10)^2+(x2-0.2)^2+(x1*x2-2)^2 %brownbadlyscaled

%f=(1.5-x1*(1-x2))^2+(2.25-x1*(1-x2^2))^2+(2.625-x1*(1-x2^3))^2 %fungsi beale %f=(10^4*x1*x2-1)^2+(exp(-x1)+exp(-x2)-1.0001)^2 %Fungsi powell badly scaled %f=10*(x2-x1^2)^2+(1-x1)^2; %rosenbrock %f=(10^-2.5)*(x1-1)^2+(10^-2.5)*(x2-1)^2+(10^-2.5)*(x3-1)^2+(10^-2.5)*(x4-1)^2+(x1^2+x2^2+x3^2+x4^2-0.25)^ x0=[_;_]; %Nilai awal eps=0.00001; try for i=1:n G(i)=diff(f,['x' num2str(i)]); for j=1:n H(i,j)=diff(G(i),['x' num2str(j)]); end end catch

disp('Permasalahan optimasi tidak dapat diselesaikan'); return end disp('Matriks Hessian=') disp(H) tic; X=x0; Hs=H; Hes=eye([n n]); for i=1:n Hs=(subs(Hs,['x' num2str(i)],X(i))); end flag=0;count=0;syms b;u=[];P=[];R=[]; grad=G' R=[grad]; for i=1:n grad=subs(grad,['x' num2str(i)],X(i)) end Ha=[Hes]; Hs=[Hs]; P=[P X]; O=[O]; Q=[Q]; ff=f for i=1:n ff=subs(ff,['x' num2str(i)],X(i)); end

29 P=[P;ff]; R=[grad]; ff=f; while max(abs(grad))>eps count=count+1;steplength=1;

fprintf('************ Iterasi ke-%g ******************\n',count) ff=f; dir=-Hes*grad for i=1:n ff=subs(ff,['x' num2str(i)],X(i)+alpha*dir(i)); end diff(ff,alpha); d=double(solve(diff(ff,alpha))); if isempty(d)==1 steplength=1; else qq=diff(diff(ff,alpha)); for i=1:length(d) if isreal(d(i))==1 if subs(qq,'alpha',d(i))>0 steplength=abs(d(i)); end end end if steplength ==0 for i=1:length(d) if isreal(d(i))==1 if d(i)>0 steplength=abs(d(i));break end end end end end

disp('Step size taken=');disp(steplength); X=X+steplength*dir; p=steplength*dir; Hss=H; for i=1:n Hss=(subs(Hss,['x' num2str(i)],X(i))); end ff=f; for i=1:n ff=subs(ff,['x' num2str(i)],X(i)); end H1=[Hss]; Hs=[Hs H1]; P1=[X;ff]; P=[P P1]; if n==2 O1=[(P(1,count+1))-(P(1,count));(P(2,count+1))-(P(2,count))]; O=[O O1]; else n==3 O1=[(P(1,count+1))-(P(1,count));(P(2,count+1))-(P(2,count));(P(3,count+1))-(P(3,count))]; O=[O O1]; end grad_new=G'; for i=1:n grad_new=subs(grad_new,['x' num2str(i)],X(i)); end q=grad_new-grad; Qq=q; Q1=[Qq]; Q=[Q Qq];

30 Hes=Hes+((1+(q'*Hes*q)/(p'*q))*(p*p')/(p'*q))-((p*q'*Hes+Hes*q*p')/(p'*q)); %untuk BFGS Hes=Hes+(p*p')/(p'*q)-(Hes*q*q'*Hes)/(q'*Hes*q); %untuk DFP grad=grad_new; Haa=Hes; H2=[Haa]; Ha=[Ha Haa]; R1=[grad]; R=[R R1]; end toc; %Hes=H; for i=1:n Hes=subs(Hes,['x' num2str(i)],X(i)); end fprintf('\n\n...Hasil...\n\n') if length(find(eig(Hes)>0))==length(eig(Hes))

disp('Pada titik tersebut fungsi konveks maka kemungkinan ada solusi lokal minimum!');

else disp('Fungsi tidak konveks'); end

disp('Hessian Matriks:'); disp(Hes)

fprintf('Titik optimum dengan error %g adalah :\n',double(max(abs(grad)))); disp(vpa(X));

fprintf('\nNilai optimum fungsi : %g\n',double(P(n+1,count+1)));

fprintf('Jumlah iterasi =%g\n',count); try

if n==2 clf

view([-50,30]);axis tight; hold on S1=max(max(P(1,:)),max(P(2,:))); S2=max(abs(min(P(1,:))),abs(min(P(2,:)))); S=max(S1,S2); S=double(S); ezsurf(f,[-2*S,1.5*S]); %surfc(str2num(a),b,C,'facecolor','green','edgecolor','b','facelighting ','gouraud')

view([-20,50]);axis tight;shading interp; plot3(P(1,:),P(2,:),P(3,:),'-mo',... 'LineWidth',2,... 'MarkerEdgeColor','k',... 'MarkerFaceColor',[.49 1 .63],... 'MarkerSize',12); end catch

disp('Plot tidak dapat dibangkitkan!');

31 Lampiran 2 Hasil komputasi program MATLAB R2011b untuk metode DFP dan

metode BFGS dalam menyelesaikan fungsi Variably dimensioned Hasil komputasi program MATLAB R2011b menggunakan metode DFP

Iterasi ke- 𝑥 ∗ Steplenght 𝜆_𝑘 ‖𝑔(𝑥∗_)‖ 𝑥1 𝑥2 0 0.5 0 1 72 1 0.5351 1.0098 0.0140 2.2618 2 1.0001 1.0083 0.2056 0.0662 3 1.0000 1.0000 8.9167 0.0000 4 1.0000 1.0000 1.2161 0.0000

Hasil komputasi program MATLAB R2011b menggunakan metode BFGS

Iterasi ke- 𝑥 ∗ Steplenght 𝜆_𝑘 ‖𝑔(𝑥∗_)‖ 𝑥₁ 𝑥₂ 0 0.5 0 1 72 1 0.5351 1.0098 0.0140 2.2618 2 1.0001 1.0083 0.2054 0.0662 3 1.0000 1.0000 8.9167 0.0000 4 1.0000 1.0000 1.2161 0.0000

32

Lampiran 3 Hasil komputasi program MATLAB R2011b untuk metode DFP dan metode BFGS dalam menyelesaikan fungsi Brown badly scaled Hasil komputasi program MATLAB R2011b menggunakan metode DFP

Iterasi ke- 𝑥 ∗ Steplenght 𝜆_𝑘 ‖𝑔(𝑥∗_)‖ 𝑥1 𝑥2 0 1 1 1 20.000 1 5.3797 1.0876 0.2190 43.2086 2 7.4912 0.1606 0.1271 12.0135 3 8.9283 0.0460 0.9502 28.6863 4 9.8493 0.2107 1.6530 1.5078 5 10.0025 0.2005 1.1345 0.1053 6 10.0001 0.2000 0.8091 0.0006 7 10.0000 0.2000 0.9879 0.0000

Hasil komputasi program MATLAB R2011b menggunakan metode BFGS

Iterasi ke- 𝑥 ∗ Steplenght 𝜆_𝑘 ‖𝑔(𝑥∗_)‖ 𝑥₁ 𝑥₂ 0 1 1 1 20.000 1 5.3797 1.0876 0.2190 43.2086 2 7.4912 0.1606 0.0224 12.0135 3 8.9283 0.0460 0.9314 28.6863 4 9.8493 0.2107 0.6047 1.5078 5 10.0025 0.2005 1.1208 0.1053 6 10.0001 0.2000 0.8078 0.0006 7 10.0000 0.2000 0.9877 0.0000