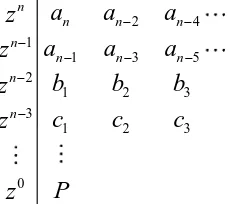MODEL PENYEBARAN PENYAKIT AIDS MELALUI TREATMENT DAN PENULARAN VERTIKAL DENGAN WAKTU TUNDAAN (TIME DELAY).

1 BAB I PENDAHULUAN

1.1. Latar Belakang

Infeksi Human Immunodeficiency Virus (HIV) merupakan salah satu masalah kesehatan utama dan salah satu penyakit menular yang dapat

mempengaruhi kematian penduduk di dunia. HIV merupakan virus penyebab terjadinya penyakit Acquired Immune Deficiency Syndrome (AIDS). Kasus HIV-AIDS telah ada di Indonesia sejak kasus pertama yang ditemukan pada tahun 1987.

Hingga saat ini kasus HIV-AIDS semakin meningkat dan telah terjadi hampir di seluruh wilayah provinsi di Indonesia. Indonesia merupakan salah satu negara di

Asia dengan epidemi HIV-AIDS yang berkembang paling cepat (UNAIDS, 2008) dan merupakan negara dengan tingkat epidemi HIV tinggi, karena terdapat daerah dengan prevalensi HIV-AIDS lebih dari 5% pada subpopulasi

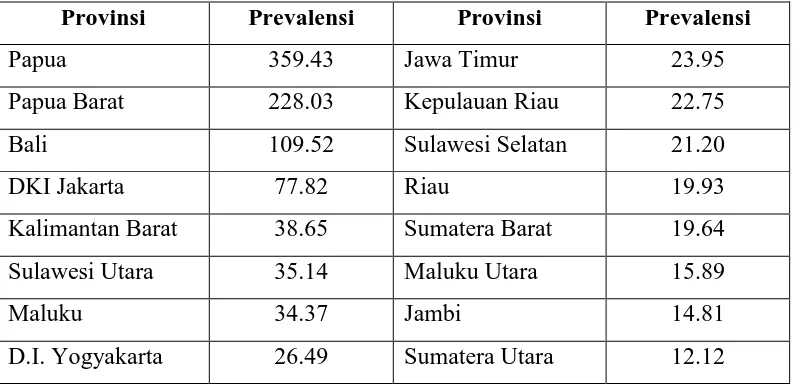
[image:1.595.115.513.522.718.2]

tertentu seperti yang ditunjukkan pada Tabel 1.1 berikut.

Tabel 1.1. Prevalensi kasus AIDS per 100.000 penduduk berdasarkan provinsi

Provinsi Prevalensi Provinsi Prevalensi

Papua 359.43 Jawa Timur 23.95

Papua Barat 228.03 Kepulauan Riau 22.75 Bali 109.52 Sulawesi Selatan 21.20

DKI Jakarta 77.82 Riau 19.93

Kalimantan Barat 38.65 Sumatera Barat 19.64 Sulawesi Utara 35.14 Maluku Utara 15.89

Maluku 34.37 Jambi 14.81

2 Bangka Belitung 26.08 Sulawesi Tenggara 11.91

Provinsi Prevalensi Provinsi Prevalensi

Jawa Tengah 11.63 Bengkulu 9.33

NTB 10.89 Gorontalo 6.54

NTT 10.59 Lampung 5.56

Kalimantan Selatan 10.04 Sumatera Selatan 5.49 Banten 9.80 Kalimantan Tengah 4.84

Sulawesi Tengah 9.75 NAD 4.29

Jawa Barat 9.73 Sulawesi Barat 0.52 Kalimantan Timur 9.34

AIDS merupakan kumpulan gejala-gejala penyakit akibat menurunnya sistem kekebalan tubuh yang disebabkan oleh HIV. Penularan HIV dapat melalui berbagai cara yang dapat diklasisfikasikan dalam penularan secara vertikal dan horisontal.

Penularan HIV-AIDS secara horisontal adalah melalui kontak langsung dengan individu terinfeksi HIV baik melalui kontak seksual maupun melalui pertukaran

substansi tubuh dengan penggunaan jarum suntik secara bersama-sama. Selain itu, penularan HIV-AIDS dapat terjadi secara vertikal, yaitu penularan dari ibu yang terinfeksi HIV-AIDS ke anak yang dilahirkannya (Riyanda & Darmawan, 2012).

Data statistik penyebaran kasus AIDS di Indonesia menurut faktor penularannya menunjukkan bahwa penularan HIV paling banyak terjadi melaui

hubungan seksual (heteroseksual, homoseksual, dan biseksual) sebanyak 35.671 kasus, pengguna NAPZA suntik (IDU/Injecting Drug Users) sebanyak 8.462 kasus, dan transmisi vertikal (penularan dari ibu hamil ke bayinya) sebanyak 1.506 kasus.

3 Indonesia hidup dengan HIV dan diperkirakan terdapat 2.250-3.250 bayi yang berisiko lahir terinfeksi HIV. Data Kementerian Kesehatan pada tahun 2012 menunjukkan dari 43.624 ibu hamil yang menjalani tes HIV, sebanyak 1.329

(3,01%) ibu hamil dinyatakan positif HIV. Hasil pemodelan Matematika epidemi HIV tahun 2012 menunjukkan prevalensi HIV pada ibu hamil

diperkirakan akan meningkat dari 0,38% menjadi 0,49% pada tahun 2016 (Kemenkes RI, 2014).

Rendahnya pengetahuan dan informasi seputar HIV dapat menyebabkan

epidemi HIV semakin meluas. Sebagian masyarakat masih belum mengetahui bahwa infeksi HIV dapat ditularkan secara vertikal. Rendahnya pengetahuan dan

informasi tentang penularan dari ibu ke anak dapat dilihat dari hasil Riskesdas 2010 yang menunjukkan bahwa persentase penduduk yang mengetahui bahwa HIV-AIDS dapat ditularkan dari ibu ke anak selama hamil, saat persalinan, dan saat

menyusui adalah masing-masing 38,1 %, 39,0 %, dan 37,4 % (Kemenkes RI, 2013). Perkembangan ilmu pengetahuan khususnya di bidang Matematika memberikan peranan penting dalam pencegahan dan pengendalian meluasnya

penyebaran penyakit. Proses penyebaran penyakit tersebut dapat dimodelkan ke dalam model Matematika dengan persamaan diferensial nonlinear. Pada tahun

1927, Kerkmark dan Kendrik memperkenalkan model penyebaran penyakit SIR (Susceptible-Infection-Recovered) yang masing-masing menyatakan banyaknya individu rentan, terinfeksi, dan sembuh pada saat t.

4 Hingga saat ini belum ditemukan obat yang dapat menyembuhkan AIDS sehingga populasi recovered R (recovered) pada model SIAR merupakan populasi yang memiliki antibodi yang mampu melawan HIV sehingga tidak kembali masuk dalam

populasi AIDS.

Dinamika suatu populasi tergantung pada hubungan antara kelahiran dan

kematian. Adanya gangguan jangka pendek dari kedua faktor ini pada umumnya tidak berpengaruh terhadap pertumbuhan maupun penurunan populasi jangka panjang. Salah satu faktor yang dapat mempengaruhi perubahan jumlah populasi

adalah efek jangka panjang pada pertumbuhan populasi yang disebabkan oleh pemisahan populasi reproduktif. Oleh karena itu, seiring dengan perkembangannya

dilakukan penelitian kembali dengan model SIA (Susceptible-Infected-AIDS). Model penyebaran penyakit HIV-AIDS ini telah digunakan untuk mensimulasikan efek populasi karantina terhadap penyebaran penyakit HIV-AIDS dengan A adalah

Abstain merupakan populasi yang terdiri dari orang-orang menahan diri untuk tidak

melakukan kontak seksual secara langsung atau dianggap tidak produktif. Hasil simulasi berdasarkan model tersebut menunjukkan bahwa populasi yang

dikarantina dapat memperlambat bahkan menurunkan populasi penderita AIDS. (Abraham dan Mahmudi, 2013).

Individu yang terinfeksi HIV dan dinyatakan positif penyakit AIDS dapat ditangani dengan melakukan terapi pengobatan untuk memperkuat sistem kekebalan tubuh. Berdasarkan hal tersebut, Liming Cai et al (2009) menambahkan

(Susceptible-Infection-Treatment-5 AIDS). Treatment merupakan populasi dari individu terinfeksi HIV yang sedang

menjalani masa pengobatan.

Penularan penyakit AIDS tidak hanya dipengaruhi oleh kontak langsung

dengan individu terinfeksi HIV-AIDS baik melalui kontak seksual maupun melalui pertukaran sustansi tubuh dengan jarum suntik, namun juga dipengaruhi oleh

adanya faktor penularan vertikal dari ibu ke anak. Basavarajaiah .D.M.B et al (2012) memodelkan penularan HIV-AIDS dengan memperhatikan penularan HIV secara vertikal dari ibu ke bayinya. Abdallah S. Waziri et al (2012) menggunakan

asumsi serupa dalam model penelitiannya, SIPTA yaitu dengan menambahkan populasi Pre-AIDS sehingga model SITA menjadi SIPTA

(Susceptible-Infection-Treatment-PreAIDS-AIDS) .

Ram Naresh dan Dileep Sharma (2011) menggunakan model SIA dengan memperhatikan penularan HIV secara vertikal dari ibu ke bayinya dan waktu

tundaan (time delay) untuk menganalisis penyebaran penyakit HIV-AIDS. Waktu tundaan tersebut merupakan waktu tundaan individu yang terinfeksi HIV secara vertikal hingga dinyatakan positif AIDS. Selain itu, model penyebaran penyakit

AIDS dengan waktu tundaan juga diteliti oleh Liming Cai et al (2009). Dalam penelitiannya, waktu tundaan tersebut merupakan waktu dimulainya terapi

pengobatan saat individu pada populasi I hingga muncul pengaruh pengobatan yang dijalaninya (populasi T).

Di Indonesia, tidak hanya perkembangan penyebaran penyakit AIDS yang

6 kekebalan tubuh. Gejala-gejala penyakit sebagai indikator individu terinfeksi HIV hingga positif dinyatakan AIDS terus diteliti hingga muncul suatu keadaan dimana individu berada dalam kondisi Pra-AIDS. Berdasarkan penelitian sebelumnya dan

realita yang terjadi, penelitian penyebaran HIV-AIDS ini dimodelkan secara matematis dengan model SIPTA (Susceptible-Infection-PreAIDS-Treatment-AIDS)

yang masing-masing merupakan populasi rentan, terinfeksi, pra-AIDS, treatment, dan AIDS. Populasi Pre-AIDS merupakan populasi yang menunjukkan kondisi dimana individu terinfeksi HIV yang mengalami munculnya gejala-gejala penyakit

AIDS sebelum dinyatakan positif AIDS. Treatment merupakan populasi yang menjalani terapi pengobatan seperti yang ada pada dewasa ini telah diketahui bahwa

belum ditemukannya obat yang dapat menyembuhkan secara total individu dari penyakit AIDS.

Pada penelitian ini, model SIPTA memperhatikan kelahiran bayi terinfeksi HIV

karena penularan secara vertikal dan pengaruh waktu tundaan yang ada merupakan waktu tundaan individu terinfeksi HIV sampai menjadi individu yang positif dinyatakan AIDS. Penularan secara vertikal diperhatikan karena berpengaruh

terhadap angka kematian ibu dan anak sedangkan waktu tundaan pada model ini akan diuji lebih lanjut pengaruh adanya waktu tundaan terhadap model penyebaran

penyakit AIDS melalui simulasi model. Model yang terbentuk disimulasikan berdasarkan data jumlah penderita positif AIDS di wilayah Daerah Istimewa Yogyakarta (DIY).

7 penularannya khususnya penularan secara vertikal. Adanya analisis waktu tundaan (time delay) pada model ini diharapkan dapat memberikan peran dalam menekan penyebaran penyakit AIDS yang selanjutnya diharapkan dapat terbentuk suatu

kebijakan khusus sebagai upaya penanggulangan pencegahan penyebaran penyakit AIDS.

1.2. Batasan Masalah

Permasalahan yang dibahas dalam skripsi ini dibatasi pada model populasi SIPTA (Susceptible-Infection-PreAIDS-Treatment-AIDS) penyebaran penyakit

HIV-AIDS berdasarkan penularan vertikal dengan mengabaikan faktor penularan melalui jarum suntik atau pada komunitas IDU (Injecting Drug User). Selanjutnya,

model disimulasikan berdasarkan data jumlah penderita positif AIDS di wilayah Daerah Istimewa Yogyakarta (DIY).

1.3. Rumusan Masalah

Berdasarkan latar belakang tersebut, maka rumusan masalah yang akan dibahas adalah sebagai berikut :

1. Bagaimana model Matematika untuk penyebaran penyakit AIDS melalui

treatment dan penularan secara vertikal dengan waktu tundaan ?

2. Bagaimana analisis kestabilan model penyebaran penyakit AIDS melalui

treatment dan penularan secara vertikal dengan dan tanpa waktu tundaan

8 1.4. Tujuan Penulisan

Berdasarkan permasalahan tersebut, tujuan dari penulisan tugas akhir ini adalah:

1. Membentuk model Matematika untuk penyebaran penyakit AIDS melalui treatment dan penularan secara vertikal dengan waktu tundaan.

2. Mengetahui kestabilan model penyebaran penyakit AIDS melalui treatment dan penularan secara vertikal dengan dan tanpa waktu tundaan pada populasi bebas infeksi HIV-AIDS dan endemik.

1.5. Manfaat Penulisan

Manfaat yang dapat diperoleh dari penulisan ini adalah :

1. Bagi mahasiswa

Menambah pengetahuan tentang model Matematika penyebaran penyakit AIDS dengan treatment dan penularan secara vertikal. Menambah

inspirasi bagi mahasiswa untuk penulisan karya ilmiah maupun tugas akhir selanjutnya.

2. Bagi masyarakat dan instansi kesehatan

Memberikan informasi penyebaran penyakit AIDS berdasarkan faktor penularannya khususnya penularan secara vertikal sehingga dapat

memprediksi endemik HIV-AIDS dalam kehidupan masyarakat. Melalui prediksi tersebut, diharapkan dapat terbentuk suatu kebijakan pemerintah dan masyarakat sadar serta turut bekerjasama dalam upaya pencegahan

penyakit AIDS.

10 BAB II

LANDASAN TEORI 2.1. Model Matematika

Model Matematika merupakan representasi matematika yang dihasilkan dari pemodelan Matematika. Pemodelan Matematika merupakan suatu proses merepresentasikan dan menjelaskan permasalahan pada dunia nyata ke dalam

pernyataan matematis (Widowati & Sutimin, 2007 : 1).

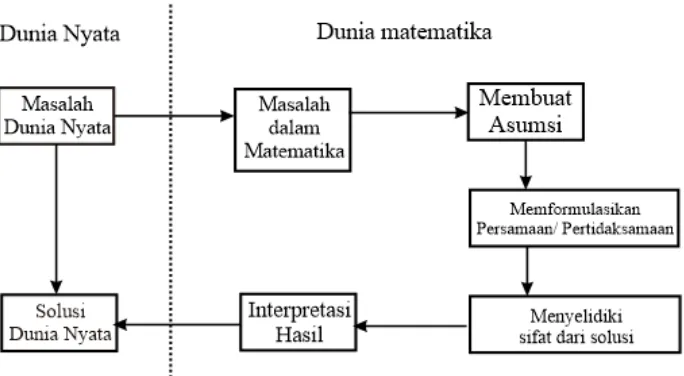
Proses pemodelan Matematika dinyatakan dalam diagram alur sebagai

[image:10.595.153.495.350.538.2]

berikut :

Gambar 2.1. Proses Pemodelan Matematika

Berdasarkan Gambar 2.1 dapat diperoleh langkah-langkah pemodelan Matematika adalah sebagai berikut :

1. Menyatakan permasalahan nyata ke dalam pengertian Matematika.

11 masalah dan membentuk beberapa hubungan antar variabel yang dihasilkan dari permasalahan tersebut.

2. Membuat Asumsi

Asumsi dalam pemodelan Matematika mencerminkan bagaimana proses berpikir sehingga model dapat berjalan.

3. Formulasi persamaan/ pertidaksamaan

Dengan pemahaman hubungan antar variabel dan asumsi, langkah selanjutnya yaitu memformulasikan persamaan atau sistem persamaan. Formulasi model

merupakan langkah yang paling penting, sehingga terkadang diperlukan adanya pengujian kembali asumsi-asumsi agar dalam proses pembentukan

formulasi dapat sesuai dan realistik. Jika pada proses pengujian kembali ditemukan ketidaksesuaian model, maka perlu dilakukan pengkajian ulang asumsi dan membentuk asumsi yang baru.

4. Menyelidiki sifat dari solusi.

Setelah membentuk formulasi model, langkah selanjutnya adalah menyelidiki sifat dari solusi yaitu menyelidiki apakah solusi sistem stabil atau tidak stabil .

5. Interpretasi Hasil

Interpretasi hasil merupakan suatu langkah yang menghubungkan formula

Matematika dengan kembali ke permasalahan dunia nyata. Interpretasi ini dapat diwujudkan dalam bentuk grafik yang digambarkan berdasarkan solusi yang diperoleh dan selanjutnya diinterpretasikan sebagai solusi dalam dunia

12 2.2. Persamaan Diferensial

Definisi 2.1 (Ross, 1984 : 3)

Persamaan diferensial adalah persamaan yang menyertakan turunan satu atau

lebih variabel tak bebas terhadap satu atau lebih variabel bebas.

Berdasarkan banyaknya variabel bebas yang dilibatkan dalam persamaan,

persamaan diferensial diklasifikasikan menjadi persamaan diferensial biasa dan persamaan diferensial parsial.

Definisi 2.2 (Ross, 1984 : 4)

Persamaan diferensial biasa adalah suatu persamaan diferensial yang melibatkan

turunan dari satu atau lebih variabel tak bebas terhadap satu variabel bebas.

Sedangkan persamaan diferensial parsial adalah suatu persamaan diferensial yang

melibatkan turunan dari satu atau lebih variabel tak bebas terhadap dua atau lebih

variabel bebas.

Contoh 2.1 :

Contoh persamaan diferensial biasa,

2 2

2 0

d y dy

xy

dx dx

   _{ } 

  (persamaan diferensial orde 2)

4 2

4 5 2 3 sin

d y d y

x t

dt  dt   (persamaan diferensial orde 4). Contoh persamaan diferensial parsial,

m m

m

s t

 _ _

 

2 2 2

2 2 2 0

v v v

x y z

 _ _ _

13 Definisi 2.3 (Ross, 1984 : 8)

Diberikan suatu persamaan diferensial orde-n berikut :

, , ', ",..., n 0

F x y y y_ y  _ (2.1)

dengan F adalah fungsi real .

1. Misalkan f adalah fungsi bilangan real yang terdefinisi untuk semua x dalam

suatu interval I dan mempunyai turunan ke-n untuk semua x yang ada di I.

Fungsi f disebut solusi eksplisit dari (2.1) dalam interval I jika fungsi f memenuhi

syarat berikut ini :

a. _{F x f x f x f} , ( ), '( ), ''( ),...,_{x f}n( ) ,_x 

  terdefinisi  x I

b. F x f x f x f_ , ( ), '( ), ''( ),...,x fn( )x    _ 0, x I

Hal ini berarti bahwa substitusi f x dan variasi turunan untuk y dan ( )

turunannya yang berkorespondensi ke (2.1) akan membuat (2.1) menjadi suatu

identitas di interval I.

2. Suatu relasi g(x,y) = 0, disebut solusi implisit dari persamaan (2.1) jika relasi

ini mendefinisikan sedikitnya satu fungsi bilangan real f dengan variabel x di

interval I .

1. _{Solusi eksplisit dan solusi implisit biasa disebut sebagai solusi sederhana.}

2.2.1. Persamaan Diferensial Linear Orde Satu Definisi 2.4 (Ross, 1984 : 5)

Persamaan diferensial orde n dengan variabel tak bebas y dan variabel bebas x,

14 1

0

( )

1

( )

1

...

1

( )

( )

( )

n n

n n

n n

d y

d

y

dy

a x

a x

a

x

a x y b x

dx

dx

dx



 



 





dengan a₀ 0.

Definisi 2.5 (Ross, 1984 : 49)

Persamaan diferensial biasa orde satu dikatakan linear jika dapat dinyatakan

dalam bentuk

( ) ( )

dy

P x y Q x

dx  . (2.2)

Persamaan (2.2) dapat dinyatakan dalam bentuk



P x y Q x dx dy

( )



( )



 

0

atau

M x y dx N x y dy

 

,



 

,



0

(2.3)

dengan

M x y

 

,



P x y Q x

( )



( )

dan

N x y

 

,



1

.

Definisi 2.6 (Ross, 1984 : 27)

Suatu persamaan diferensial berbentuk (2.3) dinamakan persamaan diferensial

eksak dalam daerah D jika terdapat suatu fungsi F sehingga F x y( , ) M x y( , )

x

 _



dan F x y( , ) N x y( , ) y

 _

 untuk semua

( , )

x y



D

.

Teorema 2.1 (Ross, 1984 : 28) Jika F x y( , ) M x y( , )

x

 _

 dan

( , )

( , ) F x y

N x y y

 _

 adalah kontinu. Persamaan

diferensial (2.3) adalah eksak jika dan hanya jika M x y( , ) N x y( , )

y x

 _

15 Persamaan (2.3) bukanlah persamaan diferensial eksak karena tidak memenuhi

Teorema 2.1. Pada persamaan tersebut

M x y

( , )

P x

( )

y







dan

( , ) 0

N x y x

 _

 maka

( , ) ( , )

M x y N x y

y x

 _

  dengan

P x

( ) 0



sehingga persamaan (2.3) merupakan

persamaan diferensial non eksak.

Solusi dari persamaan diferensial linear orde satu diperoleh melalui langkah sebagai berikut.

Perkalian persamaan (2.3) dengan faktor integrasi



 

x

diperoleh,

   

x M x y dx

,

   

x N x y dy

,

0









 

x P x y Q x dx



( )

( )



 

x dy

0













 

x P x y( )

 

x Q x dx( )

 

x dy 0

  

_  _   . (2.4)

Faktor



 

x

merupakan faktor integrasi dari persamaan (2.4) jika dan hanya jika

persamaan (2.4) merupakan persamaan diferensial eksak, yaitu jika dan hanya jika

 

x P x y

( )

 

x Q x

( )

 

x

y





x































(2.5)

Persamaan (2.5) dapat direduksi menjadi

 

x P x( ) d

 

x dx



 _



_. (2.6)

Fungsi P pada persamaan (2.6) merupakan fungsi atas variabel bebas x, sedangkan



merupakan fungsi atas x yang tidak diketahui, sehingga persamaan (2.6) dapat

dituliskan sebagai persamaan diferensial berikut :

( ) d

P x dx



16

( )

d

P x dx









. (2.7)

Untuk memperoleh solusi khusus dari persamaan (2.7), dilakukan pengintegralan pada kedua ruas persamaan (2.7) sehingga

ln || P x dx( )

 



( )

P x dx

e





 

. (2.8)

Selanjutnya, perkalian persamaan (2.2) dengan faktor integrasi (2.8) diperoleh

( ) ( ) ( )

( ) ( )

P x dxdy P x dx P x dx

e e P x y e Q x

dx

 _  _ 

( ) ( )

( )

P x dx P x dx

d

e y e Q x

dx

   

 _{ }

 

( ) ( )

( )

P x dx P x dx

d e  y e Q x dx

 _{ }

  . (2.9)

Dengan mengintegralkan kedua ruas persamaan (2.9) diperoleh solusi dari

persamaan (2.2) yang berbentuk

( ) ( )

( )

P x dx P x dx

ye







e



Q x dx c



(2.10)

dengan c adalah konstan.

Contoh 2.2

Diberikan persamaan diferensial sebagai berikut

2

(x 1)dy 4xy x dx

   . (2.11)

17

2 2

4

1 1

dy x x

y

dx x   x  . (2.12)

Dari persamaan (2.12) dapat diketahui bahwa ( ) ₂4 1

x P x

x 

 dan ( ) 2 1 x Q x x  

sehingga didapat faktor integrasi

2 2 2

2

4

( ) _{1 2.ln( 1) ln( 1) 2 2}

(

1)

x dx

P x dx _{x x x}

e

e

e

e

x

 

 _  _{ }

 















_{. (2.13)}

Substitusikan ( ) ₂ 1

x Q x

x 

 dan (2.13) ke persamaan (2.10) sehingga diperoleh,

2 2 2 2

2

2 2 2

4 2

2 2

( 1) ( 1)

1

( 1) ( 1)

2 4

( 1)

8

x

y x x dx c

x

y x x xdx c

x x

y x c

   _           





Jadi, solusi dari persamaan (2.11) adalah

4 2

2 2 2 4

( 1)

8

x x

y x    c

dengan c adalah konstan.

2.3. Sistem Persamaan Diferensial

Gabungan dari beberapa persamaan diferensial disebut sistem persamaan

diferensial. Sistem persamaan diferensial orde satu dapat dituliskan dalam bentuk

1

1( , ,1 2,..., n)

dy

f t y y y dt 

2

2( , ,1 2,..., n)

dy

18 3

3( , ,1 2,..., n)

dy

f t y y y dt  1 2 ( , , ,..., ) n n n dy

f t y y y

dt  (2.14)

untuk

t



[ , ]

a b

. Pada sistem (2.14), f f₁, ₂,...,f adalah fungsi-fungsi yang _n diketahui dalam variabel-variabel t y y, ,_{1 2},...,y . Masing-masing_n y i_i( 1, 2,..., )n adalah fungsi dalam t, yang merupakan variabel bebas (Sahid, 2012 : 400).

Sistem (2.14) dapat pula dituliskan dalam bentuk vektor. Jika dituliskan

y = [ … _� ]� , f = [� � � … �_� ]�,

dengan y dan f merupakan vektor-vektor fungsi, maka sistem (2.14) dapat ditulis

sebagai ��

�� = � ,

atau

1

1 1 2

2

2 1 2

1 2 ( , ,..., ) ( , ,..., ) ( , ,..., ) T n T n T n n n dy

dt _{f y y y}

dy

f y y y

dt

f y y y

dy dt     _{ }   _{ }   _{ }  _{   }   _{ }  _{  }       .

Selanjutnya diberikan vektor x n, dengan ( ,_{1 2}, ₃,..., )T n

x x x x



x dan

1, 2, 3,..., n

x x x x  . Jika d

dt x

dapat dinotasikan dengan

x

sehingga d dt  x

x untuk

menyatakan turunan x terhadap t, maka

1_, 2_,...,

T n dx dx dx

dt dt dt

 

 _ _

19 2.3.1. Sistem Persamaan Diferensial Linear

Sistem persamaan diferensial linear orde satu dengan variabel tak bebas

1, 2,..., n

y y y dan variabel bebas t dapat dinyatakan secara umum dalam bentuk

sebagai berikut :

1

11 1 12 2 ... 1n n 1( ) dy

a y a y a y F t

dt     

2

21 1 22 2 ... 2n n 2( ) dy

a y a y a y F t

dt     

1 1 2 2 ... ( )

n

n n nn n n

dy

a y a y a y F t

dt      . (2.15)

Jika F t dengan _i( )

i



1, 2,...,

n

bernilai nol maka sistem (2.15) disebut sistem persamaan diferensial linear homogen, sedangkan bila F t_i( ) 0 maka sistem (2.15) disebut persamaan diferensial linear nonhomogen. (Ross, 1984 : 505-506).

Sistem (2.15) dapat dinyatakan dalam bentuk

( )

dy

Ay F t

dt   (2.16)

dengan A adalah matriks n x n yang merupakan koefisien dari variabel tak bebas y,

dengan a_ij ,

i



1, 2,...,

n

,

j



1, 2,...,

n

dan

F t

( )

adalah matriks ukuran n x 1 yang merupakan fungsi dari t,

� ��

11 12 1 1 1

21 22 2 2 2

1 2

( )

( )

( )

n

n

n n nn n n

a

a

a

y

F t

a

a

a

y

F t

a

a

a

y

F t



   





   





   







   







   





   



20 Contoh 2.3

Diberikan sistem persamaan diferensial linear,

1

1 2 3

7 6

dx

x x x

dt   

2

1 2 3

10 4 12

dx

x x x

dt    

3

1 2 3 2

dx

x x x

dt     . (2.18)

Sistem persamaan diferensial (2.18) merupakan sistem persamaan diferensial linear

homogen. Berdasarkan (2.17), sistem (2.18) dapat dituliskan sebagai berikut

� ��

1 2 3

7 1 6 0

10 4 12 0

2 1 1 0

x x x



     

     

 _  _{    }       

     

 �_��

1 2 3

7 1 6

10 4 12

2 1 1

x x x



   

   

 _  _{  }     

   

.

2.3.2. Sistem Persamaan Diferensial Nonlinear Definisi 2.7 (Ross, 1984 : 5)

Persamaan diferensial nonlinear merupakan persamaan diferensial biasa yang

tidak linear.

Persamaan diferensial disebut sebagai persamaan diferensial nonlinear apabila memenuhi paling sedikit satu dari kriteria berikut (Ross, 1984 : 6),

21 Contoh 2.4

Diberikan sistem persamaan diferensial nonlinear sebagai berikut,

1

1 2 2 dx

x x x

dt   (2.19a)

2 2

1 2 dx

x x

dt   . (2.19b)

Sistem (2.19) merupakan sistem persamaan diferensial nonlinear dengan

variabel bebas t dan variabel tak bebas x dan ₁ x₂. Pada sistem (2.19), persamaan

(2.19a) memuat perkalian variabel tak bebas x dan ₁ x , pada persamaan (2.19b) ₂

terdapat kuadrat dari variabel bebas x . Berdasarkan kondisi tersebut, sistem (2.19) ₂

dapat disebut sebagai persamaan diferensial nonlinear.

2.3.3. Sistem Persamaan Diferensial Tundaan

Sistem persamaan diferensial tundaan ditunjukkan dengan persamaan berikut :

( )

t



( ( ), (

t

t





))

x

f x

x

. (2.20)

Persamaan karakteristik dari sistem (2.20) dinyatakan dalam bentuk



( , )

g



yaitu

( , )g P g( ) Q g e( ) g 0

    (2.21)

dengan  adalah lama waktu tundaan yang ditambahkan pada model persamaan

diferensial yang digunakan,

P g

( )

dan

Q g

( )

merupakan polinomial dalam

g

dan

g

merupakan akar karakteristik sistem (2.21) yang selanjutnya disebut sebagai nilai eigen (Rubono, 2009).

Contoh 2.5

22

1( ) 5 ( ) 4 ( )1 2

x t   x t  x t

2( ) 2 ( ) 4 ( ) 6 ( )1 2 2

x t   x t  x t  x t

Bila lama waktu tundaan  berpengaruh terhadap 4x , maka sistem tersebut ₂

dapat dituliskan dalam bentuk persamaan diferensial tundaan sebagai berikut,

1( ) 5 ( ) 4 (1 2 )

x t   x t  x t

2( ) 2 ( ) 4 (1 2 ) 6 ( )2

x t   x t  x t 



x t

dengan

t

 

0,



0

dan



x t x t

₁

( ), ( )

₂





2.

2.4. Titik Ekuilibrium

Titik ekuilibrium merupakan solusi dari sistem

x



f x

( )

yang tidak

mengalami perubahan terhadap waktu. Definisi 2.7 (Perko, 2001 : 102 )

Titik

x

ˆ



ndisebut titik ekuilibrium dari

x



f x

( )

jika

f x

( ) 0

ˆ



.

Contoh 2.6

Akan dicari titik ekuilibrium dari sistem (2.19). Misalkan

x



f x

( )

, maka

sistem (2.19) dapat dituliskan sebagai 1 2 ₂2

1 2

( ) x x x f x

x x



 

 _{ } _. Titik ekuilibrium sistem

(2.19) dapat diperoleh jika

f x

( ) 0

ˆ



.

Misal

x

ˆ ˆ ˆ



( , )

x x

_{1 2} Tmerupakan titik ekuilibrium sistem (2.19), maka

1 2 2

ˆ ˆ ˆ 0

23

2

1 2

ˆ ˆ 0

x x  . (2.23)

Dari persamaan (2.23) diperoleh 2

1 2

ˆ ˆ

x x . (2.24)

Selanjutnya, substitusikan persamaan (2.24) ke persamaan (2.22), sehingga

diperoleh 3

2 2

ˆ ˆ 0

x  x

2

2 2

ˆ ˆ( 1) 0

x x

  

2

ˆ 0

x

  atau xˆ₂ 1.

Selanjutnya, substitusikan xˆ₂0 ke persamaan (2.24) diperoleh xˆ₁0,

substitusikan xˆ₂ 1 dan xˆ₂  1 ke persamaan (2.24) diperoleh xˆ₁1. Jadi, titik

ekuilibrium dari sistem (2.19) adalah (0,0)T, (1,1)T, dan (1, 1) T. 2.5. Linearisasi

Linearisasi merupakan proses mengubah suatu sistem nonlinear menjadi sistem linear. Diberikan sistem persamaan diferensial nonlinear

( )

x



x f

(2.25)

dengan x  L n, f :

L



n, f fungsi nonlinear dan kontinu.

Sebelum ditunjukkan proses linearisasi dari persamaan diferensial non linear, akan

dibahas terlebih dahulu matriks Jacobian berdasarkan teorema berikut.

Teorema 2.2 (Perko, 2001 : 67 )

Jika f : n  n terdiferensial di x maka diferensial parsial ₀ i , , 1, 2,...,

j

f

i j n

x

 _

 ,

di x ada untuk semua ₀

x



n dan 0 0

1

( ) ( )

n

j

j j

f

Df x x x x

x



 





24

1

1 1

0

0 1 0 2

1 2

2

2 2

0

0 1 0 2

1 2

0 1

0 1 0 2 0

1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ... ( ) ( ) ( ) n n n n n j j j

n n n

n n f

f f

x x

x x x x

x

x x

f

f f

x x

x x x x

f

x

x x

x x x

f f f

x x x x x x

x x x

            _  _  _                 __  _{ } _{  }_        _{     }   _  _  _                   



1 1 1

0 0 0

1 2

1

2 2 2

0 0 0 2

1 2

0 0 0

1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) n n n

n n n

n

f f f

x x x

x x x

x

f f f

x x x x

x x x

x

f f f

x x x

x x x

     _{  }   _{  }    _{ } _{     }   _{  }  _{  } _{     }   _{  }    0 ( ) Df x x

 . ∎

dengan Df x disebut sebagai matriks Jacobian dari fungsi ( )_{0 f} : n  n yang

terdifrensial pada ₀ n

x  dan Df x dapat dinotasikan sebagai ( )₀ Jf x . ( )₀

Selanjutnya, akan ditunjukkan proses linearisasi dari sistem persamaan

diferensial. Misalkan xˆ( ,x xˆ ˆ_{1 2},...,xˆn)T merupakan titik ekuilibrium sistem (2.25).

Deret Taylor dari fungsi f disekitar titik ekuilibrium xˆ adalah sebagai berikut :

1

1 1

1 1 2 1 1 2 1 2 1 1 1 2

1

ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ

( , ,..., )T ( , ,..., )T ( , ,..., ) (T ) ... ( , ,..., ) (T )

n n n n n n f

n

f f

f x x x f x x x x x x x x x x x x x R

x x

 

 _   _  

2

2 2

2 1 2 2 1 2 1 2 1 1 1 2

1

ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ

( , ,..., n)T ( , ,..., n)T ( , ,..., n) (T ) ... ( , ,..., n) (T n n) f n

f f

f x x x f x x x x x x x x x x x x x R

x x

 

      

25

1 2 1 2 1 2 1 1 1 2

1

ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ

( , ,..., ) ( , ,..., ) ( , ,..., ) ( ) ... ( , ,..., ) ( )

n

T T n T n T

n n n n n n n n f

n

f f

f x x x f x x x x x x x x x x x x x R

x x

 

 _   _  

dengan

1, 2,..., n

f f f

R R R disebut sebagai bagian nonlinear yang selanjutnya dapat

diabaikan karena nilainya mendekati nol. Karena ( ,ˆ ˆ_{1 2},...,ˆ )T n

x x x titik ekuilibrium

sistem (2.25) maka ₁( ,ˆ ˆ_{1 2},...,ˆ )T ₂( ,ˆ ˆ_{1 2},...,ˆ )T ... ( ,ˆ ˆ_{1 2},...,ˆ )T 0

n n n n

f x x x  f x x x   f x x x 

sehingga diperoleh,

1 1 1

1 1 2 1 1 1 2 2 2 1 2

1 2

ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ

( , ,..., n) (T ) ( , ,..., n) (T ) ... ( , ,..., n) (T n n)

n

f f f

x x x x x x x x x x x x x x x x

x x x

  

      

  

2 2 2

2 1 2 1 1 1 2 2 2 1 2

1 2

ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ

( , ,..., ) (T ) ( , ,..., ) (T ) ... ( , ,..., ) (T )

n n n n n

n

f f f

x x x x x x x x x x x x x x x x

x x x

  

_  _   _ 

1 2 1 1 1 2 2 2 1 2

1 2

ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ

( , ,..., ) (T ) ( , ,..., ) (T ) ... ( , ,..., ) (T )

n n n

n n n n n n

n

f f f

x x x x x x x x x x x x x x x x

x x x

  

_  _   _ 

(2.26).

Sistem (2.26) dapat dituliskan dalam bentuk sebagai berikut :

1 1 1

1 2 1 2 1 2

1 2

1

2 2 2

1 2 1 2 1 2

2 1 2 1 2 1 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ( , ,..., ) ( , ,..., ) ( , ,..., ) ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ( , ,..., ) ( , ,..., ) ( , ,..., ) ˆ ˆ ˆ ( , ,..., )

T T T

n n n

n

T T T

n n n

n

n

T

n n

n

f f f

x x x x x x x x x

x x x

x

f f f

x x x x x x x x x

x

x x x

x

f f

x x x x         _{  }    _{   }       _{ }  1 1 2 2

1 2 1 2

2 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ( , ,..., ) ( , ,..., ) n n

T n T

n n n x x x x x x f

x x x x x x

x x      _{  }  _{   }  _{  }  _{  }  _{  }   _            (2.27)

26

1 1 1

1 2 1 2 1 2

1 2

1

2 2 2

1 2 1 2 1 2

2 1 2 1 2 1 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ( , ,..., ) ( , ,..., ) ( , ,..., ) ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ( , ,..., ) ( , ,..., ) ( , ,..., ) ˆ ˆ ˆ ( , ,..., )

T T T

n n n

n

T T T

n n n

n

n

T

n n

n

f f f

x x x x x x x x x

x x x

x

f f f

x x x x x x x x x

x

x x x

x

f f

x x x x         _{  }    _{   }       _{ }  1 2

1 2 1 2

2

ˆ ˆ ˆ ˆ ˆ ˆ

( , ,..., ) ( , ,..., )

n

T n T

n n n y y y f

x x x x x x

x x      _{  }  _{  }  _{  }  _{  }  _{  }  _{   }    _{ }    (2.28)

Sistem (2.28) merupakan linearisasi sistem (2.25), sehingga diperoleh matriks

Jacobian dari sistem (2.25) yaitu,

1 1 1

1 2 1 2 1 2

1 2

2 2 2

1 2 1 2 1 2

1 2

1 2 1 2

1 2 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ( , ,..., ) ( , ,..., ) ( , ,..., ) ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ( , ,..., ) ( , ,..., ) ( , ,..., ) ˆ ( ) ˆ ˆ ˆ ˆ ˆ ( , ,..., ) ( , ,...,

T T T

n n n

n

T T T

n n n

n

T

n n

n

f f f

x x x x x x x x x

x x x

f f f

x x x x x x x x x

x x x

Jf x

f f

x x x x x

x x               

  ˆ ) ( ,ˆ ˆ1 2,...,ˆ )

T n T

n n

n

f

x x x x

x                _         . Contoh 2.7

Akan dicari matriks Jacobian dari 1 2 ₂2

1 2

( ) x x x f x

x x



 

 _{ } _pada titik ₀ (1, 1)T

x   .

Matriks Jacobian dari fungsi

f x

( )

adalah

1 1

1 2 2 1

2 2 2 1 2 1 1 2 f f

x x x x

Df x f f x x     _{ }  _{  }   _{     }   _{ }    ,

maka 2 1

2

1 1 2

(1, 1)

1 2 1 2

x x Df x        _{   } _     .

Jadi, matriks Jacobian dari sistem tersebut adalah (1, 1) 1 2

1 2

27 2.6. Kestabilan Titik Ekuilibrium

Definisi 2.8 (Perko, 2001 : 102 )

Titik ekuilibrium xˆ disebut titik ekuilibrium hiperbolik dari sistem (2.25) jika tidak ada nilai eigen dari matriks

Df x

( )

ˆ

yang mempunyai bagian real nol.

Kestabilan sistem nonlinear

x



f x

( )

di sekitar titik ekuilibrium xˆ dapat dilihat dari kestabilan linearisasi sistem (2.25) di sekitar titik ekulibrium xˆ, asalkan titik ekuilibrium xˆ hiperbolik (Perko, 2001 : 103).

Definisi 2.9 (Olsder, 2004 : 57 )

Diberikan persamaan diferensial orde satu (2.25) dengan

x



n, penyelesaian

dengan keadaan awal x(0)x₀ dinotasikan oleh x t x . ( , ₀)

i. Vektor xˆ yang memenuhi

f x

( ) 0

ˆ



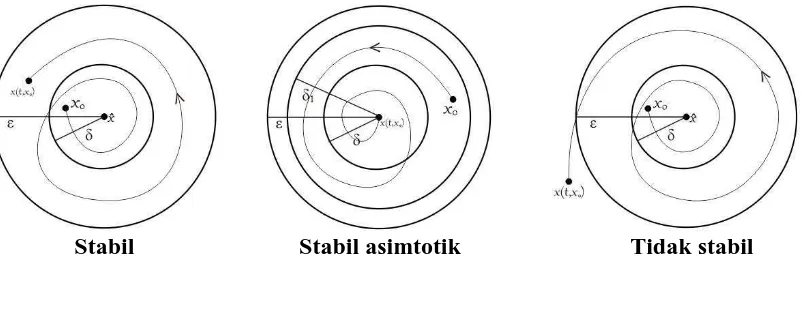
dikatakan sebagai titik ekuilibrium. ii. Titik ekulibrium xˆ dikatakan stabil jika diberikan untuk setiap



0

ada



0 sedemikian hingga jika x₀ xˆ  maka x t x( , ₀) xˆ 

untuk setiap t 0.

iii. Titik ekulibrium xˆ dikatakan stabil asimtotik jika titik ekuilibriumnya stabil dan terdapat ₁0 sedemikian sehingga lim ( , ₀) ˆ 0

t x t x  x , bila x₀ xˆ ₁

iv. Titik ekulibrium xˆ dikatakan tidak stabil jika tidak memenuhi (ii).

[image:28.595.114.515.83.238.2]

28 Stabil Stabil asimtotik Tidak stabil

Gambar 2.2. Ilustrasi Kestabilan

Dalam menganalisis kestabilan sistem di sekitar titik ekuilibrium menggunakan Definisi 2.9 masih ditemui kesulitan. Oleh karena itu, diberikan definisi dan

teorema untuk mengidentifikasi sifat kestabilan sistem nonlinear yang ditinjau dari

nilai eigen matriks Jacobian

Jf x

( ).

ˆ

Definisi 2.10 (Anton H., 1991 : 277 )

Diberikan matriks A berukuran n x n. Vektor x n,x0disebut vektor eigen dari A, jika

Ax

adalah kelipatan skalar dari

x

yaitu

A

x



g

x

untuk suatu skalar g. Skalar g disebut nilai eigen dari A.

Teorema 2.3 (Olsder, 2004)

i. Diberikan semua bagian real nilai eigen matriks Jacobian

Jf x

( )

ˆ

bernilai

negatif, maka titik ekuilibrium xˆ dari sistem (2.25) stabil asismtotik lokal. ii. Jika terdapat paling sedikit satu nilai eigen matriks Jacobian

Jf x

( )

ˆ

yang

29 Teorema 2.4 (Olsder, 2004 : 58)

Diberikan sistem persamaan diferensial linear

x



A

x

, dengan A adalah matriks

berukuran n x n, mempunyai k nilai eigen yang berbeda g g g₁, ₂, ₃,...,g dan _n .

k n

i. Titik ekuilibrium xˆ 0 stabil asimtotik jika dan hanya jika

( )_i 0, 1, 2,3,..., .

e g i k

   

ii. Titik ekuilibrium xˆ 0 stabil jika dan hanya jika

( )_i 0, 1, 2,3,...,

e g i k

    dan jika setiap nilai eigen g imaginer _i

dengane g( )_i 0, maka multiplisitas aljabar dan geometri untuk nilai eigen harus sama.

iii. Titik ekuilibrium xˆ 0 tidak stabil jika dan hanya jika terdapat paling

sedikit satu e g( )_i 0untuk i = 1,2,...k.

Bukti :

(i) Akan dibuktikan bahwa jika titik ekuilibrium xˆ 0stabil asimtotik, maka

( )_i 0, 1, 2,3,..., .

e g i k

   

Berdasarkan Definisi 2.9, titik ekuilibrium xˆ 0dikatakan stabil asimtotik

jika lim

�→∞‖ , − ̂‖. Hal ini berarti bahwa untuk → ∞, , akan

menuju xˆ 0. Karena , merupakan solusi dari sistem persamaan

diferensial, maka , memuat

e

e g t( i)

. Akibatnya untuk

e

e g t( i) yang

30 Selanjutnya, akan dibuktikan bahwa jika e g( )_i   0, i 1, 2,3,..., ,k maka titik ekuilibrium xˆ 0stabil asimtotik.

Solusi dari sistem persamaan diferensial adalah , , maka

, selalu memuat

e

e g t( i)

. Jika



e g

( ) 0

_i



, maka untuk → ∞,

, akan menuju xˆ 0. Sehingga, berdasarkan Definisi 2.9, titik

ekuilibrium xˆ 0stabil asimtotik.

(ii) Akan dibuktikan bahwa jika titik ekuilibrium xˆ 0 stabil, maka

( )_i 0, 1, 2,3,...,

e g i k

   

Andaikan



e g

( ) 0

_i



, maka solusi persamaan diferensial , yang selalu

memuat

e

e g t( i)

akan menuju ∞ (menjauh dari titik ekuilibrium ̅ = untuk → ∞, sehingga sistem tidak stabil. Hal ini bertentangan dengan yang

diketahui. Jadi terbukti bahwa jika titik ekuilibrium xˆ 0stabil, maka

( )_i 0, 1, 2,3,...,

e g i k

    .

Kemudian akan dibuktikan bahwa e g( )_i   0, i 1, 2,3,...,k maka titik ekuilibrium xˆ 0stabil dan jika ada e g( ) 0_i  , maka multiplisitas aljabar dan geometri untuk nilai eigen harus sama.

Solusi , merupakan solusi dari sistem persamaan diferensial, maka

, selalu memuat

e

e g t( i)

. Jika e g( ) 0_i  , maka

e

e g t( i)

akan menuju ˆ 0

31 multiplisitas aljabar berhubungan dengan nilai eigen sedangkan geometri berhubungan dengan vektor eigen (Widayati, 2013 : 23). Oleh karena itu, akan dibuktikan bahwa banyaknya nilai eigen dan vektor eigen adalah sama.

Tanpa mengurangi keumuman, ambil sembarang sistem pada ℝ yang

mempunyai nilai eigen bilangan kompleks murni.

1 1

2 2

0 0

g p g

g q g



 _     _ _ 

   , dengan > , > . (2.29)

Akan ditentukan nilai eigen dari sistem (2.29) |A gI | 0

0 0

0

0 0

p g

q g



  _ _

   

   

0

g p

q g

 

 _{ }

 _ 

  .

Diperoleh persamaan karakteristik

2

0

g  pq . (2.30)

Akar dari Persamaan (2.30) adalah

1,2

g = ±√− = ± �√ = ±�√

1

g = −�√ atau g₂= �√ .

Vektor Eigen untuk g₁= −�√ , diperoleh

[−�√ −

−�√ ]

1 2

0 g g

    

  (2.31)

32

[−�√ −

−�√ | ] R1 ~ R2

[ −�√

−�√ − | ] R1

[ −

� √

−�√ − | ] R2 +�√ R1

[ − �√ | ]

diperoleh

1

g −�√

g

₂



0

1

g = �√ g₂.

misal g₂t, maka g₁= �√

1 2

g g

       [

�√

], diambil t = 1 diperoleh 1

2

g g

       [

�√ ]

Sehingga vektor eigen g₁ adalah g₁= [�√ ].

Vektor Eigen untuk g₂= �√ , diperoleh

[�√ −

�√ ]

1 2

0 0 g g

   _    _{ }

  . (2.32)

Matriks augmented dari (2.32) yaitu

[�√ −

33

[ �√

�√ − | ] R1

[

� √

�√ − | ] R2 −�√ R1

[ �√ | ]

diperoleh

1

g +�√ g₂0

1

g = −�√ g ₂

misal g₂= , maka g₁= −�√

1 2

g g

       [−

�√

], diambil s = 1 diperoleh 1

2

g g

       [−

�√ ]

Sehingga vektor eigen g adalah ₂ g₂= [−�√ ].

Terbukti banyak nilai eigen sama dengan banyak vektor eigen yaitu

sebanyak 2.

(iii) Akan dibuktikan bahwa jika titik ekuilibrium xˆ 0tidak stabil, maka

( ) 0_i e g

  untuk setiap � = , , . . . , �.

34 Selanjutnya, akan dibuktikan bahwa jika e g( ) 0_i  untuk setiap � = , , . . . , �, maka titik ekuilibrium xˆ 0tidak stabil.

Diketahui bahwa jika e g( ) 0_i  maka solusi persamaan differensial , yang memuat

e

e g t( i)

akan menuju ∞. Dengan demikian, titik

ekuilibrium xˆ 0tidak stabil. ∎

Kemudian, untuk analisis kestabilan sistem persamaan diferensial tundaan

nonlinier dilakukan dengan cara linierisasi sistem di sekitar titik ekuilibrium.

Andaikan diketahui titik ekulibrium

E



( *, *, *)

s i a

, dimisalkan

*,

*,

*

u

 

s s v i i w a a

 

 

maka diperoleh sistem yang linier yaitu :

0

( ) ( ) ( )

s u u t

i J v J v t

a w w t



   

     

 _  _  _ 

     

      

     

dengan J adalah matrik Jacobian untuk parameter tanpa tundaan (non delay) dan ₀

J_ adalah matriks Jacobian untuk parameter tundaan (delay). Kestabilan titik

ekuilibrium ditunjukkan dengan mencari persamaan karakteristik dari sistem.

Persamaan karakteristik diperoleh dari J₀J e_ g gI 0 dengan I adalah matriks identitas dan g adalah nilai eigen. (Nur Aini & Subiono, 2012).

2.7. Bilangan Reproduksi Dasar (R0)

Bilangan reproduksi dasar merupakan bilangan yang menunjukkan jumlah individu rentan yang dapat menderita penyakit yang disebabkan oleh satu individu

35 bilangan yang menyatakan banyaknya rata-rata individu yang terinfeksi akibat tertular individu terinfeksi yang berlangsung dalam populasi susceptible. Bilangan

reproduksi dasar dinotasikan dengan R . Jika ₀ R₀1 penyakit tidak menyerang populasi, sedangkan jika R₀ 1 maka penyakit akan menyebar.

Misalkan ada n kelas terinfeksi dan m kelas yang tidak terinfeksi, dan misalkan

n

x



dan y m adalah subpopulasi dari masing-masing kelas. Model kompartemen (kelas) dapat dituliskan dalam bentuk berikut :

( , ) ( , ), 1, 2,...,

i i

x f x y v x y i n,

( , ),

1, 2,..., ,

j

y





x y j



m

(2.33)

dengan f merupakan matriks dari laju individu baru terinfeksi penyakit yang _i menambah kelas terinfeksi, v merupakan matriks laju perkembangan penyakit, _i kematian, dan atau kesembuhan yang mengurangi kelas ini.

Perhitungan bilangan reproduksi dasar berdasarkan linearisasi sistem (2.33) pada titik ekuilibrium bebas penyakit. Hasil linearisasi dari kelas terinfeksi pada

titik ekuilibrium bebas penyakit adalah sebagai berikut :

(

)

x

 

F V x

dengan F dan V matriks berukuran n x n,

0 (0, )

i j

f

F y

x  

 dan (0, 0)

i j

v

V y

x  



dengan (0,y merupakan titik ekuilibrium bebas penyakit. ₀)

Selanjutnya, didefinisikan

1

36 dengan K disebut sebagai next generation matrix. Bilangan reproduksi dasar (R ₀)

dari model kompartemen adalah 1

0 ( )

R  pK  p FV yaitu nilai eigen terbesar dari

matriks K (Driessche dan Watmough, 2002). Contoh 2.8

Diberikan sistem persamaan diferensial berikut :

dS

N S SI

dt 





 



( )

dI

SI I I

dt 







 

 

dA

I A

dt  

 

(2.35)

dengan S menyatakan populasi individu sehat dan rentan pada saat t, I menyatakan populasi terinfeksi pada saat t, dan A menyatakan populasi individu positif AIDS

pada saat t. Sistem (2.35) mempunyai titik ekuilibrium bebas penyakit E₀ (1,0,0).

Pada sistem (2.35) kelas terinfeksi adalah I dan kelas A. Next generation matrix dapat diperoleh dari kelas I dan kelas A dengan

0

I S I f  

 

 _

  dan

I I v

I A

 

 



 

 _{ } _.

Hasil linearisasi dari f dan v masing-masing adalah

0

0 0

S

F  

 

 _  dan

0

v

 







 

 _{  } _ .

Sehingga diperoleh Next generation matrix berikut

1

37 1

0

0 ( )

0 0 1

( )

S

K    



   

 

 

 

 _{  }

  _ _{  }

 _{  }

 

0

( )

0 0

S K

   

 

 _ 

   

 

 

(2.36)

Selanjutnya, substitusikan titik ekuilibrium bebas penyakit E₀ (1,0,0)ke (2.36)

sehingga diperoleh

0

( )

0 0

K

   

 

 _ 

  

 

 

.

Bilangan reproduksi dasar diperoleh dari nilai eigen terbesar dari matriks K.

Jadi, nilai R0 dari sistem (2.35) adalah ₀

( )

R  

  

 .

2.8. Kriteria Routh-Hurwitz

Berdasarkan Teorema 2.4, kestabilan titik ekuilibrium sistem (2.25) dapat dilihat berdasarkan nilai eigen dari matriks Jacobiannya. Namun, seringkali

dijumpai akar-akar dari persamaan karakteristik berupa parameter yang nilainya tidak mudah ditentukan. Oleh karena itu, diperlukan aturan/ kriteria yang menjamin

bahwa akar-akar persamaan karakteristik bernilai negatif atau ada persamaan karakteristik yang bernilai positif. Kriteria tersebut dikenal dengan sebutan kriteria Routh Hurwitz.

Diberikan suatu polinomial

1 2

1 2 1 0

( )

_n n _n n _n n

...

38 Akar-akar dari polinomial (2.37) dapat diketahui dengan menyusun tabel Routh sebagai berikut

2 4

1

1 3 5

2

1 2 3

3

1 2 3

0

n

n n n

n

n n n

n n

a a a

z

a a a

z

b b b

z

c c c

z

P z

 



  





dimana b b₁, ,...; , ,...₂ c c_{1 2} dan P diperoleh dari

1 2 3 1 4 5

1 2

1 1

1 3 2 1 1 5 3 1

1 2

1 1

, ,

, ,

n n n n n n n n

n n

n n n n

a a a a a a a a

b b

a a

b a b a b a b a

c c

b b

     

 

   

 

 

 

 

Kriteria Routh Hurwitz :

Semua akar-akar dari polinomial (2.37) mempunyai bagian real negatif jika dan

hanya jika semua elemen pada kolom pertama tabel Routh memiliki tanda yang

sama (semua bernilai positif atau semua bertanda negatif).

Kriteria tersebut berarti banyaknya perubahan tanda dalam kolom pertama

tabel tersebut sama dengan banyaknya akar-akar polinomial (2.37) yang bagian realnya positif. Jadi, bila pada kolom pertama dalam tabel tidak ada perubahan

[image:38.595.256.371.143.245.2]