Didownload dari ririez.blog.uns.ac.id

1 A. METODE PROGRAM LINIER

Terdapat hubungan yang erat antara teori permainan dan program linier karena setiap bentuk permainan berjumlah nol dari dua orang (yang berhingga) dapat dinyatakan sebagai suatu bentuk program linier dan sebaliknya, setiap permasalahan program linier dapat disajikan sebagai suatu permainan. Dalam penyelesaian suatu permainan dengan metode program linier ini, sering dihadapkan kepada masalah metode simpleks dualitas. Untuk suatu permainan dengan matriks pembayaran yang berukuran besar (m x n) dan tidak mempunyai titik pelana serta metode dominasi tidak dapat digunakan untuk mereduksi ukuran matriks pembayaran menjadi lebih kecil, maka program linier menawarkan suatu metode penyelesaian yang efisien. Perhatikan matriks pembayaran di bawah ini.

Pemain P2 y1 y2 …….. yn Pemain P1 x1 a11 a12 …….. a1n x2 a21 a22 a2n x3 a31 a32 a3n . . . . . . . . . xm am1 am2 …….. amn dengan

xi = probabilitas pemain P1 memilih stategi ke- i yi = probabilitas pemain P2 memilih stategi ke- j

aij = nilai pembayaran yang bersesuaian dengan strategi ke-i pemain P1 dan ke-j

pemain P2,

i = 1, 2,...,m dan j = 1, 2, ..., n.

2 Pemain P1 memilih xi,       = ≥

_∑

= m i i i x x 1 1 ,

0 yang akan menghasilkan

           

∑

∑

∑

= = = m i i in m i i i m i i i x a x a x a x 1 1 2 1 1 , ,..., min max .

Hal ini menunjukkan bahwa strategi campuran optimum pemain P1 memenuhi

           

∑

∑

∑

= = = m i i in m i i i m i i i x a x a x a x 1 1 2 1 1 , ,..., min

max berdasar pembatas :

1 1 =

∑

= m i i x dan xi ≥ 0, i = 1, 2, …, m.

Persoalan ini dapat disajikan ke bentuk program linier sebagai berikut ;

jika       =

∑

∑

∑

= = = m i i in m i i i m i i i x a x a x a v 1 1 2 1 1 , ,...,

min maka persoalan ini menjadi :

Memaksimumkan Z = v berdasarkan pembatas :

∑

= ≥ m i i ijx v a 1 , j = 1, 2, …, n

∑

= = m i i x 1 1 , xi ≥ 0 untuk semua i v = nilai permainan

Perumusan program linier di atas dapat disederhanakan dengan membagi (n+1) pembatas dengan v. Pembagian ini berlaku untuk v > 0. Jika v = 0 maka pembagian tidak berlaku. Sebaliknya, jika v < 0 maka pembagian ini juga tidak berlaku namun dapat diubah menjadi v > 0 dengan menambahkan suatu konstanta positif k pada semua elemen dalam matriks pembayaran yang akan menjamin nilai permainan untuk matriks yang dimodifikasi ini lebih besar dari nol. Sebagai pedoman, diambil k ≥ harga mutlak dari elemen yang terkecil sehingga sebelum merumuskan ke bentuk program linier perlu diperiksa nilai maximin barisnya karena jika nilai maximin tersebut negatif maka ada kemungkinan nilai permainannya negatif atau nol.

Dengan demikian matriks pembayarannya perlu dimodifikasi dahulu dan sebagai konsekuensinya adalah jika solusi optimum telah diperoleh maka

3

nilai permainan yang sebenarnya ditentukan dengan mengurangi sebesar k tadi dari nilai permainan yang dimodifikasi itu. Pada umumnya jika nilai maximinnya positif maka nilai permainannya lebih besar daripada nol (terutama permainan yang mempunyai titik pelana). Oleh karena itu di dalam pembentukan rumusan program linier diasumsikan bahwa v > 0.

Pembatas-pembatas (constraints) dalam rumusan program linier di atas menjadi :

∑

= ≥ m i i ij v x a 1 1, j = 1, 2, 3, ..., n dan

∑

= = m i i v v x 1 1 , xi≥0 untuk semua i. Atau ditulis secara lengkap :

1 ... ₁ 3 31 2 21 1 11 + + + + ≥ v x a v x a v x a v x a m m 1 ... ₂ 3 32 2 22 1 12 + + + + ≥ v x a v x a v x a v x a m m 1 ... 3 3 33 2 23 1 13 + + + + ≥ v x a v x a v x a v x a m m . . . 1 ... 3 3 2 2 1 1 + + + + ≥ v x a v x a v x a v x a m mn n n n dan v v x v x v x v x m 1 ... 3 2 1 + + + + = Jika dinotasikan v x Xi = i dengan i = 1, 2, ..., m maka v X X X X m 1 ... 3 2 1 + + + + = . Karena v V min1 max = = min [X1+X2+X3+...+Xm]

4 Meminimumkan z = v X X X X₁+ ₂ + ₃ +...+ _m =1 berdasarkan pembatas : 1 ... ₁ 3 31 2 21 1 11X +a X +a X + +am Xm ≥ a 1 ... ₂ 3 32 2 22 1 12X +a X +a X + +am Xm ≥ a 1 ... ₃ 3 33 2 23 1 13X +a X +a X + +am Xm ≥ a . . . 1 ... 3 3 2 2 1 1nX +a nX +a nX + +amnXm ≥ a 0 ..., , , 2 3 1 X X Xm ≥ X

Dari sini kemudian diselesaikan dengan metode simpleks. Penyelesaian bagi pemain P2 merupakan dual dari penyelesaian pemain P1. Jadi penyelesaian

optimum bagi salah satu pemain dapat memberikan penyelesaian optimum bagi pemain lainnya meskipun penyelesaian bagi pemain P2 merupakan dual dari

penyelesaian pemain P1. Perhitungan penyelesaian optimum pemain P2 dapat

dilakukan dengan menggunakan metode simpleks dan penyelesaian pemain P1

merupakan dualnya. Pada kenyataannya bahwa lebih mudah untuk menghitung penyelesaian pemain P2 dengan metode simpleks terlebih dahulu.

• Untuk pemain P2 (pemain kolom)

Pemain P2 memilih yj,        = ≥

∑

= 1 , 0 1 n j j j y

y yang akan menghasilkan

               

∑

∑

∑

= = = n j j mj n j j j n j j j y_j a y a y a y 1 1 2 1 1 , ,..., max min .

Hal ini menunjukkan bahwa strategi campuran optimum pemain P2 memenuhi

               

∑

∑

∑

= = = n j j mj n j j j n j j j y_j a y a y a y 1 1 2 1 1 , ,..., max min

5 berdasarkan pembatas 1 1 =

∑

= n j j y dan yj > 0 , j = 0,1,2,…,n.

Persoalan ini dapat dirumuskan ke dalam bentuk program linear sebagai berikut. Jika         =

∑

∑

∑

= = = n j j mj n j j j n j j jy a y a y a v 1 1 2 1 1 , ,..., max

Maka persoalan di atas menjadi, meminimumkan Z = v berdasarkan pembatas v y a n j j ij ≤

∑

=1 , i = 1, 2,…, m 1 1 =

∑

= n j j y , yj > 0 untuk semua j v = nilai permainan

Asumsikan bahwa v > 0 maka pembatas-pembatas dalam rumusan program linear di atas menjadi

1 1 ≤

∑

= n j j ij v y a , i = 1, 2,…, m dan v v y n j j 1 1 =

∑

= , yj > 0 untuk semua j

Atau ditulis secara lengkap

1 ... 1 ... 1 ... 3 3 2 2 1 1 2 3 23 2 22 1 21 1 3 13 2 12 1 11 ≤ + + + + ≤ + + + + ≤ + + + + v y a v y a v y a v y a v y a v y a v y a v y a v y a v y a v y a v y a n mn m m m n n n n M dan v v y v y v y _n 1 ... 2 1 + + + = Jika dinotasikan v y Y_j = j ; j = 0,1,2,…,n maka

6 v Y Y Y Y₁+ ₂ + ₃ +...+ _n =1. Karena min v = v 1 max

= max

[

Y₁+Y₂ +Y₃ +...+Y_n

]

, maka persoalan di atas menjadi

Memaksimumkan       = + + + + = v Y Y Y Y w n 1 ... 3 2 1 berdasarkan pembatas-pembatas 1 ... 1 ... 1 ... 3 3 2 2 1 1 2 3 23 2 22 1 21 1 3 13 2 12 1 11 ≤ + + + + ≤ + + + + ≤ + + + + n mn m m m n n n n Y a Y a Y a Y a Y a Y a Y a Y a Y a Y a Y a Y a M Y1, Y2, Y3,…, Yn > 0

Kemudian diselesaikan dengan metode simpleks dan penyelesaian pemain P1

merupakan dual dari penyelesaian pemain P2 dan simpleksnya lebih sederhana.

Contoh 1 :

Diberikan matriks pembayaran (3 x 3) sebagai berikut : Pemain P2 y1 y2 y3 Pemain P1 x1 2 -1 -3 x2 -2 0 1 x3 0 -3 2

dengan xi = probabilitas pemain P1 memilih stategi ke- i yi = probabilitas pemain P2 memilih stategi ke- j

Ternyata bahwa permainan ini tidak mempunyai titik pelana dan aturan dominasi tidak digunakan. Karena nilai maximin = -2, maka ada kemungkinan nilai permainannya negatif atau nol. Oleh karena itu, matriks pembayaran di atas perlu dimodifikasi dengan menambahkan konstanta positif k = 4 sedemikian rupa sehingga matriks pembayaran modifikasinya adalah

7 Pemain P2 y1 y2 y3 Pemain P1 x1 6 3 1 x2 2 4 5 x3 4 1 6

Penyelesaian dengan metode simpleks untuk pemain P2. Formulasi program linear

berdasarkan matriks pembayaran modifikasi untuk pemain P2 adalah :

Memaksimumkan z = Y1 + Y2 + Y3 (= v 1 ) berdasarkan pembatas 6Y1 + 3Y2 + Y3 ≤ 1 2Y1 + 4Y2 + 5Y3 ≤ 1 4Y1 + Y2 + 6Y3 ≤ 1 Y1, Y2, Y3 ≥ 0

Bentuk di atas dibawa ke bentuk kanonik dengan memasukkan pengubah-pengubah kelonggaran (slack), misalnya P, Q, R. Kemudian mencari Y1, Y2, Y3,

P, Q, R ≥ 0 yang memenuhi 6Y1 + 3Y2 + Y3 + P = 1

2Y1 + 4Y2 + 5Y3 + Q = 1

4Y1 + Y2 + 6Y3 + R = 1

Memaksimumkan z = Y1 + Y2 + Y3 + OP + OQ + OR. Maka,

Y = [Yj] = [Y1, Y2, Y3, P, Q, R] v = [vi] = [v1, v2, v3] = [1, 1, 1] c = [cj] = [1, 1, 1, 0, 0, 0] A = (aij) =           1 0 0 6 1 4 0 1 0 5 4 2 0 0 1 1 3 6 METODE SIMPLEKS

Metode Simpleks mulai diperkenalkan oleh George B. Dantzig pada tahun 1949 Metode penyelesaian masalah:

8

- iterasi dengan langkah-langkah perhitungan yang sama

- perhitungan yang sama diulang beberapa kali sebelum solusi optimum dicapai

Langkah-langkah penyelesaian metode Simpleks: 1. Tentukan model formulasi

2. Tambahkan slack variable pada setiap constraint 3. Buat tabel simpleks

Persamaan constraint khusus untuk slack variable harus membentuk matriks identitas

4. Hitung zj dan zj - cj

Bila zj - cj < 0 belum optimal, harus dibuat tabel baru

5. Tentukan kolom pivot = kolom di mana zj - cj paling kecil 6. Tentukan baris pivot = baris di mana Harga bagi paling kecil

Harga bagi = Harga jawab

Elemen pada kolom pivot

7. Tentukan unsur pivot = unsur (elemen) yang menjadi anggota dari kolom pivot dan baris pivot

8. Menentukan variabel yamg masuk = variabel pada kolom pivot Menentukan variabel yang keluar = variabel pada baris pivot 9. Membuat tabel baru

Bagi elemen-elemen pada baris pivot dengan unsur pivot 10.Hitung elemen-elemen untuk baris lain dengan ketentuan

nij = nij - nip. npj

nij = elemen pada baris ke-i dan kolom ke-j yang baru nij = elemen pada baris ke-i dan kolom ke-j (tabel lama) nip = elemen pada baris ke i kolom pivot lama

npj = elemen pada baris pivot kolom ke-j (tabel baru) 11.Ulangi langkah nomor 4 sampai mendapatkan tabel optimal

9

Karena A telah tereduksi lengkap (memuat matriks identitas I3) maka bentuk

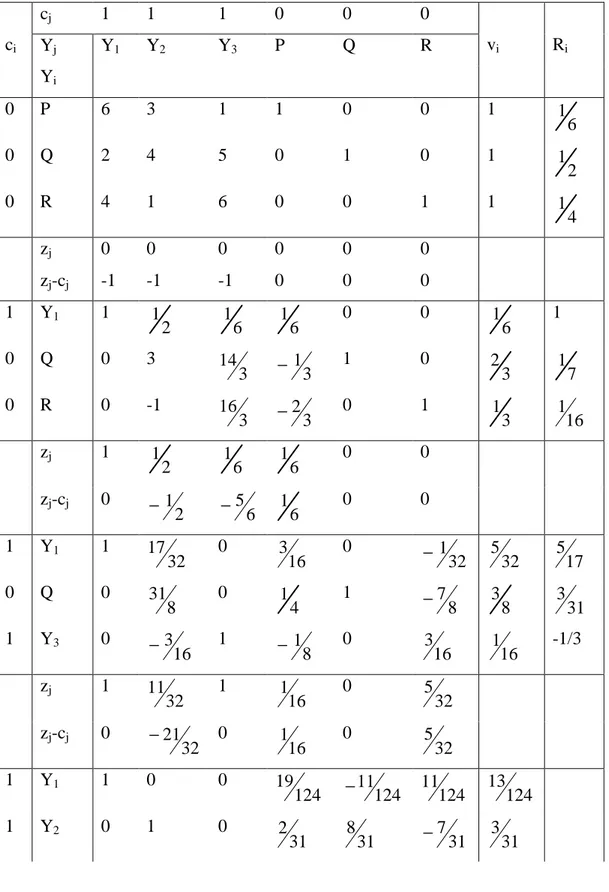
matriks itu dikatakan siap simpleks. Tabel simpleks untuk pemain P2

ci cj 1 1 1 0 0 0 vi Ri Yj Yi Y1 Y2 Y3 P Q R 0 P 6 3 1 1 0 0 1 6 1 0 Q 2 4 5 0 1 0 1 2 1 0 R 4 1 6 0 0 1 1 4 1 zj 0 0 0 0 0 0 zj-cj -1 -1 -1 0 0 0 1 Y1 1 2 1 1 ₆ 1 ₆ 0 0 6 1 1 0 Q 0 3 3 14 3 1 − 1 0 3 2 7 1 0 R 0 -1 3 16 3 2 − 0 1 3 1 16 1 zj 1 2 1 6 1 6 1 0 0 zj-cj 0 2 1 − ₋5₆ 6 1 0 0 1 Y1 1 32 17 0 16 3 0 32 1 − 5₃₂ 17 5 0 Q 0 8 31 0 4 1 1 8 7 − 8 3 31 3 1 Y3 0 16 3 − 1 8 1 − 0 16 3 16 1 -1/3 zj 1 32 11 1 16 1 0 32 5 zj-cj 0 32 21 − ₀ 16 1 0 32 5 1 Y1 1 0 0 124 19 124 11 − 11₁₂₄ 124 13 1 Y2 0 1 0 31 2 31 8 31 7 − 31 3

10 1 Y3 0 0 1 62 7 − 62 3 62 9 62 5 zj 1 1 1 124 13 124 21 124 1 124 35 zj-cj 0 0 0 124 13 124 21 124 1

Karena semua zj-cj > 0 maka telah tercapai optimum. Didapatkan bahwa

124 35 = z Y = [ Y1, Y2, Y3, P, Q, R ] =

[

13₁₂₄,3₃₁,5₆₂,0,0,0

]

Karena v y Y i i = dan z v = 1 maka z Y y i i = untuk i = 1, 2, 3. Diperoleh bahwa * 1 1 1 35 13 35 124 124 13 y x z Y y = = = = * 2 2 2 35 12 35 124 31 3 y x z Y y = = = = * 3 3 3 35 10 35 124 62 5 y x z Y y = = = =

dan nilai permainan sebenarnya adalah

35 16 4 35 124 1 * = − = − =− k z v

Jadi strategi campuran optimum pemain P1 adalah 

     = 35 10 , 35 12 , 35 13 * Y dan nilai permainan 35 16 * =− v .

Selanjutnya akan dicari solusi optimum untuk pemian P1 melalui dualitas

(berdasarkan solusi optimum matriks modifikasi). Bagi pemain P1

Y1 =13₁₂₄> 0 Y2 =3₃₁> 0 Y3 =5₆₂> 0

X1> 0 6 3 1 =1

X2> 0 2 4 5 =1

X3> 0 4 1 6 =1

11 Masalah dual :

6X1 + 2X2 + 4X3 = 1

3X1 + 4X2 + X3 = 1

X1 + 5X2 + 6X3 = 1

Merupakan sistem persamaan linier non homogen dengan 3 variabel, yaitu X1, X2,

X3 dan 3 persamaan. Sistem ini diselesaikan dengan aturan Cramer.

124 6 5 1 1 4 3 4 2 6 = = ∆ 124 13 6 5 1 1 4 1 4 2 1 1 = ∆ = X 124 21 6 1 1 1 1 3 4 1 6 2 = _∆ = X 124 1 1 5 1 1 4 3 1 2 6 3 = _∆ = X Diperoleh bahwa 124 35 1 3 2 1+ + = = = X X X v z Karena v x X i i = dan v z =1 maka z X x i i = untuk i = 1, 2, 3. Diperoleh bahwa * 1 1 1 35 13 35 124 124 13 x x z X x = = = = * 2 2 2 35 21 35 124 124 21 x x z X x = = = =

12 * 3 3 3 35 1 35 124 124 1 x x z X x = = = =     = 35 1 , 35 21 , 35 13 * x

Jadi solusi optimum permainan ini adalah

Strategi campuran pemain P1 adalah 

   = 35 1 , 35 21 , 35 13 * X

Strategi campuran pemain P2 adalah 

   = 35 10 , 35 12 , 35 13 * Y Nilai permainan 35 16 * =− v Contoh 2

Matriks pembayaran yang telah dimodifikasi.

Pemain P2 y1 y2 y3 Pemain P1 x1 6 3 1 x2 2 4 5 x3 4 1 6

Formulasi dalam program linier untuk pemain P1 adalah

Meminimumkan z = X1 + X2 + X3 (= v 1 ) berdasarkan pembatas 6X1 + 2X2 + 4X3 ≥ 1 3X1 + 4X2 + X3 ≥ 1 X1 + 5X2 + 6X3 ≥ 1 X1, X2, X3 ≥ 0

13

Bentuk di atas dibawa ke bentuk kanonik dengan menambahkan pengubah kelonggaran (slack), misalnya P, Q, R. Dicari X1, X2, X3, P, Q, R ≥ 0 yang

memenuhi : 6X1 + 2X2 + 4X3 – P = 1 3X1 + 4X2 + X3 – Q = 1 X1 + 5X2 + 6X3 – R = 1 Memaksimumkan z = X1 + X2 + X3 + 0P + 0Q + 0R Ternyata bahwa A=           − − − 1 0 0 6 5 1 0 1 0 1 4 3 0 0 1 4 2 6

belum siap simpleks.

Oleh karena itu perlu ditambah lagi dengan pengubah-pengubah semu (artificial

variables), misalnya S, T, W sehingga

Akan dicari X1, X2, X3, P, Q, R, S, T, W ≥ 0 yang memenuhi

6X1 + 2X2 + 4X3 – P + S = 1

3X1 + 4X2 + X3 – Q + T = 1

X1 + 5X2 + 6X3 – R + W = 1

Meminimumkan z = X1 + X2 + X3 + 0P + 0Q + 0R + MS + MT + MW dengan M

= bilangan positif besar. Maka, X = [X1, X2, X3, P, Q, R, S, T, W] v = [vi] = [v1, v2, v3] = [1, 1, 1] C = [cj] = [1, 1, 1, 0, 0, 0, M, M, M] A = (aij) =           − − − 1 0 0 1 0 0 6 5 1 0 1 0 0 1 0 1 4 3 0 0 1 0 0 1 4 2 6

Karena matriks A telah tereduksi lengkap maka matriks A dinamakan telah siap simpleks. Tabel simpleks untuk pemain P1 adalah sebagai berikut:

14 M S 6 2 4 -1 0 0 1 0 0 1 2 1 M T 3 4 1 0 -1 0 0 1 0 1 4 1 M W 1 5 6 0 0 -1 0 0 1 1 5 1 zj 10M 11M 11M -M -M -M M M M zj-cj 10M-1 11M-1 11M-1 -M -M -M 0 0 0 M S 5 28 0 5 8 -1 0 5 2 1 1 5 2 − 5 3 28 3 M T 5 11 0 5 19 − 0 -1 5 4 0 1 5 4 − 5 1 11 1 1 X2 5 1 1 5 6 0 0 5 1 − 0 0 5 1 5 1 1 zj 5 1 5 39 _{M +} 1 5 6 5 11 ₊ − M -M -M 5 1 5 6 _{M −} M M 5 1 5 6 ₊ − M zj-cj 5 4 5 39 _{M −} 0 5 1 5 11 ₊ − M -M -M 5 1 5 6 _{M −} 0 0 5 1 5 6 ₋ − M M S 0 0 11 124 -1 11 28 − 11 18 − 1 11 28 11 28 11 1 124 1 1 X1 1 0 11 19 − 0 11 5 − 11 4 0 11 5 11 4 − 11 1 1 X2 0 1 11 17 0 11 1 11 3 − 0 11 1 − 11 3 11 2 17 2 zj 1 1 11 2 11 124 _{M −} -M 11 4 11 28 ₋ − M 11 1 11 18 ₋ − M M 11 4 11 28 _{M +} 11 1 11 18 _{M −} zj-cj 0 0 11 13 11 124 _{M −} -M 11 4 11 28 ₋ − M 11 1 11 18 ₋ − M 0 11 4 11 17 _{M +} 11 1 11 7 _{M −}

15 1 X2 0 1 0 124 17 341 150 62 3 − 124 17 − 341 150 − 62 3 124 21 zj 1 1 1 124 13 − 341 166 − 62 5 − 124 13 341 166 62 5 124 35 zj-cj 0 0 0 124 13 − 341 166 − 62 5 − _−M 124 13 _−M 341 166 _−M 62 5

16 telah tercapai. Nilai optimumnya adalah

z = X1 + X2 + X3 (= v 1 ) = 124 35 Solusi optimum X = [X1, X2, X3, P, Q, R, S, T, W] =_ ,0,0,0,0,0,0_ 124 1 , 124 21 , 124 13 Karena v x Xi = i dan v z=1 maka z X xi = i untuk i = 1, 2, 3. Diperoleh bahwa * 1 1 1 35 13 35 124 124 13 x x z X x = = = = * 2 2 2 35 21 35 124 124 21 x x z X x = = = = * 3 3 3 35 1 35 124 124 1 x x z X x = = = =

Dan nilai permainan sebenarnya adalah

35 16 4 35 124 1 * = − = − =− k z v

Jadi strategi campuran optimum pemain P1 adalah 

   = 35 1 , 35 21 , 35 13 *

X dan nilai permainan

35 16

* =−

v . Selanjutnya akan dicari solusi optimum untuk pemian P2 melalui dualitas

(berdasarkan solusi optimum matriks modifikasi). Bagi pemain P2 Y1 > 0 Y2 > 0 Y3 > 0 X1=13₁₂₄ 6 3 1 =1 X2 =21₁₂₄ 2 4 5 =1 X3 =1₁₂₄ 4 1 6 =1 =1 =1 =1 Masalah dual 6Y1 + 3Y2 + Y3 = 1 2Y1 + 4Y2 + 5Y3 = 1

17

Sistem persamaan linier non homogen dengan tiga anu yaitu Y1, Y2, Y3 dan tiga persamaan

ini diselesaikan dengan aturan Cramer.

124 6 1 4 5 4 2 1 3 6 = = ∆ 124 13 6 1 1 5 4 1 1 3 1 1 = ∆ = Y 124 12 6 1 4 5 1 2 1 1 6 2 = _∆ = Y 124 10 1 1 4 1 4 2 1 3 6 3 = ∆ = Y Diperoleh bahwa 124 35 1 3 2 1+ + = = = Y Y Y v z Karena v y Yi = i dan v z =1 maka z Y yi = i untuk i = 1, 2, 3. Diperoleh bahwa * 1 1 1 35 13 35 124 124 13 y x z Y y = = = = * 2 2 2 35 12 35 124 124 12 y x z Y y = = = = * 3 3 3 35 10 35 124 124 10 y x z Y y = = = =     = 35 10 , 35 12 , 35 13 * Y

Jadi solusi optimum permainan ini adalah

o Strategi campuran optimum pemain P1 adalah 

   = 35 1 , 35 21 , 35 13 * X

18  35 35 35 o Nilai permainan 35 16 * =− v

Dengan demikian terlihat bahwa penyelesaian simpleks untuk pemain P1 (pemain baris ) lebih

rumit daripada penyelesaian simpleks untuk pemain P2. Oleh karena itu disarankan untuk

menyelesaikan dengan metode simpleks bagi pemain P2 (pemain kolom) dahulu dan baru

penyelesaian pemain P1 sebagai dualnya.

KESIMPULAN PENYELESAIAN BERJUMLAH NOL DARI DUA ORANG

1. Dalam studi kasus buatlah matriks pembayaran atau matriz permainannya terlebih dahulu. 2. Perhatikan baik-baik matriks pembayaran yang diberikan atau matriks pembayaran yang

baru disajikan bila studi kasus.

3. Selidi apakah mempunyai titik pelana.

4. Kalau ditemukan titik pelana, maka permainan tersebut dapat diselesaikan dengan strategi murni. Kalau titik pelana tidak ditemukan maka permainan tersebut diselesaikan dengan strategi campuran.

5. Memeriksa apakah mtriks pembayaran dapat direduksi dengan aturan dominasi. 6. Selesaikan permainan ini dengan salah satu metode penyelesaian yang cocok.

• Metode aljabar untuk ukuran 2 x 2

• Metode grafik untuk ukuran 2 x 2, 2 x n, m x 2

• Metode aljabar matriks dan metode program linier untuk usuran m x n B. PERMAINAN BERJUMLAH NOL DARI n ORANG

1. Pendahuluan

Pada bab-bab sebelumnya telah dibahas tentang permainan berjumlah nol dari 2 orang, yaitu suatu permainan yang hanya memuat dua pertentangan kepentingan (oppositing interest). Dalam bab ini akan sedikit dibahas tentang permainan berjumlah nol dari n

orang. Perbedaannya dengan bab sebelumnya adalah bahwa permainan pada bab-bab sebelumnya dimainkan hanya oleh dua orang (pihak) saja tetapi dalam bab-bab ini jumlah pemainnya lebih dari dua orang (pemain).

Ada dua asumsi yang dipakai di dalam pembahasan permainan berjumlah nol dari n orang ini, yaitu:

19

pemain yang lain untuk membuat suatu perjanjian yang mengikat. Hal ini berarti ada kerjasama di antara pemain. Barangkali perjanjian itu meliputi dua jenis, yaitu koordinasi strategi dan pembagian pembayaran. Jika suatu kelompok pemain menyatakan untuk bekerja sama maka mereka membentuk koalisi. Suatu koalisi adalah persetujuan di antara beberapa pemain untuk mengkoordinasikan strategi mereka yang ada dalam suatu cara (jalan) sedemikian sehingga seluruh anggota koalisi itu akan beruntung. Analisis mengenai bentuk koalisi inimerupakan bagian yang terpenting di dalam mempelajari permainan berjumlah nol dari n orang ini. 2. Para pemain dapat membuat pembayaran sampingan (side payment), yaitu suatu

transfer (pemindahan) pembayaran di antara pemain. Oleh karena itu mereka akan membentuk suatu koalisi jika pembayaran-pembayaran itu sedemikian rupa sehingga anggota-anggota koalisi (melalui kerjasama) dapat mencapai total pembayaran untuk koalisi itu lebih besar daripada mereka bermain secara individu. Setelah koalisi memaksimumkan total pembayarannya, penbayaran untuk para anggota koalisi itu diatur dengan pembuatan pembayaran sampingan (side

payment) itu.

Sesuai dengan definisi permainan di sini maka diasumsikan bahwa pemain-pemain di dalam permainan n orang ini dapat dibagi menjadi dua kelompok (koalisi) yang saling berhadapan (besaing). Setelah terbentuk dua koalisi (kelompok), permainan n orang ini dapat diberlakukan sebagai permainan dua orang, yaitu koalisi I melawan koalisi II.

Nilai permainan, yang mana terdaftar di dalam fungsi karakteristik untuk permainan ini adalah nilai maximin untuk koalisi I yang berarti bahwa minimum total pembayaran anggota-anggota koalisi I dapat diperoleh tanpa memperhatikan tindakan yang diberikan oleh anggota koalisi II. Oleh karena itu total pembayaran dari koalisi I sama dengan negatif dari total pembayaran koalisi II di dalam setiap vektor pembayaran dalam matriks pembayaran.

2. Bentuk Koalisi

Secara umum di dalam permainan berjumlah nol n orang terdapat 2n-1 cara yang mungkin untuk mengelompokkan n orang (pemain) itu ke dalam dua kelompok yang saling berhadapan. Misalnya, permainan yang berjumlah nol 4 orang (A, B, C, D). Para pemain dalam permainan ini dapat membentuk 24-1=8 koalisi yang berbeda yaitu:

20

1.

ABCD Ø

2.

ABC D

3.

ABD C

4.

ACD B

5.

BCD A

6.

AB CD

7.

AC BD

8.

AD BC

Kalau dilihat pada bentuk koalisi yang kesatu, yaitu ABCD VS Ø maka jelas ini tidak dipakai di sini. Karena koalisi kosong (Ø) tidak mempunyai langkah, tidak mempunyai pengaruh, tidak ada keuntungan ataupun kerugian.

Demikian juga komplemen dari koalisi kosong (Ø) ini, yaitu ABCD, walaupun mempunyai banyak anggota dan langkah juga tidak mempunyai pengaruh dan tidak ada kerugian atau keuntungan karena jelas bahwa koalisi ABCD ini tidak mempunyai lawan bersaingnya.

Dengan membagi n orang (pemain) menjadi dua grup tersebut maka permainan berjumlah nol dari n orang ini dapat diberlakukan sebagai suatu permainan berjumlah nol dari dua orang (grup).

Dengan demikian di dalam menghitung solusi optimumnya dapat menggunakan metode-metode untuk permainan berjumlah nol dari dua orang. Hanya ada sedikit perbedaan yaitu mengenai pembagian pembayaran untuk masing-masing anggota koalisi yang bersangkutan.

Contoh 3

Diberikan permainan berjumlah nol dari 3 orang (A, B, C) dengan masing-masing pemain mempunyai 2 pilihan strategi. Misalnya:

- Pemain A mempunyai 2 strategi : X1, X2. - Pemain B mempunyai 2 strategi : Y1,Y2. - Pemain C mempunyai 2 strategi : Z1, Z2.

21 A B C A B C X1 Y1 Z1 -1 1 0 X1 Y1 Z2 -3 2 1 X1 Y2 Z1 0 2 -2 X1 Y2 Z2 3 -2 -1 X2 Y1 Z1 -2 0 2 X2 Y1 Z2 0 -1 1 X2 Y2 Z1 -1 -2 3 X2 Y2 Z2 2 1 -3

Dari sini ada 3 koalisi yang mungkin, yaitu: Grup I melawan Grup II

1. A BC

2. B AC

3. C AB

Diselidiki untuk A melawan B, C; dengan matriks pembayarn sebagai berikut:

BC

A

Dalam matriks pembayaran tabel ini tidak mempunyai titik pelana. Diselesaikan metode grafik. Misalnya x1 = probabilitas pemain A memainkan strategi kesatu.

Pembayaran harapan pemain A yang berkaitan dengan strategi murni pemain (BC) adalah:

Strategi murni pemain BC Pembayaran harapan pemain A 1 2 3 4 x1 - 2 -3x1 x1-1 x1 + 2 Y1 Z1 Y 1Z2 Y2 Z1 Y2 Z2 X1 X2 -1 -3 0 3 -2 0 -1 2

ini. Dan kolom ke 3 dan ke 4 pada tabel

didominasi oleh kolom ke 1 atau garis lurus (1). D bawah ini.

Titik maximin dilalui oleh garis lurus (1) dan (2) maka: x1 – 2 = -3x1

4x1 = 2 < = > x

Sehingga berarti bahwa x v* = -

2 3

Sekarang strategi optimum pemain (BC) dengan dualitas. Misalnya Y pemain (BC) memilih kolom ke j; j = 1, 2, 3, 4.

y1 > 0 2 1 = x1 -1 2 1 = x2 -2 ǁ 3 2 Dual: -y1 – 3y2 = -3/2 -2y1 = -3/2 < = > y1 < = > y2 22

olom ke 3 dan ke 4 pada tabel atau persamaan garis lurus (3) dan (4) didominasi oleh kolom ke 1 atau garis lurus (1). Dapat diperlihatkan pada grafik 1

Grafik 1

Titik maximin dilalui oleh garis lurus (1) dan (2) maka:

< = > x1 = ½ = x1

a berarti bahwa x2 = ½ dan nilai permainan

Sekarang strategi optimum pemain (BC) dengan dualitas. Misalnya Y pemain (BC) memilih kolom ke j; j = 1, 2, 3, 4.

y2 > 0 y3 > 0 y4 > 0 -3 0 3 0 -1 2 ǁ 3 2 V 3 2 v 3 2 1 = 4 3 = y1* = 4 1 = y2*

atau persamaan garis lurus (3) dan (4) apat diperlihatkan pada grafik 1 di

Sekarang strategi optimum pemain (BC) dengan dualitas. Misalnya Yj = probabilitas

3 =

2 =

v 3 2

Strategi optimum pemain BC adalah Y dan v* =

-2 3

Diselidiki untuk B melawan AC dengan matriks pembayaran sebagai berikut:

B

Ternyata tidak mempunyai titik pelana dan

misalnya x1 = probabilitas pemain B memilih strategi ke 1. Pembayaran harapan

pemain B yang berkaitan dengan strategi murni pemain (AC) adalah: Strategi murni pemain

Ketiga garis lurus ini digambarkan sebagai fungsi dari

Ternyata titik maximum dilalui oleh garis lurus (3) dan (4) maka X1 Z Y1 Y2 1 2 23  2 2 Strategi optimum pemain BC adalah Y* = _ ,0,0_

4 1 , 4 3

Diselidiki untuk B melawan AC dengan matriks pembayaran sebagai berikut: AC

Ternyata tidak mempunyai titik pelana dan ke 1 dan 2 didominasi oleh kolom ke 3. = probabilitas pemain B memilih strategi ke 1. Pembayaran harapan pemain B yang berkaitan dengan strategi murni pemain (AC) adalah:

Strategi murni pemain AC Pembayaran harapan pemain 3

4

2x1-2

1 - 2x1

Ketiga garis lurus ini digambarkan sebagai fungsi dari x1 pada grafik 2

Grafik 2

Ternyata titik maximum dilalui oleh garis lurus (3) dan (4) maka 2 2 1 2 4 3 ⇔ 3 4 ∗ Z1 X 1Z2 X2 Z1 X2 Z2 2 0 -1 -2 -2 1

Diselidiki untuk B melawan AC dengan matriks pembayaran sebagai berikut:

ke 1 dan 2 didominasi oleh kolom ke 3. = probabilitas pemain B memilih strategi ke 1. Pembayaran harapan pemain B yang berkaitan dengan strategi murni pemain (AC) adalah:

Pembayaran harapan pemain B

pada grafik 2 di bawah ini.

24 dan 2 1 * ₌₋ v

Strategi optimum bagi pemain AC dengan dualitasnya. Misalnya = probabilitas pemain AC memilih strategi ke j; j = 3,4

y3 y4 x1 = 0 -1 =− x2 = -2 1 =− ǁ −1₂ ǁ −1₂ Dual −4 = −1_{2 ⇔} =1_{2 =} ∗ −2+ = −1_{2 ⇔} =1_{2 =} ∗

Jadi strategi optimum pemain B adalah ∗ =

,

Strategi optimum pemain AC adalah ∗ = 0,0,

, dan 2 1 * ₌₋ v

3. Untuk C melawan AB dengan matriks pembayaran : AB

C

Ternyata tidak mempunyai titik pelana dan kolom ke 1 dan 3 didomonasi oleh kolom ke 2. Misalnya = probabilitas pemain C memilih langkah ke 1. Pembayaran harapan pemain C yang berkaitan dengan strategi murni AB.

X1,Y1 X1,Y2 X2,Y1 X2,Y2

Z1

Z2

0 -2 2 3 1 -1 1 -3

Kedua garis lurus ini digambarkan sebagai fungsi

Karena titik maximum dilalui oleh dua garis lurus, yaitu (1) dan (4) maka

⇔ ∗ dan ∗

Strategi optimum pemain AB melalui dualitas. memilih strategi kej;j=2,4

x1 = x2 = Dual : 2 3 3 3 25 2 4 -x1-1 6x1-3

Kedua garis lurus ini digambarkan sebagai fungsi dari x1 pada grafik

Grafik 3

Karena titik maximum dilalui oleh dua garis lurus, yaitu (1) dan (4) maka 1 6 3

7 2 ⇔

2 7

∗

Strategi optimum pemain AB melalui dualitas. Misalnya Yj = probabilitas pemain AB memilih strategi kej;j=2,4

y2 > 0 y4 > 0 -2 3 = -1 -3 = ǁ 9 7 ǁ 9 7 ⇔ ∗ ⇔ ∗

da grafik 3 dibawah ini.

Karena titik maximum dilalui oleh dua garis lurus, yaitu (1) dan (4) maka

26

Strategi optimum pemain C adalah ∗ = 0,

, 0,

dan ∗ =

Dengan demikian didapatkan bahwa :

Nilai permainan untuk A yaitu !"# = − , !$%# = Nilai permainan untuk B yaitu !$# = −

, !"%# =

Nilai permainan untuk C yaitu !%# = −

, !"$# =

Sekarang timbul permasalahan mengenai bagaimana pembagian (pendistribusian) pembayaran setiap pemain/anggotanya. Aturan pendistribusian (pembagian) pembayaran setiap pemain (anggota) dikenal dengan imputasi (imputations)

C.IMPUTASI

Imputasi adalah suatu distribusi (pembagian) yang mungkin dari pembayaran yang tersedia yang dinyatakan sebagai vektor pembayaran untuk suatu permainan yang memenuhi kriteria.

1. Jumlah dari pembayaran-pembayaran tiap individu (pemain ) harus sama dengan nol (karena permainan berjumlah nol). Dalam permainan berjumlah nol dari n oramg yang bekerja sama (membentuk koalisi) dapat disajikan suatu imputasi sebagai vektor pembayaran P = [p1, p2, p3, ..., pn] dengan Pi I menyatakan suatu besaran pembayaran

yang diterima oleh pemain ke i ∈ I = {1, 2, ..., n}. Ini dapat disajikan sebagai

∑

=0

∈I i

i

p

2. Pembayaran untuk setiap pemain harus lebih besar atau sama dengan pembayaran yang dapat diperolehnya secara individu. Dapat disajikan sebagai

pi≥ v ({i}), untuk semua i ∈ I,

dengan v ({i}) adalah nilai permainan untuk pemain ke – i. Contoh 4

Pada contoh 3 didapatkan bahwa

V(A) = -1,5 V(AC) = 1,5 V(B) = -0,5 V(AC) = 0,5 V(C) = - 1.286 V(AB) = 1,286

27 1,5

[0,5, -0,25, 0,25]

[0,75, 0,25, -1] dan sebagainya . Contoh yang bukan imputansi :

[0,2, -0,7, 0,5] karena -0,7 < 0,5 [-2, 1,5, 0,5] karena -2 < 1,5

Dari contoh 4 di atas ternyata bahwa terdapat banyak (bahkan tak berhingga jumlahnya) imputansi dari permainan n orang itu sehingga yang menjadi masalah adalah untuk mendapatkan kriteria yang memungkinkan kita untuk menentukan salah satu imputansi terpilih dari imputansi-imputansi yang lain. Kriteria ini dinamakan criteria dominasi. Misalnya diberikan dua imputansi yang berbeda P1 dan P2. Imputansi P1 dikatakan

mendominasi imputan P2 untuk suatu koalisi jika pembayaran-pembayaran untuk semua

anggota koalisi itu lebih besar untuk P1 daripada untuk P2 dan jika total pembayaran untuk

koalisi itu adalah cukup besar untuk menyediakan pembayaran secara individu yang diberikan P1.

Contoh 5

Perhatikan contoh 4.

Misalkan P1= [-1,5 , 0,5 , 1] dan P2= [ 0,5 , -0,25 , -0,25] Maka P1 mendominasi P2 untuk menjadi koalisi (BC)

Karena [-1,5 , 0,5 , 1] > [ 0,5 , -0,25 , -0,25] >

>

Tetapi P2 tidak mendominasi P1 untuk koalisi BC karena [ 0,5 , -0,25 , -0,25] ≯ [-1,5 , 0,5 , 1]

<

28 D. DOMINANSI DARI IMPUTASI

Untuk mengetahui apakah suatu imputasi lebih baik dibandingkan imputasi lainnya, yaitu dengan melihat pada dua imputasi x dan y.

Karena

( )

∑

∑

∈ ∈ = = N i i N i i v N y x

jika untuk suatu i berlaku x_i > y_i maka pasti terdapat j sedemikian sehingga y_j >x_j. Sebab suatu imputasi tidak lebih baik dari imputasi yang lain untuk suatu pemain, tetapi terdapat kemungkinan untuk suatu koalisi istimewa, x lebih baik daripada y untuk setiap anggota. Jadi bisa dikehendaki suatu koalisi yang kuat untuk mendapatkan imputasi yang lebih baik.

Berikut ini definisi mengenai dominasi dari imputasi.

Definisi 1. (Parthasarathy dan Raghavan, 1971: 220-221) Misalkan x =

(

x₁,x₂,K,x_n

)

dan y =

(

y1,y2,K,yn

)

imputasi untuk permainan kooperatif n-pihak dimana v adalah fungsi karakteristik, dan S adalah himpunan bagian dari himpunan pemain. Imputasi

(

x1,x2,K,xn

)

mendominasi imputasi

(

y1,y2,K,yn

)

, yang dinotasikan xfy, pada S jika memenuhi: 1) S≠Ø 2) x v

( )

S S i i ≤

∑

∈ 3) x_i > y_i, ∀i∈S

Dari definisi tersebut dapat dikatakan bahwa xf_{y jika terdapat suatu himpunan} yang tidak kosong S ⊆N sedemikian sehingga

∑

( )

∈ ≤ S i i v S x dan x_i > y_i, ∀i∈S. Jika x f_{y pada S (dinotasikan x}f_{Sy), maka S harus memuat paling sedikit dua dan paling}

banyak

(

n−1

)

anggota. Sebab jika S =

{}

i dan xfSy maka yi < xi ≤v

( )

{}

i . Kondisi (2) pada Definisi 1 dilanggar.

Jika S =N dan xf_{Ny maka} i i y

x > untuk setiap i∈N sehingga

( )

N v y x N i i N i i >

∑

=

∑

∈ ∈

Maka x bukan imputasi karena tidak memenuhi kondisi (1) pada Definisi 1. Jika xf_{Sy, maka kedua kondisi berikut harus benar yaitu (Winston, 1994: 856):}

29 2. Karena x v

( )

S S i i ≤

∑

∈

, anggota S mendapat perolehan yang diberikan x

Kondisi (1) sesuai dengan kondisi (3) pada Definisi 2, sedangkan kondisi (2) menghendaki bahwa perolehan yang diberikan x cukup menjamin anggota S.

Definisi 2 (Thomas, 1984: 91) x dikatakan mendominasi y (xf_{y) jika x mendominasi y} untuk suatu koalisi S.

Jika terdapat dua imputasi dengan perolehan bagi beberapa pihak pada imputasi yang satu lebih besar daripada perolehan dari imputasi yang lain, maka pihak tersebut cenderung memilih imputasi yang paling menguntungkan baginya.

Berikut ini akan diberikan contoh mengenai dominasi dari imputasi. Contoh 5: Jika x =

(

1₂

)

2 1_, , 0 dan y =

(

₄1

)

4 1 2 1_{, ,}

Maka x mendominasi y untuk koalisi

{ }

2,3 karena 1

(

₂1

)

2 1_, , 0 f

(

)

4 1 4 1 2 1_{, ,} > >

Gambar 1. x mendominasi y untuk koalisi {2,3} Tetapi y tidak mendominasi x untuk koalisi

{ }

2,3 karena

(

4

)

1 4 1 2 1_{, , f}

(

)

2 1 2 1_, , 0 < <

Gambar 2. y tidak mendominasi x untuk koalisi {2,3}

E. PUSAT IMPUTASI (CORE)

Pusat imputasi merupakan salah satu konsep solusi yang penting untuk permainan kooperatif n-pihak, dan didefinisikan secara eksplisit oleh Gillies (1959). Konsep solusi ini didasarkan pada penggunaan ide dominasi dari imputasi.

30

kooperatif n-pihak, terlebih dahulu akan diberikan pengertian pusat imputasi. Pusat imputasi didefinisikan sebagai berikut.

Definisi 3. (Jones, 1980: 200) Himpunan semua imputasi yang tidak terdominasi pada permainan kooperatif n-pihak disebut pusat imputasi.

Pusat imputasi suatu permainan dengan fungsi karakteristik v dinotasikan dengan

( )

v

C .

Kerugian yang mungkin timbul dalam mencari solusi permainan kooperatif n-pihak dengan menggunakan konsep ini adalah pusat imputasi kosong.

Untuk lebih memahami konsep solusi di atas, akan diberikan sebuah contoh sebagai berikut.

Contoh 6:

Diketahui fungsi karakteristik dari permainan sebagai berikut:

( )

Ø = v v

( )

{}

1 =v

( )

{ }

2 =v

( )

{ }

3 =0

{ }

( )

1,2 = v v

( )

{ }

1,3 =v

(

{ }

2,3

)

=1

{ }

(

1,2,3

)

=1 v

Tentukan pusat imputasi dari permainan tersebut. Jawab:

Misalkan x =(x₁,x₂,x₃) merupakan pusat imputasi

Perolehan terbesar yang didapat jika semua pemain yaitu pemain 1, 2 dan 3 bekerjasama dalam satu koalisi adalah 1 yaitu

1

3 2

1+x +x =

x

Jika pemain 1 dan 2 bekerjasama dalam satu koalisi, maka perolehan yang didapat paling sedikit sebanyak 1 yaitu

1

2

1+x ≥

x

Jika pemain 1 dan 3 bekerjasama dalam satu koalisi, maka perolehan yang didapat paling sedikit sebanyak 1 yaitu

1

3

1+x ≥

x

Jika pemain 2 dan 3 bekerjasama dalam satu koalisi, maka perolehan yang didapat paling sedikit sebanyak 1 yaitu

1

3

2 +x ≥

31 1 2 1+x ≥ x mengakibatkan x₃ ≤0 1 3 1+x ≥ x mengakibatkan x₂ ≤0 1 3 2 +x ≥ x mengakibatkan x₁ ≤0

Kontradiksi dengan pengandaian bahwa x₁ +x₂ +x₃ =1.

Jadi tidak terdapat x =(x₁,x₂,x₃)∈C

( )

v dengan kata lain C

( )

v =Ø. F. NILAI SHAPLEY (SHAPLEY VALUE)

Terdapat konsep solusi alternatif lain untuk permainan kooperatif n-pihak, yaitu Nilai Shapley, yang dikemukakan oleh Lloyd Shapley (1953). Konsep ini memberikan solusi yang lebih adil dibandingkan pusat imputasi. Shapley melihat bahwa tiap pemain dapat membayangkan harapan perolehannya sebelum permainan dimulai. Menurut Shapley, ada tiga aksioma yang harus dipenuhi oleh suatu Φi

( )

v , dengan Φi

( )

v merupakan harapan perolehan pemain ke-i dalam permainan dengan fungsi karakteristik

v. Ketiga aksioma tersebut adalah:

S1 Φ_i

( )

v haruslah independen dari penomoran pemain. Jika

π

adalah permutasi

n

, , 2 ,

1 K dan

π

v adalah fungsi karakteristik dari permainan dengan nomor pemain telah dipermutasi oleh

π

, maka

( )i

( )

v =Φi

( )

v

Φπ π (1)

S2 Jumlah seluruh harapan perolehan pemain sama dengan harapan perolehan maksimum dalam permainan, jadi

( ) ( )

∑

∈ = Φ N i i v v N (2)

S3 Jika u,v adalah fungsi karakteristik dari dua permainan, u+v adalah fungsi karakteristik dari permainan yang dimainkan bersama-sama, maka Φ memenuhi:

(

u v

)

_i

( )

u _i

( )

v

i + =Φ +Φ

Φ (3)

Selanjutnya Shapley membuktikan bahwa terdapat satu fungsi yang memenuhi ketiga aksioma di atas, yang dituangkan dalam teorema berikut.

Teorema 1. (Thomas, 1984: 102) Hanya terdapat satu fungsi yang memenuhi S1, S2 dan S3 yaitu:

( )

∑

(

) (

) ( )

(

(

{}

)

)

∈ − − − = Φ S i S i v S v S i n S n S v : \ ! ! # ! 1 # (4)

32 pemain dalam koalisi S.

( )

v

i

Φ merupakan nilai Shapley. Contoh 7:

Diketahui fungsi karakteristik dari permainan sebagai berikut: v

( )

Ø = v

( )

{}

1 =v

( )

{ }

2 =v

( )

{ }

3 =0

{ }

( )

1,2 =

v v

( )

{ }

1,3 =v

(

{ }

2,3

)

=1

v

(

{ }

1,2,3

)

=1

Tentukan nilai Shapley dari permainan tersebut. Jawab:

( )

( )

( )

( )

3 1 1 1 ! 3 ! 0 ! 2 1 ! 3 ! 1 ! 1 1 ! 3 ! 1 ! 1 0 ! 3 ! 2 ! 0 1 = + + + − = Φ

Dengan sifat simetri, Φ1 =Φ2 =Φ3 = 13.