III PEMBAHASAN
3.1 Analisis Metode
Perhatikan persamaan integral Volterra berikut.
( ) ( ) ( , , ( )) x
a
y x = f x +λ
∫
K x t y t dt, (8) dengan y(x) merupakan fungsi yang akan ditentukan, a suatu konstanta, f(x) fungsi sembarang yang diketahui dan terdefinisi pada R, dan K(x,t,y(t)) suatu fungsi yang bentuknya tak linear dan bergantung pada variabel x, t, dan fungsi y(t). Berdasarkan bentuk fungsi K(x,t,y(t)), maka berikut ini akan dianalisis dua kasus.3.1.1 Kasus pertama
Fungsi K(x,t,y(t)) terdefinisi pada [ , ]a b . Selang [ , ]a b dibagi menjadi n selang bagian, yaitu
[
x x
i, i+1)
, i=0,1,2,3,...,n-1. Uraian deretTaylor fungsi K(x,t,y(t)) di sekitar titik (x t yn, ,n n)dengan y x( )n =yn adalah sebagai
berikut: ( , , ( )) ( , , ) ( , , ) ( ) ( , , ) ( ) ( , , ) ( ) . n n n n n n n n n n n n n n n K x t y t K x t y K x t y x x x K x t y t t t K x t y y y y = ∂ + − ∂ ∂ + − ∂ ∂ + − ∂ (9)
Jika persamaan (9) disubstitusikan ke persamaan (8) diperoleh : ( , , ) ( , , ) ( ) ( ) ( ) ( , , ) ( ) ( , , ) ( ) n n n n n n n x n n n n a n n n n K x t y K x t y x x x y x f x K x t y dt t t t K x t y y y y λ ⎡ ⎤ ⎢ ∂ ⎥ ⎢+ − ⎥ ⎢ ∂ ⎥ ⎢ ⎥ = + ⎢+ − ∂ ⎥ ∂ ⎢ ⎥ ⎢ ∂ ⎥ + − ⎢ ⎥ ∂ ⎢ ⎥ ⎣ ⎦
∫
(10) atau ( ) ( ) ( ) ( ) . ( ) x n n n n n n n a K x x J t t Q y x f x dt y y Z λ ⎡ + − + − ⎤ = + ⎢ ⎥ + − ⎣ ⎦∫
(11) dengan Kn = K x( n,tn,yn), ( n, n, n) n K x t y J x ∂ = ∂ , ( n, n, n) n K x t y Q t ∂ = ∂ , (12) ( , , ) . n n n n K x t y Z y ∂ = ∂Karena dalam integrand pada persamaan (11), t merupakan variabel bebas, y variabel tak bebas, dan x sebuah parameter, maka persamaan (11) dapat ditulis
[
]
(
)
( ) ( ) ( ) ( ) . x n a x n n n n n a x n n a y x f x Z y t dt K x x J Z y dt Q t t dt λ λ λ = + + + − − + −∫
∫
∫
(13)Jika integral pada persamaan (13) disederhanakan, maka diperoleh bentuk linear persamaan integral Volterra sebagai berikut.
2 2 1 ( ) ( ) ( ) ( ) ( ) ( ) 2 ( ) ; n n n n n n n n x n n n a K x x J y x f x x a Z y Q x t a t Z y t dt x x x λ λ λ + + − ⎡ ⎤ = + ⎢ ⎥ − − ⎣ ⎦ ⎡ ⎤ + ⎣ − − − ⎦ +
∫
≤ ≤ (14)Kemudian, jika kedua ruas pada persamaan (14) diturunkan terhadap x, maka diperoleh
'( ) '( ) (2 ) ( ) ( ) n n n n n n n n y x f x K x x a J Z y Q x x Z y x λ λ λ λ λ = + + − − − + − + (15)
atau (2 ) '( ) ( ) '( ) . ( ) n n n n n n n n K x x a J y x Z y x f x y Z Q x x λ λ⎡ + − − ⎤ − = + ⎢ ⎥ − + − ⎣ ⎦ (16)
Persamaan (16) merupakan persamaan differensial biasa orde satu dengan penyelesaian analitik dalam bentuk.
( ) ( ) ( ) exp( ) ( ) exp( ) 2 ( ) ( ) 1 1 ( ) exp( ( )) 2 ( ) 1 1 ( n x n n n n x n n n n n n n n n n n n n n n n n y x y x f x Z Z x f t Z t dt K x x x a J Z Z x t Q Z Z x x K x a J Z Z x t Z λ λ λ λ λ λ λ = + + − ⎧ ⎡ ⎤ ⎫ + − + − + ⎪ ⎢ ⎥ ⎪ ⎪ ⎣ ⎦ ⎪ − ⎨ ⎬ ⎪ + − + ⎪ ⎪ ⎪ ⎩ ⎭ + − + − + + − +
∫
( ) ) n n n f x Q ⎧ ⎡ ⎤ ⎫ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ − ⎪ ⎨ ⎢ ⎥ ⎬ ⎪ ⎢ ⎥ ⎪ ⎪ ⎣ ⎦ ⎪ ⎩ ⎭ (17) Dengan demikian untuk x=xn+1 diperoleh :1 1 1 1 1 1 1 ( ) ( ) ( ) exp( ) ( )exp( ) 2 ( ) ( ) 1 1 ( ) exp( ( n n n n n x n n n n x n n n n n n n n n n n n n y x y x f x Z Z x f t Z t dt K x x x a J Z Z x t Q Z Z x λ λ λ λ λ λ + + + + + + + = + + − ⎧ ⎡ ⎤ ⎫ + − + − + ⎪ ⎢ ⎥ ⎪ ⎪ ⎣ ⎦ ⎪ − ⎨ ⎬ ⎪ + − + ⎪ ⎪ ⎪ ⎩ ⎭ +
∫
1 )) 2 ( ) 1 ( ) 1 ( ) n n n n n n n n n n n x K x a J Z f x Z x t Q Z λ +− ⎧ ⎡ + − + ⎤ ⎫ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ − ⎪ ⎨ ⎢ ⎥ ⎬ ⎪ ⎢ + − + ⎥ ⎪ ⎪ ⎣ ⎦ ⎪ ⎩ ⎭ (18) atau 1 1 1 1 1 1 1 1 exp( ) ( )exp( ) 2 ( ) ( ) 1 1 ( ) exp( ( )) 1 2 ( ) n n x n n n n n n n x n n n n n n n n n n n n n n n n n n y y f Z Z x f t Z t dt K x x x a J Z Z x t Q Z Z x x K x a J Z Z λ λ λ λ λ λ λ + + + + + + + + = + + − ⎧ ⎡ ⎤ ⎫ + − + − + ⎪ ⎢ ⎥ ⎪ ⎪ ⎣ ⎦ ⎪ − ⎨ ⎬ ⎪ + − + ⎪ ⎪ ⎪ ⎩ ⎭ + − + − +∫
1 ( ) ( ) n n n n n n x t Q f x Z ⎧ ⎡ ⎤ ⎫ ⎪ + − + − ⎪ ⎨ ⎢ ⎥ ⎬ ⎪ ⎣ ⎦ ⎪ ⎩ ⎭ (19) dengan yn =y x( n), dan fn= f x( n).Persamaan (19) merupakan pendekatan penyelesaian persamaan integral Volterra (8).
Untuk memudahkan dalam perhitungan, misalkan x0= , a tn = dan selang [ , ]xn a b
dibagi n dengan panjang selang bagian
1
n n
x x+ x
∆ = − . Jadi persamaan (19) dapat ditulis : 1 1 1 1 1 0 0 exp( ) ( )exp( ) 2 ( ) 1 1 ( ) 2 ( ) 1 exp( ) 1 n n x n n n n n n n x n n n n n n n n n n n n n n n y y f Z Z x f t Z t dt K x x x J Z Z x Q Z K x x J Z Z x f Z Q Z λ λ λ λ λ λ λ + + + + + = + + − ⎧ ⎡ ⎤ ⎫ + ∆ + − + ⎪ ⎢ ⎥ ⎪ ⎪ ⎣ ⎦ ⎪ − ⎨ ⎬ ⎪ + ∆ + ⎪ ⎪ ⎪ ⎩ ⎭ ⎡ + − + ⎤ ⎢ ⎥ ⎢ ⎥ + ∆ − ⎢ + ⎥ ⎢ ⎥ ⎣ ⎦
∫
( )xn ⎧ ⎫ ⎪ ⎪ ⎪ ⎪ ⎨ ⎬ ⎪ ⎪ ⎪ ⎪ ⎩ ⎭ (20) Jika diasumsikan selang [ , ]a b dibagi n sama panjang dengan panjang selang bagiann
x h
∆ = , maka xn=x0+nh, sehingga
persamaan (20) menjadi seperti berikut.
1 1 1 exp( 1) ( ) exp( ) 1 2 1 ( 2) ( ) 2 ( ) 1 exp( ) ( ) 1 ) n n x n n n n n n n x n n n n n n n n n n n n n n y y f Z Z x f t Z t dt K n h J h Q Z Z Z K nh J Z Z h f x Z Q Z λ λ λ λ λ λ λ + + = + + + + − ⎧ ⎡ ⎤ ⎫ ⎪ ⎪ − ⎨ +⎢ + + ⎥ + + ⎬ ⎪ ⎣ ⎦ ⎪ ⎩ ⎭ ⎧ ⎡ + + ⎤ ⎫ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ + ⎨ ⎢ ⎥− ⎬ ⎪ ⎢ + ⎥ ⎪ ⎪ ⎣ ⎦ ⎪ ⎩ ⎭
∫
(21) Aplikasi ke dalam perhitungan numerik membutuhkan nilai f(x), λ, Kn, Jn, Qn,Zndan h. Hasilnya berupa fungsi y=y(x). 3.1.2 Kasus kedua
Misalkan K(x,t,y(t)) memiliki titik singular di
x
n, maka formulasi yang diturunkan di atas tidak berlaku. Dalam kasus ini, misalkan fungsi K(x,t,y(t)) didekati dengan uraian deret Taylor di sekitar titik (xn+1,tn+1,yn) dengan( )n n y x =y, sebagai berikut: 1 1 1 1 1 1 1 1 1 1 ( , , ( )) ( , , ) ( , , ) ( ) ( , , ) ( ) ( , , ) ( ) n n n n n n n n n n n n n n n K x t y t K x t y K x t y x x x K x t y t t t K x t y y y y + + + + + + + + + + = ∂ + − ∂ ∂ + − ∂ ∂ + − ∂ (22)
Jika persamaan (22) disubstitusi ke dalam persamaan (8), kemudian dilakukan penyederhanaan seperti yang dilakukan pada penurunan persamaan (14), maka diperoleh persamaan berikut.
[
1 1 1 1]
2 2 1 1 1 1 1 ( ) ( ) ( ) ( ) ( ) ( ) 2 ( ) ; n n n n n n n n x n n n a y x f x K x x J Z y x a Q x t a t Z y t dt x x x λ λ λ + + + + + + + + + = + + − − − ⎡ ⎤ + ⎣ − − − ⎦ +∫
≤ ≤ (23) dengan Kn+1=K x( n+1,tn+1,yn), 1 1 1 ( n ,n , n) n K x t y J x + + + ∂ = ∂ , 1 1 1 ( n , n , n) n K x t y Q t + + + ∂ = ∂ , (24) 1 1 1 ( n ,n , n) n K x t y Z y + + + ∂ = ∂ ,Persamaan (23) merupakan persamaan differensial biasa orde satu. Jika kedua ruas persamaan (23) diturunkan, maka diperoleh penyelesaian analitik yang serupa dengan persamaan (16) seperti berikut.
1 1 1 1 1 1 1 1 1 1 1 1 ( ) ( ) ( ) exp( ) ( ) exp( ) (2 ) 2 1 1 ( ) exp( ( )) n n n n x n x n n n n n n n n n n y x y x f x Z Z x f t Z t dt x x a K J Z Z x t Q Z Z x x λ λ λ λ λ λ + + + + + + + + + + + + = + + − ⎧ ⎡ − − ⎤ ⎫ ⎪ +⎢ ⎥ ⎪ ⎪ ⎢ + ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ − ⎨ ⎣ ⎦ ⎬ ⎪ ⎪ ⎪ + − + ⎪ ⎪ ⎪ ⎩ ⎭ + −
∫
1 1 1 1 1 1 1 1 1 2 (2 ) ( ) ; 1 ( ) n n n n n n n n n n n K x x a J f x Z Z x t Q Z λ + + + + + + + + ⎧ ⎡ ⎤ ⎫ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ + − − + − ⎪ ⎢ ⎥ ⎨ ⎬ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ + − + ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎣ ⎦ ⎪ ⎩ ⎭ (25) Persamaan (25) merupakan pendekatan penyelesaian persamaan integral Volterra (15) dengan yn =y x( n) dan fn = f x( n).Untuk memudahkan dalam perhitungan, misalkan x0=a , tn+1=xn+1 dan selang [ , ]a b
dibagi n, dengan panjang selang bagian
1 n n x x+ x ∆ = − , diperoleh: 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 ( ) exp( ) ( ) exp( ) 1 2 ( ) 1 exp( n n n n n n n n x n x n n n n n n n y x y f Z Z x f t Z t dt K x x J Z Z Q Z λ λ λ λ λ λ + + + + + + + + + + + + + + = + + − ⎧ ⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ − ⎨+ − + ⎬ ⎪ ⎪ ⎪ ⎪ + ⎪ ⎪ ⎪ ⎪ ⎩ ⎭ +
∫
1 1 0 1 1 1 1 ) 1 2 ( ) ( ) 1 ( ) n n n n n n n n n n n n Z x K x x x J f x Z Z x Q Z λ + + + + + + ∆ ⎧ ⎡ ⎤ ⎫ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ + − ∆ − + − ⎪ ⎢ ⎥ ⎨ ⎬ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ + − ∆ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎣ ⎦ ⎪ ⎩ ⎭ (26) Jika diasumsikan selang [ , ]a b dibagi n sama panjang dengan panjang selang bagiann x h ∆ = , maka xn=x0+nh, sehingga persamaan (26) menjadi : 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 exp( ) ( ) exp( ) ( 1) 2 1 1 ( 1) 1 exp( ) 2 n n n n n n n n x n x n n n n n n n n n n y y f Z Z x f t Z t dt n h K J Z Z Q Z K n h Z h Z Z λ λ λ λ λ λ λ + + + + + + + + + + + + + + + + + = + + − ⎧ ⎛ + ⎞ ⎫ ⎪ +⎜ ⎟ ⎪ ⎪ ⎜+ ⎟ ⎪ ⎪ ⎜ ⎟ ⎪ − ⎨ ⎝ ⎠ ⎬ ⎪ ⎪ ⎪ + ⎪ ⎪ ⎪ ⎩ ⎭ − + + +
∫
1 1 1 ( ) 1 n n n n J f x Q Z + + + ⎧ ⎡ ⎤ ⎫ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ ⎛ ⎞ ⎥ ⎪ ⎪ ⎢ ⎜ ⎟ ⎥− ⎪ ⎨ ⎢ ⎜⎜ ⎟⎟ ⎥ ⎬ ⎪ ⎢ ⎝ ⎠ ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎪ ⎢ + ⎥ ⎪ ⎪ ⎢ ⎥ ⎪ ⎣ ⎦ ⎩ ⎭ (27) Aplikasi ke dalam perhitungan numerik membutuhkan nilai f(x), λ, Kn+1,Jn+1 ,1
n
Q+ ,Zn+1 dan h. Hasilnya berupa fungsi
y=y(x).
Untuk memahami kedua kasus yang diberikan di atas, maka berikut ini dibahas beberapa contoh aplikasi.
3.2 Aplikasi dan Hasil Numerik
Dalam bagian ini akan dibahas tiga contoh kasus. Contoh yang kedua dan keempat menjelaskan kasus pertama dari metode ini. Sedangkan contoh kasus yang ketiga menjelaskan kasus kedua dari metode ini.
Contoh 2. Tinjau persamaan integral Volterra berikut pada selang [0,1].
2 0 1 ( ) exp( ) (exp(2 ) 1) ( ) 2 x y x = x− x − +
∫
y t dt (28)Penyelesaian eksak dari persamaan integral (28) adalah
( ) exp( )
y x = x (29) Berikut ini akan ditentukan penyelesaian hampiran persamaan integral (28) dengan menggunakan metode yang diuraikan di atas. Oleh karena itu, misalkan
2 ( , , ) ( ) 1 ( ) exp( ) (exp(2 ) 1) 2 1 K x t y y t f x x x λ = = − − = (30)
Dengan demikian persamaan (15) memberikan bentuk linear persamaan integral Volterra dari persamaan (28) sebagai berikut.
2 0 1 ( ) exp( ) (exp(2 ) 1) 2 ( ) ; 2 x n n y x = x − x− −y x+ y
∫
y t dt xn≤ ≤x xn+1 (31)Kemudian persamaan (27) memberikan persamaan berikut.
1
1 1 1
1
1
exp( ) (exp(2 ) 1) exp(2 )( exp( )
2 2 2
1 1
exp(2 ) 1)) 2 exp(2 ) (exp( ) (exp(2 ) 1)) exp( 2 )
2 2 n n n n n n n n n x n n n n n x y y y x x y h x x y y x t t y t dt + + + + + = + − − + − + − +
∫
− − − (32)Persamaan (32) akan digunakan untuk menentukan hampiran penyelesaian persamaan (28). Dengan menggunakan software MATLAB akan ditentukan penyelesaian y(x) untuk nilai h yang berbeda. Untuk nilai h=0.1, h=0.01 dan h=0.01 dan beberapa nilai x pada [0,1] , diperoleh nilai y(x) seperti diberikan dalam Tabel 1.
Tabel 1. Penyelesaian numerik contoh 2
x h=0.1 h=0.01 h=0.001 0.0 1.000000 1.000000 1.000000 0.1 1.104800 1.105200 1.105200 0.2 1.220500 1.221400 1.221400 0.3 1.348100 1.349800 1.349900 0.4 1.488800 1.491800 1.491800 0.5 1.643700 1.648700 1.648700 0.6 1.814000 1.822000 1.822100 0.7 2.000500 2.013600 2.013800 0.8 2.203900 2.225300 2.225500 0.9 2.423300 2.459200 2.459600 1.0 2.655600 2.717600 2.718300 Berikut ini diberikan grafik penyelesaian eksak dan hampiran penyelesaian persamaan (28) dengan nilai h yang berbeda, yakni untuk h=0.1, h=0.01, dan h=0.001.
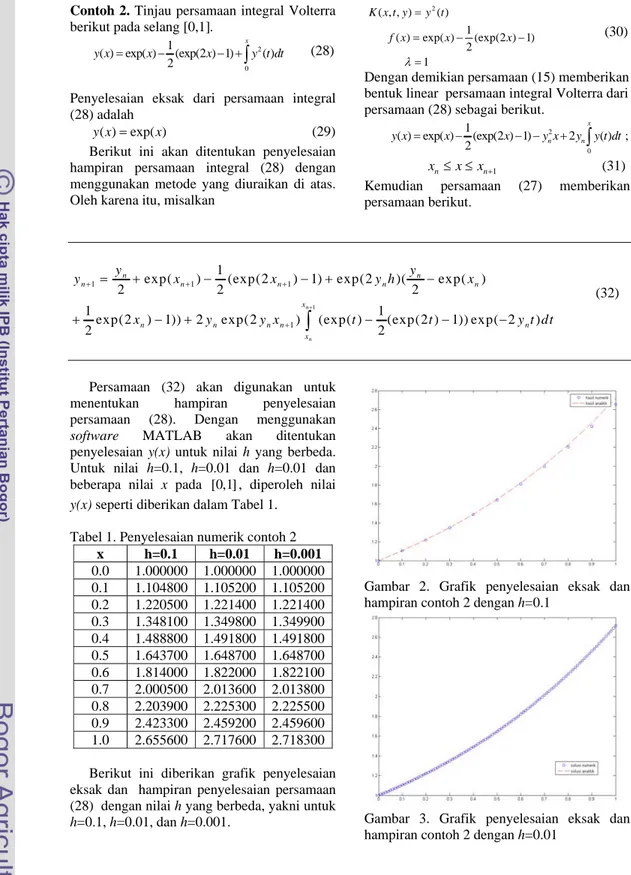
Gambar 2. Grafik penyelesaian eksak dan hampiran contoh 2 dengan h=0.1
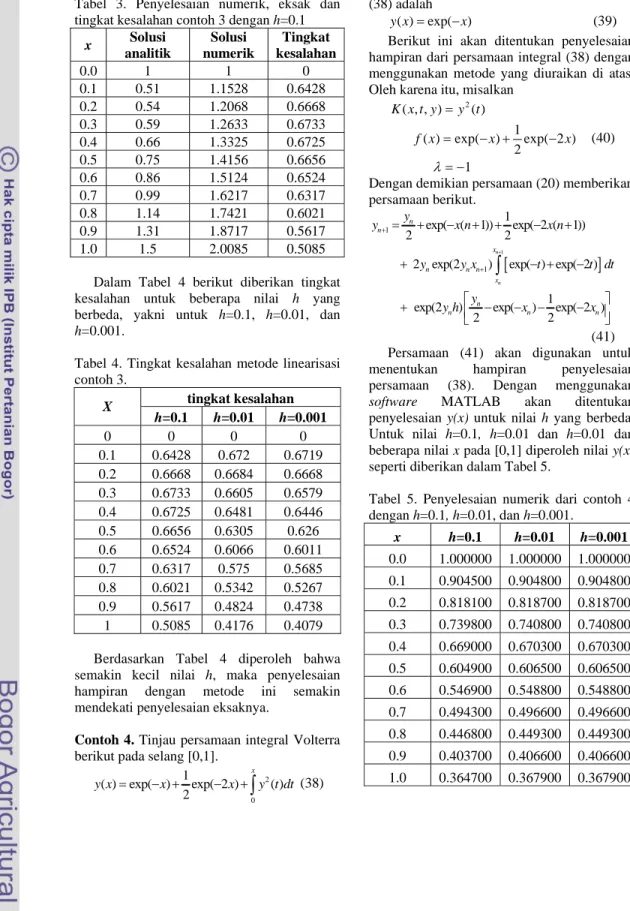
Gambar 3. Grafik penyelesaian eksak dan hampiran contoh 2 dengan h=0.01
Gambar 4. Grafik penyelesaian eksak dan hampiran contoh 2 dengan h=0.001
Gambar 2, 3, dan 4 memperlihatkan bahwa hampiran penyelesaian eksak akan cukup baik untuk h yang semakin kecil. Kesalahan yang ditimbulkan untuk pemilihan h yang berbeda-beda dapat dilihat pada Tabel 2.
Tabel 2. Tingkat kesalahan metode linearisasi contoh 2 x h=0.1 h=0.01 h=0.001 0.0 0 0 0 0.1 0.0004 0 0 0.2 0.0009 0 0 0.3 0.0018 0.0001 0 0.4 0.003 0 0 0.5 0.005 0 0 0.6 0.0081 0.0001 0 0.7 0.0133 0.0002 0 0.8 0.0216 0.0002 0 0.9 0.0363 0.0004 0 1.0 0.0627 0.0007 0
Tabel 2 menunjukkan bahwa semakin kecil h, penyelesaian hampiran semakin mendekati penyelesaian eksak, dengan kesalahan mendekati 0.
Contoh 3. Tinjau persamaan integral Volterra Hammerstein berikut pada selang [0,1].
4 2 2 0 5 3 1 ( ) ( ) 10 6 8 2 x x y x x y t dt x = − + + +
∫
(33) Titik singular dari persamaan integral (33) adalahx
0=
0
. Penyelesaian eksak dari persamaan integral (33) adalah2 1
( ) 2
y x =x + (34)
Berikut ini akan ditentukan penyelesaian hampiran dari persamaan integral (33) dengan menggunakan metode yang diuraikan di atas. Oleh karena itu, misalkan
2 4 2 1 ( , , ) ( ) 2 5 3 ( ) 10 6 8 1 K x t y y t x x f x x λ = = − + + = , (35)
Dengan demikian persamaan (23) memberikan bentuk persamaan integral Volterra linear dari persamaan (33) sebagai berikut.
2 4 2 1 1 1 1 1 0 5 3 ( ) [1 ] 10 6 8 2 ( ) ; n n n n x n n n n y x x x y x x x x x y y t dt x x x x + + + + + − = − + + − + +
∫
≤ ≤ (36) Kemudian persamaan (27) memberikan persamaan berikut. 1 4 4 2 2 1 1 1 1 1 ( 1) 5 11 5 3 ( ) (1 ) exp( ) (( ) exp( )) 2 10 6 8 10 6 8 n n x n n n n n n n n x n y n h x y t y y x x y t t dt x x x + + + + + + + = + − + + +∫
− + + − 4 2 1 1 ( 1) 5 11 exp( )( (1 ) ) 2 10 6 8 n n n n n n y y n h x h x x+ x+ − + − + − − (37)Persamaan (37) akan digunakan untuk menentukan penyelesaian numerik persamaan (33). Dengan menggunakan software MATLAB akan ditentukan penyelesaian y(x) untuk nilai h=0.1, dan beberapa nilai x pada [0,1].
Perhitungan MATLAB untuk penyelesaian eksak, penyelesaian numerik serta tingkat kesalahannya dengan nilai h=0.1 diberikan dalam Tabel 3.
Tabel 3. Penyelesaian numerik, eksak dan tingkat kesalahan contoh 3 dengan h=0.1
x Solusi analitik Solusi numerik Tingkat kesalahan 0.0 1 1 0 0.1 0.51 1.1528 0.6428 0.2 0.54 1.2068 0.6668 0.3 0.59 1.2633 0.6733 0.4 0.66 1.3325 0.6725 0.5 0.75 1.4156 0.6656 0.6 0.86 1.5124 0.6524 0.7 0.99 1.6217 0.6317 0.8 1.14 1.7421 0.6021 0.9 1.31 1.8717 0.5617 1.0 1.5 2.0085 0.5085
Dalam Tabel 4 berikut diberikan tingkat kesalahan untuk beberapa nilai h yang berbeda, yakni untuk h=0.1, h=0.01, dan h=0.001.
Tabel 4. Tingkat kesalahan metode linearisasi contoh 3. tingkat kesalahan X h=0.1 h=0.01 h=0.001 0 0 0 0 0.1 0.6428 0.672 0.6719 0.2 0.6668 0.6684 0.6668 0.3 0.6733 0.6605 0.6579 0.4 0.6725 0.6481 0.6446 0.5 0.6656 0.6305 0.626 0.6 0.6524 0.6066 0.6011 0.7 0.6317 0.575 0.5685 0.8 0.6021 0.5342 0.5267 0.9 0.5617 0.4824 0.4738 1 0.5085 0.4176 0.4079
Berdasarkan Tabel 4 diperoleh bahwa semakin kecil nilai h, maka penyelesaian hampiran dengan metode ini semakin mendekati penyelesaian eksaknya.
Contoh 4. Tinjau persamaan integral Volterra berikut pada selang [0,1].
2 0 1 ( ) exp( ) exp( 2 ) ( ) 2 x y x = − +x − x +
∫
y t dt (38)Penyelesaian eksak dari persamaan integral (38) adalah
( ) exp( )
y x = −x (39)
Berikut ini akan ditentukan penyelesaian hampiran dari persamaan integral (38) dengan menggunakan metode yang diuraikan di atas. Oleh karena itu, misalkan
2 ( , , ) ( ) 1 ( ) exp( ) exp( 2 ) 2 1 K x t y y t f x x x λ = = − + − = − (40)
Dengan demikian persamaan (20) memberikan persamaan berikut.
[
]
1 1 1 1 exp( ( 1)) exp( 2 ( 1)) 2 22 exp(2 ) exp( ) exp( 2 ) 1
exp(2 ) exp( ) exp( 2 )
2 2 n n n n x n n n x n n n n y y x n x n y y x t t dt y y h x x + + + = + − + + − + + − + − ⎡ ⎤ + ⎢ − − − − ⎥ ⎣ ⎦
∫
(41) Persamaan (41) akan digunakan untuk menentukan hampiran penyelesaian persamaan (38). Dengan menggunakan software MATLAB akan ditentukan penyelesaian y(x) untuk nilai h yang berbeda. Untuk nilai h=0.1, h=0.01 dan h=0.01 dan beberapa nilai x pada [0,1] diperoleh nilai y(x) seperti diberikan dalam Tabel 5.Tabel 5. Penyelesaian numerik dari contoh 4 dengan h=0.1, h=0.01, dan h=0.001. x h=0.1 h=0.01 h=0.001 0.0 1.000000 1.000000 1.000000 0.1 0.904500 0.904800 0.904800 0.2 0.818100 0.818700 0.818700 0.3 0.739800 0.740800 0.740800 0.4 0.669000 0.670300 0.670300 0.5 0.604900 0.606500 0.606500 0.6 0.546900 0.548800 0.548800 0.7 0.494300 0.496600 0.496600 0.8 0.446800 0.449300 0.449300 0.9 0.403700 0.406600 0.406600 1.0 0.364700 0.367900 0.367900
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0.4 0.5 0.6 0.7 0.8 0.9 1
Berikut ini diberikan grafik penyelesaian eksak dan hampiran persamaan (38) yakni untuk h=0.1 dan h=0.01.
• numerik -- analitik
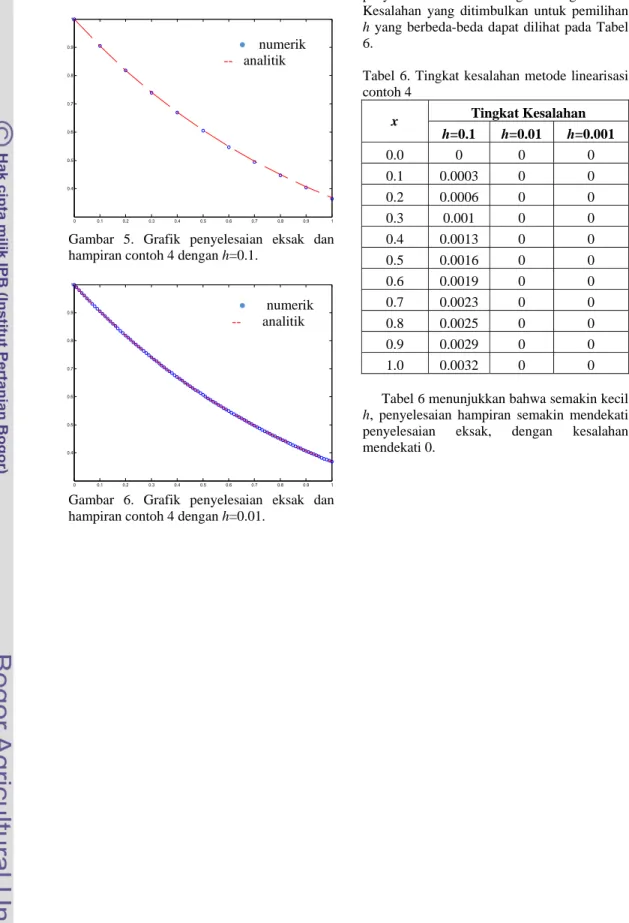
Gambar 5. Grafik penyelesaian eksak dan hampiran contoh 4 dengan h=0.1.
• numerik -- analitik
Dari Gambar 5 dan 6 terlihat bahwa penyelesaian hampiran mendekati penyelesaian eksak dengan sangat baik. Kesalahan yang ditimbulkan untuk pemilihan h yang berbeda-beda dapat dilihat pada Tabel 6.
Tabel 6. Tingkat kesalahan metode linearisasi contoh 4 Tingkat Kesalahan x h=0.1 h=0.01 h=0.001 0.0 0 0 0 0.1 0.0003 0 0 0.2 0.0006 0 0 0.3 0.001 0 0 0.4 0.0013 0 0 0.5 0.0016 0 0 0.6 0.0019 0 0 0.7 0.0023 0 0 0.8 0.0025 0 0 0.9 0.0029 0 0 1.0 0.0032 0 0
Tabel 6 menunjukkan bahwa semakin kecil h, penyelesaian hampiran semakin mendekati penyelesaian eksak, dengan kesalahan mendekati 0.
Gambar 6. Grafik penyelesaian eksak dan hampiran contoh 4 dengan h=0.01.