LAPORAN AKHIR
PENELITIAN DOSEN INTERNAL PT
NILAI EIGEN, VEKTOR EIGEN, DAN EIGENMODE DARI
MATRIKS TEREDUKSI DAN APLIKASINYA
EIGENVALUE, EIGENVECTOR, AND EIGENMODE OF REDUCIBLE
MATRIX AND ITS APPLICATION
Pelaksana:
Himmatul Mursyidah, S.Si., M.Si., NIDN: 0711029101
Dr. Subiono, M.S., NIDN: 0011045706
UNIVERSITAS MUHAMMADIYAH SURABAYA
2017
Judul Peneliti/Pelal<sana Nama
Ketua
: PerguruanTinggi
..NIDN
: JabatanFungsional
: ProgramStudi
:Alamat surel (e-mail) :
Nama Anggota
(l)
: PeryuruanTinggi
:MDN
: JabatanFungsional
: PrograrnStudi
: Nama Mahasiswa (1) : PerguruanTinggi
: ProgramStudi
:Nama Mahasiswa (2)
:
Cruschi tal-evyana ZylvyP_erguruan
Tinggi :
Universitas Muhammadiyah SurabayaNIM
:
20141112002Program
Studi
:
pendidikan MatemalikaInstitusi Mitra (Jika ada)
Nama Institusi
Mitra
:
-Alamat
:
-PenanggungJawab
:
-Tahun Pelaksanaan
:
2016 -2017Biaya
Keseluruhan
:
Rp 10.000.000 ul,Keguruan Ilmu Pendidikan
HALAMAN PENGESAHAN
Nilai
Eigen,Vehor
Eigen, dan Eigenmodedari
Matriks Tereduksi dan Aplikasinya @igmvalue, Eigenvector, and Eigenmode oJ-Reducible Matrix and lts Apptication)Himmatul Mursyidah, S.Si., M.Si.
Universitas Muhammadilah Surabaya
071 1029101
Pendidikan Matematika 085646626056
himmatul.pen&nat@fkip.um-surabaya.ac.id
Dr. Subiono, M.S.
In-stitut Teknologi Sepuluh Nopember Surabaya 001 1045706
Lektor Kepala Matematika Hadi Harianto
Universitas Muhammadiyah Surabaya
20131t12020 Pendidikan Matematika endarwati, , M.Pd.) 012.02.t .t97 s.12.06t Surabaya, 19 Juni 2017 Ketua,
(Himmatul Mursfldah, S.Si , M.Si.) NIK. 012.02.1. | 991.16.208 UMSurabaya, , M.Pd.) e o yetujui, z ? Ina s Men 1965.90 004 ll
iii RINGKASAN
. Terdapat tiga komponen penting dari matriks yang harus diketahui dan dipahami dalam proses menyelesaikan masalah penjadwalan menggunakan aljabar max-plus. Komponen tersebut meliputi nilai eigen, vektor eigen, dan eigenmode. Hasil penelitian menunjukkan bahwa matriks tereduksi tidak harus memiliki nilai eigen. Jika matriks memiliki nilai eigen, maka nilai eigen tidak harus tunggal dengan nilai-nilai yang berhingga. Adapun vektor eigen yang bersesuaian dengan nilai eigen dari matriks tereduksi juga tidak harus tunggal, dan memuat paling tidak satu elemen berhingga. Lebih lanjut, eigenmode dari matriks tereduksi regular tidak tunggal, dengan semua elemen berhingga.
iv KATA PENGANTAR
Puji syukur kehadirat Allah SWT yang telah memberikan rahmat, nikmat, dan petunjuk-Nya sehingga laporan akhir Penelitian Dosen Internal PT yang dibiayai oleh Universitas Muhammadiyah Surabaya dengan judul “Nilai Eigen, Vektor Eigen, dan Eigenmode dari Matriks Tereduksi dan Aplikasinya (Eigenvalue, Eigenvector, and Eigenmode of Reducible Matrix and Its Application)”, dapat terselesaikan dengan baik dan lancar tanpa ada halangan suatu apapun. Meskipun berada pada home base pendidikan matematika Universitas Muhammadiyah Surabaya (UMSurabaya), peneliti bersyukur mendapat dukungan dari pihak universitas sehingga dapat melakukan penelitian pada lingkup matematika murni dan aplikasinya bekerjasama dengan peneliti dari institusi lain. Pada penelitian ini, peneliti juga dibantu oleh mahasiswa pendidikan matematika yang mengambil kosentrasi matematika murni dan ilmu komputer.
Luaran dari penelitian ini adalah berupa hasil kajian teori, contoh pengaplikasian teori matematika terkait aljabar max-plus pada kehidupan sehari-hari yang ditulis dalam karya ilmiah (artikel) dan dipublikasikan dalam seminar internasional dan prosiding international terindeks bereputasi. Tersusunnya Laporan akhir ini tidak terlepas dari bantuan berbagai pihak, terutama Lembaga Penelitian dan Pengabdian Masyarakat (LPPM) UMSurabaya dan semua pihak yang tidak dapat disebutkan satu persatu, kiranya penulis sampaikan terima kasih.
Menyadari bahwa seiring perkembangan zaman, sebuah karya akan mengalami perkembangan. Penulis selalu mengharapkan kritik dan saran yang dapat memberikan motivasi bagi peneliti. Pembaca dapat menjadikan artikel yang telah disusun sebagai bahan kajian maupun sebagai bahan acuan daftar pustaka.
v DAFTAR ISI HALAMAN SAMPUL ... i HALAMAN PENGESAHAN ... ii RINGKASAN ... iii KATA PENGANTAR ... iv DAFTAR ISI ... v BAB I PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Fokus Penelitian ... 2
BAB II TINJAUAN PUSTAKA ... 3
A. Aljabar Max-Plus ... 3
B. Graf dalam Aljabar Max-Plus ... 4
C. Nilai Eigen, Vektor Eigen, dan Eigenmode dalam Aljabar Max-Plus ... 6
D. Algoritma untuk Menentukan Nilai Eigen, Vektor Eigen, dan Eigenmode dalam Aljabar Max-Plus ... 7
BAB III TUJUAN DAN MANFAAT PENELITIAN ... 9
A. Tujuan Penelitian ... 9
B. Manfaat Penelitian ... 9
BAB IV METODE PENELITIAN ... 10
BAB V HASIL DAN LUARAN YANG DICAPAI ... 12
A. Hasil yang Dicapai ... 12
B. Luaran yang Dicapai ... 12
BAB V KESIMPULAN DAN SARAN ... 13
A. Kesimpulan ... 13
B. Saran ... 13
DAFTAR PUSTAKA ... 14
LAMPIRAN ... 15
Lampiran 1 Artikel yang Telah Diseminarkan... 15
Lampiran 2 Sertifikat Seminar International... 26
1 BAB I
PENDAHULUAN
A. Latar Belakang
Salah satu aplikasi aljabar max-plus adalah untuk menyelesaikan masalah sistem penjadwalan. Suatu sistem dapat dipandang sebagai kumpulan dari beberapa sumber yang dapat digunakan oleh banyak pengguna untuk mencapai tujuan bersama (Subiono, 2012). Aktivitas dari masing-masing sumber dapat ditentukan awal dan akhirnya dengan menggunakan aljabar max-plus, sehingga dapat dilakukan sinkronisasi dan konkurensi untuk berbagai sumber pada suatu sistem.
Aplikasi aljabar max-plus berkaitan dengan suatu graf berarah 𝒢 = 𝒩,𝒟 , dengan 𝒩 adalah suatu himpunan dari seluruh titik dan 𝒟 adalah himpunan dari beberapa pasangan terurut (tidak harus berbeda) dari titik-titik, yang selanjutnya disebut arc. Dalam suatu sistem, sumber dapat dipandang sebagai titik, dan proses perpindahan dari satu sumber ke sumber yang lain dapat dipandang sebagai suatu arc. Untuk melakukan sinkronisasi dan konkurensi sumber-sumber yang ada, perlu ditentukan lama dari masing proses. Lebih lanjut, lama dari masing-masing proses dapat disebut sebagai bobot dari arc. Terdapat dua jenis graf dalam aljabar max-plus, yaitu graf terhubung kuat dan graf tidak terhubung kuat. Suatu graf dikatakan terhubung kuat jika untuk setiap titik terhubung (communicate) satu sama lain. Matriks representasi dari suatu graf terhubung kuat disebut matriks tidak tereduksi (Heidergott, Olsder, & van der Woude, 2006). Sementara itu, ketika terdapat suatu titik yang tidak terhubung (tidak communicate) dengan titik lain, graf tersebut merupakan graf tidak terhubung kuat dan matriks representasinya disebut sebagai matriks tereduksi.
Dalam proses menyelesaikan masalah penjadwalan dengan menggunakan aljabar max-plus, terdapat komponen-komponen penting yang berhubungan dengan matriks, yaitu nilai eigen, vektor eigen, dan eigenmode. Nilai eigen merepresentasikan keperiodikan dari suatu sistem. Vektor eigen merepresentasikan waktu awal untuk setiap sumber dari suatu sistem. Adapun eigenmode menunjukkan perilaku periodik dari suatu sistem.
2 Selama ini, penelitian mengenai nilai eigen, vektor eigen, dan eigenmode dalam aljabar max-plus banyak terfokus pada algoritma untuk memperoleh komponen-komponen tersebut. Hal tersebut dapat dilihat dalam (Konigsberg, 2009) dan (Zuliyanto, Siswanto, & Muslich, 2012), keduanya membahas tentang hasil penelitian algoritma eigenmode tergeneralisasi untuk matriks tereduksi regular dalam aljabar max-plus. Sedangkan untuk mengimplementasikan algoritma tersebut, perlu memahami karakter tiga komponen sesuai dengan jenis representasi matriks terlebih dahulu.
Berdasarkan peran penting nilai eigen, vektor eigen, dan eigenmode, serta penelitian yang telah dilakukan. Perlu dilakukan penelitian mengenai karakterisasi nilai eigen, vektor eigen, dan metode eigen terutama untuk matriks tereduksi. Selain karakterisasi dari ketiga komponen, juga perlu dilakukan penelitian mengenai contoh aplikasi penggunaan hasil karakterisasi ketiga komponen tersebut dalam menyelesaikan permasalahan pada kehidupan sehari-sehari, salah satunya pada masalah antrian.
B. Fokus Penelitian
Fokus dalam penelitian ini adalah melakukan karakterisasi nilai eigen, vektor eigen, dan eigenmode dari matriks tereduksi dalam aljabar max-plus. Selanjutnya, dari hasil karakterisasi tersebut dilakukan penelitian kegunaan hasil karakterisasi dalam menyelesaikan permasalahan antrian pada kehidupan sehari-hari.
3 BAB II
TINJAUAN PUSTAKA
A. Aljabar Max-Plus
Pada bagian ini diberikan konsep yang berhubungan dengan aljabar max-plus, yang meliputi definisi, operasi, dan sifat-sifat dari aljabar max-max-plus, graf dalam aljabar max-plus, nilai eigen, vektor eigen, dan eigenmode dalam alajabr max-plus, serta algoritma untuk menentukan ketiga komponen tersebut.
Definisi 1 (Baccelli, Cohen, & Olsder, 2001) Aljabar max-plus adalah suatu himpunan tidak kosong ℝε ≔ ℝ ∪ ε dengan ℝ adalah himpunan bilagan real,ε ≔ −∞, dan dua operasi biner didefinisikan sebagai berikut:
1. Operasi ⊕, yaitu ∀𝑥,𝑦 ∈ ℝε memenuhi
𝑥 ⊕ 𝑦 ≔max 𝑥 ,𝑦 2. Operasi ⊗, yaitu ∀𝑥,𝑦 ∈ ℝε memenuhi
𝑥 ⊗ 𝑦 ≔ 𝑥+𝑦.
Aljabar max-plus dinotasikan dengan ℝε,⊕,⊗ atau secara ringkas dapat ditulis ℝmax adalah semiring (Subiono, 2012). Himpunan matriks berukuran
𝑛×𝑚 pada ℝmax dinotasikan dengan ℝmaxn×m. Suatu matriks pada ℝ max
n×m disebut
regular jika matriks tersebut memuat sedikitnya satu elemen berbeda dari ε untuk setiap baris. Terdapat dua bentuk matriks dalam ℝmaxn×m yang harus dipahami, yaitu
matriks ℇ 𝑛,𝑚 dan 𝐸 𝑛,𝑚 . Matriks ℇ 𝑛,𝑚 adalah matriks berukuran 𝑛×𝑚 dengan seluruh elemen-elemennya sama dengan ε. Adapun matriks 𝐸 𝑛,𝑚 adalah matriks berukuran 𝑛×𝑚 dengan
𝐸 𝑛,𝑚 𝑖,𝑗 ≔
𝑒 untuk 𝑖=𝑗, ε untuk 𝑖 ≠ 𝑗.
dan 𝑒= 0. Jika 𝑚=𝑛, maka 𝐸 adalah suatu matriks persegi dan disebut sebagai matriks identitas.
Elemen-elemen dari ℝmaxn ≔ ℝmaxn×1 disebut vektor. Elemen ke-𝑗 dari suatu
4 ℝmaxn yang semua elemennya sama dengan 𝑒 disebut vektor satuan dan
dinotasikan dengan 𝐮.
B. Graf dalam Aljabar Max-Plus
Aplikasi aljabar max-plus sangat erat kaitannya dengan graf berarah yang dinotasikan 𝒢 = 𝒩,𝒟 , dengan 𝒩 adalah himpunan seluruh titik dan 𝒟 adalah himpunan beberapa pasangan terurut titik-titik (tidak harus berbeda). Pasangan terurut titik-titik pada graf disebut arc. Oleh karena itu, jika titik 𝑖,𝑗 ∈ 𝒩 maka arc dari 𝑖 ke 𝑗 dinotasikan dengan 𝑗,𝑖 . Suatu graf dapat direpresentasikan sebagai suatu matriks persegi dalam aljabar max-plus. Graf yang berkorespondesi dengan suatu matriks persegi 𝐴 pada ℝmax disebut graf komunikasi
(communication graph), dan dinotasikan dengan 𝒢 𝐴 . Misal diberikan 𝐴 ∈ ℝmaxn×n, elemen 𝑎
𝑖,𝑗 ≠ ε jika terdapat suatu arc dari titik 𝑗 ke titik 𝑖 pada 𝒢 𝐴 . Istilah lintasan (path) dalam suatu graf didefinisikan sebagai suatu barisan arc yang merepresentasikan keterhubungan antara suatu titik dengan titik yang lain. Suatu lintasan disebut elementer jika tidak terdapat titik yang muncul lebih dari satu kali pada lintasan tersebut. Suatu sirkuit adalah suatu lintasan elementer tertutup, yang mempunyai suatu titik asal sama dengan titik akhir. Diberikan suatu lintasan 𝑝, bobot dari lintasan tersebut dinotasikan dengan 𝑝 𝑤 adalah jumlahan dari bobot untuk setiap arc pada lintasan 𝑝. Panjang lintasan 𝑝 adalah jumlah arc pada lintasan tersebut., yang dinotasikan dengan 𝑝 𝑙. Bobot rata-rata dari lintasan 𝑝 adalah bobot dibagi dengan panjang lintasan.
Sirkuit rata-rata adalah bobot rata-rata dari suatu sirkuit. Suatu sirkuit yang mempunyai sirkuit rata-rata maksimum disebut dengan sirkuit kritis. Graf kritis dari 𝒢 𝐴 dinotasikan dengan 𝒢𝑐 𝐴 = 𝒩𝑐 𝐴 ,𝒟𝑐 𝐴 adalah suatu graf yang terdiri himpunan titik dan arc pada sirkuit kritis dari 𝒢 𝐴 . Graf dan matriks representasinya saling terkait satu sama lain. Kondisi dari suatu graf dapat diketahui berdasarkan matriks representasinya, begitu pula sebaliknya. Sebagai contoh, panjang lintasan dari suatu graf berkaitan dengan pangkat dari matriks representasinya.
5 Teorema 2 (Heidergott, Olsder, & van der Woude, 2006) Misal 𝐴 ∈ ℝmaxn×n. Untuk
setiap 𝑘 ≥1 berlaku
𝐴⊗𝑘
𝑖,𝑗 = max 𝑝 𝑤 ∶ 𝑝 ∈ 𝑃 𝑗,𝑖;𝑘 , dengan 𝐴⊗𝑘
𝑖,𝑗 = ε pada kasus dengan 𝑃 𝑗,𝑖;𝑘 adalah kosong, yaitu ketika tidak ada path dengan panjang 𝑘 dari 𝑖 ke 𝑗 dalam graf 𝒢 𝐴 .
Lebih lanjut, dapat didefinisikan matriks 𝐴+ dari Teorema 2, yaitu
𝐴+≔ 𝐴⊗𝑘 ∞
𝑘=1
Matriks 𝐴⊗𝑘 berhenti untuk 𝑘 =𝑛. Hal tersebut diberikan pada teorema berikut.
Teorema 3 (Subiono, 2012)Diberikan 𝐴 ∈ ℝmaxn×n sedemikian hingga untuk setiap sirkuit pada graf 𝒢 𝐴 mempunyai bobot sirkuit rata-rata kurang dari sama dengan 𝑒. Sehingga berlaku
𝐴+≔ 𝐴 ⊕ 𝐴⊗2⊕ … ⊕ 𝐴⊗𝑛 ∈ ℝ
max n×n
Terdapat dua jenis graf berdasarkan sifat keterhubungannya, yaitu graf terhubung kuat dan tidak terhubung kuat. Sebelum diberikan definisi dari masing-masing graf, diberikan terlebih dahulu penjelasan mengenai istilah keterjangkauan dan communicate. Untuk setiap dua buah titik 𝑖,𝑗 ∈ 𝒩, titik 𝑖 communicate dengan titik 𝑗, dinotasikan dengan 𝑗𝐶𝑖, jika dan hanya jika 𝑖=𝑗 atau titik 𝑖 terjangkau dari titik 𝑗 dan titik 𝑗 terjangkau dari titik 𝑖. Relasi 𝐶 adalah relasi ekuivalen pada 𝒩.
Suatu graf disebut terhubung kuat jika setiap titik dalam graf tersebut communicate satu sama lain, yaitu untuk setiap 𝑖,𝑗 ∈ 𝒩 memenuhi 𝑖𝐶𝑗. Suatu matriks pada ℝmaxn×n yang merepresentasikan suatu graf terhubung kuat disebut
matriks tak tereduksi. Lebih lanjut, matrik tak tereduksi adalah matriks yang tidak dapat dikontruksi menjadi matriks segitiga atas.
Jika terdapat suatu titik yang tidak communicate dengan titik lain dalam suatu graf, maka graf tersebut disebut graf tidak terhubung kuat. Suatu matriks pada ℝmaxn×n yang merepresentasikan graf tidak terhubung kuat disebut matriks
6 tereduksi. Lebih lanjut, matriks tereduksi adalah matriks yang dapat dibentuk menjadi matriks blok segitiga atas. Suatu matriks blok segitiga atas terdiri dari matriks ℰ dan matriks tak tereduksi. Matriks blok segitiga atas merepresentasikan graf tereduksi. Graf tereduksi adalah suatu hasil reduksi dari graf tidak terhubung kuat.
C. Nilai Eigen, Vektor Eigen, dan Eigenmode dalam Aljabar Max-Plus Dalam aplikasi aljabar max-plus terdapat tiga komponen penting yang berhubungan dengan matriks. Tiga komponen tersebut adalah nilai eigen, vektor eigen, dan eigenmode.
Definisi 4 (Heidergott, Olsder, & van der Woude, 2006) Diberikan suatu matriks persegi 𝐴 ∈ ℝmaxn×n. Jika 𝜇 ∈ ℝmax adalah suatu scalar dan 𝐯 ∈ ℝmaxn adalah
suatu vektor yang memuat minimal satu elemen berhingga sedemikian hingga 𝐴 ⊗ 𝐯=𝜇 ⊗ 𝐯,
maka 𝜇 disebut nilai eigen dari matriks 𝐴 dan 𝐯 merupakan vektor eigen dari matriks 𝐴 yang bersesuaian dengan nilai eigen𝜇.
Misal 𝐶 𝐴 adalah himpunan dari semua sirkuit pada 𝒢 𝐴 . Sirkuit rata-rata maksimum dinotasikan dengan 𝜆 didefinisikan sebagai
𝜆 ≔max 𝑃 𝑤 𝑃 ℓ 𝑃∈𝐶(𝐴)
Jika rata-rata maksimum dari graf 𝒢 𝐴 yaitu 𝜆 mempunyai suatu nilai berhingga, maka 𝜆 adalah nilai eigen dari matriks 𝐴. Sedangkan kolom 𝐴𝜆∗ .,𝜂 adalah vektor eigen dari matriks 𝐴 yang berasosiasi/bersesuaian dengan nilai eigen 𝜆. Pernyataan tersebut sesuai dengan Lemma 5.
Lemma 5 (Heidergott, Olsder, & van der Woude, 2006) Diberikan graf komunikasi 𝒢 𝐴 dari matriks 𝐴 ∈ ℝmaxn×n yang mempunyai bobot sirkuit rata-rata
maksimal berhingga 𝜆. Skalar 𝜆 adalah suatu nilai eigen dari 𝐴, dan kolom 𝐴𝜆∗
.,𝜂 adalah vektor eigen dari 𝐴 yang bersesuaian dengan 𝜆, untuk setiap titik 𝜂 ∈ 𝒢𝐶 𝐴 .
7 Pada proses penyelesaian masalah penjadwalan, sangat berkaitan dengan upaya mendapatkan barisan 𝐱 𝑘 ∶ 𝑘 ∈ ℕ dari model persamaan linear berikut,
𝐱 𝑘+ 1 = 𝐴 ⊗ 𝐱 𝑘 , (1)
Untuk 𝑘 ≥0, dengan 𝐴 ∈ ℝmaxn×n dan 𝐱 0 = 𝐱0 ∈ ℝmaxn adalah kondisi awal.
Definisi dari eigenmode tergeneralisasi diberikan pada berikut.
Definisi 6 (Heidergott, Olsder, & van der Woude, 2006) Pasangan vektor 𝜂,𝐯 ∈ ℝn ×ℝn disebut eigenmode tergeneralisasi dari matriks regular 𝐴 jika untuk setiap 𝑘 ≥0
𝐴 ⊗ 𝑘×𝜂+𝐯 = 𝑘+ 1 ×𝜂 +𝐯.
Perlu diketahui, eigenmode tergeneralisasiselanjutnya disebut sebagai eigenmode.
D. Algoritma untuk Menentukan Nilai Eigen, Vektor Eigen, dan Eigenmode
dalam Aljabar Max-Plus
Terdapat algoritma untuk mendapatkan nilai eigen, vektor eigen dan eigenmode dari matriks tereduksi reguler.
Algoritma 7Algoritma Power (Subiono, 2012) 1. Ambil sebarang vektor awal 𝐱 0 ≠ 𝐮 ε .
2. Iterasi persamaan (1) sampai terdapat bilangan-bilangan bulat 𝑝> 𝑞 ≥0 dan suatu bilangan real 𝑐, sedemikian hingga suatu bentuk periodic terpenuhi, yaitu
𝐱 𝑝 =𝑐 ⊗ 𝐱 𝑞 . 3. Hitung nilai eigen
𝜆= 𝑐
𝑝 − 𝑞. 4. Hitung vektor eigen
𝐯= 𝜆⊗ 𝑝−𝑞−𝑖 ⊗ 𝐱 𝑞+𝑖 −1
𝑝−𝑞
𝑖=1
8 Algoritma 8 Algoritma Eigenmode Tergeneralisasi untuk Matriks Tereduksi Reguler (Konigsberg, 2009)
1. Ambil matriks tereduksi regular 𝐴 ∈ ℝmaxn×n.
2. Tentukan suatu matriks blok segitiga atas dari matriks 𝐴.
3. Hitung nilai eigen dan vektor eigen matriks blok pada diagonal utama dari matriks blok segitiga atas. Misal 𝐴𝑞,𝑞, hitung nilai eigen 𝜆𝑞 = 𝜆 𝐴𝑞,𝑞 dan vektor eigen 𝐯𝑞 yang bersesuaian dengan nilai eigen. Kemudian, ambil 𝜉𝑞 =𝜆𝑞 dan 𝑖= 𝑞.
4. Hitung nilai eigen 𝜆 𝑖−1 dari matriks 𝐴 𝑖−1, 𝑖−1 .
5. Jika 𝜆 𝑖−1 >𝜉𝑖 lanjutkan langkah 6. Jika tidak, lanjutkan langkah 7. 6. Tentukan 𝜉𝑖−1 = 𝜆𝑖−1 dan hitung vektor 𝐯𝑖−1 sesuai persamaan berikut:
𝜉𝑖−1⊗ 𝐯𝑖−1 = 𝐴 𝑖−1 ,(𝑖−1)⊗ 𝐯(𝑖−1)⊕ 𝐴 𝑖−1,𝑗 ⊗ 𝐯𝑗. 𝑞
𝑗=1
Selanjutnya, lakukan langkah 8.
7. Tentukan 𝜉𝑖−1 = 𝜆𝑖 dan hitung vektor 𝐯𝑖−1 sesuai persamaan berikut: 𝜆𝑖 ⊗ 𝐯𝑖−1= 𝐴 𝑖−1 ,(𝑖−1)⊗ 𝐯(𝑖−1)⊕ 𝐴 𝑖−1 ,𝑗 ⊗ 𝐯𝑗.
𝑞
𝑗=1
Selanjutnya, lakukan langkah 8.
8. Jika 𝑖 −1≠ 1 kembali ke langkah 4. Jika tidak, selesai.
9 BAB III
TUJUAN DAN MANFAAT PENELITIAN
A. Tujuan Penelitian
Tujuan dilakukan penelitian ini meliputi:
1. Mendapatkan karakterisasi ketiga komponen penting, yaitu nilai eigen, vektor eigen, dan eigenmode dari matriks tereduksi dalam aljabar max-plus sehingga mempermudah pengaplikasiannya dalam menyelesaikan masalah antrian di kehidupan sehari-hari.
2. Memberikan contoh kegunaan hasil karakterisasi nilai eigen, vektor eigen, dan eigenmode dari matriks tereduksi dalam aljabar max-plus untuk menyelesaikan masalah antrian, dan dituliskan dalam artikel ilmiah.
B. Manfaat Penelitian
Manfaat penelitian yang dilakukan adalah
1. Bagi peneliti, dapat menambah wawasan dan pengalaman peneliti dalam proses karakterisasi sehingga lebih lanjut dapat dilakukan penelitian dalam menentukan karakteristik nilai eigen, vektor eigen, dan eigenmode dari matriks tereduksi dalam aljabar max-plus.
2. Bagi pengembangan ilmu, hasil penelitian ini dapat dituliskan dalam artikel yang dipublikasikan sehingga ke depannya dapat dimanfaat peneliti lain untuk menggunakan hasil karakterisasi ketiga komponen penting dalam pengaplikasiannya untuk menyelesaikan masalah-masalah antrian dalam kehidupan sehari-hari.
10 BAB IV
METODE PENELITIAN
Penelitian ini termasuk dalam jenis penelitian matematika murni sekaligus terapan. Secara garis besar terdapat dua tahapan dalam penelitian ini, yaitu tahap penelitian matematika murni berbasis studi literatur yakni melakukan karakterisasi nilai eigen, vektor eigen, dan eigenmode dari matriks tereduksi dalam aljabar max-plus berdasarkan teori-teori yang pernah ada. Berikutnya, dilakukan tahap penelitian terapan, yakni dengan pengambilan data primer pada antrian penggantian buku tabungan pada customer service suatu Bank X untuk dimodelkan menggunakan aljabar max-plus. Detail tahapan penelitian, diberikan pada Gambar 1.
Buku, Jurnal, Prosiding Mengumpulkan referensi
terkait nilai eigen, vektor eigen, dan eigenmode dari
matriks tereduksi dalam aljabar max-plus Mulai
Karakterisasi nilai eigen, vektor eigen, dan eigenmode dari matriks tereduksi dalam aljabar
max-plus Hasil karakterisasi Observasi dan pengambilan data primer Waktu kedatangan pelanggan, waktu pengambilan antrian, waktu servis teller, wak- tu servis oleh customer servis
Membuat model
11 Gambar 1. Tahapan Penelitian
Membentuk persamaan berdasarkan model Petri net
Nilai eigen, vektor eigen, dan eigenmode Penyelesaian matriks tereduksi Matriks tereduksi Kesimpulan Menarik kesimpulan Membuat artikel dan diseminasi Laporan Menyusun laporan Selesai Artikel terdiseminasi/ Prosiding
12 BAB V
HASIL DAN LUARAN YANG DICAPAI
A. Hasil yang Dicapai
Hasil dari penelitian ini adalah
1. Diperoleh karakterisasi ketiga komponen penting sebagai berikut:
a. Suatu matriks tereduksi dalam aljabar max-plus tidak harus memiliki nilai eigen. Jika matriks memiliki nilai eigen, maka nilai eigen tidak harus tunggal dengan nilai-nilai yang berhingga.
b. Vektor eigen yang bersesuaian dengan nilai eigen dari matriks tereduksi juga tidak harus tunggal, dan memuat paling tidak satu elemen berhingga. c. Eigenmode dari matriks tereduksi regular tidak tunggal, dengan semua
elemen-elemennya berhingga.
2. Diberikan contoh kegunaan hasil karakterisasi nilai eigen, vektor eigen, dan eigenmode dari matriks tereduksi dalam aljabar max-plus untuk menyelesaikan masalah antrian layanan penggantian buku tabungan oleh customer service pada suatu Bank X, dan dituliskan dalam artikel ilmiah. B. Luaran yang Dicapai
Luaran yang berhasil dicapai sampai diselesaikan laporan ini sebagai berikut:
1. Artikel ilmiah berbahasa inggris
2. Diseminasi artikel ilmiah pada International Conference on Mathematics:
Pure, Applied and Computation (ICoMPAC), “Empowering Engineering Using Mathematics”, 23 November 2016 di Hotel Pullman Surabaya,
13 BAB VI
KESIMPULAN DAN SARAN
A. KESIMPULAN
Penelitian ini berhasil sampai pada penyusunan dan diseminasi artikel mengenai karakterisasi nilai eigen, vektor eigen, dan eigenmode dari matriks tereduksi dalam aljabar max-plus, serta aplikasinya dalam menyelesaikan masalah antrian di kehidupan sehari-hari. Adapun untuk prosiding terindeks bereputasi masih sampai pada pengisian copyright transfer agreement, belum sampai pada tahap publish.
B. SARAN
Dari hasil penelitian ini diharapkan dapat dikembangkan baik oleh peneliti sendiri ke depannya maupun bagi peneliti-peneliti lain mengenai karakter dari nilai eigen, vektor eigen, dan eigenmode dari matriks tereduksi dalam aljabar max-plus. Selain itu, dapat diteliti lebih lanjut aplikasi karakterisasi yang sudah diperole untuk menyelesaikan permasalahan lain selain antrian.
14 DAFTAR PUSTAKA
Baccelli, F., Cohen, G., & Olsder, J. G. (2001). Synchronization and Linearity, An Algebra for Discrete Event System. New York: Wiley-Interscience. Heidergott, B., Olsder, G. J., & van der Woude, J. (2006). Max Plus at Work,
Modelling and Analysis of Synchronized System: A Course on Max-Plus Algebra and Its Application. United Kingdom: Princeton University. Konigsberg, Z. R. (2009). A generalized eigenmode algorithm for reducible
reguler matrices over the max-plus algebra. Chinese Control and Decision Conference (pp. 5598-5603). Guilin, China: IEEE.
Subiono. (2012). Aljabar Maxplus dan Terapannya. Surabaya: Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Teknologi Sepuluh Nopember Surabaya.
Zuliyanto, A., Siswanto, & Muslich. (2012). Algoritma eigenmode tergeneralisasi untuk matriks tereduksi reguler di dalam aljabar max-plus. Seminar Nasional Matematika (pp. 7-14). Surakarta: Universitas Sebelas Maret Surakarta.
15 LAMPIRAN
MAX-PLUS ALGEBRA
In this section, we give some concepts related to max-plus algebra, they are definition, operation, and the properties of max-plus algebra, graph in max-plus algebra, eigenvalues, eigenvectors, and eigenmode in max-plus algebra, and algorithms to determine those three components.
Definition 1 [5] Max-plus algebra is non empty setRε :=R∪ {ε}whereRis the set of real numbers,ε :=−∞, and two binary operations are defined as follows:
1. the operation⊕, that is∀x,y∈Rεsatisfy
x⊕y:=max{x,y},
2. the operation⊗, that is∀x,y∈Rεsatisfy
x⊗y:=x+y.
Max-plus algebra denoted by (Rε,⊕,⊗) or simply writtenRmaxis semiring [see 1]. The set ofn×mmatrices on
Rmaxdenoted byRnmax×m. A matrix inRnmax×mis called regular if it contains at least one element different fromεin each
row. There are two forms of matrix inRn×m
max that need to be understood, they are matrixE(n,m) andE(n,m). Matrix
E(n,m) isn×mmatrix where all elements equal toε. While matrixE(n,m) isn×mmatrix where [E(n,m)]i,j:=
(
e untuk i= j,
ε untuk i, j.
ande=0. Ifm=n, thenEis a square matrix and called the identity matrix. Elements ofRn
max:=Rnmax×1 called a vector. The j-th element of a vectorx∈Rnmaxdenoted byxjor can be written as [x]j. A vector inRnmaxwhere all elements equal toeis called a unit vector, and denoted byu.
Graph in Max-Plus Algebra
Max-plus algebra application is closely related to the directed graph denoted byG=(N,D), whereNis a set of all nodes andDis a set of some ordered (not necessarily different) pairs of nodes. Ordered pair of nodes in a graph called arc. Therefore, if nodesi,j ∈ Nthen the arc fromito jdenoted by (j,i). A graph can be represented into a square matrix in max-plus algebra. A corresponding graph to a square matrixAonRmaxis called a communication graph,
and denoted byG(A). SupposeA∈Rnmax×n, elementai,j,εif there is an arc from node jto nodeiinG(A).
The path term in graph is defined as an arc sequence that represents the link between a node with another node. A path is called elementary if no nodes appear more than once in it. A circuit is a closed elementary path, that has an initial node as same as final node. Suppose a pathp, the weight of it denoted by|p|wis the sum of weights for each arc in the pathp. The length of pathpis the number of arcs in it, which is denoted by|p|`. The average weight of path
pis the weight divided by the length of path.
Average circuit is an average weight of a circuit. A circuit that has a maximum average circuit called critical circuit. Critical graph ofG(A), denoted byGc(A)=(Nc(A),Dc(A)) is a graph consisting of a set of nodes and arcs in critical circuits ofG(A). Graph and its matrix representation are related each other. A graph condition can be known according to the matrix representation, and vice versa. For example, the path length in a graph associated with the power of its matrix representation.
Theorem 2 [2] Let A∈Rnmax×n. It holds for all k≥1that
[A⊗k]i,j=max{|p|w:p∈P(j,i;k)},
where[A⊗k]
i,j=εin the case where P(j,i;k)is empty, i.e., when no path of length k from i to j exists inG(A). Furthermore, we can defineA+matrix from Theorem 2, i.e.,
A+:=
∞ M
k=1
A⊗k.
Theorem 3 [1] Let A∈Rnmax×n be such that any circuit inG(A)has average circuit weight less than or equal to e. Then, it holds that
A+:=A⊕A⊗2⊕. . .⊕A⊗n∈Rnmax×n.
There are two types of graphs based on the connectedness property, they are strongly and not strongly connected graph. The main topic discussed in this paper is not strongly connected graph. Before we discuss the definition both types of graph, we must understand the reachable and communicate terms first. For any two nodesi,j∈ N, nodeiis said to be reachable from nodej, denoted byjRi, if there exist a path from i to j. While the nodeicommunicates with node j, denoted by jCi, if and only ifi= jor nodeiis reachable from the node jand node jis reachable from nodei. RelationCis equivalence relation inN.
A graph is called strongly connected if all nodes in the graph communicate with each other another i.e., for everyi,j∈ NsatisfyiCj. A matrix inRnmax×n representation of a strongly connected graph is called irreducible matrix.
Furthermore, irreducible matrix is a matrix that can not be constructed into upper triangular form.
If there is a node that does not communicate to the other nodes, the graph is called not strongly connected. A matrix inRn×n
maxrepresentation of not strongly connected graph is called reducible matrix. Furthermore, reducible
matrix is a matrix that can be constructed into a block upper triangular matrix form. A block upper triangular matrix consists of matricesE and irreducible matrices, and it is representation of reduced graph. The reduced graph is a reduction result of not strongly connected graph.
Eigenvalue, Eigenvector, and Eigenmode in Max-Plus Algebra
In the max-plus algebra application, there are three essential components associated with the matrix. They are eigen-value, eigenvector, and eigenmode.
Definition 4 [2] Let A∈Rn×n
maxbe a square matrix. Ifµ∈Rmaxis a scalar andv ∈Rnmaxis a vector that contains
at least one finite element such that
A⊗v=µ⊗v,
thenµis called an eigenvalue of A andvan eigenvector of A associated with eigenvalueµ.
SupposeC(A) is a set of all circuits inG(A). The maximum average circuit, denoted byλis defined as
λ:= max
p∈C(A)
|p|w
|p|`.
If the maximum average of graphG(A) i.e.,λhas a finite value, then it is the eigenvalues of matrixA. While the column [A∗λ].,η is an eigenvector of Aassosiated with eigenvaluesλ. The statement is according with the following lemma.
Lemma 5 [2] Let the communication graphG(A)of matrix A∈Rn×n
maxhave finite maximal average circuit weight λ. Then, the scalarλis an eigenvalue of A, and the column[A∗λ].,η is an eigenvector of A assosiated withλ, for any nodeη∈ Gc(A).
In the process of resolving scheduling problem, closely related to efforts getting sequence{x(k) :k∈N}of this linear equation model
x(k+1)=A⊗x(k), (1)
fork≥0, whereA∈Rn×n
maxandx(0)=x0∈Rnmaxis the initial state.
The definition of generalized eigenmode is given in Definition 6.
Definition 6 [2] A pair of vectors(η,v)∈Rn×
Rnis called a generalized eigenmode of the regular matrix A if for
all k≥0
A⊗(k×η+v)=(k+1)×η+v.
Algorithm for Determining The Eigenvalue, Eigenvector, and Eigenmode in Max-Plus Algebra
In this paper, we use thepower algorithmand the generalized eigenmode algorithm for reducible regular matrices.
Algorithm 7 Power Algorithm [1]
1. Take an arbitrary initial vectorx(0),u[ε].
2. Iterate equation (1) until there are integers p > q ≥ 0 and a real number c, such that a periodic regime is reached i.e.,
x(p)=c⊗x(q).
3. Compute as the eigenvalue
λ= c
p−q. 4. Compute as the eigenvector
v= p−q M i=1 λ⊗(p−q−i)⊗x(q+i−1) .
Algorithm 8 Generalized Eigenmode Algorithm for Regular Reducible Matrices [3]
1. Take a regular reducible matrix A∈Rn×n
max.
2. Specify a block upper triangular matrix form of matrix A.
3. Compute eigenvalue and eigenvector of the last block matrix in the main diagonal of block upper triangular matrix. Suppose Aq,q, compute eigenvalueλq=λ(Aq,q)and eigenvectorvqassociated with the eigenvalue. Then,
takeξq =λqand i=q.
4. Compute eigenvalueλ(i−1)of matrix A(i−1),(i−1).
5. Ifλ(i−1)> ξigo to 6. If not, go to 7.
6. Setξ(i−1)=λ(i−1)and compute vectorv(i−1)according to this following equation: ξ(i−1)⊗v(i−1)=A(i−1),(i−1)⊗v(i−1)⊕ q M j=i A(i−1),j⊗vj. Then, go to 8.
7. Setξ(i−1)=λiand compute vectorv(i−1)according to this following equation: λi⊗v(i−1)=A(i−1),(i−1)⊗v(i−1)⊕ q M j=i A(i−1),j⊗vj. Then, go to 8.
8. If i−1,1go back to 4, if not finish.
EIGENVALUE, EIGENVECTOR, AND EIGENMODE OF REDUCIBLE MATRIX IN MAX-PLUS ALGEBRA
In this section, we discuss about eigenvalue, eigenvector, and eigenmode characterization of reducible matrix. Then, we use the characterization result to solve a problem. The problem that we have learned is the queue problem.
To obtain the eigenvalue and eigenvector of a matrixA ∈ Rn×n
max, we use the algorithm repeatedly of this linear
equation
x(k+1)=A⊗x(k), k=0,1,2, . . . . (2)
The periodic regime of equation (2) for reducible matrixAclosely related to cycle time vector, i.e.,
lim
k→∞
x(k)
The limit is exist for allx(0),u(ε), whereu(ε)= ε ε . . . ε T.
If the matrixAin the equation (2) is reducible matrix, then we can always establishAbe a block upper triangular matrix: A1,1 A1,2 . . . A1,q E A2,2 . . . A2,q E E A3,3 ... .. . ... ... ... ... E E . . . E Aq,q , (3)
MatrixAi,iis irreducible matrix orAi,i=εfor alli∈q.
Eigenvalue, Eigenvector, and Eigenmode Characterization of Reducible Matrix
Some of reducible matrix that represent not strongly connected graph have eigenvalues and some are not. Here is an existence eigenvalues and eigenvectors theorem of reducible matrix.
Theorem 9 [1] Letx(0),u[ε]be an arbitrary initial condition. If the equation system (2) satisfiesx(p)=c⊗x(q) for several integers p,q with p>q≥0and real number c, then
lim k→∞ x(k) k = λ λ .. . λ ,
whereλ= p−cq. Furthermore,λis an eigenvalue of matrix A with the eigenvector
v= p−q M i=1 λ⊗(p−q−i)⊗ x(q+i−1).
A reducible matrix does not necessarily have a unique eigenvalue. The following example shows the eigenvalue of reducible matrix is not unique.
Example 10 Given a reducible matrix represents not strongly connected graphG(A)as follows:
A= 1ε ε
3
!
.
Eigenvalue of matrix A is not unique. It is clear from the following description:
1 ε ε 3 ! ⊗ 0ε ! = 1ε ! =1⊗ 0ε ! , and 1 ε ε 3 ! ⊗ ε 0 ! = ε3 ! =3⊗ ε 0 ! .
We can conclude that1and3are eigenvalues of matrix A.
Furthermore, we also give an example that a reducible matrix has a unique eigenvalue.
Example 11 Given a reducible matrix represents not strongly connected graphG(B)as follows:
B= 1ε 0
0
!
Eigenvalue of matrix B is unique. It is clear from the following description: 1 0 ε 0 ! ⊗ 0ε ! = 1ε ! =1⊗ 0ε ! . While 1 0 ε 0 ! ⊗ a 0 ! =λ⊗ a 0 ! , we get max{1+a,0}=λ+a, (4) and max{ε,0}=λ. (5)
From equation (5) we getλ=0, and if it is substituted to the equation (4),
max{1+a,0}=a. (6)
So, we can not find a that satisfies equation (6).
Eigenvector of reducible matrix is not unique because some eigenvectors of reducible matrix can be formed by operation⊗any scalar real number with an eigenvector.
Theorem 12 For all reducible matrices A∈Rnmax×nthat have eigenvalue, having not unique eigenvector. Ifv∈Rnmax
is an eigenvector associated with eigenvalueλ, thenα⊗vis also eigenvector associated with eigenvalueλfor any
α∈R.
Proof Letλas eigenvalue of reducible matrixAandv∈Rnmaxis an eigenvector associated with eigenvalueλsuch that
A⊗v=λ⊗v. (7)
Multiply any scalarα∈Ron both sides of the equation (7),
α⊗A⊗v=α⊗λ⊗v. (8)
Operation⊗is commutative, so the equation (8) becomes
A⊗α⊗v = λ⊗α⊗v A⊗(α⊗v) = λ⊗(α⊗v).
From the description, we also getα⊗v∈Rnmaxas eigenvector of matrixAassociated with eigenvalueλ, and we can conclude that the eigenvector of reducible matrix is not unique.
Eigenvalue of reducible matrix has finite value. The statement is given in this following theorem.
Theorem 13 If reducible matrix A ∈ Rn×n
max has eigenvalue, then the eigenvalue has finite value element of real
number.
Proof According to the Theorem 9, if a reducible matrixA∈Rn×n
maxhas eigenvalue, it means the equation system
(2) satisfiesx(p)=c⊗x(q) for several integersp>q≥0 and real numbercsuch that we get eigenvalue ofAi.e.,
λ(A)= c
p−q.
Sincecis real number and p−q is integer, then we get the eigenvalue of reducible matrixAis finite real number. Moreover, if we take the distinct eigenvalue belongs to one of the block matrix in the main diagonal of upper triangular block matrix, then obviously the eigenvalue has finite value because the matrix blocks in the main diagonal are irreducible that have finite value for its eigenvalue, or the matrix blocks areεthat do not have eigenvalue.
While eigenvector of reducible matrix based on Example 10 and Definition 4, obtained that the eigenvector of reducible matrix contains at least one finite element.
The next discussion is about eigenmode characterization of regular reducible matrix. Before we discuss about the eigenmode existence of regular reducible matrix, first we discuss about solution of equationx=(A⊗x)⊕band inhomogeneous recurrent equations.
Solution of equationx=(A⊗x)⊕bis given in the following theorem.
Theorem 14 [1] Let A∈Rn×n
maxandb∈Rnmax. If the average weight of circuit in the graphG(A)less than or equal
0, thenx=A∗⊗bwith A∗:=E⊕A+=L∞ i=0A
⊗iis solution ofx=(A⊗x)⊕b. Furthermore, if the circuit weight in
G(A)is negative, then the solution is unique.
The inhomogeneous recurrent equation is an extension of the linear recurrent equationx(k+1)=A⊗x(k). The following theorem concerning inhomogeneous recurrent equation.
Theorem 15 [3] Consider the inhomogeneous recurrent equation
x(k+1)=A⊗x(k)⊕ m M j=1 Bj⊗uj(k), (9) with A ∈ Rn×n
max irreducible matrix with eigenvalueλ, or A ∈ Rmax i.e., A = εwithλ = ε, matrix Bj ∈ Rnmax×mj with
mj ≥1satisfies Bj,E, whileuj(k)∈Rmmaxj satisfiesuj(k)=τkj⊗wj(k), k≥0withwj∈Rmmaxj andτj ∈R. For some
τ=L
j∈mτj, there exists an integer K≥0and vectorv∈R
nsuch that the sequencex(k)=µ⊗k⊗v, withµ=λ⊗τ
satisfies the recurrent equation (9) for all k≥K.
In the previous discussion, it is known that the reducible matrixAcan be presented in an upper triangular block matrix form, with the matrix blockAi,iis irreducible matrix, soλi = λ(Ai,i) orAi,i = ε, and we getλi = ε. Then, suppose we take vectorx(k) correspondence to an upper triangular block matrix 3, i.e.,
x(k)= x1(k) x2(k) .. . xq(k) .
The upper triangular block matrix of reducible matrixAsatisfy recurrent equation (9), i.e.,
xi(k+1)=Ai,i⊗xi(k)⊕ q M
j=i+1
Ai,j⊗xj(k); i∈q, k≥0. (10)
In particular, equation (10) becomesxq(k+1)=Aq,q⊗xq(k) fori=q. AssumingAis a regular matrix, thenAq,q is also regular. So,Aq,q ,E, and the maximal strongly connected subgraph correspondence with matrixAq,qhas non empty arc set, as a resultAq,qis an irreducible matrix. Therefore, there is a vector with all the finite elementvqand a scalarξq∈Rsuch that
xq(k)=ξ⊗qk⊗vq
satisfiesxq(k+1)=Aq,q⊗xq(k) for allk≥0. In this case,vqis the eigenvector of matrixAq,qcorrespondence with eigenvaluesλq=λ(Aq,q), whereξq =λq.
Then, fori∈qis generally given in the following theorem.
Theorem 16 [3] Consider the recurrent equation given by equation (10). Assume that Aq,qis irreducible and that
for i∈q−1either Ai,iis an irreducible matrix or is equal toε. Assume also, that the Ai,imatrices are different from
Efor i,j=i+1; i∈q. Then there exist finite vectorsv1,v2, . . . ,vqof suitable size and scalarξ1, ξ2, . . . , ξq ∈Rsuch
that the sequances:
satisfy equation (10) for all k≥0. The scalarsξ1, ξ2, . . . , ξq∈Rare determined by: ξi= M j∈Hi ξj⊕λi, whereHi={j∈q: j>i,Ai,j,E}.
Theorem 16 yields a result which indicates the eigenmode existence of regular reducible matrix.
Corollary 17 [3] Let A∈Rn×n
maxbe a regular reducible matrix, then there exist a pair of vectors(η,v)∈Rn×Rn, a
generalized eigenmode, such that for all k≥0:
A⊗(k×η+v)=(k+1)×η+v.
Eigenmode of regular educible matrix is not unique. It is caused the vectorvis not unique.
Theorem 18 For all regular reducible matrix A∈Rn×n
maxhave non unique eigenmode, i.e., if(η,v)is eigenmode of
matrix A, then(η, α⊗v)is also eigenmode of matrix A whereα∈R. Proof Suppose (η,v) is eigenmode of regular reducible matrixA∈Rn×n
max, then for allk≥0ηandvsatisfy
A⊗(k×η+v)=(k+1)×η+v. (11)
Multiply any scalar numberα∈Rto both sides equation (11)
α⊗A⊗(k×η+v)=α⊗(k+1)×η+v. (12)
Since the operation⊗is commutative, then equation (12) becomes
A⊗(α⊗k×η+v) = (k+1)×η+α⊗v A⊗(k×η+(α⊗v)) = (k+1)×η+(α⊗v). We get (η, α⊗v) is also eigenmode of regular reducible matrixAfor anyα∈R.
The last discussion in the characterization of regular reducible matrix is about the value of vector elements in the eigenmode. Eigenmode of regular reducible matrix has finite elements for each component of the vector.
Theorem 19 For all regular reducible matrix A ∈ Rn×n
max have eigenmode i.e., pair of vectors with all vector
elements are finite.
Proof Suppose the upper triangular block matrix (3) is the construction of reducible matrixA. Eigenmode of upper triangular block matrix construction results from the reducible matrixAbe a pair of vectors (η,v). It was explained that the vector
η=
uT[ξ1] uT[ξ2] . . . uT[ξq] T
is cycle time vector, whereξi,i∈qis real numbers by Theorem 16. So that the vectorηconsists of finite elements. Then, vectorvconsists of vectorsvi,i∈q. According to Theorem 16, all elements of the vectorvi,i∈qare finite, i.e., real numbers. So that the vectorvonly contains finite element. Then we can conclude eigenmode of reducible matrix is couple of vectors with all finite elements.
Characterization Result Application in The Queue System Problem
In the end of the discussion, we give an example the application of eigenvalue, eigenvector, and eigenmode characteri-zation result in the queue system problems, i.e., in the queue system of the replacement saving types servicing process in a bank for a customer service officer.
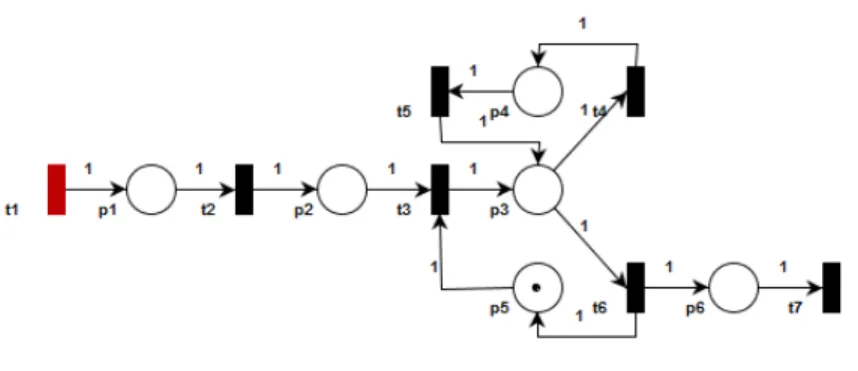
We will analyze the queue system of the replacement saving types servicing process in a customer service officer of bank. Then for the customer service process, start from customer comes to the bank, serviced by customer service officers, until leave the bank are given in a Petri net form, Figure 1. Based on Figure 1, The Petri net of replacement saving types servicing process in a customer service officer consists of seven transitions and sixth places.
FIGURE 1.The Petri Net of Replacement Saving Types Servicing Process in A Customer Service Officer
The description of seven transitions is given as follows:
t1 : a customer comes to the bank,
t2 : a customer takes the queue number,
t3 : a costumer is serviced by a customer service officer,
t4 : a customer service officer carries the customer files to the teller,
t5 : customer files have been processed by the teller,
t6 : a customer has been served by customer service officer,
t7 : a customer leaves the bank,
and six places, i.e.,
p1 : a customer who was waiting to take a queue number,
p2 : a customer who was waiting to be served by a customer service officer,
p3 : a customer being served by a customer service officer,
p4 : a customer who was waiting for files processing by the teller,
p5 : idle or a customer services officer who is not busy,
p6 : a customer who has been served by a customer service officer.
Furthermore, we also give the definition of the variables used in the modeling process. The variables that show the time as follows:
t1(k) : time of thekth customer arrival,
t2(k) : time of thekth customer taking a queue number,
t3(k) : time of thekth customer begin to be served by a customer service officer,
t4(k) : time of thekth customer service officer carries the customer files to the teller,
t5(k) : time of thekth customer files have been processed by the teller,
t6(k) : time of thekth customer has been served,
t7(k) : time of thekth customer leaves the bank.
Then, the variables that determine the length of time i.e.,
vt1,k : the time length of thekth customer arrival,
vt2,k : the time length of thekth customer taking a queue number, vt5,k : the time length of thekth files processing by the teller,
vt6,k : the time length of thekth customer served by the customer service officer, vt7,k : the time length of thekth customer leaves the bank.
TABLE 1.The List of Replacement Saving Types Servicing Process in A Bank.
Codes Processes The Length of Time(minutes)
vt1,k The time length of thekth customer arrival 8
vt2,k The time length of thekth customer taking a queue number 0,5 vt5,k The time length of thekth files processing by the teller 5 vt6,k The time length of thekth customer served by the customer service officer 20
Based on petri net Figure 1, we obtain a model of the queue system of the replacement saving types servicing process in a customer service officer as follows:
t1(k) t5(k) t6(k) = vt1,k ε ε vt5,k⊗vt2,k⊗vt1,k vt5,k vt5,k vt6,k⊗vt5,k⊗vt2,k⊗vt1,k vt6,k⊗vt5,k vt6,k⊗vt5,k ⊗ t1(k−1) t5(k−1) t6(k−1) . If the time length of each process is given in Table 1, we obtain equation:
t1(k) t5(k) t6(k) = 8 ε ε 13,5 5 5 33,5 25 25 ⊗ t1(k−1) t5(k−1) t6(k−1) .
The matrix of the model obtained is a reducible matrix. Furthermore, we will analyze eigenvalue, eigenvector, and eigenmode of the matrix
B= 8 ε ε 13,5 5 5 33,5 25 25 .
Based on the eigenvalue and eigenvector of reducible matrix characterization result, we get that reducible matrix does not necessarily have eigenvalue. Therefore, we use the power algorithm to find eigenvalue of reducible matrix
B. With an arbitrary initial statex(0) , u(ε), we can not find integers p > q ≥ 0 and real number cthat satisfy
x(p) = c⊗x(q). Thus Bhas no eigenvalues. Nevertheless, sinceBis regular reducible matrix, then we can search eigenmode i.e., pair of vectors with finite element.
First, we must determine an upper triangular block matrix form of regular reducible matrixBto get eigenmode i.e., A= 5 5 13,5 25 25 33,5 ε ε 8 .
Then, we compute the eigenvalue of matrixA2,2i.e.,λ2=8, so we can takeξ2=λ2=8 and suppose we takev2=0.
The next step, we compute eigenvalue of matrixA1,1=
5 5
25 25
!
by the power algorithm. With an arbitrary initial statex(0),u(ε), we get the eigenvalue of matrixA1,1isλ1=25. Sinceλ1 > ξ2, thenξ1=λ1 =25 and we compute
vectorv1: ξ1⊗v1 = A1,1⊗v1⊕ A1,2⊗v2 25⊗ v1 v2 ! = 5 5 25 25 ! ⊗ v1 v2 !! ⊕ 13,5 33,5 ! ⊗0 ! (13)
Based on equation (13), we getv1 =
−11,5 8,5
!
. Therefore, a pair of vector (η,v) where η =
25 25 8 andv = −11,5 8,5 0
is eigenmode of matrixAbecause fork=0, the vectors satisfy:
A⊗(0×η+v)= 13,5 33,5 8 =1×η+v,
fork=1, satisfy: A⊗(1×η+v)= 38,5 58,5 16 =2×η+v,
and so on, vectorsηandvsatisfy
A⊗(k×η+v)=(k+1)×η+v.
fork=0,1,2, . . ..
Based on the eigenmode result, we can determine the time ofkth customer completed in each service process. Suppose the earliest time is 08.00, then forkequal to 0 and 1 we get the result as shown in the Table 2.
TABLE 2.The Time of The First and Second Customer Service Process Descriptions Time of Customer
First Second
Customer files have been processed by the teller 08:05:30 08:30:30 A Customer has been served by customer service officer 08:25:30 08:50:30 customer arrival 08:00:00 08:08:00
CONCLUSIONS
Based on the eigenvalue, eigenvector, and eigenmode characterization of reducible matrix, we obtain that reducible matrix does not necessarily have eigenvalue. If the reducible matrix has eigenvalue, the eigenvalue is not necessarily unique and has a finite value. Eigenvector corresponding to the eigenvalue of reducible matrix is not unique, and contains at least a finite element. Then, Regular reducible matrix does not have a unique eigenmode, with all elements are finite.
ACKNOWLEDGMENTS
We are really grateful because we managed to complete this paper. This paper was prepared for Interna-tional Conference on Mathematics: Pure, Applied and Computation (ICoMPAC), ”Empowering Engineering Using Mathematics”, 23rd November 2016 at Pullman Hotel Surabaya, Indonesia. This paper can not be completed without the effort and co-operation from our group member as our supervisor too. So we also sincerely thank to him for the guidance and encouragement in finishing this paper. Last but not least, we would like to express our gratitude to our friends for their support.
REFERENCES
[1] Subiono,Aljabar Maxplus dan Terapannya(Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Teknologi Sepuluh Nopember, Surabaya, 2012), pp. 1–46.
[2] B. Heidergott, G. J. Olsder, and J. van der Woude,Max Plus at Work, Modelling and Analysis of Synchronized System: A Course on Max-Plus Algebra and Its Applications(Princeton University, United Kingdom, 2006), pp. 13–91.
[3] Z. R. Konigsberg, “A generalized eigenmode algorithm for reducible reguler matrices over the max-plus al-gebra,” inChinese Control and Decision Conference(Chinese, 2009), pp. 5598–5603.
[4] A. Zuliyanto, Siswanto, and Muslich, “Algoritma eigenmode tergeneralisasi untuk matriks tereduksi reguler di dalam aljabar max-plus,” inProsiding Seminar Nasional Matematika(Surakarta, 2012).
[5] F. Baccelli, G. Cohen, and G. J. Olsder,Synchronization and Linearity, An Algebra for Discrete Event System
26 Lampiran 2 Sertifikat Seminar Internasional
27 Lampiran 3 Copyright Transfer Agreement Artikel